二项式定理测试题
2022高三总复习数学 二项式定理(含解析)

二项式定理A 级——基础达标1.(2021·栖霞模拟)⎝⎛⎭⎫x -2x 6的展开式中的常数项为( ) A .-150 B .150 C .-240D .240解析:选D ⎝⎛⎭⎫x -2x 6的二项展开式的通项公式为T k +1=C k 6x 6-k ·⎝⎛⎭⎫-2x k =C k 6x 6-k·(-2)k ·x -k 2=(-2)k C k 6x 6-32k .令6-32k =0,解得k =4,故所求的常数项为T 5=(-2)4·C 46=240. 2.(2021·深圳市统一测试)⎝⎛⎭⎫x -2x 7的展开式中x 3的系数为( ) A .168 B .84 C .42D .21解析:选B ⎝⎛⎭⎫x -2x 7的展开式的通项公式为T r +1=C r 7x 7-r ⎝⎛⎭⎫-2x r =(-2)r C r 7x 7-2r,令7-2r =3,则r =2,所以⎝⎛⎭⎫x -2x 7的展开式中x 3的系数为(-2)2C 27=84,故选B. 3.⎝⎛⎭⎪⎫x +13x n的展开式中各项系数之和大于8,但小于32,则展开式中系数最大的项是( )A .63x B .4xC .4x 6xD .4x或4x 6x 解析:选A 令x =1,可得⎝⎛⎭⎪⎫x +13x n的展开式中各项系数之和为2n 即8<2n<32,解得n =4,故第3项的系数最大,所以展开式中系数最大的项是C 24(x )2⎝ ⎛⎭⎪⎫13x 2=63x . 4.(2021·贵阳市适应性考试)在⎝⎛⎭⎫x +3x n 的二项展开式中,各项系数之和为A ,二项式系数之和为B ,若A +B =72,则二项展开式中常数项的值为( )A .6B .9C .12D .18解析:选B 在⎝⎛⎭⎫x +3x n 中,令x =1,得A =4n ,由题意知B =2n ,所以4n +2n =72,得n =3,⎝⎛⎭⎫x +3x 3的二项展开式的通项公式为T r +1=C r 3(x )3-r ⎝⎛⎭⎫3x r =3r C r 3x 3-3r 2,令3-3r 2=0,得r =1,所以常数项为T 2=3C 13=9.5.已知(x +2)(2x -1)5=a 0+a 1x +a 2x 2+a 3x 3+a 4x 4+a 5x 5+a 6x 6,则a 0+a 2+a 4=( ) A .123 B .91 C .-120D .-152解析:选D 法一:因为(2x -1)5的展开式的通项T r +1=C r 5(2x )5-r·(-1)r (r =0,1,2,3,4,5),所以a 0+a 2+a 4=2×C 55×20×(-1)5+[1×C 45×21×(-1)4+2×C 35×22×(-1)3]+[1×C 25×23×(-1)2+2×C 15×24×(-1)1]=-2-70-80=-152,故选D.法二:令x =1,得a 0+a 1+a 2+a 3+a 4+a 5+a 6=3 ①;令x =-1,得a 0-a 1+a 2-a 3+a 4-a 5+a 6=-243 ②.①+②,得a 0+a 2+a 4+a 6=-120.又a 6=1×25=32,所以a 0+a 2+a 4=-152,故选D.6.(多选)在二项式⎝⎛⎭⎫3x 2-2x 5的展开式中,有( ) A .含x 的项 B .含1x 2的项C .含x 4的项D .含1x4的项解析:选ABC 二项式⎝⎛⎭⎫3x 2-2x 5的展开式的通项公式为T r +1=C r 5·35-r ·(-2)r ·x 10-3r,r =0,1,2,3,4,5,故展开式中含x 的项为x 10-3r ,结合所给的选项,知ABC 的项都含有.故选A 、B 、C .7.(多选)(2021·沈阳模拟)已知(3x -1)n =a 0+a 1x +a 2x 2+…+a n x n ,设(3x -1)n 的展开式的二项式系数之和为S n ,T n =a 1+a 2+…+a n ,则( )A .a 0=1B .T n =2n -(-1)nC .n 为奇数时,S n <T n ;n 为偶数时,S n >T nD .S n =T n解析:选BC 由题意知S n =2n ,令x =0,得a 0=(-1)n ,令x =1,得a 0+a 1+a 2+…+a n =2n ,所以T n =2n -(-1)n ,故选B 、C .8.(多选)若(1-ax +x 2)4的展开式中x 5的系数为-56,则下列结论正确的是( ) A .a 的值为-2B .展开式中各项系数和为0C .展开式中x 的系数为4D .展开式中二项式系数最大为70解析:选BD (1-ax +x 2)4=[(1-ax )+x 2]4,故展开式中x 5项为C 14C 33(-ax )3x 2+C 24C 12(-ax )(x 2)2=(-4a 3-12a )x 5,所以-4a 3-12a =-56,解得a =2.(1-ax +x 2)4=(x -1)8,则展开式中各项系数和为0,展开式中x 的系数为C 78(-1)7=-8,展开式中二项式系数最大为C 48=70.故选B 、D.9.(2020·天津高考)在⎝⎛⎭⎫x +2x 25的展开式中,x 2的系数是________. 解析:二项式⎝⎛⎭⎫x +2x 25的展开式的通项为T r +1=C r 5·x 5-r ·⎝⎛⎭⎫2x 2r =C r 5·2r ·x 5-3r.令5-3r =2得r =1.因此,在⎝⎛⎭⎫x +2x 25的展开式中,x 2的系数为C 15·21=10. 答案:1010.若⎝⎛⎭⎫x +12x n (n ≥4,n ∈N *)的二项展开式中前三项的系数依次成等差数列,则n =________.解析:⎝⎛⎭⎫x +12x n 的展开式的通项T r +1=C r n x n -r ⎝⎛⎭⎫12x r =C r n 2-r x n -2r ,则前三项的系数分别为1,n 2,n (n -1)8,由其依次成等差数列,得n =1+n (n -1)8,解得n =8或n =1(舍去),故n =8.答案:811.已知(a 2+1)n 展开式中的二项式系数之和等于⎝⎛⎭⎫165x 2+1x 5的展开式的常数项,而(a 2+1)n 的展开式的二项式系数最大的项等于54,则正数a 的值为________.解析:⎝⎛⎭⎫165x 2+1x 5展开式的通项为T r +1=C r 5⎝⎛⎭⎫165x 25-r ·⎝⎛⎭⎫1x r =C r 5⎝⎛⎭⎫1655-r x 20-5r 2. 令20-5r =0,得r =4, 故常数项T 5=C 45×165=16, 又(a 2+1)n 展开式中的二项式系数之和为2n ,由题意得2n =16,∴n =4.∴(a 2+1)4展开式中二项式系数最大的项是中间项T 3,从而C 24(a 2)2=54,∴a = 3.答案: 312.已知f (x )=(1+2x )m +(1+2x )n (m ,n ∈N *)的展开式中x 的系数为24,则展开式中x 2的系数的最小值为________.解析:由f (x )的展开式中x 的系数为24,可得C 1m 2x +C 1n 2x =2mx +2nx =24x ,解得m +n =12.设f (x )的展开式中x 2的系数为t ,则t =C 2m 22+C 2n 22=2(m 2+n 2-m -n )=2(m 2+n 2-12)≥2⎣⎢⎡⎦⎥⎤(m +n )22-12=2×(72-12)=120.当且仅当m =n =6时,t 有最小值120. ∴f (x )的展开式中x 2的系数的最小值为120. 答案:120B 级——综合应用13.(多选)已知(2x -m )7=a 0+a 1(1-x )+a 2(1-x )2+…+a 7(1-x )7,若a 0+a 12+a 222+…+a 727=-128,则有( ) A .m =2 B .a 3=-280 C .a 0=-1D .-a 1+2a 2-3a 3+4a 4-5a 5+6a 6-7a 7=14解析:选BCD 令1-x =12,即x =12,可得⎝⎛⎭⎫2×12-m 7=(1-m )7=a 0+a 12+a 222+…+a 727=-128,得m =3,则令x =1,得a 0=(-1)7=-1,(2x -3)7=[-1-2(1-x )]7,所以a 3=C 37×(-1)7-3×(-2)3=-280.对(2x -3)7=a 0+a 1(1-x )+a 2(1-x )2+…+a 7(1-x )7两边求导得14(2x -3)6=-a 1-2a 2(1-x )-…-7a 7(1-x )6,令x =2得-a 1+2a 2-3a 3+4a 4-5a 5+6a 6-7a 7=14.故选B 、C 、D.14.若⎝⎛⎭⎫x +a x ⎝⎛⎭⎫2x -1x 5的展开式中各项系数的和为2,则该展开式中的常数项为( ) A .10 B .20 C .30D .40解析:选D 令x =1,得(1+a )(2-1)5=1+a =2,所以a =1.因此⎝⎛⎭⎫x +1x ⎝⎛⎭⎫2x -1x 5的展开式中的常数项为⎝⎛⎭⎫2x -1x 5的展开式中x 的系数与1x 的系数的和.⎝⎛⎭⎫2x -1x 5的展开式的通项T r +1=C r 5(2x )5-r⎝⎛⎭⎫-1x r =C r 525-r x 5-2r ·(-1)r . 令5-2r =1,得r =2,因此⎝⎛⎭⎫2x -1x 5的展开式中x 的系数为C 2525-2×(-1)2=80; 令5-2r =-1,得r =3,因此⎝⎛⎭⎫2x -1x 5的展开式中1x 的系数为C 3525-3×(-1)3=-40,所以⎝⎛⎭⎫x +1x ⎝⎛⎭⎫2x -1x 5的展开式中的常数项为80-40=40. 15.中国南北朝时期的著作《孙子算经》中,对同余除法有较深的研究.设a ,b ,m (m >0)为整数,若a 和b 被m 除得的余数相同,则称a 和b 对模m 同余,记为a =b (mod m ).若a =C 020+C 120·2+C 220·22+…+C 2020·220,a =b (mod 10),则b 的值可以是( ) A .2 011 B .2 012 C .2 013D .2 014解析:选A ∵a =(1+2)20=320=910=(10-1)10=C 0101010-C 110109+…-C 01010+1,∴被10除得的余数为1,而2 011被10除得的余数是1,故选A .。
二项式定理(1)

x 二项式定理1.【来源】浙江省 2017 届高三“超级全能生”3 月联考数学试题 在二项式(2x - 1)6的展开式中,常数项是( C )xA .-240B .240C .-160D .160答案及解析:2.【来源】安徽省黄山市 2019 届高三第一次质量检测(一模)数学(理)试题在(1+x )6(1-2x )展开式中,含 x 5 的项的系数是( D ) A. 36B. 24C. -36D. -243.【来源】新疆维吾尔自治区 2018 届高三第二次适应性(模拟)检测数学(理)试题若⎛ 2 1 ⎫n- x ⎪ 展开式中含 x 项的系数为-80,则 n 等于( A )⎝ ⎭A .5B .6 C.7 D .84.【来源】浙江省金丽衢十二校联考 2017 届高考二模数学试题在(1+x 3)(1﹣x )8 的展开式中,x 5 的系数是( A ) A .﹣28B .﹣84C .28D .84答案及解析:【考点】二项式定理的应用.【分析】利用二项式定理的通项公式求解即可.【解答】解:由(1+x 3)展开可知含有 x 3 与(1﹣x )8 展开的 x 2 可得 x 5 的系数; 由(1+x 3)展开可知常数项与(1﹣x )8 展开的 x 5,同样可得 x 5 的系数; ∴含 x 5 的项+=28x 5﹣56x 5=﹣28x 5;∴x 5 的系数为﹣28, 故选 A【点评】本题主要考查二项式定理的应用,求展开式的系数把含有 x 5 的项找到.从而可以利用通项求解.属于中档题5.【来源】北京东城景山学校 2016-2017 学年高二下学期期中考试数学(理)试题设(3x -1)4 = a + a x + a x 2 + a x 3 + a x 4 ,则 a + a + a + a的值为( A ).12341234A .15B .16C .1D .-15答案及解析: 在(3x -1)4= a + a x + a x 2 + a x 3 + a x 4 中,令 x = 0 ,可得 a = 1 ,1234再令 x = 1可得 a 0 + a 1 + a 2 + a 3 + a 4 = 16 , 所以 a 1 + a 2 + a 3 + a 4 = 15 .n 7 7 7 故选 A .6.【来源】北京西城八中少年班 2016-2017 学年高一下学期期末考试数学试题在(x + y )n的展开式中,若第七项系数最大,则 n 的值可能等于( D ).A .13,14B .14,15C .12,13D .11,12,13答案及解析:(x + y )n 的展开式第七项系数为 C 6 ,且最大,可知此为展开式中间项,当展开式为奇数项时: n= 6 , n = 12 ,2当有偶数项时 n + 1= 6 , n = 11, 2 或 n + 1 = 7 , n = 13 ,2故 n = 11,12 ,13 . 选 D .7.【来源】广东省广州市海珠区 2018 届高三综合测试(一)数学(理)试题(x + y )(2x - y )6 的展开式中 x 4 y 3 的系数为( D )A .-80B .-40C. 40D .808.【来源】广东省潮州市 2017 届高三数学二模试卷数学(理)试题 在(1﹣2x )7(1+x )的展开式中,含 x 2 项的系数为( B ) A .71 B .70 C .21 D .49答案及解析:【分析】先将问题转化为二项式(1﹣2x )7 的系数问题,利用二项展开式的通项公式求出展开式的第 r+1 项,令 x 的指数分别等于 1,2 求出特定项的系数【解答】解:(1﹣2x )7(1+x )的展开式中 x 2 的系数等于(1﹣2x )7 展开式的 x 的系数+(1﹣2x )7 展开式的 x 2 的系数,(x+1)7 展开式的通项为 T r+1=(﹣2)r C r x r ,故展开式中 x 2 的系数是(﹣2)2C 2+(﹣2)•C 1=84﹣14=60,故选:B .9.【来源】浙江省新高考研究联盟 2017 届第四次联考数学试题 在二项式(x 2- 1)5 的展开式中,含 x 7的项的系数是( C )xA . -10B. 10C. -5D. 510.【来源】辽宁省重点高中协作校 2016-2017 学年高二下学期期末考试数学(理)试题 已知(1 + x )n的展开式中只有第 6 项的二项式系数最大,则展开式奇数项的二项式系数和为( D ) A .212B .211C.210D .2911.【来源】上海市浦东新区 2018 届高三上学期期中考试数学试卷展开式中的常数项为( C )x -A.-1320B.1320C.-220D.22012.【来源】浙江省绍兴一中2017 届高三上学期期末数学试题在(x﹣y)10 的展开式中,系数最小的项是(C )A.第4 项B.第5 项C.第6 项D.第7 项答案及解析:【考点】二项式定理的应用.【分析】由二项展开式可得出系数最小的项系数一定为负,再结合组合数的性质即可判断出系数最小的项.【解答】解:展开式共有11 项,奇数项为正,偶数项为负,且第6 项的二项式系数最大,则展开式中系数最小的项第 6项.故选C.13.【来源】浙江省金华十校联考2017 届高三上学期期末数学试题在(1﹣x)n=a0+a1x+a2x2+a3x3+…+a n x n中,若2a2+a n﹣5=0,则自然数n的值是(B)A.7 B.8 C.9 D.10答案及解析:【考点】二项式定理的应用.【分析】由二项展开式的通项公式T r+1=•(﹣1)r x r可得a r=(﹣1)r•,于是有2(﹣1)2+(﹣1)n﹣5=0,由此可解得自然数n 的值.【解答】解:由题意得,该二项展开式的通项公式•(﹣1)r x r,∴该项的系数,∵2a2+a n﹣5=0,∴2(﹣1)2+(﹣1)n﹣5=0,即+(﹣1)n﹣5•=0,∴n﹣5 为奇数,∴2==,∴2×=,∴(n﹣2)(n﹣3)(n﹣4)=120.∴n=8.故答案为:8.14.【来源】浙江省重点中学2019 届高三上学期期末热身联考数学试题⎛ 2 ⎫5 1⎪1展开式中,x2的系数是( B )⎝⎭A、80B、-80C、40D、-4015.【来源】山东省德州市2016-2017 学年高二下学期期末考试数学(理)试题a 2 4如果x + x - 的展开式中各项系数之和为2,则展开式中x 的系数是( C ) x xA.8 B.-8 C.16 D.-1616.【来源】云南省昆明市第一中学2018 届高三第八次月考数学(理)试题x x2 ⎪ ⎛1- 1 ⎫ (1+ x )6x 3⎝ ⎭ 展开式中 x 的系数为(B )A .-14B .14C. 15D .3017.【来源】安徽省安庆一中、山西省太原五中等五省六校(K12 联盟)2018 届高三上学期期末联考数学(理)试题在二项式(x - 1)n 的展开式中恰好第 5 项的二项式系数最大,则展开式中含有 x 2项的系数是( C )xA .35B .-35C .-56D .56答案及解析:第五项的二项式系数最大,则,通项,令,故系数.18.【来源】辽宁省实验中学、沈阳市东北育才学校等五校 2016-2017 学年高二下学期期末联考数学(理)试题 在( - 2)n 的展开式中,各项的二项式系数之和为 64,则展开式中常数项为( A )xA .60B .45C . 30D .1519.【来源】湖北省武汉市 2018 届高三四月调研测试数学理试题 在(x + 1-1)6 的展开式中,含 x 5项的系数为( B )xA .6B .-6C .24D .-24答案及解析:的展开式的通项 .的展开式的通项=. 由 6﹣r ﹣2s=5,得 r+2s=1,∵r ,s ∈N ,∴r=1,s=0. ∴的展开式中,含 x 5 项的系数为 . 故选:B .20.【来源】辽宁省抚顺市 2018 届高三 3 月高考模拟考试数学(理)试题在(2 -1)6 的展开式中,含 1项的系数为( C )xA. -60B. 160C. 60D. 6421.【来源】2018 年高考真题——数学理(全国卷Ⅲ)(x 2+ 2)5 的展开式中 x 4 的系数为( C )xA .10B .20C .40D .80答案及解析:由题可得 令 ,则所以x2× 4x9 n故选 C.22.【来源】浙江省金华市十校联考 2016-2017 学年高二下学期期末数学试卷在(x 2﹣4)5 的展开式中,含 x 6 的项的系数为( D ) A .20 B .40 C .80 D .160答案及解析:【分析】=(﹣4)r,令 10﹣2r=6,解得 r=2,由此能求出含 x 6 的项的系数.【解答】解:∵(x 2﹣4)5, ∴T r+1==(﹣4)r,令 10﹣2r=6,解得 r=2, ∴含 x 6 的项的系数为=160. 故选:D .23.【来源】浙江省诸暨市牌头中学 2018 届高三 1 月月考数学试题 在⎛x 2 - ⎝2 ⎫6的展开式中,常数项为( D )⎪⎭ A .-240 B .-60 C .60 D .24024.【来源】浙江省湖州市 2017 届高三上学期期末数学试题在(1﹣x )5+(1﹣x )6+(1﹣x )7+(1﹣x )8 的展开式中,含 x 3 的项的系数是( D ) A .121 B .﹣74C .74D .﹣121答案及解析:【考点】二项式定理的应用.【分析】利用等比数列的前 n 项公式化简代数式;利用二项展开式的通项公式求出含 x 4 的项的系数,即是代数式的含 x 3 的项的系数.【解答】解:(1﹣x )5+(1﹣x )6+(1﹣x )7+(1﹣x )8 ==,(1﹣x )5 中 x 4 的系数 ,﹣(1﹣x )9 中 x 4 的系数为﹣C 4=﹣126,﹣126+5=﹣121. 故选:D25.【来源】甘肃省兰州市第一中学 2018 届高三上学期期中考试数学(理)试题在(x 2-1)(x +1)4 的展开式中,x 3 的系数是( A ) A .0B .10C .-10D .20答案及解析:(x +1)4 的展开式的通项, 因此在(x 2-1)(x +1)4 的展开式中,x 3 的系数是26.【来源】山西重点中学协作体 2017 届高三暑期联考数学(理)试题在二项式 + 1的展开式中,前三项的系数成等差数列,把展开式中所有的项重新排成一列,有理项都互 x xx 1 ⎝ ⎭不相邻的概率为( D ) A . 16B . 14C. 1 3D . 51227.【来源】湖北省孝感市八校 2017-2018 学年高二上学期期末考试数学(理)试题已知C 0- 4C 1+ 42C 2- 43C 3+ + (-1)n 4nC n= 729 ,则C 1+ C 2+ + C n的值等于( C )nnnnnA .64B .32 C.63 D .31答案及解析:nnn因为 ,所因,选 C. 28.【来源】辽宁省重点高中协作校 2016-2017 学年高二下学期期末考试数学(理)试题若òn(2x -1)dx = 6 ,则二项式(1 - 2x )n的展开式各项系数和为( A ) A .-1 B .26 C .1 D . 2n29.【来源】浙江省金华十校 2017 届高三数学模拟试卷(4 月份)数学试题若(x -1)8=1+a 1x +a 2x 2+…+a 8x 8,则 a 5=( B ) A .56B .﹣56C .35D .﹣35答案及解析:利用通项公式即可得出. 解:通项公式 T r+1=(﹣1)8﹣r x r ,令 r=5,则(﹣1)3=﹣56.故选:B .30.【来源】广东省茂名市五大联盟学校 2018 届高三 3 月联考数学(理)试题6⎛ 1 ⎫ x 4在( + x ) 1+ y ⎪ 的展开式中, y 2 项的系数为( C )A .200B .180 C. 150 D .120答案及解析:展开式的通项公式,令可得:,,展开式的通项公式 ,令可得,据此可得: 项的系数为 .本题选择 C 选项.31.【来源】吉林省长春外国语学校 2019 届高三上学期期末考试数学(理)试题 (2-x )(1+2x )5 展开式中,含 x 2 项的系数为( B )x x 0 1 2 2017 3n nx A . 30 B . 70 C .90 D .-15032.【来源】浙江省新高考研究联盟 2017 届第三次联考数学试题若(1 + x )3 + (1 + x )4 + (1 + x )5 + + (1 + x )2017 = a + a x + a x 2 + + a x 2017 ,则 a 的值为( D )3 2017 32018 420174201833.【来源】广东省肇庆市 2017 届高考二模数学(理)试题若(x 6+ 1 )n的展开式中含有常数项,则 n 的最小值等于( C )A .3B .4C .5D .6答案及解析:【分析】二项式的通项公式 T r+1=C )r ,对其进行整理,令 x 的指数为 0,建立方程求出 n 的最小值.【解答】解:由题意 )n 的展开式的项为)r =C n r=C r令r=0,得 r ,当 r=4 时,n 取到最小值 5故选:C .【点评】本题考查二项式的性质,解题的关键是熟练掌握二项式的项,且能根据指数的形式及题设中有常数的条 件转化成指数为 0,得到 n 的表达式,推测出它的值.34.【来源】上海市金山中学 2017-2018 学年高二下学期期中考试数学试题 设(3x -1)6= a x 6+ a x 5+ + a x + a ,则| a | + | a | + | a | + + | a| 的值为…( B )651126(A) 26(B) 46(C) 56(D) 26+ 4635.【来源】浙江省台州市 2016-2017 学年高二下学期期末数学试题x -已知在( 2 1 )n的展开式中,第 6 项为常数项,则 n =( D )A .9B .8C .7D .6答案及解析:【考点】二项式系数的性质. 【分析】利用通项公式即可得出. 【解答】解:∵第 6 项为常数项,由 =﹣ •x n ﹣6,可得 n ﹣6=0.解得 n=6. 故选:D .36.【来源】山东省潍坊寿光市 2016-2017 学年高二下学期期末考试数学(理)试题⎛ 1 ⎫6+ 2x ⎪ ⎝ ⎭的展开式中常数项为( B ) A .120B .160C. 200D .24037.【来源】北京西城八中少年班 2016-2017 学年高一下学期期末考试数学试题 (2x + 3)4 = a + a x + a x 2 + a x 3 + a x 4(a + a + a )2 - (a + a )2若0 1 2 3 4,则 0 2 41 3 的值为( A ). 5 x A . C B . C C . C D . Cx x A .1 B .-1 C .0 D .2答案及解析:令 x = 1, a + a + + a = (2 + 3)4 ,1 4令 x = -1, a - a + a - a + a= (-2 + 3)4 ,1234而 (a + a + a )2 - (a + a )22413= (a 0 + a 2 + a 4 + a 1 + a 3 )(a 0 - a 1 + a 2 - a 3 + a 4 )= (2 + 选 A .3)4 (-2 + 3)4 = (3 - 4)4 = 1. 38.【来源】云南省曲靖市第一中学 2018 届高三 4 月高考复习质量监测卷(七)数学(理)试题设 i 是虚数单位,a 是(x + i )6的展开式的各项系数和,则 a 的共轭复数 a 的值是( B ) A . -8iB . 8iC . 8D .-8答案及解析:由题意,不妨令 ,则,将转化为三角函数形式,,由复数三角形式的乘方法则,,则,故正确答案为 B.39.【来源】福建省三明市 2016-2017 学年高二下学期普通高中期末数学(理)试题 a 2 52x + x - 的展开式中各项系数的和为-1,则该展开式中常数项为( A ) x xA .-200B .-120 C.120 D .20040.【来源】甘肃省天水一中 2018 届高三上学期第四次阶段(期末)数学(理)试题已知(1+ax )(1+x )5 的展开式中 x 2 的系数为 5,则 a =( D )A.-4B.-3C.-2D.-141.【来源】广东省深圳市宝安区 2018 届高三 9 月调研测数学(理)试题(1 + 1)(1 + x )5 展开式中 x 2 的系数为 ( A )xA .20B .15C .6D .142.【来源】甘肃省民乐一中、张掖二中 2019 届高三上学期第一次调研考试(12 月)数学(理)试题⎛ a ⎫ ⎛1 ⎫5x + ⎪ 2x - ⎪ ⎝ ⎭ ⎝⎭ 的展开式中各项系数的和为 2,则该展开式中常数项为( D )A .-40B .-20C .20D .4043.【来源】浙江省名校协作体 2018 届高三上学期考试数学试题⎛ 1+ 2⎫(1- x )4 展开式中 x 2 的系数为( C ) x ⎪ ⎝ ⎭A .16B .12C .8D .444.【来源】山西省太原市 2018 届高三第三次模拟考试数学(理)试题已知(x -1)(ax +1)6展开式中 x 2 的系数为 0,则正实数a = ( B ) 22 A .1B .C.53D . 2x 4 5 5 答案及解析:的展开式的通项公式为.令 得 ;令得.展开式 为. 由题意知,解得(舍).故选 B. 45.【来源】吉林省松原市实验高级中学、长春市第十一高中、东北师范大学附属中学 2016 届高三下学期三校联合模拟考试数学(理)试题(x +1)2 (x - 2)4的展开式中含 x 3 项的系数为( D )A .16B .40 C.-40 D .846.【来源】海南省天一大联考 2018 届高三毕业班阶段性测试(三)数学(理)试题若(2x - 3)2018= a + a x + a x 2 + L + ax 2018 ,则 a + 2a + 3a + L + 2018a= ( D )122018A .4036B .2018C .-2018D .-4036123201847.【来源】湖北省天门、仙桃、潜江 2018 届高三上学期期末联考数学(理)试题(1 + x )8 (1 + y )4 的展开式中 x 2y 2 的系数是 ( D )A .56B .84C .112D .168答案及解析:因的展开式 的系数 ,的展开式 的系数 ,所的系数.故选 D.48.【来源】北京西城八中 2016-2017 学年高一下学期期末考试数学试题 ⎛ x 2 - 在二项式⎝ 1 ⎫5⎪⎭ 的展开式中,含 x 的项的系数是( C ). A .-10B .-5C .10D .5答案及解析:解: ⎛ x 2 - 1 ⎫5⎪ 的展开项T = C k (x 2 )k (-x -1 )5-k = (-1)5-k C k x 3k -5 ,令3k - 5 = 4 ,可得 k = 3, ⎝x ⎭ k +1 5 5∴ (-1)5-k C k = (-1)5-3 C 3= 10 . 故选 C .49.【来源】广东省化州市 2019 届高三上学期第二次模拟考生数学(理)试题 已知(x +1)(ax - 1)5的展开式中常数项为-40,则 a 的值为( C )xA. 2B. -2C. ±2D. 450.【来源】福建省“华安一中、长泰一中、南靖一中、平和一中”四校联考 2017-2018 学年高二下学期第二次联考试题(5 月)数学(理)试题若(1 - 2 x )n(n ∈ N *) 的展开式中 x 4的系数为 80,则(1 - 2 x )n的展开式中各项系数的绝对值之和为( C ) A .32B .81C .243D .256。
二项式定理

和简捷性.
3.求常数项、有理项和系数最大的项时,要根据通 项公式讨论对 r的限制;求有理项时要注意到指数 及项数的整数性.
nr 4. 性质 1 是组合数公式 Cr 的再现,性质 2 是从 C n n 函数的角度研究的二项式系数的单调性,性质3 是
利用赋值法得出的二项展开式中所有二项式系数的
和.
“我们很聪明,这不需要再验证,也不是门萨的目的。 它的意义在于,我们在智慧的碰撞中享受欢娱。” 如果您觉得自己的智商在130之上,包括130,想要加 入门萨俱乐部的话,可以通过门萨中国官方网站进行申 请,入会测试费260元(全日制学生130元)。
从近两年的高考试题来看,求二项展开式中特定项及特
定项的系数是考查的热点,题型为选择题或填空题,属容易题,
0 (4)二项式的系数从 Cn
, C1 n
1 ,一直到 Cn n ,
Cn n .
3.二项式系数的性质 (1)对称性:与首末两端“等距离” 的两个二项式
nm 系数相等,即 Cm C . n n
n 1 k k (2)增减性与最大值:二项式系数C n,当 2
时,二项式系数是递增的;当
k
n 1 2
二项展开式中,偶数项的二项式系数的和 等于 奇数
1 3 5 2 项的二项式系数的和,即 Cn Cn Cn = C0 C n n
C4 n =
2n1 .
思想方法 感悟提高
方法与技巧
1.通项公式最常用,是解题的基础. 2.对三项或三项以上的展开问题,应根据式子的特 点,转化为二项式来解决,转化的方法通常为集 项、配方、因式分解,集项时要注意结合的合理性
1 n 项式系数是指 C0 n,Cn,„,Cn,它只与各项的项数有关,而
排列组合二项式定理练习题

排列组合二项式定理练习题1.有5本不同的书,其中语文书2本,数学书2本,物理书1本.若将其并排摆放在书架的同一层上,则同一科目书都不相邻的放法种数是( ).A .24B .48C .72D .962.某校开设A 类选修课3门,B 类选修课4门,一位同学从中选3门.若要求两类课程中各至少选一门,则不同的选法共有( ).A .30种B .35种C .42种D .48种3.某外商计划在4个候选城市中投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有( ).A .16种B .36种C .42种D .60种4.2013年春节放假安排:农历除夕至正月初六放假,共7天.某单位安排7位员工值班,每人值班1天,每天安排1人.若甲不在除夕值班,乙不在正月初一值班,而且丙和甲在相邻的两天值班,则不同的安排方案共有( )A .1 440种B .1 360种C .1 282种D .1 128种5.二项式⎝ ⎛⎭⎪⎫2x -1x 6的展开式中的常数项是( ) A .20 B .-20 C .160 D .-1606.已知⎝ ⎛⎭⎪⎫x -a x 8展开式中常数项为1 120,其中实数a 是常数,则展开式中各项系数的和是( ).A .28B .38C .1或38D .1或287.设⎝ ⎛⎭⎪⎫5x -1x n的展开式的各项系数之和为M ,二项式系数之和为N ,若M -N =240,则展开式中x 的系数为( ).A .-150B .150C .300D .-3008.广州亚运会火炬传递在A ,B ,C ,D ,E ,F 六个城市之间进行,以A 为起点,F 为终点,B 与C 必须接连传递,E 必须在D 的前面传递,且每个城市只经过一次,那么火炬传递的不同路线共有__________种9.在某次中外海上联合搜救演习中,参加演习的中方有4艘船、3架飞机;外方有5艘船、2架飞机.若从中、外两组中各选出2个单位(1架飞机或1艘船都可作为1个单位,所有的船只两两不同,所有的飞机两两不同),则选出的4个单位中恰有1架飞机的不同选法共有多少种?10.已知10件不同的产品中有4件次品,现对它们一一测试,直至找到所有4件次品为止.(1)若恰在第2次测试时,才测试到第一件次品,第8次才找到最后一件次品,则共有多少种不同的测试方法?11.已知a为如图所示的程序框图中输出的结果,求二项式(a x-1x)6的展开式中含x2项的系数.。
二项式定理

第三讲 二项式定理(理)A 组基础巩固一、选择题1.(2021·广东深圳、汕头、潮州、揭阳联考)⎝⎛⎭⎫1x -x 10的展开式中x 4的系数是( B ) A .-210 B .-120 C .120D .210[解析] ⎝⎛⎭⎫1x -x 10的展开式的通项T r +1=C r 10⎝⎛⎭⎫1x 10-r (-x )r =(-1)r C r 10x 2r -10,由2r -10=4得r =7,∴x 4的系数为(-1)7C 710=-120.故选B.2.(2020·河北保定期末)⎝⎛⎭⎫3x -1x 6的展开式中,有理项共有( D ) A .1项 B .2项 C .3项D .4项[解析] ⎝⎛⎭⎫3x -1x 6的展开式的通项公式为T r +1=C r 6·(-1)r ·36-r·x 6-32r ,令6-32r 为整数,求得r =0,2,4,6,共计4项.3.(2019·全国)(2x +1)6的展开式中x 的系数是( B ) A .120 B .60 C .30D .15[解析] 由二项式(2x +1)6的展开式的通项为 T r +1=C r 6(2x )6-r =26-r C r 6x 6-r 2, 令6-r2=1,解得r =4, 则(2x +1)6的展开式中x 的系数是22C 46=60,故选B.4.(2020·山东省临沂市期末)⎝⎛⎭⎪⎫2x -134x 6的展开式的中间项为( B )A .-40B .-40x 2C .40D .40x 2[解析] ⎝⎛⎭⎪⎫2x -134x 6的展开式的通项为T k +1=C k 6(2x )6-k⎝⎛⎭⎪⎫-134x k ,则中间项为T 4=C 36(2x )3⎝⎛⎭⎪⎫-134x 3=20×23×⎝⎛⎭⎫-14×x 2=-40x 2.故选B. 5.(2021·湖南省六校联考)设常数a ∈R .若⎝⎛⎭⎫x 2+ax 5的二项展开式中x 7项的系数为-15,则a =( D )A .-2B .2C .3D .-3[解析] ⎝⎛⎭⎫x 2+ax 5的二项展开式的通项公式为 T r +1=C r 5·(x 2)5-r ·⎝⎛⎭⎫a x r =a r ·C r 5·x 10-3r , r =0,1,2,3,4,5.令10-3r =7,得r =1,所以展开式中x 7项的系数为a ·C 15=-15,解得a =-3. 故选D.6.(2021·广州测试)使⎝⎛⎭⎫3x +1x x n (n ∈N +)的展开式中含有常数项的最小的n 为( B )A .4B .5C .6D .7[解析] T r +1=C r n (3x )n -r ·x -32r =C r n ·3n -r·xn -5r 2(r =0,1,2,…,n ),若T r +1是常数项,则有n -52r =0,即2n =5r (r =0,1,…,n ),当r =0,1时,n =0,52,不满足条件:当r =2时,n =5,故选B.7.(2021·四川达州诊断)已知(2+x )8=a 0+a 1(1-x )+a 2(1-x )2+…+a 8(1-x )8,则a 6=( B )A .-252B .252C .112D .-112[解析] (2+x )8=[3-(1-x )]8=a 0+a 1(1-x )+…+a 8(1-x )8,其通项T r +1=C r 838-r [-(1-x )]r =(-1)r 38-r C r 8(1-x )r ,∴a 6=32C 68=252,故选B.8.(2021·广西南宁二中、柳铁一中联考)(1-x )(1+2x )3展开式中x 2项的系数为( B ) A .5 B .6 C .-6D .-4[解析] x 2项为1×C 23(2x )2+(-x )×C 13(2x )=6x 2.9.(2021·四川绵阳南山中学诊断)已知(2x -1)5=a 0+a 1(x -1)+a 2(x -1)2+a 3(x -1)3+a 4(x -1)4+a 5(x -1)5,则a 2=( C )A .10B .80C .40D .120[解析] 由已知得令x -1=t 有(2t +1)5=a 0+a 1t +a 2t 2+a 3t 3+a 4t 4+a 5t 5,又T r =C r 5(2t )5-r=25-r C r 5t 5-r.令5-r =2得r =3.∴a 2=25-3C 35=40.故选C.10.(2021·新高考八省联考)(1+x )2+(1+x )3+…+(1+x )9的展开式中x 2的系数是( D ) A .60 B .80 C .84D .120[解析] (1+x )2+(1+x )3+…+(1+x )9的展开式中x 2的系数是C 22+C 23+C 24+…+C 29, 因为C m -1n +C m n =C m n +1且C 22=C 33, 所以C 22+C 23=C 33+C 23=C 34, 所以C 22+C 23+C 24=C 24+C 34=C 35,以此类推,.C 22+C 23+C 24+…+C 29=C 39+C 29=C 310=10×9×83×2×1=120. 故选D.11.(2021·河南信阳调研)已知(x +1)2⎝⎛⎭⎫x +1x 3n 的展开式中没有x 2项,n ∈N *,则n 的值可以是( C )A .5B .6C .7D .8[解析] 因为(x +1)2⎝⎛⎭⎫x +1x 3n 的展开式中没有x 2项,所以⎝⎛⎭⎫x +1x 3n 的展开式中不含常数项,不含x 项,不含x 2项⎝⎛⎭⎫x +1x 3n 的展开式的通项为:T r +1=C r n x n -r ⎝⎛⎭⎫1x 3r =C r n x n -4r,r =0,1,2,…,n ,所以当n 取5,6,7,8时,方程n -4r =0,n -4r =1,n -4r =2无解,检验可得n =7,故选C.12.(2021·江苏南京调研)已知(2+x )(1-2x )5=a 0+a 1x +a 2x 2+a 3x 3+a 4x 4+a 5x 5+a 6x 6,则不正确...的是( D ) A .a 0的值为2 B .a 5的值为16C .a 1+a 2+a 3+a 4+a 5+a 6的值为-5D .a 1+a 3+a 5的值为120[解析] 令x =0,得a 0=2,故A 正确;2×(-2)5C 55+(-2)4C 45=16,故a 5=16,B 正确;令x =1,得a 0+a 1+a 2+a 3+a 4+a 5+a 6=-3①,又a 0=2,∴a 1+a 2+a 3+a 4+a 5+a 6=-5,故C 正确;令x =-1,得a 0-a 1+a 2-a 3+a 4-a 5+a 6=243②,由①②得:a 1+a 3+a 5=-123,D 错误.故选D.二、填空题13.(2018·天津高考)在⎝⎛⎭⎫x -12x 5的展开式中,x 2的系数为 52 .[解析] ⎝⎛⎭⎫x -12x 5的展开式的通项为T r +1=C r 5x 5-r ⎝⎛⎭⎫-12x r =⎝⎛⎭⎫-12r C r 5x 5-3r 2. 令5-3r2=2,可得r =2.所以⎝⎛⎭⎫x -12x 5的展开式中的x 2的系数为⎝⎛⎭⎫-122C 25=52. 14.(2021·山西大同学情调研)在(2x -1)7的二项展开式中,第四项的系数为 -560 .[解析] 在(2x -1)7的二项展开式中,第四项的系数为:C 37·24·(-1)3=-560.15.(2020·安徽池州统测)已知⎝⎛⎭⎫x -2x n 的展开式中二项式系数之和为512,则展开式中常数项为 -672 .[解析] 由题意得:C 0n +C 1n +…+C n n =2n =512,解得:n =9,∴⎝⎛⎭⎫x -2x 9展开式的通项公式为 T r +1=C r 9(x )9-r ⎝⎛⎭⎫-2x r =(-2)r C r 9x 9-3r 2, 当9-3r =0,即r =3时,T 4=(-2)3C 39=-672, ∴常数项为-672.16.(2020·广东省东莞市期末)若(3+ax )(1+x )4展开式中x 的系数为13,则展开式中各项系数和为 64 .(用数字作答)[解析] 由题意得3C 14+a =13,∴a =1.令x =1得(3+ax )(1+x )4的展开式中各项系数和为(3+1)(1+1)4=64.B 组能力提升1.(2019·浙江,13)在二项式(2+x )9的项的个数是 5 .[解析] (2+x )9展开式的通项T r +1=C r 9(2)9-r x r=C r 9·29-r 2·x r(r =0,1,2,…,9),令r =0,得常数项T 1=C 09·292·x 0=292=162,要使系数为有理数,则只需9-r 2∈Z ,则r 必为奇数,满足条件的r 有1,3,5,7,9,共五种,故系数为有理数的项的个数是5.2.(2021·中原名校质量测评)若⎝⎛⎭⎫x -2x 2n 的展开式中只有第六项的二项式系数最大,则展开式中各项的系数和是 1 .[解析] 由⎝⎛⎭⎫x -2x 2n 的展开式中只有第六项的二项式系数最大,所以展开式中共有11项,所以n =10;令x =1,可求得展开式中各项的系数和是(1-2)10=1.故答案为1.3.(2021·上海普陀区二模)502 019+1被7除后的余数为 2 .[解析] 502 019+1=(1+72)2019+1=1+C 12 019·72+C 22 019·74+…+C 2 0192 01974 038+1=72C 12 019+74C 22 019+…+74 038C 2 0192 019+2.故余数为2. 4.(2021·内蒙古包头模拟)已知(2x -1)5=a 5x 5+a 4x 4+a 3x 3+a 2x 2+a 1x +a 0,则|a 0|+|a 1|+…+|a 5|=( B )A .1B .243C .121D .122[解析] 令x =1,得a 5+a 4+a 3+a 2+a 1+a 0=1,① 令x =-1,得-a 5+a 4-a 3+a 2-a 1+a 0=-243,② ①+②,得2(a 4+a 2+a 0)=-242, 即a 4+a 2+a 0=-121.①-②,得2(a 5+a 3+a 1)=244, 即a 5+a 3+a 1=122.所以|a 0|+|a 1|+…+|a 5|=122+121=243.故选B.5.(2021·衡水模拟)S =C 127+C 227+…+C 2727除以9的余数为( B )A .8B .7C .6D .5[解析] 依题意S =C 127+C 227+…+C 2727=227-1=89-1=(9-1)9-1=C 09×99-C 19×98+…+C 89×9-C 99-1=9(C 09×98-C 19×97+…+C 89)-2.∵C 09×98-C 19×97+…+C 89是正整数,∴S 被9除的余数为7.6.(2021·湖北武汉襄阳荆门宜昌四地六校考试联盟联考)(2x +y +1)6的展开式中,xy 3的系数为( A )A .120B .480C .240D .320[解析] 解法一:(2x +y +1)6=[2x +(y +1)]6,其展开式通项T r +1=C r 6(2x )6-r (y +1)r , 令r =5得,T 6=2C 56x (y +1)5, 又(y +1)5展开式通项P s +1=C s 5y 5-s , 令s =2得P 3=C 25y 3, ∴xy 3的系数为2C 56·C 25=120,故选A.解法二:(2x +y +1)6=(2x +y +1)·(2x +y +1)…(2x +y +1)6个从六个括号中1个取2x,3个取y 、2个取1即得xy 3项,其系数为2C 16·C 35·C 22=120,故选A.7.(2021·江西重点中学联考)若多项式(2x +3y )n 展开式仅第5项的二项式系数最大,则多项式⎝⎛⎭⎫x 2+1x 2-4n -4展开式中x 2的系数为( A ) A .-304 B .304 C .-208D .208[解析] 多项式(2x +3y )n 展开式仅第5项的二项式系数最大,故n =8,多项式⎝⎛⎭⎫x 2+1x 2-44展开式中x 2的系数为C 14·(-4)3+C 24·C 12·(-4)=-256-48=-304,故选A.。
高考数学二轮复习考点十八《二项式定理》课件

Tr
+
1
=
C
r 12
(2
+
x )12 -
r·-2x0202212 rቤተ መጻሕፍቲ ባይዱ必须满足 r=0,T1=(2+ x)12,x5 的系数为 22C1102=264.故选
B.
二、选择题(在每小题给出的四个选项中,有多项符合题目要求)
17.(2021·湖南第三次模拟)在3x-
1xn的展开式中,各项系数和与二项
式系数和之和为 128,则( )
三、填空题 19.(2021·北京高考)x3-1x4 展开式中常数项为________.
答案 -4 解析 x3-1x4 的展开式的通项公式为 Tr+1=C4r(x3)4-r-1xr=(-1)rCr4x12 -4r,令 12-4r=0,得 r=3,则常数项为 T4=(-1)3C34=-4.
20.(2021·山东青岛一中模拟)(x2+2)x-1x10的展开式中,x6 的系数为 ________.
6.(2021·湖南长沙一中模拟)(1- x)10 的二项展开式中,x 的系数与 x4 的系数之差为( )
A.-220 B.-90 C.90 D.0
答案 D
r
解析 因为(1- x)10 的二项展开式中,通项公式为 Tr+1=C1r0·(-1)r·x2, 故 x 的系数与 x4 的系数之差为 C210-C810=0.故选 D.
数为 C16×-23×25=-128.故选 D.
3.(2021·福建福州高三 5 月调研)在(x+y+z)6 的展开式中,xyz4 的系数 是( )
A.15 B.30 C.36 D.60 答案 B
解析 (x+y+z)6 相当于 6 个(x+y+z)相乘,由二项式定理的原理可知 xyz4 的系数是 C16C15C44=6×5×1=30.故选 B.
排列组合二项式定理综合测试卷(B卷)

演练篇 核心考点AB 卷 """""t""高二数学 2021年5月 T 于王"排"#合二&式()综合测试卷(B -)■河南省南乐县第一高级中学吉晓波D. 3医院了:果店一、选择题1 -已知 A ' = 100 A ',则'=( )。
A. 11 B. 12#. 13 D. 142. 满足条件C )>#6的正整数"的个数是( )。
A. 10B. 9#. 43. 小张从家出发去看望生病的同学,他需要先去 水果店买水果,然后 去花店买花,最后到达医院。
相关.........................的网格纸上,网格线是道........图1路,则小张所走路程最短的走法种数为!)。
A. 72B. 56#. 48 D. 404. 在一-次运动会上有四项比赛的冠军在甲、乙、丙3人中产生,那么不同的夺冠情况共有()种。
A. A )B. 43#. 34 D. #3/ 2 \ 65. (2' — 3;?"的展开式中'3的系数为( )。
#. 64D. —1286. 由0,1,2,5四个数组成没有重复数字的四位数中,能被5整除的个数是()$A. 24B. 12#. 10 D. 67. 从2名教师和5名学生中选出3人参加“我爱我的祖国”主题活动,要求入选的3人中至少有1名教师,则不同的选取方案数是( )$A. 20B. 25#. 30 D. 558. 将4张座位编号分别为1,2,3,4的电影票全部分给3人,每人至少1张$如果分给同一人的2张电影票具有连续的编号,那 么不同的分法数是!)$A. 24B. 18#. 12 D. 69.从6种不同的颜色中选出一些颜色给如图2所示的4个格子涂色,每个格子涂图2一种颜色,且相邻的两个格子颜色不同,则不同的涂色方法有()$A.360 种B.510 种#.630 种 D.750 种10.如图 3, *MON的边O8上有4个点A i 、A 2、A 3、A 4,ON 上有 3 个点 21、22、2,,则以 O 、A 1>A 2>A 3>A 4>21、22、23中的3个点为顶点的三角形的个数为()$A. 30B. 42#. 54 D. 5611. A 、2、C 、/4名学生报名参加学校的 甲、乙、丙、丁 4个社团,若学生A 不参加甲社团,2不参加乙社团,且4名学生每人报一个社团,每个社团也只能1人报名,则不同的 报名方法数为( )$A. 14B. 18#. 12 D. 412.为了提高命题质量,命题组指派5名 教师对数学卷的选择题、填空 题和解答题这3种题型进行改编,则每种题型至少指派1名教师的不同分派方法种数为( )$A. 90B.36#. 150D. 10813. 2020年春节期间新型冠状病毒肺炎疫情在湖北爆发,为了打赢疫情防控阻击战&某医院呼吸科要从3名男医生,2名女医生中选派3人到湖北省的A , 2, C 三地参加疫情防控工作,若这3人中至少有1名女医生&则选派方案有( )$A. 9 种B. 12 种#. 54 种D.72 种14.(2------2)(1 + "y )6 展开式中'23315中孝生皋捏化演练篇核心考点AB卷高二数学2021年5月项的系数为160,则a=!"$A.2B.4C-—22-—2215.计划展出10幅不同的画,其中1幅水彩画、4幅油画、5幅国画,排成一行陈列,要求同一品种的画必须连在一起,并且水彩画不放在两端,那么不同的陈列种数为!"$A.A4A5B.A3A4A5C.C1A4A5 2.A2A4A516.若(2+a'"$(a(0)的展开式中各项的二项式系数之和为512,且第6项的系数最大,则a的取值范围为("$A.(—7,0)UC.+317.已知二项式(1+丄一2'),则展开式中常数项为!)$A.49B.—47C.—1 2.11)已知二项式(2'2+1)的展开式中二项式系数之和等于64,则展开式中常数项等于()A.240B.120C.48 2.361*.某校实行选科走班制度(语文、数学、英语为必选科目,此外学生需在物理、化学、生物、历史、地理、政治六科中任选三科),根据学生选科情况,该校计划利用三天请专家对九个学科分别进行学法指导,每天依次安排三节课,每节课一个学科,语文、数学、英语只排在第二节,物理、政治排在同一天,化学、地理排在同一天,生物、历史排在同一天,则不同的排课方案数为()$A.36B.48C.144 2.28820.包括甲、乙、丙3人的7名同学站成一排拍纪念照,其中丙站正中间,甲不站在乙的左边,且不与乙相邻,则不同的站法有()$A.240种B.252种C.264种 2.288种21.已知(3—')(2'—3)8"a$+a1('—1)+a2('—1)2+…+a g('—1)9,则a6"()$A.—1792B.1792C.—5376 2.537622.5名护士上班前将外衣放在护士站,下班后从护士站取外衣,由于灯光暗淡,只有2人拿到了自己的外衣,另外3人拿到别人外衣的情况有!)$A.60种B.40种C.20种 2.10种23.停车场划出一排9个停车位置,今有5辆不同的车需要停放,若要求剩余的4个空车位连在一起,则不同的停车方法有!)$A.A5种B.2A5A4种C.5A5种 2.6A5种24.从正方体的8个顶点中选取4个作为顶点,可得到四面体的个数为()$A.C;—12B.C;—8C.C4—6 2.C8—425.从装有$+1个不同小球的口袋中取出,个小球(0V,'$,,,$#N$),共有C,+1种取法$在这C,+1种取法中,可以分为两类:第一类是某指定的小球未被取到,共有C$・C,种取法;第二类是某指定的小球被取到,共有C1・C,1种取法。
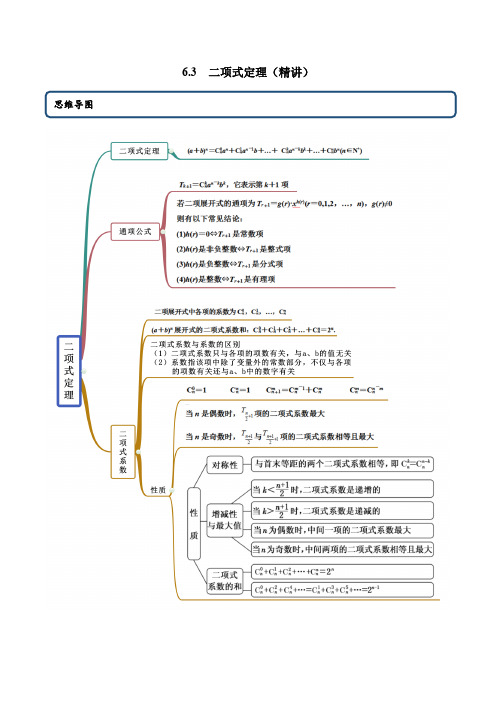
高中试卷-6.3 二项式定理(精讲)(含答案)
6.3 二项式定理(精讲)考法一 二项式定理展开式【例1】(1)求4+的展开式为 .(2)(2020·江苏省太湖高级中学高二期中)已知012233444(1)4729nnnn n n n n C C C C C -+-++-=L ,则n 的值为【答案】(1)1x 2+12x+54+108x +81x 2【解析】(1)方法一 (14=4+C 143·1)+C 2421)2+C 341)3+C41)4=81x 2+108x +54+12x+1x2.方法二 (14=3x +14=1x 2(1+3x )4=1x 2·[1+C 14·3x +C 24(3x )2+C 34(3x )3+C 4(3x )4]=1x2(1+12x +54x 2+108x 3+81x 4)=1x2+12x+54+108x +81x 2.(2)由012233444(1)4729n n nn n n n n C C C C C-+-++-=L 得()()()()()0120312312301414141414729nn n n n n n n n n n C C C C C ---××-+××-××-+××-×-+++=×L 则()12479n-=,即()()672933n =-=-,解得6n =.【一隅三反】1.(2021·全国课时练习)化简多项式(2x+1)5-5(2x+1)4+10(2x+1)3-10(2x+1)2+5(2x+1)-1的结果是( )A .(2x+2)5B .2x 5C .(2x-1)5D .32x 5【答案】D【解析】依题意可知,多项式的每一项都可看作()()55211rrr C x -+-,故为()5211x éù+-ëû的展开式,化简()()555211232x x x éù+-==ëû.故选D.2.(2020·江苏宿迁市·宿迁中学高二期中)化简:2012222412333...3n n n n n n n n C C C C ---×+×+×++×=_________.【答案】101n -【解析】()()()()011020201211212(31)3131...3131n n n n n nn n n n n C C C C ----+=´´+´´++´´+´´则2012222412233331(31)10n n n n n nn n n n C C C C ---×+×+×++×+=+=L 所以2012222412333...3101nn n n n n n n n C C C C ---×+×+×++×=-故答案为:101n -.考法二 二项式指定项的系数与二项式系数【例2】(1)(2020·全国高二单元测试)在(x 10的展开式中,x 6的系数是(2)(2020·广东佛山市·高二期末)二项式81x x æö+ç÷èø的展开式中常数项是______(用数字作答)(3)(2020·安徽省蚌埠第三中学高二月考)30的有理项共有 项【答案】(1)9410C (2)70(3)6【解析】(1)由T k +1=10kC x 10-k k ,令10-k =6,解得k =4,∴系数为)4410C =9410C (2)二项式81x x æö+ç÷èø的展开式的通项公式8821881r r r rr r T C x C x x --+==,令820r -=,得4r =,则常数项为4588765==704321T C ´´´=´´´,故答案为:70(3)30的通项公式为:53010613030rrrrr r T C C x--+==,061051730300,,6,r T x r T x C C ====,12180513********,,18,r T x r T x C C -====,243010152531303024,,30,r T x r T x C C --====,所以有理项共有6项,故选:C 【一隅三反】1.(2020·北京市鲁迅中学高二月考)二项式261(2)x x-的展开式中的常数项是_______.(用数字作答)【答案】60【解析】有题意可得,二项式展开式的通项为:()62612316612(1)2rrr r r r rr T C xC xx ---+æö=-=-ç÷èø令1230r -=可得4r = ,此时2456260T C ==.2.(2021·上海青浦区)在6212x x æö+ç÷èø二项展开式中,常数项是_______.【答案】60【解析】展开式的通项公式是()626123166122rrrr r r r T C xC x x ---+æö=××=××ç÷èø,当1230r -=时,4r = 24416260T C +=×=.故答案为603..(2020·青海西宁市)若8x æ+çè的展开式中4x 的系数为7,则实数a =______.【答案】12【解析】根据二项展开式的通项公式可得:4888331888=rr r r r r r r r r r T C x C a x C a x ----+==,令4843r -=,可得3r =,3388==7r r C a C a ,解得:12a =,故答案为:124.(2020·梁河县)已知31(2)nx x+的展开式的常数项是第7项,则n =________.【答案】8【解析】根据题意,可知第7项为()666366324122n n n nn C xC x x ---æö××=××ç÷èø,而常数项是第7项,则3240n -=,故8n =.故答案为:8.考法三 多项式系数或二项式系数【例3】(1)(2020·福建三明市·高二期末)52212x x æö+-ç÷èø的展开式中常数项是( )A .-252B .-220C .220D .252(2).(2021·四川成都市)若5(2)a x x x æö+-ç÷èø的展开式中常数项为80-,则a =( )A .2B .1C .2-D .1-【答案】(1)A (2)C 【解析】(1)由2510211(2)()x x x x+-=-,可得二项式101()x x-的展开式通项为10102110101()(1)rrr r r r r T C xC x x--+=-=-,令1020r -=,解得=5r ,所以展开式的常数项为5510(1)252C -=-.故选:A.(2)Q 5a x x æö-ç÷èø的展开式的通项公式为:55251(1)r r r r r T C a x --+=×××-,显然,25r -为奇数,Q 若求5(2)a x x x æö+-ç÷èø展开式的常数项,251r \-=-,解得2r =故5(2)a x x x æö+-ç÷èø的展开式的常数项等于:23580C a ×=-2a \=-故选:C.【一隅三反】1.(2020·全国高三专题练习)4211x x æö+-ç÷èø展开式中常数项为( ).A .11B .11-C .8D .7-【答案】B【解析】将21x x +看成一个整体,展开得到:41421()(1)r r rr T C x x-+=+- 421(r x x-+的展开式为:4243144m r m m m r mm r r T C x x C x -----+--=×=取430r m --= 当0m =时,4r = 系数为:4440(1)1C C ´´-= 当1m =时,1r = 系数为:11143(1)12C C ´´-=- 常数项为11211-=- 故答案选B2.(2020·全国高三专题练习)52431x x x ææö-+ç÷çèøè的展开式中常数项为( )A .30-B .30C .25-D .25【答案】C【解析】51æçè 的通项为15(1)r r r r T C +=-, 55224311x x x x æææö-+=-ç÷ççèøèè 554311x x ææ-+ççèè,根据式子可知当4r = 或2r = 时有常数项,令4r = 41455(1)T C Þ=- ; 令232352(1)r T C =Þ=-;故所求常数项为13553C C -´ 53025=-=- ,故选C.3.(2020·河南商丘市)()64111x x æö++ç÷èø的展开式的常数项为( )A .6B .10C .15D .16【答案】D【解析】由题意得611x æö+ç÷èø的展开式的通项为()160,1,2,,6r r r T C x r -+=×=×××,令4r =,则4615C =,所以()64111x x æö++ç÷èø的展开式的常数项为11516+=.故选:D.4.(2020·枣庄市第三中学高二月考)在1020201(1)x x++的展开式中,x 2项的系数为( )A .30B .45C .60D .90【答案】B 【解析】在1020201(1)x x++的展开式中,通项公式为T r +110rC=•20201rx x æö+ç÷èø.对于20201rx x æö+ç÷èø,通项公式为T k +1kr C =•x r ﹣2021k ,k ≤r ,r 、k ∈N ,r ≤10.令r ﹣2021k =2,可得r =2+2021k ,故k =0,r =2,故x 2项的系数为210C •02C =45,故选:B .5.(2020·全国高二专题练习)若()1021x a x x æö-+ç÷èø的展开式中6x 的系数为30,则a 等于( )A .13B .12C .1D .2【答案】D【解析】将题中所给式子可化为()10101022111x a x x x a x x x x æöæöæö-+=+-+ç÷ç÷ç÷èøèøèø根据二项式定理展开式通项为1C rn rrr nT a b -+=,101x x æö+ç÷èø的通项为10102110101rr r r r r T C x C x x --+æö=×=ç÷èø令1024r-= 解得3r =所以6x 的项为234610120x C xx ×=令1026r -=解得2r =所以6x 的项为2661045a C x ax -×=-综上可知, 6x 的系数为1204530a -= 解得2a = 故选:D考法四 二项式定理的性质【例2】(1)(多选)(2020·全国高二单元测试)111x x æö-ç÷èø的展开式中二项式系数最大的项是( )A .第5项B .第6项C .第7项D .第8项(2)(2020·山东省桓台第一中学高二期中)(多选)二项式1121x x æö+ç÷èø的展开式中,系数最大的项为( ).A .第五项B .第六项C .第七项D .第八项(3)(2020·绵阳市·四川省绵阳江油中学高二开学考试)若1nx x æö-ç÷èø的展开式中只有第7项的二项式系数最大,则展开式中含2x 项的系数是A .462-B .462C .792D .792-【答案】(1)BC (2)BC (3)D【解析】(1)因为n =11为奇数,所以展开式中第1112+项和第11112++项,即第6项和第7项的二项式系数相等,且最大.故选:BC(2)二项式1121x x æö+ç÷èø的展开式中,每项的系数与二项式系数相等,共有12项所以系数最大的项为第六项和第七项故选:BC(3)∵1nx x æö-ç÷èø的展开式中只有第7项的二项式系数最大,∴n 为偶数,展开式共有13项,则12n =.121x x æö-ç÷èø的展开式的通项公式为()1212211C r r r r T x -+=-,令1222r -=,得5r =.∴展开式中含2x 项的系数是()12551C 792-=-,故选D .【一隅三反】1.(2020·辽宁沈阳市·高二期中)在()()1nx n N +-Î的二项展开式中,若只有第5项的二项式系数最大,则næçè的二项展开式中的常数项为( )A .960B .1120C .-560D .-960【答案】B【解析】在(x ﹣1)n (n ∈N +)的二项展开式中,若只有第5项的二项式系数最大,则n=8,则n =8æ-çè的二项展开式的通项公式为T r+1=8r C •28﹣r •(﹣1)r •x 4﹣r ,令4﹣r=0,求得r=4,可得展开式中的常数项为48C •24•(﹣1)4=1120,故选B .2.(2021·湖南常德市)(ax +1x )(2x ―1)5的展开式中各项系数的和为2,则该展开式中常数项为( )A .B .C .10D .20【答案】C【解析】由已知,当x =1时,(a +11)(2―1)5=2,即a =1,所以(x +1x )(2x ―1)5展开式中常数项为1x ×C 452x ×(―1)4=10,故选C .3.(多选)(2020·三亚华侨学校高二开学考试)已知()na b +的展开式中第5项的二项式系数最大,则n 的值可以为( )A .7B .8C .9D .10【答案】ABC【解析】∵已知()na b +的展开式中第5项的二项式系数4n C 最大,则7n =或n =8或n =9故选:ABC .4.(2020·全国高二课时练习)已知6(31)x +展开式中各项系数的和为m ,且2log n m =,求2nx ö-÷ø展开式中二项式系数最大的项的系数 .【答案】59136【解析】设6260126(31)x a a x a x a x +=++++L ,令1x =,得6612(31)42m =+==,所以2log 12n m ==,则122x ö÷ø展开式中有13项,且中间一项(第7项)的二项式系数最大,该项为6666633712122(2)59136T C C x x x --æö=-=-=ç÷èø.故所求的系数为59136.5.(2020·重庆市第七中学校高二月考)二项式()*122nx n N x æö-Îç÷èø的展开式中,二项式系数最大的项是第4项,则其展开式中的常数项是_________.【答案】-20【解析】由题意知,展开式中有7项,6n =.因为()661122rrrTr C x x -æö+=-ç÷èø()6262612r r r r C x --=-令620r -=,得3r =,所以常数项为()336120C -=-.考法五 二项式系数或系数和【例5】(2020·安徽省泗县)若2701277()(12)f x x a a x a x a x =+=++++L .求:(1)017a a a ++¼+;(2)1357a a a a +++;(3)0127a a a a ++++L .【答案】(1)27;(2)14;(3)27.【解析】(1)令1x =,可得301235674()3271f a a a a a a a a ==+++++++=,∴4012356727a a a a a a a a ++++++=+.①(2)令1x =-可得301235674(1)(1)f a a a a a a a a -=-=-+-+-+-,∴401235671a a a a a a a a +-+-+-=--.②由①-②得13572()28a a a a +++=,∴135714a a a a +++=.(3)由题意得二项式7(12)x +展开式的通项为177(2)2rrrr rr T C x C x +==,∴每项的系数0(0,1,2,,7)i a i >=L ,∴01235017647227a a a a a a a a a a a a ++++=++++++=+L .【一隅三反】1.(2020·北京朝阳区·高二期末)在5(21)x +的二项展开式中,二项式系数之和为___________;所有项的系数之和为_______.【答案】32 243【解析】根据二项展开式的性质,展开式的二项式系数之和为52232n ==,令1x =可得所有项的系数之和为55(211)3243==´+,故答案为:32,2432.(2020·全国高二单元测试)若-x )10=a 0+a 1x +a 2x 2+…+a 10x 10,则(a 0+a 2+…+a 10)2-(a 1+a 3+…+a 9)2= 【答案】1【解析】令1x =,得)1001101a a a +++=-L ,令1x =-,得)100123101a a a a a -+-++=+L ,()()220210139a a a a a a +++-+++L L ()()0110012310a a a a a a a a =+++-+-++L L))1010111==.故选:A.3.(2020·福建厦门市·厦门双十中学高二期中)已知()1121011012101112x a a x a x a x a x +=+++++L ,则12101121011a a a a -+-+=L _____.【答案】22【解析】对等式112012(12)x a a x a x +=++10111011a x a x +++L 两边求导,得101222(12)2x a a x +=+91010111011a x a x +++L ,令1x =-,则1210112101122a a a a -+-+=L .4.(2020·宁县第二中学高二期中)设2012(21)n n n x a a x a x a x -=++++L 展开式中只有第1010项的二项式系数最大.(1)求n ;(2)求012n a a a a ++++L ;(3)求.312232222n na a a a ++++L .【答案】(1)2018;(2)20183;(3)-1.【解析】(1)由二项式系数的对称性,1101020182n n +=\= (2)201801220180122018=3a a a a a a a a ++++-+++=L L (3)令0x = ,得20180(10)1a =-=,令12x =,得21232018232018(11)02222a a a a ++++=-=L ,故3201812023201812222a a a a a +++=-=-.考法六 二项式定理运用【例6】(1)(2020·上海市七宝中学高二期中)7271除以100的余数是________(2)(2020·全国高二单元测试)6(1.05)的计算结果精确到0.01的近似值是_________【答案】(1)41(2)1.34【解析】(1)()727217172727270727127270170177070C C C C +==++++L 21072701()m m N =+´+Îg 2105041m =+g 即7271除以100的余数为41.故答案为:41.(2)()()66122661.0510.051+0.05+0.05+1+0.3+0.0375=1.3375 1.34C C =+=××»»L 故答案为:1.34【一隅三反】1.(2020·四川棠湖中学高二月考)已知202074a +能够被15整除,则a =________.【答案】14【解析】由题可知,()0202020275714=-Q ()()()()0120192020020201201920191202002020202020202020751751751751C C C C =-+-++-+-L 0202012019201912020202020207575751C C C =-+-+L 所以0202012019201912020202022020200775754751C C C a a =-++-++L ,而75能被15整除,要使202074a +能够被15整除,只需1a +能被15整除即可,所以115a +=,解得:14a =.故答案为:14.2.(2020·江苏泰州市·泰州中学高二期中)83被5除所得的余数是_____________.【答案】1【解析】因为883(52)=-0817********8888855(2)5(2)5(2)5(2)C C C C C =×+×´-+×´-++×´-+×´-K 071625277808888885(55(2)5(2)(2))5(2)C C C C C =×+×´-+×´-++-+×´-K ,所以转化为求80885(2)256C ×´-=被5除所得的余数,因为2565151=´+,所以83被5除所得的余数是1,故答案为:13.(2021·河北保定市)60.99的计算结果精确到0.001的近似值是【答案】0.941【解析】()()()()6620126666330.9910.0110.010.010.01...C C C C =-=´-´+´-´ 10.060.00150.00002...=-+- 0.941»故选B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二项式定理测试题
一、选择题
1.设二项式⎝
⎛⎭⎪⎫33x +1x n 的展开式的各项系数的和为P ,所有二项式系数的和为S ,若P
+S =272,则n =( )
A .4
B .5
C .6
D .8
2.⎝
⎛⎭⎫x 2+1
x n 的展开式中,常数项为15,则n 等于( ) A .3 B .4 C .5
D .6
3.(1+2x )3(1-3
x )5的展开式中x 的系数是( ) A .-4 B .-2 C .2
D .4
4.在⎝
⎛⎭⎪⎫
x 2-2x 6的二项展开式中,x 2的系数为( )
A .-15
4
B.154 C .-38
D.38
5.C 331+C 332+C 333+…+C 3333除以9的余数是( ) A .7
B .0
6.已知C n 0+2C n 1+22C n 2+…+2n C n n =729,则C n 1+C n 3+C n 5的值等于( ) A .64 B .32 C .63
D .31
7.(1+2x )2(1-x )5=a 0+a 1x +a 2x 2+…+a 7x 7,则a 1-a 2+a 3-a 4+a 5-a 6+a 7=( ) A .32 B .-32 C .-33
D .-31
8.(1+ax +by )n 展开式中不含x 的项的系数绝对值的和为243,不含y 的项的系数绝对值的和为32,则a ,b ,n 的值可能为( )
A .a =2,b =-1,n =5
B .a =-2,b =-1,n =6
C .a =-1,b =2,n =6
D .a =1,b =2,n =5
二、填空题(每小题5分,共10分)
9.若(1-2x )2 004=a 0+a 1x +a 2x 2+…+a 2 004x 2 004(x ∈R ),则(a 0+a 1)+(a 0+a 2)+(a 0+a 3)+…+(a 0+a 2 004)=________.(用数字作答)
10.若多项式x 3+x 10=a 0+a 1(x +1)+a 2(x +1)2+…+a 9(x +1)9+a 10(x +1)10,则a 9=________.
11.(1-x )20的二项展开式中,x 的系数与x 9的系数之差为__________. 12.若⎝⎛⎭
⎫x -
a x 2
6
展开式的常数项为60,则常数a 的值为________.
三、解答题(每小题10分,共20分)
13.已知⎝
⎛⎭⎪⎫x -124x n
的展开式中,前三项系数的绝对值依次成等差数列,
(1)证明展开式中没有常数项; (2)求展开式中所有的有理项.
14.求0.9986的近似值,使误差小于0.001.
15.(10分)已知f (x )=(1+2x )m +(1+4x )n (m ,n ∈N *)的展开式中含x 项的系数为36,求展开式中含x 2项的系数最小值.
16.在(x -y )11的展开式中,求 (1)通项T r +1;
(2)二项式系数最大的项; (3)项的系数绝对值最大的项; (4)项的系数最大的项; (5)项的系数最小的项; (6)二项式系数的和; (7)各项系数的和.
17.已知(2x-3y)9=a0x9+a1x8y+a2x7y2+…a9y9,求:
(1)各项系数之和;
(2)所有奇数项系数之和;
(3)系数绝对值的和;
(4)分别求出奇数项的二项式系数之和与偶数项的二项式系数之和.
18.已知(1+x)+(1+x)2+…+(1+x)n=a0+a1x+a2x2+…+a n x n,若a1+a2+…+a n-1=29-n,求n.。
