正方体侧面展开图
北师大版数学七年级上册1.2.1正方体的展开图课件
4. 所有侧棱长都相等.
什么样的图形能折成棱柱?
观察下面的四个图形,想一想哪几个能围成棱柱
(1)、(3)不行
为什么(1)、(3)不行? 在(1)、(3)的基础上进行修改, 使其能围成一个棱柱
展开图能围成棱柱的条件:
1、中间部分是几个长方形,可以围成棱柱的侧面。 2、上、下底面形状大小要相同,
面 侧棱(条) 侧面(个) (个)
三棱柱
6
四棱柱
95 3 3
8 12 6 4 4
五棱柱
10 15 7 5 5
六棱柱
12 18 8 6 6
……
n棱柱
2n 3n n+2 n n
(Ⅱ)动手操作、认识棱柱
侧面
底面
1.棱柱有上下两个底面, 它们的形状相同.
2.侧面的形状都是长方形.
3.侧面数、侧棱数、底面 侧棱 边数和底面多边形的顶点
作业: 位于侧面部分的两 侧
侧面数、侧棱数、底面 边数和底面多边形的顶点数相等.
4.三习棱柱题底面1边.长3为的3cm知, 识技能1、2、3。
五、课堂小结,布置作业
侧面的动形状手都是制长方作形.一个正方体的纸盒及圆柱圆锥
1、课本P12随堂练习 1、棱柱的特征、棱柱的顶点数、棱数、面数的规律 4.三棱柱底面边长为3cm, 2、写出下面图形能折叠成什么多面体。 2、写出下面图形能折叠成什么多面体。
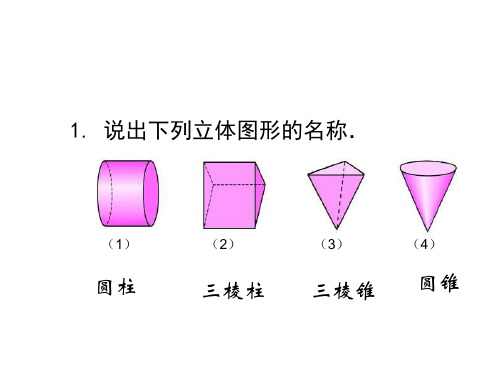
1. 说出下列立体图形的名称.
(1)
圆柱
(2)
三棱柱
(3)
三棱锥
(4)
圆锥
展开
折叠
展开 折叠
展开与折叠(1)
用一个词来形容之前的活动
有些立体图形 展开 平面图形 有些平面图形 折叠 立体图形
常见几何体的表面展开图
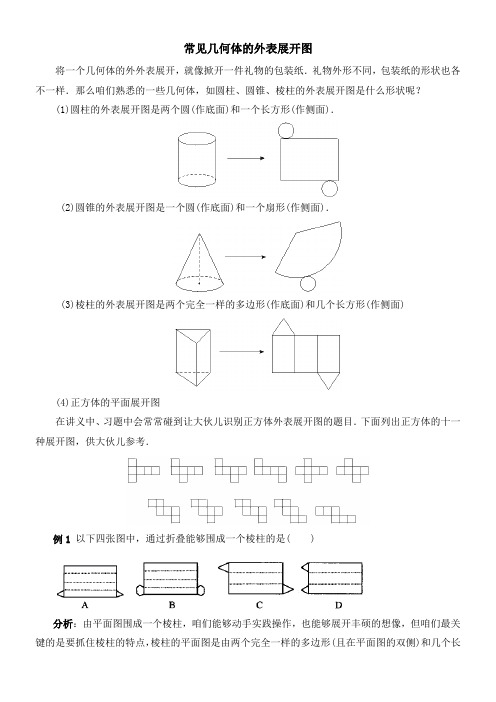
常见几何体的外表展开图将一个几何体的外外表展开,就像掀开一件礼物的包装纸.礼物外形不同,包装纸的形状也各不一样.那么咱们熟悉的一些几何体,如圆柱、圆锥、棱柱的外表展开图是什么形状呢?(1)圆柱的外表展开图是两个圆(作底面)和一个长方形(作侧面).(2)圆锥的外表展开图是一个圆(作底面)和一个扇形(作侧面).(3)棱柱的外表展开图是两个完全一样的多边形(作底面)和几个长方形(作侧面)(4)正方体的平面展开图在讲义中、习题中会常常碰到让大伙儿识别正方体外表展开图的题目.下面列出正方体的十一种展开图,供大伙儿参考.例1 以下四张图中,通过折叠能够围成一个棱柱的是( )分析:由平面图围成一个棱柱,咱们能够动手实践操作,也能够展开丰硕的想像,但咱们最关键的是要抓住棱柱的特点,棱柱的平面图是由两个完全一样的多边形(且在平面图的双侧)和几个长方形组成的.解:正确答案选C.点评:专门要注意的是两个完全一样的多边形是棱柱的上下两个底面图形(棱柱展开后,这两个图形是位于展开图的双侧),故不选D,另外定几个长方形,究竟是几个呢,它的个数确实是上下底多边形的边数,应选C.例2如以下图的平面图形是由哪几种几何体的外表展开的?(1) (2) (3)分析:找几何体的外表展开图,关键是看侧面和底面的形状.底面是圆的几何体有圆柱、圆锥、圆台.侧面是扇形的几何体是圆锥.侧面是长方形的几何体是棱柱、圆柱.解答:(1)圆锥;(2)圆柱;(3)圆台.例3如以下图,在正方体的两个相距最远的极点处停留着一只苍蝇和一只蜘蛛,蜘蛛能够从哪条最短的途径爬到苍蝇处?说明你的理由.分析:在解这道题时,正方体的展开图对解题有专门大的帮忙,由于作展开图有各类不同的方式,因此从蜘蛛到苍蝇能够用6种不同方式选择最短途径,而其中每一条途径都通过连结正方体2个极点的棱的中点.解:由于蜘蛛只能在正方体的外表爬行,因此只需作出那个正方体的展开图并用点标出苍蝇和蜘蛛的位置,依照“两点之间线段最短〞这一常识可知,连结这两个点的线段确实是最短的途径.点评:这种求最短路程是多少及求与棱的夹角是多少等问题,同窗们容易犯的错误是:用棱柱来计算路程,可求出的却不是最短的.通过对该节内容的学习,咱们必然要养成擅长观看,随时寻觅规律的良好适应,只有如此,才能把所学知识融会贯穿.。
北师大版七年级上册数学课件1.2.1正方体的展开图

提示:可以是生活中的常用物品,也可以是正方 体、长方体、圆柱、圆锥、棱柱、棱锥等几何体 或者它们的组合体。
学生合作讨论:
仔细观察,下面各种包装盒分别 下面六个正方形连在一起的图形,经折叠后能围成正方体的图形有哪几个?
开启 智慧
是什么几何体? 将下图中五角星状的图形沿虚线折叠,得到一个几何体,你在生活中见过和这个几何体形状类似的物体吗?
下列图形哪个不是长方体的表面展开图? 仔细观察,下面各种包装盒分别是什么几何体?
下列图形哪个不是长方体的表 面展开图?
B A
C
D
把下面的正三角形沿 虚线折叠后的几何体是 什么?
将下图中五角星状的图形沿虚线 折叠,得到一个几何体,你在生 活中见过和这个几何体形状类似 的物体吗?
下面六个正方形连在一起的图形,经 折叠后能围成正方体的图形有哪几个?
A
B
C
D
E
F
G
4、如图,这是一个正方体的展 开图,如果将它组成原来的正 方体,哪些点与点P重合。
5、有一个正方体,在它的各个面上分别涂了白、红、黄、兰、绿、黑六种颜色。
下面请发挥你的聪明才智,与小组内的其他同学合作,设计并制作一个模型,尽可能使设计美观、大方。
下面请发挥你的聪明才智,与小组内的其他同学合作,设计并制作一个模型,尽可能使设计美观、大方。
6、有一正方体木块,它的六个面分别标上数字1-6,下图是这个正方体木块从不同面所观察到的数字情况。
第三类,中间二连方,两侧各有二个,只有一种.
(1)如果A面在多面体的底部,哪一面会在上面?
第一章 第2节
把圆锥、圆柱的侧面展开,会得到什么图形?
正方体的11种展开图及判断方法教案-参考模板

正方体的11种展开图及判断方法教案今天这节课我分成了两大块,前一部分:学习正方体的展开图;后一部分:动手操作、验证。
因为我在课前已经布置了学生预习,“找几个正方体纸盒,把它剪开,看看可以有哪些不同的展开图?”我在检查预习作业时,我就发现有的同学已经能找出10种不同的展开图。
但有也一些学生根本就没有完成预习作业。
为了,使不同的学生在本课上都能得到不同的发展,所以我把这节课分成了上面两大板块,第一板块:我直接就将11种不同的情况的展开图出示给学生,因为好学生在课前已经完成过“剪”的操作活动,如果课上再安排去剪,对于他们来说本课对他们来说没有什么收获。
而那些没有认真去做预习的同学,往往是那些成绩暂差生,如果上课再慢慢地安照教材给他们去动手再剪,一节课下来可能无法完成“11种”不同展开图的教学任务。
我直接告诉他们这些不同的展开图,至少可以应付后面的练习,有的学生虽然没有动手剪,但是在课堂上他们可以去想象,我想这样同样也可以培养学生的空间观念。
到了六年级,我个人认为有的操作是可有可无的。
我想操作的目的也是为了不操作,最后终归要回到抽象中,比如今天的“展开图教学”,一般的教学顺序应该是找一个正方体实物剪开,观察、认识展开图;然后把几种展开图动手折叠判断看看哪些展开图能做成正方体。
最后,运用获得的一些展开图的知识去判断、练习。
我在备课时,就产生了这样的疑问:1、通过剪的操作能不能找全部11种不同的展开图吗?2、通过什么活动能让学生发现11种不同的展开图?第一个问题:我想通过剪的操作不可能得全11种展开图,难道要学生去准备11个正方体纸盒吗?况且课堂时间也不允许,因为这部分知识只有1课时。
所以,我认为正方体的11种展开图用自主探索的方法可能不太可能,所以,我就运用讲授法,直接将这个结果告诉学生。
但是我在教学这个知识点的时候并不是生硬的直接出示,我是这样教学第一部分知识的:第一板块:师:如果给你一张硬纸板,你能做成一个正方体纸盒吗?怎么做?教学长方体展开图:(这时,我先教学长方体的展开图,拿出事先准备好的长方体的展开图,重点是让学生能判断,“谁和谁是对面?”。
正方体展开图--判断哪些图形能围成正方体
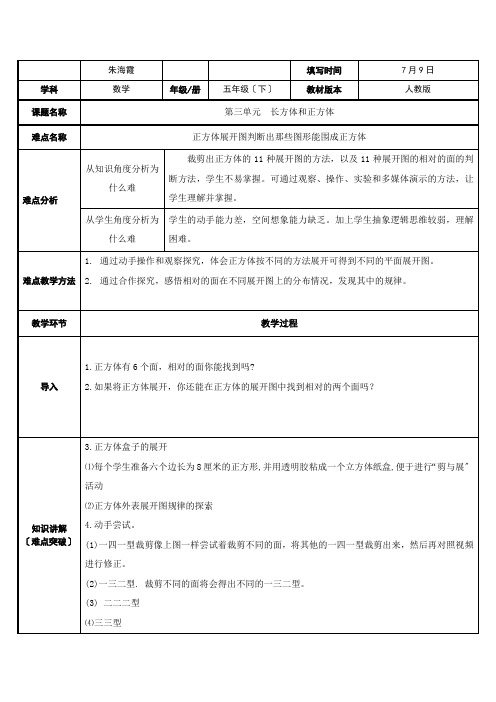
5.由平面展开图判断哪两个面是对面?
6.总结正方体展开图的11情况
正方体有6个面,12条棱,当沿着某棱将正方体剪开,可以得到正方体的展开图形,很显然,正方体的展开图形不是唯一的,但也不是无限的,事实上,正方体的展开图形有且只有11种,11种展开图形又可以分为4种类型:
⑴1141型
中间一行4个作侧面,上下两个各作为上下底面,共有6种根本图形
⑵231型
中间一行3个作侧面,共3种根本图形。
⑶222型
中间两个面,只有1种根本图形。
⑷33型
中间没有面,两行只能有一个正方形相连,只有1种根本图形。
课堂练习〔难点稳固〕7.下列图是一个正方体的展开图,请说出1号、2号、3号面相对的各是几号?
8.如果“你〞在前面,那么哪个字在后面?
小结
通过今天的学习,我们会准确识别和区别正方体的展开图,并会在展开图中找到相对面和相邻面。
其实也可以用下面的口诀来帮助记忆今天的知识哦!
正方体展有规律,十一种图看仔细;
中间四个成一行,两边各一无规矩;
二三紧连错一个,三一相连一随意;
两两相连各错一,三个两排一对齐。
一条线上不过四,田七凸凹要放弃;
相间之端是对面,间二拐角面相邻。
正方体的11种展开图形

02
CHAPTER
正方体的展开图形分类
一字型展开图形
总结词
一字型展开图形是最简单的正方体展 开图形,它由两个矩形和四个等长的 三角形组成。
详细描述
在展开后,正方体的一个面完全展开 ,与底面平行,其他五个面则形成等 长的三角形。这种展开图形通常用于 折叠正方体纸盒。
L型展开图形
总结词
L型展开图形由一个矩形和两个等长的三角形组成,展开后的形状类似于英文 字母"L"。
VS
详细描述
在正方体的展开图形中,面数相等是判断 是否能够还原成正方体的一个重要标准。 如果展开图形中的面数与正方体的面数相 等,那么这个图形就有可能通过折叠还原 成正方体。
04
CHAPTER
正方体展开图形的应用
折纸艺术
折纸艺术是一种以纸张为主要材料的艺术形式,通过折叠、剪裁、拼贴等手法创 造出各种形态和形象。正方体的展开图形在折纸艺术中有着广泛的应用,如千纸 鹤、纸盒等。
在展开后,正方体的八个角完全展开, 形成等长的三角形,同时还有一个正 方形面完全展开。这种展开图形通常 用于折叠正方体纸盒的顶部和底部以 及四个侧面。
混合型展开图形
总结词
混合型展开图形由多种形状组成,包括矩形、三角形和正方形等。
详细描述
混合型展开图形是最复杂的正方体展开图形,它由多种形状组合而成,通常用于折叠复杂的正方体纸盒结构。这 种展开图形需要较高的空间想象能力和手工技巧才能完成。
谢谢
折纸艺术不仅可以培养人的创造力和动手能力,还可以作为装饰品和礼物赠送给 亲朋好友,传递美好祝福。
空间几何教学
空间几何是数学中的一门学科,主要研究空间图形的性质和 关系。正方体的展开图形是空间几何教学中的一个重要内容 ,通过让学生亲手制作正方体的展开图形,可以帮助学生更 好地理解空间几何的概念和原理。
苏教版六年级上册数学《长方体正方体的展开图》课件

用1根长88分米的铝条焊接成一 个长方体框架模型,这个模型的长 12分米,宽6分米.可以焊多高?
方 法 二
方 法 三
88÷4=22 22-12-6=4
(12+6+x) ×4=88
动动手:
用棱长1厘米的小正方体 摆成稍大一些的正方体, 至少需要多少个小正方体? 动手摆一摆看。
复习:
1、长方体有( 6 )个面,( 12 )条棱, ( )个顶点。长方体相对的面是 8 ( 相等 )的( )形。长方体的棱分为 长方 ( )组,每组( )条棱长度相等。 3 4 2、长方体相交于同一顶点的三条棱 叫做长方体的( 长 、 宽 、 )。 高
3、判断 ①正方体的长、宽、高都相等。 (√ ) ②正方体是特殊的长方体。(√ ) ③长方体的三条棱分别叫做长、宽、 高。 ( × ) ④有两个面是正方形的长方体一定是 正方体。( × ) ⑤有三个面是正方形的长方体一定是 正方体。 (√ )
(√ )
(√ )
(√ )
(√ )
(× )
(√ )
1
5 2 3 4
方案1:正方体
1 2
方案2:长方体(一般) 方案3:长方体(特殊)
3 1 3 3 3 3 5 3 1 4 2 4 2 4 4 5 4 4
1
1
1
2
说一说,把两个长5分米,宽4 分米,高3分米的长方体拼成 一个大长方体,有几种拼法?
把一个长方体的盒子沿棱剪 开,想一想:它的展开图是什 么样子?
上 后 左 下 前 右
你的长方体展成了哪一种?
(A)
(B)
(E)
(D) (C)
下图中的那些图形可以沿虚线折叠 成长方体包装盒,先想一想,再折一折。
长方体正方体的展开图

在运输领域的应用
包装设计:利用展开图进行包 装结构设计,提高包装效率和 降低成本
集装箱设计:利用展开图进行 集装箱结构设计,提高集装箱 的装载效率和空间利用率
物流规划:利用展开图进行物 流规划,优化运输路线和降低 运输成本
仓储管理:利用展开图进行仓 储管理,提高仓储效率和降低 库存成本
在生产制造领域的应用
03
长方体和正方体的共同点:都有八个顶点、十 二条棱和六个面。
02
正方体:由六个正方形围成的立体图形,每个 面都是正方形。
04
长方体和正方体的区别:长方体的六个面形状 不同,正方体的六个面形状相同。
长方体正方体的特征
长方体:由六个长方形围成的 立体图形,相对的两个面是长 方形,其余四个面是正方形。
3
完成手绘展开图,并标注 尺寸和文字说明
6
使用CAD软件绘制展开图的方法
打开CAD软件,新建一个 文件。
在CAD中绘制长方体或正 方体的三维模型。
选择要展开的表面,点击 “展开”命令。
1
2
3
在展开的平面上绘制展开 图,可以添加尺寸和标注。
保存并关闭CAD文件。
4
5
长方体正方体的展开图的 实例分析
性。
实际应用案例2
包装设计:根据长方体正方体的展开图,设计合适的包装盒,节省材料, 提高空间利用率。
建筑设计:利用长方体正方体的展开图,设计建筑物的外墙和内部结构, 提高建筑的稳定性和美观性。
家具设计:根据长方体正方体的展开图,设计家具的各个部分,提高家具 的实用性和舒适性。
机械设计:利用长方体正方体的展开图,设计机械设备的各个部件,提高 设备的性能和可靠性。
长方体正方体的展开图的 未来发展与展望
