三角函数的图像和性质题型归纳总结
三角函数的图像与性质 知识点与题型归纳

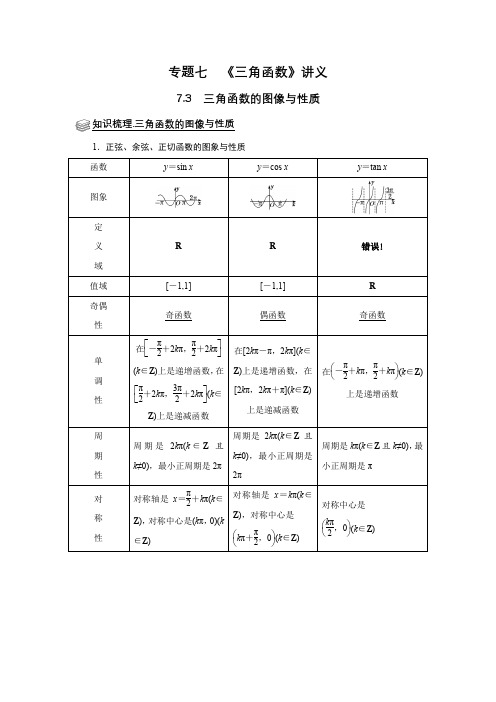
1●高考明方向1.能画出y =sin x ,y =cos x ,y =tan x 的图象, 了解三角函数的周期性.2.理解正弦函数、余弦函数在[0,2π]上的性质(如单调性、 最大值和最小值,图象与x 轴的交点等),理解正切函数在区间⎝ ⎛⎭⎪⎫-π2,π2内的单调性.★备考知考情三角函数的周期性、单调性、最值等是高考的热点,题型既有选择题、填空题、又有解答题,难度属中低档,如2014课标全国Ⅱ14、北京14等;常与三角恒等变换交汇命题,在考查三角函数性质的同时,又考查三角恒等变换的方法与技巧,注重考查函数方程、转化化归等思想方法.《名师一号》P552二、例题分析: (一)三角函数的定义域和值域 例1.(1)《名师一号》P56 对点自测3函数y =lg(sin x )+ cos x -12的定义域为____________解析 要使函数有意义必须有⎩⎪⎨⎪⎧ sin x >0,cos x -12≥0, 即⎩⎪⎨⎪⎧sin x >0,cos x ≥12,解得⎩⎪⎨⎪⎧2k π<x <π+2k π,-π3+2k π≤x ≤π3+2k π (k ∈Z).∴2k π<x ≤π3+2k π,k ∈Z.∴函数的定义域为{x |2k π<x ≤π3+2k π,k ∈Z}.例1.(2)《名师一号》P56 高频考点 例1(1) 函数y =sin x -cos x 的定义域为________.3解:(1)要使函数有意义,必须有sin x -cos x ≥0,即sin x ≥cos x ,同一坐标系中作出y =sin x ,y =cos x ,x ∈[0,2π]的图象如图所示.结合图象及正、余弦函数的周期是2π知,函数的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2k π+π4≤x ≤2k π+54π,k ∈Z .注意:《名师一号》P56 高频考点 例1 规律方法 (1)求三角函数的定义域实质就是解三角不等式(组). 一般可用三角函数的图象或三角函数线确定 三角不等式的解.例2.(1)《名师一号》P56 对点自测4函数y =2sin ⎝ ⎛⎭⎪⎫πx 6-π3(0≤x ≤9)的最大值与最小值之和为( )A .2- 3B .0C .-1D .-1- 34解:∵0≤x ≤9,∴-π3≤π6x -π3≤7π6.∴sin ⎝ ⎛⎭⎪⎫π6x -π3∈⎣⎢⎡⎦⎥⎤-32,1. ∴y ∈[-3,2],∴y max +y min =2- 3. 注意:《名师一号》P56 高频考点 例1 规律方法2 求三角函数的值域的常用方法之一: 利用sin x 和cos x 的值域(图像)直接求;例2.(2)8月月考第17题(1)17.(满分12分)已知函数22()3cos 2cos sin sin f x x x x x =++.(I )当[0,]2x π∈时,求()f x 的值域;222()3cos 2cos sin sin 12cos sin 2f xx x x x x x =++=++………2分5)2x π=++ …………3分……4分即()f x 的值域为2]+. …………………6分注意:《名师一号》P56 高频考点 例1 规律方法2 求三角函数的值域的常用方法之二: 化为求sin()=++y A x b ωϕ的值域 如:①sin cos y a x b x =+sin()y A x ϕ=+ ②22sin sin cos cos y a x b x x c x =++ sin2cos2y d x e x f =++ sin(2)y A x b ϕ=++注意弦函数的有界性!变式:《名师一号》P58 特色专题 典例1降幂 合一变换 合一变换6若函数f (x )=a sin x -b cos x 在x =π3处有最小值-2,则常数a ,b 的值是( )A .a =-1,b = 3B .a =1,b =- 3C .a =3,b =-1D .a =-3,b =1解:函数f (x )=a sin x -b cos x 的最小值为-a 2+b 2. f (x )=a 2+b 2sin(x -φ)⎝⎛⎭⎪⎫其中cos φ=a a 2+b 2,sin φ=b a 2+b 2,则⎩⎨⎧-a 2+b 2=-2,f ⎝ ⎛⎭⎪⎫π3=32a -12b =-2,解得⎩⎨⎧a =-3,b =1.【名师点评】 解答本题的两个关键:①引进辅助角,将原式化为三角函数的基本形式; ②利用正弦函数取最值的方法建立方程组.例2.(3)《名师一号》P56 高频考点 例1(2)当x ∈⎣⎢⎡⎦⎥⎤π6,7π6时,函数y =3-sin x -2cos 2x 的最小值是________,最大值是________.7解:∵x ∈⎣⎢⎡⎦⎥⎤π6,7π6,∴sin x ∈⎣⎢⎡⎦⎥⎤-12,1.又y =3-sin x -2cos 2x =3-sin x -2(1-sin 2x )=2⎝ ⎛⎭⎪⎫sin x -142+78.∴当sin x =14时,y min =78;当sin x =-12或sin x =1时,y max =2.注意:《名师一号》P56 高频考点 例1 规律方法2 求三角函数的值域的常用方法之三:把sin x 或cos x 看作一个整体,转换成二次函数求值域.练习: (补充)(1)求函数22tan 1()tan 1x f x x -=+的值域【答案】[)1,1-(2)求函数22sin 1()0,sin 22x f x x x π+⎛⎫⎛⎫=∈ ⎪ ⎪⎝⎭⎝⎭的值域8【答案】)+∞2222sin 13sin cos ()sin 22sin cos 3tan 1113tan 2tan 2tan 0,tan 0211()23tan 32tan x x x f x x x xx x x x x x f x x xπ++==+⎛⎫==+ ⎪⎝⎭⎛⎫∈∴> ⎪⎝⎭≥=注意:求三角函数的值域的常用方法之三:求三角函数的值域的常用方法: 化为求代数函数的值域注意约束条件----三角函数自身的值域!例2.(4)(补充)求函数()sin cos sin cos =+-f x x x x x 的值域【答案】12⎡⎤-+⎢⎥⎣⎦9注意:求三角函数的值域的常用方法之四: 《名师一号》P56 问题探究 问题3 如何求三角函数的值域或最值?③形如y =a sin x cos x +b (sin x ±cos x )+c 的三角函数,可先设t =sin x ±cos x ,化为关于t 的二次函数求值域(或最值).利用22sin cos 1x x +=转化为二次函数在指定区间 上的值域问题变式:求函数()sin cos sin cos +=+f x x x x x 的值域例2.(5)详见 第一章 第二讲函数值域 7.数形结合法: 例7(2)《名师一号》P14 问题探究 问题(6) 当一个函数图象可作时,通过图象可求其值域和最值;或利用函数所表示的几何意义,借助于几何方法求出函数的值域.(补充)如两点间距离、直线斜率等等求函数4sin 12cos 4+=-x y x 的值域10解:()114sin sin 4422cos 2cos 2⎛⎫⎛⎫+-- ⎪ ⎪⎝⎭⎝⎭==--x x y x x 可视作单位圆外一点12,4⎛⎫- ⎪⎝⎭P 与圆221+=x y 上的点()cos ,sin x x 所连线段斜率的2倍,设过点12,4⎛⎫- ⎪⎝⎭P 的点的直线方程为()12+=-y k x 即1204---=kx y k1=解得34=-k 或512=k 答案:35,26⎡⎤-⎢⎥⎣⎦注意:求三角函数的值域的常用方法之五: 数形结合法练习:求函数[]cos 10,sin 2-=∈-x y x x π的值域11答案:40,3⎡⎤⎢⎥⎣⎦变式:求函数cos 1,sin 222-⎡⎤=∈-⎢⎥-⎣⎦x y x x ππ的值域答案:10,2⎡⎤⎢⎥⎣⎦拓展:8月月考第16题函数22)24()2cos x x xf x x xπ+++=+的最大值是M ,最小值是m ,则M m +的值是 .22222)2sin cos 2sin 4()12cos 2cos 2cos x x xx x x x x x f x x x x x x x π+++++++===++++,记2sin ()2cos x xg x x x+=+,则()g x 是奇函数且()1()f x g x =+,所以()f x 的最大值是max 1()M g x =+,最小值是min 1()m g x =+,因为()g x 是奇函数, 所以max min ()()0g x g x +=,所以max min 1()1()2M m g x g x +=+++=.12(三)三角函数的周期性、奇偶性、对称性 例1.(1)《名师一号》P56 对点自测5设函数f (x )=sin ⎝ ⎛⎭⎪⎫2x -π2,x ∈R ,则f (x )是( )A.最小正周期为π的奇函数B.最小正周期为π的偶函数C.最小正周期为π2的奇函数D.最小正周期为π2的偶函数答案 B例1.(2)《名师一号》P57 高频考点 例3(2)(2014·新课标全国卷Ⅰ)在函数①y =cos|2x |,②y =|cos x |,③y =cos ⎝⎛⎭⎫2x +π6,④y =tan ⎝⎛⎭⎫2x -π4中,最小正周期为π的所有函数为( )A .①②③B .①③④C .②④D .①③解:由于y =cos|2x |=cos2x ,所以该函数的周期为2π2=π;由函数y =|cos x |的图象易知其周期为π;函数y =cos ⎝⎛⎭⎫2x +π6的周期为2π2=π;函数y =tan ⎝⎛⎭⎫2x -π4的周期为π2,故最小正周期为π的函数是①②③,故选A.13注意:《名师一号》P56 问题探究 问题1 如何求三角函数的周期? (1)利用周期函数的定义. (2)利用公式:y =A sin(ωx +φ)和y =A cos(ωx +φ)的最小正周期为2π|ω|, y =tan(ωx +φ)的最小正周期为π|ω|.例1.(3)《名师一号》P58 特色专题 典例2函数f(x)=sin ⎝⎛⎭⎫ωx +π3+sin ωx(ω>0)相邻两对称轴之间的距离为2,则ω=________【规范解答】 相邻两对称轴之间的距离为2,即T =4.f(x)=sin ⎝⎛⎭⎫ωx +π3+sin ωx =12sin ωx +32cos ωx +sin ωx =32sin ωx +32cos ωx =3sin ⎝⎛⎭⎫ωx +π6,又因为f(x)相邻两条对称轴之间的距离为2,所以T =4,所以2πω=4,即ω=π2.注意:【名师点评】 函数f(x)=A sin (ωx +φ),f(x)=A cos (ωx +φ)图象上一个最高点和它相邻的最低点的横坐标之差的绝对值14是函数的半周期π|ω|,纵坐标之差的绝对值是2A .在解决由三角函数图象确定函数解析式的问题时,要注意使用好函数图象显示出来的函数性质、函数图象上特殊点的坐标及两个坐标轴交点的坐标等.练习:《加加练》P3 第11题例2.(1)《名师一号》P57 高频考点 例3(1)(1)若函数f (x )=sin x +φ3(φ∈[0,2π])是偶函数,则φ=( ) A.π2 B.2π3 C.3π2 D.5π3解: (1)∵f (x )=sin x +φ3是偶函数,∴f (0)=±1.∴sin φ3=±1,∴φ3=k π+π2(k ∈Z).∴φ=3k π+3π2(k ∈Z).又∵φ∈[0,2π],∴当k =0时,φ=3π2.故选C.15变式:若函数f (x )=sin x +φ3(φ∈[0,2π])是奇函数,则φ=?例2.(2)《名师一号》P57 高频考点 例3(3)(3)如果函数y =3cos(2x +φ)的图象关于点⎝ ⎛⎭⎪⎫4π3,0中心对称,那么|φ|的最小值为( ) A.π6 B.π4 C.π3 D.π2解:(3)由题意得3cos ⎝⎛⎭⎫2×4π3+φ=3cos ⎝⎛⎭⎫2π3+φ+2π =3cos ⎝⎛⎭⎫2π3+φ=0,∴2π3+φ=k π+π2,k ∈Z. ∴φ=k π-π6,k ∈Z ,取k =0,得|φ|的最小值为π6.注意:【规律方法】(1)若f (x )=A sin(ωx +φ)为偶函数,则当x =0时,f (x )取得最大或最小值,若f (x )=A sin(ωx +φ)为奇函数,则当x =0时,f (x )=0.(2)对于函数y =A sin(ωx +φ),其对称轴一定经过图象的最高点或最低点,对称中心一定是函数的零点,因此在判断16直线x =x 0或点(x 0,0)是否是函数的对称轴或对称中心时,可通过检验f (x 0)的值进行判断. 《名师一号》P56 问题探究 问题4如何确定三角函数的对称轴与对称中心?若f (x )=A sin(ωx +φ)为偶函数, 则当x =0时,f (x )取得最大值或最小值.若f (x )=A sin(ωx +φ)为奇函数, 则当x =0时,f (x )=0. 如果求f (x )的对称轴,只需令ωx +φ=π2+k π(k ∈Z),求x .(补充)结果写成直线方程! 如果求f (x )的对称中心的横坐标,只需令ωx +φ=k π(k ∈Z)即可. (补充)结果写点坐标!同理对于y =A cos(ωx +φ),可求其对称轴与对称中心, 对于y =A tan(ωx +φ)可求出对称中心.练习1:《名师一号》P58 特色专题 典例3已知f(x)=sin x +3cos x(x ∈R),函数y =f (x +φ)⎝⎛⎭⎫|φ|≤π2为偶函数,则φ的值为________.17【规范解答】 先求出f (x +φ)的解析式,然后求解.∵f (x )=sin x +3cos x =2sin ⎝⎛⎭⎫x +π3. ∴f (x +φ)=2sin ⎝⎛⎭⎫x +φ+π3. ∵函数f (x +φ)为偶函数,∴φ+π3=π2+k π,k ∈Z ,即φ=π6+k π(k ∈Z).又∵|φ|≤π2,∴φ=π6.练习2:《计时双基练》P247 第3题(四)三角函数的单调性 例1.(1)《名师一号》P56 对点自测6下列函数中,周期为π,且在⎣⎡⎦⎤π4,π2上为减函数的是( )A .y =sin ⎝⎛⎭⎫2x +π2B .y =cos ⎝⎛⎭⎫2x +π2C .y =sin ⎝⎛⎭⎫x +π2D .y =cos ⎝⎛⎭⎫x +π2解析 由函数的周期为π,可排除C ,D.又函数在⎣⎡⎦⎤π4,π2上为减函数,排除B ,故选A.18练习1:《计时双基练》P247 第7题函数y cos x π⎛⎫=- ⎪⎝⎭24的单调递减区间为练习2:《加加练》P1 第11题(2)《名师一号》P57 高频考点 例2已知函数f (x )=4cos ωx ·sin ⎝⎛⎭⎫ωx +π4(ω>0)的最小正周期为π. (1)求ω的值;(2)讨论f (x )在区间⎣⎡⎦⎤0,π2上的单调性.解:(1)f (x )=4cos ωx ·sin ⎝⎛⎭⎫ωx +π4=22sin ωx ·cos ωx +22cos 2ωx =2(sin2ωx +cos2ωx )+2=2sin ⎝⎛⎭⎫2ωx +π4+ 2. 因为f (x )的最小正周期为π,且ω>0.从而有2π2ω=π,故ω=1.(2)由(1)知,f (x )=2sin ⎝⎛⎭⎫2x +π4+ 2. 若0≤x ≤π2,则π4≤2x +π4≤5π4.当π4≤2x +π4≤π2,即0≤x ≤π8时,f (x )单调递增; 当π2≤2x +π4≤5π4,即π8≤x ≤π2时,f (x )单调递减.19综上可知,f (x )在区间⎣⎡⎦⎤0,π8上单调递增, 在区间⎣⎡⎦⎤π8,π2上单调递减.注意:《名师一号》P56 问题探究 问题2 如何求三角函数的单调区间?(1)求函数的单调区间应遵循简单化原则,将解析式先化简,并注意复合函数单调性规律“同增异减”.(2)求形如y =A sin(ωx +φ)或y =A cos(ωx +φ)(其中,ω>0)的单调区间时,要视“ωx +φ”为一个整体,通过解不等式求解.但如果ω<0,那么一定先借助诱导公式将ω化为正数,防止把单调性弄错.例2.《名师一号》P58 特色专题 典例4(2014·全国大纲卷)若函数f (x )=cos2x +a sin x 在区间⎝ ⎛⎭⎪⎫π6,π2是减函数,则a 的取值范围是________.【规范解答】 先化简,再用换元法求解. f (x )=cos2x +a sin x =1-2sin 2x +a sin x .20令t =sin x ,∵x ∈⎝⎛⎭⎫π6,π2, ∴t ∈⎝⎛⎭⎫12,1.∴g (t )=1-2t 2+at =-2t 2+at +1⎝⎛⎭⎫12<t <1, 由题意知-a 2×(-2)≤12,∴a ≤2.∴a 的取值范围为(-∞,2].课后作业一、计时双基练P247 基础1-11、 课本P56变式思考1二、计时双基练P247培优1-4课本P56变式思考2、3 预习 第五节练习:1、设函数f (x )=2sin(2πx +5π).若对任意x ∈R ,都有f (x 1)≤f (x )≤f (x 2)成立,则|x 1-x 2|的最小值为( )A .4B .2C .1 D.1221 分析:∵f (x )的最大值为2,最小值为-2,∴对∀x ∈R ,-2≤f (x )≤2.取到最值时x =2π+k π,|x 1-x 2|取最小值,即f (x 1)为最小值,f (x 2)为最大值且(x 1,f (x 1)),(x 2,f (x 2))为相邻的最小(大)值点,即半个周期.解析:f (x )的周期T =4,|x 1-x 2|min =2T =2. 故选B.2、为了使函数)0(sin >=ωωx y 在区间]1,0[上至少出现50次最大值,求ω的最小值。
三角函数图像与性质知识点总结

三角函数图像与性质知识点总结The Standardization Office was revised on the afternoon of December 13, 2020函数图像与性质知识点总结一、三角函数图象的性质 1.“五点法”描图(1)y =sin x 的图象在[0,2π]上的五个关键点的坐标为(0,0) ⎝ ⎛⎭⎪⎪⎫π2,1 (π,0)⎝ ⎛⎭⎪⎪⎫32π,-1 (2π,0) (2)y =cos x 的图象在[0,2π]上的五个关键点的坐标为 (0,1),⎝ ⎛⎭⎪⎪⎫π2,0,(π,-1),⎝ ⎛⎭⎪⎪⎫3π2,0,(2π,1)2.三角函数的图象和性质函数 性质y =sin x y =cos x y =tan x 定义域 R R{x |x ≠k π+π2,k∈Z}图象值域[-1,1][-1,1]R对称性对称轴: x =k π+π2(k ∈Z);对称轴:x =k π(k ∈Z) 对称中心:对称中心:⎝ ⎛⎭⎪⎪⎫k π2,0 (k ∈Z)3.一般地对于函数(),如果存在一个非零的常数,使得当取定义域内的每一个值时,都有f(x+T)=f(x),那么函数f(x)就叫做周期函数,非零常数T 叫做这个函数的周期,把所有周期中存在的最小正数,叫做最小正周期(函数的周期一般指最小正周期)4.求三角函数值域(最值)的方法:(1)利用sin x、cos x的有界性;关于正、余弦函数的有界性由于正余弦函数的值域都是[-1,1],因此对于∀x∈R,恒有-1≤sin x≤1,-1≤cos x≤1,所以1叫做y=sin x,y=cos x的上确界,-1叫做y=sin x,y=cos x的下确界.(2)形式复杂的函数应化为y =A sin(ωx +φ)+k 的形式逐步分析ωx +φ的范围,根据正弦函数单调性写出函数的值域;含参数的最值问题,要讨论参数对最值的影响.(3)换元法:把sin x 或cos x 看作一个整体,可化为求函数在区间上的值域(最值)问题.利用换元法求三角函数最值时注意三角函数有界性,如:y =sin 2x -4sin x +5,令t =sin x (|t |≤1),则y =(t -2)2+1≥1,解法错误.5.求三角函数的单调区间时,应先把函数式化成形如y =A sin(ωx +φ) (ω>0)的形式,再根据基本三角函数的单调区间,求出x 所在的区间.应特别注意,应在函数的定义域内考虑.注意区分下列两题的单调增区间不同;利用换元法求复合函数的单调区间(要注意x 系数的正负号) (1)y =sin ⎝ ⎛⎭⎪⎪⎫2x -π4;(2)y =sin ⎝ ⎛⎭⎪⎪⎫π4-2x .6、y =A sin(ωx +φ)+B 的图象求其解析式的问题,主要从以下四个方面来考虑:①A 的确定:根据图象的最高点和最低点,即A =最高点-最低点2;②B 的确定:根据图象的最高点和最低点,即B =最高点+最低点2;③ω的确定:结合图象,先求出周期,然后由T =2πω(ω>0)来确定ω;④φ的确定:把图像上的点的坐标带入解析式y =A sin(ωx +φ)+B ,然后根据φ的范围确定φ即可,例如由函数y =A sin(ωx +φ)+K 最开始与x 轴的交点(最靠近原点)的横坐标为-φω(即令ωx +φ=0,x =-φω)确定φ.二、三角函数的伸缩变化先平移后伸缩sin y x =的图象ϕϕϕ<−−−−−−−→向左(>0)或向右(0)平移个单位长度得sin()y x ϕ=+的图象()ωωω−−−−−−−−−→横坐标伸长(0<<1)或缩短(>1)1到原来的纵坐标不变 得sin()y x ωϕ=+的图象()A A A >−−−−−−−−−→纵坐标伸长(1)或缩短(0<<1)为原来的倍横坐标不变 得sin()y A x ωϕ=+的图象(0)(0)k k k ><−−−−−−→ 得sin()y A x k ϕ=++的图象. 先伸缩后平移sin y x =的图象(1)(01)A A A ><<−−−−−−−−−→纵坐标伸长或缩短为原来的倍(横坐标不变)得sin y A x =的图象(01)(1)1()ωωω<<>−−−−−−−−−→横坐标伸长或缩短到原来的纵坐标不变 得sin()y A x ω=的图象(0)(0)ϕϕϕω><−−−−−−−→向左或向右平移个单位得sin ()y A x x ωϕ=+的图象(0)(0)k k k ><−−−−−−−→向上或向下平移个单位长度得sin()y A x k ωϕ=++的图象. .。
三角函数的图像与性质知识点及题型归纳总结

三角函数的图像与性质知识点及题型归纳总结知识点讲解1.“五点法”作图原理在确定正弦函数])2,0[(sin π∈=x x y 的图像时,起关键作用的5个点是)0,2(),1,23(),0,(),1,2(),0,0(ππππ-.在确定余弦函数])2,0[(cos π∈=x x y 的图像时,起关键作用的5个点是)1,2(),0,23(),1,(),0,2(),1,0(ππππ-.2.3.)sin(ϕ+=wx A y 与)0,0)(cos(>>+=w A wx A y ϕ的图像与性质 (1)最小正周期:wT π2=. (2)定义域与值域:)sin(ϕ+=wx A y ,)ϕ+=wx A y cos(的定义域为R ,值域为[-A ,A ]. (3)最值假设00>>w A ,. ①对于)sin(ϕ+=wx A y ,⎪⎩⎪⎨⎧-∈+-=+∈+=+;)(22;)Z (22A Z k k wx A k k wx 时,函数取得最小值当时,函数取得最大值当ππϕππϕ ②对于)ϕ+=wx A y cos(,⎩⎨⎧-∈+=+∈=+;)(2;)Z (2A Z k k wx A k k wx 时,函数取得最小值当时,函数取得最大值当ππϕπϕ (4)对称轴与对称中心. 假设00>>w A ,. ①对于)sin(ϕ+=wx A y ,⎪⎪⎩⎪⎪⎨⎧+==+∈=+=+=±=+∈+=+).0,()sin(0)sin()()sin(1)sin()(2000000x wx y wx Z k k wx xx wx y wx Z k k wx 的对称中心为时,,即当的对称轴为时,,即当ϕϕπϕϕϕππϕ ②对于)ϕ+=wx A y cos(,⎪⎪⎩⎪⎪⎨⎧+==+∈+=+=+=±=+∈=+).0,()cos(0)cos()(2)cos(1)cos()(000000x wx y wx Z k k wx x x wx y wx Z k k wx 的对称中心为时,,即当的对称轴为时,,即当ϕϕππϕϕϕπϕ 正、余弦曲线的对称轴是相应函数取最大(小)值的位置.正、余弦的对称中心是相应函数与x 轴交点的位置.(5)单调性. 假设00>>w A ,. ①对于)sin(ϕ+=wx A y ,⎪⎩⎪⎨⎧⇒∈++∈+⇒∈++-∈+.)](223,22[)](22,22[减区间增区间;Z k k k wx Z k k k wx ππππϕππππϕ ②对于)ϕ+=wx A y cos(,⎩⎨⎧⇒∈+∈+⇒∈+-∈+.)](2,2[)](2,2[减区间增区间;Z k k k wx Z k k k wx πππϕπππϕ (6)平移与伸缩由函数x y sin =的图像变换为函数3)32sin(2++=πx y 的图像的步骤;方法一:)322(ππ+→+→x x x .先相位变换,后周期变换,再振幅变换,不妨采用谐音记忆:我们“想欺负”(相一期一幅)三角函数图像,使之变形.−−−−−→−=个单位向左平移的图像3sin πx y 的图像)3sin(π+=x y 12−−−−−−−−→所有点的横坐标变为原来的纵坐标不变的图像)32sin(π+=x y 2−−−−−−−−−→所有点的纵坐标变为原来的倍横坐标不变的图像)32sin(2π+=x y−−−−−→−个单位向上平移33)32sin(2++=πx y方法二:)322(ππ+→+→x x x .先周期变换,后相位变换,再振幅变换.的图像x y sin =12−−−−−−−−→所有点的横坐标变为原来的纵坐标不变−−−−−→−=个单位向左平移的图像62sin πx y的图像)22sin()6(2sin ππ+=+=x x y 2−−−−−−−−−→所有点的纵坐标变为原来的倍横坐标不变−−−−−→−+=各单位向上平移的图像3)32sin(2πx y 3)32sin(2++=πx y注:在进行图像变换时,提倡先平移后伸缩(先相位后周期,即“想欺负”),但先伸缩后平移(先周期后相位)在题目中也经常出现,所以必须熟练掌握,无论哪种变化,切记每一个变换总是对变量x 而言的,即图像变换要看“变量x ”发生多大变化,而不是“角ϕ+wx ”变化多少.例如,函数x y 2sin =的图像向右平移6π个单位,得到的图像表达式是)32sin()6(2sin ππ-=-=x x y ,而不是)62sin(π-=x y ;再如,将图像)6sin(π+=x y 上各点的横坐标扩大到原来的2倍(纵坐标不变),得到的函数图像表达式是)621sin(x x y +=,而不是)6(21sin π+=x y .此点要引起同学们的的别注意.题型归纳及思路提示思路提示一般将所给函数化为)sin(ϕ+=wx A y 或)cos(ϕ+=wz A y ,0.0>>w A ,然后依据x y x y cos ,sin ==的性质整体求解.题型1 三角函数性质的应用一、函数的奇偶性例4.16函数)0)(sin(πϕϕ≤≤+=x y 是R 上的偶函数,则ϕ等于( ) A .0 B .4π C .2πD .π 解析 因为函数)sin(ϕ+=x y 是R 上的偶函数,所以其图像关于y 轴对称,有正弦函数的对称性知,当0=x 时,1sin ±=ϕ,又πϕ≤≤0,所以2πϕ=.故选C.评注 由x y sin =是奇函数和x y cos =是偶函数可拓展得到关于三角函数奇偶性的重要结论: (1)若)sin(ϕ+=x A y 为奇函数,则)(Z k k ∈=πϕ; (2)若)sin(ϕ+=x A y 为偶函数,则)(2Z k k ∈+=ππϕ; (3)若)cos(ϕ+=x A y 为奇函数,则)(2Z k k ∈+=ππϕ;(4)若)cos(ϕ+=x A y 为偶函数,则)(Z k k ∈=πϕ; 若)tan(ϕ+=x A y 为奇函数,则)(2Z k k ∈=πϕ,该函数不可能为偶函数. 变式1 已知R a ∈,函数)(sin )(R x a x x f ∈-=为奇函数,则a 等于( ). A .0 B .1 C .-1 D .1±变式2 设R ∈ϕ,则“0=ϕ”是“))(cos()(R x x x f ∈+=ϕ为偶函数”的( ).A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不比哟啊条件 变式3设)sin()(ϕ+=wx x f ,其中0>w ,则)(x f 是偶函数的充要条件是( ).A .1)0(=fB . 0)0(=fC . 1)0(='fD . 0)0(='f 例4.17设函数))(22sin()(R x x x f ∈-=π,则)(x f 是( ).A. 最小正周期为π的奇函数B. 最小正周期为π的偶函数C. 最小正周期为2π的奇函数 D. 最小正周期为2π的偶函数解析 x x x f 2cos )22sin()(-=-=π,所以是最小正周期为x 的偶函数.故选B.变式1 若函数)(21sin )(2R x x x f ∈-=,则)(x f 是( )A. 偶函数且最小正周期为πB. 奇函数且最小正周期为πC. 偶函数且最小正周期为π2D. 奇函数且最小正周期为π2变式2 下列函数中,既是)2,0(π上的增函数,又是以π为周期的偶函数的是( )A .x y 2cos =B .x y 2sin =C .x y cos =D .x y sin = 二、函数的周期性 例4.18函数)62cos()62sin(ππ++=x x y 的最小正周期为( )A .2π B .4πC .π2D .π 解析 函数)34sin(21)62cos()62sin(πππ+=++=x x x y ,242ππ==T .故选A评注 关于三角函数周期的几个重要结论:(1)函数b wx A y b wx A y b wx A y ++=++=++=)tan(,)cos(,)sin(ϕϕϕ的周期分别为wT π2=,wT π=. (2)函数)cos(,)sin(ϕϕ+=+=wx A y wx A y ,)tan(ϕ+=wx A y 的周期均为wT π=(3)函数)0()cos(),0()sin(≠++=≠++=b b wx A y b b wx A y ϕϕ的周期均wT π2=.变式1 函数)32cos()62sin(ππ++=x x y 的最小正周期和最大值分别为( )A .1,πB .2,πC .1,2πD .2,2π变式2 已知函数))(cos (sin sin )(R x x x x x f ∈-=,则)(x f 的最小正周期为_____. 变式3 设函数x x x f 3sin 3sin )(+=,则)(x f 为( )A. 周期函数,最小正周期为3πB. 周期函数,最小正周期为32πC. 周期函数,最小正周期为π2D. 非周期函数 二、函数的单调性 例4.19函数]),0[)(26sin(2ππ∈-=x x y 为增函数的区间是( )A .]3,0[πB .]127,12[ππC .]65,3[ππD .],65[ππ解析 因为)62sin(2)26sin(2ππ--=-=x x y ,所以)26sin(2x y -=π的递增区间实际上是 )62sin(2π-=x y 的递减区间.令)(2326222Z k kx x k ∈+≤-≤+ππππ, 解得)(653Z k k x k ∈+≤≤+ππππ. 令0=k ,得653ππ≤≤x ,又因为],0[π∈x , 所以653ππ≤≤x .即函数]),0[)(26sin(2ππ∈-=x x y 的增区间为]65,3[ππ.故选C评注 三角函数的单调性,需将函数)sin(ϕ+=wx A y 看成由一次函数和正弦函数组成的复合函数,利用复合函数单调区间的单调方法转化为解一元一次不等式.如函数)0,0)(sin(>>+=w A wx A y ϕ的单调区间的确定基本思想是吧ϕ+wx 看做是一个整体,如由)(2222Z k kx wx k ∈+≤+≤-πϕππ解出x 的范围,所得区间即为增区间;由)(23222Z k kx wx k ∈+≤+≤+πϕππ解出x 的范围,所得区间即为减区间.若函数)sin(ϕ+=wx A y 中0,0>>w A ,可用诱导公式将函数变为)sin(ϕ---=wx A y ,则)sin(ϕ--=wx A y 的增区间为原函数的减区间,减区间为原函数的的增区间.如)4sin()4sin(ππ--=-=x x y ,令22422πππππ+≤-≤-k x k ,即)(43242Z k k x k ∈+≤≤-ππππ,可得)](432,42[Z k k k ∈+-ππππ为原函数的减区间.对于函数)tan(),cos(ϕϕ+=+=wx A y wx A y 的单调性的讨论与以上类似处理即可. 变式1 若函数)(sin x f x y +=在]43,4[ππ-内单调递增,则)(x f 可以是( ).A .1B .x cosC .x sinD .x cos -变式2 已知0>w ,函数)4sin()(π+=wx x f 在),2(ππ上单调递减,则w 的取值范围是( ) A .]45,21[ B .]43,21[ C .]21,0( D .]2,0( 变式3 已知函数)0(,),3cos()3cos(sin 3)(>∈-+++=w R x wx wx wx x f ππ.(1)求函数)(x f 的值域; (2)若)(x f 的最小正周期为]2,0[,2ππ∈x ,求)(x f 的单调递减区间. 四、函数的对称性(对称轴、对称中心) 例4.30函数)32sin(π+=x y 图像的对称轴方程可能是( )A .6π-=x B .12π-C .6π=x D .12π=x解析 解法一:已知x y sin =的对称轴方程是)(2Z k k x ∈+=ππ令)(232Z k k x ∈+=+πππ,得)(122Z k k x ∈+=ππ, 当0=k 时,12π=x ,故选D.解法二,当6π-=x 时,032=+πx .其正弦值为0;当12π-=x 时,632ππ=+x ,其正弦值不等于1或-1当6π=x 时,3232ππ=+x ,其正弦值不等于1或-1 当12π=x 时,232ππ=+x ,这时12sin=π.故选D评注 关于三角函数对称的几个重要结论; (1)函数x y sin =的对称轴为)(2Z k k x ∈+=ππ,对称中心为))(0.(Z k k ∈π;(2)函数x y cos =的对称轴为)(Z k k x ∈=π,对称中心为))(0,2(Z k k ∈+ππ;(3)函数x y tan =函数无对称轴,对称中心为))(0,2(Z k k ∈π;(4)求函数)0()sin(≠++=w b wx A y ϕ的对称轴的方法;令)(2Z k k wx ∈+=+ππϕ,得)(2Z k w k x ∈-+=ϕππ;对称中心的求取方法;令)(Z k k wx ∈=+πϕ,得wk x ϕπ-=,即对称中心为)(b wk ,ϕπ-.(5)求函数)0()cos(≠++=w b wx A y ϕ的对称轴的方法;令)(Z k k wx ∈=+πϕ得wk x ϕππ-+=2,即对称中心为))(,2(Z k b wk ∈-+ϕππ变式1 已知函数)0)(3sin()(>+=w wx x f π的最小正周期为π,则该函数的图像( ).A .关于点)0,3(π对称 B .关于直线4π=x 对称 C .关于点)0,4(π对称 D .关于直线3π=x 对称变式2 )4sin(π-=x y 的图像的一个对称中心是( )A .)0,(π-B .)0,43(π-C . )0,43(πD .)0,2(π变式3 52sin52cos xx y +=的图像中,相邻两条对称轴之间的距离是______. 变式4 将函数x x y cos 3sin -=的图像沿x 轴向右平移a 个单位)0(>a ,所得图像关于y 轴对称,则a 的最小值是( ).A .67πB .2πC .6πD .3π五、三角函数性质的综合 思路提示三角函数的性质(如奇偶性、周期性、单调性、对称性)中,尤为重要的是对称性.因为对称性⇒奇偶性(若函数图像关于坐标原点对称,则函数)(x f 为奇函数;若函数图像关于y 轴对称,则函数)(x f 为偶函数);对称性⇒周期性(相邻的两条对称轴之间的距离是2T ;相邻的对称中心之间的距离为2T;相邻的对称轴与对称中心之间的距离为4T);对称性⇒单调性(在相邻的对称轴之间,函数)(x f 单调,特殊的,若0,0),sin()(>>=w A wx A x f ,函数)(x f 在],[21θθ上单调,且],[021θθ∈,设{}21,max θθθ=,则θ≥4T深刻体现了三角函数的单调性与周期性、对称性之间的紧密联系)例4.21设x b x a x f 2cos 2sin )(+=,其中,0,,≠∈ab R b a 若)6()(πf x f ≤对一切R x ∈恒成立,则①;0)1211(=πf ②)5()107(ππf f <; ③)(x f 既不是奇函数也不是偶函数; ④)(x f 的单调递增区间是)](32,6[Z k k k ∈++ππππ; ⑤存在经过点),(b a 的直线与函数)(x f 的图像不相交. 以上结论正确的是_______(写出所有正确命题的序号)分析 函数)2sin()(22ϕ++=x b a x f ,a b =ϕtan ,其中一条对称轴为6π=x ,函数的最小正周期π=T ,通过对称轴⇒对称中心(对称轴与零点相距4T的奇数倍)通过对称轴⇒奇偶性(若函数)(x f 为奇函数,则6π等于4T 的奇数倍;若函数)(x f 为偶函数,则6π等于4T的偶数倍);通过对称性⇒单调性(在相邻的两条对称轴之间,)(x f 单调递增或单调递减).解析 )2sin()(22ϕ++=x b a x f ,其中a b =ϕtan ,))6((πf x f ≤对一切R x ∈恒成立,知直线6π=x 是)(x f 的对称轴,又)(x f 的最小正周期为π. 对于①:)436()1211(πππ+=f f 可看做6π=x ,加了43个周期所对应的函数值,所以0)1211(=πf .故①正确对于②:函数)(x f y =周期2π=T ,因为25107πππ=-,所以)5()107(ππf f =,因此)5()107(ππf f <错误,故②不正确. 对于③:因为6π既不是4T 的奇倍数,也不是4T的偶倍数,所以函数)(x f 的图像既不关于原点对称,也不关于y 轴对称,所以函数)(x f 既不是奇函数也不是偶函数,故③正确 对于④:依题意,函数)(x f 相邻两条对称轴32,621ππ==x x ,在区间)](32,6[Z k k k ∈++ππππ上函数)(x f 单调,不能确定是单调递增,还是单调递减,故④不正确.对于⑤:因为x b x a x f 2cos 2sin )(+=)2sin(22ϕ++=x b a (其中ab =ϕtan ),所以22)(b a x f +≤,又0≠ab ,所以22b a b +≤,因此经过点),(b a 的直线与函数)(x f 的图像相交,⑤不正确,应填①③. 例4.22设)2cos(sin )6cos(4)(ππ+--=wx wx wx x f ,其中0>w(1)求)(x f 的值域; (2)若)(x f y =在区间]2,23[ππ-上为增函数,求w 的最大值. 解析12sin 32cos 2cos 12sin 32cos sin 2cos sin 322cos sin )6sin sin 6cos(cos 42cos sin )6cos(4)(12+=+-+=++=++=+-=wx wx wx wx wxwx wx wx wxwx wx wx wxwx wx x f πππ)(因为]1,1[2sin -∈wx 所以函数)(x f 的值域为]31,31[+-. (2)解法一:12sin 3)(+=wx x f ,由)(x f y =在区间]2,23[ππ-上为增函数,的)0](2,2[],3[>-⊆-w w w ππππ 故⎪⎩⎪⎨⎧≤-≥-223ππwx wx ,得610≤<w ,则w 的最大值为61. 解法二:由12sin 3)(+=wx x f )0(>w 在区间]2,23[ππ-上为增函数,含原点的增区间的对称型可知函数)(x f 在]23,23[ππ-上也为增函数,故π32≥T ,即π6≥T ,得ππ622≥w ,故610≤<w ,则w 的最大值为61评注 一般的,若))((R x x f ∈为奇函数,在],[21θθ上为增函数,其中210θθ<<,若令},max{21θθθ=,则4T≤θ,即可求出w 的范围. 变式1 已知函数)sin(2)(wx x f =,其中常数0>w ,若)(x f y =在]32,4[ππ-上单调递增,求w 的取值范围.变式2 已知函数)0)(sin(2)(>=w wx x f ,)3()6(ππf f =在]4,3[ππ-上的虽小值为-2,则w 的最小值为_____.例4.23若)0)(3sin()(>+=w wx x f π,)3()6(ππf f =且在)3,6(ππ上有最小值无最大值,则______. 解析 依题意,如图4-24所示,在4236πππ=+=x 处)(x f 取得最小值,故Zk k w ∈+=+,2323ππππ得3148+=k w.取0=k ,得314=w .评注 本题融汇了三角函数)sin()(ϕ+=wx x f 的最值(对称轴)、周期性、单调性之间的相互关系与转化 题型2 根据条件确定解析式方向一:“知图求式”,即已知三角形函数的部分图像,求函数解析式. 思路提示已知函数图像求函数)0,0)(sin(>>+=w A wx A y ϕ的解析式时,常用的解析方法是待定系数法,由图中的最大值或最小值确定A ,由周期确定w ,由适合解析式点的坐标确定ϕ,但有图像求得的)0,0)(sin(>>+=w A wx A y ϕ的解析式一般不唯一,只有限定ϕ的取值范围,才能得出唯一解,将若干个点代入函数式,可以求得相关特定系数ϕ,,w A ,这里需要注意的是,要认清选择的点属于“五点”中的哪一个位置点,并能正式代入式中,依据五点列表法原理,点的序号与式子的关系是:“第一点”(及图像上升时与x 轴的交点)为0=+ϕwx ;“第二点”(即图像曲线的最高点)为2πϕ=+wx ;“第三点”(及图像下降时与轴的交点),为πϕ=+wx ;“第四点”(及图像曲线的最低点)为23πϕ=+wx ;“第五点”(及图像上升时与x 轴的交点)为πϕ2=+wx .例4.24函数),)(2(sin )(R A x A x f ∈+=ϕϕ的部分图像如图4-25所示,那么)0(f =( A .21-B .-1C .23-D .3-分析 对于)sin(ϕ+=wx A y 的解析式的确定,通过最值确定A ,周期T 确定w ,特征点(尤其是极值点)来确定ϕ;对于零点要分析向上零点还是向下零点. 解析 解法一:依题意Z k k A ∈+=+=,2232,2ππϕπ得Z k k ∈-=,62ππϕ, 所以1)62sin(2sin 2)0(-=-==ππϕk f ,故选B解法二:由函数)2(sin )(ϕ+=x A x f ,得π=T ,则相邻的零点与对称轴之间的距离为44π=T ,因此图中向上的零点是120π=x ,则满足0)122sin()12(=+⨯=ϕππA f 所以.,62Z k k ∈-=ππϕ故1)62sin(2sin 2)0(-=-==ππϕk f ,故选B评注 对于三角函数问题中的“知图求式”(及其性质),应重点关注以下方面 (1)周期(可推出w 的值域范围) (2)振幅(可推出A (A >0))(3)特征点(可形成三角方程,以求ϕ的值)对于本题代入零点)0,(0x ,(0x 为上零点),则满足0)sin(0=+ϕwx A ,所以)sin()sin(sin )0(,,2000wx A wx A A f Z k wx k -=-==∈-=ϕπϕ1)122sin(2-=⨯-=π,对于正弦型函数),0)(sin()(R w wx A x f ∈>+=ϕϕ,若已知上零点0x ,则)sin()0(0wx A f -=.同理,若已知下零点0x ',则)sin()0(0x w A f '=. 变式一 函数0,0,,,)(sin()(>>+=w A w A wx A x f是常数ϕϕ所示,则=)0(f _______.变式二 已知函数)cos()(ϕ+=wx A x f 的图像如图4-27所示,32)(-=πf ,则=)0(f ( ) A .32- B .32C .21- D .21例4.25已知函数),0,0)(sin(πϕϕ<>>+=w A wx A y 的部分图像如图4-28所示,求函数)(x f 的解析式.分析 有最小值为-2确定A ,由周期确定w ,但本题的周期不易求解,我们可抓住,2127T >π,且12743π>T ,建立周期 T 的不等关系,从而得到w 的取值范围,在建立w 的等量关 系(根据零点),最终建立求得w ,而ϕ的确定可通过特征点(0,1)得到.解析 有图知2=A ,将点(0,1),代入)sin(ϕ+=wx A y 中,得ϕsin 21=,即21sin =ϕ,又πϕπ<<-,且(0,1)点在函数的单调增区间上,故6πϕ=,又431272T T <<π,得6797π<<T T ,又因为wT π2=,得67297ππ<<w T ,故718712<<w ,又点)0,127(π-在函数图像上,且127π-为函数)(x f 的下零点,所以Z k k ∈+=+-,26127ππππ,解得Z k k w ∈--=,710724,因此7187********<--<k ,得121167-<<-k ,又Z k ∈,因此1-=k ,此时2=w . 所以).62sin(2)(π+=x x f变式一 已知),)((cos )(2为常数ϕϕw wx x f +=,如果存在正整数w 常数ϕ使得函数)(x f 的图像经过点(1,0)如图4-29所示,求w 的值.方向二:知性质(如奇偶性、单调性、对称性、最值) 求解函数解析式(即ϕ,,w A 的值的确定)例4.26已知函数)0,0)(sin()(πϕϕ<≤>+=w wx x f 为)0,43π是一个对称中心,且在区间]2,0[π上为单调函数,求函数)(x f 的解析式.分析 本题的目标是求φ,w 因为)sin(ϕ+=wx y 为偶函数,则必关于y 轴对称,因此化为wx y cos =的形式,由函数在]2,0[π上单调,则]2,0[π最多只会是半个周期,即22π≥T ,从而得wT π2=得w 的范围,再代入对称中心求解.解析 由函数)0,0)(sin()(πϕϕ<≤>+=w wx x f 为R 上的偶函数,则2πϕ=,得wx x f cos )(=,且在区间]2,0[π上为单调函数,得22π≥T ,即π≥T ,故ππ≥w 2,又0>w 得20≤<w .,同时点)0,43(π为函数)(x f 的一个对称中心,的Z k k w ∈+=,243πππ,则Z k k w ∈+=,324,因此23240≤+<k ,得Z k k ∈≤<-,121所以0=k 或1得32=w 或2,所以函数)(x f 的解析式为x y 32cos =或x y 2cos =.评注 根据函数必关于y 轴对称,在三角函数中联想到wx y cos =的模型,从图象、对称轴、对称中心、最值点或单调性来求解.变式一:已知函数),20,0)(sin(4)(R x w wx x f ∈<<>+=πϕϕ图像的两条相邻对称轴的距离为3π,且经过点(0,2).(1)求)(x f 的最小正周期; (2)求函数)(x f 的解析式.题型3 函数的值域(最值) 思路提示求三角函数的最值,通常要利用正、余弦函数的有界性,一般是通过三角变换化归为下列基本类型处理. (1)b x a y +=sin ,设x t sin =,化为一次函数b at y +=在]1,1[-上的最值求解. (2)c x b x a y ++=cos sin ,引入辅助角)(tan ab=ϕϕ,化为c x b a y +++=)sin(22ϕ,求解方法同类型(1)(3)c x b x a y ++=sin sin 2,设x t sin =,化为二次函数c bt at y ++=2在闭区间]1,1[-∈t 上的最值求解,也可以是c x b x a y ++=sin cos 2或c x b x a y ++=sin 2cos 型.(4)c x x b x x a y +±+=)cos (sin cos sin ,设x x t cos sin ±=,则x x t cos sin 212±=,故21cos sin 2-±=t x x ,故原函数化为二次函数c bt t a y ++-±⋅=)21(2在闭区间]2,2[-上的最值求解.(5)d x c b x a y ++=sin sin 与dx c bx a y ++=cos sin ,根据正弦函数的有界性,即可用分析法求最值,也可用不等式法求最值,更可用数形结合法求最值.这里需要注意的是化为关于x sin 或x cos 的函数求解释务必注意x sin 或x cos 的范围.例4.27函数x x x f cos sin )(=的最小值是( )A .-1B .21-C .21D .1分析 将函数)(x f 转化为)sin(ϕ+=wx A y 的形式求最值 解析 函数).(2sin 21cos sin )(R x x x x x f ∈==最小值为21-,故选B. 评注 若本题改为“]4,0[,cos sin )(π∈=x x x x f ”则最小值为0,在解题过程中,若存在换元环节,应注意新元取值范围的限定.变式1 函数)6cos(sin )(π+-=x x x f 的值域为( ).A .[-2,2]B .]3,3[-C .[-1,1]D .]23,23[-变式2 函数x x x x f cos sin 3sin )(2+=在区间]2,4[ππ-上的最大值是( ). A .1 B .231+ C .23D .31+ 例4.28函数)6sin(3)3sin(4x x y -++=ππ的最大值为( )A .7B .2332+ C .5 D .4 分析 由263πππ=-++x x ,利用诱导公式把)6(x -π转化为)3(π+x ,化不同角为相同角,将函数化为)sin()(ϕ+=wx A x f 的形式.解析 )]6(2cos[3)3sin(4x x y --++=πππ)3cos(3)3sin(4x x +++=ππ )43tan )(3sin(5=++=ϕϕπ其中x ,所以5=wax y .故选C.变式1 求函数)(2cos 2)32cos()(2R x x x f ∈++=ππ的值域 变式2 求函数])2,12[)(4sin()4sin(2)32cos()(πππππ-∈+-+-=x x x x x f 的值域.例4.29求函数x x x x f cos 4sin 2cos 2)(2-+=的最大值和最小值.分析 通过二倍角公式和同角公式将函数)(x f 的公式化简为)(cos cos 2R x c x b x a y ∈++=的形式,换元转化为求二次函数在给定区间上的最值.解析 ,1cos 4cos 3cos 4)cos 1()1cos 2(2)(222--=--+-=x x x x x x f 令]1,1[cos -∈=x t ,则])1,1[(37)32(3143)(22-∈--=--=t t t t t g ,因为]1,1[-∈t ,所以当1-=t 时,)(t f 取最大值6,即)(x f 的最大值为6;当32=t 时,)(t g 取最小值37-,即)(x f 的最小值为37-.变式1 已知4π≤x ,求函数x x y sin cos 2+=的最小值.变式2 求函数)20(2385cos sin 2π≤≤-+=x a xa x y 的最大值. 变式3 若0cos sin 2=++a x x 有实数解,试确定实数a 的取值范围. 变式4 若关于x 的方程0sin cos 2≥+-a x x 在]2,0(π上恒成立,求实数a 的取值范围.例4.30对于函数)0(sin 1sin )(π<<+=x xx x f ,下列结论中正确的是( ).A .有最大值无最小值B .有最小值无最大值C .有最大值且有最小值D .既无最大值又无最小值分析 形如dx c bx a y ++=sin sin 的函数的最值,可考虑用函数的有界性求解.解析 解法一:x x f sin 11)(+=,令]1,0(sin ∈=x t ,则ty 11+=在区间]1,0(上单调递减,即)(x f 只有最小值无最大值.故选B 解法二:1sin sin sin 1sin =-⇒+=x x y xx y ,得111sin 0≤-=<y x ,解得2≥y ,所以)(x f 只有最小值无最大值.故选B 变式1 求函数xxy sin 2cos 3+=的值域.变式2 若24ππ<<x ,则函数x x y 2tan 2tan =的最大值为_______.题型4 三角函数图像变换 思路提示由函数x y sin =的图像变换为函数)0,()sin(>++=w A b wx A y ϕ的图像.方法一:)(ϕϕ+→+→wx x x 先相位变换,后周期变换,再振幅变换.x y sin =的图像→<ΦΦ>ΦΦ)个单位(向左平移)个单位(向左平移00)sin(ϕ+=x y 的图像→<ΦΦ>ΦΦ)个单位(向左平移)个单位(向左平移00ϖϖ)sin(ϕ+=wx y 的图像→横坐标不变倍来的所有点的纵坐标变为原A)sin(ϕ+=wx A y 的图像→<>)个单位(向下平移)个单位(向上平移00b b b b b wx A y ++=)sin(ϕ 例4.31把函数12cos +=x y 的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1分析 利用三角函数的图像与变换求解解析 12cos +=x y →纵坐标不变倍横坐标伸长2−−−−−−→−+=个单位长度向左平移11cos x y −−−−−−→−++=个单位长度向下平移11)1cos(x y ).1cos(+=x y结合选项可知,函数图像过)0,12(-π.故选A变式1 为得到函数)32cos(π+=x y 的图像,只需将函数x y 2sin =的图像( ).A .向左平移125π个单位 B . 向右平移125π个单位 C .向左平移65π个单位 D . 向右平移65π个单位变式2 已知)2sin()(π+=x x f ,)2cos()(π-=x x g ,则)(x f 的图像( ).A .与)(x g 图像相同B .与)(x g 图像关于y 轴对称C .是由)(x g 的图像向左平移2π个单位得到D .是由)(x g 的图像向右平移2π个单位得到 变式3 已知函数)0,)(4sin()(>∈+=w R x wx x f π的最小正周期为π,为了得到)cos()(wx x g =的图像,只要将)(x f y =的图像( )C DA .向左平移8π个单位长度 B .向右平移8π个单位长度 C .向左平移4π个单位长度 D .向右平移4π个单位长度例4.32已知函数)0)(2sin(21cos cos sin 2sin 21)(2πϕϕπϕϕ<<+-+=x x x f ,其图像过点)21,6(π.(1)求ϕ的值(2)将)(x f 图像上各点的横坐标缩短为原来的21,纵坐标不变,得到函数)(x g y =的图像,求函数)(x g 在]4,0[π上的最大值和最小值解析 由题意把点)21,6(π代入函数的解析式得21cos 21cos 43sin 3sin 21=-+ϕϕϕπ 1)6sin(cos 21sin 23=+=+⇒πϕϕϕ (1)1)6sin(=+πϕ,.3,26),67,6(6),,0(πϕππϕπππϕπϕ==+∈+∈ (2)41cos 21232sin 21)(2-+⋅=x x x f )62sin(2141)2cos 1(412sin 43π+=-++=x x x , 依题意)64sin(21)622sin(21)(ππ+=+⋅=x x x g , 当6764ππ=+x ,即4π=x 时,)(x g 取最小值41-;当264ππ=+x ,即12π=x 时,)(x g 取最大值21.变式1已知向量)0)(2cos 2,cos 3(),1,(sin >==A x Ax A n x m ,函数n m x f ⋅=)(的最大值为6.(1)求A(2)求将函数)(x f y =的图像向左平移12π个单位,再将所的图像上各点的横坐标缩短到原来的21倍,,纵坐标不变,得到函数)(x g y =的图像,求)(x g 在]245,0[π上的值域最有效训练题1.已知函数)02,0)(sin()(<<->+=ϕπϕA wx A x f ,在65π=x 时取得最大值,则)(x f 在]0,[π-上的单调增区间是( ).A .]65,[ππ-- B .]6,65[ππ-- C .]0,3[π- D .]0,6[π- 2.若直线t x =与函数)42sin(π+=x y 和)42cos(π+=x y 的图像分别交于P ,Q的最大值为( )A .2B .1C .3D .2 3.已知函数x x x f sin cos )(2+=,那么下列命题中假命题是( )A .)(x f 既不是奇函数也不是偶函数B .)(x f 在]0,[π-上恰有一个零点C .)(x f 是周期函数D .)(x f 在)65,2(ππ上是增函数4,.已知函数)46sin()(π+=x x f 的图像上各点的横坐标伸长到原来的3倍,再向右平移8π个单位,得到的函数一个对称中心是( ).A .)0,16(π B .)0,9(π C .)0,4(π D .)0,2(π5.如图4-30所示,点P 是函数0,)(sin(2>∈+=w R x wx y ϕx 轴的交点,若0=⋅PN PM ,则w 的值为( )A .8π B .4πC .4D .8 6.已知],0(π∈x ,关于x 的方程a x =+)3sin(2π,( )..[2]A 2]B 2]C 2)D7.已知函数22()2sin cos f x x x x x ωωω=+,其中0ω>,且()f x 的最小正周期为π,则()f x 的单调递增区间为 . 8.已知函数()3sin()(0)6f x x πωω=->的图象和()2cos(2)1g x x ϕ=++的图象对称轴完全相同,若[0,]2x π∈,则()f x 的取值范围为 .9.定义一种运算12341423(,)(,)a a a a a a a a ⊗=-,将函数()2sin )(cos ,cos 2)f x x x x =⊗的图象向左移(0)n n >个单位长度所得图像对应的函数为偶函数,则n 的最小值为 .10.某学生对函数()2cos f x x x =进行研究后,得出如下四个结论:①函数()f x 在[,0]π-上为单调递增,在[0,]π上单调递减;②存在常数0M >,使()f x M x ≤对一切实数x 均成立;③点(,0)2π是函数()y f x =图像的一个对称中心;④函数()y f x =的图象关于直线x π=对称.其中正确的是 .(把所有正确的命题的序号都填上). 11.已知函数22()cos(2)sin cos .3f x x x x π=-+-(1)求函数()f x 的最小正周期及图像的对称轴方程; (2)设函数2()[()]()g x f x f x =+,求()g x 的值域.12.已知函数()sin()f x A x ωϕ=+,其中 (,0,0,)22x R A ππωϕ∈>>-<<的部分图 像如图4-31所示.(1)求函数()f x 的解析式;(2)已知函数()f x 图像上三点M,N,P的横坐标分别为-1,1,5,求sin MNP ∠ 的值.。
三角函数图像与性质知识点总结优秀版

优秀版函数图像与性质知识点总结一、三角函数图象的性质 1.“五点法”描图(1)y =sin x 的图象在[0,2π]上的五个关键点的坐标为(0,0) ⎝ ⎛⎭⎪⎪⎫π2,1 (π,0)⎝ ⎛⎭⎪⎪⎫32π,-1 (2π,0) (2)y =cos x 的图象在[0,2π]上的五个关键点的坐标为 (0,1),⎝ ⎛⎭⎪⎪⎫π2,0,(π,-1),⎝ ⎛⎭⎪⎪⎫3π2,0,(2π,1)函数 性质y =sin x y =cos x y =tan x定义域 R R{x |x ≠k π+π2,k ∈Z}图象值域[-1,1][-1,1]R对称性对称轴: x =k π+π2(k ∈Z);对称轴: x =k π(k ∈Z)对称中心:对称中心:⎝ ⎛⎭⎪⎪⎫k π2,0 (k ∈Z)f+T)=f(x),那么函数f(x)就叫做周期函数,非零常数T叫做这个函数的周期,把所有周期中存在的最小正数,叫做最小正周期(函数的周期一般指最小正周期) 4.求三角函数值域(最值)的方法:(1)利用sin x、cos x的有界性;关于正、余弦函数的有界性由于正余弦函数的值域都是[-1,1],因此对于∀x∈R,恒有-1≤sin x≤1,-1≤cos x≤1,所以1叫做y=sin x,y=cos x的上确界,-1叫做y=sin x,y=cos x的下确界.(2)形式复杂的函数应化为y=A sin(ωx+φ)+k的形式逐步分析ωx+φ的范围,根据正弦函数单调性写出函数的值域;含参数的最值问题,要讨论参数对最值的影响.(3)换元法:把sin x 或cos x 看作一个整体,可化为求函数在区间上的值域(最值)问题.利用换元法求三角函数最值时注意三角函数有界性,如:y =sin 2x -4sin x +5,令t =sin x (|t |≤1),则y =(t -2)2+1≥1,解法错误.5.求三角函数的单调区间时,应先把函数式化成形如y =A sin(ωx +φ) (ω>0)的形式,再根据基本三角函数的单调区间,求出x 所在的区间.应特别注意,应在函数的定义域内考虑.注意区分下列两题的单调增区间不同;利用换元法求复合函数的单调区间(要注意x 系数的正负号) (1)y =sin ⎝ ⎛⎭⎪⎪⎫2x -π4;(2)y =sin ⎝ ⎛⎭⎪⎪⎫π4-2x .6、y =A sin(ωx +φ)+B 的图象求其解析式的问题,主要从以下四个方面来考虑:①A 的确定:根据图象的最高点和最低点,即A =最高点-最低点2;②B 的确定:根据图象的最高点和最低点,即B =最高点+最低点2;③ω的确定:结合图象,先求出周期,然后由T =2πω(ω>0)来确定ω;④φ的确定:把图像上的点的坐标带入解析式y =A sin(ωx +φ)+B ,然后根据φ的范围确定φ即可,例如由函数y =A sin(ωx +φ)+K 最开始与x 轴的交点(最靠近原点)的横坐标为-φω(即令ωx +φ=0,x =-φω)确定φ.二、三角函数的伸缩变化 先平移后伸缩sin y x =的图象ϕϕϕ<−−−−−−−→向左(>0)或向右(0)平移个单位长度得sin()y x ϕ=+的图象()ωωω−−−−−−−−−→横坐标伸长(0<<1)或缩短(>1)1到原来的纵坐标不变 得sin()y x ωϕ=+的图象()A A A >−−−−−−−−−→纵坐标伸长(1)或缩短(0<<1)为原来的倍横坐标不变 得sin()y A x ωϕ=+的图象(0)(0)k k k ><−−−−−−→ 得sin()y A x k ϕ=++的图象. 先伸缩后平移sin y x =的图象(1)(01)A A A ><<−−−−−−−−−→纵坐标伸长或缩短为原来的倍(横坐标不变)得sin y A x =的图象(01)(1)1()ωωω<<>−−−−−−−−−→横坐标伸长或缩短到原来的纵坐标不变 得sin()y A x ω=的图象(0)(0)ϕϕϕω><−−−−−−−→向左或向右平移个单位得sin ()y A x x ωϕ=+的图象(0)(0)k k k ><−−−−−−−→向上或向下平移个单位长度得sin()y A x k ωϕ=++的图象. .高中数学必修4三角函数知识点总结一、角的概念和弧度制:(1)在直角坐标系内讨论角:注意:若角的终边在坐标轴上,就说这个角不属于任何象限,它叫象限界角。
高中数学三角函数及反三角函数图像性质、知识点总结

高中数学三角函数及反三角函数图像性质、知识点总结高中数学中,三角函数及反三角函数是重要的内容之一。
在学习这一部分知识时,需要掌握其图像性质以及相关的知识点。
下面将对这些内容进行总结。
一、三角函数的图像性质1. 正弦函数(sin)的图像性质:- 周期性:sin函数的周期为2π,即在每个周期内,函数的图像重复出现;- 奇函数性质:sin函数关于原点对称;- 取值范围:sin函数的取值范围为[-1,1],即函数的值始终在该区间内波动。
2. 余弦函数(cos)的图像性质:- 周期性:cos函数的周期为2π;- 偶函数性质:cos函数关于y轴对称;- 取值范围:cos函数的取值范围也为[-1,1]。
3. 正切函数(tan)的图像性质:- 周期性:tan函数的周期为π;- 奇函数性质:tan函数关于原点对称;- 无界性:tan函数的值域为实数集,即函数在某些点无界。
二、三角函数的知识点1. 基本正弦函数的性质:- 特殊角的正弦值:0°、90°、180°、270°和360°对应的正弦值分别为0、1、0、-1和0;- 正弦函数的增减性:在0°到180°的区间上,sin函数是单调递增的;- 正弦函数的奇偶性:sin(-x)=-sin(x),即sin函数关于原点对称。
2. 基本余弦函数的性质:- 特殊角的余弦值:0°、90°、180°、270°和360°对应的余弦值分别为1、0、-1、0和1;- 余弦函数的增减性:在0°到180°的区间上,cos函数是单调递减的;- 余弦函数的奇偶性:cos(-x)=cos(x),即cos函数关于y轴对称。
3. 基本正切函数的性质:- 特殊角的正切值:0°、90°、180°和270°对应的正切值分别为0、无穷大、0和无穷大;- 正切函数的周期性:tan(x+π)=tan(x),即tan函数的周期是π。
三角函数经典题型总结

三角函数的经典题型主要包括以下几个方面:
1. 三角函数的基本性质和公式应用:
-三角函数的基本关系:sin²θ+ cos²θ= 1,tanθ= sinθ/cos θ等。
-诱导公式:sin(α±β),cos(α±β),tan(α±β)等的公式。
-二倍角公式、半角公式、和差化积、积化和差公式等。
2. 解三角形问题:
-正弦定理:a/sinA = b/sinB = c/sinC。
-余弦定理:a²= b²+ c²- 2bc cosA,同理可得其他边和角的关系。
-利用正弦定理和余弦定理解决边角关系问题。
3. 三角函数图像和性质:
-正弦函数、余弦函数、正切函数的图像及其周期性、奇偶性、单调性、对称性等性质。
-利用图像解三角函数方程和不等式。
4. 三角函数的应用问题:
-在物理中的应用,如振动问题、波动问题、光学问题等。
-在地理学中的应用,如地图上的方位角、距离计算等。
-在工程学中的应用,如结构力学、电路分析等。
5. 三角函数的复合与逆运算:
-复合三角函数的运算,如sin(cosx),cos(sinx)等。
-三角函数的反函数,如arcsin(x),arccos(x),arctan(x)等。
6. 三角恒等式的证明:
-利用三角函数的基本关系和公式进行恒等式的变形和证明。
以上就是三角函数的一些经典题型总结,掌握这些题型的解题方法和技巧,可以有效地提高解决三角函数问题的能力。
三角函数图像与性质-知识点总结及题型归纳讲义
专题七《三角函数》讲义7.3 三角函数的图像与性质知识梳理.三角函数的图像与性质1.正弦、余弦、正切函数的图象与性质函数y=sin x y=cos x y=tan x 图象定义域R R错误!值域[-1,1][-1,1]R奇偶性奇函数偶函数奇函数单调性在⎣⎡⎦⎤-π2+2kπ,π2+2kπ(k∈Z)上是递增函数,在⎣⎡⎦⎤π2+2kπ,3π2+2kπ(k∈Z)上是递减函数在[2kπ-π,2kπ](k∈Z)上是递增函数,在[2kπ,2kπ+π](k∈Z)上是递减函数在⎝⎛⎭⎫-π2+kπ,π2+kπ(k∈Z)上是递增函数周期性周期是2kπ(k∈Z且k≠0),最小正周期是2π周期是2kπ(k∈Z且k≠0),最小正周期是2π周期是kπ(k∈Z且k≠0),最小正周期是π对称性对称轴是x=π2+kπ(k∈Z),对称中心是(kπ,0)(k∈Z)对称轴是x=kπ(k∈Z),对称中心是⎝⎛⎭⎫kπ+π2,0(k∈Z)对称中心是⎝⎛⎭⎫kπ2,0(k∈Z)题型一. 三角函数图像的伸缩变换1.要得到函数y =3sin (2x +π3)的图象,只需要将函数y =3cos2x 的图象( ) A .向右平行移动π12个单位 B .向左平行移动π12个单位C .向右平行移动π6个单位D .向左平行移动π6个单位2.(2017•新课标Ⅰ)已知曲线C 1:y =cos x ,C 2:y =sin (2x +2π3),则下面结论正确的是( )A .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2B .把C 1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 2C .把C 1上各点的横坐标缩短到原来的12,纵坐标不变,再把得到的曲线向右平移π6个单位长度,得到曲线C 2D .把C 1上各点的横坐标缩短到原来的12,纵坐标不变,再把得到的曲线向左平移π12个单位长度,得到曲线C 23.(2021春•闵行区校级期中)函数y =cos (2x +φ)的图象向右平移π2个单位长度后与函数y =sin (2x +2π3)的图象重合,则|φ|的最小值为 .4.(2016春•南通期末)将函数f(x)=sin(ωx +φ),(ω>0,−π2<φ<π2)图象上每一点的横坐标缩短为原来的一半,纵坐标不变,再向右平移π4个单位长度得到y =sin x 的图象,则f(π6)= .5.(2015•湖南)将函数f (x )=sin2x 的图象向右平移φ(0<φ<π2)个单位后得到函数g (x )的图象.若对满足|f (x 1)﹣g (x 2)|=2的x 1、x 2,有|x 1﹣x 2|min =π3,则φ=( ) A .5π12B .π3C .π4D .π6题型二. 已知图像求解析式1.图是函数y =A sin (ωx +φ)(x ∈R )在区间[−π6,5π6]上的图象,为了得到这个函数的图象,只要将y =sin x (x ∈R )的图象上所有的点( )A .向左平移π3个单位长度,再把所得各点的横坐标缩短到原来的12,纵坐标不变B .向左平移π3个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C .向左平移π6个单位长度,再把所得各点的横坐标缩短到原来的12,纵坐标不变D .向左平移π6个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变2.已知函数y =sin(ωx +φ)(ω>0,|φ|<π2)的部分图象如图所示,则( )A .ω=π2,φ=−π4 B .ω=π2,φ=π4C .ω=π,φ=−π4D .ω=π,φ=π43.已知函数f (x )=A cos (ωx +φ)的图象如图所示,f (π2)=−23,则f (0)=( )A .−23B .−12C .23D .124.已知函数f (x )=A tan (ωx +φ)(ω>0,|φ|<π2)的部分图象如图所示,下列关于函数g (x )=A cos (ωx +φ)(x ∈R )的表述正确的是( )A .函数g (x )的图象关于点(π4,0)对称B .函数g (x )在[−π8,3π8]递减 C .函数g (x )的图象关于直线x =π8对称D .函数h (x )=cos2x 的图象上所有点向左平移π4个单位得到函数g (x )的图象题型三. 三角函数的性质 考点1.单调性1.函数y =sin (﹣2x +π3)的单调递减区间是( ) A .[k π−π12,k π+5π12],k ∈Z B .[2k π−π12,2k π+5π12],k ∈ZC .[k π−π6,k π+5π6],k ∈ZD .[2k π−π6,2k π+5π6],k ∈Z2.已知函数f(x)=Asin(x +φ)(A >0,−π2<φ<0)在x =5π6时取得最大值,则f (x )在[﹣π,0]上的单调增区间是( ) A .[−π,−5π6] B .[−5π6,−π6] C .[−π3,0]D .[−π6,0]3.已知函数f (x )=sin (2x +π3)在区间[0,a ](其中a >0)上单调递增,则实数a 的取值范围是( ) A .{a |0<a ≤π12} B .{a |0<a ≤π2} C .{a |a =k π+π12,k ∈N *} D .{a |2k π<a ≤2k π+π12,k ∈N *} 4.已知ω>0,函数f (x )=sin (ωx +π4)在区间(π2,π)上单调递减,则实数ω的取值范围是( ) A .[12,54] B .[12,34]C .(0,12]D .(0,2]考点2.周期性、奇偶性、对称性1.已知函数f (x )=cos 2x +sin 2(x +π6),则( )A .f (x )的最小正周期为π,最小值为12B .f (x )的最小正周期为π,最小值为−12C .f (x )的最小正周期为2π,最小值为12D .f (x )的最小正周期为2π,最小值为−122.已知f (x )=sin2x +|sin2x |(x ∈R ),则下列判断正确的是( ) A .f (x )是周期为2π的奇函数 B .f (x )是值域为[0,2]周期为π的函数 C .f (x )是周期为2π的偶函数 D .f (x )是值域为[0,1]周期为π的函数3.将函数y =sin2x −√3cos2x 的图象沿x 轴向右平移a 个单位(a >0)所得图象关于y 轴对称,则a 的最小值是( ) A .712π B .π4C .π12D .π64.已知函数f (x )=a sin x ﹣b cos x (ab ≠0,x ∈R )在x =π4处取得最大值,则函数y =f (π4−x )是( )A .偶函数且它的图象关于点(π,0)对称B .偶函数且它的图象关于点(3π2,0)对称 C .奇函数且它的图象关于点(3π2,0)对称 D .奇函数且它的图象关于点 (π,0)对称考点3.三角函数性质综合1.(2019•天津)已知函数f (x )=A sin (ωx +φ)(A >0,ω>0,|φ|<π)是奇函数,将y =f (x )的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为g (x ).若g (x )的最小正周期为2π,且g (π4)=√2,则f (3π8)=( )A .﹣2B .−√2C .√2D .22.(2015•天津)已知函数f (x )=sin ωx +cos ωx (ω>0),x ∈R ,若函数f (x )在区间(﹣ω,ω)内单调递增,且函数y =f (x )的图象关于直线x =ω对称,则ω的值为 .3.(2014•大纲版)若函数f (x )=cos2x +a sin x 在区间(π6,π2)是减函数,则a 的取值范围是 .4.(2016•新课标Ⅰ)若函数f (x )=x −13sin2x +a sin x 在(﹣∞,+∞)单调递增,则a 的取值范围是( ) A .[﹣1,1]B .[﹣1,13]C .[−13,13]D .[﹣1,−13]5.(2013•安庆二模)已知函数f (x )=sin (ωx +π6),其中ω>0,若f (π6)=f (π3),且f (x )在区间(π6,π3)上有最小值、无最大值,则ω等于( )A .403B .283C .163D .436.(2014•北京)设函数f (x )=A sin (ωx +φ)(A ,ω,φ是常数,A >0,ω>0)若f (x )在区间[π6,π2]上具有单调性,且f (π2)=f(2π3)=﹣f (π6),则f (x )的最小正周期为 .题型四. 三角函数最值1.函数f (x )=15sin (x +π3)+cos (x −π6)的最大值为( ) A .65B .1C .35D .152.函数f (x )=cos (ωx +π3)(ω>0)在[0,π]内的值域为[﹣1,12],则ω的取值范围为( ) A .[32,53]B .[23,43]C .[23,+∞)D .[23,32]3.已知函数f (x )=cos2x +sin x ,则下列说法中正确的是( ) A .f (x )的一条对称轴为x =π4 B .f (x )在(π6,π2)上是单调递减函数C .f (x )的对称中心为(π2,0)D .f (x )的最大值为14.若0<x ≤π3,则函数y =sin x +cos x +sin x cos x 的值域为 .5.已知函数f(x)=2sinωx ⋅cos 2(ωx 2−π4)−sin 2ωx(ω>0)在区间[−2π5,5π6]上是增函数,且在区间[0,π]上恰好取得一次最大值1,则ω的取值范围是( ) A .(0,35]B .[12,35]C .[12,34]D .[12,52)6.已知函数f (x )=cos x •sin (x +π3)−√3cos 2x +√34,x ∈R (1)求f (x )的最小正周期;(2)求f (x )在闭区间[0,π2]上的最大值和最小值及相应的x 值;(3)若不等式|f (x )﹣m |<2在x ∈[0,π2]上恒成立,求实数m 的取值范围.题型五.三角函数零点1.已知函数f (x )=sin ωx −√3cos ωx (ω>0),若方程f (x )=﹣1在(0,π)上有且只有四个实数根,则实数ω的取值范围为 .2.已知函数f (x )=√3sin ωx cos ωx +cos 2ωx −12,(ω>0,x ∈R ),若函数f (x )在区间(π2,π)内没有零点,则ω的取值范围( ) A .(0,512] B .(0,512]∪[56,1112]C .(0,58]D .(0,56]∪[1112,1)3.函数f(x)=2sin(2ωx +π6)(ω>0)图象上有两点A (s ,t ),B (s +2π,t )(﹣2<t <2),若对任意s ∈R ,线段AB 与函数图象都有五个不同交点,若f (x )在[x 1,x 2]和[x 3,x 4]上单调递增,在[x 2,x 3]上单调递减,且x 4−x 3=x 2−x 1=23(x 3−x 2),则x 1的所有可能值是课后作业. 三角函数的图像与性质1.函数f (x )=A sin (ωx +φ)(A >0,ω>0,﹣π<φ<0)的部分图象如图所示,为了得到g (x )=A sin ωx 的图象,只需将函数y =f (x )的图象( )A .向左平移π3个单位长度B .向左平移π12个单位长度 C .向右平移π3个单位长度D .向右平移π12个单位长度2.关于函数y =2sin (3x +π4)+1,下列叙述正确的是( ) A .其图象关于直线x =−π4对称 B .其图象关于点(π12,1)对称 C .其值域是[﹣1,3]D .其图象可由y =2sin (x +π4)+1图象上所有点的横坐标变为原来的13得到 3.已知函数f (x )=(12a −√3)sin x +(√32a +1)cos x ,将f (x )的图象向右平移π3个单位长度得到函数g (x )的图象,若对任意x ∈R ,都有g (x )≤g (π4),则a 的值为 . 4.已知函数f (x )=sin (ωx +φ)(ω>1,0≤φ≤π)是R 上的偶函数,其图象关于点M (3π4,0)对称,且在区间[0,π2]上是单调函数,则ω和φ的值分别为( )A .23,π4B .2,π3C .2,π2D .103,π25.已知函数f (x )=sin (ωx +φ),其中ω>0,|φ|≤π2,−π4为f (x )的零点:且f (x )≤|f (π4)|恒成立,f (x )在区间(−π12,π24)上有最小值无最大值,则ω的最大值是( )A .11B .13C .15D .176.已知函数f (x )=2sin (ωx −π6)sin (ωx +π3)(ω>0),若函数g (x )=f (x )+√32在[0,π2]上有且只有三个零点,则ω的取值范围为( )A .[2,113) B .(2,113) C .[73,103) D .(73,103)。
三角函数的图像与性质(名师经典总结)

三角函数的图像与性质(正弦、余弦、正切)【知识点1】函数y =sin x ,y =cos x ,y =tan x 的图象性质题型1:定义域例1:求下列函数的定义域(1)xx y cos 2cos 1+=; (2)x y 2sin = 2lg(4)x -题型2:值域 例2:求下列函数值域 (1))3π2,6π(,sin 2-∈=x x y (2)y=2sin(2x-3π),x 5,46ππ⎡⎤∈⎢⎥⎣⎦(3) )3π,2π(),3π2cos(2-∈+=x x y(4)函数1)6π21cos(2++-=x y 的最大值以及此时x 的取值集合题型3:周期例3:求下列函数的周期: (1)f(x)=2sin2x (2)y=cos(123x π-) (3)y=tan(2x 4π-) (4)y=sin x 例4: 若函数()2sin(2)3f x kx π=+的最小正周期T 满足12T <<,则自然数k 的值为______.例5:若)10(sin 2)(<<=ϖϖx x f 在区间[0,]3π上的最大值是2,则ϖ=________.例6:使x y ωsin =(ω>0)在区间[0,1]至少出现2次最大值,则ω的最小值为【 】A .π25B .π45C .πD .π23例7:设函数f(x)=2sin(25x ππ+),若对于任意的x R ∈,都有f(1x )2()()f x f x ≤≤成立,则12x x -的最小值是A.4B.2C.1D.12题型4:奇偶性 例8:函数y =sin (x +2π)(x ∈[-2π,2π])是【 】A.增函数B.减函数C.偶函数D.奇函数例9:判断下列函数的奇偶性 (1)y=xsin(x π+) (2)y=cos 1sin x x+例10:已知函数f(x)=x 3cosx+1,若f(a)=11,则f(-a)=________ 题型5:单调性例11:函数y =21log sin(2x +4π)的单调递减区间是【 】 A.(k π-4π,k π](k ∈Z ) B.(k π-8π,k π+8π](k ∈Z ) C.(k π-83π,k π+8π](k ∈ D.(k π+8π,k π+83π](k ∈Z )例12:.求1cos()3412logx y π+=的单调区间例13:求下列函数的单调增区间(1))3π21cos(-=x y ; (2) ]0,π[),6π2sin(2-∈+=x x y ;(3))23πsin(2x y -=例14:(1)求函数y=2sin(2x-3π)的单调递减区间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角函数的图像与性质题型归纳总结题型归纳及思路提示题型1 已知函数解析式确定函数性质【思路提示】一般所给函数为y =A sin(ω x +φ)或y =A cos(ω x +φ),A>0,ω>0,要根据 y =sin x ,y =cos x 的整体性质求解。
一、函数的奇偶性例1 f (x )=sin ()x ϕ+(0≤ϕ<π)是R 上的偶函数,则ϕ等于( )B .4π C .2πD .π 【评注】由sin y x =是奇函数,cos y x =是偶函数可拓展得到关于三角函数奇偶性的重要结论:sin()();y A x k k Z ϕϕπ=+=∈(1)若是奇函数,则sin()+();2y A x k k Z πϕϕπ=+=∈(2)若是偶函数,则 cos()();2y A x k k Z πϕϕπ=+=+∈(3)若是奇函数,则cos()();y A x k k Z ϕϕπ=+=∈(4)若是偶函数,则tan()().2k y A x k Z πϕϕ=+=∈(5)若是奇函数,则.()sin ||a R f x x a a ∈=-变式1已知,函数为奇函数,则等于( )B .1C .1-D .1±2.0()cos()()R f x x x R ϕϕϕ∈==+∈变式设,则“”是“为偶函数”的( )A 充分不必要条件B .必要不充分条C .充要条件D .无关条件3.()sin()0()f x x f x ωϕω=+>变式设,其中,则是偶函数的充要条件是( )A.(0)1f = B .(0)0f = C .'(0)1f = D .'(0)0f =2.()sin(2)()()2f x x x R f x π=-∈例设,则是( )A.π最小正周期为的奇函数 B .π最小正周期为的偶函数 C .2π最小正周期为的奇函数 D .2π最小正周期为的偶函数2()sin 1()()f x x x R f x =-∈变式1.若,则是( )A.π最小正周期为的奇函数 B .π最小正周期为的偶函数 C .π最小正周期为2的奇函数 D .π最小正周期为2的偶函数2.(0,)2ππ变式下列函数中,既在递增,又是以为周期的偶函数的是( )A.cos 2y x = B .|sin 2|y x = C .|cos 2|y x = D .|sin |y x =二、函数的周期性3.sin(2)cos(2)66y x x ππ=++例函数的最小正周期为( )A.2π B .4πC .2πD .π【评注】关于三角函数周期的几个重要结论:sin()b,cos()b,tan()b22,,.||||||y A x y A x y A x ωϕωϕωϕπππωωω=++=++=++(1)函数的周期分别为|sin()|,|cos()|,|tan()|.||y A x y A x y A x πωϕωϕωϕω=+=+=+(2)函数的周期均为2|sin()b |(b 0),|cos()b |(b 0).||y A x y A x πωϕωϕω=++≠=++≠(3)函数的周期均为1.sin(2)cos(2)63y x x ππ=+++变式函数的最小正周期和最大值分别为( )A.,1π B.π C .2,1π D.2π()sin (sin cos ),()f x x x x f x =-变式2.若则的最小正周期是________.()sin 3|sin 3|()f x x x f x =+变式3.若则是( )A.3π最小正周期为的周期函数 B .23π最小正周期为的周期函数 C .π最小正周期为2的周期函数 D .非周期函数三、函数的单调性.sin(2)([0,])6y x x ππ=-∈例4函数的递增区间是( )A.[0,]3π B .7[,]1212ππ C .5[,]36ππD .5[,]6ππ【评注】求三角函数的单调区间:sin()(0,0)y A x A ωϕω=+>>若函数则22()22322()22(3)sin()0,0sin()sin()(4)cos()tan()k x k k Z k x k k Z y A x A y A x y A x y A x y A x πππωϕππππωϕπωϕωωϕωϕωϕωϕ-≤+≤+∈+≤+≤+∈=+><=---=--=+=+(1)函数的递增区间由决定;(2)函数的递减区间由决定;若函数中,可将函数变为则的增区间为原函数的减区间,减区间为原函数的增区间;对于函数和单调性的讨论同上。
31.sin ()[()44y x f x f x ππ=+-变式函数在,]内单调递增,则可以是( )A.1 B .cos x C .sin x D .cos x-()sin()(0)(42f x x ππωωπω=+>变式2.若在,)上单调递增,则的取值范围是( )A.15[,]24 B .13[,]24 C .1(0,]2 D .(0,2]3.()cos()cos()(0)33(1)()(2)(),[0,]()22f x x x x f x f x x f x ππωωωωππ=+++->∈变式已知函数求的值域;若的最小正周期为,的单调递减区间.四、函数的对称性(对称轴、对称中心).sin(2)3y x π=+例5函数图象的对称轴方程可能是( )A.6x π=- B .12x π=- C .6x π= D .12x π=【评注】关于三角函数对称性的几个重要结论:sin (),(,0)();2cos (),(,0)();2tan (,0)();22sin()(),=();2:y x x k k Z k k Z y x x k k Z k k Z k y x k Z k y A x b x k k Z x k Z x k πππππππππϕπωϕωϕπωωϕπ==+∈∈==∈+∈=∈+-=+++=+∈∈+=(1)函数的对称轴为对称中心(2)函数的对称轴为对称中心(3)函数无对称轴,对称中心(4)函数的对称轴的求法:令得对称中心的求法令()=(),(,)()cos()(),=();22:()=(),(,)()2k k k Z x k Z b k Z k y A x b x k k Z x k Z k k x k k Z x k Z b k Z πϕπϕωωπϕωϕωϕπωπππϕπϕπωϕπωω--∈∈∈-=+++=∈∈+-+-+=+∈∈∈得对称中心为;(5)函数的对称轴的求法:令得对称中心的求法令得对称中心为1.sin()(0)()3y x f x πωωπ=+>变式已知函数的最小正周期为,则的图象( )A.(,0)3π关于点对称 B .4x π=关于直线对称C .(,0)4π关于点对称D .3x π=关于直线对称.sin()4y x π=-变式2函数的图象的一个对称中心是( )A.(,0)π- B .3(,0)4π- C .3(,0)4π D .(,0)2π 223.()sin cos .55x xf x =+变式函数的图象中,相邻两条对称轴之间的距离是__________.sin 0x x a a a =>变式4若函数y 的图象向右平移个单位()后的图象关于y 轴对称,则的最小值是( )A.76π B .2π C .6π D .3π五、三角函数性质的综合【思路提示】三角函数的性质(奇偶性、周期性、单调性、对称性)中,对称性尤为重要;121()()()()(2)224(3)()()sin(),00()[,]f x y f x f x f x T T Tf x f x A x A f x ωωθθ⇒⇒⇒=>>()对称性奇偶性:若函数的图象关于轴对称,则是偶函数;若函数的图象关于原点对称,则是奇函数;对称性周期性:相邻两条对称轴之间的距离为;相邻两个对称中心的距离为;相邻的对称中心与对称轴之间的距离为;对称性单调性:在相邻的对称轴之间,函数单调;特殊的,若,函数在上单调12120[,]{||,}4Tmax θθθθθθ∈=≥,且设,则。
6.()sin 2cos 2,0,()(),6117(1)()0;(2)()();(3)()121052()[,]()63(5)(,)().f x a x b x ab f x f x R f f f f x f x k k k Z a b f x ππππππππ=+≠≤∈=<++∈例设若对任成立则不具奇偶性;(4)的单调递增区间是;存在经过点的直线与函数的图象不相交.以上结论中正确的是__________________7.()4cos()sin cos(2)(0)63(1)()(2)()[,].22f x x x x f x f x πωωωπωππω=--+>-例已知函数求的值域;若在区间为增函数,求的最大值21.()2sin (0),()[,].43f x x f x ππωωω=>-变式已知函数若在上递增,求的取值范围8.()sin()(0),()()(,)=______.36363f x x f f πππππωωω=+>=例若且在上有最小值无最大值,则题型2 根据条件确定解析式方向一:“知图求式”,即已知三角函数的部分图象,求函数解析式。
【思路提示】由图象求得y =A sin(ω x +φ) (A >0,ω>0)的解析式一般不唯一,只有限定φ的取值范围,才能得到唯一解。
依据五点法原理,点的序号与式子的关系是:第一点(即图象上升时与横轴的交点)为0x ωϕ+=,第二点(即图象最高点)为2x πωϕ+=,第三点(即图象下降时与横轴的交点)为x ωϕπ+=,第四点(即图象最低点)为32x πωϕ+=,第五点(即图象上升时与横轴的交点)为2.x ωϕπ+=。
.()sin(2)(,)(0)f x A x A R f ϕϕ=+∈=例9函数部分图象如下图所示,则( )A.12-B .1-C .32-D .31.()sin()(0,0)(0)________.f x A x A f ωϕω=+>>=变式函数部分图象如下图所示,则2.()cos()()(0)________.23f x A x f f πωϕ=+=-=变式2部分图象如下图所示,,则.()sin()(0,0,||)()f x A x A f x ωϕωϕπ=+>><例10已知函数部分图象如下图所示,求的解析式。
变式1.已知)(cos )(2ϕω+=x x f (ω,ϕ为常数),如果存在正整数ω和实数ϕ使得函数()f x 的图象如图所示(图象经过点(1,0)),求ω的值.112yOx方向二:知性质(如奇偶性、单调性、对称性、最值)求函数解析式。
