大学物理波动22011第二部分讲解
大二物理上-课件-第12章-波动

x 2π x
u
λ
y(x,t) y(x,t T ) (波具有时间的周期性)
12– 1
第十二章 平面简谐波
波线上各点的简谐运动图
12– 1
第十二章 平面简谐波
y
A c os [ (t
x) u
0]
A c os [2 π
(t T
x
)
0
]
2) 当 t 一定时,波函数表示该时刻波线上各
u
x
点 O 振动方程 yO Acos(t 0 )
波 函 数
y
A c os [ (t
-
x) u
0]
u 沿x 轴正向
y
A c os [ (t
x) u
0]
u 沿x 轴负向
12– 1
第十二章 平面简谐波
二 波函数的物理意义
y
A c os [ (t
x) u
0]
A c os [2 π
(t T
x
)
0
]
1) 当 x 固定时, 波函数表示该点的简谐运
一 机械波的形成
机械波:机械振动在弹性介质中的传播.
产生条件:1)波源;2)弹性介质.
注意
媒质中任一质元在平衡位置附近振动,不“随 波
逐流”(如河中足球) 即:波传播的是振动,位相,能量,而非质元
波是运动状态的传播,介质的质点并不随波传播.
12– 1
第十二章 平面简谐波
二 横波与纵波
横波:质点振动方向与波的传播方向相垂直的波. (仅在固体中传播 )
(t
-
6) 20
- π ]cm 3
0.10cos[4π t - 23π ]cm
2024年大学物理波动课件

大学物理波动课件引言波动是物理学中的一个重要概念,涉及到的领域广泛,包括声波、电磁波、机械波等。
本文旨在介绍大学物理中波动的基本概念、波动方程、波动特性以及波动在各个领域的应用,以帮助读者更好地理解和掌握波动知识。
一、波动的基本概念1.1波的定义波是一种能量传递的方式,它是由振源产生的振动在介质中传播的过程。
波可以分为两大类:机械波和电磁波。
机械波需要介质来传播,如声波和水波;而电磁波不需要介质,可以在真空中传播,如光波和无线电波。
1.2波的参数波的参数包括波长、波速、频率和振幅。
波长是相邻两个波峰(或波谷)之间的距离,通常用λ表示;波速是波在介质中传播的速度,通常用v表示;频率是单位时间内通过某一点的完整波的个数,通常用f表示;振幅是波的振动幅度,即波的最大偏离度。
二、波动方程2.1机械波方程机械波的波动方程可以表示为:y=Asin(2πft2πx/λ+φ)其中,y表示介质中某一点的位移,A表示振幅,f表示频率,λ表示波长,x表示该点距离振源的距离,φ表示初相位。
2.2电磁波方程电磁波的波动方程可以表示为:E=E0sin(2πft2πx/λ+φ)其中,E表示电场强度,E0表示振幅,其他参数与机械波方程相同。
三、波动特性3.1干涉干涉是指两个或多个波相遇时,它们的振动叠加产生的现象。
当两个波峰相遇时,振动加强;当波峰与波谷相遇时,振动减弱。
干涉现象广泛应用于光学、声学等领域。
3.2衍射衍射是指波传播过程中遇到障碍物或通过狭缝时,波的传播方向发生改变的现象。
衍射现象广泛应用于光学、声学等领域,如光栅、声呐等。
3.3折射折射是指波从一种介质传播到另一种介质时,波的传播方向发生改变的现象。
折射现象广泛应用于光学领域,如透镜、棱镜等。
3.4反射反射是指波遇到界面时,部分能量返回原介质的现象。
反射现象广泛应用于光学、声学等领域,如镜子、回声等。
四、波动应用4.1声学领域波动在声学领域有着广泛的应用,如声音的产生、传播、接收和利用。
波动大学物理-PPT文档资料

Y(x,t)的函数形式称为波函数,它也就 是波传播时媒质质元的运动函数。
x 称为行波的波函数。 y (x ,t) f ( t ) u
(二) 简谐波(波函数) 一、一维简谐波的表达式(波函数) 讨论:沿+x方向传播的一维简谐波(u , )
波速u 假设 : 媒质无吸收 参考点 a 任一点p (质元振幅均为A) o ·x d · 已知:参考点a的振动表达式为 x
§1
机械波的产生和传播
一. 机械波的产生 1. 产生条件: 波源 媒质 2. 弹性波: 机械振动在弹性媒质中的传播 • 横波 • 纵波 3. 简谐波: 波源作简谐振动, 在波传到的区域, 媒质中的质元均作简谐振动 。
· · · · · · · ·t = 0 · · · · · ·· · · · · · · · · · · · · · ·· · · · · · · · · · · · · · ·· · · · · ·t = T/4 · · · · · · · · · ·· · · · · · · · · · · · · · t = T/2 · · · · · · · · · · · ·t = 3T/4 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · t=T · · · · ·· ·
结论:
u
a b 沿波的传播 · · 方向 , 各质元的相 x 位依次落后。 2 图中b点比a点的相位落后 x
传播方向
x
三. 波形曲线(波形图) y u t • 不同时刻对应有 o 不同的波形曲线 • 波形曲线能反映横 波 纵波的位移情况 四. 波的特征量 1.波长 : 两相邻同相点间的距离 2. 波的频率 : 媒质质点(元)的振动频率 即单位时间传过媒质中某点的波的个数 3. 波速u : 单位时间波所传过的距离
大学物理《波动》课件

t 1.0s
波形方程
y 1.0 cos( π - π x) 2
1.0 sin(π x)
y/m
1.0
o
2.0
x/m
-1.0
t 1.0 s 时刻波形图
第二节 波动学基础
3) x 0.5m 处质点的振动规律并做图 . y (1.0m) cos[2 π( t - x ) - π] 2.0s 2.0m 2
x 0.5m 处质点的振动方程
y (1.0m)cos(π t - π)
y
y/m
3
1.0
3*
2
4
4O
2
0 * 1.0 * 2.0 * t / s
1 -1.0*1
*
x 0.5 m 处质点的振动曲线
第二节 波动学基础
讨 论 1)给出下列波函数所表示的波的传播方向
和 x 0 点的初相位.
y -Acos2π ( t - x )
-
x)
2π T 2π
C
B
u B
TC
2π d dC
第二节 波动学基础
3 ) 如图简谐波 以余弦函数表示,
求 O、a、b、c 各
点振动初相位.
(-π ~ π )
t =0 A y
Oa
-A
A
O
y o π
O
A
O
y
a
π 2
O A
u
b c
A
y
y
t=T/4
x
b 0
c
-π 2
§8.5 波的干涉与衍射
波程差 r2 - r1
k k 0,1,2,
A A1 A2 振动始终加强
3 ) (k 1 2) k 0,1,2,
大学物理II(二)2波动
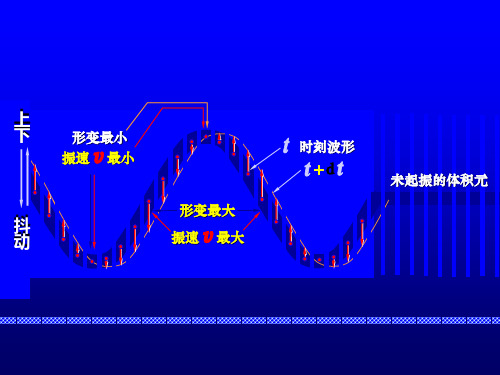
体积元总能量
x W Wk Wp (V ) A sin (t ) u
u p RT M mol
u F l
: 比热容比
在柔软绳索和弦线中,横波的波速
F :绳中的张力 l :单位长度的质量
三.机械波的波长、周期和频率
a、波长 (一个完整波形的长度) 沿波传播方向、位相差为2的两个 质点间的距离(即相邻的运动状态相同的 两个质点间的距离)
设体积元体积为 V, 质量为m=V
1 1 2 2 Wk m v (V )v 2 2 1 x 2 2 2 V A sin (t ) 2 u
2.弹性势能 体积元应变:y / x
f S E l l
y 体积元所受弹性力 f ES ky x
横波:质元的振
动方向与波动的 传播方向垂直
特征:波峰、波谷
纵波:质元的振
动方向与波动传 播方向平行 特征:密部、疏部
三.波线和波阵面 波射线(波线):波的传播方向 波阵面 ( 波面 ) : 某一时刻振动相位相 同的各点连成的面(同相面) 波前:最前面的波面 各向同性媒介中,波线与波面垂直
讨论: 1.上式反映一切平面波的共同特征 2.服从该式的任何物理量或系统,一定 是以u速度沿x方向传播的平面波
y 1 y 2 2 2 x u t
2 2
3.波线上任一点的振动速度
y v A sin t x u t
是 t 的函数,而波的传播速度u(即相速), 与 t 无关
----体积模量
f
1 1 V 压缩系数 K V0 p
2.弹性体的拉伸和压缩变形 设柱体受拉力作用
应力 f / S 应变 l / l 定义 E
大学物理解题方法(第2章 波动)

6. 波的叠加 (1) 波的叠加原理 1) 独立性 2) 位移可加性 (2) 驻波 •“驻”字的三层含义 驻波波形不传播;驻波相位不传播; 驻波不传播能量。 •两相邻波节或波腹间的距离为 /2 •同一分段中的各质元振动相位相同; •相邻分段中的质元振动相位相反。 •半波损失。波疏介质→波密介质
2.设在介质中有一振源作简谐振动并产生平面简谐波。 (1)振动的频率与波动频率是否相同? (2)振动速度与波速有何不同?方向是否相同?
解:(1)波源相对介质静止时,相同。 波源相对介质运动时,不相同。 (2)振动速度为 A sin( t ) 速度随时间作周期性变化; 而在同一介质中,波传播的速度 u 为定值。
2
5
5 yo 0.02 cos( t ) 2 2
11 2
5. 如下图所示,一平面简谐波以速度 u 沿 x 轴正 向传播,O点为坐标原点,已知P点的振动表达式 为 y P A cos t
则波动表达式为何?C点的振动表达式为何?
u
O d P
x
2d
C
x
解:波动是振动状态的传播, 沿着波的传播方向,振动总是依次延迟的;
7. 惠更斯原理 --- 仅解决波的传播方向问题 介质中任一波阵面上的各点, 都可以看作是发射球面子波的波源, 其后任一时刻,这些子波的包迹就是新的波阵面。
t时刻波面 t+t时刻波面
波传播方向
· · · · ·
ut
波的反射定律:i=i’ 折射定律: sin i u1 n21 sin r u2
2d
A cos t
2n
d
u
u 6. 一右行的平面简谐波 波疏 波密 在波密界面处发生全反射, O 在某一时刻的波形如图所 示。试画出同一时刻反射 u 波的波形图,再画出经 波疏 波密 1/4周期后入射波与反射 反 射 O 波的波形图。 波 解: 入射波在O点引起的振动方向是向下的; 反射点O必须是波节; 反射波在O点引起的振动方向应向上;
大学物理波动课件(2024)

电磁波能量传递与衰减
能量传递
电磁波传递能量时,其能量与振幅的平方成正比。在传播过程中,电磁波的能量可以转化为其他形式的能量,如 热能、机械能等。
衰减
电磁波在传播过程中会受到各种因素的影响而逐渐减弱,如空气的吸收、物体的反射和折射等。衰减的程度取决 于电磁波的频率、传播介质和距离等因素。为了减小衰减,可以采取一些措施,如使用高增益天线、选择合适的 传播介质等。
2024/1/28
12
电磁波谱及应用领域
2024/1/28
电磁波谱
按照频率从低到高,电磁波谱包括无线电波、微波、红外线、可见光、紫外线、 X射线和伽马射线等。
应用领域
电磁波在通信、广播、电视、雷达、遥感、医疗、科学研究等领域有广泛应用。 例如,无线电波用于移动通信和广播,微波用于卫星通信和微波炉,红外线用于 遥控和夜视仪,可见光用于照明和显示,紫外线用于消毒和防伪等。
机械波可以用波动方程来描述,波动 方程反映了波的振幅、频率、波长等 参数与传播距离和时间的关系。
9
机械波能量传递与衰减
能量传递
机械波在传播过程中,介质中的质点通过振动将能量传递给相邻的质点,从而实现能量的传递 。波的振幅越大,传递的能量越多。
衰减
机械波在传播过程中,由于介质的吸收、散射等原因,波的振幅会逐渐减小,这种现象称为波 的衰减。衰减程度与介质的性质、波的频率等因素有关。
2024/1/28
8
机械波参数与描述方法
波长
波长是指相邻两个同相位点之间的距 离,用λ表示。波长反映了波的空间
周期性。
波速
波速是指波在介质中传播的速度,用 v表示。波速与波长和频率的关系为
v=λf。
2024/1/28
大学物理课件-波动

平面波、柱面波與球面波
平面波的波陣面為平面,對應波函數:
u(x,t) Acost kx 0
柱面波的波陣面為柱面,對應波函數:
u(x,t)
a r
cost
kr
0
,
r
x2 y2
球面波的波陣面為球面,對應波函數:
u(
x,
t)
b r
cost
kr
0
,
r
x2 y2 z2
平面波、柱面波與球面波
一維波動方程及其通解
問:一靜止觀察者在機車前和機車後所聽到的聲音頻率 各為多少?已知空氣中聲波的速率為340m/s。
解:
v
340
f前
v vs
f
500 531Hz
340 20
f后
v
v vs
f
340 500 472Hz 340 20
例:雷達測速儀
波源靜止,接收器運動(vs=0) 對汽車而言,頻率變為:
F (x) E u S , F (x) G u S
x x
x x
均勻彈性棒中縱波和橫波的波動方程
F
F+dF
O
x
x+dx x
根據楊氏/剪切模量的定義,在x+dx處的拉伸/剪切
應力應當為:
u
F(x) E S ,
質元所受合力
x xdx
u F(x) G S
x xdx
F(x
dx)
F ( x)
E
u x
S
將其改寫為:
u(x,t) A(x) cost
A(
x)
2
A0
c
osk
x
各質點都在作同 頻率的簡諧運動
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
波动方程
任意点比参考点晚振动,减去传播时间; 任意点比参考点早振动,加上传播时间。
例. 已知 P 点的振动方程
Y
u
p
L
y p A cos( t )
X
0
x
试写以 O 为原点的波动方程
x L u
解:选择 P 点为参考点,任选一点‘ x ’ 波由参考点传到 x 点,需时间 : 波动方程为:
2 2 2
x u
)
结论: (1)波动动能与势能数值 相同,位相相同。同时变大, 同时变小。
Wk Wk
p
vm
u
最大则 W 也最大,如平衡位置。 与振动能量 最小则 W 也最小,如最大位移处。 不 同!
p
(2) V 中 Δ
W 总随 t
W总 Wk W
p
VA sin ( t
2 2 2
Wk 1 2 1 2
2
mv
2
1 2
m(
2
y t
2
ΔV
)
2
u
x
Δ VA sin ( t
x u
)
形变势能
W
p
? 可证明 W p W k
1 2
Δ VA sin ( t
2 2 2
x u
)
W p Wk
1 2
Δ VA sin ( t
2 2
r1
S1
S2
A 1 4 r1
2
2
2 2 2 A 2 4 r2
A 1 r1 A 2 r2
1 r
r2
A1 A2
r2 r1
A
y
A r
cos ( t
r u
)
振动的位相随距离的增加而落后的关系与平面波类似
例1.用聚焦超声波的方法在水中可以产生强度达到
I 120 kW cm
大学物理 电子教案
(波动2)
波动
第1节 第2节
机械波
机械波的产生和传播 波的描述
第3节
第4节 第5节 第6节
简谐波 波动方程
波的能量 多普勒效应 机械波的干涉
第7节 机械驻波 第8节 惠更斯原理和波的衍射
回顾: 波动方程的建立与意义 波动是振动的传播。
y
u
o
x
p
x
设原点o 振动方程为 y o A cos( t )
声强级(dB)
0 20 50 80 90 100 120 120 150 210
响度
轻 正常 响 很响 震耳
§5 多普勒效应 当波源S或接收器R相对于介质运动时, 接收器所测 得的频率 不等于波源振动频率 的现象。
• 参考系 : 介质
• 波源振动频率
S
·
Vs
VR
· R
1. 波源和接收器都静止 (VS=0,VR=0)
2
A ,
2
2
2、能流、能流密度 (1)能流 P :单位时间通过某面的能量
P wu Δ s
平均能流
P w us
u
Δs
(2)能流密度 i :单位时间内通过 垂直于波的传播方向单位面积的能量。
i P Δs wu
P w u Δ s cos
u
n
Δs
u
平均能流密度I(又称波的强度,如光强、声强):
1 . 27 10
5
m
因在水中传播的声波是纵波,此振幅值表示媒质各体积元 作振动时,在波线方向上相对于各自平衡位置的最大位移。
★声波 一般意义上的声波,是指能引起人的听觉、 频率在 20 ~ 20 000 Hz 的机械波,又称声音或声。 在声学中,声波的频率范围包括 10 4 10 12 Hz 的机械波。 声强 声波的平均能流密度 单位: 米 –2 ( W· –2 ) 瓦· m 10
'
10 Hz
3
uV
R收到 2 拍频
u u V
2
u uV '
u V
反射壁发出
'
频率
1129 Hz
1 129 Hz
注意:
1)若观察者与波源的运动不在两者的连线上 只须将速度在连线上的分量代入公式 2)光波的多普勒效应 设光源和接收器的相对速度V
x u
)
、 x 变,不守恒 ! 能量传输! 最大位移 平衡位置,能量增大,从前面输入; 平衡位置 最大位移,能量减小,向后面输出。
(3)能量密度:单位体积中的能量
w W
V
A sin ( t
2 2 2
x u
)
能量密度周期平均值
w 1 T
T 0
wdt
1 2
A
2
变大 变小
s
VR
R
R 远离 s 则 2
u VR u
u
3. 接收器静止,波源运动(VR=0,VS 0)
波长变化,左边变长,右边变短
V sT uT V sT
'
'
u Vs
s
Vs
R
V sT uT V sT
'
u Vs
2
的超声波,设该超声波的频率为
1000
Kg m
3
500 kHz
,水的密度为
s
,其中声
速为
u 1500 m
。 求这时液体质元振动的振幅。
1 A 2 2 u 解: I 2
A 1
2I u
2
7
1
2I u
1 3 2 500 10
2 120 10 1000 1500
I i P Δs wu 1 2
A u
2 2
A
2
单位:W 2 m 例:讨论在无吸收的理想介质中球面波的振幅 对无吸收的理想介质,一个周期内通过两个波 面的能量应该相等。 解:通过波面 S1, S2 的平均能流应相等 P1 P 2
P w uΔs 1
机械波
A us
波一发出就会脱离波源运动。 每隔一周期画一波面,间隔为 , 波速 u 与波源和 接收器无关。 单位时间通过 R 的波的个数, 即为 R 收到的频率 u
1
s
R
u
2. 波源静止,接收器运动 (VS =0, VR 0)
R 收到的频率为
2
u VR u VR u u VR u
y A cos[ ( t
xL u
xL u
) ]
Y
例. 若是下图情况,波动方程如何?
u
P
y A cos[ ( t
) ]
X
x
0
L
x
y A cos[ ( t
L x u
) ]
例.给出波形曲线 由波动方程 y=f(x,t) 令 作出的函数图线。
t=t0
0 1
, 由y=f(x) u =12(m.s-1)
y(m )
如右图, 可看出:
0
1
2
4
x(m )
3
10
t0=T/4 t=0 A=0.1m, =4m, T= /u = 4/12=1/3(s) =2/T=6
20各质点在 t0 时刻的实际位置(对横波)。
30各质点在 t0 时刻(或下时刻)的运动方向。
3
V s 10 m/s
R
S
u 330 m/s
求:(1)R 直接从 S 收到的频率?
1
u u Vs
330 330 10
10
3
970 Hz
4
u ቤተ መጻሕፍቲ ባይዱR u VS
(2)
R 从反射波 收到的频率?
反射壁对入射波而言,相当于观察者; 反射壁对反射波而言,相当于波源。 反射壁 收到的频率
3
2
4
50 根据 A、 、0 坐标原点振动方程:
可写出 波动方程。
y 0 0 1 cos( 6 t )
波动方程: y 0 1 cos[6 ( t
x 12
) ](m)
§4 波的能量 1、波的能量 不论纵波和横波各媒质块中都有振动动能和 形变势能。 u x) 设 y A cos ( t u 考虑 Δ V体积中物质的 ΔV 振动动能
40各质点的初位相(找出 t=0 时刻的波形图即可)。
50根据波形曲线 可写出波动方程。
40 由旋转矢量知 0、1、2、3、4等各点的初位相。
1
y(m )
u =12(m.s-1)
2
y
0
4
3
0
1
2
0 1
t=0
x(m )
4
3
t=T/4
0
1
2
2 0
、u
2
u u Vs
330 330 10
10
3
1030 Hz
反射壁接收与发出的频率相同,
故R从反射波收到的频率为1030Hz. (3)R收到的拍频?
2
R
S
V
1 1030 970 60 Hz
