空间向量的坐标运算(人教A版)(含答案)
数学人教A版选择性必修第一册13.2空间向量运算的坐标表示课件
2、用向量法解决立体几何问题的一般步骤
①建系，读取点坐标 ②构造向量并坐标化 ③进行向量的坐标运算，获得几何结论
且 a ⊥b .求x的值 且a //b. 求x+y的值 且a与b的夹角
例题分析
如图，在正方体ABCD-A₁BC₁D₁中 ， 点E,F 分别是AB,CD 的一个四等分点， 求BE 与 DF₁ 所成角的余弦值.
法一：几何法(定义) 法二：向量法
பைடு நூலகம்题分折
如图，在正方体ABCD-A₁BC₁D₁ 中 ， 点E,F 分别是AB,CD 的一个四等分点， 求BE 与 DF₁ 所成角的余弦值.
法一：几何法(定义) 法二：向量法
【方法提炼】①建系、读取点坐标 ②构造向量并坐标化 ⑤进行向量的坐标运算， 获得几何结论
变式1:若点E,F 分别是BB,D₁B₁的中点，求证EF⊥DA.
变式2:G 是 BB₁ 的一个靠近点B 的四等分点，H 为DD₁ 上的一点， 若GH⊥DF, 试确定H点的位置.
演练反馈
减法： a-b=(a₁-a₂,b₁-b₂,c₁c₂)
你能对这些运
算的生标表示
加以证明吗?
数乘： λa=(λa,λb,2c₁)
O
数量积：抓a.住b=根aa₂本+b：₁b₂空+c₁间C₂向量的坐标表示!
探究新知
2、 空间向量平行与垂直的坐标表示
平行：a lIb(b≠0)→a=λb⇔a=λa₂,b₁=λb₂,c₁=λc₂ (λ∈R)
探究新知
在空间直角坐标系中，已知点 A(a,b,c₁),B(a₂,b₂,C₂),
新教材2022版人教A版数学选择性必修第一册学案：1.3.2 空间向量运算的坐标表示(含解析)
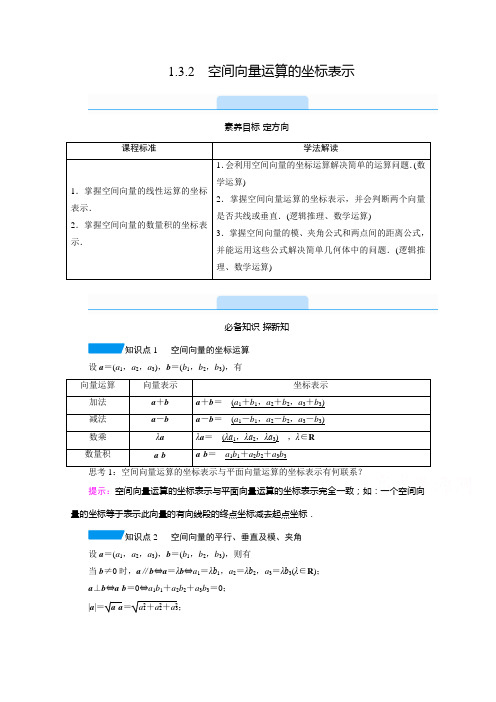
1.3.2空间向量运算的坐标表示素养目标·定方向课程标准学法解读1．掌握空间向量的线性运算的坐标表示．2．掌握空间向量的数量积的坐标表示．1．会利用空间向量的坐标运算解决简单的运算问题．(数学运算)2．掌握空间向量运算的坐标表示，并会判断两个向量是否共线或垂直．(逻辑推理、数学运算)3．掌握空间向量的模、夹角公式和两点间的距离公式，并能运用这些公式解决简单几何体中的问题．(逻辑推理、数学运算)必备知识·探新知知识点1 空间向量的坐标运算设a＝(a1，a2，a3)，b＝(b1，b2，b3)，有向量运算向量表示坐标表示加法a＋b a＋b＝__(a1＋b1，a2＋b2，a3＋b3)__减法a－b a－b＝__(a1－b1，a2－b2，a3－b3)__数乘λaλa＝__(λa1，λa2，λa3)__，λ∈R数量积a·b a·b＝__a1b1＋a2b2＋a3b3__提示：空间向量运算的坐标表示与平面向量运算的坐标表示完全一致；如：一个空间向量的坐标等于表示此向量的有向线段的终点坐标减去起点坐标．知识点2 空间向量的平行、垂直及模、夹角设a＝(a1，a2，a3)，b＝(b1，b2，b3)，则有当b≠0时，a∥b⇔a＝λb⇔a1＝λb1，a2＝λb2，a3＝λb3(λ∈R)；a⊥b⇔a·b＝0⇔a1b1＋a2b2＋a3b3＝0；|a|＝a·a＝a21＋a22＋a23；cos 〈a ，b 〉＝a ·b|a ||b |＝a 1b 1＋a 2b 2＋a 3b 3a 21＋a 22＋a 23b 21＋b 22＋b 23．知识点3 空间两点间的距离公式设P 1(x 1，y 1，z 1)，P 2(x 2，y 2，z 2)是空间中任意两点，则P 1P 2＝|P 1P 2→|＝__(x 2－x 1)2＋(y 2－y 1)2＋(z 2－z 1)2__．思考2：已知点A (x ，y ，z )，则点A 到原点的距离是多少？ 提示：OA ＝|OA →|＝x 2＋y 2＋z 2．关键能力·攻重难题型探究题型一 空间向量的坐标运算典例1 已知在空间直角坐标系中，A (1，－2,4)，B (－2，3,0)，C (2，－2，－5)．(1)求AB →＋CA →，CB →－2BA →，AB →·AC →；(2)若点M 满足AM →＝12AB →＋34AC →，求点M 的坐标；(3)若p ＝CA →，q ＝CB →，求(p ＋q )·(p －q )．[分析] 先由点的坐标求出各个向量的坐标，再按照空间向量运算的坐标运算法则进行计算求解．[解析] (1)因为A (1，－2,4)，B (－2,3,0)，C (2，－2，－5)， 所以AB →＝(－3,5，－4)，CA →＝(－1,0,9)． 所以AB →＋CA →＝(－4,5,5)．又CB →＝(－4,5,5)，BA →＝(3，－5,4)， 所以CB →－2BA →＝(－10,15，－3)． 又AB →＝(－3,5，－4)，AC →＝(1,0，－9)， 所以AB →·AC →＝－3＋0＋36＝33．(2)由(1)知，AM →＝12AB →＋34AC →＝12(－3,5，－4)＋34(1，0，－9)＝⎝⎛⎭⎫－34，52，－354， 若设M (x ，y ，z )，则AM →＝(x －1，y ＋2，z －4)，于是⎩⎪⎨⎪⎧ x －1＝－34，y ＋2＝52，z －4＝－354，解得⎩⎪⎨⎪⎧x ＝14，y ＝12，z ＝－194，故M ⎝⎛⎭⎫14，12，－194． (3)由(1)知，p ＝CA →＝(－1,0,9)，q ＝CB →＝(－4,5,5)． (方法1)(p ＋q )·(p －q )＝|p |2－|q |2＝82－66＝16． (方法2)p ＋q ＝(－5,5,14)，p －q ＝(3，－5,4)， 所以(p ＋q )(p －q )＝－15－25＋56＝16．[规律方法] 空间向量的坐标运算注意以下几点：(1)一个向量的坐标等于这个向量的终点的坐标减去起点的坐标．(2)空间向量的坐标运算法则类似于平面向量的坐标运算，牢记运算公式是应用的关键． (3)运用公式可以简化运算：(a ±b )2＝a 2±2a ·b ＋b 2；(a ＋b )·(a －b )＝a 2－b 2． 【对点训练】❶ 在△ABC 中，A (2，－5,3)，AB →＝(4,1,2)，BC →＝(3，－2,5)． (1)求顶点B ，C 的坐标； (2)求CA →·BC →；(3)若点P 在AC 上，且AP →＝12PC →，求点P 的坐标．[解析] (1)设B (x ，y ，z )，C (x 1，y 1，z 1)，所以AB →＝(x －2，y ＋5，z －3)，BC →＝(x 1－x ，y 1－y ，z 1－z )． 因为AB →＝(4,1,2)， 所以⎩⎪⎨⎪⎧x －2＝4，y ＋5＝1，z －3＝2，解得⎩⎪⎨⎪⎧x ＝6，y ＝－4，z ＝5，所以点B 的坐标为(6，－4,5)．因为BC →＝(3，－2,5)， 所以⎩⎪⎨⎪⎧x 1－6＝3，y 1＋4＝－2，z 1－5＝5，解得⎩⎪⎨⎪⎧x 1＝9，y 1＝－6，z 1＝10，所以点C 的坐标为(9，－6,10)．(2)因为CA →＝(－7,1，－7)，BC →＝(3，－2,5)， 所以CA →·BC →＝－21－2－35＝－58．(3)设P (x 2，y 2，z 2)，则AP →＝(x 2－2，y 2＋5，z 2－3)，PC →＝(9－x 2，－6－y 2,10－z 2)，于是有(x 2－2，y 2＋5，z 2－3)＝12(9－x 2，－6－y 2,10－z 2)，所以⎩⎪⎨⎪⎧ x 2－2＝12(9－x 2)，y 2＋5＝12(－6－y 2)，z 2－3＝12(10－z 2)，解得⎩⎪⎨⎪⎧x 2＝133，y 2＝－163，z 2＝163.故点P 的坐标为⎝⎛⎭⎫133，－163，163． 题型二 空间向量的平行与垂直典例2 已知空间三点A (－2,0,2)，B (－1,1,2)，C (－3，0,4)．设a ＝AB →，b ＝AC →．(1)若|c |＝3，c ∥BC →，求c ；(2)若k a ＋b 与k a －2b 互相垂直，求k ．[分析] (1)根据c ∥BC →，设c ＝λBC →，则向量c 的坐标可用λ表示，再利用|c |＝3求λ值； (2)把k a ＋b 与k a －2b 用坐标表示出来，再根据数量积为0求解． [解析] (1)∵BC →＝(－2，－1,2)且c ∥BC →， ∴设c ＝λBC →＝(－2λ，－λ，2λ)(λ∈R )． ∴|c |＝(－2λ)2＋(－λ)2＋(2λ)2＝3|λ|＝3，解得λ＝±1．∴c ＝(－2，－1,2)或c ＝(2,1，－2)． (2)∵a ＝AB →＝(1,1,0)，b ＝AC →＝(－1,0,2)，∴k a ＋b ＝(k －1，k,2)，k a －2b ＝(k ＋2，k ，－4)． ∵(k a ＋b )⊥(k a －2b )，∴(k a ＋b )·(k a －2b )＝0， 即(k －1，k,2)·(k ＋2，k ，－4)＝2k 2＋k －10＝0， 解得k ＝2或k ＝－52．[规律方法] 向量平行与垂直问题主要题型 (1)平行与垂直的判断．(2)利用平行与垂直求参数或解其他问题，即平行与垂直的应用．解题时要注意：①适当引入参数(比如向量a ，b 平行，可设a ＝λb )，建立关于参数的方程；②最好选择坐标形式，以达到简化运算的目的．【对点训练】❷ 已知a ＝(λ＋1,1,2λ)，b ＝(6,2m －1,2)． (1)若a ∥b ，分别求λ与m 的值；(2)若|a |＝5，且a 与c ＝(2，－2λ，－λ)垂直，求a ． [解析] (1)由a ∥b ，得(λ＋1,1,2λ)＝k (6,2m －1,2)， ∴⎩⎪⎨⎪⎧λ＋1＝6k ，1＝k (2m －1)，2λ＝2k ，解得⎩⎪⎨⎪⎧λ＝k ＝15，m ＝3.∴λ＝15，m ＝3．(2)∵|a |＝5，且a ⊥c ，∴⎩⎪⎨⎪⎧(λ＋1)2＋12＋(2λ)2＝5，(λ＋1，1，2λ)·(2，－2λ，－λ)＝0，化简，得⎩⎪⎨⎪⎧5λ2＋2λ＝3，2－2λ2＝0，解得λ＝－1．因此，a ＝(0,1，－2)．题型三 空间向量夹角及长度的计算 角度1 向量法求夹角典例3 在棱长为1的正方体ABCD －A 1B 1C 1D 1中，E ，F 分别为D 1D ，BD 的中点，G 在棱CD 上，且CG ＝14CD ．(1)求证：EF ⊥B 1C ；(2)求cos 〈EF →，C 1G →〉．[解析] (1)如图，建立空间直角坐标系Dxyz ，D 为坐标原点，则有E ⎝⎛⎭⎫0，0，12，F ⎝⎛⎭⎫12，12，0，C (0,1,0)，C 1(0,1,1)，B 1(1,1,1)，G ⎝⎛⎭⎫0，34，0． EF →＝⎝⎛⎭⎫12，12，0－⎝⎛⎭⎫0，0，12＝⎝⎛⎭⎫12，12，－12， B 1C →＝(0,1,0)－(1,1,1)＝(－1,0，－1)．所以EF →·B 1C →＝12×(－1)＋12×0＋⎝⎛⎭⎫－12×(－1)＝0，所以EF →⊥B 1C →，即EF ⊥B 1C ． (2)因为C 1G →＝⎝⎛⎭⎫0，34，0－(0,1,1)＝⎝⎛⎭⎫0，－14，－1． 所以|C 1G →|＝174．又EF →·C 1G →＝12×0＋12×⎝⎛⎭⎫－14＋⎝⎛⎭⎫－12×(－1)＝38，|EF →|＝32， 所以cos 〈EF →，C 1G →〉＝EF →·C 1G →|EF →||C 1G →|＝5117．角度2 向量法求模典例4 如图，在直三棱柱ABC －A 1B 1C 1中，CA ＝CB ＝1，∠BCA ＝90°，棱AA 1＝2，M ，N 分别是AA 1，CB 1的中点．(1)求BM ，BN 的长；(2)求△BMN 的面积．[分析] 建立空间直角坐标系，写出B ，M ，N 等点的坐标，从而得出BM →，BN →的坐标．然后利用模的公式求得BM ，BN 的长度．对于(2)，可利用夹角公式求得cos ∠MBN ，再求出sin ∠MBN 的值，然后套用面积公式计算．[解析] 以C 为原点，以CA ，CB ，CC 1所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系(如图)．则B (0,1,0)，M (1,0,1)，N ⎝⎛⎭⎫0，12，1． (1)∵BM →＝(1，－1,1)， BN →＝⎝⎛⎭⎫0，－12，1， ∴|BM →|＝12＋(－1)2＋12＝3， |BN →|＝02＋⎝⎛⎭⎫－122＋12＝52． 故BM 的长为3，BN 的长为52． (2)S △BMN ＝12·|BM |·|BN |·sin ∠MBN ．∵cos ∠MBN ＝cos 〈BM →，BN →〉＝BM →·BN →|BM →||BN →|＝323×52＝155，∴sin ∠MBN ＝1－⎝⎛⎭⎫1552＝105，故S △BMN ＝12×3×52×105＝64．即△BMN 的面积为64．[规律方法] 利用空间两点间的距离公式求线段长度问题的一般步骤【对点训练】❸ 已知点M (3,2,1)，N (1,0,5)，求： (1)线段MN 的长度；(2)到M ，N 两点的距离相等的点P (x ，y ，z )的坐标满足的条件．[解析] (1)根据空间两点间的距离公式得线段MN 的长度|MN |＝(3－1)2＋(2－0)2＋(1－5)2＝26， 所以线段MN 的长度为26．(2)因为点P (x ，y ，z )到M ，N 两点的距离相等，所以有下面等式成立： (x －3)2＋(y －2)2＋(z －1)2 ＝(x －1)2＋(y －0)2＋(z －5)2，化简得x ＋y －2z ＋3＝0，因此，到M ，N 两点的距离相等的点P (x ，y ，z )的坐标满足的条件是x ＋y －2z ＋3＝0．易错警示混淆两向量平行与两向量同向典例5 已知向量a ＝(1,2，－1)，b ＝(m ，m 2＋3m －6，n )，若向量a ，b 同向，求实数m ，n 的值．[错解] 由题意可知a ∥b ，所以m 1＝m 2＋3m －62＝n－1，即⎩⎪⎨⎪⎧ m 2＋3m －6＝2m ，n ＝－m ，解得⎩⎪⎨⎪⎧ m ＝－3，n ＝3或⎩⎪⎨⎪⎧m ＝2，n ＝－2. 故m ＝－3，n ＝3或m ＝2，n ＝－2．[辨析] “两向量同向”是“两向量平行”的充分不必要条件．错解中错认为“同向”就是“平行”，从而导致错误．[正解] 由题意可知a ∥b ，所以m 1＝m 2＋3m －62＝n －1，即⎩⎪⎨⎪⎧m 2＋3m －6＝2m ，n ＝－m ， 解得⎩⎪⎨⎪⎧ m ＝－3，n ＝3或⎩⎪⎨⎪⎧m ＝2，n ＝－2.当m ＝－3，n ＝3时，b ＝(－3，－6,3)＝－3a ，向量a ，b 反向，不符合题意，舍去； 当m ＝2，n ＝－2时，b ＝(2,4，－2)＝2a ，向量a ，b 同向，符合题意． 综上，m ＝2，n ＝－2．。
1.3 空间向量的坐标表示及其运算(同步课件)-【优选组合】2021-2022学年高二(人教A版20
∴ || =
22 + 12 + (−3)2 = 14, || =
32 + (−2)2 + (−1)2 = 14, ⋅
= 2 × 3 + 1 × (−2) + (−3) × (−1) = 7,
∴ cos = cos＜, ＞ =
=
−4
3×2 5
=
2 5
−
15
.
12 + 22 + (−2)2 = 3, || =
探究点三 空间向量坐标运算的运用
例 [2021山东师大附中高二月考] 已知在空间直角坐标系中
,(0,2,3),(−2,1,6),(1, −1,5).
（1） 若点在直线上,且 ⊥ ,求点的坐标;
= (4,2,0), = (−1,2, −1),所以 ⋅ = −4 + 4 + 0 = 0,所以 ⊥ ,
即 ⊥ ,故B中结论正确;
易知 = − = (2,3,4) ,若 // ,则存在实数 ,使得 =
−1 = 2,
,即 ቐ 2 = 3, 此方程组无解,故 不平行于 ,故C中结论错误;
读 式.
标运算解决立体几何问题.
3.能用空间向量的坐标运算解决
平行、垂直、夹角、长度等问题.
要点一 空间向量运算的坐标表示
设 = (1 , 2 , 3 ), = (1 , 2 , 3 )，空间向量的坐标运算法则如下表所示：
运算
加法
减法
数乘
数量积
坐标表示
1 1 + 2 2 + 3 3
2. 已知 = (1,1,0), = (0,1,1), = (1,0,1), = − , = + 2 − ,则 ⋅
空间向量及其运算的坐标表示高中数学人教A版(2019)选择性必修第一册
【解析】如图，建立空间直角坐标系 Oxyz，
则(3,0,0)，(0,3,0)，
又由 = 2，所以(1,2,0)，
因为(3,3,0)，′(0,3,3)， = 2 ′ ，所以(1,3,2),
所以 = 1,3,2 − 1,2,0 = (0,1,2)，即 = 02 + 12 + 22 = 5，
③ 2 ⋅ − , ④ + ⋅ − .
【解析】 + = 2, −1 − 2 + 0, −1,4 = 2, −2,2
⋅ = 2, −1, −2 ⋅ 0, −1,4 = 2 × 0 + −1 × −1 + −2 × 4 = −7
2 ⋅ − = −2 ⋅ = −2 × −7 = 14
1
2
1− +0
3∙
15
15
.
5
4
=
15
15
.
五、课堂小结
1、向量坐标运算一些技巧
2
2
(1)相关公式的运用：如 + ⋅ − = − =
或者 + ⋅ + = +
2
(2)可以直接代入坐标运算，也可先化简再带入坐标运算
2
−
2
2、空间向量垂直、平行问题
1.3 空间向量及其运算的
坐标表示提升课
学业要求
学科素养
1.能够运用空间向量坐标法解决一
1．通过空间直角坐标系的研究，培
些简单的实际问题．
养直观想象的核心素养.
2.能够理解空间向量坐标运算和作
2．通过空间向量的坐标运算，培养
空间向量及其运算的坐标表示高二上学期数学人教A版(2019)选择性必修第一册
我国著名数学家吴文俊先生在《数学教育 现代化问题》中指出:“数学研究数量关系与 空间形式,简单讲就是形与数,欧几里得几何体 系的特点是排除了数量关系,对于研究空间形 式,你要真正的‘腾飞’,不通过数量关系,我 想不出有什么好的办法…….”
空间几何“代数化”
类比平面直角坐标系，如何建立空间直角坐标系？
类比平面向量，我们能利用空间向量的坐标解决哪些问题？ 应用4 判定垂直
a b a b 0. a b a1b1 a2b2 a3b3 0
例 1 如图,在直三棱柱 ABC-A B C 中,CA=CB=1,∠BCA=90°,棱 AA =2,M,N
111
1
分别是 AA ,CB 的中点.（4）求 BM 在 BN 上投影向量的坐标. 11
空间向量坐标表示 空间向量四大应用：平行、垂直、角度、模长
则 x, y, z 是OP的坐标，即OP= x, y, z x, y, z也是点P的坐标，即P x, y, z .
（横，纵，竖）
例 1 如图,在直三棱柱 ABC-A B C 中,CA=CB=1,∠BCA=90°,棱 AA =2,M,N
111
1
分别是 AA ,CB 的中点.（1）求三棱柱各顶点及 M,N 点的坐标； MN 的坐标. 11
1.建立空间直角坐标系的叙述规范
以…为原点，以…所在直线为x、y、z轴，
建立如图空间直角坐标系.（图上务必标出）
2.建立空间直角坐标系的原则 有垂直用垂直，无垂直作垂直； 使尽可能多的点落在坐标轴上或坐标平面内.
类比平面向量，我们能利用空间向量的坐标解决哪些问题？
向量的坐标运算法则
设a a1, a2 , a3 , b b1, b2 , b3 ,则容易得到
人教A版高中数学选修2-1课件-空间向量运算的坐标表示
＝12a2－12a2cos
60°＋a2cos
60°－12a2cos
60°
＝12a2－a42＋a22－a42＝a22．
又∵|A→N|＝|M→C|＝ 23a，
∴A→N·M→C＝|A→N||M→C|cos θ＝ 23a× 23a×cos θ＝a22．
∴cos θ＝23．
∴向量
A→N
②设P(x，y，z)，则A→P＝(x－2，y＋1，z－2)．
x－2＝3， ∵A→P＝12(A→B－A→C)＝3，32，－2，∴y＋1＝32，
z－2＝－2，
解得x＝5，y＝21，z＝0，则点P的坐标为5，12，0．
1．一个向量的坐标等于表示这个向量的有向线段的终点坐标减 去起点坐标．
2．在确定了向量的坐标后，使用空间向量的加减、数乘、数量 积的坐标运算公式进行计算就可以了，但要熟练应用下列有关乘法 公式：(1)(a＋b)2＝a2＋2a·b＋b2；(2)(a＋b)·(a－b)＝a2－b2．
m＋1＝3λ，
∴n－2＝－λ， －2＝λ，
解得λ＝－2，m＝－7，n＝4．
∴m＋n＝－3．]
4．已知a＝(－ 2，2， 3)，b＝(3 2，6,0)，则|a|＝________， a与b夹角的余弦值等于________．
3
6 9
[|a|＝ － 22＋22＋ 32＝ 9＝3，
cos〈a，b〉＝|aa|·|bb|＝3× －36＋2122＋62＝ 96．]
(4)∵2a＝(4，－2，－4)， ∴2a·(－b)＝(4，－2，－4)·(0,1，－4) ＝4×0＋(－2)×1＋(－4)×(－4)＝14． (5)(a＋b)·(a－b)＝a2－b2＝4＋1＋4－(0＋1＋16)＝－8．
利用向量的坐标运算解决平行、垂直问题
空间向量及其运算的坐标表示(15张PPT)——高中数学人教A版选择性必修第一册
点的位置
向量位置
坐标
特点
x轴上
平行于x轴
(x,0,0)
纵、竖坐标均为0
y轴上
平行于y轴
(0,y,0)
横、竖坐标均为0
z轴上
平行于z轴
(0,0,z)
横、纵坐标均为0
Oxy平面上
平行于Oxy平面
(x,y,0)
竖坐标为0
Oyz平面上
平行于Oyz平面
(0,y,z)
横坐标为0
Ozx平面上
平行于Ozx平面
典例分析
例4如图，在正方体ABCD-A₁B₁C₁D₁ 中 ，E,F分别是BB₁ ,D₁B₁ 的中点，求证：EF⊥DA₁证明：不妨设正方体的棱长为1,建立如图所示的空间直角坐标系Oxyz, 则
典例分析
所以EF ·所以EF⊥DA₁,即EF⊥DA₁
,又A₁(1,0,1),D(0,0,0),
所以DA₁=(1,0,1)
深度探究
空间向量的坐标：在空间直角坐标系0xyz 中，给定向量a,作 0A=a,
由空间向量基本定理，
(1) 垂面法：过点A作三个平面分别垂直于x轴 ，y 轴 ，z轴于B,C,D三点，点B,C,D在x轴 ，y 轴 ，z 轴上的坐标分别为x,y,z,则(x,y,z)就是点 A的坐标。(2) 垂线段法：先确定点A在0xy平面内的射影A₁,由A₁A的长度及与z轴正方向的异同，确定竖坐标z, 再在0xy平面内确定点A₁ 的横坐标x 和纵坐标y, 那么点A的坐标就是(x,y,z).(3) 向量法：当向量的起点是原点时，向量坐标与向量终点的坐标相同。
例 1 如图，在长方体OABC-D'A'B'C′中 ，OA=3,0C=4,0D'=2,以为单位正交基底，建立如图所示的直角坐标系Oxyz。
2020秋高中数学人教版2-1达标练习：3.1-3.1.5 空间向量运算的坐标表示含解析
2020秋高中数学人教A版选修2-1达标练习：3.1-3.1.5 空间向量运算的坐标表示含解析A级基础巩固一、选择题1．设M（5，－1,2），A(4,2，－1)．若错误!＝错误!,则点B的坐标为（）A．（－1，3，－3）B．（9，1，1)C．（1，－3，3) D．（－9，－1，－1）解析：错误!＝（5，－1，2）,错误!＝（4，2,－1）．又错误!＝错误!＝错误!－错误!，所以错误!＝错误!＋错误!＝（9，1，1)。
答案：B2．已知错误!＝(2，4，5)，错误!＝（3，x，y),若错误!∥错误!,则() A．x＝6，y＝15 B．x＝3，y＝错误!C．x＝3，y＝15 D．x＝6，y＝错误!答案：D3．点P(x，2，1）到点Q(1，1，2），R（2，1,1)的距离相等，则x的值为()A。
12B．1C.错误!D．2答案：B4.如图所示的空间直角坐标系中，正方体ABCD—A1B1C1D1棱长为1，B1E1＝14A1B1，则错误!等于（）A．(0，14,－1）B．(－错误!,0,1)C．(0,－错误!，1)D．(错误!，0，－1）解析：因为B（1，1,0），A1（1，0，1），B1(1，1,1）．所以E1错误!，所以错误!＝错误!.答案：C5．若a＝（x，2，0），b＝（3，2－x，x2)，且a与b的夹角为钝角,则x的取值范围是（）A．x〈－4 B．－4<x〈0C．0<x<4 D．x〉4解析：因为a与b的夹角为钝角，所以a·b＜0所以3x＋2(2－x)＜0，解得x＜－4.若a与b的夹角为180°,则存在λ＜0，使a＝λb(λ＜0)，即(x,2,0)＝λ（3，2－x,x2）所以错误!此方程组无解，即a与b不可能共线．答案：A二、填空题6．已知a＝（1，－1，1），则与向量a共线的单位向量是________．答案：±错误!7．已知向量a＝(－1，0，1）,b＝（1，2，3)，k∈R，若ka －b与b垂直，则k＝________．解析:因为（ka－b）⊥b,所以(ka－b）·b＝0，所以ka·b－｜b｜2＝0,所以k（－1×1＋0×2＋1×3）－（错误!)2＝0，解得k＝7.答案：78．若a＝（2，2，0），b＝（1，3,z)，<a，b〉＝错误!,则z等于________．解析：cos<a，b〉＝cos错误!＝错误!＝错误!＝错误!。
空间向量及其运算的坐标表示 人教A版(2019)选择性必修第一册高中数学精品课件
A．30°
B．45°
C．60°
D．90°
→
→
→
设向量P→
1P2与P1P3的夹角为θ，因为P1P2＝(3，1，0)－(1，－1，2)＝(2，2，－2)，P1P3＝(0，1，3)－(1，
－1，2)＝(－1，2，1)，所以 cos θ＝
→
P→
1P2·P1P3
＝0.因为 0°≤θ≤180°，所以θ＝90°.故选 D.
标为( D )
1
1
A．( ，1，－ )
2
2
1
1
C．(－ ，1， )
2
2
1
1
B．( ，－1， )
2
2
1
1
D．( ，1， )
2
2
由题可知，M 为 DC1 的中点，
1
1
1
1
→
→
→
→
→
→
→
→
→
→
→
→，
∴AM＝AD＋DM＝AD＋ (DD1＋DC)＝AD＋ (AA1＋AB)＝ AA1＋AD＋ AB
2
2
2
2
1
1
∴坐标为( ，1， )．
B
)
A． (0，－4,6)
B． (0，－2,3)
C． (0,2,3)
D． (0，－2,6)
【答案】B
−3+3 1−5 −4+10
【解析】根据线段的中点坐标公式可得线段 AB 的中点 M 的坐标是(
即(0，－2,3)．故选 B.
2
，2 ，
2
)，
例题解析
例 4.点 A(2，－3,1)关于原点的对称点 A′的坐标是(
2018秋人教A版高中数学选修2-1习题：3.1.5空间向量运算的坐标表示(精编含解析)
3.1.5 空间向量运算的坐标表示1.在空间直角坐标系Oxyz中,已知点A的坐标为(-1,2,1),点B的坐标为(1,3,4),则( )A. =(-1,2,1)B. =(1,3,4)C. =(2,1,3)D. =(-2,-1,-3)【答案】C【解析】【分析】由向量坐标公式可求得向量的坐标。
【详解】=(2,1,3).选C.【点睛】若点，则。
2.已知A(2,-5,1),B(2,-2,4),C(1,-4,1),则向量的夹角为( )A. 30°B. 45°C. 60°D. 90°【答案】C【解析】【分析】先求得向量的坐标，再用向量夹角公式可求解。
【详解】由已知得=(0,3,3),=(-1,1,0),因此cos<>=,所以向量的夹角为60°.选C.【点睛】求平面向量夹角公式：，若若，则3.已知a=(1,0,1),b=(-2,-1,1),c=(3,1,0),则|a-b+2c|等于( )A. 3B. 2C.D. 5【答案】A【解析】【分析】先求向量坐标，再由向量模的坐标公式求解。
【详解】因为a-b+2c=(1,0,1)-(-2,-1,1)+(6,2,0)=(3,1,0)+(6,2,0)=(9,3,0),所以|a-b+2c|=3.选A.【点睛】若点，则。
.4.在空间直角坐标系中,O为坐标原点,设A,B,C,则有( )A. OA⊥ABB. AB⊥ACC. AC⊥BCD. OB⊥OC【答案】B【解析】【分析】由向量坐标表示求得,,再由=0可知选项B对。
【详解】由已知得,,因此=0,故,即AC⊥BC.选B.【点睛】用向量的数量积为0可判定两向量所在直线垂直，如果不为0，则两向量所在直线不垂直。
5. 已知点A(1，－2，11)，B(4，2，3)，C(6，－1，4)，则△ABC的形状是( )A. 锐角三角形B. 钝角三角形C. 直角三角形D. 等边三角形【答案】C【解析】，，．所以，故△ABC是直角三角形．选C．6.下列各组向量中共面的组数为( )①a=(1,2,3),b=(3,0,2),c=(4,2,5);②a=(1,2,-1),b=(0,2,-4),c=(0,-1,2);③a=(1,1,0),b=(1,0,1),c=(0,1,-1);④a=(1,1,1),b=(1,1,0),c=(1,0,1).A. 0B. 1C. 2D. 3【答案】D【解析】【分析】根据平面向量基本定理，用向量做基底表示向量，如果能表示则共面，不能表示则不共面。
高中数学人教A版选修2-1课件3.1.4空间向量的正交分解及其坐标运算(系列三)
∴O→E＝12(O→A＋O→B)， C→G＝2C→E＝2(O→E－O→C)
33 ∴O→G＝O→C＋C→G＝ O→C＋2(O→E－O→C)＝
3 13(O→A＋O→B＋O→C) ∴λ＝3.
答案：3
5．如图 2，四棱锥 P—OABC 的底面为一矩形， 设O→A＝a，O→C＝b，O→P＝c，E、F 分别是 PC 和 PB 的中点，用 a，b，c 表示B→F、B→E、A→E、E→F.
D．既不充分也不必要条件
解析：当非零向量a，b，c不共面时，{a，b，c}可以当基底， 否则不能当基底，当{a，b，c}为基底时，一定有a，b，c为 非零向量．
答案：B
2．已知{a，b，c}是空间的一个基底，则可以和向量p＝a＋b， q＝a－b构成基底的向量是( )
A．a
B．b
C．a＋2b
有序实数组{x，y，z}，使得p＝xa＋yb＋zc.
2．基底的概念
如果三个向量a、b、c不共面，那么空间所有向量组成的集合 就是{p|p＝xa＋yb＋zc，x、y、z∈R}这个集合可以看作是由 向 量 a 、 b 、 c 生 成 的 ， 我 们 把 {a ， b ， c} 叫 做 空 间 的 一 个 基 底．a、b、c叫做基向量．空间任何三个不共面的向量都可构 成空间的一个基底．
人教版 选修2-1
第三章 空间向量与立体几何
3.1空间向量及其运算
空间向量的正交分解及其坐标 表示
学习目标
1.了解空间向量的正交分解的含义． 2．掌握空间向量的基本定理，并能用空间向量基本定理
解决一些简单问题． 3．掌握空间向量的坐标表示，能在适当的坐标系中写出
向量的坐标.
新知导入
1．空间向量基本定理 如果三个向量a，b，c不共面，那么对空间任一向量p，存在
空间向量运算的坐标表示(教学课件)(人教A版2019选择性必修第一册)
又因为A(1, 0, 2), B(1, 3,1), MA MB , 所以 (1 0)2 (0 0)2 (2 a)2 (1 0)2 (3 0)2 (1 a)2 ,
解得a 3, 所以M(0, 0, 3).
4. 如图, 正方体OABC DABC的棱长为a, 点N , M分别在AC , BC 上, AN 2CN , BM 2MC, 求MN的长.
人教A版2019选择性必修第一册
1
环节一：创设情境，引入课题
我们所在的教室即是一个三维 立体图,如果以教室的一个墙角为 始点,沿着三条墙缝作向量可以得 到三个空间向量.
这三个空间向量是不共面的, 那么如何用这三个向量表示空间 中任意的向量呢？
平面向量运算的坐标表示
空间向量运算的坐标表示
设a (a1, a2 ), b (b1, b2 ) a b ___(_a_1___b_1,_a_2___b_2_)____, a b ____(_a_1__b_1_,_a_2___b_2_)___,
(4) a b (3)1 2 5 5 (1) 3 10 5 2
2.已知a (2, 1, 3), b (4, 2, x), 且a b, 求x的值.
因为a b, 所以a b 8 2 3x 0, 解得x 10 . 3
3. 在z轴上求一点M, 使点M到点A(1,0, 2)与点B(1, 3,1)的距离相等.
a __(__a_1,___a_2_, __a_3_),_____R_,
a b ____a_1b_1___a_2_b_2 __a_3_b_3___ .
问题1：有了空间向量的坐标表示，你能类比平面向量的坐标运 算，得出空间向量运算的坐标表示并给出证明吗？
知识点1 空间向量及其运算的坐标表示
人教A版(新教材)高二数学选择性必修第一册重点题型n1(含答案)
人教A版（新教材）高二选择性必修第一册重点题型N1第一章空间向量与立体几何考试范围：1.1空间向量及其运算；1.2空间向量基本定理；1.3空间向量及其运算的坐标表示；考试时间：100分钟；命题人：LEOG学校:___________姓名：___________班级：___________考号：___________题型1、利用向量方法解决立体几何的证明问题1．已知向量＝（1，x2，2），＝（0，1，2），＝（1，0，0），若，，共面，则x 等于（）A．﹣1B．1C．1或﹣1D．1或0【考点】共线向量与共面向量．【分析】利用共面向量定理直接求解．【解答】解：∵向量＝（1，x2，2），＝（0，1，2），＝（1，0，0），，，共面，∴，m≠0，n≠0，∴（1，x2，2）＝（n，m，2m），∴，解得x2＝m＝1，∴x＝±1．故选：C．【点评】本题考查实数值的求法，考查共面向量定理等基础知识，考查运算求解能力，是基础题．2．如果向量＝（2，﹣1，3），＝（﹣1，4，2），＝（1，﹣1，m）共面，则实数m的值是（）A．﹣1B．1C．﹣5D．5【考点】共线向量与共面向量．【分析】由各量共面，可知存在x，y，使得，列出方程组，求出实数m的值．【解答】解：∵向量＝（2，﹣1，3），＝（﹣1，4，2），＝（1，﹣1，m）共面，∴存在x，y，使得，∴（2，﹣1，3）＝（﹣x+y，4x﹣y，2x+my），∴，解得x＝，y＝，m＝1．∴实数m的值是1．故选：B．【点评】本题考查实数值的求法，共面向量的性质等基础知识，考查运算求解能力，是基础题．3．已知，﹣1，3），，4，﹣2），，3，λ），若、、三向量共面，则实数λ等于（）A．1B．2C．3D．4【考点】共线向量与共面向量．【分析】由向量、、共面得出＝x+y，列方程组可求得λ的值．【解答】解：向量、、共面，则＝x+y，其中x，y∈R；则（1，3，λ）＝（2x，﹣x，3x）+（﹣y，4y，﹣2y）＝（2x﹣y，﹣x+4y，3x﹣2y），∴，解得x＝1，y＝1，λ＝1．故选：A．【点评】本题考查了空间向量的坐标表示与共面定理的应用问题，是基础题．4．已知，，若与共线，则（）A．x＝6，y＝15B．x＝3，y＝10C．x＝3，y＝15D．x＝6，y＝9【考点】共线向量与共面向量．【分析】利用向量平行的性质直接求解．【解答】解：∵，，与共线，∴，解得x＝6，y＝9．故选：D．【点评】本题考查实数值的求法，考查向量平行的性质等基础知识，考查运算求解能力，是基础题．5．已知＝（2，﹣1，3），＝（﹣1，4，﹣2），＝（7，5，λ），若、、三向量共面，则实数λ等于（）A．B．C．D．【考点】共线向量与共面向量．【分析】由已知中＝（2，﹣1，3），＝（﹣1，4，﹣2），＝（7，5，λ），若、、三向量共面，我们可以用向量、作基底表示向量，进而构造关于λ的方程，解方程即可求出实数λ的值．【解答】解：∵＝（2，﹣1，3），＝（﹣1，4，﹣2）∴与不平行，又∵、、三向量共面，则存在实数X，Y使＝X+Y即解得λ＝故选：D．【点评】本题考查的知识点是共线向量与共面向量及平面向量基本定理，其中根据、、三向量共面，与不共线，则可用向量、作基底表示向量，造关于λ的方程，是解答本题的关键题型2、空间向量平行和垂直坐标表示1．若向量＝（0，1，﹣1），＝（1，1，0），且（+λ）⊥，则实数λ的值是（）A．﹣1B．0C．﹣2D．1【考点】空间向量的数量积运算．【分析】利用向量垂直与数量积的关系即可得出．【解答】解：∵（+λ）⊥，∴（+λ）•＝+＝+λ×（0+1+0）＝0，解得λ＝﹣2．故选：C．【点评】本题考查了向量垂直与数量积的关系，属于基础题．2．已知向量＝（1，1，0），＝（﹣1，0，1）且k与互相垂直，则k＝（）A．B．C．D．【考点】空间向量的数量积运算．【分析】根据与互相垂直，（k+）•＝0，列出方程求出k的值．【解答】解：∵向量，，∴k+＝（k﹣1，k，1）；又与互相垂直，∴（k+）•＝0，即（k﹣1）×1+k＝0，解得k＝．故选：B．【点评】本题考查了空间向量的坐标运算与数量积的应用问题，是基础题目．3．已知＝（﹣1，﹣2，1），＝（1，x，﹣2）且•＝﹣13，则x的值为（）A．3B．4C．5D．6【考点】空间向量的数量积运算．【分析】根据空间向量数量积的坐标运算，列方程求出x的值．【解答】解：＝（﹣1，﹣2，1），＝（1，x，﹣2），所以•＝﹣1﹣2x﹣2＝﹣13，解得x＝5．故选：C．【点评】本题考查了空间向量数量积的坐标运算问题，是基础题．4．已知，且，则x•y＝（）A．B．2C．D．﹣1【考点】空间向量的数量积运算．【分析】由，可得存在实数k使得＝k（），利用向量相等即可得出．【解答】解：＝（1+2x，4，4+y），＝（2﹣x，3，2y﹣2），∵，∴存在实数k使得＝k（），∴，解得x＝，y＝4．∴x•y＝2．故选：B．【点评】本题考查了向量坐标运算性质、向量共线定理、空间向量基本定理，考查了推理能力与计算能力，属于基础题．5．已知向量＝（﹣1，2，3），＝（2，y，0），且，那么y等于（）A．﹣1B．4C．﹣4D．1【考点】空间向量的数量积运算．【分析】，可得＝0，解得y．【解答】解：∵，∴＝﹣2+2y+0＝0，解得y＝1．故选：D．【点评】本题考查了向量垂直与数量积的关系，考查了推理能力与计算能力，属于基础题．6．已知向量＝（2m+1，3，m﹣1），＝（2，m，﹣m），且∥，则实数m的值等于（）A．B．﹣2C．0D．或﹣2【考点】共线向量与共面向量．【分析】根据两向量平行的充要条件建立等式关系，然后解二元一次方程组即可求出m 的值．【解答】解：∵空间平面向量＝（2m+1，3，m﹣1），＝（2，m，﹣m），且∥，∴（2m+1，3，m﹣1）＝λ（2，m，﹣m）＝（2λ，λm，﹣λm），∴，解得m＝﹣2．故选：B．【点评】本题主要考查了平空间向量共线（平行）的坐标表示，以及解二元一次方程组，属于基础题．7．已知＝（λ+1，0，1），＝（3，2μ﹣1，2），其中λ，μ∈R，若∥，则λ+μ＝（）A．0B．1C．2D．3【考点】共线向量与共面向量；向量的数量积判断向量的共线与垂直．【分析】根据可得出，然后即可得出，从而解出λ，μ即可．【解答】解：∵∥，∴设，∴（3，2μ﹣1，2）＝（kλ+k，0，k），∴，解得，∴λ+μ＝1．故选：B．【点评】本题考查了共线向量基本定理，向量坐标的数乘运算，相等向量的坐标关系，考查了计算能力，属于基础题．8．已知向量＝（2，1，﹣5），＝（4，y，z），且∥，则y+z＝（）A．﹣8B．﹣12C．8D．12【考点】共线向量与共面向量；向量的数量积判断向量的共线与垂直．【分析】直接利用向量共线定理得到，再利用向量相等的坐标表示求出y和z，即可得到答案．【解答】解：因为向量＝（2，1，﹣5），＝（4，y，z），且∥，所以，则有，解得y＝2，z＝﹣10，所以y+z＝﹣8．故选：A．【点评】本题考查了空间向量共线定理的应用，涉及了空间向量的坐标表示以及空间向量相等的充要条件的应用，属于基础题．9．已知向量，且，则x+y的值为（）A．11B．6C．7D．15【考点】共线向量与共面向量；向量的数量积判断向量的共线与垂直．【分析】由向量平行的充要条件可得答案，【解答】解：向量，且，则＝λ，即（x，3，4）＝（6，y，12），解得x＝2，y＝9，则x+y＝2+9＝11，故选：A．【点评】本题考查向量平行的充要条件，属于基础题．10．已知空间向量＝（3，1，3），＝（﹣1，λ，﹣1），且∥，则实数λ＝（）A．﹣B．﹣3C．D．6【考点】共线向量与共面向量．【分析】由∥，可设k＝，可得，解出即可得出．【解答】解：∵∥，∴可设k＝，∴，解得λ＝k＝﹣．故选：A．【点评】本题考查了向量共线定理、方程的解法，考查了推理能力与计算能力，属于基础题．题型3、空间向量的夹角应用1．已知A（1，0，0），B（0，﹣1，1），O是坐标原点，+与的夹角为120°，则λ的值为（）A．±B．C．﹣D．±【考点】空间向量的夹角与距离求解公式．【分析】首先求出空间向量的坐标，及向量的模，进一步利用向量的夹角求出结果．【解答】解：因为+λ＝（1，0，0）+λ（0，﹣1，1）＝（1，﹣λ，λ），所以＝，＝，（+λ）•＝2λ，所以cos 120°＝＝﹣，所以λ＜0，且4λ＝﹣解得：λ＝﹣．故选：C．【点评】本题考查的知识要点：空间向量的数量积，空间向量的模及夹角的运算．属于基础题型．2．已知：＝（x，4，1），＝（﹣2，y，﹣1），＝（3，﹣2，z），∥，⊥，求：（1），，；（2）（+）与（+）所成角的余弦值．【考点】空间向量的夹角与距离求解公式；向量的数量积判断向量的共线与垂直．【分析】（1）由向量的平行和垂直可得关于xyz的关系式，解之即可得向量坐标；（2）由（1）可得向量与的坐标，进而由夹角公式可得结论．【解答】解：（1）∵，∴，解得x＝2，y＝﹣4，故＝（2，4，1），＝（﹣2，﹣4，﹣1），又因为，所以＝0，即﹣6+8﹣z＝0，解得z＝2，故＝（3，﹣2，2）（2）由（1）可得＝（5，2，3），＝（1，﹣6，1），设向量与所成的角为θ，则cosθ＝＝【点评】本题考查空间向量平行和垂直的判断，涉及向量的夹角公式，属基础题．3．已知＝（3，﹣2，﹣3），＝（﹣1，x﹣1，1），且与的夹角为钝角，则x的取值范围是（）A．（﹣2，+∞）B．（﹣2，）∪（，+∞）C．（﹣∞，﹣2）D．（，+∞）【考点】空间向量的夹角与距离求解公式．【分析】根据两个向量的夹角是钝角，则两个向量的夹角的余弦小于零，从而得到两个向量的数量积小于零，用坐标形式表示向量的数量积，解不等式，得到变量的范围．【解答】解：∵与的夹角为钝角，∴cos＜，＞＜0．且与不共线∴•＜0．且（3，﹣2，﹣3）≠λ（﹣1，x﹣1，1）∴﹣3﹣2（x﹣1）﹣3＜0．且x≠∴x的取值范围是（﹣2，）∪（，+∞）．故选：B．【点评】两个向量的数量积是一个数量，它的值是两个向量的模与两向量夹角余弦的乘积，结果可正、可负、可以为零，其符号由夹角的余弦值确定．4．已知＝（1，1，1），＝（0，y，1）（0≤y≤1），则cos＜，＞最大值为（）A．B．C．D．【考点】空间向量的夹角与距离求解公式．【分析】【解法一】利用作图法，构造正方体，考虑极端情况，可快速得出答案；【解法二】根据两向量的数量积求出夹角的余弦值cos＜，＞，再利用换元法求出它的最大值即可．【解答】解：【解法一】利用作图法，构造正方体，设正方体的棱长为1，如图所示；则＝＝（1，1，1），＝＝（0，y，1），且E在线段D′C′上移动，当E在D′位置时，cos＜，＞＝＝＝；当E在C′位置时，cos＜，＞＝＝＝为最大值．【解法二】∵＝（1，1，1），＝（0，y，1）（0≤y≤1），∴•＝y+1，||＝，||＝，∴cos＜，＞＝＝；设t＝，则t2﹣1＝y2，∴y＝（1≤t≤），∴f（t）＝•＝（+）；设sinα＝，则1≥sinα≥，即≤α≤，∴g（α）＝（+sinα）＝（cosα+sinα）＝sin（α+），∴当α＝时，g（α）取得最大值为＝．故选：D．【点评】本题考查了利用向量的数量积求夹角的应用问题，也考查了函数在闭区间上的最值问题，是基础题目．5．已知空间三点A（﹣1，2，1），B（0，1，﹣2），C（﹣3，0，2）（1）求向量的夹角的余弦值，（2）若向量垂直，求实数k的值．【考点】空间向量运算的坐标表示．【分析】（1）＝（1，﹣1，﹣3），＝（﹣2，﹣2，1），计算可得＝．（2）∵向量垂直，可得•＝3+（3k ﹣1）﹣k＝0，即可得出．【解答】解：（1）＝（1，﹣1，﹣3），＝（﹣2，﹣2，1），||＝＝，＝3．＝﹣2+2﹣3＝﹣3．∴＝＝＝﹣．（2）∵向量垂直，∴•＝3+（3k﹣1）﹣k＝0，3×11+（3k﹣1）×（﹣3）﹣9k＝0，解得k＝2．【点评】本题考查了向量夹角公式、向量垂直与数量积的关系，考查了推理能力与计算能力，属于基础题．题型4、空间向量模的坐标表示1．已知＝（1﹣t，2t﹣1，0），＝（3，t，t），则|﹣|的最小值为（）A．B．C．D．【考点】空间向量运算的坐标表示．【分析】根据空间向量的坐标表示与数量积定义，利用二次函数的性质求出|﹣|的最小值．【解答】解：＝（1﹣t，2t﹣1，0），＝（3，t，t），则﹣＝（2+t，1﹣t，t），∴＝（2+t）2+（1﹣t）2+t2＝3t2+2t+5＝3+，∴t＝﹣时|﹣|取得最小值为＝．故选：B．【点评】本题考查了空间向量的坐标运算与模长的计算问题，是基础题．2．若向量，，则＝（）A．B．C．3D．【考点】空间向量的夹角与距离求解公式．【分析】利用向量坐标运算法则求解＝（3，0，﹣1），由此能求出的值．【解答】解：∵向量，，∴＝（3，0，﹣1），∴＝＝．故选：D．【点评】本题考查向量的模的求法，考查向量坐标运算法则、向量的模等基础知识，考查函数与方程思想，考查运算求解能力，是基础题．3．已知＝（1﹣t，1，0），＝（2，t，t），则|﹣|的最小值是（）A．1B．C．D．【考点】空间向量的夹角与距离求解公式．【分析】利用向量的坐标运算法则得到＝（1+t，t﹣1，t），从而||＝＝，由此能求出当t＝0时，|﹣|取最小值．【解答】解：∵＝（1﹣t，1，0），＝（2，t，t），∴＝（1+t，t﹣1，t），∴||＝＝，∴当t＝0时，|﹣|取最小值．故选：B．【点评】本题考查向量的模的最小值的求法，考查向量坐标运算法则、向量的模等基础知识，考查运算求解能力，是基础题．4．已知空间向量＝（t，1，t），＝（t﹣2，t，1），则|﹣|的最小值为（）A．B．C．2D．4【考点】空间向量及其线性运算；空间向量的夹角与距离求解公式．【分析】由已知求得，再由向量模的计算公式求||，利用配方法求最值．【解答】解：∵＝（t，1，t），＝（t﹣2，t，1），∴＝（2，1﹣t，t﹣1），则|﹣|＝，∴当t＝1时，|﹣|取最小值为2．故选：C．【点评】本题考查向量的坐标运算与向量模的求法，训练了利用配方法求最值，是基础题．5．已知空间三点A（0，2，3），B（2，5，2），C（﹣2，3，6），则以AB，AC为邻边的平行四边形的面积为6．【考点】空间向量运算的坐标表示．【分析】＝（2，3，﹣1），＝（﹣2，1，3）．可得＝﹣4，，．可得cos∠BAC＝．可得sin∠BAC＝．以AB，AC为邻边的平行四边形的面积S＝••sin∠BAC．【解答】解：＝（2，3，﹣1），＝（﹣2，1，3）．∴＝﹣4+3﹣3＝﹣4，＝＝，＝＝．∴cos∠BAC＝＝＝﹣．∴sin∠BAC＝＝．∴以AB，AC为邻边的平行四边形的面积S＝••sin∠BAC＝×＝6．故答案为：6．【点评】本题考查了向量数量积运算性质、向量夹角公式、平行四边形面积计算公式，考查了推理能力与计算能力，属于中档题．题型5、平面的法向量的求法与应用1．若两个向量＝（1，2，3），＝（3，2，1），则平面ABC的一个法向量为（）A．（﹣1，2，﹣1）B．（1，2，1）C．（1，2，﹣1）D．（﹣1，2，1）【考点】平面的法向量．【分析】设平面ABC的一个法向量＝（x，y，z），则，由此能求出平面ABC的一个法向量．【解答】解：两个向量，设平面ABC的一个法向量＝（x，y，z），则，取x＝﹣1，得平面ABC的一个法向量为（﹣1，2，﹣1）．故选：A．【点评】本题考查平面的法向量的求法，考查平面的法向量的性质等基础知识，考查运算求解能力，是基础题．2．平面α经过三点O（0，0，0），A（2，2，0），B（0，0，2），则平面α的法向量可以是（）A．（1，0，1）B．（1，0，﹣1）C．（0，1，1）D．（﹣1，1，0）【考点】平面的法向量．【分析】求出＝（2，2，0），＝（0，0，2），设平面α的法向量＝（x，y，z），由，能求出平面α的法向量．【解答】解：∵平面α经过三点O（0，0，0），A（2，2，0），B（0，0，2），∴＝（2，2，0），＝（0，0，2），设平面α的法向量＝（x，y，z），则，取x＝﹣1，得＝（﹣1，1，0），∴平面α的法向量可以是（﹣1，1，0）．故选：D．【点评】本题考查平面的法向量的求法，考查平面的法向量等基础知识，考查运算求解能力，是基础题．3．已知A（0，2，3），B（﹣2，1，6），C（1，﹣1，5）（1）求平面ABC的一个法向量；（2）证明：向量与平面ABC平行．【考点】平面的法向量．【分析】（1）设＝（x，y，z）为平面ABC的一个法向量，则有•＝0且•＝0，由此求出平面ABC的一个法向量；（2）假设存在实数m、n，使＝m+n，利用向量相等列出方程组求出m、n的值，即可证明结论成立．【解答】解：（1）∵A（0，2，3），B（﹣2，1，6），C（1，﹣1，5），∴＝（﹣2，﹣1，3），＝（1，﹣3，2），设＝（x，y，z）为平面ABC的一个法向量，则有•＝（x，y，z）•（﹣2，﹣1，3）＝﹣2x﹣y+3z＝0，•＝（x，y，z）•（1，﹣3，2）＝x﹣3y+2z＝0；由，解得，令x＝y＝z＝1，得平面ABC的一个法向量为（1，1，1）；（2）证明：若存在实数m、n，使＝m+n，即（3，﹣4，1）＝m（﹣2，﹣1，3）+n（1，﹣3，2），则，解得，所以＝﹣+，即向量∥平面ABC．【点评】本题考查了空间向量的坐标运算问题，也考查了求平面法向量的应用问题，是基础题．4．已知向量＝（1，2，1），＝（0，1，﹣2），则平面ABC的一个法向量可以是（）A．（5，﹣2，﹣1）B．（﹣6，2，2）C．（3，1，﹣2）D．（4，﹣3，1）【考点】平面的法向量．【分析】平面ABC的一个法向量与向量，的数量积都为0．【解答】解：由＝（1，2，1），＝（0，1，﹣2），知：在A中，∵，∴平面ABC的一个法向量可以是（5，﹣2，﹣1），故A正确；在B中，，故B错误；在C中，，故C错误；在D中，，故D错误．故选：A．【点评】本题考查平面的法向量的求法，是基础题，解题时要认真审题，注意法向量的性质的合理运用．5．设平面α内两个向量的坐标分别为（1，2，1）、（﹣1，1，2），则下列向量中是平面的法向量的是（）A．（﹣1，﹣2，5）B．（﹣1，1，﹣1）C．（1，1，1）D．（1，﹣1，﹣1）【考点】平面的法向量．【分析】利用非零向量⇔即可找出平面的法向量．【解答】解：∵（﹣1，1，﹣1）•（1，2，1）＝﹣1+2﹣1＝0，（﹣1，1，﹣1）•（﹣1，1，2）＝1+1﹣2＝0，∴向量（﹣1，1﹣1）是此平面的法向量．故选：B．【点评】正确理解平面的法向量是解题的关键．6．在三角形ABC中，A（1，﹣2，﹣1），B（0，﹣3，1），C（2，﹣2，1），若向量与平面ABC垂直，且||＝，则的坐标为（2，﹣4，﹣1）或（﹣2，4，1）．【考点】空间两点间的距离公式；平面的法向量．【分析】根据条件求出平面的法向量，结合向量的长度公式即可得到结论．【解答】解：设平面ABC的法向量为＝（x，y，z），则＝0，且•＝0，∵＝（﹣1，﹣1，2），＝（1，0，2），∴，即，令z＝1，则x＝﹣2，y＝4，即＝（﹣2，4，1），若向量与平面ABC垂直，∴向量∥，设＝λ＝（﹣2λ，4λ，λ），∵||＝，∴•|λ|＝，即|λ|＝1，解得λ＝±1，∴的坐标为（2，﹣4，﹣1）或（﹣2，4，1），故答案为：（2，﹣4，﹣1）或（﹣2，4，1）【点评】本题主要考查空间向量坐标的计算，根据直线和平面垂直求出平面的法向量是解决本题的关键．7．已知点A（1，0，0），B（0，，0），C（0，0，1）求平面ABC的一个法向量．【考点】平面的法向量．【分析】由已知中A，B，C三点的坐标，我们可以求出向量，的坐标，进而根据平面的法向量与平面内任一向量都垂直，其数量积均为0，可以构造法向量坐标的方程组，解方程组可得答案．【解答】解：∵点A（1，0，0），B（0，，0），C（0，0，1）∴＝（﹣1，，0），＝（﹣1，0，1），设平面ABC的一个法向量为则，即令x＝1，则即为平面ABC的一个法向量【点评】本题考查的知识点是用向量语言表述线面垂直关系，其中根据平面的法向量与平面内任一向量都垂直，数量积均为0，构造关于法向量坐标的方程组是解答的关键．8．若和分别为平面α和平面β的一个法向量，且α⊥β，则实数λ＝3．【考点】平面的法向量．【分析】由于α⊥β，可得＝0，解出即可得出．【解答】解：∵α⊥β，∴，∴＝λ﹣6+3＝0，解得λ＝3．故答案为：3．【点评】本题考查了向量垂直与数量积的关系、面面垂直的性质，考查了推理能力与计算能力，属于中档题．9．已知平面α的法向量为＝（3，﹣1，2），＝（﹣3，1，﹣2），则直线AB与平面α的位置关系为（）A．AB∥αB．AB⊂αC．AB与α相交D．AB⊂α或AB∥α【考点】平面的法向量．【分析】由＝﹣，即可判断出位置关系．【解答】解：∵＝﹣，∴∥，∴直线AB与平面α的位置关系为相交．故选：C．【点评】本题考查了线面位置关系、向量共线定理，考查了推理能力与计算能力，属于中档题．10．若，，是平面α内的三点，设平面α的法向量，则x：y：z＝2：3：（﹣4）．【考点】平面的法向量．【分析】求出、的坐标，由•＝0，及•＝0，用y表示出x和z的值，即得法向量的坐标之比．【解答】解：，∴．故答案为2：3：﹣4．【点评】本题考查平面的法向量的性质以及两个向量垂直的性质，两个向量的数量积公式的应用．。
2022-2023学年人教A版选择性必修第一册 1-3-2 空间向量运算的坐标表示 课件(48张)
1．3 空间向量运算的坐标表示/
新课程标准
新学法解读 1.会利用空间向量的坐标运算解决简单的运算
问题． 1.掌握空间向量的线性
2．掌握空间向量运算的坐标表示，并会判断两 运算的坐标表示．
个向量是否共线或垂直． 2．掌握空间向量的数量
数量积
a·b
a·b＝_____a_1_b_1＋__a_2_b_2_＋__a_3b_3___________
知识点二 空间向量的平行、垂直及模、夹角 设 a＝(a1，a2，a3)，b＝(b1，b2，b3)，则有
当 b≠0 时，a∥b⇔a＝λb⇔a1＝λb1，a2＝λb2，a3＝λb3(λ∈R)；
a⊥b⇔a·b＝0⇔a1b1＋a2b2＋a3b3＝0；
|a|＝ a·a＝ a12＋a22＋a32； cos〈a，b〉＝|aa|·|bb|＝ a21＋a1ba122＋＋aa232b2b＋21＋a3bb223＋b23.
知识点三 空间两点间的距离公式 设 P1(x1，y1，z1)，P2(x2，y2，z2)是空间中任意两点，则 P1P2＝|P→1P2|＝
_____x_2－__x_1__2＋___y_2_－__y1__2＋___z_2_－__z1__2 ____.
2．已知向量 a＝(0，－1,1)，b＝(4,1,0)，|λa＋b|＝ 29，且 λ>0，则 λ 等于( C ) A．5 B．4 C．3 D．2
解析：λa＋b＝λ(0，－1,1)＋(4,1,0)＝(4,1－λ，λ)，由已知得|λa＋b|＝ 42＋1－λ2＋λ2 ＝ 29，且 λ>0，解得 λ＝3.
研习 1 空间向量的坐标运算 [典例 1] (1)已知 a＝(2，－1，－2)，b＝(0，－1,4)，求 a＋b，a－b，a·b，(2a)·(－b)， (a＋b)·(a－b)．
2023年高中数学人教A版选择性必修第一册1.3空间向量及其运算的坐标表示 课时分层练习题含答案解析
1.3 空间向量及其运算的坐标表示1.3.1空间直角坐标系 ................................................................................................................ 1 1.3.2空间向量运算的坐标表示 (7)1.3.1空间直角坐标系基础练习一、单选题1．已知空间点(3,1,4)P --，则点P 关于y 轴对称的点的坐标为（ ） A ．(3,1,4)--- B ．(3,1,4)-- C ．(3,1,4)- D ．(3,1,4)【答案】D【分析】利用空间直角坐标系点关于坐标轴对称的特点求解作答. 【详解】依题意，点(3,1,4)P --关于y 轴对称的点的坐标为(3,1,4).2．（2022·广东·高二阶段练习）如图所示的空间直角坐标系中，四棱锥P ABCD -的底面ABCD 是正方形，PB ⊥平面ABCD ，且2PB A B ==，若3PC P Q =，则点Q 的空间直角坐标为（ ）A ．()3,2,1B ．44,2,33⎛⎫⎪⎝⎭C ．()1,2,3D ．()1,2,1【答案】B【分析】根据空间向量的坐标运算直接计算.【详解】由题意得()0,2,0C ，()2,2,2P ，所以()2,0,23PC PQ =--=， 所以()22,0,33PQ =--，所以Q 的坐标为()()()2244,0,2,2,2,2,3333--+=．3．点()3,4,5A -关于坐标平面Oxy 对称的点的坐标是（ ） A ．()3,4,5B ．()3,4,5--C ．()3,4,5--D ．()3,4,5---【答案】C【分析】本题根据关于坐标平面对称的点的坐标直接求解即可. 【详解】因为点(,,)x y z 关于Oxy 平面对称的点的坐标是(,,)x y z -， 所以点()3,4,5A -关于xOz 平面对称的点的坐标是()3,4,5--， 二、多选题4．如图，在正三棱柱111ABC A B C -中，已知ABC 的边长为2，三棱柱的高为111,,BC B C 的中点分别为1,D D ，以D 为原点，分别以1,,DC DA DD 的方向为x 轴､y 轴､z 轴的正方向建立空间直角坐标系，则下列空间点及向量坐标表示正确的是（ ）A ．()1A B ．()11,0,1CC ．()10,AD = D ．()13,1B A =-【答案】ABC【分析】求出等边三角形的高AD 的长，根据三棱柱的棱长可得各点坐标，然后求得向量的坐标即可判断．【详解】在等边ABC 中，2,1AB BD ==，所以AD =，则()()()111,,1,0,1,)(0,0,1A A C D ，()11,0,1B -，则()()110,3,1,1,3,1AD B A =-=-. 三、填空题5．在空间直角坐标系中，点()3,1,4-A 关于xOy 平面对称的点B 的坐标为______． 【答案】(3,1,4)--【分析】空间直角坐标系中任一点(,,)P a b c 关于坐标平面xOy 的对称点(,,)P a b c - ，写出结果即可【详解】由题意可得：点(3,1,4)A -关于xOy 平面的对称点的坐标是(3,1,4)B -- ， 6．（2022·全国·高二课时练习）在空间直角坐标系中，已知点(,,)P x y z ，下列叙述中，正确的序号是_______.①点P 关于x 轴的对称点是1(,,)P x y z - ②点P 关于yOz 平面的对称点是2(,,)P x y z -- ③点P 关于y 轴的对称点是3(,,)P x y z -④点P 关于原点的对称点是4(,,)P x y z --- 【答案】④【分析】根据空间坐标的对称性进行判断即可．【详解】解：①点P 关于x 轴的对称点的坐标是(x ，y -，)z -，故①错误； ②点P 关于yOz 平面的对称点的坐标是(x -，y ，)z ，则②错误； ③点P 关于y 轴的对称点的坐标是(x -，y ，)z -，则③错误； ④点P 关于原点的对称点的坐标是(x -，y -，)z -，故④正确， 故正确的序号是④. 三、解答题7．在正方体1111ABCD A B C D -中建立空间直角坐标系，若正方体的棱长为1，分别求AB ，1DC ，1B D 的坐标．【分析】利用正方体的几何特征建立空间直角坐标系，求出点的坐标，由此即可求出向量坐标.【详解】如图所示建立空间直角坐标系，则()0,0,0A ，()1,0,0B ，()0,1,0D ，()11,1,1C ，()11,0,1B ， ∴()1,0,0AB =，()11,0,1DC =，()11,1,1B D =--.8．（2022·全国·高二课时练习）在空间直角坐标系中，分别求点(2,1,4)P -关于x 轴、xOy 平面、坐标原点对称的点的坐标．【答案】关于x 轴对称()2,1,4---，关于xOy 平面对称()2,1,4--，关于坐标原点对称()2,1,4-- 【分析】根据空间直角坐标系中点关于x 轴、xOy 平面、坐标原点对称的点的特征即可得出答案.【详解】解：点(2,1,4)P -关于x 轴对称的点的坐标为()2,1,4---， 关于xOy 平面对称的点的坐标为()2,1,4--， 关于坐标原点对称的点的坐标为()2,1,4--.提升训练一、单选题1．点P 是棱长为1的正方体1111ABCD A B C D -的底面ABCD 上一点，则1PA PC ⋅的取值范围是（ ） A ．1[1,]4--B ．11[,]24--C ．[1,0]-D ．1[,0]2-【答案】D【分析】以点D 为原点，以DA 所在的直线为x 轴，以DC 所在的直线为y 轴，以1DD 所在的直线为z 轴，建立空间直角坐标系，写出各点坐标，同时设点P 的坐标为(,,)x y z ，其中01,01,1x y z ≤≤≤≤=，用坐标运算计算出1PA PC ⋅，配方后可得其最大值和最小值，即得其取值范围．【详解】以点D 为原点，以DA 所在的直线为x 轴，以DC 所在的直线为y 轴，以1DD 所在的直线为z 轴，建立空间直角坐标系，如图所示；则点1(1,0,0),(0,1,1)A C 设点P 的坐标为(,,)x y z ，由题意可得 01,01,1x y z ≤≤≤≤=， 1(1,,1),(,1,0)PA x y PC x y ∴=---=--22221111(1)(1)0222PA PC x x y y x x y y x y ⎛⎫⎛⎫∴⋅=----+=-+-=-+-- ⎪ ⎪⎝⎭⎝⎭， 由二次函数的性质可得，当12x y ==时1PA PC ⋅取得最小值为12-；当0x =或1，且0y =或1时，1PA PC ⋅取得最大值为0，则1PA PC ⋅的取值范围是1,02⎡⎤-⎢⎥⎣⎦2．已知点A(3,3,-5),B(2,-3,1),C 为线段AB 上一点,且23AC AB = ,则点C 的坐标为( ) A ． 715(,,)222-B ． 3(,3,2)8-C ． 7(,1,1)3--D ． 573(,,)222-【答案】C【分析】设出C 点的坐标，根据A ，B ，C 三个点的坐标，写出两个向量的坐标，根据两个向量之间的关系，得到关于x ，y ，z 的关系式，在每一个关系式中解出变量的结果，得到要求的点的坐标．【详解】设C 的坐标是（x ，y ，z ） ∵A(3,3,-5),B(2,-3,1)，∴166,335AB AC x y z =--=--+（，，）（，，） ∵23AC AB =， ∴2335166,3x y z --+=--（，，）（，，） 由此解得7,1,1,3x y z ==-=- ，3．如图，在空间直角坐标系中，正方体ABCD －A 1B 1C 1D 1的棱长为1，B 1E 1＝14A 1B 1，则1BE 等于A ．10,,14⎛⎫- ⎪⎝⎭B ．1,0,14⎛⎫- ⎪⎝⎭C ．10,,14⎛⎫- ⎪⎝⎭D ．1,0,14⎛⎫- ⎪⎝⎭【答案】C【分析】根据空面向量运算法则，利用 BE OE OB =- ，即可得出．【详解】由题，在空间直角坐标系中，正方体1111ABCD A B C D －的棱长为1，111B E A B ＝， 则3110(11)4B E （，，），，，，31(11)110(01)44BE OE OB ∴=-=-=-，，（，，），，，二、填空题4．如图，在长方体ABCD -A 1B 1C 1D 1中，E ，F 分别为D 1C 1，B 1C 1的中点，若以{}1,,AB AD AA 为基底，则向量AE 的坐标为___，向量AF 的坐标为___，向量1AC 的坐标为___.【答案】 1,1,12⎛⎫⎪⎝⎭1112⎛⎫⎪⎝⎭,, (1,1,1) 【分析】利用向量的运算用1,,AB AD AA 表示向量AE ，AF ，1AC ，即可得出答案.【详解】因为11112AE AD DD D E AB AD AA =++=++，所以向量AE 的坐标为1,1,12⎛⎫ ⎪⎝⎭. 因为11112AF AB BB B F AB AD AA =++=++， 所以向量AF 的坐标为1112⎛⎫⎪⎝⎭,,. 因为11AC AB AD AA =++，所以向量1AC 的坐标为(1,1,1). 三、解答题5．已知A(1,0,0),B(0,1,0),C(0,0,2). (1)若DB AC,DC AB ,求点D 的坐标;(2)问是否存在实数α,β,使得AC =αAB +βBC 成立?若存在,求出α,β的值;若不存在,说明理由. 【答案】（1）()1,1,2D -；（2）1αβ==【分析】（1）设D(x,y,z )，由向量平行的坐标运算可求得D 点坐标．（2）假设存在，由待定系数法求解．【详解】(1)设D(x,y,z ),则DB =(-x,1-y,-z),AC =(-1,0,2),DC =(-x,-y,2-z),AB =(-1,1,0). 因为DB AC,DC AB ,所以(-,1-,-)(-1,0,2),(-,-,2-)(-1,1,0),x y z m x y z n =⎧⎨=⎩解得-1,1,2.x y z =⎧⎪=⎨⎪=⎩即D(-1,1,2).(2)依题意AB =(-1,1,0),AC =(-1,0,2),BC =(0,-1,2).假设存在实数α,β,使得AC =αAB +βBC 成立,则有(-1,0,2)=α(-1,1,0)+β(0,-1,2)=(-α,α-β,2β),所以1,-0,22,ααββ=⎧⎪=⎨⎪=⎩故存在α=β=1,使得AC =αAB +βBC 成立.1.3.2空间向量运算的坐标表示基础练习一、单选题1．已知()()1,2,5,1,,1a b x =-=-，且2a b ⋅=，则x 的值是（ ） A ．3 B ．4 C ．5 D ．6【答案】B【分析】由向量数量积的坐标表示列方程求参数. 【详解】由题设，1252a b x ⋅=-+-=，可得4x =. 2．已知向量()3,2,1a =，()2,4,0b =，则42a b -=（ ） A ．()16,0,4 B ．()8,16,4 C ．()8,16,4- D ．()8,0,4【答案】D【分析】根据向量的数乘以及减法运算，即可求得答案.【详解】()()()()()4243,2,122,4,012,8,44,8,08,0,4a b -=-=-=,3．已知直线2,l l l 的方向向量分别为()()1,4,2,2,1,a b m =-=-，若12l l ⊥，则m 等于（ ） A ．0 B ．1 C ．2 D ．3【答案】B【分析】根据12l l ⊥列方程，化简求得m 的值.【详解】由于12l l ⊥，所以()()124120,1m m ⨯-+⨯+-⨯==.4．已知()1,4,4a =--，(),2,21b m m =-+，若a b ∥，则m 的值为（ ） A ．－2 B ．2C ．12-D ．12【详解】因为a b ∥，所以m 5．（2022·福建龙岩·高二期中）已知直线l 的一个方向向量为，平面的一个法向量为()3,1,2n =-r，若l α∥，则x =（ ）A ．6-B ．6C ．4-D ．4【答案】D【分析】若//l α，则m n ⊥，从而0m n ⋅=r r即可求解【详解】若//l α，则m n ⊥，从而0m n ⋅=r r即32100x --=,解之得：4x =6．（2022·全国·高二）设,x y ∈R ，向量(,1,1),(1,,1),(2,4,2)a x b y c ===-，且,a c b c ⊥∥，则||x y +=（ ） A ．1 B ．2C ．3D ．4【详解】02a c a c x ⊥⇒⋅=⇒b ∥1224yc y ⇒=⇒=--， ∴1x y +=.7．已知()2,3,1a =-，()2,0,3b =，()0,0,2c =，则()a b c ⋅+=（ ） A ．5 B ．4 C ．7 D ．9【答案】D【分析】根据空间向量的坐标运算，即可求解.【详解】()=2,0,5b c +,()2,3,1a =-,()()220351=9a b c ∴⋅+=⨯+⨯-+⨯ 8．已知向量()1,0,1a =-，则下列向量中与a 成3π夹角的是（ ） A ．()1,1,0- B ．()1,1,0- C ．()0,1,1- D ．()1,0,1--【分析】利用空间向量夹角公式进行逐一判断即可：因为向量(1,0,1a =-12=-，所以向量(1,0,1a =-：因为向量(1,0,1a =-所以向量()1,0,1a =-与向量：因为向量(1,0,1a =-所以向量()1,0,1a =-与向量：因为向量(1,0,1a =-，所以向量(1,0,1a =-9．在正三棱柱111-ABC A B C 中，12=，E 为棱AB 的中点，F 为线段1上的一点，且1AC EF ⊥，则1B FFB=（ ） A ．10 B ．12 C ．15 D ．20且与1AA 同向的方向分别为⎫⎪⎭，设F ⎛ ⎝132AC EF ⎛⋅= ⎝10．（2022·全国·高二专题练习）给出下列命题：①若空间向量a b ，满足a b =则a b = ②空间任意两个单位向量必相等③若空间向量a b c ，，满足a c b c ⋅=⋅，则a b = ④在正方体ABCD ﹣A 1B 1C 1D 1中，必有11BD B D =⑤向量a =（1，1，0 其中假命题的个数是（ ） A ．1 B ．2C ．3D ．4若空间向量a b ，满足a b =，向量a 与b 方向不一定相同，在②中，空间任意两个单位向量的模必相等，但方向不一定相同，故②是假命题；在③中，若空间向量a b c ，，满足a c b c ⋅=⋅，，则向量a 与b 不一定相等，故③是假命题；ABCD ﹣A 1B 1C 1D 1中，由向量相等的定义得必有11BD B D =，故④是真命在⑤中，由模的定义得向量a =（1，1，故⑤是真命题． 11．（多选）已知向量()1,0,1a =-r，则下列向量中与a 的夹角为60°的是（ ）A ．()1,1,0-B ．()1,1,0-C ．()0,1,1--D ．()1,0,1-【分析】设向量(),,b x y z =1,=2ba b a a b >⋅<=，再结合选项逐一判断即可【详解】解：不妨设向量(),,b x y z =， 若(1,1,0b =-111,=22a b a b a b -⨯=>-⋅<≠=若(1,1,0b =-1,=2ba b a b a ⋅=>⨯若(0,1,b =--1,2a a b a b b⋅==<>⨯若(1,0,1b =-2,22a b a a b b=-⨯⋅=<>12．（2022·全国·高二）已知空间向量(2,1,1a =--，()3,4,5b =，则下列结论正确的是（ ） A ．()2//a b a + B ．53a b =。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
空间向量的坐标运算（人教A版）
一、单选题(共10道，每道10分)
1.已知点的坐标分别为与，则向量的相反向量的坐标是( )
A. B.
C. D.
答案：A
解题思路：
试题难度：三颗星知识点：空间向量运算的坐标表示
2.已知空间直角坐标系中且，则点的坐标为( )
A. B.
C. D.
答案：A
解题思路：
试题难度：三颗星知识点：空间向量运算的坐标表示
3.若向量，，则向量的坐标是( )
A. B.
C. D.
答案：D
解题思路：
试题难度：三颗星知识点：空间向量运算的坐标表示
4.已知向量，，则=( )
A. B.
C. D.
答案：C
解题思路：
试题难度：三颗星知识点：空间向量运算的坐标表示
5.已知向量是空间的一组单位正交基底，若向量在基底下的坐标为，那么向量在基底下的坐标为( )
A. B.
C. D.
答案：C
解题思路：
试题难度：三颗星知识点：空间向量的基本定理及其意义
6.已知为空间的一组单位正交基底，而是空间的另一组
基底，若向量在基底下的坐标为，则向量在基底下的坐标为( )
A. B.
C. D.
答案：A
解题思路：
试题难度：三颗星知识点：空间向量的基本定理及其意义
7.已知三点不共线，点为平面外的一点，则下列条件中，能使得平面成立的是( )
A. B.
C. D.
答案：B
解题思路：
试题难度：三颗星知识点：共线向量与共面向量
8.已知，，，若，，三向量共面，则实数=( )
A. B.
C. D.
答案：D
解题思路：
试题难度：三颗星知识点：共线向量与共面向量
9.已知空间三点的坐标为，，，若三点共线，则=( )
A. B.
C. D.
答案：D
解题思路：
试题难度：三颗星知识点：共线向量与共面向量
10.已知点，点和点，则三角形的边上的中线长为( )
A. B.
C. D.
答案：D
解题思路：
试题难度：三颗星知识点：空间向量模的运算。