估算畦灌土壤入渗参数的线性回归法
土壤入渗实验报告.doc
土壤入渗实验报告一、实验目的:进行土壤入渗试验,对土壤入渗规律有大致了解,并且利用测的数据绘出土壤累积入渗量和时间的关系曲线,利用该曲线求出入渗强度和时间的关系。
二、实验仪器:直径4.5cm的土柱圆筒、宽5cm长4cm的马氏瓶三、实验步骤:(1)把准备好的土装入圆筒中,每装5cm就夯实一次,直至土的的顶端位于圆筒进水孔的下缘。
(2)检测马氏瓶是否漏气。
如果漏气就换试验设备或者用凡士林涂抹。
(3)将水灌入马氏瓶,把马氏瓶的出水孔和圆筒的进水口用橡胶管连接好,调节圆筒和马氏瓶的相对高度使得马氏瓶的出水孔刚好出水。
(4)读取马氏瓶中水的高度。
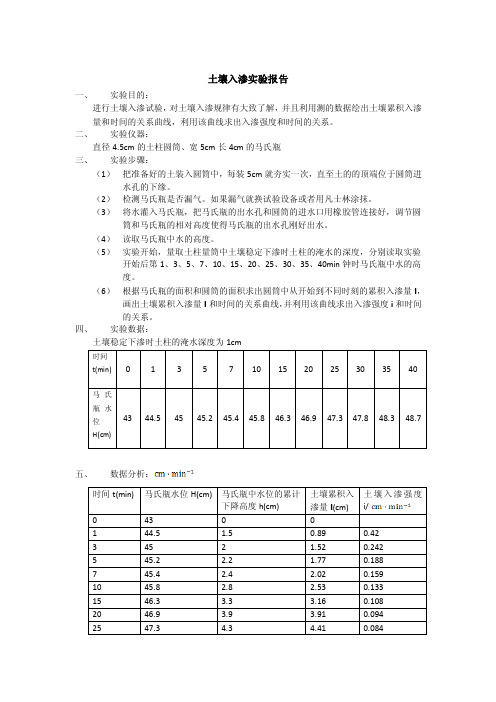
(5)实验开始,量取土柱量筒中土壤稳定下渗时土柱的淹水的深度,分别读取实验开始后第1、3、5、7、10、15、20、25、30、35、40min钟时马氏瓶中水的高度。
(6)根据马氏瓶的面积和圆筒的面积求出圆筒中从开始到不同时刻的累积入渗量I,画出土壤累积入渗量I和时间的关系曲线,并利用该曲线求出入渗强度i和时间的关系。
四、实验数据:土壤稳定下渗时土柱的淹水深度为1cm五、数据分析:i/012345651015202530354045入渗时间t/min土壤累积入渗量I 和时间t 的关系曲线图根据土壤累积入渗量I 和时间t 的拟合函数求导得到土壤入渗强度i 和时间t 的关系00.050.10.150.20.250.30.350.40.451020304050入渗时间t/min土壤入渗强度i/cm·min土壤入渗强度i 和时间t 的关系曲线图六、 体会:1. 土壤渗流试验看似简单,不过做成功很难。
实验室中大多数仪器损坏。
实验条件艰难,但是还是尽量利用实验室中的其他条件勉强把实验做完了。
2.土壤入渗要现实土壤足够湿润,然后才能开始记录试验数据,否则会出错。
3.土壤入渗强度开始较强,后来变小,逐渐稳定。
关于农业投入产出的线性回归模型

关于农业投入产出的线性回归模型农业投入产出是农业经济学中一个非常重要的问题,它直接关系到农业生产的效率和可持续发展。
为了深入了解农业投入产出的关系,可以使用线性回归模型来分析相关数据,从而预测农业生产的产出。
线性回归模型是一种统计模型,它可以用来描述自变量和因变量之间的线性关系。
在农业投入产出领域,我们可以将农业产出视为因变量,而农业投入则是自变量。
通过线性回归模型,我们可以了解农业投入对农业产出的影响,从而帮助农业生产者制定更有效的生产计划和资源配置。
我们需要收集相关的农业投入和产出数据。
农业投入包括土地、劳动力、肥料、农药等资源的投入,而农业产出可以用农作物产量、养殖业产量等指标来衡量。
这些数据可以通过调查和统计部门、农业生产企业、农户等途径来获取。
接下来,我们可以利用统计软件或编程语言来建立线性回归模型。
假设我们的数据集包括n组数据,每组数据包括农业产出Y和农业投入X。
线性回归模型可以表示为:Y = β0 + β1X + εY表示农业产出,X表示农业投入,β0和β1是回归系数,ε是误差项。
通过拟合得到的回归系数,我们可以了解农业投入对农业产出的影响程度。
如果β1大于0,说明农业投入的增加会促进农业产出的增长;反之,如果β1小于0,说明农业投入的增加会抑制农业产出的增长。
我们还可以通过回归模型的显著性检验和模型拟合度来评估模型的可靠性。
在得到线性回归模型后,我们可以利用模型进行预测。
假设我们要预测未来某一年的农业产出,我们可以将该年的农业投入代入线性回归模型中,从而获得预测值。
这有助于农业生产者和政府部门制定相应的生产计划和政策。
需要注意的是,线性回归模型的建立和应用需要考虑到多种因素的综合影响。
农业生产受到天气、市场需求、技术进步等多种因素的影响,这些因素也需要纳入考虑范围。
线性回归模型也有一定的局限性,不能完全描述复杂的实际情况。
在建立线性回归模型的还需要综合考虑其他统计方法和实地调查等手段,从多个角度来分析农业投入产出的关系。
灌溉工程节水潜力计算方法(全文)

灌溉工程节水潜力计算方法(全文)1、计算参数的确定我省地下水一直处于严重超采状态,随着水位埋深不断加大,地下水的赋存运移规律发生了变化,与水资源有关的一些参数必然发生相应的变化。
计算参数主要为:大埋深灌溉入渗补给系数、渠系输水节水前后扣除蒸发损失水量系数、潜水蒸发系数、土面蒸发占作物总蒸发量的比例等。
1.1大埋深灌溉入渗补给系数的确定(1)地下水位深埋时降雨(灌溉)入渗补给浅埋时地下水和上部土壤存在水分的双向交换;深埋时,地下水只承受上部土壤水分的入渗补给,水分总是由上而下迁移的,地下水常年承受入渗补给。
分析了地下水深埋条件下入渗补给和土壤水疏干的特征。
(2)渠灌田间入渗系数和井灌回归系数在灌溉过程中用于渠道周边下渗,有一部分会下渗补给地下水,当灌水到达田面后,因农田表土疏松且包气带土壤的渗透性较强,将有较多的水量入渗补给地下水。
灌溉入渗补给系数层为灌溉入渗补给地下水的水量与灌溉水量的比值。
渠灌田间入渗补给系数为渠灌区斗渠(包括斗渠)以下田间渠灌入渗补给量与斗渠引水量比值;而井灌回归系数β是指田间灌溉水入渗补给地下水的水量与灌溉水深的比值。
β值可通过灌溉入渗试验或动态资料分析确定。
1.2渠系输水节水前后扣除蒸发损失水量系数的确定渠系水蒸腾蒸发损失量(包括全部渠系面积的蒸腾蒸发量和渠系侧渗影响带面积的附加蒸腾蒸发损失量),约占渠系输水过程总损失的l0%一15%(该百分比以下简称“渠系水蒸发损失系数”代表渠系输水时蒸发损失除以渠系渗漏损失的系数),约占小麦播种面积上总蒸腾蒸发量的6%一10%(包括田间与渠系)。
渠系防渗后,渠系水蒸腾蒸发损失量一般只占防渗以前渠系输水过程中总损失量的3%一4%,约占节水前小麦播种面积上总蒸腾蒸发量的2%一3%。
由此可见,对于土渠输水的大型灌溉区在小麦全生育期,由渠系节水所能够减少的无效蒸腾蒸发量一般只占节水前农田蒸腾蒸发总量的4%一7%。
同样可以得出,对于土渠输水的井灌区在小麦全生育期,由土渠输水改为管道化输水所能够减少的无效蒸腾蒸发量一般只占节水前农田蒸腾蒸发总量的3%左右。
土透水性渗透系数计算公式

土透水性渗透系数计算公式土壤渗透性是土壤水分运移的重要指标,也是评价土壤水分保持能力和排水能力的重要参数。
土壤渗透性通常通过土壤渗透性系数来表示,而土壤渗透性系数则可以通过土壤渗透性渗透系数计算公式来计算。
本文将介绍土壤渗透性渗透系数计算公式及其应用。
土壤渗透性渗透系数计算公式一般采用Kostiakov方程或Philip方程来表示。
Kostiakov方程是最常用的土壤渗透性渗透系数计算公式之一,其表达式为:K = a t^b。
其中,K为土壤渗透性渗透系数,a和b为经验常数,t为时间。
Philip方程则是另一种常用的土壤渗透性渗透系数计算公式,其表达式为:K = a S^b。
其中,K为土壤渗透性渗透系数,a和b为经验常数,S为土壤孔隙度。
这两种计算公式都是经验公式,可以根据实际情况进行参数的调整,以更好地适用于不同类型的土壤和不同的水文条件。
土壤渗透性渗透系数计算公式的应用范围非常广泛,主要用于土壤水分运移模型的建立和水文模拟的参数化。
在土壤水分运移模型中,土壤渗透性渗透系数是一个重要的参数,它直接影响着土壤中水分的运移速度和分布规律。
通过计算土壤渗透性渗透系数,可以更准确地描述土壤水分运移过程,为农业灌溉、水资源管理等提供科学依据。
另外,在水文模拟中,土壤渗透性渗透系数也是一个重要的参数。
水文模拟是研究流域水文过程和水资源管理的重要手段,而土壤渗透性渗透系数则是模拟土壤水分平衡和地下水补给的关键参数。
通过计算土壤渗透性渗透系数,可以更准确地模拟流域水文过程,为水资源管理和防洪减灾工作提供科学依据。
除了在水文模拟和土壤水分运移模型中的应用,土壤渗透性渗透系数计算公式还可以用于土壤改良和排水工程的设计。
通过计算土壤渗透性渗透系数,可以评估土壤的排水能力和保水能力,为土壤改良和排水工程的设计提供科学依据。
例如,在农田排水工程中,通过计算土壤渗透性渗透系数,可以确定排水管道的设计规格和排水系统的布局,提高农田排水效果,增加农田产量。
关于农业投入产出的线性回归模型

关于农业投入产出的线性回归模型
农业投入产出的线性回归模型是用于评估农业生产中投入与产出之间的关系。
模型的基本思路是通过分析不同的农产品产出、耕作过程中的投入、天气因素、土地利用情况以及其他因素之间的关系,建立一个可以预测生产结果的模型。
这个模型可以为农业生产者提供决策支持,帮助其更好地规划生产计划和决策投入。
农业投入产出的线性回归模型是基于统计学的方法建立的。
建立这个模型需要先对数据进行搜集,对数据进行处理和拟合,然后计算出各种参数和预测值。
在实际运用需要考虑到不同的农业因素对生产的影响,进行相应的数据分组和调整。
线性回归模型的基本形式是y=a+bx,其中y表示产出,x表示投入。
a为截距,b为斜率。
截距即当投入为0时的产出值,斜率表示投入对产的变化量,这个变化量通常用敏感度(Sensitivity)代码的比率来度量。
建立农业投入产出的线性回归模型时,需要先考虑投入要素,如人工成本、肥料、种子、农具等,然后再考虑产出因素,如产量、出售价格等。
通过统计学的方法计算出二者之间的关系,得出各种参数。
实际上,在建立模型时,我们还需要考虑到非线性因素的影响。
因为农业生产的结果是受到多种因素的影响的,模型可能无法描述这些因素的复杂性。
因此,在农业投入产出的线性回归模型中,有时还需要引入一些非线性因素,如神经网络(Neural Networks)等技术,以确保模型的有效性。
总之,农业投入产出的线性回归模型是一种简单而有效的预测模型。
它对农业生产的决策至关重要,有助于农业生产者做出更为明智的决策。
关于农业投入产出的线性回归模型

关于农业投入产出的线性回归模型
农业投入产出的线性回归模型是一种用于分析农业产出与投入之间关系的统计方法。
该模型是建立在线性关系的基础上,通过拟合数据来估计产出与投入之间的数学关系。
农业投入通常包括土地、劳动力、资本、肥料、农药和灌溉等因素,而农业产出则是指农作物或畜牧产品的产量。
线性回归模型的目标是通过找到最佳拟合直线来描述投入与产出之间的关系。
最常用的线性回归模型是一元线性回归模型,该模型可以表示为:
Y = a + bX + e
Y表示农业产出,X表示农业投入,a和b是待估计的参数,e是误差项。
在建立线性回归模型之前,需要收集相关的农业投入和产出数据。
这些数据可以来自农业调查、统计年鉴或农业生产资料企业等。
收集到的数据包括投入和产出的量,可以是数量、重量或货币单位。
接下来,使用统计软件或编程语言,通过最小二乘法来拟合数据,估计出模型中的未知参数a和b。
最小二乘法是一种常用的回归分析方法,它通过找到使得误差平方和最小的参数估计。
估计出参数后,可以使用模型来预测农业产出。
将农业投入的值带入模型中,即可得到对应的预测产出值。
还可以通过模型中的参数来解释农业投入对产出的影响。
如果b的值为正,则表示增加投入会使产出增加;如果b的值为负,则表示增加投入会使产出减少。
需要注意的是,线性回归模型假设了投入与产出之间是线性关系。
在现实情况中,农业产出往往受到众多因素的影响,线性模型可能无法完全解释这种复杂关系。
应该对模型的合理性进行验证,如检验模型的拟合优度和统计显著性。
土壤水文学2下渗计算过程

大多数的入滲公式都是描述土壤的入滲能力(infiltration capacity),一般常用的有霍顿公式、菲利普公式、格林-安
普公式以及美國水土保持局的入滲公式。
入渗量与入渗率
入渗量是入渗开始后一定时间内,通过地表单位面积 入渗到土壤中的总水量,通常用水深表示(mm):
L
F (t) (z, t) (z,0)dz
3. Green-Ampt模型
原理:
• Green-Ampt模型研究的 是初始干燥的土壤在薄层 积水时的入渗问题。基本 假定是,入渗时存在着明 确的水平湿润锋面,将湿 润的和未湿润的区域截然 分开。也可以说含水量 的分布呈阶梯状,湿润区 为饱和含水量s,湿润峰 前即为初始含水量i,如 图示。这种模型又称活塞 模型。
ln
f0 f
fc fc
累積入滲量Fp = itpo,且此 時之入滲率f = i,故可得
t po
1 ik
f0
i
fc
ln
f0 fc i fc
入滲公式修正
入滲公式所計算出之單位時間入滲
水量,称为入滲能力fp(t)。所以
f(t) = min [fp(t),i(t)]
例題5-5 已知土壤起始入滲率f0 = 5 cm/hr、稳定入滲率fc
5
0.4 3
1
e
3 t 60
F20
0.510 1.510
1 60
0.33
f 20
5 3.19 5
0.33 0 0.67 0
4.11
t
4.11
0.4
5
0.4e
3 60
t' 4.3min
k ttpo t
f fc fo fc e 60
由实灌观测资料确定土壤渗吸特征值的渐近法应用实例

由实灌观测资料确 定土壤渗 吸特 征值 的渐近 法应用实例
赵 文 源
( 甘肃省水 利科 学研究 院 , 肃 兰州 甘 700 ) 3 00
摘要 : 利用畦灌 中的观测 资料 , 将不 同位 置不 同下渗历 时的资料 , 用迭代渐近 法求 出代表畦 田的渗 吸特征 值 z 分析 , 中对 空间、 时间均未作 简化处理 。本法采用 简单 的电算程序 , 可适 用于底坡 不规格 的畦田 , 更实用方便 。并可检 验 z
的可信度 , 而求 出灌水的质量指标。经典型灌 区多组试验 , 进 效果 良好 。 关键 词: 实灌; 土壤 渗吸 ; 征值 ; 特 渐近 法; 应用
中 图分 类 号 :2 53 ¥7. 1 渐 近 法 简 要 说 明 文献标识码 : B 数 据 再 回归 求 解 , 出 : 得 z = 1t M ・ 这 是第一次 的近似值 。 () 3
L B・ = t a () 1
精 度要 求 , 重复上述计算 , 达到 满意精度 即为解答。设式 ( ) 4 为解答 , 将式 ( ) 4 代人畦流到达 各等分 点的时间来计算 , 求出 tt : 、 ……t的全畦平均 下渗值 即 Z ,应分别 为观 测 的 Z 、 i ^
… …
Z3K3 N =  ̄ t
一
的在理论 上更有依 据 的方 法( 或称为迭代 逼近法 ) 简要说 明
如下 : ,
() 4
般计算至此 , 一K 、 , 2
, 可作 为解答 。 或确定某个
( )将 观测 到 的畦流输水 时间 ( 1 畦首进 水开 始计 时 ) 与推进 距离 厶 的数据 回归分 析 , 出: 求
m n 畦首水深降为零时为 8 i。 i; 5 m n 由每 1 f 个观测点处 0 r一 l
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
估算畦灌土壤入渗参数的线性回归法王维汉1,2,缴锡云1,彭世彰1,马海燕1,2(1. 河海大学水文水资源与水利工程科学国家重点实验室,南京 210098;2. 河海大学现代农业工程系,南京 210098)摘要:将畦灌地表水深与水流推进距离按指数函数进行非线性最小二乘拟合,并根据水量平衡原理提出了估算土壤入渗参数的线性回归法。
实例计算表明:地表水深与水流推进距离之间呈现较好的指数函数关系;线性回归法估算土壤入渗参数计算工作量较小,计算精度较高。
关键词:入渗参数;畦灌;地表水深;线性回归法土壤入渗特性是影响地面灌溉过程的一个十分重要的因素。
土壤入渗参数的估算是地面灌溉研究中的一个重要内容。
早在1956年,Haise就提出了利用筒测仪来测量土壤入渗参数,但由于入渗过程的时空变异性很大[1-2],土壤入渗参数常常难以准确估算。
国内外学者对估算土壤入渗参数进行了大量研究,提出了多种计算方法。
Elliott和Walker[3](1982)针对沟灌提出了估算土壤入渗参数的两点法,需要分别观测水流前锋推进到沟长中点和沟末端的时间及沟首过流断面面积,在水量平衡的基础上估算入渗参数。
两点法需要观测的数据少,计算简单,但计算结果精度往往不够。
Maheshwari[4](1988)首次将优化技术应用到土壤入渗参数的估算中,通过测量水流推进过程和畦首地表水深的变化过程来计算土壤入渗参数。
这种方法(以下简称M法)适用于任何入渗模型,精度较高,使用较为广泛,但计算量偏大。
Shepard[5](1993)提出了估算土壤入渗参数的一点法,该方法需要测量水流推进到沟末端的时间和沟中的平均过水面积来计算土壤入渗参数,但它只适用于Philip入渗模型,从而其应用受到一定的限制。
Esfandiari[6](1997)对M法进行改进,提出了利用水流推进资料和沿沟长若干点地表水深资料采用模式搜索技术来估算土壤入渗参数的方法,但同样是存在计算量较大的问题。
国内学者也提出了许多估算土壤入渗参数的计算方法。
王文焰[7](1993)提出了利用两个畦田的水流推进消退过程来估算土壤入渗参数的方法。
费良军[8](1999)提出了利用畦灌水流的地表水深资料及水流推进过程来估算土壤入渗参数的方法。
这两种方法都需要至少观测两个畦田的灌水资料才能估算土壤入渗参数,精度较高,但试验工作量较大,且不便于评价入渗模型的合理性。
缴锡云[9](2001)对M法的计算方法进行了改进(以下简称M-J法),张新民[10](2005)又对M法的计算方法做了改进(以下简称M-Z法),这两种改进减少了一定的试验工作量,但计算量较大的问题仍算存在。
综上所述,在以上估算土壤入渗参数的方法中,两点法、M法等采用地表储水形状系数计算地表储水量,但当畦田长度较长时(大于100m),地表储水形状系数变化较大,会给计算带来较大误差[11]。
本文依据水位传感器观测的地表水深资料,规避地表储水形状系数,提出计算精度较高的线性回归法,来估算土壤入渗参数。
1理论分析1.1水量平衡方程式建立x,地表水面线与入渗水量分布曲线如图1所示。
在畦灌地表水流推进过程中,对应于推进距离a基金项目:河海大学水文水资源与水利工程科学国家重点实验室开放研究基金资助项目(2005405811);河海大学科技创新基金资助项目(2084-40401105)作者简介:王维汉(1981—),男,河南南阳市人,在读博士研究生,从事节水灌溉理论与技术研究。
通讯作者:缴锡云(1962—),男,河北文安县人,博士,教授,主要从事节水灌溉理论与技术研究。
根据水量平衡原理有z h V V qt += (1)式中:q 为入畦的单宽流量,L 2·T -1;t 为灌水历时,T ;h V 为水流前锋推进至a x 处时,单位畦宽上的地表储水量,L 2;z V 为对应的单位畦宽上的入渗水量, L 2。
1.1.1 地表储水量在畦灌水流推进过程中, 假定地表水深h 与水流推进距离a x 符合如下的指数函数关系式)1(0s h a b e h h h −+= (2)式中:h 为地表水深,L;0h 为畦首地表水深,L ;a h 、b h 为拟合参数; s 为沿畦长方向上距畦首的距离,L。
则地表储水量可表示为h V =∫ax hds 0ds e h h ab x s h a ])1([00∫−+=bx h a a a h e h x h h a b )1()(0−++= (3)式中:h V 为单位畦田宽度的地表储水量,L 2;a x 为水流推进距离,L。
1.1.2 地下储水量地下储水量的计算涉及到土壤入渗模型,常用的入渗模型有Kostiakov 模型、Kostiakov-Lewis 模型、Green-Ampt 模型、Philip 模型、Horton 模型等。
在实际计算中Kostiakov 经验模型应用较为广泛[12]。
本文采用Kostiakov 入渗模型ατK Z = (4)式中:Z 为单位畦田面积上的累积入渗量,以水深表示,L ;K 为入渗系数,L·T -α;α为入渗指数,无量纲;τ为入渗历时,s t t −=τ,T ;s t 为水流前锋推进时间,T ;假定水流前锋推进过程符合幂函数规律[13],即rs ps t = ,p 和r 为拟合参数。
于是,地下储水量可表示为ds ps t K V ax r z ∫−=)(α (5)根据Fok 和Bishop 对式(5)的推导[13],上式可表示为z V =a x Kt r r αααα)1)(1()1(11[++−++ (6) 1.1.3 水量平衡方程式综合式(1)、式(3)和式(6)有Fig .1 Sketch of water surface profiles and infiltration waterdistribution for border irrigation地表水深ha b x h a a a x Kt r r h e h x h h qt a b αααα])1)(1()1(11[)1()(0++−+++−++= (7) 1.2 公式推导及计算方法对式(7)移项,令bx h a a a z h e h x h h qt V a b )1()(0−−+−= (8) =)(αf )1)(1()1(11r r ++−++ααα (9) 则式(7)可简化为ααKt x f V az=)( (10)式中:z V 表示地下入渗水量的观测值,L 2。
对式(10)两边取对数得t K x f V azln ln )(ln[αα+= (11)为了便于说明计算过程,令])(ln[azx f V Y α= t X ln = (12)则式(11)可转化为X K Y α+=ln (13)于是可利用线性回归法来估算入渗参数K 和α,具体计算步骤如下:(1)线性回归。
对灌水过程中的不同时刻i t (=i 1,2,3…),计算i X ;设入渗指数初始值5.0)0(=α,将)0(α代入到)(αf 中并计算得一系列i Y ,视等式(13)右边的K ln 和α分别为线性回归的截距和斜率,对i Y 和i X 进行线性回归,便可得到入渗参数的第一次回归值,记为)1(K 和)1(α。
(2)迭代。
用)1(α代替)0(α,重复步骤(1)的计算过程,可得到入渗参数的第二次回归值,记为)2(K 和)2(α,如此进行m 次迭代便可得到入渗参数的回归值)(、m m Kα)(。
(3) 误差控制。
对第1−m 次和第m 次线性回归得到的入渗参数)(、1)1(−−m m K α和)(、m m K α)(,利用式(14)计算两次回归求得参数之间的误差。
)1(1−−−=m m m K K K δ,)1()(1−−−=m m m a ααδ (14)式中:1−m Kδ,1−m aδ分别为K 和α的第m 次回归和第1−m 次回归之间的误差。
如果两次回归得到的入渗参数同时满足式(15),则停止迭代,得到最终参数为)(m K K =,)(m αα=。
K m Kεδ≤−1,ααεδ≤−1m (15)式中:εK 和αε分别为K 和α的允许误差。
(4)精度计算。
精度用残差平方和e S 表示,计算式如下2)(zj zj e V V S −= (16) 式中:zj V 为由试验测得的水流推进到第j 个水深控制点时的单宽入渗水量,L 2;zj V 为利用入渗参数计算得到的第j 个水深控制点时的单宽入渗水量,L 2。
对)0(α在0到1之间任意取值,计算发现,)0(α的不同取值不影响迭代的稳定性,为了加快迭代的收敛速度,建议)0(α在0.3到0.7之间取值。
采用上述线性回归及迭代计算入渗参数,比目前使用广泛的M 法大大减少了计算工作量,而且在计算地表储水量时,避开了难以定值的地表储水形状系数,因而具有更高的计算精度。
2 试验验证2.1 试验区概况及试验方法试验于2005年在中科院南皮生态农业试验站内进行。
试验区位于河北省沧州市南约40km ,地处北纬38。
06′,东经116。
40′。
该地区多年平均降水量550mm ,平均日照时间2318h ,水面蒸发1025~1218mm ,地下水埋深5~7m ,耕地土壤为轻质壤土,灌前测定试验地土层1m 内的土壤含水量15.85%~19.63%,土壤干容重1.42g/cm 3。
在2条畦田(编号分别为B 1和B 2)中分别进行了2次灌水试验,畦田规格及入畦流量见表1。
表1 畦田规格及入畦流量 Table 1 Border data and inflow discharge 畦宽畦长平均纵坡单宽流量畦田编号 /m /m% /m 3/min·mB 1 2.0 95 0.043 0.140 B 22.0 95 0.0640.081为了方便观测地表水流的推进过程和地表水深资料,在畦田两侧从畦首起每隔5m 布置一个标杆,并在畦田中心线上每隔10m 布置一个水位传感器。
灌水过程中用水表和秒表分别记录灌水流量和水流前锋推进时间;用奥得赛电容式水位传感器(Odyssey™4.5,精度0.1mm, 量程0.5m)记录距畦首0m 、10m 、20m 、30m 、40m 、50m 、60m 、70m 和80m 处的地表水深,直至灌水结束试验。
用水来自机井抽取的地下水。
2.2 水流推进过程及地表水深对畦田B 1的地表水流推进资料,用幂函数拟合得到水流推进过程函数关系式如下7721.10151.0st s = 9999.02=R (17)式中:s t 、s 的意义同前。
对畦田B 1的水深数据采用式(2)建立不同时刻的地表水深与水流推进距离的函数关系式,拟合参数及其相关系数见表2。
畦田B 1、B 2地表水深与水流推进距离拟合曲线见图2,图3。
