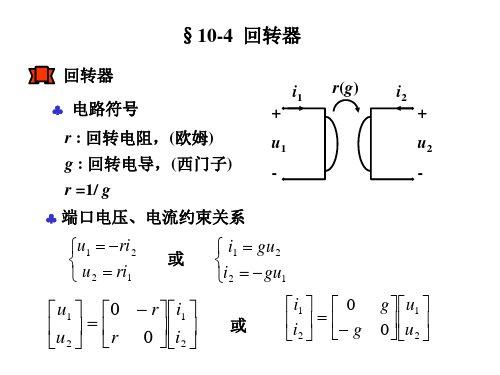
回转器
回转器
级联后的双口网络的[T]=[T1][T2]
例10.5-1 求图示电路的传输参数[T],已知 R1=1 、 R2=2、 R3=3、L=1H、C=1F、n=2、=1rad/s L 1 R1 n:1 * * R2 1‘ . . I1 R1=1 I2 + . U1 R2=2 . I . L j1 I1 2:1 + . * * U1 图(b) 2‘ . I2 + . U2 + . U1 . I1 R3 C 2
例10-3.1: 求图示回转器端口的输入阻抗。 . g I1 1 + . U1 1‘
. I2 2 + . U2 2‘
ZL
例10.3-2: 已知 r=2 C=0.5F 求:u1
i1 5 2 cos 3 t ( A )
. I1 r . I2 2 + . U2 2‘
1 + . U1 1‘
1 j C
由于: Z12Z21 Y12Y21 等效电路
i1 gu 2 i 2 gu 1
所以回转器不具有互易性。
u 1 ri 2 u 2 ri 1
i1
+ u1 gu2
i2
+ u2 + u1 -
i1 + -ri2 + ri1
i2 + u2 -
-gu1
回转器的功率 1-1‘端口输入的瞬时功率 p1=u1i1 +
u1 0 r u 2
或
i1 0 g i2
g u1 0 u 2
回转器的Z参数矩阵和Y参数矩阵为:
0 [Z ] r r 0 0 [Y ] g g 0
16.6 回转器和负阻抗变换器
本节介绍两种特殊的二端口器件: 本节介绍两种特殊的二端口器件:
回转器和负阻抗变换器
一、回转器
回转器是一种线性非互易的多端元件。 回转器是一种线性非互易的多端元件。 回转器是一种阻抗逆变器,可用于将电容回转成电感。 回转器是一种阻抗逆变器,可用于将电容回转成电感。 1、电路符号图 、 i2 i1 + u1 + u2 -
0 − r Z= r 0 0 g Y== - r i2 u2 = r i1 或 i1 = g u2 i2 = -g u1
u1i1+u2i2= - r i2 i1 + r i1 i2 = 0
理想回转器既不消耗功率又不发出功率, 理想回转器既不消耗功率又不发出功率,它 是一个无源线性元件 无源线性元件。 是一个无源线性元件。且互易定理不适用于回转 器。
4、回转器的应用 、 回转器具有把一个端口上的电流 回转” “回转”为另一端口上的电压或相反过 程的性质。 程的性质。 应用这一性质回转器可以把一个电 容回转为一个电感, 容回转为一个电感, 这在微电子器件中为用易于集成的 电容来实现难于集成的电感提供了可能 来实现难于集成的电感 电容来实现难于集成的电感提供了可能 性。
0 U 2 − I 1 2
4、负阻抗的实现(以电流反向型为例) 、负阻抗的实现 I1 + U1 NIC I2
Z2
U1 1 0 U 2 I = 0 − k − I 2 + 1
U2 U2 = - Z2I2
U1 ( s ) U 2 (s) = 输入阻抗 Zin= I1 ( s ) kI 2 ( s )
电容回转为电感. 若C=1µF,r = 50k ,则L=2500H.电容回转为电感 , 电容回转为电感
回转器——精选推荐

回转器一、实验目的1. 掌握回转器的基本特性2. 测量回转器的基本参数3. 了解回转器的应用 二、原理说明1. 回转器是一种有源非互易的新型两端口网络元件, 电路符号及其等效电路如图23-1(a)、(b)所示。
图 23-1 理想回转器的导纳方程如下: I 1 0 g u 1= ,或写成 i 1=gu 2 ,i 2=-gu 1 I 2 -g 0 u 2也可写成电阻方程:u 1 0 -R i 1= ,或写成u 1=-R i 2 ,u 2=R i 1 u 2 R 0 i 2式中g 和R 分别称为回转电导和回转电阻,统称为回转常数。
2. 若在2-2'端接一电容负载C ,则从1-1'端看进去就相当于一个电感,即回转器能把一个电容元件“回转”成一个电感元件;相反也可以把一个电感元件“回转”成一个电容元件,所以也称为阻抗逆变器。
2-2'端接有C 后,从1-1'端看进去的导纳Y i 为2222211/i u g g i gu u i Y i -=-== C j Z i u L ω122=-= Lj C j g Y i ωω1/2==∴,式中2g C L =为等效电感。
3. 由于回转器有阻抗逆变作用,在集成电路中得到重要的应用。
因为在集成电路制造中,制造一个电容元件比制造电感元件容易得多,我们可以用一带有电容负载的回转器来获得数值较大的电感。
图23-2为用运算放大器组成的回转器电路图。
11,2,2u i1i 2u 2(a )11,u i1(b )图 23-2三、实验设备四、实验内容实验线路如图23-3所示。
R S 跨接于DG06挂箱中G 线路板左下部的二个插孔间。
1. 在图23-3的2-2'端接纯电阻负载(电阻箱), 信号源频率固定在1KHz ,信号源电压≤3伏。
图 23-3用交流毫伏表测量不同负载电阻R L 时的 U 1、U 2 和U RS , 并计算相应的电流I 1、I 2和回转常数g ,一并记入表23-1中。
回转器

的回转器电路。
其端口特性
i1
1 R u2
i2
1 R
u1
根据回转器定义式,可得g=1/R。
2.在输入为正弦电压,负载阻抗是一个电容C时, 输入阻抗为:
Zin
1 g2ZL
g2
1 1
jC
g2
j L
jC
可见,在回转器输出端接入一个电容元件,从输入
端看入时可等效为一电感元件,等效电感L=C/g2
。所以,回转器也是一个阻抗变换器,它可以使容
性负载变换为感性负载。
3.如图3(a)所示,用模拟电感器可以组成一个
RLC并联谐振电路,图3(b)是其等效电路。
R
+
u1
C1
C2
-
图3(a) RLC并联谐振电路图
R
+
u1
C1
L
-
图3(b) RLC并联谐振电路等效电路图
此并联谐振电路的幅频特性为:
U ()
I
I
G2 (C 1 )2 G 1 Q2 ( 0 )2
3. 绘制不同频率下,电路中采样电阻两端的幅频特 性。
实验现象
1. 在模拟电感器实验中,回转器的负载接电容时, 其端口的电压相位超前于端口电流相位,说明回 转器将电容转换成了电感。
2. 电阻、电容和模拟电感器串联当输入信号频率等 于谐振频率时电路发生了谐振,此时电阻上的电 压最大。
实验结果分析
1. 如果直接将通道1测量 us,通道2测量uro,会产 生什么后果?为什么? 答:会造成功率函数发生器输出端短路。因为 示波器两通道的“地”是同一个“地”。
1台
交流毫伏表
1只
数字示波器
1台
有源电路实验板
16.6回转器及负阻抗
u i 2
0
r
1
或
r 0 2
i u
1
i u 2
0 g 1
g
0
2
性质:
把一个端口上的电流回转为另一端口
上的电压,或相反的过程。
i1 1
i2 2
u1
u2
C
1’
2’
结论:从端口1-1’看相当于一个电感,Le=r2C
运放实现的回转器
ia
ib
i u gu
1 1 R
2
2
i u gu
I I 1 0 k 2
U U
1
k 0
2
I I 1 0 1 2
电流反向型 电压反向型
Z i
u1 i1
u2 ki2
1 k
ZL
运放实现的负阻抗变换器
I3
I1
U 1
I4 I2
U 2
2 1 R
1
1
B
i1
A
U1
D
C E
F
i2
U2
回转器的等效电路
i1 1
i2 2
u1
u2
1’
2’
i
1
gu2
i
2
gu1
i1
i2
u1 gu2
-gu1 u2
二、负阻抗变换器
负阻抗变换器(NIC)也为一个二端口, 其图形符号如下图:
i1
i2
i1
i2
u1
NIC
u2
u1
ห้องสมุดไป่ตู้
NIC
u2 ZL
U U
1
1
0
2
16.6 回转器与负阻抗变换器
回转器

数字示波器
1台
数字万用表
1只
可调电容箱
1只
可调电阻箱
1只
直流毫安表
1只
交流毫伏表
1只
有源电路实验板 1块
直流稳压电源
用表
可调电容箱
可调电阻箱
直流毫安表
交流毫伏表
有源电路实验板
实验步骤
1. 测量回转器的回转电导
Ro ro
uro
实验标准报告
一、实验目的 1.学习和了解回转器的特性。
2.研究如何用运算放大器构成回转器,学习回转器 的测试方法。
2. 回转器可以由晶体管或运算放大器等有源器件
构成。图5.16.2所示电路是一种用两个负阻抗变换器
来实现的回转器电路。
其端口特性:
i1
1 R
u2
i2
1 R
u1
根据回转器定义式,可得 g=1/R。
+ +
R0
-
R0
R0
i5
i6
R
i3
i1 u1
A
i
Rin
R i7
Rin
B
-
R0
3. 绘制不同频率下,电路中采样电阻两端的幅频特 性。
实验现象
1. 在模拟电感器实验中,回转器的负载接电容时, 其端口的电压相位超前于端口电流相位,说明回 转器将电容转换成了电感。
2. 电阻、电容和模拟电感器串联当输入信号频率等 于谐振频率时电路发生了谐振,此时电阻上的电 压最大。
实验结果分析
1. 如果直接将通道1测量 us,通道2测量uro,会产 生什么后果?为什么? 答:会造成功率函数发生器输出端短路。因为 示波器两通道的“地”是同一个“地”。
回转器实验报告

回转器实验报告回转器实验报告引言:回转器是一种常见的实验装置,用于研究物体在旋转时产生的力和动力学特性。
本次实验旨在通过构建一个简单的回转器装置,探究回转器的基本原理和运行机制,并分析其在不同条件下的性能表现。
一、实验目的本实验的主要目的如下:1. 理解回转器的基本原理和结构;2. 探究回转器在不同转速下的性能变化;3. 分析回转器在不同负载条件下的工作特性;4. 讨论回转器在实际应用中的局限性和改进方向。
二、实验装置与方法1. 实验装置:本次实验所使用的回转器装置主要包括一个电动机、一个转轴、一个负载轮和一套数据采集系统。
电动机通过转轴将动力传递给负载轮,数据采集系统用于记录转轴转速和负载轮的转动情况。
2. 实验方法:在实验开始前,首先将电动机与转轴连接,并将负载轮安装在转轴上。
然后,通过调节电动机的转速,记录不同转速下转轴的转动情况。
接着,改变负载轮上的负载,记录不同负载条件下转轴的转速和负载轮的转动情况。
最后,根据实验数据进行分析和讨论。
三、实验结果与讨论1. 回转器转速与负载关系:根据实验数据,我们可以得出回转器的转速与负载之间存在一定的关系。
当负载增加时,回转器的转速会下降;当负载减小时,回转器的转速会增加。
这是因为负载的增加会增加回转器所需的力矩,从而降低转速。
2. 回转器转速与电动机转速关系:实验还表明,回转器的转速与电动机的转速之间存在一定的关系。
当电动机的转速增加时,回转器的转速也会增加;当电动机的转速减小时,回转器的转速也会减小。
这是因为电动机提供的动力直接影响着回转器的转速。
3. 回转器的性能与负载轮材料的关系:在实验中,我们还发现负载轮的材料对回转器的性能有一定的影响。
当负载轮的材料较轻时,回转器的转速会相对较高;当负载轮的材料较重时,回转器的转速会相对较低。
这是因为负载轮的材料质量会影响回转器所需的力矩。
四、实验结论通过本次实验,我们得出了以下结论:1. 回转器的转速与负载之间存在一定的关系,负载增加会导致转速下降。
回转器与负阻抗变换器

电流反向型和电压反向型
电路符号
i1 +
u1
NIC
_
i2 + u2 _
电流反向型定义:
u1 i1
= =
u ki
2 2
k >0
电压反向型定义:
u
1
i1
= =
− ku − i2
2
电流反向型NIC情况下:
I&1
+
U& 1
NIC
_
I&2
+ U&_2
可实现
Z in
=
U&1 I&1
=
U& 2 k1 I&2
第十章 双口网络
§10-4 回转器与负阻抗变换器
1、回转器
+ 1 i1 u1
r (或g)
i2 2+ u2
1′
2′
箭头表示回转器的回转方向,在图示参考方
向下,端口电压、电流的约束关系为
uu12==−rrii12 (1)
或
i2i1
= =
gu2 − gu1
(2)
若回转方向相反,则上述各式的等号右边加一负号。
I&2 2 +
U& -
2
ZL
2′
Zi
=
U&1 I&1
=
− rI&2 U& 2
=
−r 2
I&2 U& 2
=
r2
1 ZL
r
因此当 ZL
=
1 jωC
时,
Zi
=
jωr 2C =
jωL
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
回转器实验目的实验原理 实验仪器 实验步骤 实验报告要求 实验现象 实验结果分析 实验相关知识 实验标准报告实验目的• 学习和了解回转器的特性。
• 研究如何用运算放大器构成回转器,学习回转器的测试方法。
•学习用回转器和电容,来替代电感的方法。
实验原理• 回转器是理想回转器的简称。
它是一种新型的双 口元件,其符号如图5.16.1所示。
其特性表现为它能 将一端口上的电压(或电流)¡°回转¡±为另一端口上 的电流(或电压)。
端口量之间的关系为: 或上式中,回转系数g 具有电导的量纲,称为回转电导,α=1/g 称为回转比。
• 回转器可以由晶体管或运算放大器等有源器件 构成。
图5.16.2所示电路是一种用两个负阻抗变换器1221i gui gu =⎧⎨=-⎩1221u i u iαα=-⎧⎨=⎩来实现的回转器电路。
其端口特性:根据回转器定义式,可得 g =1/R 。
图2.16.2 回转器电路图• 在输入为正弦电压,负载阻抗是一个电容C 时,输入阻抗为:因此,在回转器输出端接入一个电容元件,从输入 端看入时可等效为一电感元件,等效电感L =C /g 2。
所以,回转器也是一个阻抗变换器,它可以使容性 负载变换为感性负载。
122111i u R i u R ⎧=⎪⎪⎨⎪=-⎪⎩Lin 222111Lj C Z j Lg Z ggj Cωωω====• 如图5.16.4(a )所示,用模拟电感器可以组成 一个RLC 并联谐振电路,图5.16.4(b )是其等效电 路。
图5.16.4(a ) RLC 并联谐振电路图图5.16.4(b ) RLC 并联谐振电路等效电路图图5.16.4(a )图5.16.4(b )此并联谐振电路的幅频特性为:2C U LU ()U ω==其中, ; ,称为谐振角频率;品质因数为:实验仪器直流稳压电源 1台 功率函数发生器 1台 数字示波器 1台 数字万用表 1只 可调电容箱 1只 可调电阻箱 1只 直流毫安表 1只 交流毫伏表 1只 有源电路实验板 1块直流稳压电源 功率函数发生器数字示波器 数字万用表 可调电容箱 可调电阻箱 直流毫安表 交流毫伏表有源电路实验板实验步骤•测量回转器的回转电导1G R=0ω=001CQ GG Lωω===图5.16.5 测量回转电导电路图1. 按图2.16.5所示电路接线,回转器输入端u 1接正弦 信号U S ,电阻R 0为51Ω,电阻R 为1k Ω,负载电阻R L 取 2k Ω,采样电阻r 0取2k Ω。
固定正弦信号源频率在3k H z 左右,在0~3V 范围内,从低到高逐渐增加正弦信号u 1 幅值,每增加约0.5V 取一个点,记录下此时的u 1、u 2和 u r 0的读数。
根据u r 0可得出输入电流i 1,由u 1、u 2和i 1可 得出回转电导g 和输入电阻R i n ,并与理论计算值进行比 较。
表5.16.1 测量回转器的回转电导LR2. 模拟电感器的测量按图5.16.5所示电路接线,将负载R L 换成电容箱, 电容调到 1µF 。
为了观察不同频率 f 时,输入电压与 输入电流的相位超前滞后关系以及u ro 的波形。
测量数 据填入表5.16.2•用模拟电感器作RLC 并联谐振实验C 2图5.16.6 RLC并联谐振电路图⑴实验电路如图2.16.6所示,R0为51Ω、R为1kΩ、r0为2kΩ,C1、C2为电容箱。
给定正弦信号发生器输出电压(有效值)不变,用万用表测量R两端的电压u R,记录下谐振频率。
C1为0.1µF,改变电容箱C2的值,重复实验,最后将所记录谐振频率与理论谐振频率进行比较。
表5.16.3 RLC串联诣振实验报告要求•根据实验数据,计算回转器的回转电导、输入阻抗,并与理论值相比较。
•用示波器观察并记录模拟电感器的u-i波形,解释相位超前滞后关系。
根据实验数据,计算输入电阻,并与理论值相比较。
•绘制不同频率下,电路中采样电阻两端的幅频特性。
实验现象•在模拟电感器实验中,回转器的负载接电容时,其端口的电压相位超前于端口电流相位,说明回转器将电容转换成了电感。
•电阻、电容和模拟电感器串联当输入信号频率等于谐振频率时电路发生了谐振,此时电阻上的电压最大。
实验结果分析•如果直接将通道1测量u s,通道2测量u ro,会产生什么后果?为什么?答:会造成功率函数发生器输出端短路。
因为示波器两通道的¡°地¡±是同一个¡°地¡±。
•可以只用一个通道直接测量u ro吗?答:不可以,因为用一个通道测量,只能得到r o的某一端对¡°地¡±的电压。
实验相关知识•预习要求•相关知识点•注意事项预习要求•预习运算放大器的基本工作原理,以及构成回转达器的基本方法。
•预习回转性的特性及用回转器构成模拟电感器的原理。
•预习RLC串联谐振的基本概念。
相关知识点二端口器件回转器串联谐振注意事项•回转器电路的电源极性及工作电压不能接错,以免损坏运算放大器。
•更换实验内容时,必须首先关断实验板的电源,不能在带电情况下更改接线。
•交流电源的输出不能太大,否则,运算放大器饱和,正弦电压波形出现畸变,影响实验测量准确性。
•注意信号源和示波器公共接地点的选取。
实验标准报告一、实验目的1.学习和了解回转器的特性。
2.研究如何用运算放大器构成回转器,学习回转器的测试方法。
3.学习用回转器和电容,来替代电感的方法。
二、实验内容1.测量回转器的回转电导。
2.模拟电感的测量。
3.用模拟电感器测RLC并联谐振频率。
三、实验仪器双路稳压电源1台函数发生器1台交流毫伏表1只数字示波器1台有源电路实验板1块四、实验用详细电路图1.测量回转电导。
R L2.用模拟电感器测RLC 并联谐振频率。
五、实验原理及计算公式回转器是理想回转器的简称。
它是一种新型的 双口元件。
其特性表现为它能将一端口上的电压( 或电流)¡°回转¡±为另一端口上的电流(或电压) 。
端口量之间的关系为:或上式中,回转系数g 具有电导的量纲,称为回转电 导,α=1/g 称为回转比。
回转器可以由晶体管或运算放大器等有源器件构 成。
图1所示电路是一种用两个负阻抗变换器来实现C 21221i gu i gu =⎧⎨=-⎩1221u i u i αα=-⎧⎨=⎩的回转器电路。
其端口特性根据回转器定义式,可得g =1/R 。
2.在输入为正弦电压,负载阻抗是一个电容C 时,输入阻抗为:可见,在回转器输出端接入一个电容元件,从输入 端看入时可等效为一电感元件,等效电感L =C /g 2 。
所以,回转器也是一个阻抗变换器,它可以使容 性负载变换为感性负载。
3.如图3(a )所示,用模拟电感器可以组成一个RLC 并联谐振电路,图3(b )是其等效电路。
图3(a ) RLC 并联谐振电路图122111i u R i u R⎧=⎪⎪⎨⎪=-⎪⎩222111in Lj C Z j Lg Z ggj Cωωω====u C 2图3(b ) RLC 并联谐振电路等效电路图此并联谐振电路的幅频特性为:其中, ;,称为谐振角频率;,称为品质因数。
六、实验数据记录1.测量回转器的回转电导按图1电路接线,回转器输入端u 1接正弦信号U s , 电阻R 0为51Ω,电阻R 为1k Ω,负载电阻R L 取2k Ω, 采样电阻r 0取2k Ω。
正弦信号源的频率固定在3kHz 左 右,在0~3V 范围内,从低到高逐渐增大正弦电压u 1 ,每增加约0.5V 取一个点,记录下此时的u 1、u 2和u r0 的读数。
根据u r0可得出输入电流i 1,由u 1、u 2和i 1可得 出回转电导g 和输入电阻R in ,并与理论计算值进行比较。
表5.15.1 测量回转器的回转电导u 1L()U ω==1G R=0ω=001C Q GG Lωω===2.模拟电感器的测量按图2所示电路接线,将负载R L换成电容箱,电容调到1µF。
为了观察不同频率f 时,输入电压与输入电流i1的相位超前滞后关系,同时保证示波器两路输入共地,不能直接测量u ro的波形。
把u s和u1分别输入通道1和通道2,利用示波器的数学计算功能,按下Math按钮,选择CH1-CH2功能,示波器上显示出M波形,此波形即为u s和u1的差值,即u ro的波形。
;3.用模拟电感器作RLC并联谐振实验图5.15.6 RLC并联谐振电路图实验电路如图5.15.6所示,R0为51Ω、R为1kΩ、r0为2kΩ,C1、C2为电容箱。
给定正弦信号发生器输出电压(有效值)不变,从低到高改变电源频率(在谐振频率附近,频率变化量要小一些),用交流毫伏表测量R两端的电压u R,记录下电压u R值最小时的电源频率,即为谐振频率,改变电容箱C2的值,重复实验,将所记录谐振频率与理论谐振频率进行比较。
表5.16.2 RLC并联谐C2七、实验数据计算、分析1.测量回转器的回转电导等效电阻(理论值):等效电阻(实验值):(计算结果见表5.16.1)回转电导(理论值):回转电导(实验值):(计算结果见表5.16.1)2.模拟电感器测量。
从示波器上可以看到u 1相位超前于i 1相位,说明 回转器容性负载回转成感性负载。
3. 用模拟电感器作RLC 并联谐振实验谐振频率(理论值)计算公式:22in L1000500 /2000RR R ===Ω11in r01o /u u R u i r ==Ω110.001 /S1000g R ===12i g u =计算结果参见表5.15.2。
谐振频率(测量值):测量时保持输入正弦信 号幅值不变,改变输入信号频率,测量取样电阻电 压,当电阻电压上的电压最小时,输入信号的频率 即为并联谐振频率。
测量结果参见表5.16.2。
0z f ==。
