微波介质陶瓷的介电特性数值计算
闭腔谐振法测试微波介质陶瓷介电参数.
收稿日期:2003212208.作者简介:周东祥(19412),男,教授;武汉,华中科技大学电子科学与技术系(430074).E 2mail :Zhou -Dx @基金项目:国家高技术研究发展计划资助项目(2001AA325110);湖北省科技攻关计划资助项目(2002AA101C01).闭腔谐振法测试微波介质陶瓷介电参数周东祥 胡明哲 姜胜林 龚树萍(华中科技大学电子科学与技术系,湖北武汉430074)摘要:研究用闭腔谐振法测量微波介质陶瓷介电参数的方法,采用TE 01δ模,开波导法研究了闭腔谐振器的谐振频率和导体的表面损耗,并由此计算了材料的微波介电常数、微波介电损耗,研究了谐振频率、介电损耗随体系结构参数的变化.研究证明开波导法的采用和此计算模型对体系谐振频率的计算误差小于5%.低损耗介质基片的采用不但可降低体系的谐振频率,还可有效提高金属板的品质因子,减小测量误差.关 键 词:闭腔;介电参数;TE 01δ模;介质谐振器中图分类号:TB973 文献标识码:A 文章编号:167124512(2004)0820050204Microw ave measurement of dielectric properties of ceramicsby the closed cavity resonator methodZhou Dongxiang Hu M i ngz he Jiang S hengli n Gong S hupi ngAbstract :Microwave measurement of dielectric properties of ceramics by the closed cavity resonator method was discussed.By working in TE 01δmode ,the resonant frequencies and the conductor surface loss were studied using DWM theory.Based on the analysis ,the microwave dielectric constant and dielectric loss of the material were calculated.The relationships among the resonant frequency ,dielectric loss and the struc 2ture of the cavity were studied.The results were verified by comparing with other experiments ,and a total error with less than 5%was achieved.With the low 2loss dielectric substrate being presented ,the resonant frequency of the system was suppressed while the Q value of the conductor increased.K ey w ords :closed cavity ;dielectric properties ;TE 01δmode ;dielectric resonatorZhou Dongxiang Prof.;Dept.of Electronics Sci.&Tech.,Huazhong Univ.of Sci.&Tech.,Wuhan430074,China. 随着多种低损耗、高介电常数、高温度稳定性的微波介质陶瓷材料的发展,微波介质陶瓷介电参数的测量成为材料性能评价及器件设计中的重要环节.目前的介质测试通常采用介质谐振法,它又可分为开式腔法[1]和闭式腔法[2],其中由于闭式腔法不但可有效防止电磁能的辐射,提高无载品质因数,而且可为谐振频率温度系数的测试带来方便.因而本研究采用了介质体在屏蔽腔中谐振的方法来测量低损耗、高介电常数材料的复介电常数.其中高介电常数材料放置于低损耗、低介电常数的聚四氟乙烯基片上,使得电磁场在介质试样内为传输模式,在试样外的空气介质和基片内为截止模式,这样介质试样外的电磁能可以尽量小,从而使体系有很高的能量填充系数.采用TE 01δ模不但可避免介质试样与基片之间、基片与导电板之间以及上下导电板与侧壁之间的缝隙耦合电容,还可使该体系有较高的无载Q 值.1 测试原理本研究计算模型为开波导法,它是一种常用的计算介质谐振器的二阶近似方法[3].图1所示为闭腔测试的结构模型图,并作如下几点假设:介质试样各向同性;介质垫片无损耗;整个器件工作第32卷第8期 华 中 科 技 大 学 学 报(自然科学版) Vol.32 No.82004年 8月 J.Huazhong Univ.of Sci.&Tech.(Nature Science Edition ) Aug. 2004于TE 01δ模.图1 闭腔谐振法测试微波介质陶瓷结构示意图谐振时把整个结构分为5个区域,绝大部分的电磁能储存于区域Ⅱ中,区域Ⅰ,Ⅲ,Ⅳ中为衰减场,并忽略区域Ⅴ中的双重衰减场.针对TE 01δ模进行研究,并设空气、基片及介质试样的磁导率均为μ0(4π×10-7H/m ).对于图1所示的模型,由于轴向磁场分量与角分量θ无关,根据亥姆霍兹波动方程[4],可求得非零电磁场分量为:H z 1=A 1J 0(k r r )sinh α1(z +h 1+h 2);H z 2=A 2J 0(k r r )cos (βz +<);H z 3=A 3J 0(k r r )sinh α3(h 2+h 3-z );H z 4=A 4C 0(p r r )cos (βz +<),(1)式中,A 1,A 2,A 3,A 4及<为待定系数,它们可由介质谐振器界面上的连续性边界条件导出;J 0(・)为第一类零阶贝塞耳函数;k r ,p r 为径向波数;β为轴向传播常数;α1,α3为轴向衰减常数;且k 2r =εr k 20-β2;p 2r =β2-k 20;α21=k 2r -ε1k 20;α23=k 2r-k 20;k 2=ω2ε0μ0.另外, C 0(p r r )=[J 0(k r r 1)/K 0(p r r 1)]{K 0(p r r )-[K ′0(p r r 2)/I ′0(p r r 2)]I 0(p r r )},式中,r 1,r 2分别代表试样及腔体半径;K 0(・)为第二类零阶修正贝塞耳函数;I 0(・)为第一类修正贝塞耳函数[5].各区域中电磁场的其余分量可由麦克斯韦方程组求得:E θi =(j ωμ0/k 2t )(5H zi /5r );H ri =(1/k 2t )[52H zi /(5r 5z )],(2)以及E ri =E zi =H θi =0,式(2)中,i =Ⅰ,Ⅱ,Ⅲ,Ⅳ.k t =k r (i =Ⅰ,Ⅱ,Ⅲ),k t =p r (i =Ⅳ).再由边界连续条件:a .在Ⅰ区、Ⅱ区交界处可得α1coth (α1h 1)=βtan (βh 2-<); b .在Ⅱ区、Ⅲ区交界处可得α3coth (α3h 3)=βtan (βh 2+<).(3)另一个连续性方程可由介质谐振器边界处(r =r 1)容抗匹配条件给出:Y + Y =0,(4)式中, Y =H z 4/E θ4|r =r 1,Y χ=-H z 3/E θ3|r =r 1.由方程(1),(2)及(4)即可得出 J ′0(k r r 1)/(k r J 0(k r r 1))+[K 1(p r r 1)-CI 1(p r r 1)]/{p r [K 0(p r r 1)+CI 0(p r r 1)]}=0,(5)式中C =K 1(p r r 2)/[I 1(p r r 2)].该谐振器的介质基片材料可采用低介电常数材料,如聚四氟乙烯,其介电参数为ε1=2.05,已知体系的谐振频率f 0后,用数值迭代法解超越方程组(3)和(5)即可得陶瓷材料的介电常数εr .经验证,一般可以用不超过6次的迭代求得该谐振器材料的介电常数.2 介电损耗假定基片是无损耗的,整个体系的无载Q 值可写为 Q 0=ωW tot /P tot =ω0(W spec +W matrix +W air3+W air4)/(P walls +P spec ),(6)式中,W tot 代表谐振时体系中总存储的电磁能;P tot 则代表一周期内介质谐振器内的平均能耗.W tot 包括待测试样、介质基片以及空气中存储的电磁能,P tot 则包括待测试样中的介质损耗以及腔壁中的导体损耗.其中介质试样的损耗功率又可表示为 P spec =(ω0ε0εr tanδ/2)・∫V s pec|E 2(θ)|2d V =ω0tan δW spec ,代入式(6)后整理得:tan δ=(1+A )/Q 0-B ,(7)式中,A =(W matrix +W air3+W air4)/W spec ;B =P walls /(ω0W spec ).对于由金属壁引发的导体损耗则包括上、下板的损耗及区域Ⅳ中的边壁损耗.P walls =12∫sR s |H tan |2d S ,式中H tan 代表金属壁上的切向磁场,它是诱发表面电流密度的因素,代入切向场分量后上式可写为 P walls =P endplates +P sidewalls =12∫s R s |H r 1|2d S +12∫sR s |H r 3|2d S +12∫sR s|H z 4|2d S.(8) 在微波频率下,金属壁引起的损耗近似与表面阻抗的实部有关,即R s =1/(δσ)[6],式中δ=2/(ω0μ0σ),表示微波频率时金属表面电流的15第8期 周东祥等:闭腔谐振法测试微波介质陶瓷介电参数 趋肤深度;σ为电导率.δ及σ可由空腔时TE 011模的谐振频率及品质因素算出,这里根据文献[6]取σ=91%.另外由前述场方程可分别求得上述分量如下:W i =ε0εi 2∫V i|E i (θ)|2d V ,(9)式中,W i ,εi ,V i ,E i 分别代表第i 区(i =Ⅰ,Ⅱ,Ⅲ,Ⅳ)中存储的电磁能、相对介电常数、体积和角向电场分量.将式(8)和(9)代入式(7)中,即可求得介质材料的介电损耗.3 模拟结果及讨论图2为体系谐振频率随介质基片归一化厚度图2 基片归一化厚度对谐振频率的影响ε1=2.05ε0,h 3=3mm ,h 2=3mm ,r 1=6mm ,r 2=15mm的变化关系,它与上盖板到试样上表面归一化距离的变化对体系谐振频率的影响有类似的规律,但由于介质基片的介电常数大于空气的介电常数,因此介质基片厚度h 1对频率的影响略大于h 3.例如当ε1=8.05,h 1从0.1mm 到0.6mm ,f 0的变化率为0.2GHz/mm ,而h 3从0.1mm 到0.6mm ,f 0的变化率为0.19GHz/mm .因此对h 1的测量比对h 3的测量更为重要.另外对于80<εr <100的材料,h 1及h 3对体系的调节范围分别为10.78%和10.32%.实际上当h 1,h 3≥1.2h 2时,它们对频率的影响就已经饱和了.本研究还就r 2趋于无穷大,ε1=2.05ε0时,对于特定结构的谐振器谐振频率进行计算,并与文献[7,8]的结论进行了比较,结果表明本文的计算误差在1%～5%之间.图3表示由体系的谐振频率可对应计算出试样的介电常数.整个计算过程中随h 2的变化均保持试样长径比为0.5,从图中可以看到当试样尺寸较小时(例如试样长3mm ,直径6mm ,εr 为80时,f 0=6.073GHz ),谐振频率较大,易引起较大的导体损耗;但若试样尺寸较大,则频率变化率也较大,易引入较大误差.图3 不同尺寸试样介电常数与谐振频率的关系ε1=2.05ε0,h 1=3mm ,h 3=3mm ,r 1=2h 2,r 2=15mm图4为计算的介质品质因子与导体品质因子随h 1的变化关系,并且它与介质品质因子及导体品质因子随h 3的变化规律类似.这里假定测量的器件的品质因子为Q u =5000.可以发现随h 1(或h 3)的增加导体损耗迅速减小,介质的品质因子越来越趋近于测量值,这与整个体系的品质因子公式Q -1u =Q -1d +Q -1c 非常符合.另外介质基片的作用h 1对损耗的影响大于h 3.虽然减小金属损耗对于低损耗介质材料的测量是至关重要的,但h 1(或h 3)的值并非越大越好,因为对于图示结构,当h 1>6.5mm ,h 3>7.0mm 时金属板损耗值已趋近于饱和,而且当h 1+2h 2+h 3>λ0/2时,介质谐振器将处于漏模状态,体系品质因子将急剧下降[9].图4 试样品质因子(Q d )与导体品质因子(Q c )随h 1的变化关系(假定Q u =5000)εr =98.71ε0,ε1=2.05ε0,h 3=3mm ,h 2=3mm ,r 1=6mm ,r 2=15mm ,σ=91%图5示出了基片介电常数对金属板品质因子的贡献.当80<εr <100随ε1从1到9变化,金属板的品质因子可提高15%,谐振频率降低0.67%,这对低损耗材料的测量及提高整个器件25 华 中 科 技 大 学 学 报(自然科学版) 第32卷的品质因子是非常重要的.图5 导体品质因子(Q c )与基片介电常数(ε1)的关系h 1=3mm ,h 3=3mm ,h 2=3mm ,r 1=6mm ,r 2=15mm ,σ=91%参考文献[1]Hakki B W ,Coleman P D.A dielectric resonatormethod of measuring inductive capacities in the mil 2limeter range.IRE Trans.Microwave Theory Tech.,1960,6:402～410[2]G eyer R G ,K abos P ,Jarvis J B.Dielectric sleeve res 2onator techniques for microwave complex permittivity evaluation.IEEE Trans.Microwave Theory Tech.,2002,51:383～392[3]Itoh T ,Rudokas R.New method for com puting theresonant frequency ofdielectric resonator.IEEETrans.Microwave Theory Tech.,1977,25:52～54[4]Maystre D ,Vincent P ,Mage J C.Thoretical and ex 2perimental study of the resonant frequency of a cylin 2drical dielectric resonator.IEEE Trans.Microwave Theory Tech.,1983,31:844～848[5]Zaki K A ,Atia A.Modes in dielectric 2loaded waveg 2uides and resonators.IEEE Trans.Microwave Theory Tech.,1983,31:1039～1045[6]K obayashi Y ,Latoh M.Microwave measurement of di 2electric properties of low 2loss materials by the dielectric rod resonator method.IEEE Trans.Microwave Theo 2ry Tech.,1985,33:586～592[7]Fiedziuszko S ,Jelenski A.The influence of conductin gwalls on resonant frequencies of the dielectric res 2onator.IEEE Trans.Microwave Theory Tech.,1971,19:778～781[8]Pospieszalski M W.Cylindrical dielectric resonators andtheir applications in TEM line microwave circuits.IEEE Trans.Microwave Theory Tech.,1979,27:233～238[9]Mongia R K.Resonant frequency of cylindrical dielectricresonator placed in an MIC environment.IEEE Trans.Microwave Theory Tech.,1990,38:802～804(上接第32页)拱桥在规定的淹没高度范围内的安全,因此,建议在本文的研究基础上进一步研究流水压力、动水压力对拱桥内力的影响,在保证结构安全的前提下,具体设计时放松有关拱桥拱圈淹没高度的规定,因地制宜地降低桥梁高度,以节省桥梁造价.参考文献[1]孙菊芳.有限元法及其应用.北京:北京航空航天大学出版社,1990.[2]肖 盛,凌天清,陈世民等.公路与桥梁抗洪分析.北京:人民交通出版社,1999.[3]交通部.公路桥涵设计规范.北京:人民交通出版社,1987.35第8期 周东祥等:闭腔谐振法测试微波介质陶瓷介电参数 。
微波介质陶瓷的介电贡献
微波介质陶瓷的介电贡献
微波介质陶瓷的介电贡献是指它在微波频段中对电场的响应和传播起到的作用。
介电贡献包括介电常数和介电损耗两个方面。
介电常数是描述介质对电场响应程度的参数，它的大小决定了介质对电场的屏蔽和传输能力。
介电常数可以分为实部和虚部两部分，实部决定了介质对电场的相位延迟和折射率，虚部决定了介质对电场的能量吸收和损耗。
介电损耗是微波介质材料对电磁波能量损失的过程，它与介质内部分子的摩擦导致的能量转化为热能有关。
介电损耗通常由介电常数的虚部表示，其大小决定了材料的吸收性能和功率损耗。
微波介质陶瓷的介电贡献通常由其成分、结构和制备工艺等参数决定。
不同的陶瓷材料具有不同的介电常数和介电损耗，可以通过调整材料成分和制备工艺等方式来改变介电贡献。
微波介质陶瓷广泛应用于无线通信、雷达、卫星通信等领域，其介电贡献对于电磁波的传输和控制起到重要作用。
微波介质陶瓷 参有B2O3–ZnO–La2O3玻璃的BaTi4O9的低温烧结和微波介电特性
参有B2O3–ZnO–La2O3玻璃的BaTi4O9的低温烧结和微波介电特性梗概：一个高Q值低温烧结陶瓷材料的制造是由80wt%的BaTi4O9粉末和20wt%B2O3–ZnOLa2O3玻璃熔剂构成的。
样品在900℃下烧结3小时拥有最大的体积密度。
B2O3-ZnO –La2O3玻璃具有烧结辅助作用。
材料在包含有BaTi4O9的900℃环境下烧结3小时，LaBO3是一种不明的结晶相和残余玻璃相并具有良好的微波介电性能：介电常数≈27，品质因数Q×f=20000GHz，谐振频率τf≈6.5ppm/℃。
1.简介：低温共烧陶瓷技术由于应用于可使微波器件微型化的的微波原件而得到广泛的研究。
在多分子层结构中，电介质材料的烧结温度必须降至900℃甚至低于900℃以便能以像Ag这样的高导电嵌入式电极进行共烧。
（Ag的熔点是961℃）。
一般来说，添加低软化点玻璃是一个降低陶瓷致密化温度的十分有效、廉价的途径。
一些包括参有ZnO–B2O3玻璃的BaO–TiO2–WO3，参有MgO–CaO–SiO2–Al2O3玻璃的Ba2Ti9O20，参有3ZnO–B2O3玻璃的Ba2Ti9O20的调查研究已被计划进行，然而，复合材料的烧结温度通常都高于900℃，这对于共烧内嵌电极Ag来说确是很高。
参有La2O3–B2O3–TiO2玻璃的BaO–Nd2O3–TiO2陶瓷也被Jung et al进行了研究，尽管可使致密化温度低于900℃，但玻璃添加物部分高达60wt%，这无疑对BaNd2Ti5O14的微波特性具有巨大的影响。
为了减少玻璃添加剂对陶瓷本质微波特性的有害影响，研究者们必须找到良好的玻璃熔剂，可以在使用少量添加剂的情况下大幅降低烧结温度而又不太大影响主体材料的微波特性。
B2O3–ZnO–La2O3玻璃被用作光学玻璃具有高折射率系数。
它还没被报导文献作为LTCCs的烧结助剂。
以目前的研究，我们发现B2O3–ZnO–La2O3玻璃可用作降低BaTi 4O9-基复合材料烧结温度的烧结助剂，并且对烧结复合材料烧结进程和微波介电特性也进行了研究。
BSZN微波介质陶瓷介电常数的异常
Ｄｉ ｌ ｃ ｒ ｃ Ｃｏ ｔ ｎ ｎｏ ｍ ｉｙ ｏ ＺＮ ｉ ｒ ｗａ ｅ Ｄｉ ｌ ｃ ｒ ｃ Ｃｅ ａ ｉ ｓ ｅ ｅ ｔ ｉ ｎｓ ａ ｔＡｂ ｒ ｆ ＢＳ ｔ Ｍ ｃ ｏ ｖ ｅ ｅ ｔｉ ｒ ｍ ｃ
Ｓ ＩＦｅ ｇ Ｈ ｎ
（ ｃ ｏ ｌｏ ｙ ｉｓａ ｅ ｔｏ ｃ ｈ ｎ ｎｇ Ｎｏｒ ａ ｎｖ ｒｉｙ，Ｊｎ ｎ ２ ０ ４， ｉａ Ｓ ｈ ｏ ｆＰｈ ｓｃ ｎｄＥｌｃ ｒｎｉ，Ｓ ａ Ｄｏ ｍ ｌ Ｕ ｉｅｓｔ ｉ ａ ５ ０１ ｈ ｏ －ｉ ｅ ｒｔ ｈ ｎ ｅ ａ ｄ ｔ ｅｒ ａ ｏ ｆ ｂ ｏ ｍｉ ｆ ｉｌｃ ｒ ｏ ｓ ａ ｔｏ Ｂ 一 ｒ ） Ｚ ， Ｎｂ ／ ） ｅｎ ｎ ｌ ａ ｉｙ ｃ ａ ｇ ｎ ｈ ｅ ｓ ｎ ｏ ｎ ｒ ｔ ｏ ｅｅ ｔ ｉ ｃ ｎ ｔ ｎ ｆ（ １ Ｓ ｘ （ ｎ ／ ｎ ａ ｙ ｄ ｃ ３ ｚａ
维普资讯
第３卷第４ ０ 期
２ ８年 ８月 ００
压
电
与
声
光
Ｖｏ ． Ｏ ＮＯ ４ １３ ．
Ａ ｕｇ ２ ８ ． ００
Ｐ ＥＺ Ｉ ＯＥＬＥＣＴＥＣＴＲＩ ＣＳ ＆ ＡＣＯＵＳ ＴＯＯＰＴＩ ＣＳ
文 章 编 号 ：０ ４ ２ ７ （ ０ ８ ０ — ４ ５ ０ １ ０—４ ４ ２ ０ ） ４０ ９—３
Ｋｅ ｒ ｓ ｍｉｒ ｗａ ｅ ｄ ｅｅ ｔ ｉ ｃ ｒ ｍ ｉｓ ｉｌｃ ｒ ｏ ｓ ａ ｔ ｂ ｏ ｍｉｙ ｙ ｗｏ ｄ ： ｃ ｏ ｖ ｉｌ ｃｒｃ ｅ ａ ｃ ；ｄ ｅｅ ｔ ｉ ｃ ｎ ｔ ｎ ￣ａ ｎ ｒ ｔ ；ｐ ａ ｅ ｔ ａ ｓｔ ｎ ｅ ｏ ｄ ｒ ｈ ｓ ｓ ｃ ｈ ｓ ｒ ｎ ｉ ｏ ；ｓ ｃ ｎ ａ ｙ ｐ ａ ｅ ｉ
微波介电陶瓷
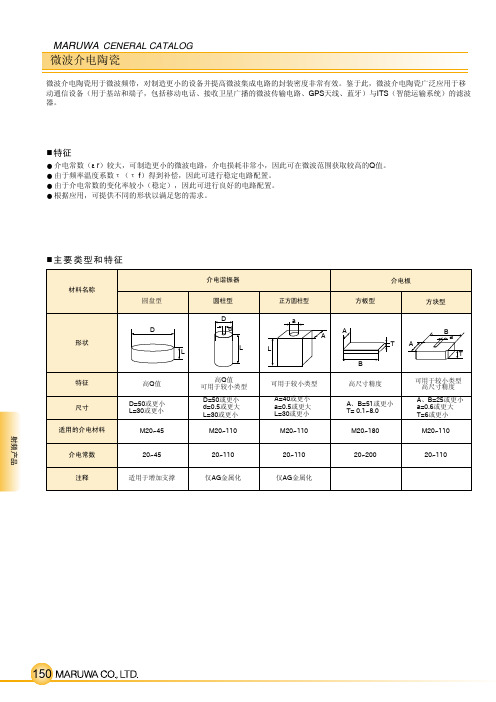
天线
LNA放大器
BRF
LNB
混合器 IF输出
Lo 本机振荡器
金属外壳
调节螺钉
DR
支撑
树脂板
耦合电路
形状
DR
支撑固定类型
支撑 （镁橄榄石）
仅谐振器
MARUWA生产的产品处于4GHz至20GHz频率范围内，共有 两种类型：支撑固定型、仅谐振器。
尺寸根据频率而有所不同。提供了不同的温度特征材料。
3. 天线块、底板
• 用于汽车导航设备（GPS天线）的平面天线。 也称作接线天线。
电极尺寸A
馈电点
形状
偏心率d
至放大电路
接地
天线块
底板（50mm square）
2.95
9.00
1.50
60SS
5.90
2.13
10.00
1.00
51SS
5.05
1.95
10.00
0.15
41SS
3.93
1.50
10.00
0.50
40SS
3.90
1.20
10.00
1.00
34SS
3.40
1.15
10.00
0.20
33SS
3.35
0.75
10.00
0.20
31SS
3.05
0.小类型 A=40或更小 a=0.5或更大 L=30或更小 M20~110
A T
B 高尺寸精度 A、B=51或更小 T= 0.1~8.0 M20~180
介电常数的测量实验报告(附数据)
实验题目：介电常数的测量实验目的：测量陶瓷电容的介电常数介电体（又称电介质）最基本的物理性质是它的介电性，对介电性的研究不但在电介质材料的应用上具有重要意义，而且也是了解电介质的分子结构和激化机理的重要分析手段之一，探索高介电常数的电介质材料，对电子工业元器件的小型化有着重要的意义。
介电常数（又称电容率）是反映材料特性的重要参量，电介质极化能力越强，其介电常数就越大。
测量介电常数的方法很多，常用的有比较法，替代法，电桥法，谐振法，Q 表法，直流测量法和微波测量法等。
各种方法各有特点和适用范围，因而要根据材料的性能，样品的形状和尺寸大小及所需测量的频率范围等选择适当的测量方法。
本实验要求学生了解多种测量介电常数的方法及其特点和适用范围，掌握替代法，比较法和谐振法测固体电介质介电常数的原理和方法，用自己设计与制作的介电常数测试仪，测量压电陶瓷的介电常数。
实验原理：介质材料的介电常数一般采用相对介电常数εr 来表示，通常采用测量样品的电容量，经过计算求出εr ，它们满足如下关系：SCdr 00εεεε==（1）式中ε为绝对介电常数，ε0为真空介电常数，m F /1085.8120-⨯=ε，S 为样品的有效面积，d 为样品的厚度，C 为被测样品的电容量，通常取频率为1kHz 时的电容量C 。
一、替代法当实验室无专用测量电容的仪器，但有标准可变电容箱或标准可变电容器时，可采用替代法设计一简易的电容测试仪来测量电容。
这种方法的优点是对仪器的要求不高，由于引线参数可以抵消，故测量精度只取决于标准可变电容箱或标准可变电容器读数的精度。
若待测电容与标准可变电容的损耗相差不大，则该方法具有较高的测量精度。
替代法参考电路如图2.2.6-1(a)所示，将待测电容C x （图中R x 是待测电容的介电损耗电阻），限流电阻R 0(取1k Ω)、安培计与信号源组成一简单串联电路。
合上开关K 1，调节信号源的频率和电压及限流电阻R 0，使安培计的读数在毫安范围恒定（并保持仪器最高的有效位数），记录读数I x 。
SrTi(1-1.25x)NbxO3陶瓷结构及介电性能
SrTi(1-1.25x)NbxO3陶瓷结构及介电性能傅文平;李蔚;韩蕊【摘要】采用传统固相法制备了按化学计量比掺杂Nb2O5的SrTi(1-1.25x)NbxO3微波介质陶瓷材料,研究了x为0～0.005时陶瓷的相组成、显微结构和微波介电性能.结果表明:在x增大过程中,SrTi(1-1.25x)NbxO3的相组成并没有太大的变化,其体积密度也是呈现基本不变的趋势.随着Nb5+离子的增加,晶体中的小晶粒数量在不断减少,大晶粒的尺寸迅速增大,同时SrTi(1-1.25x) NbxO3的介电常数(εr)保持基本不变,品质因素(Q×f值)则一直加速增长.当x为0.005时,陶瓷SrTi0.99375Nb0.005O3获得最佳的微波介电性能:εr=296.41,Q×f=6 953 GHz.【期刊名称】《华东理工大学学报（自然科学版）》【年(卷),期】2018(044)006【总页数】5页(P845-848,895)【关键词】SrTi(1-1.25x)NbxO3;微波介质陶瓷;掺杂;Nb2O5;介电性能【作者】傅文平;李蔚;韩蕊【作者单位】华东理工大学材料科学与工程学院,上海200237;华东理工大学材料科学与工程学院,上海200237;上海三思电子工程有限公司,上海201100【正文语种】中文【中图分类】TQ174.75近几年来，随着5G移动通信的提出，通信技术的发展受到越来越多的关注。
微波介质陶瓷作为通信领域应用最广泛的材料[1-2]，人们对其介电性能也提出了更高的要求，包括适当的介电常数(εr)、尽可能高的品质因素(Q×f值)以及接近于零的频率温度系数(τf)。
SrTiO3陶瓷具有很高的介电常数(εr≈200)和极大的正频率温度系数(τf≈+1.7×10-3 (℃)-1)[3]，可与一些频率温度系数为负值的材料复合制备出性能优良的微波介质材料。
如Huang等[4]采用SrTiO3与负频率温度系数(τf≈-4.2×10-5 (℃)-1)的Nd(Zn1/2Ti1/2)O3复合，可得到介电常数(εr)为54.2、Q×f值为 84 000 GHz、τf≈0×10-6/℃的(1-x) Nd(Zn1/2Ti1/2)O3-xSrTiO3复合陶瓷(x=0.52)。
功能陶瓷 电介质陶瓷和绝缘陶瓷 中介 微波介质陶瓷讲解
5
5
5.5 微波介质陶瓷
实现微波设备的小型化、高稳定性和廉价的途径是微波电
路的集成化。由于金属谐振腔和金属波导体积和重量过大，
大大限制了微波集成电路的发展，而微波介质陶瓷制作的
谐振器与微波管、微带线等构成的微波混合集成电路，可
使器件尺寸达到毫米量级。这就使微波陶瓷成为实现微波 控制功能的基础和关键材料。它的应用大致分为两个方面. 从而对性能也有两种不同要求: 一种是用于介质谐振器(dielectric resonator )DR的功能 陶瓷，其中用于包括带通(阻）滤波器(filters )、分频器、 耿氏二极管、双工器和多工器、调制解调器(modem）等 固体振荡器(oscillators)中的稳倾元件;
P.R.China: 6 companys mainly
浙江正原电气股份有限公司、潮州三环(集团)股份有限公司、景华电子有限责任 公司(999厂)、苏州捷嘉电子有限公司、浙江嘉康电子有限公司、福建南安讯通电 子公司、高斯贝尔公司、嘉兴佳利电子有限公司、西安广芯电子科技有限公司、 张家港燦勤电子元件有限公司、武汉凡谷电子技术股份有限公司、江苏江佳电子 股份有限公司
11
11
1.4.5 微波介质陶瓷
最简单的电介质谐振器是一个相对介电常数为εr的陶瓷圆 柱体，其εr值很高，足以使得电介质－空气界面上反射的 电磁波仍维持在体腔内。
Avoidance Sensors Dielectric Resonator Antennas Motion Detectors
9
9
Famous company
Japan: Murata村田制作所 Germany: EPCOS(S+M) USA: Skyworks Solutions Inc. 陶瓷分部 Trans-Tech USA: Narda Microwave-West Mini-Circuits England: Morgan Electro Ceramics
Ca1-3xLn2xTiO3陶瓷的微波介电性能
［ 摘
要］ 采用 固相反应法制备 ｃ Ｌ ： ｉ ３ Ｘ ０ １ ，．０ Ｌ ａ ｎ Ｏ （ ＝ ．３ ０２ ；ｎ＝Ｌ ， ｄ Ｓ 陶瓷 ， Ｔ ａＮ ，ｍ） 探讨 了 Ｌ ｎ系元素 的含量对其 物相组成 、
显微结构及微波介 电性能的影响 。结果表 明： Ｃ Ｓ ＴＯ 陶瓷 含有少量 的 Ｓ Ｔ 除 ａ ｍ ｉ。 ｍ： ｉ 第二 相外 ， Ｏ 其他 均形成 了正交钙 钛 矿 结构单相 固溶体 ； Ｌ 的含量增加 ， 电常数随之降低 ， 随 ｎ 介 同时谐振频 率温度 系数 明显 降低 。ｘ＝ ．３时的微波介 电性 能 ０１
信 Ｅ益集 成化 、 ｔ 片式 化 、 型化 的发 展趋 势 。 小
（９ ５ ） 末 为原 料 ， 别 根 据 化 学 式 ｃ Ｌ ９ ．％ 粉 分 ａ ｎ
Ｃ ＴＯ 陶瓷 … 具 有 高 的介 电 常 数 （～１０ ， ａｉ ７ ） 但 ＴＯ （ ｉ ３ ｘ＝０ １ ， ． ０ Ｌ ． ３ ０ ２ ； ｎ＝Ｌ ， ｄ Ｓ 按 摩 尔 比 配 ａ Ｎ ， ｍ）
Ｋｅ ｒ ｓ Ｃａ ３Ｌ ２Ｔ Ｏ３ ｙ ｗｏ ｄ ： ｎ ｉ ；ｍｉ ｒｗａ ｅ ｄ ｅｅ ｔ ｃ ｐ ｏ ｅ ｔ ｓ ｏ ｅ ａ ｃ ａ ｔｒ ｖ ｒ ｇ ｏ ｄ ｖ ｅ ｃ ｃ ｏ ｖ ｉｌ ｃｒ ｒ ｐ ｒｉ ；ｔｌ ｒ ｎ ｅ ｆｃ ｏ ；ａ ｅ ａ ｅ ｂ ｎ ａ ｎ ｅ ｉ ｅ ｌ
０。 ｈ排 分别 于 １０ 。 ～１ ５ 。 ３０Ｃ ３ ０ Ｃ烧 等价 置换 ｃ 。ＩＳ Ｋｍ 等人 研 究 了（ 一ｘ Ｃ Ｔ 在 ６ ０ Ｃ保 温 １ 塑 ， ａ ．． ｉ １ ）ａ．
ｈ ｉ３ｘ ａ ｉ 系 ， 出 随着 Ｌ 量 的增 加 ， 电 结 ３ 。 Ｏ－ Ｌ ＴＯ 体 － 指 ａ含 介
中介电常数高q值微波介质陶瓷材料及其制备方法
中介电常数高q值微波介质陶瓷材料及其制备方法引言随着无线通信和雷达技术的迅猛发展，对于微波介质材料的需求越来越大。
中介电常数高q值微波介质陶瓷材料由于其优异的电磁性能，在通信、雷达、无线电等领域有着广泛的应用。
本文将介绍中介电常数高q值微波介质陶瓷材料的定义、特性以及制备方法。
中介电常数高q值微波介质陶瓷材料的定义中介电常数高q值微波介质陶瓷材料是指具有高介电常数和高品质因子（q值）的微波介质材料。
介电常数是材料对电场响应的量度，而q值则是材料对电磁波的损耗情况的量度。
中介电常数高q值微波介质陶瓷材料具有低损耗、高效率、稳定性好等特点，能够在高频率下实现更好的电磁波传输和能量转换。
中介电常数高q值微波介质陶瓷材料的特性1.高介电常数：中介电常数高q值微波介质陶瓷材料具有高介电常数，可以增加电场的聚集效应，从而提高电磁波的传播速度和能量转换效率。
2.高q值：中介电常数高q值微波介质陶瓷材料具有高品质因子，即能够存储更多的电磁波能量并减少能量的损耗。
这使得材料在高频率下能够实现低损耗的电磁波传输。
3.低损耗：中介电常数高q值微波介质陶瓷材料具有低损耗特性，能够减少电磁波的能量损失，提高传输效率。
4.稳定性好：中介电常数高q值微波介质陶瓷材料在高温、高湿度等恶劣环境下仍能保持稳定的电磁性能，具有较好的耐久性。
中介电常数高q值微波介质陶瓷材料的制备方法中介电常数高q值微波介质陶瓷材料的制备方法通常包括以下几个步骤：1.原料选择：选择具有高介电常数和低损耗的陶瓷材料作为主要原料，如氧化锆（ZrO2）、氧化钛（TiO2）等。
2.材料配比：根据所需的介电常数和q值要求，对各种原料进行适当的配比，以获得预期的材料性能。
3.粉体制备：将所选原料进行粉碎、混合和球磨等处理，以获得均匀的粉体。
4.成型：将粉体通过压制、注塑等方式进行成型，以得到所需形状的陶瓷坯体。
5.烧结：将成型后的陶瓷坯体进行高温烧结处理，使其颗粒之间发生结合，形成致密的陶瓷材料。
功能陶瓷--电介质陶瓷和绝缘陶瓷-中介-微波介质陶瓷概要
浙江正原电气股份有限公司、潮州三环(集团)股份有限公司、景华电子有限责任 公司(999厂)、苏州捷嘉电子有限公司、浙江嘉康电子有限公司、福建南安讯通电 子公司、高斯贝尔公司、嘉兴佳利电子有限公司、西安广芯电子科技有限公司、 张家港燦勤电子元件有限公司、武汉凡谷电子技术股份有限公司、江苏江佳电子 股份有限公司
Dielectric Filter
7
7
在微波电路中的应用主要有以下几方面： 用作微波电路的介质基片 起着电路元器件及线路的承载、支撑和绝缘作用； 用作微波电路的电容器 起着电路或元件之间的耦合及储能作用； 用作微波电路的介质天线 起着集中吸收储存电磁波能量的作用； 用作微波电路的介质波导 起着导引电磁波沿一定方向传播的作用； 用作微波电路的介质谐振器件（最主要应用） 起着类似于一般电子线路中LC谐振电路的作用
微波谐振器的频率特征曲线
17
17
1.4.5 微波介质陶瓷
在微波频段 εr基本上为定值，不随频率而变化。 要使微波介质陶瓷具有高εr值。除需考虑微观晶相类型及 其组合外，应在工艺上保证晶粒生长充分，结构致密。
18
18
在微波频段，品质因数Q值与微波频率f有关，因此微波 介质陶瓷材料的介电损耗与品质因数则可表示为：
27
测试频率<1GHz,可用阻抗分析仪如HP4294A
28
28
1.4.5 微波介质陶瓷
Q值的测量
样品Q值可以通过测量TE011, 谐振峰的宽度计算出来。
Q fr f
相 对
△f为3dB频带宽度(BW)
辐 射
功
率
τf值的测量
f
f2 f1 f1 T2 T1
微波介质陶瓷研究报告
微波介质陶瓷研究报告微波介质陶瓷是一种应用广泛的高性能陶瓷材料，其性能优异，可广泛应用于微波电子器件、高频电子玻璃等领域。
针对微波介质陶瓷的研究报告如下：一、微波介质陶瓷的基本概念微波介质陶瓷是一种用于制作微波电子器件的陶瓷材料，主要用于制作高性能陶瓷薄膜、陶瓷电容器、微波电子器件等。
其特点是介电常数高、损耗低、温度稳定性好、化学稳定性好等。
二、微波介质陶瓷的制备方法微波介质陶瓷的制备方法主要包括干燥压制、共烧法、化学气相沉积法、反应烧结法等。
其中，干燥压制方法是最常用的一种方法，通过将陶瓷粉末进行混合、干燥后压制成型，再进行烧结得到微波介质陶瓷材料。
三、微波介质陶瓷的性能要求微波介质陶瓷的性能要求主要包括介电常数、品质因数、温度系数、热膨胀系数等。
一般来说，介电常数越高、品质因数越大、温度系数越小、热膨胀系数越小，微波介质陶瓷的性能就越优异。
四、微波介质陶瓷的应用领域微波介质陶瓷的应用领域很广，包括微波天线、微波滤波器、微波隔离器、微波振荡器、微波天线等。
其中，微波滤波器是应用最为广泛的一种器件，其主要功能是将无用信号分离出来，只将需要的信号传输到下一个电路中。
五、微波介质陶瓷的发展趋势随着微波电子技术的发展，微波介质陶瓷材料的应用领域也在不断扩展。
未来，随着5G通信、人工智能等技术的不断发展，微波介质陶瓷材料的需求量也将会持续增长。
同时，人们对微波介质陶瓷材料性能的要求也会越来越高，因此，微波介质陶瓷材料的制备方法和性能要求也将不断创新和改进。
综上所述，微波介质陶瓷是一种应用广泛的高性能陶瓷材料，其制备方法和性能要求都需要进一步研究和改进。
未来，随着微波电子技术的发展和应用越来越广泛，微波介质陶瓷材料的市场前景也将会持续看好。
开路型微波陶瓷介电参数测试的研究
１ 引言
微波 介质 陶瓷是 在微 波 频段 使川 的 ｌ 陶瓷 ，川该 材料 制作 的谐 振器 和滤 波 器等 介质器件 ， Ｕ子 具 有 易 于 小 型 化 、损 耗 低 、温 度 系 数 小 的 特 点 ，在 移 动 通 信 技 术 领 域 得 剑 广 泛 麻 川 ｌ３ １ １ 波 陶 瓷 －．微
Ｇ ｅ ｒ ＩＮｏ ７ ｎｅ ａ ．６
文章编 号：０ ８７ ２ （０ ００ ＿Ｏ ６０ １０ —８ ６２ ｌ ）ｌ０ ６ ．４
开 路 型 微 波 陶瓷 介学院 物理 ｌ 范 予信息：程 系，祸建 漳州 ３ ３ ０ ） １ ： ６ ０ ０
２１ ００年第 ｌ 期 （ 总第 ６ ７期）
漳州 ｊ 范学院学报 （ ｌ Ｉ ｉ ｌ ｊ ｆ然科学版）
Ｊ ｕ ｎ ｌ ｆ ａ ｇ ｈ ｕ Ｎｏ ｍａ ｉｅ ｓｔ Ｎａ ． ｉ ｏ ｒ ａ ｏ Ｚｈ ｎ ｚ ｏ ｒ ｌ Ｕｎ ｖ ｒ ｉ ｙ ｔ Ｓｃ． ）
Ｎ ． ． ０ ０年 ｏ １２ １
Ａｂｓ ｒ ｃ ：Ａ ｅ ｈｎｉ ｅ ｆ ｅ ｔｎｇ ｄｉ ｌｃ ｒｃ ｐ ｒｍ ｉｔｖｉｙ ａ ｏ ｓ ｏ ａｍ ｐｌ ａｓｐｒ ｓ ｔ ｄ ａｓ ｄ ｏｎ ａｒ ｌｅ－ ｔａｔ ｔｃ ｑｕ ｏｒ ｔ ｓ ｉ ｅｅ ｔ ｉ ｅ ｔｉ ｔ ｎｄ ｌ ｓ ｆｓ ｅ ｗ ｅ ｅｎ ｅ ｂ ｅ ｐ ａｌ ｌ
程研 究 的重要课 题． 介 电参 数 测 试 主 要 取 决 ＿ 样 的 ． 频 率 ，介 电 常 数 高 低 ，损 耗 人 小 及 试 样 尺 寸 等 ．介 质 谐 ＿ ｒ试 作
振 器 法 根 据 微 波 介 质 谐 振 器 的 谐 振 频 率 及 － 因 数 计 算 得 到 介 质 材 料 的 介 Ｉ 参 数 ， 土 要 分 为 两 质 ｌ 三 类 ： 短 路 型 和 开 路 型 平 行 板 介 质 谐 振 器 １６ 前 者 ． ｝ 两 端 短 路 的 介 质 传 输 线 转 变 而 米 的 谤 振 器 ， ４１ － 足 ｔ Ｉ
Li2Mg3TiO6型陶瓷微波介电性能研究
学校代号10532 学号S151301165分类号TB321 密级公开硕士学位论文Li2Mg3TiO6型陶瓷微波介电性能研究学位申请人姓名郭爱芬培养单位材料科学与工程学院导师姓名及职称李玉平教授学科专业材料科学与工程研究方向高性能结构与功能陶瓷论文提交日期2018 年05 月29 日学校代号：10532学号：S151301165密级：公开湖南大学硕士学位论文Li2Mg3TiO6型陶瓷微波介电性能研究学位申请人姓名郭爱芬导师姓名及职称李玉平教授培养单位材料科学与工程学院专业名称材料科学与工程论文提交日期2018 年05 月29 日论文答辩日期2018 年05 月30 日答辩委员会主席肖汉宁教授The Research on Microwave Dielectric Properties of Li2Mg3TiO6 CeramicsbyGUO AifenB.E.( Hunan University ) 2015A thesis submitted in partial satisfaction of therequirements for the degree ofMaster of scienceinMaterials Science and Engineeringin theGraduate schoolofHunan UniversitySupervisorProfessor Li YupingMay,2018湖南大学学位论文原创性声明本人郑重声明：所呈交的论文是本人在导师的指导下独立进行研究所取得的研究成果。
除了文中特别加以标注引用的内容外，本论文不包含任何其他个人或集体已经发表或撰写的成果作品。
对本文的研究做出重要贡献的个人和集体，均作者签名：日期：年月日学位论文版权使用授权书本学位论文作者完全了解学校有关保留、使用学位论文的规定，同意学校保留并向国家有关部门或机构送交论文的复印件和电子版，允许论文被查阅和借阅。
微波介质陶瓷介电性能影响因素分析
微波介质陶瓷介电性能影响因素分析微波介质陶瓷产品性能的好坏主要由其介电性能决定，介电性能的好坏则由陶瓷材料的配方主导。
当材料配方一定时，微波介质陶瓷的介电性能主要由其结构中的杂质、气孔、晶粒、晶格缺陷决定。
1、杂质杂质常以两种形态存在于陶瓷材料中，一种存在于晶粒内部，一种则在晶界中析出存在。
进入陶瓷晶粒内部的杂质通常可分为等价原子掺杂与异价原子掺杂两种。
等价原子掺杂时，被掺入的原子如果为少量小质量原子，陶瓷的本征损耗降低，其性能反而可以得到部分优化；如果被掺入的为其它类型原子，其本征损耗往往存在增加现象，陶瓷整体介电性能变差。
异价原子掺杂时，往往会使陶瓷体系产生多余电荷，破坏其内部平衡，从而增加其电导损耗，本征损耗变大，介电性能恶化。
2、气孔气孔的存在在陶瓷中往往不可避免，通常残留气孔越多、大小越大，其介电性能越差。
在陶瓷微观形貌观察中，主要观察的就是气孔的大小、多少，产品烧结越致密，其气孔形状越规则，晶粒形态越饱满，其介电性能越好。
通常可将气孔看做相对介电常数为1的相，气孔越多，微波介质陶瓷材料体系的相对介电常数也被拉低的越多。
气孔的大量存在也增加了陶瓷的本征损耗，进而使得材料的品质因数降低。
同时由于气孔具有较低的热稳定性，在温度变化时，掺杂的气孔会使材料的线性膨胀系数增大，降低了陶瓷材料的热稳定性，增大了其谐振频率温度系数。
3、晶粒晶粒的大小、形貌、均匀度均能影响微波介质陶瓷材料的介电性能。
晶粒生长越充分、大小越均匀、形貌越饱满、镶嵌越紧密、致密性越好，其形成的微波介质陶瓷材料性能越好。
4、晶格缺陷陶瓷中的晶格缺陷可大体分为点缺陷、线缺陷、面缺陷、体缺陷四类。
其中点缺陷对材料性能的影响最多。
其通常是由离子掺杂引起，与晶粒内部杂质对陶瓷材料影响机制类似，但其所带来的影响结果通常是不好的。
当分析微波介质陶瓷材料介电性能的影响因素时，可以着重从第二点气孔入手，气孔的多少通常由其余三项所决定，直接影响着其相对介电常数、品质因数、谐振频率温度系数，并可直观的从体积密度去推导，当其体积密度达到最大时，往往是是烧结温度最优、晶粒生长最好、气孔率最低时，此时也往往是微波介质陶瓷材料介电性能最好之时。
介电常数30的微波介质陶瓷材料
介电常数30的微波介质陶瓷材料微波介质陶瓷材料是一种具有较高介电常数的陶瓷材料，常用于微波器件和电子设备中。
本文将介绍以介电常数30为特点的微波介质陶瓷材料的性质、应用以及制备工艺。
一、性质微波介质陶瓷材料的介电常数是其重要的性能参数之一。
介电常数是材料对电场的响应能力的度量，它决定了材料在电场中的极化程度。
对于介电常数较高的材料，它们在电场作用下极化的能力较强，因而能够有效地储存和传导电能。
以介电常数30的微波介质陶瓷材料为例，它具有以下特点：1. 高介电常数：介电常数30意味着该陶瓷材料在电场作用下具有较强的极化能力，能够有效地储存和传导电能。
2. 低损耗：微波介质陶瓷材料通常具有较低的介电损耗，即在电场作用下能量的损失较小。
这一特点使得它们在微波器件中能够实现高效的能量传输和信号传导。
3. 良好的稳定性：微波介质陶瓷材料具有良好的化学稳定性和热稳定性，能够在高温、高湿等恶劣环境下保持较好的性能稳定性。
4. 良好的机械性能：微波介质陶瓷材料通常具有较高的硬度和强度，能够抵抗外界的机械应力和冲击。
二、应用以介电常数30的微波介质陶瓷材料为基础，可以制备各种微波器件和电子设备，如滤波器、耦合器、天线、射频开关等。
这些器件在通信、雷达、卫星导航等领域中起着重要的作用。
1. 微波滤波器：微波介质陶瓷材料具有较高的介电常数和较低的损耗，能够实现对特定频率的微波信号进行滤波和选择性传输。
通过合理设计和选择介电常数30的陶瓷材料，可以制备出具有良好滤波性能的微波滤波器。
2. 微波耦合器：微波介质陶瓷材料的高介电常数和低损耗使其成为制备微波耦合器的理想选择。
微波耦合器是用于将微波信号从一个传输线传输到另一个传输线的器件，常用于微波通信和雷达系统中。
3. 微波天线：微波介质陶瓷材料具有较高的机械强度和较好的热稳定性，能够满足微波天线对材料性能的要求。
通过制备具有介电常数30的陶瓷材料，可以实现对微波信号的有效接收和辐射。
11-介电陶瓷材料3
BaTiO 3 120oC
多元复合化合物
~ RT
介电常数：可增大至20000、温度系数增大 添加 Bi 2 ( SnO3 )3 , NiSnO3 , LiSb2O6 可降低介电常数及其温度系数 改变添加物的组成及含量可调节介电常数、温度系数为合适的值
3、高电压电容器陶瓷
使用在高压下
BaTiO 3 : 高介电常数、介电常数随电压变化较大（铁电性） SrTiO 3 : 介电常数小、介电常数随电压变化
驰豫型铁电陶瓷 的电致伸缩远大 2 2 2 驰豫型铁电陶瓷的应变：X E ( P ) r 于一般压电材料 （ r 比一般压电材料大许多） 驰豫型铁电陶瓷的另一个特点：居里点附近的热膨胀系数很小
一般压电材料的应变： X
E( P) r
0.9Pb(Mg1/ 3 Nb2 / 3 )O3 0.1PbTiO3热膨胀系数： 1106 K 1 o ( 100 ~ 100 C) 适于制造微位移器
n0 : E0 0 时、介质的折射率；
a、b：常数、通常很小 场强很强时、后面的项才显著 电光效应：外加电场引起介质材料折射率变化的现象
aE0 :
bE02 :
线性电光效应或 Pockels 效应 二次电光效应或 kerr 效应
PLZT透明铁电陶瓷具有显著的电光效应
1 外电场诱发的双折射的折射率差： n n13 c E 2 c : 一次电光系数 c (1.0 ~ 1.6) 1010 (m / V ) （PLZT） 组分的不同 n1 : 与电场垂直方向的折射率
介电陶瓷材料
一、电容器陶瓷
用作介电目的（利用其介电性能）的陶瓷、主要用于电容器 和微波元件中
1、温度补偿电容器陶瓷
温度的变化会引起电路元件参数的变化
(Mg_(4-x)Li_(2x))(Nb_(1.92)V_(0.08))O_9陶瓷微波介电性能
(Mg_(4-x)Li_(2x))(Nb_(1.92)V_(0.08))O_9陶瓷微波介电性能姚国光;裴翠锦;刘鹏【期刊名称】《硅酸盐通报》【年(卷),期】2007(26)6【摘要】采用固相合成法制备了(Mg_(4-x)Li_(2x))(Nb_(1.92)V_(0.08))O_9系列微波介质陶瓷。
通过XRD、SEM以及HP网络分析仪等测试手段对其烧结特性、晶体结构和微波介电性能进行了系统研究。
结果表明:x<0.3时形成了(Mg_(4-x)Li_(2x))(Nb_(1.92)V_(0.08))O_9固溶体;x≥0.3时,除主相(Mg_(4-x)Li_(2x))(Nb_(1.92)V_(0.08))O_9外,还有少量第二相Li3Mg2NbO6生成。
微波介电常数ε随x的增大持续升高,品质因数Q则先增大后减小。
x=0.2,950℃,5h烧结样品的微波介电性能达到最佳:ε=12.7,Q.f=14078GHz(f0=8GHz)。
【总页数】4页(P1122-1124)【关键词】(Mg4-xLi2x)(Nb1.92V0.08)O9陶瓷;微波介质陶瓷;介电性能;低温烧结【作者】姚国光;裴翠锦;刘鹏【作者单位】西安邮电学院应用数理系;运城学院应用化学系;陕西师范大学【正文语种】中文【中图分类】TQ174【相关文献】1.ZnO-B_2O_3-SiO_2玻璃对Ca[(Li_(1/3)Nb_(2/3))_(0.95)Zr_(0.15)]O_(3+δ)陶瓷微波介电性能的影响 [J], 熊钢;周东祥;龚树萍2.(1-y)Ca_(1-x)La_(2x/3)TiO_3-yCa(Mg_(1/3)Nb_(2/3))O_3复合体系的微波介电性能 [J], 王浩;陈文;刘涛3.B_2O_3对Ca[(Li_(1/3)Nb_(2/3))_(0.95)Zr_(0.15)]_(3+δ)陶瓷微波介电性能的影响 [J], 熊钢;周东祥;龚树萍4.粉体的球磨方式对 Li_(1.0)Nb_(0.6)Ti_(0.5)O_3锂铌钛陶瓷烧结行为及微波介电性能的影响 [J], 曾群;李蔚;施剑林;董显林;郭景坤5.稀土离子对0.6Ca_(0.6)La_(0.267)TiO_3-0.4Ca(Mg_(1/3)Nb_(2/3))O_3陶瓷微观组织结构及微波介电性能的影响 [J], 徐越;杨薇;任帅;雷沛沅;杨扬;傅仁利因版权原因，仅展示原文概要，查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
HUAZHONG UNIVERSITY OF SCIENCE AND TECHNOLOGY Wuhan 430074, Hubei, P. R. China 中国·武汉 Tel(027)《计算材料学》课程设计指导老师：江建军教授电子科学与技术系 2004 年 6 月电子 0102B3 组1HUAZHONG UNIVERSITY OF SCIENCE AND TECHNOLOGY Wuhan 430074, Hubei, P. R. China 中国·武汉 Tel(027)微波介质陶瓷的介电特性数值计算万文涛 洪毅 黄文佳 陈婷 杨伟伟 王旭曦 袁大双 黄钏 饶伟 贺策林 李树平 （华中科技大学电子科学与技术系，武汉 430074）摘要：对于微波介质陶瓷,建立数学模型,讨论了介电常数与组分，温度，频率的关系。
对于组分，重点讨论运用蒙特卡罗有限元法计算出波介质陶瓷的宏观介电常数 ε m ，结果显示由二维模型和三维模型计 算得出的介电常数 ε m 大小位于串并联模型之间,而且由二维模型计算得出的介电常数 ε m 比由三维模型得 出的结果小，因为实际的一个由两相构成的微波介质陶瓷的相都是以三维形式分布的,所以由三维模型计 算出的介电常数 ε m 比用二维计算的结果要精确；对于频率，介电常数随它的变化不明显；由于温度的变 化灰引起结构以及组成物质的相的变化，只讨论了BaTiO3一类MWDC和温度的变化关系。
关键词：微波介质陶瓷；蒙特卡罗有限元法；介电常数；二相化合物Dielectric Properties Culculated of MicroWave Dielectric Ceremoes(MWDC) ( Department of Electronics Science & Technology,Huazhong university,Wuhan 430074,China)Abstract: As to the MicroWave Dielectric Ceremoes, the mathematics model is established,and the relations between dielectric constant and many factors is discussed,such as component,temperature and frequency.In the aspect of component, great importance is taken to using monte carlo and finite element method to culculate the macro dielectric constant of MWDC 。
The results are displayed in curves ,which use two-dimension and three-dimension models and are manifested between the results of serial model and parallelmodel.Furthermore,the values which are simulated in two-dimension model are smaller than the ones in three-dimension,for the two-phase MWDC are distributed in three dimensions actually.So it’s preciser to use the three-dimemsion model.In the frequency of microwave,the dielectric constant doesn’t vary obviously.Besides, the changes of temperature can lead to the varieties of the construction and phases of materials,so we only discuss the changes with temperature of BaTiO3。
Keywords:MWDC,Monte Carlo method,finite element method,two-phased materies电子 0102B3 组2HUAZHONG UNIVERSITY OF SCIENCE AND TECHNOLOGY Wuhan 430074, Hubei, P. R. China 中国·武汉 Tel(027)1 引言微波介质陶瓷(MWDC)是近十余年才迅速发展起来的一类新型功能电子陶瓷。
以其优异的微波介电 性能在微波电路系统中发挥着介质隔离，介质波导以及介质谐振等一系列电路功能，并正在为微波电路 的小型化，集成化，商品化做出重要贡献。
应用于微波电路的介质陶瓷，除了必备的机械强度，化学稳 定性及经时稳定性外，应满足如下介电性能的要求：在微波频率下相对介质常数εr应大;在微波频率下 的介质损耗tanδ应很小，或换言之品质因数Q(1/tanδ)应很高;谐振频率温度系数τf应很小。
微波介 质陶瓷的介电常数的影响因素有组分,频率,温度. 对于组分,一般情况下，对于单一相的由某一化合物构成的微波介质陶瓷，除非能够用实验仪器直 接测量其介电常数，否则很难直接从公式计算出其介电常数，而在微波介质陶瓷这一领域，也有很多是 以两相和多相存在的，对于每一相的介电常数的具体值，我们往往都能通过查找各种关于微波介质陶瓷 介电特性的资料得到，这样如何从各相的介电常数比较精确地计算出混合相的介电常数问题，我们就必 须解决了。
微波介质陶瓷是一个典型的多相体系，一般说来，它既含有主晶相，又含有副相。
例如：在 BaO-Sm2O3-TiO2体系中，除了有BaO•Sm2O3•TiO2主晶相外，还有一定的副相Ba2Ti9O20存在。
多相体系 的介电常数取决于各相的介电常数，体积浓度，以及相与相之间的配置情况。
， 对于多相的情况,设每相的介电常数分别为 ε1 , ε 2 ,… ε t ，浓度分别为X1,X2,…Xt（X1+X2+…+Xt =1） 现阶段可用于计算的模型有串并联和对数模型:ε = x1ε1 + x2ε 2 + " + xt ε tε −1 = x1ε1−1 + x2ε 2−1 + " + xt ε t−1ln ε = x1 ln ε1 + x2 ln ε 2 + " + xt ln ε t(并联模型) (串联模型) (对数模型)并联模型和串联模型实际上代表了两种极端的情况,它们分别给出了 ε m 的上限和下限,用它们计算 ε m 与 实验结果相差很大,实际中很少采用.对数模型在计算 ε m 时相对精确一些,应用比较广泛,但是这种模型并 未真正从材料介电特性的物理本质出发,它只能定性反映复合介质介电常数的大致变化趋势,不能作为精 确的定量计算公式.为了更加精确的计算微波介质陶瓷的宏观介电常数,引入蒙特卡罗有限元分析,得到了 比较精确的模型. 对于频率和温度,由于用于微波频段的微波介质陶瓷器件应该在该频段稳定工作,所以介电常数在该 频段应该为一常数.至于温度,由于其变化会引起微波介质陶瓷的结构和它的组成相发生变化,所以也较难 讨论,但是对于钙钛矿型的微波介质陶瓷我们可以通过简单的模型来讨论它的介电常数与温度的关系.2 介电常数与组分的关系电子 0102B3 组 3HUAZHONG UNIVERSITY OF SCIENCE AND TECHNOLOGY Wuhan 430074, Hubei, P. R. China 中国·武汉 Tel(027)2.1 由二相化合物构成的 MWDC 的介电常数的计算2.1.1 电磁学原理 用右图 1 所示的长方形方格代表一微波介质陶瓷，在 x,y 方向的边 长分别为 nx , n y (图 1)。
介质区介质的（相对）介电常数不是常量，而 是坐标的函数，即 ε = ε ( x, y ) 。
介质区的底面（y=0）为负电极，施加 零电位；顶面（y= n y ）为正电极，施加正电位 u0 。
从而介质内部电位 分布 u = u ( x, y ) 满足： u ( x,0) = 0 ； u ( x, n y ) = u0 介质内任一点的电场强度为： E = −∇u (1)图 1:长方形单元格及其划分在忽略介质区外电场能量的情况下，电容器的总静电储能为：W=→ 1 1 ε ( x , y ) | E ( x, y ) |2 dxdy = ∫∫ ε ( x, y ) | ∇u ( x, y ) |2 dxdy （2） ∫∫ 2 S 2 S式中积分域 S 为整个介质区域（ （2）式及（4）式省去了真空电容率 ε 0 项，对问题的实质及计算结果 并无影响） 。
根据电磁场中的汤姆逊原理，在一定的边界条件和初始条件下，电磁场的分布必使该电 磁场所具有的能量达到最小，因此有∂W / ∂u ( x, y ) = 0 ， ∀( x, y ) ∈ S （3）根据（2）式和（3）式，并结合边界条件（1）式，设法求得介质内的电位分布 u ( x, y ) ，在代入（2） ，则其电容量和储 式可求出储能 W。
对于上述平行板电容器，如果介质的宏观介电常数为 ε m （未知） 能分别为： C = ε m nx / n y （4）1 2 （5） W = Cu0 2由（4） ， （5）二式可得 ε m 的计算公式： ε m = 2n yW / nxu0 （6）22.1.2 用 MC-FET 法建模 上述（1）~（3）式为连续形式，为了便于计算机求解，按照有限元法的 思想，利用完全二次多项式插值将介质区的连续场离散化，最终（1）~（3） 式转化为线性方程组求解。
作为实际两相复合介质中两相以微粒形式混合情况的近图 2:单元格的填充，并将这些单元格按照图 1） 所示 似，将长方形方格划分为 nx × n y 个单位正方形单元格（如图 1）电子 0102B3 组 4HUAZHONG UNIVERSITY OF SCIENCE AND TECHNOLOGY Wuhan 430074, Hubei, P. R. China 中国·武汉 Tel(027)的规律编号，第 I 个单元格的介电常数为 ε i 。
用计算机产生两相的随机 分布，使两相体积比为 V1 : V 2 。