第二定律习题及解答
热力学第二定律复习题及解答

第三章 热力学第二定律一、思考题1. 自发过程一定是不可逆的,所以不可逆过程一定是自发的。
这说法对吗?答: 前半句是对的,后半句却错了。
因为不可逆过程不一定是自发的,如不可逆压缩过程。
2. 空调、冰箱不是可以把热从低温热源吸出、放给高温热源吗,这是否与第二定律矛盾呢?答: 不矛盾。
Claususe 说的是“不可能把热从低温物体传到高温物体,而不引起其他变化”。
而冷冻机系列,环境作了电功,却得到了热。
热变为功是个不可逆过程,所以环境发生了变化。
3. 能否说系统达平衡时熵值最大,Gibbs 自由能最小?答:不能一概而论,这样说要有前提,即:绝热系统或隔离系统达平衡时,熵值最大。
等温、等压、不作非膨胀功,系统达平衡时,Gibbs 自由能最小。
4. 某系统从始态出发,经一个绝热不可逆过程到达终态。
为了计算熵值,能否设计一个绝热可逆过程来计算?答:不可能。
若从同一始态出发,绝热可逆和绝热不可逆两个过程的终态绝不会相同。
反之,若有相同的终态,两个过程绝不会有相同的始态,所以只有设计除绝热以外的其他可逆过程,才能有相同的始、终态。
5. 对处于绝热瓶中的气体进行不可逆压缩,过程的熵变一定大于零,这种说法对吗? 答: 说法正确。
根据Claususe 不等式TQS d d ≥,绝热钢瓶发生不可逆压缩过程,则0d >S 。
6. 相变过程的熵变可以用公式H ST∆∆=来计算,这种说法对吗?答:说法不正确,只有在等温等压的可逆相变且非体积功等于零的条件,相变过程的熵变可以用公式THS ∆=∆来计算。
7. 是否,m p C 恒大于 ,m V C ?答:对气体和绝大部分物质是如此。
但有例外,4摄氏度时的水,它的,m p C 等于,m V C 。
8. 将压力为101.3 kPa ,温度为268.2 K 的过冷液体苯,凝固成同温、同压的固体苯。
已知苯的凝固点温度为278.7 K ,如何设计可逆过程?答:可以将苯等压可逆变温到苯的凝固点278.7 K :9. 下列过程中,Q ,W ,ΔU ,ΔH ,ΔS ,ΔG 和ΔA 的数值哪些为零?哪些的绝对值相等?(1)理想气体真空膨胀; (2)实际气体绝热可逆膨胀; (3)水在冰点结成冰;(4)理想气体等温可逆膨胀;(5)H 2(g )和O 2(g )在绝热钢瓶中生成水;(6)等温等压且不做非膨胀功的条件下,下列化学反应达到平衡:H 2(g )+ Cl 2(g )(g )答: (1)0Q WU H ==∆=∆=(2)0, R Q S U W =∆=∆= (3)e 0, , P G H Q A W ∆=∆=∆= (4)e 0, =, U H Q W G A ∆=∆=-∆=∆ (5)e = 0V U Q W ∆==(6)0=W,H U Q ∆=∆=,0=∆=∆G A10. 298 K 时,一个箱子的一边是1 mol N 2 (100 kPa),另一边是2 mol N 2 (200 kPa ),中间用隔板分开。
牛顿第二定律练习题及答案解析

(本栏目内容,在学生用书中以活页形式分册装订!) 1.由牛顿第二定律知道,无论怎样小的力都可以使物体产生加速度,可是当我们用一个很小的力去推很重的桌子时,却推不动它,这是因为() A.牛顿第二定律不适用于静止的物体B.桌子的加速度很小,速度增量极小,眼睛不易觉察到C.推力小于静摩擦力,加速度是负的D.桌子所受的合力为零解析:F=ma中F指合力,用很小的力推桌子时,合力为零,故无加速度.答案: D2.关于速度、加速度和合外力之间的关系,下述说法正确的是()A.做匀变速直线运动的物体,它所受合外力是恒定不变的B.做匀变速直线运动的物体,它的速度、加速度、合外力三者总是在同一方向上C.物体受到的合外力增大时,物体的运动速度一定加快D.物体所受合外力为零时,一定处于静止状态解析:匀变速直线运动就是加速度恒定不变的直线运动,所以做匀变速直线运动的物体的合外力是恒定不变的,选项A正确;做匀变速直线运动的物体,它的加速度与合外力的方向一定相同,但加速度与速度的方向就不一定相同了.加速度与速度的方向相同时做匀加速运动,加速度与速度的方向相反时做匀减速运动,选项B错误;物体所受的合外力增大时,它的加速度一定增大,但速度不一定增大,选项C错误;物体所受合外力为零时,加速度为零,但物体不一定处于静止状态,也可以处于匀速运动状态,选项D错误.答案: A3.如右图所示,质量为10 kg的物体在水平面上向左运动,物体与水平面间的动摩擦因数为μ=0.2,与此同时,物体还受到一个水平向右的推力F=20 N,则物体产生的加速度是(g=10 m/s2)()A.0B.4m/s2,水平向右C.2 m/s2,水平向左D.2 m/s2,水平向右答案: B4.搬运工人沿粗糙斜面把一个物体拉上卡车,当力沿斜面向上,大小为F时,物体的加速度为a1;若保持力的方向不变,大小变为2F时,物体的加速度为a2,则()A.a1=a2B.a1<a2<2a1C.a2=2a1D.a2>2a1解析:设总的阻力为F′,第一次推时F-F′=ma1,式子两边同乘以2,得2F-2F′=m·2a1第二次推时,2F-F′=ma2,比较两个式子可以看出a2>2a1,所以D正确.答案: D5.力F1单独作用于某物体时产生的加速度是3 m/s2,力F2单独作用于此物体时产生的加速度是4 m/s2,两力同时作用于此物体时产生的加速度可能是() A.1 m/s2B.5 m/s2C.4 m/s2D.8m/s2解析:由题意,力F1作用于物体的加速度a1=3 m/s2,F2作用于物体的加速度a2=4 m/s2,F1与F2的合力F的范围|F1-F2|≤F≤F1+F2,故两力同时作用于此物体的加速度|a1-a2|≤a≤a1+a2.即1 m/s2≤a≤7 m/s2,故选项A、B、C正确.答案:ABC6.如右图所示,位于水平地面上的质量为m的小木块,在大小为F,方向与水平方向成α角的拉力作用下沿地面做匀加速运动.若木块与地面之间的动摩擦因数为μ,则木块的加速度为()A.F/mB.F cos α/mC.(F cos α-μmg)/mD.[F cos α-μ(mg-F sin α)]/m解析:对木块作受力分析,如右图所示,在竖直方向上合力为零,即F sin α+F N=mg,在水平方向上由牛顿第二定律有F cos α-μF N=ma.联立可得a=F cos α-μ?mg-F sin α?m,故选项D正确.答案: D7.如右图所示,物体在水平拉力F的作用下沿水平地面做匀速直线运动,速度为v.现让拉力F逐渐减小,则物体的加速度和速度的变化情况应是() A.加速度逐渐变小,速度逐渐变大B.加速度和速度都在逐渐变小C.加速度和速度都在逐渐变大D.加速度逐渐变大,速度逐渐变小解析:物体向右做匀速直线运动,滑动摩擦力F f=F=μF N=μmg,当F逐渐减小时,F f=μmg不变,所以产生与v方向相反即向左的加速度,加速度的数值a=F f-Fm随F逐渐减小而逐渐增大.因为a与v方向相反,所以v减小.答案: D8.在倾角为37°的光滑斜面上,质量为m的物体以加速度a匀加速下滑.现用沿斜面向上的推力,使物块以1.2a的加速度匀加速向上滑动,则推力的大小是(sin 37°=0.6,cos 37°=0.8)()A.1.2mg B.1.32mgC.1.96mg D.2.2mg解析:在沿斜面方向上,物块匀加速下滑时,有mg sin 37°=ma,①匀加速上滑时,有F-mg sin 37°=1.2ma.②①②联立解得推力F=1.32mg.答案: B9.如右图所示,水平面上质量相等的两木板A、B用一轻质弹簧相连,整个系统处于静止状态.现用一竖直向上的力F拉动木块A,使木块A向上做匀加速直线运动.研究从力F刚作用在木块A上的瞬间到木块B刚离开地面的瞬间这一过程,并且选定该过程中木块A的起点位置为坐标原点,则下列图中可以表示力F和木块A 的位移x之间的关系的是()解析:弹簧的形变量用x′表示,系统处于静止状态时,易知弹簧的压缩量为mg/k;研究从F刚作用在木板A上的瞬间到弹簧刚恢复原长的瞬间这个过程,由牛顿第二定律得:F+kx′-mg=ma,又因为x+x′=mg/k,所以得F=kx+ma;研究从弹簧恢复原长时到木块B刚离开地面的瞬间这个过程,同理得到F=kx+ma.故选项A正确.答案: A10.质量均为m的A、B两个小球之间系一个质量不计的弹簧,放在光滑的台面上.A 紧靠墙壁,如右图所示,今用恒力F将B球向左挤压弹簧,达到平衡时,突然将力撤去,此瞬间()A.A球的加速度为F/(2m)B.A球的加速度为零C.B球的加速度为F/(2m)D.B球的加速度为F/m解析:恒力F作用时,A和B都平衡,它们的合力都为零,且弹簧弹力为F.突然将力F撤去,对A来说水平方向依然受弹簧弹力和墙壁的弹力,二力平衡,所以A球的合力为零,加速度为零,A项错,B项对.而B球在水平方向只受水平向,故C项错,D项对.右的弹簧的弹力作用,加速度a=Fm答案:BD11.如右图所示,电梯与水平面夹角为30°,当电梯加速向上运动时,梯面对人的支持力是其重力的6/5,则人与梯面间的摩擦力是其重力的多少倍?解析:本题分解加速度比分解力更显方便.对人进行受力分析:重力mg、支持力F N、摩擦力F f(摩擦力的方向一定与接触面平行,由加速度的方向可推知F f水平向右).建立直角坐标系:取水平向右(即F f 方向)为x 轴正向,此时只需分解加速度,其中a x =a cos 30°,a y =a sin 30°(如下图所示). 建立方程并求解:x 方向:F f =ma cos 30°y 方向:F N -mg =ma sin 30°所以F f /(mg )=3/5.答案: 3512.某一旅游景区,建有一山坡滑草运动项目.该山坡可看成倾角θ=30°的斜面,一名游客连同滑草装置总质量m =80 kg ,他从静止开始匀加速下滑,在时间t =5 s 内沿斜面滑下的位移x =50 m .(不计空气阻力,取g =10 m/s 2,结果保留2位有效数字)问(1)游客连同滑草装置在下滑过程中受到的摩擦力F 为多大?(2)滑草装置与草皮之间的动摩擦因数μ为多大?解析: (1)由位移公式x =12at 2 沿斜面方向,由牛顿第二定律得mg sin θ-F f =ma联立并代入数值后,得F f =m ⎝ ⎛⎭⎪⎫g sin θ-2x t 2=80 N (2)在垂直斜面方向上,F N -mg cos θ=0,又F f =μF N联立并代入数值后,得μ=F f mg cos θ=0.12. 答案: (1)80 N (2)0.12。
牛顿第二定律典型题习题与答案

2.光滑斜面上,放有质量为M的木板,木板上表面粗糙,为使木板能在斜面上静止不动,今有一质量为m的猫在上面奔跑,求猫的运动方向和加速度大小。
解:木板不动,其受力平衡。
设斜面夹角为α则木板受到猫给的沿着斜面向上的力大小为Mgsinα。
则猫受到沿着斜面向下的力总共是(m+M)gsinα其加速度为 a = (m+M)gsinα/m3.在倾斜角α=30°的光滑斜面上,通过定滑轮连接着质量mA=mB=1kg的两个物体,开始使用手拖住A,其离地高h=5m,B位于斜面底端撤去手后,求(1)A即将着地时A的动能(2)物体B离低端的最远距离(斜面足够长)解:1,将AB看作整体,用动能地理,设A的动能为E,则B的动能也为E。
有2E = mgh - mgh/2,带入数据求的E =2,机械能守恒,B的动能完全转化为重力势能,设上升高度为H,则mgH = E ,对应的斜面长度L = 2H =所以,物体B离低端的最远距离为 5+L =4.质量为一千克的木板静止在粗糙的水平地面上,木板与地面间的摩擦因素为,在木板左端放置一块质量为一千克,大小不算的铁块,铁块与动摩擦因素为,取g等于10。
求,当木板长为1m,在铁块上加一个水平向右的恒力8N,多少时间铁块运动到木板右端?解:已知μ=,μ′= 对铁块分析,设铁块的加速度为a ma=F拉-μ′mg 解得a=4m/s²对木板分析,设木板加速度为a′ ma′=μ′mg-μ(m+m)g 解得a′=2m/s² 根据S= 1/2 (a-a′)t² 已知S=1m 将a ,a′ 解得t=1s铁块对地的加速度a1 = (8 - *1*g)/1 = 4木板对地的加速度a2 = (*1*g - *2*g)/1 = 2则铁块对木板的相对加速度a = a1 - a2 = 2 ,铁块对木板的初速度为0有 *at^2 = 1 ,得t = 1s5.如图所示。
已知斜面倾角30°,物体A质量mA=㎏,物体B质量mB=㎏,H=。
物化热力学第二定律习题解答

热力学第二定律习题解答1.已知每克汽油燃烧时可放热 46.86 kJ 。
(1) 若用汽油作以水蒸气为工作物质的蒸汽机的燃料时,该机的高温热源为 378 K ,冷凝器即低温热源为 303 K ;(2) 若用汽油直接在内燃机内燃烧,高温热源温度可达到 2273 K ,废气即低温热源亦 为 303 K ; 试分别计算两种热机的最大效率是多少?每克汽油燃烧时所能做出的最大功为多少?T 2 T 1378 303(1)210.20T 2378W Qg48.86 0.20 k J 9.37 kJT 2 T 12273 303(2)210.87T 22273W Qg 48.86 0.87 k J 40.7 kJ652.在 300 K 时, 2 mol 的 N 2 (假设为理想气体)从 106 Pa 定温可逆膨胀到 105Pa ,试计算其 S 。
解38.3 J K53.10 g H 2 (假设为理想气体 )在 300 K,5 105 Pa时,在保持温度为 300 K 及恒定外压为66106Pa 下进行压缩,终态压力为 106Pa ( 需注意此过程为不可逆过程 ) 。
试求算此过程 的 S ,并与实际过程的热温商进行比较。
解 定温过程:108.314ln 5 160 J K -1 28.8J K 2 106Q W p 外 V 2 V 1p 2 V 2 V 1nRT 1 p21.247 104 Jp1Q1.247 104 J 300 K 41.6 J K TS nRln2 8.314 lnp 2106105JK-1S nRlnp 1p2所以 S QT4.在 293 K 时,将一方形容器用隔板从正中间分开,然后将 1 mol N 2和 1 mol He 分别 放在容器的两边, 当将中间隔板抽去以后, 两种气体自动混合。
在此过程中系统的温度 不变,与环境没有热交换,试求此混合过程的S ,并与实际过程的热温商进行比较。
大学物理习题详解 热力学第二定律

©物理系_2012_09《大学物理AII 》作业 No.12 热力学第二定律一、判断题:(用“T ”和“F ”表示)[ T ] 1.任何可逆热机的效率均可表示为:高低T T -=1η 解:P301,根据卡诺热机的效率[ F ] 2.若要提高实际热机的效率, 可采用摩尔热容量较大的气体做为工作物质。
解:P294-295,根据热机效率的定义吸净Q A =η,显然工作物质从高温热源吸收的热量越少,对外作的功越多,其效率越高。
根据热量的定义T C MmQ ∆=,温差一定的时候,摩尔热熔C 与热量成正比。
[ F ] 3.一热力学系统经历的两个绝热过程和一个等温过程,可以构成一个循环过程 解:P308题知循环构成了一个单热源机,这违反了开尔文表述。
[ F ] 4.不可逆过程就是不能沿相反方向进行的过程。
解:P303 [ T ] 5.一定量的理想气体向真空作绝热自由膨胀,体积由1V 增至2V ,在此过程中A =0,Q =0,0=∆T ,0>∆S 。
解:P292,P313二、选择题:1.如果卡诺热机的循环曲线所包围的面积从图中的a b c d a 增大为 a b ′c ′d a ,那么循环a b c d a 与a b ′c ′d a 所作的功和热机效率变化情况是: [ D ] (A) 净功增大,效率提高(B) 净功增大,效率降低(C) 净功和效率都不变 (D) 净功增大,效率不变 解:卡诺循环的效率121T T-=η只与二热源温度有关,曲线所围面积在数值上等于净功,所以净功增大,效率不变。
2.对于循环热机,在下面节约与开拓能源的几个设想中,理论上可行的是: [ B ] (A) 改进技术,使热机的循环效率达100%(B) 利用海面与海面下的海水温差进行热机循环作功 (C) 从一个热源吸热,不断作等温膨胀,对外作功 (D) 从一个热源吸热,不断作绝热膨胀,对外作功解:根据热力学第二定律,(A)是第二类永动机,是不可能制成的;(C)是单热源机;(D)是从热源吸热怎么作绝热膨胀。
牛顿第二定律习题(含答案)

牛顿第二定律习题一、不定向选择1、下列说法正确的是()A、物体所受合外力减小,速度可能增大B、只要有力作用在物体上,加速度就不为零C、物体所受合外力的大小不变,其加速度也一定不变D、一个物体不论处于什么运动状态,合外力相同,加速度就相同2、一个物体受到的重力10N,将该物体竖直上抛,运动中受到的空气阻力大小恒为2N,则上升、下降过程中的加速度大小之比是()A. 1:1B. 3:2C. 2:3D. 4:13.设洒水车的牵引力不变,所受阻力与车重成正比,洒水车在平直路面上行驶原来是匀速的,开始洒水后,它的运动情况将是( C )A.继续作匀速运动. B.变为作匀加速运动.C.变为作变加速运动. D.变为作匀减速运动.4.甲车质量是乙车质量的2倍,把它们放在光滑水平面上,用力F作用在静止的甲车上时,得到2m/s2的加速度.若用力F作用在静止的乙车上,经过2s,乙车的速度大小是( D )A.2m/s. B.4m/s.C.6m/s. D.8m/s.5.如果力F在时间t内能使质量m的物体移动距离s,那么( AD )A.相同的力在相同的时间内使质量是一半的物体移动2s的距离.B.相同的力在一半时间内使质量是一半的物体移动相同的距离.C.相同的力在两倍时间内使质量是两倍的物体移动相同的距离.D.一半的力在相同时间内使质量是一半的物体移动相同的距离.6.原来作匀加速直线运动的物体,当它所受的合外力逐渐减小时,则( B )A.它的加速度将减小,速度也减小.B.它的加速度将减小,速度在增加.C.它的加速度和速度都保持不变.D.它的加速度和速度的变化无法确定.二、填空题7、一个物体受到两个互相垂直的外力的作用,已知F1=6N,F2=8N,物体在这两个力的作用下获得的加速度为2.5m/s2,那么这个物体的质量为kg。
8、一个质量为m=2kg的物体,受到F1=6N、F2 =5N、F3 =4N三个力的作用处于静止状态,若将F1撤除,物体的加速度大小为,方向。
第三章第二定律习题与解答
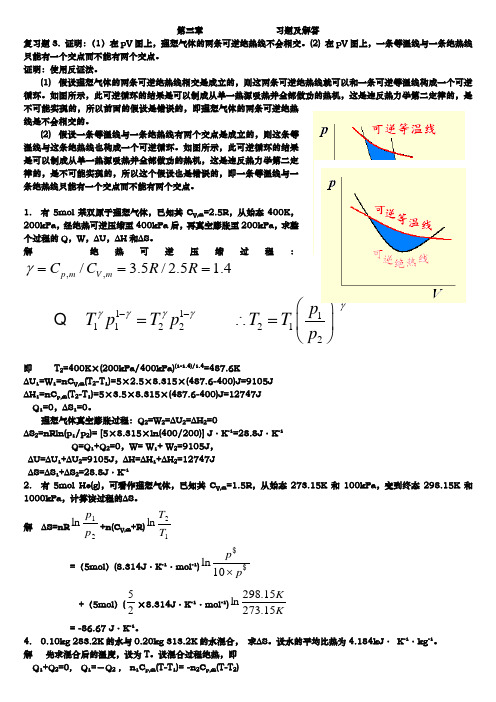
第三章 习题及解答复习题3. 证明:(1)在pV 图上,理想气体的两条可逆绝热线不会相交。
(2) 在pV 图上,一条等温线与一条绝热线只能有一个交点而不能有两个交点。
证明:使用反证法。
(1) 假设理想气体的两条可逆绝热线相交是成立的,则这两条可逆绝热线就可以和一条可逆等温线构成一个可逆循环。
如图所示,此可逆循环的结果是可以制成从单一热源吸热并全部做功的热机,这是违反热力学第二定律的,是不可能实现的,所以前面的假设是错误的,即理想气体的两条可逆绝热线是不会相交的。
(2) 假设一条等温线与一条绝热线有两个交点是成立的,则这条等温线与这条绝热线也构成一个可逆循环。
如图所示,此可逆循环的结果是可以制成从单一热源吸热并全部做功的热机,这是违反热力学第二定律的,是不可能实现的,所以这个假设也是错误的,即一条等温线与一条绝热线只能有一个交点而不能有两个交点。
1. 有5mol 某双原子理想气体,已知其C V,m =2.5R ,从始态400K ,200kPa ,经绝热可逆压缩至400kPa 后,再真空膨胀至200kPa ,求整个过程的Q ,W ,ΔU ,ΔH 和ΔS 。
解 绝热可逆压缩过程:,,/3.5/2.5 1.4p m V m C C R R γ===11111122212p T p T p T T p γγγγγγ---⎛⎫=∴= ⎪⎝⎭Q即 T 2=400K×(200kPa/400kPa)(1-1.4)/1.4=487.6KΔU 1=W 1=nC V,m (T 2-T 1)=5×2.5×8.315×(487.6-400)J=9105J ΔH 1=nC p,m (T 2-T 1)=5×3.5×8.315×(487.6-400)J=12747J Q 1=0,ΔS 1=0。
理想气体真空膨胀过程:Q 2=W 2=ΔU 2=ΔH 2=0ΔS 2=nRln(p 1/p 2)= [5×8.315×ln(400/200)] J·K -1=28.8J·K -1Q=Q 1+Q 2=0,W= W 1+ W 2=9105J ,ΔU=ΔU 1+ΔU 2=9105J ,ΔH=ΔH 1+ΔH 2=12747J ΔS=ΔS 1+ΔS 2=28.8J·K -12. 有5mol He(g),可看作理想气体,已知其C V,m =1.5R ,从始态273.15K 和100kPa ,变到终态298.15K 和1000kPa ,计算该过程的ΔS 。
物理化学热力学第二定律练习题及答案

第二章 热力学第二定律练习题一、判断题(说法正确否):1.自然界发生的过程一定是不可逆过程。
2.不可逆过程一定是自发过程。
3.熵增加的过程一定是自发过程。
4.绝热可逆过程的S = 0,绝热不可逆膨胀过程的S > 0,绝热不可逆压缩过程的S < 0。
5.为了计算绝热不可逆过程的熵变,可以在始末态之间设计一条绝热可逆途径来计算。
6.由于系统经循环过程后回到始态,S = 0,所以一定是一个可逆循环过程。
7.平衡态熵最大。
8.在任意一可逆过程中S = 0,不可逆过程中S > 0。
9.理想气体经等温膨胀后,由于U = 0,所以吸的热全部转化为功,这与热力学第二定律矛盾吗10.自发过程的熵变S > 0。
11.相变过程的熵变可由T HS ∆=∆计算。
12.当系统向环境传热时(Q < 0),系统的熵一定减少。
13.一切物质蒸发时,摩尔熵都增大。
14.冰在0℃,p 下转变为液态水,其熵变T HS ∆=∆>0,所以该过程为自发过程。
15.自发过程的方向就是系统混乱度增加的方向。
16.吉布斯函数减小的过程一定是自发过程。
17.在等温、等压下,吉布斯函数变化大于零的化学变化都不能进行。
18.系统由V 1膨胀到V 2,其中经过可逆途径时做的功最多。
19.过冷水结冰的过程是在恒温、恒压、不做其他功的条件下进行的,由基本方程可得G = 0。
20.理想气体等温自由膨胀时,对环境没有做功,所以 -p d V = 0,此过程温度不变,U = 0,代入热力学基本方程d U = T d S - p d V ,因而可得d S = 0,为恒熵过程。
21.是非题:⑴“某体系处于不同的状态,可以具有相同的熵值”,此话对否⑵“体系状态变化了,所有的状态函数都要变化”,此话对否⑶ 绝热可逆线与绝热不可逆线能否有两个交点⑷ 自然界可否存在温度降低,熵值增加的过程举一例。
⑸ 1mol 理想气体进行绝热自由膨胀,体积由V 1变到V 2,能否用公式:⎪⎪⎭⎫⎝⎛=∆12ln VV R S计算该过程的熵变22.在100℃、p时,1mol 水与100℃的大热源接触,使其向真空容器中蒸发成100℃、p 的水蒸气,试计算此过程的S 、S (环)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章 习题及解答复习题3. 证明:(1)在pV 图上,理想气体的两条可逆绝热线不会相交。
(2) 在pV 图上,一条等温线与一条绝热线只能有一个交点而不能有两个交点。
证明:使用反证法。
(1) 假设理想气体的两条可逆绝热线相交是成立的,则这两条可逆绝热线就可以和一条可逆等温线构成一个可逆循环。
如图所示,此可逆循环的结果是可以制成从单一热源吸热并全部做功的热机,这是违反热力学第二定律的,是不可能实现的,所以前面的假设是错误的,即理想气体的两条可逆绝热线是不会相交的。
(2) 假设一条等温线与一条绝热线有两个交点是成立的,则这条等温线与这条绝热线也构成一个可逆循环。
如图所示,此可逆循环的结果是可以制成从单一热源吸热并全部做功的热机,这是违反热力学第二定律的,是不可能实现的,所以这个假设也是错误的,即一条等温线与一条绝热线只能有一个交点而不能有两个交点。
1. 有5mol 某双原子理想气体,已知其C V,m =,从始态400K ,200kPa ,经绝热可逆压缩至400kPa 后,再真空膨胀至200kPa ,求整个过程的Q ,W ,ΔU ,ΔH 和ΔS 。
解 绝热可逆压缩过程:,,/ 3.5/2.5 1.4p m V m C C R R γ===11111122212p T pT pT T p γγγγγγ---⎛⎫=∴= ⎪⎝⎭Q即 T 2=400K×(200kPa/400kPa)/= ΔU 1=W 1=nC V,m (T 2-T 1)=5×××J=9105J ΔH 1=nC p,m (T 2-T 1)=5×××J=12747J Q 1=0,ΔS 1=0。
理想气体真空膨胀过程:Q 2=W 2=ΔU 2=ΔH 2=0ΔS 2=nRln(p 1/p 2)= [5××ln(400/200)] J·K -1=·K -1Q=Q 1+Q 2=0,W= W 1+ W 2=9105J ,ΔU=ΔU 1+ΔU 2=9105J ,ΔH=ΔH 1+ΔH 2=12747JΔS=ΔS 1+ΔS 2=·K -12. 有5mol He(g),可看作理想气体,已知其C V,m =,从始态和100kPa ,变到终态和1000kPa ,计算该过程的ΔS 。
解 ΔS=nR 21lnp p +n(C V,m+R)12lnT T=(5mol )·K -1·mol-1)ln10p p ⨯$$+(5mol )(25×·K-1·mol-1)KK 15.27315.298ln= J·K -1。
4. 0.10kg 的水与0.20kg 的水混合, 求ΔS 。
设水的平均比热为· K -1·kg -1。
解 先求混合后的温度,设为T 。
设混合过程绝热,即 Q 1+Q 2=0, Q 1=-Q 2 , n 1C p,m (T-T 1)= -n 2C p,m (T-T 2)得 n 1 (T-T 1)= -n 2(T-T 2) (0.10kg) = -( 0.20kg)T=ΔS 1=⎰TTp dT T C 1=(0.10kg) · K -1·kg-1)KK 2.2831.303lnΔS 2=⎰TTp dT TC 2=(0.20kg) · K-1·kg-1)KK 2.3131.303lnΔmix S=ΔS 1+ΔS 2=·K -1。
6.有2mol 理想气体,从始态300K ,20dm 3,经下列不同过程等温膨胀至50 dm 3,计算各过程的Q ,W ,ΔU ,ΔH 和ΔS 。
(1)可逆膨胀; (2)真空膨胀;(3)对抗恒外压100kPa 膨胀。
解 (1)可逆膨胀:ΔU 1=ΔH 1=0,W 1=-Q 1=-nRTln(V 2/V 1)=-[2××300×ln(50/20)]J =-4571JΔS 1= nRln(V 2/V 1)=·K -1。
(2) 真空膨胀: ΔU 2=ΔH 2=0,ΔS 2= ·K -1。
W 2=-Q 2=0(3)对抗恒外压100kPa 膨胀: ΔU 3=ΔH 3=0,W 3=-Q 3=-p 环(V 2-V 1)=- 100kPa(50-20) dm 3=-3000J ,ΔS 3= ·K -1。
7. 有1mol 甲苯CH 3C 6H 5(l)在其沸点383K 时蒸发为气体,计算该过程的Q ,W ,ΔU ,ΔH ,ΔS ,ΔA 和ΔG 。
已知在该温度下,甲苯的汽化热为362kJ ·kg -1。
解 M 甲苯=92×10-3k g·mol -1,Δvap H m =362k J·kg -1×92×10-3k g·mol -1= k J·mol -1,Q=ΔH=n Δvap H m =1mo l× k J·mol -1= kJW=-p[V(g)-V(l)]=-pV(g)=-nRT=(-1××383)J =-3184JΔU= Q+ W= kJ=ΔS=ΔH/T= ×103J/383K=·K -1ΔA=ΔU-T ΔS= kJ= ΔG=ΔH-T ΔS= kJ=08.在及p 下,一摩尔过冷水蒸气变为同温同压下的水,求此过程的ΔG 。
已知时水的蒸气压为3167Pa 。
解 实际过程为不可逆相变过程,设计成可逆途径容易计算,设计可逆途径为ΔG=ΔG 1+ΔG 2+ΔG 3=⎰21p p g dp V + 0 +⎰21p p l dp V≈⎰21p p g dp V =nRTln(p 2/p 1)= (1mol)·K -1·mol -1)×ln PaPa 1013253167= -8590J9. 实验室中有一个大恒温槽的温度为400K ,室温为300K 。
因恒温槽绝热不良而有4000J 的热传给了室内的空气,用计算说明这一过程是否为可逆 解 ΔS 体=1104004000-⋅-=-=K J KJ T Q R 体 ΔS 环=133.133004000-⋅==-K J KJT Q 环 ΔS 隔离=ΔS 体+ΔS 环=·K -1>0由计算知该过程为不可逆过程。
10. 有1mol 过冷水,从始态,变成同温、同压的冰,求该过程的熵变。
并用计算说明这一过程的可逆性。
已知水和冰在该温度范围内的平均摩尔定压热容分别为:C p,m (H 2O,l)=·K -1·mol -1,C p,m (H 2O,s)=·K -1·mol -1;在273K ,101kPa 时水的摩尔凝固热为Δfus H m (H 2O,s)=·mol -1。
解 在273K ,101kPa 时水转变为冰是可逆相变。
263 K ,101kPa 时水转变为冰是不可逆相变。
计算时设计可逆途径如下:本过程恒压,Q p =ΔH(T)=ΔH l +ΔH(T f )+ΔH s ΔH l =nC p,m (H 2O,l)(273-263)K=1××10J=753J ΔH(T f )=n Δfus H m (H 2O,s)= [1×]kJ=ΔH s = nC p,m (H 2O,s)(263-273)K=1××(-10)J=-377J ΔH(T)= 753J-5900J-377J=-5524J= 计算系统熵变ΔS(T)=ΔS l +ΔS(T f )+ΔS sΔS l =nC p,m (H 2O,l)ln(273/263)=[1××]J·K -1= J·K -1ΔS(T f )= ΔH(T f )/ T f =273K= J·K -1ΔS s =nC p,m (H 2O,s)ln(263/273)=[1××]J·K -1= J·K -1ΔS(T)= J·K -1计算环境熵变ΔS 环=- Q p /T 环=-(-5524)J/263K=21 J·K -1隔离系统熵变ΔS iso =ΔS(T)+ΔS 环=+21)J·K -1= J·K -1ΔS iso >0,过程不可逆。
12. 将、1mol O 2从p 绝热可逆压缩到6×p ,试求Q 、W 、ΔU、ΔH、ΔF、ΔG、ΔS 和ΔS iso (C p,m=27R)。
已知2(,)mS O g =$ J·K -1·mol -1。
解 设氧为理想气体。
绝热可逆过程Q R =0ΔS 体=Q R /T=0, ΔS 环= -Q R /T=0 ΔS iso =0求其它变量应先求出体系终态温度,由绝热可逆过程方程γγγ--=12111p T p , 5/7=γ1271212(298.2)6p p T T K p p γγ--⎛⎫⎛⎫== ⎪⎪⨯⎝⎭⎝⎭$$= W=nC V,m (T 1-T 2)=(1mol)25·K-1·mol -1) =-4142JΔU=-W=4142J ΔH=dT C T T p ⎰21= nCp,m(T 2-T 1)=(1mol)27·K-1·mol -1)( =5799JΔF=ΔU -SΔT=4142J-(1mol)·K -1·mol -1)×( =-36720JΔG=ΔH -SΔT=5799J-(1mol)·K -1·mol -1) ×( =-35063J13. 将1mol 双原子理想气体从始态298K 、100kPa ,绝热可逆压缩到体积为5dm 3,试求 终态的温度、压力和过程的Q 、W 、ΔU、ΔH、和ΔS。
解 理想气体的初始体积V 1=nRT 1/p 1=(1××298/100) dm 3= dm 3理想气体为双原子分子,,,(7/2) 1.4(5/2)p m V mC R C Rγ=== 理想气体的终态温度11.412112(/)298K(24.78/5)565.29K T T V V γ--===理想气体的终态压力1.42112(/)100kPa(24.78/5)940kPap p V V γ===Q = 0()2118.314565.29298()J 5555.6J1 1.41nR T T W γ⨯⨯--===-- ΔU =nC V,m (T 2-T 1)=1×××J =ΔH=nC p,m (T 2-T 1)=1×××J =ΔS= nC p,m ln(T 2/ T 1)-nRln(p 2/p 1)=014. 将1mol 苯C 6H 6(l)在正常沸点353K 和压力下,向真空蒸发为同温、同压的蒸气,已知在该条件下,苯的摩尔汽化焓为Δvap H m =·mol -1,设气体为理想气体。
