71Credit Default Swap V3
《草民经济学》-南勇

《草民经济学》-南勇名词解释GDPGDP,就是英文GrossDomesticProduct的简称,翻译成中文意思就是“国内生产总值”。
它是指在一定时期内(比如一个季度或一年),一个国家或地区的经济中所生产出的全部最终产品和劳务的价值,常被公认为衡量国家经济状况,即经济表现如何、国民财富的多寡、国家实力强弱的最佳指标。
GNP“国民生产总值”(英文简称为GNP)这个概念,要把你的人在外国创造,然后汇回国内来的收入都算进去,而将外国人在你的国家所创造的,却要汇回人家地盘的收入刨掉。
汇率汇率说白了就是一个国家货币的“价格”,当然参照物是别的国家的货币。
决定价格的因素是“供需关系”,汇率也不例外。
避险式储蓄老百姓为了应付充满了不确定性的生活压力而不得已为之的事。
供需关系价格是由供需关系决定的。
当某种东西买的多、卖的少,即“供不应求”的时候,价格就会上涨;反之,价格就会下降。
通货膨胀当通胀来临的时候,通常都意味着一个国家的经济形势相当不错,经济发展、收入增加、工作好找、生活稳定,大家都放开了花钱,抢着买东西,从而使该国的经济生活总体上呈现出一种由需求旺盛带来的“供不应求”局面。
因此,适度的通胀,预示着一个国家的生活水平总体上不错,是一个值得高兴的信号。
通缩通缩意味着所有的东西都降价,降价也没多少人买,所以经济长期处在一种物价过于低迷,货币购买力过强的局面。
消费者物价指数-CPI用来反映与居民生活有关的商品及劳务价格变动情况的指标。
CPI超过3%就可以算通胀,超过5%就基本上属于“较严重通胀”的范畴了。
生产者物价指数-PPI用来衡量工业企业产品出厂价格变动趋势和变动程度的指标。
它就站在CPI的前边,直接影响着CPI的变动。
就是说,一个物件儿从“工厂”到“商场”是需要一个过程的,“工厂”这边涨价(或降价),迟早会影响到“商场”那边的价格变化。
采购经理人指数-PMI用来监测制造业生产活动的活跃度的指标,就是说,可以用来反映一国经济还处在“工厂生产”阶段时的景气度。
credit default swap 通俗解释

credit default swap 通俗解释信用违约互换(Credit Default Swap,CDS)是指一种金融衍生品,通过将信用风险从一方转嫁给另一方,用于对冲信用违约风险。
信用违约互换是由债券市场衍生而来的金融产品,最早在20世纪90年代出现,并在其后几十年中迅速发展。
这篇文章将试图通过通俗的方式解释信用违约互换的概念、作用、运作机制以及其在金融市场中的影响。
信用违约互换是一种合约,通常由两个相互信任的当事人签订,即买方和卖方。
买方支付一定的保费给卖方,以换取其对一份特定债券债务违约风险的保护。
如果债务发行人(即债券发行方)违约,买方将获得赔偿,相当于债务违约的损失。
与此同时,卖方则承担相应的风险,并在发生违约时向买方支付赔偿。
信用违约互换的作用是用于对冲信用违约风险。
投资者可以利用这种工具来降低持有债务所面临的风险。
例如,一家银行持有大量的债券,但担心债券发行方可能违约,导致损失。
为了对冲这种风险,该银行可以购买信用违约互换,以便在债务违约时获得赔偿。
通过购买信用违约互换,银行可以降低其持有债务的风险,从而保护其财务状况。
信用违约互换的运作机制可以简单解释如下。
假设投资者A购买了一份债券,且担心发行方会违约。
投资者A可以与投资者B签订信用违约互换合约。
根据合约的内容,投资者A将支付给投资者B一定的保费。
如果发行方违约,投资者A将向投资者B索赔,获得赔偿。
通常情况下,合约中还规定了其他一些条款,比如违约定义、赔偿金额计算方法等。
这样,投资者A通过购买信用违约互换,实际上在投资者B那里获得了对债务违约的保护。
信用违约互换在金融市场中扮演着重要的角色。
它不仅对投资者降低风险提供了有力的工具,同时也对金融系统的稳定性起到了促进作用。
然而,信用违约互换也存在一些问题和风险。
首先,由于信用违约互换市场规模巨大且高度复杂,管理和监控这一市场变得更加困难。
其次,信用违约互换的流动性也可能受到影响。
Credit Default Swap函数包用户指南说明书

Package‘credule’October12,2022Version0.1.4Date2020-05-09Title Credit Default Swap FunctionsMaintainer Bertrand Le Nezet<**************************>Depends R(>=2.14.1)DescriptionIt provides functions to bootstrap Credit Curves from market quotes(Credit Default Swap-CDS-spreads)and price Credit Default Swaps-CDS.License MIT+file LICENSEURL https:///blenezet/creduleBugReports https:///blenezet/credule/issuesSuggests knitrVignetteBuilder knitrNeedsCompilation yesAuthor Bertrand Le Nezet[cre,aut,cph],Richard Brent[ctb,cph],John Burkardt[ctb,cph]Repository CRANDate/Publication2020-05-1021:20:12UTCR topics documented:credule-package (2)bootstrapCDS (3)priceCDS (6)Index912credule-package credule-package Credit Default Swap pricing and Credit Curve bootstrappingDescriptionCredit Curve boostrapping from market quotes(Credit Default Swap-CDS-spreads)and Credit Default Swap-CDS-pricingDetailsPackage:creduleType:PackageVersion:0.1.3Date:2015-08-03License:MIT+file LICENSEA Credit Default Swap(CDS)is afinancial swap agreement that the seller of the CDS will com-pensate the buyer(usually the creditor of the reference loan)in the event of a loan default(by the debtor)or other credit event.This is to say that the seller of the CDS insures the buyer against some reference loan defaulting.The buyer of the CDS makes a series of payments(the CDS"fee"or "spread")to the seller and,in exchange,receives a payoff if the loan defaults.It was invented by Blythe Masters from JP Morgan in1994.April82009saw a"Big Bang"in the market for credit default swap(CDS)contracts and the way in which they are traded.Both contract and convention changes were implemented simultaneously.These changes were designed to make CDS more standardised to help support efforts for central clearing of CDS trades,make strides towards T+0trade processing and facilitate operational effi-ciency.The CDS"Big Bang"has introduced standardized coupon dates and maturity dates.The functions provided in this package do not use these"new"conventions(i.e.they use the conventions pre-April2008);therefore it’s not recommended to use them in a production context.In most cases the differences are marginal,therefore these functions are good enough for preliminary research.See vignette("credule")for more details.Note.I’m planning to update this package with proper CDS ISDA conventions handling at a later stage.Author(s)Bertrand Le Nezet Maintainer:Bertrand Le Nezet<bertrand dot lenezet at gmail dot com>ReferencesISDA Standard CDS Example /cdsmodel/assets/cds-model/docs/ Standard%20CDS%20Examples.pdfCDS Bing Bang /assets/en/docs/markit-magazine/issue-4/60-cds-big-bang.pdfExampleslibrary(credule)yieldcurveTenor=c(1,2,3,4,5,7)yieldcurveRate=c(0.0050,0.0070,0.0080,0.0100,0.0120,0.0150)creditcurveTenor=c(1,3,5,7)creditcurveSP=c(0.99,0.98,0.95,0.92)cdsTenors=c(1,3,5,7)cdsSpreads=c(0.0050,0.0070,0.00100,0.0120)premiumFrequency=4defaultFrequency=12accruedPremium=TRUERR=0.40#CDS pricingres_price=priceCDS(yieldcurveTenor,yieldcurveRate,creditcurveTenor,creditcurveSP,cdsTenors,RR,premiumFrequency,defaultFrequency,accruedPremium)res_price#Credit curve bootstrapping from CDS spreadsres_bootstrap=bootstrapCDS(yieldcurveTenor,yieldcurveRate,res_price$tenor,res_price$spread,RR,premiumFrequency,defaultFrequency,accruedPremium)res_bootstrapbootstrapCDS Bootstrap a Credit CurveDescriptionA function that bootstrap a credit curve from a set of Credit Default Swap spreads givent for variousmaturity.UsagebootstrapCDS(yieldcurveTenor,yieldcurveRate,cdsTenors,cdsSpreads,recoveryRate,numberPremiumPerYear=c(4,2,1,12),numberDefaultIntervalPerYear=12,accruedPremium=c(TRUE,FALSE))ArgumentsyieldcurveTenorA double vector.Each value represents a tenor of the yield curve expressed inyear(e.g.1.0for1Y,0.5for6M)yieldcurveRate A double vector.Each value represents the discount rate(continuously com-pounded)for a partical tenor(e.g.0.005means0.5%,0.02means2 cdsTenors A double vector.Each value represents the maturity expressed in year of a Credit Default Swap which we want to price(e.g5.0means5Y)cdsSpreads A double vector.Each value represents the CDS spread(expressed in decimal,e.g.0.0050represent0.5%or50bp)for a given maturityrecoveryRate A double.It represents the Recovery Rate in case of default(e.g0.40means 40%recovery which is a standard value for Senior Unsecured debt) numberPremiumPerYearAn Integer.It represents the number of premiums paid per year.CDS premiumspaid quaterly(i.e.numberPremiumPerYear=4)and sometimes semi-annually(i.e.numberPremiumPerYear=2)numberDefaultIntervalPerYearAn Integer.It represents the number of timesteps used to perform the numeri-cal integral required while computing the default leg value.It is shown that amonthly discretisation usually gives a good approximation(Ref.Valuation ofCredit Default Swaps,Dominic O Kane and Stuart Turnbull) accruedPremium A boolean.If set to TRUE,the accrued premium will be taken into account in the calculation of the premium leg value.DetailsIn brief,a CDS is used to transfer the credit risk of a reference entity(corporate or sovereign)from one party to another.In a standard CDS contract one party purchases credit protection from another party,to cover the loss of the face value of an asset following a credit event.A credit event isa legally defined event that typically includes bankruptcy,failure-to-pay and restructuring.Thisprotection lasts until some specified maturity date.To pay for this protection,the protection buyer makes a regular stream of payments,known as the premium leg,to the protection seller.This size of these premium payments is calculated from a quoted default swap spread which is paid on the face value of the protection.These payments are made until a credit event occurs or until maturity, whichever occursfirst.Modeling Credit Using a Reduced-Form Approach The world of credit modelling is divided into two main approaches,one called the structural and the other called the reduced-form.In the struc-tural approach,the idea is to characterize the default as being the consequence of some company event such as its asset value being insufficient to cover a repayment of debt.Structural models are generally used to say at what spread corporate bonds should trade based on the internal structure of thefirm.They therefore require information about the balance sheet of the firm and can be used to establish a link between pricing in the equity and debt markets.However, they are limited in at least three important ways:they are hard to calibrate because internal company data is only published at most four times a year;they generally lack theflexibility tofit exactly a given term structure of spreads;and they cannot be easily extended to price credit derivatives.In the reduced-form approach,the credit event process is modeled directly by modeling the prob-ability of the credit event ing a security pricing model based on this approach,this prob-ability of default can be extracted from market prices.Reduced form models also generally have theflexibility to refit the prices of a variety of credit instruments of different maturities.They can also be extended to price more exotic credit derivatives.It is for these reasons that they are used for credit derivative pricing.See vignette("credule")for more details.ValueReturns a Dataframe with3columns:tenor,survprob and hazrate.The tenor column contains the tenor value given in parameter cdsTenors,the survprob column gives the survival probability(in decimal)for each tenor(e.g.0.98menas98%)and the hazrate column gives the non-cumulative hazard rate(intensity of the poisson process)for each tenor(e.g.0.01means1%hazard rate). Author(s)Bertrand Le NezetExampleslibrary(credule)yieldcurveTenor=c(1,2,3,4,5,7)yieldcurveRate=c(0.0050,0.0070,0.0080,0.0100,0.0120,0.0150)cdsTenors=c(1,3,5,7)cdsSpreads=c(0.0050,0.0070,0.0090,0.0110)premiumFrequency=4defaultFrequency=12accruedPremium=TRUERR=0.40bootstrapCDS(yieldcurveTenor,yieldcurveRate,cdsTenors,cdsSpreads,RR,premiumFrequency,defaultFrequency,accruedPremium)priceCDS Credit Default Swap PricingDescriptionA function that calculates the spreads of several Credit Default Swaps(different maturities)from ayield curve and a credit curve.UsagepriceCDS(yieldcurveTenor,yieldcurveRate,creditcurveTenor,creditcurveSP,cdsTenors,recoveryRate,numberPremiumPerYear=c(4,2,1,12),numberDefaultIntervalPerYear=12,accruedPremium=c(TRUE,FALSE))ArgumentsyieldcurveTenorA double vector.Each value represents a tenor of the yield curve expressed inyear(e.g.1.0for1Y,0.5for6M)yieldcurveRate A double vector.Each value represents the discount rate(continuously com-pounded)for a partical tenor(e.g.0.005means0.5%,0.02means2%) creditcurveTenorA double vector.Each value represents a tenor of the credit curve expressed inyear(e.g.1.0for1Y,0.5for6M)creditcurveSP A double vector.Each value represents the survival probability for a partical tenor(e.g.0.98means98%)cdsTenors A double vector.Each value represents the maturity expressed in year of a Credit Default Swap which we want to price(e.g5.0means5Y)recoveryRate A double.It represents the Recovery Rate in case of default(e.g0.40means 40%recovery which is a standard value for Senior Unsecured debt) numberPremiumPerYearAn Integer.It represents the number of premiums paid per year.CDS premiumspaid quaterly(i.e.numberPremiumPerYear=4)and sometimes semi-annually(i.e.numberPremiumPerYear=2)numberDefaultIntervalPerYearAn Integer.It represents the number of timesteps used to perform the numeri-cal integral required while computing the default leg value.It is shown that amonthly discretisation usually gives a good approximation(Ref.Valuation ofCredit Default Swaps,Dominic O Kane and Stuart Turnbull) accruedPremium A boolean.If set to TRUE,the accrued premium will be taken into account in the calculation of the premium leg value.DetailsIn brief,a CDS is used to transfer the credit risk of a reference entity(corporate or sovereign)from one party to another.In a standard CDS contract one party purchases credit protection from another party,to cover the loss of the face value of an asset following a credit event.A credit event isa legally defined event that typically includes bankruptcy,failure-to-pay and restructuring.Thisprotection lasts until some specified maturity date.To pay for this protection,the protection buyer makes a regular stream of payments,known as the premium leg,to the protection seller.This size of these premium payments is calculated from a quoted default swap spread which is paid on the face value of the protection.These payments are made until a credit event occurs or until maturity, whichever occursfirst.Modeling Credit Using a Reduced-Form Approach The world of credit modelling is divided into two main approaches,one called the structural and the other called the reduced-form.In the struc-tural approach,the idea is to characterize the default as being the consequence of some company event such as its asset value being insufficient to cover a repayment of debt.Structural models are generally used to say at what spread corporate bonds should trade based on the internal structure of thefirm.They therefore require information about the balance sheet of the firm and can be used to establish a link between pricing in the equity and debt markets.However, they are limited in at least three important ways:they are hard to calibrate because internal company data is only published at most four times a year;they generally lack theflexibility tofit exactly a given term structure of spreads;and they cannot be easily extended to price credit derivatives.In the reduced-form approach,the credit event process is modeled directly by modeling the prob-ability of the credit event ing a security pricing model based on this approach,this prob-ability of default can be extracted from market prices.Reduced form models also generally have theflexibility to refit the prices of a variety of credit instruments of different maturities.They can also be extended to price more exotic credit derivatives.It is for these reasons that they are used for credit derivative pricing.See vignette("credule")for more details.ValueReturns a Dataframe with2columns:tenor and spread.The tenor column contains the tenor value given in parameter cdsTenors,the spread column give the Credit Default Swap spreads(in decimal) for each tenor(e.g.0.0050is equivalent to0.5%or50bp).Author(s)Bertrand Le NezetExampleslibrary(credule)yieldcurveTenor=c(1,2,3,4,5,7)yieldcurveRate=c(0.0050,0.0070,0.0080,0.0100,0.0120,0.0150)creditcurveTenor=c(1,3,5,7)creditcurveSP=c(0.99,0.98,0.95,0.92)cdsTenors=c(1,3,5,7)cdsSpreads=c(0.0050,0.0070,0.00100,0.0120)premiumFrequency=4 defaultFrequency=12 accruedPremium=TRUERR=0.40priceCDS(yieldcurveTenor,yieldcurveRate,creditcurveTenor,creditcurveSP,cdsTenors,RR,premiumFrequency,defaultFrequency,accruedPremium)Index∗CDS spreadbootstrapCDS,3credule-package,2priceCDS,6∗Credit Default Swaps bootstrapCDS,3credule-package,2priceCDS,6∗Credit Default SwapbootstrapCDS,3credule-package,2priceCDS,6∗bootstrappingbootstrapCDS,3credule-package,2priceCDS,6∗credit curvebootstrapCDS,3credule-package,2priceCDS,6∗default probabilitiesbootstrapCDS,3credule-package,2priceCDS,6∗default probabilitybootstrapCDS,3credule-package,2priceCDS,6∗hazard ratebootstrapCDS,3credule-package,2priceCDS,6∗poisson processbootstrapCDS,3credule-package,2priceCDS,6∗pricingbootstrapCDS,3credule-package,2priceCDS,6∗survival probabilitiesbootstrapCDS,3credule-package,2priceCDS,6∗survival probabilitybootstrapCDS,3credule-package,2priceCDS,6bootstrapCDS,3credule-package,2priceCDS,69。
信用联结票据运作流程

信用联结票据运作流程Credit linking bills, also known as credit linked notes, are financial instruments that combine a debt obligation with a derivative component, typically a credit default swap. With the emergence of credit linked notes in the late 1990s, this financial product has become increasingly popular in the global financial markets.信用联结票据,也称为信用联结债券,是将债务义务与衍生品部分(通常是信用违约掉期)相结合的金融工具。
随着信用联结票据于20世纪90年代后期的出现,这种金融产品在全球金融市场上变得越来越受欢迎。
From an operational perspective, the process of credit linking bills involves several key steps. First, the issuer of the credit linked notes enters into a credit default swap agreement with a counterparty, typically a financial institution or another institutional investor. This agreement serves as the derivative component of the credit linked notes, allowing the issuer to transfer the credit risk associated with a specific reference entity to the counterparty.从运作的角度来看,信用联结票据的流程涉及几个关键步骤。
金融行业必备的100个专业名词

进入金融行业必须知道的100个专有名词1. 股票(Stock): 公司的所有权证券,持有股票意味着持有公司的一部分所有权。
2. 债券(Bond): 债务工具,投资者购买债券即借钱给发行者,预期在未来获得利息和本金回报。
3. 资产配置(Asset Allocation): 投资组合中不同资产类别的分配,以实现风险和回报的平衡。
4. 流动性(Liquidity): 资产能够迅速买卖并转化为现金的能力,流动性越高,市场风险越低。
5. 市盈率(P/E Ratio): 股票价格与每股收益之比,用于衡量一家公司的估值。
6. 资本市场(Capital Market): 提供长期融资的市场,包括股票和债券市场。
7. 衍生品(Derivative): 派生自其他资产的金融合约,如期货合约和期权。
8. 投资组合(Portfolio): 拥有多种资产的集合,旨在实现投资目标。
9. 财务杠杆(Financial Leverage): 利用借款来增加投资回报的策略。
10. 通货膨胀(Inflation): 货币购买力下降的过程,影响资产和投资的价值。
11. 市值(Market Capitalization): 公司的总市场价值,等于其股票价格乘以已发行股票的总数。
12. 利率(Interest Rate): 借款或存款的价格,通常以百分比形式表示。
13. 复利(Compound Interest): 利息在每个计息周期内基于原始本金和之前利息的计算。
14. 企业治理(Corporate Governance): 确保公司管理层履行职责,保护股东权益的体系和原则。
15. 信用评级(Credit Rating): 评估借款人信用风险的分级系统,影响债券和贷款的利率。
16. 流通股(Outstanding Shares): 公司已发行并在市场上交易的股票总数。
17. 市场风险(Market Risk): 由市场波动引起的投资损失的风险。
信用衍生性金融商品简介
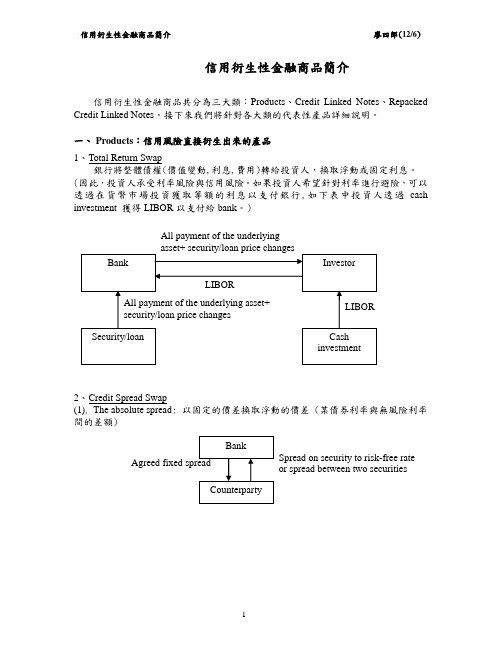
信用衍生性金融商品簡介信用衍生性金融商品共分為三大類:Products 、Credit Linked Notes 、Repacked Credit Linked Notes 。
接下來我們將針對各大類的代表性產品詳細說明。
一、 Products :信用風險直接衍生出來的產品 1、Total Return Swap銀行將整體債權(價值變動,利息,費用)轉給投資人,換取浮動或固定利息。
(因此,投資人承受利率風險與信用風險。
如果投資人希望針對利率進行避險,可以透過在貨幣市場投資獲取等額的利息以支付銀行,如下表中投資人透過cash investment 獲得LIBOR 以支付給bank 。
)2、Credit Spread Swap(1). The absolute spread : 以固定的價差換取浮動的價差 (某債券利率與無風險利率間的差額)All payment of the underlying Spread on security to risk-free rate or spread between two securities(2). The relative spread: 以浮動換取浮動 (例: 以甲債券與無風險利率間的利差換取乙債券與無風險利率間的利差)3、Credit Default Swap避險銀行透過支付對手銀行固定的費用, 將該公司承受的信用風險轉由對手銀行承擔。
當發生倒閉時對手銀行須支付避險銀行該債券的倒閉損失。
(EX: the default payment is: (national amount)(fair market value of reference bond before default - fair market value of reference bond after default))4、Basket- Linked Credit Default Swap是Credit Default Swap 的一種,但是標的信用資產為一籃子債券或債權,因此使整體信用品質較單一標的Credit Default Swap 之信用品質低。
英语语法词汇详解default

英语语法词汇详解defaultdefault英[dɪˈfɔːlt]美[dɪˈfɔːlt]n.不履行;违约;拖欠;未到庭;默认值v.不履行;拖欠;未到庭;自动转到;因未到场而取消…参赛资格第三人称单数:defaults现在分词:defaulting过去式:defaulted过去分词:defaulted英文释义:1. [uncountable, countable] failure to do something that must be done by law, especially paying a debt【不可数,可数】未能做法律规定必须做的事情,尤指偿还债务2. [uncountable, countable, usually singular] (computing) what happens or appears if you do not make any other choice or change【不可数,可数,通常单数】(计算)如果你不做任何其他选择或改变,会发生或出现什么举个例子:1.When you start a fresh letter the system will default to its own style.你要重新写封信的时候,系统会自动转到默认格式。
2.It will have to restructure its debts to avoid default.必须重新整合债务才能避免拖欠。
3.I became a presenter by default rather than by design.我成为主持人是因为当时我未考虑其他选择就接受了,并非我刻意要求得此职。
常用短语:1.by default(比赛)因其他参赛者不到场, 由于对手缺席(而胜出)2.in default拖欠违约;不出庭罪3.in default of因缺少;在缺乏…时;由于没有协议;租金将由房产稽查员决定4.go by default因一方未提出反对而判另一方获胜5.judgement in default缺席审判6.default value默认值7.default gateway默认网关;缺省网关8.default setting默认设置;默认设定;缺省设置9.default risk违约风险;违约的风险10.credit default swaps信用违约互换;信用违约掉期;信贷违约互换11.default interest拖欠利息;违约利息;过期罚金12.default option默认选项;默认选择;违约期权13.default rate违约率;拖欠率;交易违约率14.credit default swap信用违约互换;信贷违约互换15.default position默认立场;默认位置;默认的观点。
CDS简介

信用违约互换简介一、什么是CDS信用风险缓释(Credit Risk Mitigation, CRM)是指金融机构运用信用衍生工具等方式转移或降低信用风险。
信用风险缓释功能体现为违约概率、违约损失率或违约风险暴露的下降。
常用的信用风险缓释工具包括信用违约互换(Credit Default Swap, CDS)、总收益互换(Total Return Swap, TRS)、信用价差期权(Credit Spread Option, CSO)以及其他信用衍生产品。
按照市场规模来看,CDS 市值规模占全部信用衍生工具市场的97%以上,是最为重要的CRM工具。
CDS又被称为信贷违约掉期和贷款违约保险(第三种名称更为贴近产品的本意),是信用衍生工具的一种,是用来防止特定公司或产品破产的一种保险安排。
一般情况下,CDS的购买者拥有一种权力,在发行某种债券或金融产品的特定公司破产的时候,持有该公司债券或金融产品并购买了CDS合约的人,就可以以原债券或金融产品的面值出售或按一定的市场价位赎回现金。
特定公司所发行的特定债券或金融产品,被称为“推荐义务”(Reference Obligation,RO),在CDS合约下可出售的债券或金融产品的总面值,被称为是CDS合约的“名义本金”(Notional Principal,NP)。
二、CDS发展历程1992年,国际互换与衍生品协会(ISDA)提出了信用衍生品的原理和机制,探索分散、转移或对冲信用风险。
这种衍生品常用模式是信用保障买方向卖方支付一笔固定费用,一旦发生买卖双方所指定的信用问题,信用保障卖方就按合同约定赔偿对方损失。
信用违约互换最初形成于1993年,当时,美国信孚银行为了防止其向日本银行提供的贷款遭受损失,与金融衍生品的交易对手达成了一项合同:由交易商对日本银行的违约行为予以保护,如果日本银行发生信用问题、出现还款困难等问题,交易商将对信孚银行予以补偿,但信孚银行需要向交易商支付一笔固定费用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 0 0 0 0 0 0 0 0 0.601993 1.219133 3.017073 5 5 5 5 5 7 8
0 0 0 0 0 0 2.46894 5 5 5 9
1368.075 877.2098 550.5152 548.8993 331.4283 187.7073 330.5776 187.4558 95.10703 38.60097 195.1318 95.22534 39.06958 9.198755 0 0 1 2 3 4
CDS value time Annual Premium of CDS 0.125337
116.4247 116.4247 115.0323 106.4691 81.67133 40.60058 5
114.9302 114.9302 114.9302 112.1104 97.3361 60.56896 27.21539 6
113.346 113.346 113.346 113.346 107.6354 82.91483 40.60058 18.24302 7
swap termination (year) 5 10 Annual Premium of CDS 0.125337 0.0706 0.1253 Premium is defined as the annual payment for the CDS for the tenor of the swap Interim Calculations
Credit Default Swap Model reference number Version publication date author affiliation email address last revised date references Descriptions financial model class issuer/modeler model type risk sources risk distribution economic assumptions technical assumptions key words Links data financial models Inputs Face Value of Bond Bond Maturity Coupon rate Firm Value Firm Volatility Risk-free Rate swap termination (year) swap amount upward jump size p 1-p Outputs
ate the annual premium of credit default swap
bond's principal amount, coupon rate, initial firm value, firm value volatility, risk-free rate, swap termination date, notional amount annual premium of CDS Thomas S.Y. Ho and Sang Bin Lee, 2004, Oxford University Press
/ 7. Bond Arithmetic, 8. Bond Model
100 10 0.08 300 0.4 0.06 10 5 1.4918 0.4766 0.5234
Coupons are paid annually.
Swap termination year ≤10
CDS pays an amount at the event of a default on the bond. Convertibles, MBS/CMO and other Bonds: The Behavioral Models swap desks credit derivatives firm value lognormal structural model annual compounding digital credit default swap
111.6668 111.6668 111.6668 111.6668 111.6668 100.1018 60.56896 27.21539 12.22866 8
109.8868 109.8868 109.8868 109.8868 109.8868 109.8868 86.46591 40.60058 18.24302 8.197117 9
0.035789 0.169026 0.309718 0.454413 0.766356 1.269986 0.92249 1.454434 2.247673 3.39554 0 1 2 3
0 0.072479 0.561235 2.060905 5 4
reserved by Thomas Ho Company, NY, NY. tom.ho@
7248.092 3195.286 1374.243 555.9955 188.3332 34.69686 0 0 0 8
10869.58 4823.507 2106.83 886.1483 337.6606 91.20922 3.892355 0 0 0 9
0 0 0 0 0 0.146782 0.297257 1.002941 1.760456 3.260456 5 5 5 5 6
16379.45 7359.759 3306.953 1485.91 667.6623 300 134.7987 60.56896
201.096 134.7987 90.35826 60.56896 40.60058 27.21539 90.35826 60.56896 40.60058 27.21539 18.24302 12.22866 40.60058 27.21539 18.24302 12.22866 8.197117 5.494692 5 6 7 8 9 10 108 108 108 108 108 108 108 60.56896 27.21539 12.22866 5.494692 10 16271.45 7251.759 3198.953 1377.91 559.6623 192 26.79869 0 0 0 0 10 0 0 0 0 0 0 0 5 5 5 5 10
1485.91 996.0351 667.6623
firm value time
667.6623 447.5474 300 447.5474 300 201.096 134.7987 300 201.096 134.7987 90.35826 60.56896 0 1 2 3 4
debt time
2100.292 879.6103 332.5151 94.62687 8.686931 0 5
3192.023 1370.98 552.7321 18ቤተ መጻሕፍቲ ባይዱ.8896 37.46259 0 0 6
4820.048 2103.371 882.6891 334.2014 93.46063 7.443436 0 0 7
© copyright THC 2003. All rights reserved by Thomas Ho Compan 69 classification# 00501 1 Instructions 1.0 level basic To calculate the annual premium of credit d May-03 Hanyang Financial Engineering Lab. Hanyang University input bond's principal amount, coupon leesb@hanyang.ac.kr risk-free rate, swap termination Dec-03 output annual premium of CDS Ch.10 of "The Oxford Guide to Financial Modeling " by Thomas S.Y. Ho and Sang Bin Le
118.8253 118.763 116.1191 116.9698 112.5442 105.989 104.8682 105.8707 95.72911 81.15951 0 1 2 3
117.8346 117.1471 112.2927 96.19772 60.56896 4
equity time
3306.953 2216.717 1485.91 996.0351 667.6623 447.5474 300
7359.759 4933.394 3306.953 2216.717 1485.91 996.0351 667.6623 447.5474 300 201.096 134.7987
10979.47 4933.394 2216.717 996.0351 447.5474 201.096 90.35826
