初三数学九下锐角三角函数所有知识点总结和常考题型练习题
最新初三锐角三角函数知识点总结、典型例题、练习(精选)
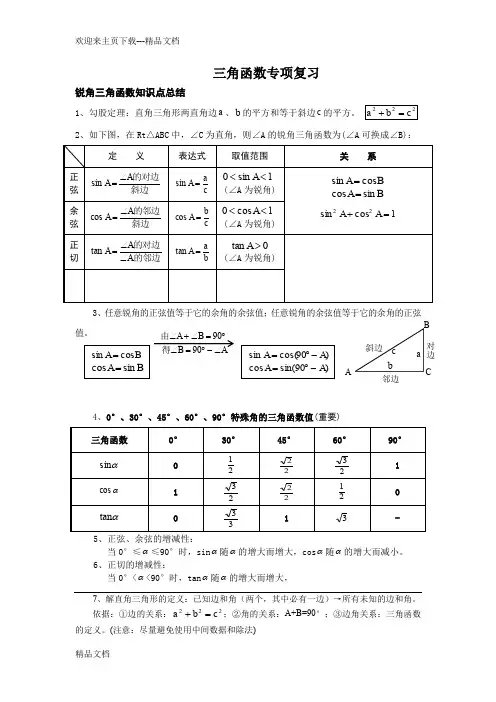
三角函数专项复习锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
222c b a =+2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):定 义表达式取值范围关 系正弦 斜边的对边A A ∠=sin c aA =sin 1sin 0<<A (∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A (∠A 为锐角) 正切 的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A (∠A 为锐角)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、0°、30°、45°、60°、90°特殊角的三角函数值(重要) 三角函数 0° 30°45°60°90° αsin 0 21 22 23 1 αcos1 23 2221 0 αtan33 1 3-5、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
6、正切的增减性:当0°<α<90°时,tan α随α的增大而增大,7、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法) )90cos(sin A A -︒=)90sin(cos A A -︒=BA cos sin =BA sin cos =A90B 90∠-︒=∠︒=∠+∠得由B A对边邻边斜边 ACBba c8、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
初三年级锐角三角函数知识点总结、典型例题、练习[精选]
![初三年级锐角三角函数知识点总结、典型例题、练习[精选]](https://uimg.taocdn.com/c22c33565f0e7cd18425367b.webp)
初三年级锐角三角函数知识点总结、典型例题、练习[精选]锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
222c b a =+2、如下图;在Rt △ABC 中;∠C 为直角;则∠A 的锐角三角函数为(∠A 可换成∠B):定 义表达式取值范围关 系正弦 斜边的对边A A ∠=sin c aA =sin 1sin 0<<A (∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A (∠A 为锐角) 正切 的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A (∠A 为锐角)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、0°、30°、45°、60°、90°特殊角的三角函数值(重要) 三角函数 0° 30°45°60°90° αsin 0 21 22 23 1 αcos1 23 2221 0 αtan33 1 3-5、正弦、余弦的增减性:当0°≤α≤90°时;sin α随α的增大而增大;cos α随α的增大而减小。
6、正切的增减性:当0°<α<90°时;tan α随α的增大而增大;7、解直角三角形的定义:已知边和角(两个;其中必有一边)→所有未知的边和角。
)90cos(sin A A -︒=)90sin(cos A A -︒=BA cos sin =BA sin cos =A90B 90∠-︒=∠︒=∠+∠得由B A对边邻边斜边 ACBba c依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
初三数学九下锐角三角函数所有知识点总结和常考题型练习题
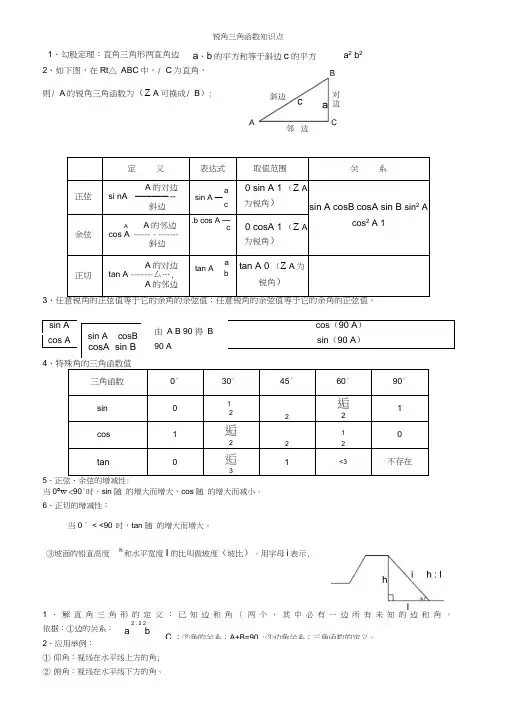
锐角三角函数知识点③坡面的铅直高度h和水平宽度I 的比叫做坡度(坡比)。
用字母i 表示,2、如下图,在Rt △ ABC 中,/ C 为直角, 则/ A 的锐角三角函数为(Z A 可换成/ B ):定义 表达式取值范围 关 系正弦A 的对边si nA ———— --斜边 asin A —c 0 sin A 1 (Z A为锐角)sin A cosB cosA sin B sin 2 Acos 2 A 1余弦AA 的邻边cos A ------ - -------斜边 .b cos A —c0 cosA 1 (Z A为锐角)正切A 的对边tan A -------- 厶…,A 的邻边atan Abtan A 0 (Z A 为锐角)3 cos (90 A ) sin A sin (90 A )cos A4三角函数 0° 30°45° 60° 90° sin 0 122逅21 cos1 逅2212 0 tan逅31<3不存在5当0°w <90°时,sin 随 的增大而增大,cos 随 的增大而减小。
6、正切的增减性:当0 ° < <90°时,tan 随 的增大而增大。
1、解直角三角形的定义:已知边和角(两个,其中必有一边所有未知的边和角。
依据:①边的关系: 2 . 2 2a bC ;②角的关系:A+B=90°;③边角关系:三角函数的定义。
2、应用举例:① 仰角:视线在水平线上方的角; ② 俯角:视线在水平线下方的角。
1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方a 2b 2sin A cosBcosA sin B由 A B 90 得 B 90 A6、计算 tan60o 「2 sin45o 2cos30o 的结果是)i ——即 l 。
坡度一般写成1:m 的形式,女口 i 1:5等。
初三锐角三角函数知识点总结、典型例题、练习47903
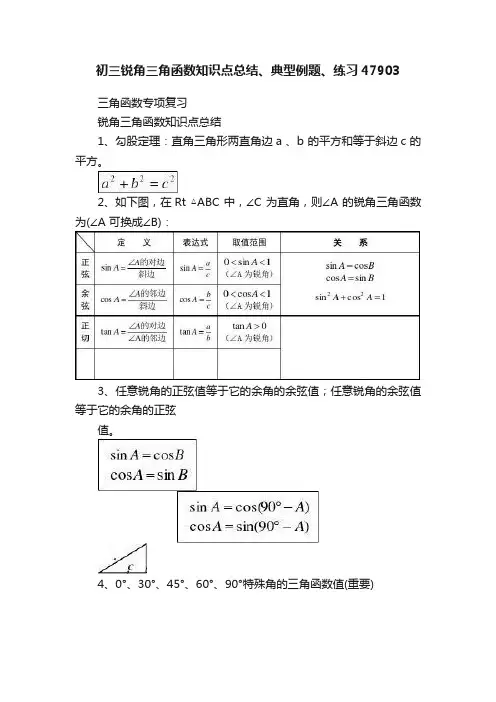
初三锐角三角函数知识点总结、典型例题、练习47903三角函数专项复习锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、0°、30°、45°、60°、90°特殊角的三角函数值(重要)当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
6、正切的增减性:当0°<α<90°时,tan α随α的增大而增大,7、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法)A90B 90∠-?=∠?=∠+∠得由B A 邻 C B8、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
仰角铅垂线水平线视线视线俯角(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示,即hi l=。
坡度一般写成1:m 的形式,如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角),那么tan hi lα==。
3、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。
4、指北或指南方向线与目标方向线所成的小于90°的水平角,叫做方向角。
如图4,OA 、OB 、OC 、OD 的方向角分别是:北偏东45°(东北方向),南偏东45°(东南方向),南偏西45°(西南方向),北偏西45°(西北方向)。
初三锐角三角函数知识点总结、典型例题、练习(精选)[免费专享]
![初三锐角三角函数知识点总结、典型例题、练习(精选)[免费专享]](https://uimg.taocdn.com/5443e4a8d15abe23492f4d36.webp)
三角函数专项复习锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
222c b a =+2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):定 义表达式取值范围关 系正弦 斜边的对边A A ∠=sin c aA =sin 1sin 0<<A (∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A (∠A 为锐角) 正切 的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A (∠A 为锐角)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、0°、30°、45°、60°、90°特殊角的三角函数值(重要)三角函数 0° 30°45°60°90° αsin 0 2122 23 1 αcos1 23 2221 0 αtan33 1 3-5、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
6、正切的增减性:当0°<α<90°时,tan α随α的增大而增大,7、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法)8、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
)90cos(sin A A -︒=)90sin(cos A A -︒= B A cos sin =B A sin cos =A 90B 90∠-︒=∠︒=∠+∠得由B A 对边邻边 斜边 A C Bb a c仰角铅垂线水平线视线视线俯角(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
人教版九年级数学下册《锐角三角函数》知识小结与练习

知识点总结一、锐角三角函数的概念: 在Rt △ABC 中,∠C 为直角,∠A 、∠B 、∠C 对的边分别是a 、b 、c ,则锐角A 的各三角函数的定义如下:1、角A 的正弦:锐角A 的对边与斜边的比叫做∠A 的正弦,记作sinA ,即sinA =ac; 2、角A 的余弦:锐角A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即cosA = bc ; 3、角A 的正切:锐角A 的对边与邻边的比叫做∠A 的正切,记作tanA ,即tanA = ab.二、特殊角的三角函数值:三、解直角三角形:1、直角三角的边角关系:如图,在Rt △ABC 中,∠A 、∠B 为锐角,∠C=90º,它们所对的边分别为a,b,c ,其中除直角∠C 外,其余的5个元素之间有以下关系:(1)三边之间的关系:a 2+b 2=c 2(勾股定理); (2)锐角之间的关系:∠A+∠B=90º; (3)边角之间的关系:sinA=cosB=a c ,cosA=sinA=b c,tanA=a b ,tanB=ba. 2、解直角三角型的类型与解法:三角函数 三角 值函数300450600a sin21 22 23 a cos23 22 21 a tan33 13角四、解直角三角形的简单应用:1、与仰角俯角有关的实际问题2、与方向角有关的实际问题3、与坡度坡角有关的实际问题4、与生活有关的实际问题易错点知识分析一、对锐角三角函数的定义理解错误:例1 如图所示,在△ABC中,AB=AC=3,BC=4,求sinB的值.∴sinB=53AD AB =【点评】锐角三角函数是在直角三角形中定义的,而△ABC 不是直角三角形,必须构建直角三角形解决问题.二、混淆特殊角的三角函数值例2、计算:tan45°-cos60°sin60°·tan30°三、对仰角、俯角、坡角、坡度方向角等概念理解错误例3、如图,某飞机于空中A 处探测到目标C ,此时飞行高度AC=h 米,从飞机上看地面控制点B 的俯角为α,则BC 的距离约为( ). A. h ·tan α米 B. tan hα米 C.sin hα米 D. h ·sin α米课堂学习检测一、填空题二、解答题2.求下列各式的值.(1)o 45cos 230sin 2-︒(2)tan30°-sin60°·sin30°(3)cos45°+3tan30°+cos30°+2sin60°-2tan45°(4)︒+︒+︒+︒-︒45sin 30cos 30tan 130sin 145cos 2223.求适合下列条件的锐角α .(1)21cos =α(2)33tan =α(3)222sin =α (4)33)16cos(6=-οα4.用计算器求三角函数值(精确到0.001).(1)sin23°=______; (2)tan54°53′40″=______. 5.用计算器求锐角α (精确到1″).(1)若cos α =0.6536,则α =______;(2)若tan(2α +10°31′7″)=1.7515,则α =______.综合、运用、诊断6.已知:如图,在菱形ABCD 中,DE ⊥AB 于E ,BE =16cm ,⋅=1312sin A 求此菱形的周长.7.已知:如图,在△ABC 中,∠BAC =120°,AB =10,AC =5.求:sin ∠ACB 的值.8.已知:如图,Rt △ABC 中,∠C =90°,∠BAC =30°,延长CA 至D 点,使AD =AB .求:(1)∠D 及∠DBC ;(2)tan D 及tan ∠DBC ;(3)请用类似的方法,求tan22.5°.9.已知:如图,Rt △ABC 中,∠C =90°,3==BC AC ,作∠DAC =30°,AD 交CB 于D 点,求:(1)∠BAD ;(2)sin ∠BAD 、cos ∠BAD 和tan ∠BAD .10.已知:如图△ABC 中,D 为BC 中点,且∠BAD =90°,31tan =∠B ,求:sin ∠CAD 、cos ∠CAD 、tan ∠CAD .拓展、探究、思考11.已知:如图,∠AOB =90°,AO =OB ,C 、D 是上的两点,∠AOD >∠AOC ,求证:(1)0<sin ∠AOC <sin ∠AOD <1;(2)1>cos ∠AOC >cos ∠AOD >0;(3)锐角的正弦函数值随角度的增大而______; (4)锐角的余弦函数值随角度的增大而______.12.已知:如图,CA ⊥AO ,E 、F 是AC 上的两点,∠AOF >∠AOE .(1)求证:tan ∠AOF >tan ∠AOE ;(2)锐角的21世纪教育网值随角度的增大而______.13.已知:如图,Rt △ABC 中,∠C =90°,求证:(1)sin 2A +cos 2A =1; (2)⋅=AAA cos sin tan。
初三数学九下锐角三角函数所有知识点总结和常考题型练.doc
锐角三角函数知识点1、勾股定理:直角三角形两直角边a、b的平方和等于斜边C的平方。
a2+h2 =c22、如下图,在RtAABC中,ZC为直角,则ZA的锐角三角函数为(ZA叮换成ZB):定义表达式取值范围关系正弦.A 的对边sin A =————斜边人asin A =—c0 < sin A < 1(ZA为锐角)sin A = cos B cos A = sin Bsin2 A + cos2A = 1余弦4乙4的邻边cos A=———T—斜边A b cos A=—c0<cosA< 1(ZA为锐角)正切人,4的对边曲“ZA的邻边tan A =—btan A > 0 (ZA为锐角)3sin A - cos B由ZA + ZB = 90。
、sin A = cos(90° - A) cos A = sin B 得ZB = 90° - ZA>cos A - sin(90°一A)4三角函数0°30°45°60°90°sin a01T VI2迴21COSO1迴2VT ~2~10tana0迥31不存在5、正弦、余弦的增减性:当0。
W Q W90°时,sina随。
的增大而增大,cos 6^随Q的增大而减小。
6、正切的增减性:当0。
<«<90°时,tan(7随Q的增大而增大。
1、解直角三角形的定义:已知边和角(两个,其屮必有一边)一所有未知的边和角。
依据:①边的关系:a2+h2=c2.②角的关系:A+B二90。
;③边角关系:三角函数的定义。
2、应用举例:①仰角:视线在水平线上方的角;②俯角:视线在水平线下方的角。
③ 坡面的铅直高度h 和水平宽度I 的比叫做坡度(坡比)o 用字母:表示,,=h即 7。
坡度一般写成1:加的形式,如,=1:5等。
把坡面与水平面 ・h ,i = — = tana的夹角记作Q (叫做坡角),那么 I 。
初三锐角三角函数知识点总结、典型例题、练习(精选)
例 2.已知:如图,⊙O 的半径 OA=16cm,OC⊥AB 于 C 点, sin AOC 3 4
求:AB 及 OC 的长.
2
例 3.已知 A 是锐角, sin A 8 ,求 cos A , tan A 的值 17
对应训练:
1.在 Rt△ABC 中,∠ C=90°,若 BC=1,AB= 5 ,则 tanA 的值为
B.
3
3
C.
4
4
D.
3
8. 如图,在△ABC 中,∠ACB=∠ADC= 90°,若 sinA= 3 ,则 cos∠BCD 的值为 . 5
C
9.计算: 2 cos 30 2 sin 45 tan 60
A
D
B
10.计算 2sin 60 2 cos 45 3 tan 30 tan 45 .
11.计算: 2 sin 60o 4 cos2 30o+ sin 45o tan 60o.
8
12.已知在 Rt△ABC 中,∠C=90°,a= 4 6 ,b=12 2 .解这个直角三角形
13. 已知:在⊙O 中,AB 是直径,CB 是⊙O 的切线,连接 AC 与⊙O 交于点 D,
C
(3) 求证:∠AOD=2∠C
则 sin B 的值是(
)
3
2
A.
3
3
B.
2
3
C.
4
4
D.
3
4. 如图 4,沿 AE 折叠矩形纸片 ABCD ,使点 D 落在 BC 边的点 F 处.已知 AB 8 ,
BC 10 ,AB=8,则 tan∠EFC 的值为 ( )
A
D
3
A.
☆人教版九年级数学下册第28章-锐角三角函数知识点及典型例题
人教版九年级数学下册第28章 锐角三角函数知识点及典型例题知识点一:锐角三角函数的定义: 一、 锐角三角函数定义:在Rt △ABC 中,∠C=900, ∠A 、∠B 、∠C 的对边分别为a 、b 、c , 则∠A 的正弦可表示为:sinA= , ∠A 的余弦可表示为cosA=∠A 的正切:tanA= ,它们弦称为∠A 的锐角三角函数 例1.如图所示,在Rt △ABC 中,∠C =90°.第1题图①斜边)(sin =A =______, 斜边)(sin =B =______; ②斜边)(cos =A =______,斜边)(cos =B =______;③的邻边A A ∠=)(tan =______,)(tan 的对边B B ∠==______.例2. 锐角三角函数求值:在Rt △ABC 中,∠C =90°,若a =9,b =12,则c =______,sin A =______,cos A =______,tan A =______, sin B =______,cos B =______,tan B =______.例3.已知:如图,Rt △TNM 中,∠TMN =90°,MR ⊥TN 于R 点,TN =4,MN =3.求:sin ∠TMR 、cos ∠TMR 、tan ∠TMR .典型例题:类型一:直角三角形求值1.已知Rt △ABC 中,,12,43tan ,90==︒=∠BC A C 求AC 、AB 和cos B .2.已知:如图,⊙O 的半径OA =16cm ,OC ⊥AB 于C 点,⋅=∠43sin AOC求:AB 及OC 的长.3.已知:⊙O 中,OC ⊥AB 于C 点,AB =16cm ,⋅=∠53sin AOC (1)求⊙O 的半径OA 的长及弦心距OC ; (2)求cos ∠AOC 及tan ∠AOC .4. 已知A ∠是锐角,178sin =A ,求A cos ,A tan 的值对应训练:(西城北)3.在Rt △ABC 中,∠ C =90°,若BC =1,AB 5tan A 的值为A .55 B .255 C .12D .2 (房山)5.在△ABC 中,∠C =90°,sin A=53,那么tan A 的值等于( ).A .35B . 45C . 34D . 43类型二. 利用角度转化求值:1.已知:如图,Rt △ABC 中,∠C =90°.D 是AC 边上一点,DE ⊥AB 于E 点.DE ∶AE =1∶2.求:sin B 、cos B 、tan B .2. 如图,直径为10的⊙A 经过点(05)C ,和点(00)O ,,与x 轴的正半轴交于点D ,B 是y 轴右侧圆弧上一点,则cos ∠OBC 的值为( )A .12B .32C .35D .453.(孝感中考)如图,角α的顶点为O ,它的一边在x 轴的正半轴上,另一边OA 上有一点P (3,4),则 sin α= .4.(庆阳中考)如图,菱形ABCD 的边长为10cm ,DE ⊥AB ,3sin 5A =,则这个菱形的面积D C B A Oy x第8题图= cm 2.5.(齐齐哈尔中考)如图,O ⊙是ABC △的外接圆,AD 是O ⊙的直径,若O ⊙的半径为32,2AC =,则sin B 的值是( )A .23B .32C .34D .436. 如图4,沿AE 折叠矩形纸片ABCD ,使点D 落在BC 边的点F 处.已知8AB =,10BC =,AB=8,则tan EFC ∠的值为 ( )A.34 B.43C.35D.45AD EC B F7. 如图6,在等腰直角三角形ABC ∆中,90C ∠=︒,6AC =,D 为AC 上一点,若1tan 5DBA ∠= ,则AD 的长为( )A .2B .2C .1D .228. 如图6,在Rt △ABC 中,∠C =90°,AC =8,∠A 的平分线AD =3316求 ∠B 的度数及边BC 、AB 的长.DABC图6类型三. 化斜三角形为直角三角形例1 (安徽)如图,在△ABC 中,∠A=30°,∠B=45°,AC=23,求AB 的长.例2.已知:如图,△ABC 中,AC =12cm ,AB =16cm ,⋅=31sin A(1)求AB 边上的高CD ; (2)求△ABC 的面积S ; (3)求tan B .例3.已知:如图,在△ABC 中,∠BAC =120°,AB =10,AC =5.求:sin ∠ABC 的值.对应训练1.(重庆)如图,在Rt △ABC 中,∠BAC=90°,点D 在BC 边上,且△ABD 是等边三角形.若AB=2,求△ABC 的周长.(结果保留根号)2.已知:如图,△ABC 中,AB =9,BC =6,△ABC 的面积等于9,求sin B .3. ABC 中,∠A =60°,AB =6 cm ,AC =4 cm ,则△ABC 的面积是3 cm 23 cm 23 cm 2D.12 cm 2类型四:利用网格构造直角三角形例1 (内江)如图所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为( ) A .12 B .55 C .1010 D .255对应练习:1.如图,△ABC 的顶点都在方格纸的格点上,则sin A =_______.2.如图,A 、B 、C 三点在正方形网络线的交点处,若将ABC ∆绕着点A 逆时针旋转得到''B AC ∆,则'tan B 的值为CBAA.41B. 31C.21D. 13.正方形网格中,AOB ∠如图放置,则tan AOB ∠的值是( )A . 5 5 B. 2 5 5 C.12 D. 2特殊角的三角函数值当 时,正弦和正切值随着角度的增大而 余弦值随着角度的增大而例1.求下列各式的值.(昌平)1).计算:︒-︒+︒60tan 45sin 230cos 2.(朝阳)2)计算:︒-︒+︒30cos 245sin 60tan 2.(黄石中考)计算:3-1+(2π-1)0-33tan30°-tan45°ABO(石景山)4.计算:030tan 2345sin 60cos 221⎪⎪⎭⎫ ⎝⎛︒-︒+︒+.(通县)5.计算:tan 45sin 301cos 60︒+︒-︒;例2.求适合下列条件的锐角α .(1)21cos =α(2)33tan =α(3)222sin =α(4)33)16cos(6=- α(5)已知α 为锐角,且3)30tan(0=+α,求αtan 的值(6)在ABC ∆中,若0)22(sin 21cos 2=-+-B A ,B A ∠∠,都是锐角,求C ∠的度数.例3. 三角函数的增减性 1.已知∠A 为锐角,且sin A <21,那么∠A 的取值范围是 A. 0°< A < 30° B. 30°< A <60° C. 60°< A < 90° D. 30°< A < 90° 2. 已知A 为锐角,且030sin cos <A ,则 ( )A. 0°< A < 60°B. 30°< A < 60°C. 60°< A < 90°D. 30°< A < 90° 例4. 三角函数在几何中的应用1.已知:如图,在菱形ABCD 中,DE ⊥AB 于E ,BE =16cm ,⋅=1312sin A 求此菱形的周长.2.已知:如图,Rt △ABC 中,∠C =90°,3==BC AC ,作∠DAC =30°,AD 交CB 于D 点,求:(1)∠BAD ;(2)sin ∠BAD 、cos ∠BAD 和tan ∠BAD .3. 已知:如图△ABC 中,D 为BC 中点,且∠BAD =90°,31tan =∠B ,求:sin ∠CAD 、cos ∠CAD 、tan ∠CAD .4. 如图,在Rt △ABC 中,∠C=90°,53sin =B ,点D 在BC 边上,DC= AC = 6,求tan ∠BAD 的值.5.如图,△ABC 中,∠A=30°,3tan B =,43AC =AB 的长.DCBAACB解直角三角形:1.在解直角三角形的过程中,一般要用的主要关系如下(如图所示):在Rt △ABC 中,∠C =90°,AC =b ,BC =a ,AB =c ,①三边之间的等量关系:________________________________.②两锐角之间的关系:__________________________________. ③边与角之间的关系:==B A cos sin ______;==B A sin cos _______;==BA tan 1tan _____;==B A tan tan 1______. ④直角三角形中成比例的线段(如图所示).在Rt △ABC 中,∠C =90°,CD ⊥AB 于D .CD 2=_________;AC 2=_________;BC 2=_________;AC ·BC =_________.类型一例1.在Rt △ABC 中,∠C =90°.(1)已知:a =35,235=c ,求∠A 、∠B ,b ;(2)已知:32=a ,2=b ,求∠A 、∠B ,c ;(3)已知:32sin =A ,6=c ,求a 、b ;(4)已知:,9,23tan ==b B 求a 、c ;(5)已知:∠A=60°,△ABC的面积,3S求a、b、c及∠B.12例2.已知:如图,△ABC中,∠A=30°,∠B=60°,AC=10cm.求AB及BC的长.例3.已知:如图,Rt△ABC中,∠D=90°,∠B=45°,∠ACD=60°.BC=10cm.求AD的长.例4.已知:如图,△ABC中,∠A=30°,∠B=135°,AC=10cm.求AB及BC的长.类型二:解直角三角形的实际应用仰角与俯角:例1.(福州)如图,从热气球C处测得地面A、B两点的俯角分别是30°、45°,如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是()A . 200米B . 200米C . 220米D . 100()米例2.已知:如图,在两面墙之间有一个底端在A 点的梯子,当它靠在一侧墙上时,梯子的顶端在B 点;当它靠在另一侧墙上时,梯子的顶端在D 点.已知∠BAC =60°,∠DAE =45°.点D 到地面的垂直距离m 23=DE ,求点B 到地面的垂直距离BC .例3(昌平)19.如图,一风力发电装置竖立在小山顶上,小山的高BD =30m .从水平面上一点C 测得风力发电装置的顶端A 的仰角∠DCA =60°,测得山顶B 的仰角∠DCB =30°,求风力发电装置的高AB 的长.例4 .如图,小聪用一块有一个锐角为30︒的直角三角板测量树高,已知小聪和树都与地面垂直,且相距33米,小聪身高AB 为1.7米,求这棵树的高度.例5.已知:如图,河旁有一座小山,从山顶A 处测得河对岸点C 的俯角为30°,测得岸边点D 的俯角为45°,又知河宽CD 为50m .现需从山顶A 到河对岸点C 拉一条笔直的缆绳AC ,求山的高度及缆绳AC 的长(答案可带根号).A B C D E例5.(泰安)如图,为测量某物体AB的高度,在D点测得A点的仰角为30°,朝物体AB 方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为()A.10米B.10米C.20米D.米例6.益阳)超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学尝试用自己所学的知识检测车速.如图,观测点设在A处,离益阳大道的距离(AC)为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从B处行驶到C处所用的时间为8秒,∠BAC=75°.(1)求B、C两点的距离;(2)请判断此车是否超过了益阳大道60千米/小时的限制速度?(计算时距离精确到1米,参考数据:,,,3,60千米/小时米/秒)类型四. 坡度与坡角例.(广安)如图,某水库堤坝横断面迎水坡AB的坡比是13BC=50m,则应水坡面AB的长度是()A .100mB .1003mC .150mD .503m类型五. 方位角1.已知:如图,一艘货轮向正北方向航行,在点A 处测得灯塔M 在北偏西30°,货轮以每小时20海里的速度航行,1小时后到达B 处,测得灯塔M 在北偏西45°,问该货轮继续向北航行时,与灯塔M 之间的最短距离是多少?(精确到0.1海里,732.13 )2.(恩施州)新闻链接,据[侨报网讯]外国炮艇在南海追袭中国渔船被中国渔政逼退2012年5月18日,某国3艘炮艇追袭5条中国渔船.刚刚完成黄岩岛护渔任务的“中国渔政310”船人船未歇立即追往北纬11度22分、东经110度45分附近海域护渔,保护100多名中国渔民免受财产损失和人身伤害.某国炮艇发现中国目前最先进的渔政船正在疾速驰救中国渔船,立即掉头离去.(见图1)解决问题如图2,已知“中国渔政310”船(A )接到陆地指挥中心(B )命令时,渔船(C )位于陆地指挥中心正南方向,位于“中国渔政310”船西南方向,“中国渔政310”船位于陆地指挥中心南偏东60°方向,AB=海里,“中国渔政310”船最大航速20海里/时.根据以上信息,请你求出“中国渔政310”船赶往出事地点需要多少时间.综合题:三角函数与四边形:(西城二模)1.如图,四边形ABCD中,∠BAD=135°,∠BCD=90°,AB=BC=2,tan∠BDC=6 3.(1) 求BD的长;(2) 求AD的长.18.如图,在平行四边形ABCD中,过点A分别作AE⊥BC于点E,AF⊥CD于点F.(1)求证:∠BAE=∠DAF;(2)若AE=4,AF=245,3sin5BAE∠=,求CF的长.三角函数与圆:1.如图,直径为10的⊙A经过点(05)C,和点(00)O,,与x轴的正半轴交于点D,B是y轴右侧圆弧上一点,则cos ∠OBC 的值为( )A .12 BC .35D .45(延庆)19. 已知:在⊙O 中,AB 是直径,CB 是⊙O 的切线,连接AC 与⊙O 交于点D,(1) 求证:∠AOD=2∠C(2) 若AD=8,tanC=34,求⊙O 的半径。
中考数学复习《锐角三角函数和解直角三角形》经典题型及测试题(含答案)
中考数学复习《锐角三角函数和解直角三角形》经典题型及测试题(含答案)知识点一:锐角三角函数的定义 1.锐角三角函数 正弦: sin A =∠A 的对边斜边=ac余弦: cos A =∠A 的邻边斜边=bc正切: tan A =∠A 的对边∠A 的邻边=ab.来源:学&科&网]2.特殊角的三角函数值[来 度数三角函数[来源:Z 。
xx 。
]30°[来源:学#科#网] 45° 60°sinA1222 32 cosA32 2212tanA 331 33、锐角三角函数的增减性当角度在0°~90°之间变化时,(1)正弦值随着角度的增大(或减小)而增大(或减小) (2)余弦值随着角度的增大(或减小)而减小(或增大) (3)正切值随着角度的增大(或减小)而增大(或减小) 变式练习1:如图,在平面直角坐标系中,点A 的坐标为注意:根据定义求三角函数值时,一定根据题目图形来理解,严格按照三角函数的定义求解,有时需要通过辅助线来构造直角三角形.[(4,3),那么cos α的值是( ) A. 34 B. 43 C. 35 D. 45【解析】D 如解图,过点A 作AB ⊥x 轴于点B ,∵A (4,3),∴OB =4,AB =3,∴OA =32+42=5,∴cos α=OB OA =45.变式练习2:在Rt △ABC 中,∠ABC =90°,AB =3,BC =4,则sinA =________. 【解析】∵在Rt △ABC 中,由勾股定理得AC =22AB BC +=32+42=5,∴sin A =BC AC =45. 变式练习3:在Rt △ABC 中,∠C =90°,sin A =35,BC =6,则AB =( D )A .4B .6C .8D .10变式练习4:如图,若点A 的坐标为(1,3),则sin ∠1=__32__. ,知识点二 :解直角三角形 1.解直角三角形的概念在直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角,由直角三角形中除直角外的已知元素求出所有未知元素的过程叫做解直角三角形. 2.解直角三角形的常用关系在Rt △ABC 中,∠C=90°,∠A ,∠B ,∠C 所对的边分别为a ,b ,c (1)三边之间的关系:a 2+b 2=c 2;(2)锐角之间的关系:∠A +∠B =90°; (3)边角之间的关系:,tan ,cos ,sin ;,tan ,cos ,sin abB c a B c b B b a A c b A c a A ======(sinA==cosB=ac,c osA=sinB=bc,tanA=ab.)变式练习1:在Rt△ABC中,已知a=5,sinA=30°,则c=10,b=5.变式练习2:如图,Rt△ACB中,∠B=30°,∠ACB=90°,CD⊥AB交AB于D.以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作Rt△FGC,∠FCG=90°,继续用同样的方法作Rt△HIC,∠HCI =90°.若AC=a,求CI的长.解:在Rt△ABC中,∠B=30°,∠ACB=90°,CD⊥AB,∴∠A=60°,∵AC=a,∴CD=AC·sin60°=32a,依此类推CH=(32)3a=338a,在Rt△CHI中,∵∠CHI=60°,∴CI=CH·tan60°=338a×3=98a.变式练习3:如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( D )A.433B.4 C.8 3 D.4 3,灵活选择解直角三角形的方法顺口溜:已知斜边求直边,正弦、余弦很方便;已知直边求直边,理所当然用正切;已知两边求一边,勾股定理最方便;已知两边求一角,函数关系要记牢;已知锐角求锐角,互余关系不能少;已知直边求斜边,用除还需正余弦.变式练习4:如图,一山坡的坡度为i=1∶3,小辰从山脚A出发,沿山坡向上走了200米到达点B,则小辰上升了__100__米., ,变式练习5:一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3小时后到达小岛的北偏西45°的C处,则该船行驶的速度为___40+4033___海里/小时.知识点三:解直角三角形的应用1.仰角、俯角、坡度、坡角和方向角(1)仰、俯角:视线在水平线上方的角叫做仰角.视线在水平线下方的角叫做俯角.(如图①)(2)坡度:坡面的铅直高度和水平宽度的比叫做坡度(或者叫做坡比),用字母i表示.坡角:坡面与水平面的夹角叫做坡角,用α表示,则有i=tanα.(如图②)(3)方向角:平面上,通过观察点Ο作一条水平线(向右为东向)和一条铅垂线(向上为北向),则从点O出发的视线与水平线或铅垂线所夹的角,叫做观测的方向角.(如图③)2.解直角三角形实际应用的一般步骤(1)弄清题中名词、术语,根据题意画出图形,建立数学模型;(2)将条件转化为几何图形中的边、角或它们之间的关系,把实际问题转化为解直角三角形问题;(3)选择合适的边角关系式,使运算简便、准确;(4)得出数学问题的答案并检验答案是否符合实际意义,从而得到问题的解.注意:解直角三角形中“双直角三角形”的基本模型:(1)叠合式(2)背靠式解题方法:这两种模型种都有一条公共的直角边,解题时,往往通过这条边为中介在两个三角形中依次求边,或通过公共边相等,列方程求解变式练习1:如图,某数学兴趣小组想测量一棵树CD 的高度,他们先在点A 处测得树顶C 的仰角为30°,然后沿AD 方向前行10 m ,到达B 点,点B 处测得树顶C 的仰角为60°(A 、B 、D 三点在同一直线上).请你根据他们的测量数据计算这棵树CD 的高度(结果精确到0.1 m).(参考数据:2≈1.414,3≈ 1.732)解:如解图,由题意可知∠CAB =30°,∠CBD =60°,AB =10 m ,∵∠CBD =∠CAB +∠BCA ,∴∠BCA =∠CBD -∠CAB =60°-30°=30°=∠CAB , ∴BC =AB =10 m . 在Rt △BCD 中,∵sin ∠CBD =CDBC,∴CD =BC ·sin ∠CBD =10×sin60°=10×32=53≈5×1.732≈8.7 m . 答:这棵树CD 的高度大约是8.7 m .变式练习2:如图,小山岗的斜坡AC 的坡度是tan α=34,在与山脚C 距离200米的D 处,测得山顶A 的仰角为26.6°,求小山岗的高AB (结果取整数;参考数据:sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50).解:设AB =x 米,在Rt △ABD 中,∠D =26.6°,∴BD =tan 26.6x≈2x ,在Rt △ABC 中,tan α=AB BC =34,∴BC =43x ,∵BD -BC =CD ,CD =200,∴2x-43x=200,解得x=300.答:小山岗的高AB约为300米.变式练习3:如图,小明所在教学楼的每层高度为3.5 m,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°,他在二楼窗台B 处测得M的仰角为30°,已知每层楼的窗台离该层的地面高度均为1 m,求旗杆MN的高度(结果精确到0.1 m).(参考数据:2≈1.414,3≈1.732)解:如解图,过点M的水平线交直线AB于点H,由题意,得∠AMH=∠MAH=45°,∠BMH=30°,AB=3.5 m,设MH=x m,则AH=x m,BH=x·tan30°=33x≈0.58x m,∴AB=AH-BH=x-0.58x=0.42x=3.5 m,解得x≈8.3,则MN=x+1=9.3 m.答:旗杆MN的高度约为9.3 m.变式练习4:小明去爬山,如图,在山脚看山顶的角度为30°,小明在坡比为5∶12的山坡上走了1300米,此时小明看山顶的角度为60°,则山高为( )A. (600-2505)米B. (6003-250)米C. (350+3503)米D. 500 3 米【解析】B如解图,∵BE∶AE=5∶12,∴设BE=5k,AE=12k,∴AB=2()5K+(12k)2=13k,∴BE∶AE∶AB=5∶12∶13,∵AB=1300米,∴AE=1200米,BE =500米,设EC=FB=x米,∵∠DBF=60°,∴DF=3x米,则DC=(3x+500)米,又∵∠DAC=30°,∴AC=3CD,即1200+x=3(3x+500),解得x=600-2503,∴DF=3x=(6003-750)米,∴CD=DF+CF=(6003-250)米,即山高CD为(6003-250)米.变式练习5:某兴趣小组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)解:如解图,过点A作AD⊥BC交BC于点D,过点B作BH⊥水平线交水平线于点H,由题意∠ACH=75°,∠BCH=30°,AB∥CH,∴∠ABC=30°,∠ACB=45°,∵AB=4×8=32米,∴CD=AD=AB·sin30°=16米,BD=AB·cos30°=32×32=163米,∴BC=CD+BD=(16+163)米,∴BH=BC·sin30°=(16+163)×12=(8+83)米.答:这架无人飞机的飞行高度为(8+83)米.变式练习6:如图,我国渔政船在钓鱼岛海域C处测得钓鱼岛A在渔政船的北偏西30°的方向上,随后渔政船以80海里/小时的速度向北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在渔政船的北偏西60°的方向上,求此时渔政船距钓鱼岛A的距离AB.(结果保留小数点后一位,其中3≈1.732) 解:∵CD∥BE,∴∠EBC+∠DCB=180°.∵∠ABE=60°,∠DCB=30°,∴∠ABC=90°.…………(4分)由题知,BC=80×12=40(海里),∠ACB=60°.在Rt△ABC中,AB=BC·tan60°=403≈40×1.732≈69.3(海里).答:此时渔政船距钓鱼岛A的距离AB的长约为69.3海里.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、如下图,在Rt△ ABC中,/ C为直角,
定义表达式取值范围关系
正弦
.A ZA的对边
sin A =————---
斜边
a
sin A =—
c
0 < sin A < 1
(Z A为锐角)sin A = cosB cosA= sin B
sin2 A + cos2 A = 1
余弦
ZA的邻边
S斜边
.b cos A
=—c
0 < cosA < 1
(Z A为锐角)
正切丄“ Z A的对边tan A
= ------------- 厶…,
Z A的邻边
a
tan A =—
b
tan A a 0 (Z A
为锐角)
3
4、特殊角的三角函数值
三角函数0°30°45°60°90°
sin a01
2匹
2
迴
2
1
cos。
1
逅
221
2
ta na
V'3
1
.—
03V3不存在
5
当0°w二<90°时,sin二随一的增大而增大,cos二随J的增大而减小。
6、正切的增减性:
当0 ° <二<90°时,tan二随二的增大而增大。
1、解直角三角形的定义:已知边和角(两个,其中必有一边所有未知的边和角。
依据:①边的关系:
2 2 2
a b c
;②角的关系:A+B=90°;③边角关系:三角函数的定义。
2、应用举例:
①仰角:视线在水平线上方的角;
②俯角:视线在水平线下方的角。
锐角三角函数知识点
1、勾股定理:直角三角形两直角边a、b的平方和等于斜边c的平
方。
a2+ b2 = c2则/ A的锐角三角函数为(Z A可换成/ B):
sin A = cosB cosA =sin B 由.A .B =90 得乙B
匚90 术
sin A = cos(90 -
A) cos A = sin(90
斜边
a
邻边
b
对
5、如图,在厶 ABC 中,/ ACB=90 , CD! AB 于 D,若
AC
二 5 6 , AB =
5
,则 tan / ACD 的值为()
③ 坡面的铅直高度 h 和水平宽度I 的比叫做坡度(坡比)。
用字母i 表示,
.h i
即 1。
坡度一般写成1:m 的形式,如i 二1:5等。
把坡面与水平面
i 亠ana
的夹角记作:(叫做坡角),那么 I。
④ 从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图3, OA OB OC 0D 的方向角分别是: 45 °、135 °、225 °。
⑤ 指北或指南方向线与目标方向 线所成的小于 90°的水平角,叫 做方向角。
如图4: OA OB OC 0D 的方向角分别是: 北偏东30° (东北方向), 南偏东45°(东南方向),南偏西60°(西南方向),北偏西60° (西北方向)。
锐角三角函数练习
1、 A.
2、选择题
把Rt △ ABC 各边的长度都扩大 2倍得Rt △ A' B ' C',那么锐角 si nA = si nA ' B . si nA = 2s inA
A 、 的正弦值的关系为(
)•
A.
3、 在 Rt △ ABC 中,/ C = 90°,若 AB= 5, AC = 4,贝
U 3 4 3 4
B .
C .
D . 5 5 4 3
如图,△ ABC 的顶点都是正方形网格中的格点,贝U
C . 2sinA = sinA '
D .不能确定
sinA 的值是(
sin / BAC 等于(
)
10
C.
5
4、如果/ 1
A.
2
a 是等腰直角三角形的一个锐角,则
B.
2
C. 1
D.
COS a 的值是(
)
16.如图,已知 Rt △ ABC 中,AC=3 , BC= 4,过直角顶点 C 作CA 1丄AB ,垂足为A 1,再过A 1作AQ 丄 BC ,垂
足为C 1,过C 1作C 1A 2丄AB ,垂足为A 2,再过A ?作A 2C 2丄BC ,垂足为C ?,…,这样一直做下去, 得到了一组线段 CA 1,
A 1C 1,
C 1A 2,…,贝V CA 1=
三、解答题
,BD 丄AC 于 D , / CBD= a , AB=3 , ?BC=4 , ?求 tan a 的值.
、5
B. 5
30
C. 6
D. '' 6
6、计算 tan60; 、:2sin45; -2cos30‘:的结果是( )
A.
B .
、、2
C. 1
7、
A.
& 如图,已知等腰梯形 25 B . 26 C
如图,小明利用一个含 眼高AB 为1.6m (即小明的眼睛距地面的距离) 0 3「
A.(
ABCD 中, AB// CD / A=60°, AB=10, CD=3 则此梯形的周长为( .27 D . 28 . 60°角的直角三角板测量一栋楼的高度, 已知他与楼之间的水平距离 ,那么这栋楼的高是(
3 5
BD 为 10m,
21.6m C
10
- 3
m D .
CD
9
、如图,
已知 AB 是半圆 O 的直径,弦 AD BC 相交于
点 P ,若/ DPB=a ,那么AB 等于(
A. sin a
COS a C . tan a
tan 、*
10. 填空题
在 Rt △ ABC 中,/ C=90°, a 、b
、c 分别是/ A 、/ B 、/ C 的对边,若 b=3a ,则 tanA= 11. 在厶 ABC 中,/ C = 90°, cosA = 4 , c = 4,贝U a =
如图,P 是/ a 的边OA 上一点,且 P 点坐标为(2, 3),贝U sin a
7 小
13 .已知:a 是锐角,tan a =—,贝V
24
12. COS a
14.在Rt △ ABC 中,两边的长分别为
3和4,求最小角的正弦值为
2
15. tan 30° +2sin60 ° -
2
sin90 ° -tan60° +cos
30°
C 4 A 5 A 5 C 5
17、如图,在△ ABC 中,/ ABC=90 B
第8题图
18、先化简,再求值:
+1
,其中,x =ta n 60c
1
19、如图,在 Rt △ ABC 中,CD CE 分别为斜边 AB 上的高和中线, BC=a AC=b ( b > a ),若tan / DCE=2 , 求b 的值.
20、如图,Rt △ ABC 中,/ C=90°, D 为 CA 上一点,/ DBC=30 , DA=3 AB”
19
,求 tanA 的值.
已知:如图,在山脚的 C 处测得山顶A 的仰角为45,沿着坡度为30 的斜坡前进400米到D 处(即
DCB =30 , CD =400米),测得A 的仰角为60,求山的高度 AB
22、如图,台风中心位于点 P ,并沿东北方向PQ 移动,已知台风移动的速度为 的半径为200千米,B 市位于点P 的北偏东75°方向上,距离点 P 320千米处.
(1)说明本次台风会影响 B 市; 2)求这次台风影响 B 市的时间.
x 2 -1
■■
21、 30千米/时,受影响区域。
