留数法在有理函数积分中的应用
探究留数定理在求解不同类型积分上的应用

探究留数定理在求解不同类型积分上的应用
留数定理是复变函数理论中的一项重要定理,它在求解各种类型的复积分问题中起到了关键作用。
留数定理的基本思想是将复变函数沿一个简单闭曲线的积分转化为沿该曲线内部的全纯函数的留数的和。
留数定理可以用来求解以下几种类型的积分。
1. 辐角积分:辐角积分是将函数沿曲线的导数与辐角的乘积积分。
对于单位圆周C上的函数f(z),如果f(z)是C上的全纯函数,那么辐角积分可以通过留数定理转化为沿圆周内部的全纯函数的留数的和。
2. 函数局部奇点:当函数在某一点z0具有奇点,但其余部分是全纯函数时,可以使用留数定理求解积分。
留数定理将积分转化为奇点z0处的留数乘以2πi。
3. 积分围道选择问题:在复平面上,通常有多个围道可供选择。
留数定理可以帮助确定选择哪个围道。
4. 多值函数积分:在复平面上,有一些函数在某些点上具有多个值。
留数定理可以帮助确定积分路径,以确保积分的正确性。
留数定理的应用不仅限于上述几种情况,还可以扩展到更复杂的函数和积分类型。
它为复变函数的积分提供了一种有力的工具,使得计算积分变得更加简单和直观。
理解和掌握留数定理对于学习和应用复变函数理论具有重要的意义。
《高等数学教学资料》第三节 留数在计算积分上的应用

2
2
二、计算形如
2
0
(cos
, sin
)d
的积分
这虽然是一种沿实轴上区间[0,2 ] 的定积分,我们
将通过适当的变换把它化为围道积分。
令 z ei ,则
dz iei d izd , 即
d dz ,
iz
cos 1 ( ei ei ) 1 ( z 1 ) z2 1 ;
2
2 z 2z
sin
1
( ei
ei
)
1
(z1)
z2 1 ;
2i
2i z 2iz
0 2 映为 z 1 。故
2
(cos ,sin )d
( z2 1, z2 1 ) 1 dz.
0
z 1 2z 2iz iz
例2:计算积分 I
2 0
1
2
cos 2 p cos
p2d (
p 1 ).
解:令
z
ei
,则 cos 2
2i z 2
z 2
1
4ez
[0
dz ]
2i
z 2 z
1 2 i ( 4e0 ) 4 .
2i
在
z
1
的去心邻域,
(
z
1
)3
cos
z
1
1
的
Laurent
展开式为
( z 1 )3 cos
1 z 1
( z 1 )3 [1
1 2!
1 ( z 1 )2
1 4!
1 ( z 1 )4
L
I
1 2
2i{Re
s[
(
z2
a2
z2 )(
留数在求实积分中的应用
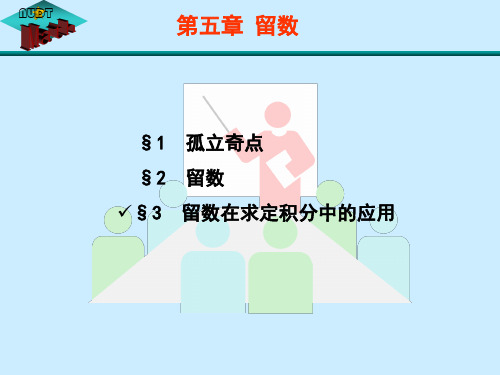
Ñ f ( z )dz 2 i Res[ f ( z ), zk ].
k 1 k 1 k 1
(1)
p
s
l
R( x)dx 2i Res[ R( z ), zk ]
k 1
l
NUDT
§3 留数在定积分计算中的应用
R( x)dx lim R R( x)dx lim 0 R( x)dx
R1
1
0
R2
p.v. R( x)dx lim
z2 (2) R( z ) 6 在上半平面上有三个简 单极点: z 1 z1 e 6 , z 2 e
i
i
3 6
, z3 e
i
5 6
( z 6 1 z k ?)
B1 1 1 1 , B2 , B3 . 6i 6i 6i
其中 z1, z2 ,, zs 为 R(z ) 在上半平面上所有的极点.
y
k 1
CR [R, R]
CR
( R 1)
.z .z
R
1
s
.z . .z
k
2
x
O
R
ÑR( z )dz
(1)
CR
R( z )dz R( x)dx
R
R
NUDT
§3 留数在定积分计算中的应用
探究留数定理在求解不同类型积分上的应用

探究留数定理在求解不同类型积分上的应用
留数定理是复变函数理论中的一项重要定理,它在求解不同类型积分上具有广泛的应用。
以下将从留数定理在求解简单闭合曲线上的积分、无穷远点上的积分以及奇点上的积
分三个方面进行探究。
留数定理适用于求解简单闭合曲线上的积分。
对于一个解析函数的闭合路径,如果函
数在路径内部有有限个奇点,并且这些奇点都是一阶可去奇点,那么函数在路径内的积分
等于其中所有奇点的留数之和。
这个定理可以用来简化复杂函数的积分计算。
留数定理也适用于求解无穷远点上的积分。
当函数在有限区域外的无穷远点处解析时,可以通过将积分路径围绕无穷远点转换成围绕原点的路径,然后利用留数定理求解。
这种
方法在求解指数函数、三角函数等在无穷远点处有定义的函数积分时非常有效。
留数定理还可以用于求解奇点上的积分。
当函数在奇点处有极点时,可以通过计算奇
点的留数来求解积分。
这种方法在求解带有简单极点的函数积分时非常有用,可以大大简
化计算过程。
留数定理及其在积分中的运用

江西师范大学数学与信息科学学院学士学位论文留数定理及其在积分中的运用(Residue theorem and the use in the Calculus)姓名:刘燕学号:0507010122学院:数学与信息科学学院专业:数学与应用数学指导老师:易才凤(教授)完成时间:2009年*月*日留数定理及其在积分中的应用【摘要】本文首先在预备知识中介绍了复函数积分,并介绍了留数的计算方法等。
在此基础上,我们叙述并证明了本文的主要内容--留数定理,并得到留数定理的推广。
然后利用留数定理探讨分析学中的积分计算问题,并利用积分技巧得到它们的一般计算方法和公式,进而更简捷的解决了分析学中积分的计算问题.【关键词】解析孤立奇点留数留数定理Residue theorem and the use in the Calculus 【Abstract】This paper, we first introduce the prior knowledge of complex function Calculus,and introduce the method of calculating the residue, etc.On this basis,We described and proved the main contents of this article--the Residue theorem,and the promotion of the Residue theorem .This paper discussed the calculating problems of intgral in analysis with the theorem of residue, got the general computating method and formula by using analysical skills, and then made it easier to resolve the calculating problems.【Key words】Analysis Isolated singular point Residue Residue theorem目录1引言 .................................................. 2预备知识.......................................2.1 复积分.............................................2.2 解析函数极点及留数.................................2.3留数的计算方法.................................3留数定理..........................................3.1留数定理........................................3.2 留数定理的证明...................................3.3 留数定理的推广..............................4 应用留数定理计算积分............................4.1复积分的计算.....................................4.2实积分的计算....................................5参考文献6 致谢1 引言众所周知,在数学分析以及实际应用中,往往要计算一些定积分或反常积分.而这些积分中被积函数的原函数,有时不能用初等函数表示出来,或者即使可以求出原函数,如果用数学分析中的计算积分的方法往往十分局限而且繁琐.因此需要寻求新的计算方法.例如,可以考虑把实积分转化为复积分,以便利用复积分的理论,而留数定理正是这方面的重要工具.在此我们将重点介绍复变函数中运用留数定理计算积分的方法. 其基本思想是:为了求实函数)(x f 在实数轴上的某一段Γ上的积分,我们在Γ上适当附加某一曲线使其构成一简单闭曲线C ,从而将积分转化为复变函数的围线积分,然后再运用留数定理即可解决.留数是复变函数论中重要的基本概念之一,它与解析函数在孤立奇点出的洛朗展开式,柯西复合闭路定理等都有密切的联系.留数定理是复变函数论中的重要定理,它是复积分和复级数想结合的产物,在实际中有重要的应用,特别是它可以为积分的计算提供新的方法,对复变函数论的发展起到一定的推动作用.那么留数定理能不能计算出所有的积分呢?答案是否定的.留数定理在积分中的应用也具有一定的局限性.通过研究留数定理及其在积分中的应用,我们可以更好的理解这一重要定理一节它在积分中的应用.此外,应用留数定理,我们还可以证明重要的辐角原理和儒歇定理等重要定理,利用这些定理可以考察区域内函数的零点分布情况等.2 预备知识2.1 复积分复变函数积分的定义定义2.1 设有向曲线C :)(),(βα≤≤=t t z z顺着C 从a 到b 的方向在C 上取分点:b z z z z a n n ==-,,,,110把曲线C 分成若干个弧段(如图1)。
留数的应用
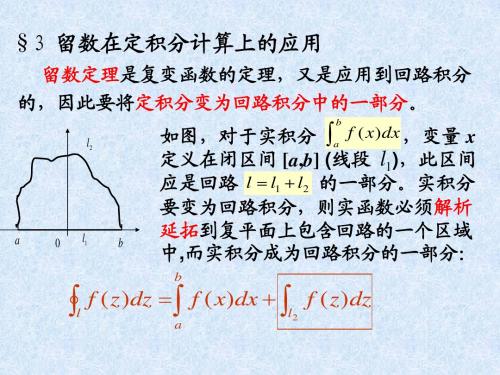
2. 形如 R( x)d x的积分 当被积函数 R(x)是 x 的有理 函数, 而分母的次数至少比分子的次数高二次, 并且 R(x)在实轴上没有孤立奇点时, 积分是存在的.
不失一般性, 设 z n a1 z n 1 an R( z ) m ,m n 2 m 1 z b1 z bm
y
z3 CR
z2
为一已约分式. O R x R 取积分路线如图所示, 其中CR是以原点为中心, R为半 径的在上半平面的半圆周. 取R适当大, 使R(z)所有的 在上半平面内的极点zk都包在这积分路线内.
此等式不因CR的半径R不断增大而有所改变.
y CR z2
R
O
z3 z1
可以证明
R x
C Rz e
R
iaz
dz 0.
R
因此
也可写为
-
2 π i Res[ R( z )eiaz , zk ] R x e dx
iax
2 π i Res[ R ( z )e aiz , zk ] A iB
例3
计算
1 2 5 3 sin
2 0
2
0
d
解: q 令 2
2 令z e i
iq
2
5 3 sinq
1
2
dq
z z 1 (3z i) 2 ( z 3i) 2 dz
i 被积函数在 z 1 内只有一个二阶极点:z 3
1 2 dq 1 I 2 0 1 cos q 2
留数的求法及应用总结

留数的求法及应用总结留数是一种在复变函数理论中用于计算复数函数在奇点处的残留的方法。
留数的计算方法有多种,例如通过直接计算留数公式、Laurent级数展开、辅助函数法、计算围道积分等。
留数的应用非常广泛,包括在计算复积分、求解微分方程、计算极限、求解物理问题等方面都有重要的应用。
首先,我们来看留数的求法。
在复变函数中,函数在奇点点处的留数可以通过以下方法求解:1. 直接计算留数公式:对于简单的函数,可以直接使用留数公式计算。
对于一阶奇点,留数可通过函数在该点的极限值计算:Res[f(z), z=a] = lim(z->a) [(z-a) * f(z)]。
对于高阶奇点,留数可以通过多次取导数再计算极限来求解。
2. Laurent级数展开:对于复变函数,在奇点附近可以进行Laurent级数展开。
然后通过观察Laurent级数的形式,可以读出相应奇点的留数。
3. 辅助函数法:对于一些复杂的函数,可以通过引入辅助函数来计算留数。
通过构造辅助函数,可以使得计算留数的过程变得更加简单。
4. 计算围道积分:复平面上的围道积分可以通过计算围道上的奇点处的留数之和来求解。
通过将围道逐步缩小,将围道上的奇点都计算在内,然后将结果相加即可得到围道积分值。
接下来,我们来看留数的应用。
1. 计算复积分:复积分可以通过计算围道上的奇点处的留数之和来进行计算。
通过围道积分的方法,可以将复积分转化为留数的求和问题,从而简化计算过程。
2. 求解微分方程:在微分方程的求解过程中,往往需要对复函数积分。
通过留数的方法,可以将复积分转化为留数的计算,从而简化问题的求解过程。
3. 计算极限:对于一些复杂的极限问题,可以通过计算极限点处的留数来进行求解。
通过将极限问题转化为留数问题,可以简化问题的求解过程。
4. 物理问题求解:在物理学中,通过留数的方法可以求解一些边界值问题、传热问题、电磁问题等。
通过将物理问题转化为留数问题,可以利用留数的性质来求解物理问题。
留数定理及其应用

留数定理及其应用
留数定理是复变函数理论中的重要定理,用于计算函数在奇点处的留数。
具体来说,如果函数f(z)在区域D内解析,除了有
限个孤立奇点外,则对于D内的任意简单闭曲线C,有如下
留数定理:
∮Cf(z)dz = 2πi * sum(Res(f, z_k))
其中,∮C表示沿C的积分,Res(f, z_k)是函数f(z)在奇点z_k
处的留数。
留数定理的应用主要包括以下几个方面:
1. 计算积分:通过计算函数在奇点处的留数,可以用留数定理来计算复变函数沿闭合曲线的积分。
这样可以简化积分计算,尤其对于实数不易计算的积分,留数定理非常有用。
2. 计算极限:通过留数定理,可以计算复变函数在某个奇点处的极限。
如果函数的极限存在,那么它等于该点处的留数。
3. 解析延拓:通过计算函数在奇点处的留数,可以确定函数在奇点处的性质,如极点的类型(一级极点、二级极点等)以及解析延拓的可能性。
4. 解析函数恢复:留数定理可以用于还原函数原本的性质,即通过计算函数在奇点处的留数,可以还原函数在奇点前的数值。
总之,留数定理是复变函数理论中的重要工具,广泛应用于多个数学和工程领域,如积分计算、边界值问题、电路分析等。
它简化了复变函数的计算和研究,为解决实际问题提供了有效的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理 函数 的 积 分 . 关 键 词 有理 函数 ; 留数 法 ; 待定 系数 中 图分 类号 O12 2 7 .
设 (,z 是的项 , 苦 有 真式以 涉到 分 函均 有真 P)(都 多 式 且 为理 分 ( 及 的式 数 为理 zQ) 并 下 分 ) 算 如苦 z有 函的 分由数 理可 , 母 (可解 , 式. 形j d 理数 积 .代学 论知当 Q)分时l 计 I 的 分 z ! p
维普资讯
l4 l
高 等 数 学研 究
20 年 1 08 月
这种 方法 和复变 函数 中求 留数 的方法类 似 , 即分式 函数 在一 级极 点 n 点 的 留数 就是 A 故称 , 之 为“ 留数 法” . ( )当 ( )一 2 z
例 不 积 jj ≠ x l求 定 分 d .
解 设 一 + + + 测
A 赫
一 —
Iz , B一 6 。 等 一
I 一, 一2 ~
将 A、 的值代人 含有 待定系数 的等 式并整 理得 : B
6 — l z B2 。 B1 B 2+ B1 z+ 1 ( ) —— — — = — — — —。十 — + — = —= —— 1 — — . ( — — -= ( — — ) ‘z— 一 = — — z+ —— —一 ’ — — —) z+ 1 = — — + —一 z —1 — — =l — — —— —— 。 . ( — ) 二
l i n
…
一
.
当 — a 时取极 限得 : 】
A一
P( 1 口) 口2 … ( ) 口l— n )
同理得 :
p( a) A,一 ( ~ “1 ( 一 a )… ( 一 nH ) 口 “ )Ⅱ 2 “, ( 一 “ ) ( 一 “ ’ 斗1 … 口 )
一
三±垡 一 一 兰± 一 一 …一 一 竺 _ 里一 _ _ 生兰±堡 ! 一… 一 ! _ _
( + + q) (
l
+
+ q。 ) l 十 l
r z 十 5 2 2
rI ,十 5 ”
( + z
+ )
—
时, 可令
( z一 6 )
立
一
( z一 6 。 ( ) z一 6 )
旦 ! +
旦
+… +
。
。( 一 6 ’ )
星
上 式两 边 同乘 以最高 次幂 ( z一6 当 z— b ), 时取极 限得 B 一 户 6 , () 再将 B 代人 上式 , 由多项 式理
论 可知 p z 一 p 6 () ( )一 ( z— b p ( ) 加 以整理得 : ) 1z 并
法 时 总要 化归 为解线 性方程组 . 当分式越 多时 , 分分式 会越 复杂 , 程就越 困难 . 部 方 以下介 绍一种确
定 待定 系数 的新 方法 —— 留数法 , 种方法 简单 明 了. 这
下 面分情 况来看 :
( )当 厂z 一 = 1 ()
( 中 啦互不相同 , ) z的多项式 , T N) , 其 p 为  ̄ 2 时 令
( z。+ 髓 + ) 2
( + z
+ ) ’
其 中 A ~ A , 一, P , “, , , ,1S .' , 均 为待定 系数 . , B B , 1g P q … r, . 确定 待定 系数 的常用方 法有 : 比较 系数法 , 赋值法 及这 两种 方 法 的综 合使 用 . 但在 使 用这 些方
兰
上式 两边 同乘 以( z— a ) : 得
二
: 垒 +
+… + !
’z — a 。
( — a1 z — a ) ( ~ 口” z )( 2… z )
z — a1 ’z 一 口 ’ 2
予 二 一 ( a( + + 呈 A+x  ̄ 全 … -)
维普资讯
Vo . 1 No 1 11 , . Jn a .,2 0 08
S TUDI S I C LEGE ATH E ATI E N oL M M CS
高 等 数 学 研 究
13 1
留数 法在 有 理 函数 积 分 中的应 用
刘 玉玲 ( 宁夏职业技术学院信息工程系 银川 700) 502
Q( z)一 ( z一 口 ( 一 6 z )… z ) ( + + q r 一( + )『 z 1 . + ) , ”
则 有
Q)南 口 口+. 口+. — 6 . 上 b ( 一 ) . ) . 6 ) .( f z )( 0 .( . )( .x + + 一 + 一 + +一 + +-
善2 垒 一 生 ! : 旦 二 2 一
( z一 6 ) ( z一 6 )
( 一 6 1 。 z )
+… + 旦
。( 一 6 ’ 。 z ).
同理得 B = P ( )依 此类 推 , 高到低 直 到算 出 B -6 . 从 为止. 值得 注意 的是 , 当求 B , 时 , 。B 若用 比
一
用 留数 法先求 出 A 和 B ,
A = = , B 一 : ,
再 将 A 及 B 人 加 以 整理 后 为 : , 代
坌
( z~ 6 一 )
一 旦: 上…
( z一 6 ) 。
里
。( 一 6 ‘ z )
( ( 是低 于 一 1次的多项式 ) 用 留数 法求 出 Br ) , , 。一 P () 以下算法 同情 形 ( ) 。6 , 2.
较 系数法 将更为 简捷.
( ) , z 一 石『 3 当 () 二
—. —
=
时, 这是前两种情况的混合型, 可令
( j)( 一6) 一z — a+ z 旦 + z一 +…+( 里6)’ “ 坚z一 ! 星6 . 。( 一 6 。( ) ) 。 。 z一
