浙江省温州市高一上学期数学期末测试卷

温州市高一数学第一学期期末试卷

温州市高一数学第一学期期末试卷一、选择题（每题3分，共36分）1、设集合M ={}(,)1,R,R x y x y x y -=∈∈,则下列关系成立的是(* )A ．0∈MB ．1∈MC ．(0,1)∈MD ．(1,0)∈M 2、函数2xy =的值域为（*）A ．(),-∞+∞B ．(0,)+∞C ．(0,1)D ．(1,)+∞3、已知{}n a 是等比数列，21a =，58a =，则{}n a 的公比是(*) A. 1 B.2 C. 2- D. 2或2-4、“2a c b +=”是c ,b ,a 成等差数列的(* ) A ．充分非必要条件 B ．必要非充分条件 C ．充要条件 D ．既非充分又非必要条件5、数列{}n a 的首项为2，且12n n a a +=-（n ≥2），则{}n a 的通项公式是(*) A ．3n a n =- B ．42n a n =- C ．1n a n =+ D ．42n a n =-6、若命题 “p 且q ”是假命题，命题“非q”是假命题.那么(* )A ．命题p 和命题q 都是真命题B ．命题p 和命题q 都是假命题C ．命题p 是假命题，命题q 是真命题D ．命题p 是真命题，命题q 是假命题 7、在等比数列{a n }中，若374a a =，则19a a =(*)A ．-4B ．-2C ． 2D ．4 8、已知24,23ab==,则22ab -=(*)A B ．1 C ．32D ．6 9、若xx x f 1)(-=，则方程x x f =)4(的根是(*) A ．21 B ．－21C ．2D ．－210、已知等差数列{}n a 的公差为1，若134,,a a a 成等比数列，则3a 等于(*)A ．-4B ．-2C ．2D ．4 11、（普通）函数y =lg x 和y =1lgx的图象关于(*) A ．x 轴对称 B ．y 轴对称 C ．y =x 对称 D ．原点对称（重点）已知图甲中的图象对应的函数为)(x f y =，则图乙中的图象对应的函数在下列给出的四式中，只可能是(*)A．d＜0B．a1＜0C．a7=0D．a10＜0二、填空题（每题3分，共18分）13、函数y=_____________ .14、两个数的等差中项为5，等比中项为±4,则这两个数为.15、若函数2()(0)f x x x=>，则1(4)f-=_____________ .16、仓库里堆放着一些盒子，如右图所示，最高一层2盒，第二层6盒，第三层12盒，第四层20盒，……。

浙江省温州市2022-2023学年高一上学期期末考试数学(A卷)含答案

2022学年第一学期温州市高一期末教学质量统一检测数学试题（A 卷）（答案在最后）选择题部分一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{1,3,5}A =，{0,1,2,3,4,5}B =，则B C A =（） A ．{2,4}B ．{1,3,5}C ．{0,2,4}D ．{0,1,2,3,4,5}2．已知幂函数()f x x α=，则“0α>”是“此幂函数图象过点()1,1”的（） A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件3．已知3log 41a =，26b=则（） A ．1a b =+ B ．1b a =+ C ．12a b =+ D ．12b a =+ 4．已知某扇形的周长为4cm ，面积为1cm 2，则该扇形圆心角的弧度数为（）A ．1B ．2C ．3D ．45．函数()lne xf x e x-=+的图象大致为（） A ． B ．C ．D ．6．已知函数21()max ,f x x x ⎧⎫=⎨⎬⎩⎭，其中,max{,},a a ba b b a b ≥⎧=⎨<⎩，若[2,4]x ∃∈，使得关于x 的不等式()()f x f a ≤成立，则正实数a 的取值范围为（）A ．2a ≥或102a <≤B ．2a ≥或104a <≤C ．4a ≥或102a <≤D ．4a ≥或104a <≤7．已知()bg x x x =+，若对任意的1x ，()21,2x ∈，都有()()12211g x g x x x ->-（12x x ≠），则实数b 的取值范围为（） A ．2b ≥ B ．2b ≤C ．8b ≥D ．8b ≤8．已知1718a =，1cos 3b =，13sin 3c =，则（） A ．a b c << B ．c a b << C ．b a c <<D ．c b a <<二、选择题：本大题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得2分． 9．已知a b >，则下列不等式恒成立的是（） A ．11a b< B ．22a b >C ．33a b >D ．a a b b >10．已知函数()()sin 3(0)f x x ϕϕπ=+<<对任意实数t 都有33f t f t ππ⎛⎫⎛⎫+=-+ ⎪ ⎪⎝⎭⎝⎭，记()()cos 3g x x ϕ=+，则（）A ．()6g x g π⎛⎫≤-⎪⎝⎭B ．()g x 图象可由()f x 图象向左平移6π个单位长度得到 C ．03g π⎛⎫=⎪⎝⎭D ．()g x 在,3ππ⎡⎤⎢⎥⎣⎦上单调递减 11．已知正实数x ，y 满足2x y xy +=，则（） A ．8xy ≥B ．6x y +≥C ．1841x y+≥- D ．22248x y y +≥12．已知()f x 为非常值函数，若对任意实数x ，y 均有()()()()()1f x f y f x y f x f y ++=+⋅，且当0x >时，()0f x >，则下列说法正确的有（） A ．()f x 为奇函数 B ．()f x 是()0,+∞上的增函数 C ．()1f x <D ．()f x 是周期函数非选择题部分三、填空题：本大题共4小题，每小题5分，共20分．13．已知角α的顶点在原点，以x 轴非负半轴为始边，若角α的终边经过点()P ，则()cos πα+=_________．14．黑嘴鸥被世界自然保护联盟列为易危物种，全球数量只有2万只左右．据温州网2022年11月26日的报道，今年越冬候鸟黑嘴鸥已到达温州湾，人们可以在密集的芦苇丛中进行观赏．研究发现黑嘴鸥的飞行速度（单位：m/s ）可以表示为函数310log 20v x =-，其中x 表示黑嘴鸥每秒耗氧量的单位数．已知黑嘴鸥在飞往温州湾的过程中，最低飞行速度为10m/s ，最高飞行速度为30m/s ，则黑嘴鸥每秒耗氧量的单位数的取值范围是_________．15．若()cos 202cos sin10x x ︒︒-=，则tan x =_________． 16．已知函数1|1|,2()(2),2x x f x f x x --≤⎧=⎨-->⎩，若关于x 的方程22[()]()10f x mf x --=在(0,2)n （N n +∈）内恰有7个实数根，则n m -=_________．四、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分10分）已知集合3{|1}1A x x =>+，集合2{|0}B x x a =-<．（I ）若1a =，求A B ⋂；（II ）若A B A ⋃=，求实数a 的取值范围．18．（本小题满分12分）已知tan 147tan 14παπα⎛⎫+- ⎪⎝⎭=⎛⎫++ ⎪⎝⎭．（I ）求cos2α的值；（II ）求22sin sin 21tan ααα-+的值．19．（本小题满分12分）已知函数()22cos cos 23f x x x πωω⎛⎫=-+ ⎪⎝⎭（0ω>）．（I ）若函数()f x 的周期是π，求ω的值；（II ）若函数()f x 在0,2x π⎡⎤∈⎢⎥⎣⎦上的值域为3,22⎡⎤⎢⎥⎣⎦，求ω的取值范围． 20．（本小题满分12分）车流密度是指在单位长度（通常为1km ）路段上，一个车道或一个方向上某一瞬时的车辆数，用以表示在一条道路上车辆的密集程度在理想的道路和交通条件下，某城市普通道路的车流速度v （千米/小时）是车流密度x （辆/千米）的函数．研究表明：该城市普通道路车流密度达到160辆/千米时，会造成堵车，此时车流速度为0千米/小时；当车流密度不超过60辆/千米时，车流的速度为60千米/小时；当60160x ≤≤时，车流速度v 是车流密度x 的一次函数．（I ）当0160x <≤时，求车流速度函数()v x 的表达式：（II ）求该城市普通道路的最大通行能力（通行能力=车流速度×车流密度），并结合生活实际给出该道路合理限速建议．21．（本小题满分12分）已知函数()42x xaf x +=为偶函数．（I ）求出a 的值，并写出单调区间；全科免费下载公众号-《高中僧课堂》（II ）若存在[]0,1x ∈使得不等式()()21bf x f x +≥成立，求实数b 的取值范围． 22．（本小题满分12分）已知函数()22f x ax b ax bx =-++（0a >）．（I ）若1a b ==，求函数()f x 的最小值：（II ）若函数()f x 存在两个不同的零点1x 与2x ，求2112x x x x +的取值范围．2022学年第一学期温州市高一期末教学质量统一检测数学试题（A 卷）参考答案及评分标准一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求的．二、多选题：本题共四小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求的，全部选对的得5分，有选错的得0分，部分选对的得2分．三、填空题：本题共4小题，每小题5分，共20分． 13 14．[]27,24315．16．4四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．（本小题满分10分）解析：（1）由311x >+，即201xx ->+，解得12x -<<；由210x -<得11x -<<，所以{11}A B xx ⋂=-<<∣．（2）因为A B A ⋃=，所以B A ⊆，若B φ=，得0a ≤；若B φ≠，有01a >⎧⎪≤，得01a <≤，故1a ≤．18．（本小题满分12分）（I ）解一：由己知得4tan 43πα⎛⎫+=- ⎪⎝⎭，则tan 7α=，若α为第一象限角，则cos 10sin 10αα⎧=⎪⎪⎨⎪=⎪⎩，若α为第三象限角，则cos 10sin 10αα⎧=-⎪⎪⎨⎪=-⎪⎩，故2224cos 2cos sin 25ααα=-=-．（说明：此解法中对角α的象限讨论只有一种情形扣1分）解二：由已知得4tan 43πα⎛⎫+=- ⎪⎝⎭，则tan 7α=，则22221tan 24cos 2cos sin 1tan 25ααααα-=-==-+．解三：由已知得4tan 43πα⎛⎫+=- ⎪⎝⎭，则22tan 244cos 2sin 22251tan 4παπααπα⎛⎫+ ⎪⎛⎫⎝⎭=+==- ⎪⎛⎫⎝⎭++ ⎪⎝⎭．（II ）解一：由（I ）知tan 7α=，则249sin 50α=，7sin 225α=，故22sin sin 2211tan 100ααα-=+．解二：由己知得tan 7α=，则()()()()2222222sin sin 22sin 2sin cos 2tan 2tan 211tan 1001tan sin cos 1tan tan 1ααααααααααααα---===+++++．解三：由己知得4tan 43πα⎛⎫+=- ⎪⎝⎭，则22tan 174sin 2cos 22251tan 4παπααπα⎛⎫+- ⎪⎛⎫⎝⎭=-+== ⎪⎛⎫⎝⎭++ ⎪⎝⎭，则()22sin cos sin cos 2sin sin 2sin 2211tan sin cos 100tan 4αααααααπαααα--==-=++⎛⎫+ ⎪⎝⎭．（说明：此题由教材复习参考5第18题改编） 19．（本小题满分12分）（I ）解：()222cos cos 21cos 2cos 233f x x x x x ππωωωω⎛⎫⎛⎫=-+=+-+ ⎪ ⎪⎝⎭⎝⎭11cos 221cos 223x x x πωωω⎛⎫=+=+- ⎪⎝⎭，则由2ππω=得1ω=．（说明：若()1sin 26f x x πω⎛⎫=++⎪⎝⎭类似给分）（II ）由（I ）知()1cos 23f x x πω⎛⎫=+-⎪⎝⎭，当0,2x π⎡⎤∈⎢⎥⎣⎦时，2333x πππωωπ-≤-≤-，则()302f =，故033ππωπ≤-≤，可得1233ω≤≤． 20．（本小题满分12分）解析：（1）设v kx b =+，则316005606096k b k k b b ⎧⎧+==-⎪⎪⇒⎨⎨+=⎪⎪=⎩⎩，所以60,060396,601(6)05x x x v x <≤-⎧+=<≤⎪⎨⎪⎩．（2）当060x <≤时，通行能力603600y x =≤辆/小时；当60160x <≤时，通行能力()2339680384055y x x x ⎛⎫=-+⋅=--+ ⎪⎝⎭，当80x =时，道路通行能力最大值为3840辆/小时；此时车速()48v x =千米/小时，因此，应给该道路合理限速50千米/小时．备注：生活实际中，道路限速一般30，40，50，60等，学生写“50千米/小时”，或“不超过50千米/小时”，“限速50”，都给1分；写“48千米/小时”其他扣一分。

浙江省温州市高一数学上学期期末试卷(含解析)

2015-2016学年浙江省温州市高一（上）期末数学试卷一、选择题（本大题共18个小题，每小题3分，共54分．在每小题给出的四个选项中，只有一项符合题目要求）1．cos600°=（）A．B．﹣C．D．﹣2．已知集合A={x|2x+a＞0}（a∈R），且1∉A，2∈A，则（）A．a＞﹣4 B．a≤﹣2 C．﹣4＜a＜﹣2 D．﹣4＜a≤﹣23．若幂函数y=f（x）的图象经过点（，3），则该幂函数的解析式为（）A．y=x﹣1B．y=x C．y=x D．y=x34．已知a=log32，b=log2，c=2，则（）A．c＞a＞b B．c＞b＞a C．a＞c＞b D．a＞b＞c5．下列各式中正确的是（）A．﹣=（﹣x）B．x=﹣C．（﹣x）=x D．x=x6．下列函数中，值域为C．（﹣∞，﹣2） D．（﹣∞，﹣2]18．存在函数f（x）满足：对任意x∈R都有（）A．f（|x|）=x B．f（|x|）=x2+2x C．f（|x+1|）=x D．f（|x+1|）=x2+2x二、填空题（本大题共4个小题，每小题4分，共16分）19．计算：（log23）•（log34）= ．20．函数f（x）=2的单调递增区间为．21．对a，b∈R，记max{a，b}=，则函数f（x）=max{|x+1|，x+2}（x∈R）的最小值是．22．已知函数f（x）=log2（x+2）与g（x）=（x﹣a）2+1，若对任意的x1∈，使得f（x1）=g（x2），则实数a的取值范围是．三、解答题（本大题共3个小题，共30分．解答应写出文字说明、证明过程或演算步骤）23．设全集为实数集R，函数f（x）=lg（2x﹣1）的定义域为A，集合B={x||x|﹣a≤0}（a∈R）（Ⅰ）若a=2，求A∪B和A∩B（Ⅱ）若∁R A∪B=∁R A，求a的取值范围．24．已知△ABC的三个内角分别为A，B，C，且A≠．（Ⅰ）化简；（Ⅱ）若角A满足sinA+cosA=．（i）试判断△ABC是锐角三角形还是钝角三角形，并说明理由；（ii）求tanA的值．25．已知定理：“实数m，n为常数，若函数h（x）满足h（m+x）+h（m﹣x）=2n，则函数y=h（x）的图象关于点（m，n）成中心对称”．（Ⅰ）已知函数f（x）=的图象关于点（1，b）成中心对称，求实数b的值；（Ⅱ）已知函数g（x）满足g（2+x）+g（﹣x）=4，当x∈时，都有g（x）≤3成立，且当x∈时，g（x）=2k（x﹣1）+1，求实数k的取值范围．2015-2016学年浙江省温州市高一（上）期末数学试卷参考答案与试题解析一、选择题（本大题共18个小题，每小题3分，共54分．在每小题给出的四个选项中，只有一项符合题目要求）1．cos600°=（）A．B．﹣C．D．﹣【考点】运用诱导公式化简求值．【专题】三角函数的求值．【分析】利用诱导公式把要求的式子化为﹣cos60°，从而求得结果．【解答】解：cos600°=cos=cos240°=cos=﹣cos60°=﹣，故选：B．【点评】本题主要考查利用诱导公式进行化简求值，属于基础题．2．已知集合A={x|2x+a＞0}（a∈R），且1∉A，2∈A，则（）A．a＞﹣4 B．a≤﹣2 C．﹣4＜a＜﹣2 D．﹣4＜a≤﹣2【考点】元素与集合关系的判断．【专题】集合思想；定义法；集合．【分析】根据元素和集合的关系，解不等式组即可得到结论．【解答】解：∵1∉A，2∈A，∴，解得﹣4＜a≤﹣2，故选：D．【点评】本题主要考查元素和集合关系的应用，根据条件解不等式是解决本题的关键，比较基础．3．若幂函数y=f（x）的图象经过点（，3），则该幂函数的解析式为（）A．y=x﹣1B．y=x C．y=x D．y=x3【考点】幂函数的概念、解析式、定义域、值域．【专题】函数思想；综合法；函数的性质及应用．【分析】利用幂函数的形式设出f（x），将点的坐标代入求出函数的解析式．【解答】解：∵f（x）是幂函数设f（x）=xα∴图象经过点（，3），∴3=，∴α=﹣1∴f（x）=x﹣1故选：A．【点评】本题考查利用待定系数法求知函数模型的解析式．4．已知a=log32，b=log2，c=2，则（）A．c＞a＞b B．c＞b＞a C．a＞c＞b D．a＞b＞c【考点】对数值大小的比较．【专题】计算题；转化思想；函数的性质及应用．【分析】利用对数函数、指数函数性质求解．【解答】解：∵0=log31＜a=log32＜log33=1，b=log2＜log21=0，c=2＞20=1，∴c＞a＞b．故选：A．【点评】本题考查三个数大小的比较，是基础题，解题时要认真审题，注意对数函数、指数函数性质的合理运用．5．下列各式中正确的是（）A．﹣=（﹣x）B．x=﹣C．（﹣x）=x D．x=x【考点】根式与分数指数幂的互化及其化简运算．【专题】计算题；转化思想；综合法；函数的性质及应用．【分析】利用根式与分数指数幂性质、运算法则求解．【解答】解：在A中，﹣=﹣≠（﹣x），故A错误；在B中，x=≠﹣，故B错误；在C中，（﹣x）=x，故C正确；在D中，x=±x≠，故D错误．故选：C．【点评】本题考查命题真假的判断，是基础题，解题时要认真审题，注意根式与分数指数幂性质的合理运用．6．下列函数中，值域为=﹣sin（α+）=﹣．故选：C．【点评】本题主要考查了诱导公式的应用，属于基础题．15．在一块顶角为120°、腰长为2的等腰三角形钢板废料OAB中裁剪扇形，现有如图所示两种方案，则（）A．方案一中扇形的周长更长B．方案二中扇形的周长更长C．方案一中扇形的面积更大D．方案二中扇形的面积更大【考点】扇形面积公式．【专题】计算题；转化思想；数形结合法；三角函数的求值．【分析】由已知利用弧长公式，扇形面积公式求出值比较大小即可．【解答】解：∵△AOB为顶角为120°、腰长为2的等腰三角形，∴A=B=30°=，AM=AN=1，AD=2，∴方案一中扇形的周长=2=4+，方案二中扇形的周长=1+1+1×=2+，方案一中扇形的面积=2×=，方案二中扇形的周长==，故选：A．【点评】本题主要考查了弧长公式，扇形面积公式的应用，考查了计算能力，属于基础题．16．某种型号的电脑自投放市场以来，经过三次降价，单价由原来的5000元降到2560元，则平均每次降价的百分率是（）A．10% B．15% C．16% D．20%【考点】函数的值．【专题】计算题；函数思想；综合法；函数的性质及应用．【分析】设降价百分率为x%，由题意知5000（1﹣x%）2=2560，由此能够求出这种手机平均每次降价的百分率．【解答】解：设降价百分率为x%，∴5000（1﹣x%）3=2560，解得x=20．故选：D．【点评】本题考查数列的性质和应用，解题时要注意挖掘隐含条件，寻找数量关系，建立方程．17．已知函数f（x）=x|x|，若对任意的x≤1有f（x+m）+f（x）＜0恒成立，则实数m的取值范围是（）A．（﹣∞，﹣1） B．（﹣∞，﹣1] C．（﹣∞，﹣2） D．（﹣∞，﹣2]【考点】函数恒成立问题．【专题】函数思想；转化思想；函数的性质及应用．【分析】根据函数f（x）的解析式判断函数的奇偶性和单调性，利用函数奇偶性和单调性的关系将不等式进行转化，利用参数分离法转化为求函数的最值即可．【解答】解：f（x）=x|x|=，则函数f（x）在定义域为增函数，且f（﹣x）=﹣x|﹣x|=﹣x|x|=﹣f（x），则函数f（x）为奇函数，则若对任意的x≤1有f（x+m）+f（x）＜0恒成立，等价为若对任意的x≤1有f（x+m）＜﹣f（x）=f（﹣x），即x+m＜﹣x恒成立，即m＜﹣2x恒成立，∵x≤1，∴﹣2x≥﹣2，则m＜﹣2，故选：C【点评】本题主要考查不等式恒成立问题，根据条件判断函数的奇偶性和单调性是解决本题的关键．利用参数分离法是解决不等式恒成立问题的常用方法．18．存在函数f（x）满足：对任意x∈R都有（）A．f（|x|）=x B．f（|x|）=x2+2x C．f（|x+1|）=x D．f（|x+1|）=x2+2x【考点】函数的对应法则；函数的概念及其构成要素．【专题】计算题；转化思想；综合法；函数的性质及应用．【分析】在A、B中，分别取x=±1，由函数性质能排除选项A和B；令|x+1|=t，t≥0，则x2+2x=t2﹣1，求出f（x）=x2﹣1，能排除选项C．【解答】解：在A中，取x=1，则f（1）=1，取x=﹣1，则f（1）=﹣1，不成立；在B中，令|x|=t，t≥0，x=±t，取x=1，则f（1）=3，取x=﹣1，则f（1）=﹣1，不成立；在C中，令|x+1|=t，t≥0，则x2+2x=t2﹣1，∴f（t）=t2﹣1，即f（x）=x2﹣1，故C不成立，D成立．故选：D．【点评】本题考查抽象函数的性质，是中档题，解题时要认真审题，注意函数性质的合理运用．二、填空题（本大题共4个小题，每小题4分，共16分）19．计算：（log23）•（log34）= 2 ．【考点】对数的运算性质．【专题】计算题；函数思想；定义法；函数的性质及应用．【分析】根据换底公式计算即可．【解答】解：（log23）•（log34）=•=2，故答案为：2．【点评】本题考查了换底公式，属于基础题．20．函数f（x）=2的单调递增区间为，使得f（x1）=g（x2），则实数a的取值范围是∪．【考点】对数函数的图象与性质．【专题】函数思想；分类法；函数的性质及应用．【分析】分别求出f（x1）和g（x2）的值域，令f（x1）的值域为g（x2）的值域的子集列出不等式解出a．【解答】解：∵x1∈上是增函数，∴g（0）≤g（x2）≤g（2），即g（x2）的值域为，∴，解得﹣1≤a≤0．（2）若a≥2，则g（x）在上是减函数，∴g（2）≤g（x2）≤g（1），即g（x2）的值域为，∴，解得2≤a≤3．（3）若0＜a≤1，则g min（x）=g（a）=1，g max（x）=g（2）=a2﹣4a+5，∴g（x）的值域为，∴，解得0．（4）若1＜a＜2，则g min（x）=g（a）=1，g max（x）=g（0）=a2+1，∴g（x）的值域为，∴，解得a＜2．综上，a的取值范围是∪∪（0，2﹣）∪（，2）=∪．故答案为∪．【点评】本题考查了二次函数的值域，对数函数的单调性与值域，集合间的关系，分类讨论思想，属于中档题．三、解答题（本大题共3个小题，共30分．解答应写出文字说明、证明过程或演算步骤）23．设全集为实数集R，函数f（x）=lg（2x﹣1）的定义域为A，集合B={x||x|﹣a≤0}（a∈R）（Ⅰ）若a=2，求A∪B和A∩B（Ⅱ）若∁R A∪B=∁R A，求a的取值范围．【考点】交、并、补集的混合运算；并集及其运算；交集及其运算．【专题】计算题；集合思想；综合法；集合．【分析】（Ⅰ）先求出A=（），由a=2便可求出B=，然后进行并集、交集的运算即可；（Ⅱ）根据条件便有B⊆C R A，可求出，可讨论B是否为空集：B=∅时会得到a＜0；而B≠∅时得到a≥0，且B={x|﹣a≤x≤a}，这样便可得到，这两种情况下得到的a的范围求并集便可得出a的取值范围．【解答】解：（Ⅰ）A=；a=2时，B=；∴A∪B=时，都有g（x）≤3成立，且当x∈时，g（x）=2k（x﹣1）+1，求实数k的取值范围．【考点】抽象函数及其应用．【专题】综合题；新定义；分类讨论；分析法；函数的性质及应用；不等式的解法及应用．【分析】（Ⅰ）由对称性可得f（1+x）+f（1﹣x）=2b，化简整理，即可得到b=2；（Ⅱ）由g（2+x）+g（﹣x）=4可得g（x）的图象关于点（1，2）对称，且g（1）=2，对k讨论，当k=0，k＞0，k＜0，结合对称性和单调性，要使g（x）≤3，只需g（x）max≤3，运用单调性求得最大值，解不等式即可得到所求范围．【解答】解：（Ⅰ）函数f（x）=的图象关于点（1，b）成中心对称，可得f（1+x）+f（1﹣x）=2b，即有+=4=2b，解得b=2；（Ⅱ）由g（2+x）+g（﹣x）=4可得g（x）的图象关于点（1，2）对称，且g（1）=2，当k=0时，g（x）=2（0≤x≤1），又g（x）关于（1，2）对称，可得g（x）=2（0≤x≤2），显然g（x）≤3恒成立；当k＞0时，g（x）=2k（x﹣1）+1在递增，又g（x）关于点（1，2）对称，可得g（x）在递增，g（x）≤3，只需g（x）max=g（2）≤3，又g（2）+g（0）=4，则g（0）≥1即21﹣k≥1，即有0≤k≤1；当k＜0时，g（x）=2k（x﹣1）+1在递减，又g（x）关于（1，2）对称，可得g（x）在递减，要使g（x）≤3，只需g（x）max=g（0）≤3，即21﹣k≤3，解得1﹣log23≤k＜0．综上可得，1﹣log23≤k≤1．【点评】本题考查函数的对称性和运用，同时考查函数的单调性的运用，以及不等式恒成立问题的解法，考查运算能力，属于中档题．11。

浙江省温州市高一数学上学期期末试卷(含解析)

2015-2016学年浙江省温州市高一（上）期末数学试卷一、选择题（本大题共18个小题，每小题3分，共54分．在每小题给出的四个选项中，只有一项符合题目要求）1．cos600°=（）A．B．﹣C．D．﹣2．已知集合A={x|2x+a＞0}（a∈R），且1∉A，2∈A，则（）A．a＞﹣4 B．a≤﹣2 C．﹣4＜a＜﹣2 D．﹣4＜a≤﹣23．若幂函数y=f（x）的图象经过点（，3），则该幂函数的解析式为（）A．y=x﹣1B．y=x C．y=x D．y=x34．已知a=log32，b=log2，c=2，则（）A．c＞a＞b B．c＞b＞a C．a＞c＞b D．a＞b＞c5．下列各式中正确的是（）A．﹣=（﹣x）B．x=﹣C．（﹣x）=x D．x=x6．下列函数中，值域为[1，+∞）的是（）A．y=2x+1B．y=C．y=+1 D．y=x+7．下列函数中，与函数y=2x表示同一函数的是（）A．y=B．y=C．y=（）2D．y=log24x8．已知函数f（x）=，则f（﹣1）+f（0）=（）A．3 B．4 C．5 D．69．函数f（x）=x﹣2+lnx的零点所在的一个区间是（）A．（0，1）B．（1，2）C．（2，3）D．（3，4）10．已知函数f（x）=（x﹣a）（x﹣b）（其中a＞b）的图象如图所示，则函数g（x）=a x+b 的图象是（）A．B．C．D．11．已知函数f（x）=e x﹣e﹣x，e为自然对数的底，则下列结论正确的是（）A．f（x）为奇函数，且在R上单调递增B．f（x）为偶函数，且在R上单调递增C．f（x）为奇函数，且在R上单调递减D．f（x）为偶函数，且在R上单调递减12．已知sinα=3cosα，则sinα•cosα的值为（）A．B．C．D．13．已知定义在R上的函数f（x）满足：对任意x1，x2∈R（x1≠x2），均有＞0，e为自然对数的底，则（）A．f（）＜f（）＜f（e） B．f（e）＜f（）＜f（） C．f（e）＜f（）＜f（）D．f（）＜f（）＜f（e）14．设＜α＜π，若sin（α+）=，则cos（+α）=（）A．﹣B．C．﹣D．15．在一块顶角为120°、腰长为2的等腰三角形钢板废料OAB中裁剪扇形，现有如图所示两种方案，则（）A．方案一中扇形的周长更长B．方案二中扇形的周长更长C．方案一中扇形的面积更大D．方案二中扇形的面积更大16．某种型号的电脑自投放市场以来，经过三次降价，单价由原来的5000元降到2560元，则平均每次降价的百分率是（）A．10% B．15% C．16% D．20%17．已知函数f（x）=x|x|，若对任意的x≤1有f（x+m）+f（x）＜0恒成立，则实数m的取值范围是（）A．（﹣∞，﹣1） B．（﹣∞，﹣1] C．（﹣∞，﹣2） D．（﹣∞，﹣2]18．存在函数f（x）满足：对任意x∈R都有（）A．f（|x|）=x B．f（|x|）=x2+2x C．f（|x+1|）=x D．f（|x+1|）=x2+2x二、填空题（本大题共4个小题，每小题4分，共16分）19．计算：（log23）•（log34）= ．20．函数f（x）=2的单调递增区间为．21．对a，b∈R，记max{a，b}=，则函数f（x）=max{|x+1|，x+2}（x∈R）的最小值是．22．已知函数f（x）=log2（x+2）与g（x）=（x﹣a）2+1，若对任意的x1∈[2，6），都存在x2∈[0，2]，使得f（x1）=g（x2），则实数a的取值范围是．三、解答题（本大题共3个小题，共30分．解答应写出文字说明、证明过程或演算步骤）23．设全集为实数集R，函数f（x）=lg（2x﹣1）的定义域为A，集合B={x||x|﹣a≤0}（a∈R）（Ⅰ）若a=2，求A∪B和A∩B（Ⅱ）若∁R A∪B=∁R A，求a的取值范围．24．已知△ABC的三个内角分别为A，B，C，且A≠．（Ⅰ）化简；（Ⅱ）若角A满足sinA+cosA=．（i）试判断△ABC是锐角三角形还是钝角三角形，并说明理由；（ii）求tanA的值．25．已知定理：“实数m，n为常数，若函数h（x）满足h（m+x）+h（m﹣x）=2n，则函数y=h（x）的图象关于点（m，n）成中心对称”．（Ⅰ）已知函数f（x）=的图象关于点（1，b）成中心对称，求实数b的值；（Ⅱ）已知函数g（x）满足g（2+x）+g（﹣x）=4，当x∈[0，2]时，都有g（x）≤3成立，且当x∈[0，1]时，g（x）=2k（x﹣1）+1，求实数k的取值范围．2015-2016学年浙江省温州市高一（上）期末数学试卷参考答案与试题解析一、选择题（本大题共18个小题，每小题3分，共54分．在每小题给出的四个选项中，只有一项符合题目要求）1．cos600°=（）A．B．﹣C．D．﹣【考点】运用诱导公式化简求值．【专题】三角函数的求值．【分析】利用诱导公式把要求的式子化为﹣cos60°，从而求得结果．【解答】解：cos600°=cos=cos240°=cos=﹣cos60°=﹣，故选：B．【点评】本题主要考查利用诱导公式进行化简求值，属于基础题．2．已知集合A={x|2x+a＞0}（a∈R），且1∉A，2∈A，则（）A．a＞﹣4 B．a≤﹣2 C．﹣4＜a＜﹣2 D．﹣4＜a≤﹣2【考点】元素与集合关系的判断．【专题】集合思想；定义法；集合．【分析】根据元素和集合的关系，解不等式组即可得到结论．【解答】解：∵1∉A，2∈A，∴，解得﹣4＜a≤﹣2，故选：D．【点评】本题主要考查元素和集合关系的应用，根据条件解不等式是解决本题的关键，比较基础．3．若幂函数y=f（x）的图象经过点（，3），则该幂函数的解析式为（）A．y=x﹣1B．y=x C．y=x D．y=x3【考点】幂函数的概念、解析式、定义域、值域．【专题】函数思想；综合法；函数的性质及应用．【分析】利用幂函数的形式设出f（x），将点的坐标代入求出函数的解析式．【解答】解：∵f（x）是幂函数设f（x）=xα∴图象经过点（，3），∴3=，∴α=﹣1∴f（x）=x﹣1故选：A．【点评】本题考查利用待定系数法求知函数模型的解析式．4．已知a=log32，b=log2，c=2，则（）A．c＞a＞b B．c＞b＞a C．a＞c＞b D．a＞b＞c【考点】对数值大小的比较．【专题】计算题；转化思想；函数的性质及应用．【分析】利用对数函数、指数函数性质求解．【解答】解：∵0=log31＜a=log32＜log33=1，b=log2＜log21=0，c=2＞20=1，∴c＞a＞b．故选：A．【点评】本题考查三个数大小的比较，是基础题，解题时要认真审题，注意对数函数、指数函数性质的合理运用．5．下列各式中正确的是（）A．﹣=（﹣x）B．x=﹣C．（﹣x）=x D．x=x【考点】根式与分数指数幂的互化及其化简运算．【专题】计算题；转化思想；综合法；函数的性质及应用．【分析】利用根式与分数指数幂性质、运算法则求解．【解答】解：在A中，﹣=﹣≠（﹣x），故A错误；在B中，x=≠﹣，故B错误；在C中，（﹣x）=x，故C正确；在D中，x=±x≠，故D错误．故选：C．【点评】本题考查命题真假的判断，是基础题，解题时要认真审题，注意根式与分数指数幂性质的合理运用．6．下列函数中，值域为[1，+∞）的是（）A．y=2x+1B．y=C．y=+1 D．y=x+【考点】函数的值域．【专题】计算题；函数思想；综合法；函数的性质及应用．【分析】前三项都可由解析式看出值域：y=2x+1＞0，y=，y=，从而判断出这三项不正确，对于D，先得到，两个不等式相加便可得到，这样便可得出该函数的值域，即得出D正确．【解答】解：A.2x+1＞0，∴y=2x+1的值域为（0，+∞），∴该选项错误；B.，∴的值域为[0，+∞），∴该选项错误；C．|x|＞0；∴；∴；∴的值域为（1，+∞），∴该选项错误；D．x﹣1≥0；∴；∴；即y≥1；∴的值域为[1，+∞），∴该选项正确．故选：D．【点评】考查函数值域的概念，指数函数的值域，以及反比例函数的值域，一次函数的值域，根据不等式的性质求值域的方法．7．下列函数中，与函数y=2x表示同一函数的是（）A．y=B．y=C．y=（）2D．y=log24x【考点】判断两个函数是否为同一函数．【专题】对应思想；定义法；函数的性质及应用．【分析】根据两个函数的定义域相同，对应关系也相同，即可判断它们是同一函数．【解答】解：对于A，y==2x（x≠0）与y=2x（x∈R）的定义域不同，∴不是同一函数；对于B，y==2|x|（x∈R）与y=2x（x∈R）的解析式不同，∴不是同一函数；对于C，y==2x（x≥0）与y=x（x∈R）的定义域不同，∴C是同一函数；对于D，y=log24x=log222x=2x（x∈R）与y=2x（x∈R）的定义域相同，对应关系也相同，∴是同一函数．故选：D．【点评】本题考查了判断两个函数是否为同一函数的应用问题，是基础题目．8．已知函数f（x）=，则f（﹣1）+f（0）=（）A．3 B．4 C．5 D．6【考点】函数的值．【专题】计算题；函数思想；综合法；函数的性质及应用．【分析】根据函数的表达式求出f（﹣1）和f（0）的值，求和即可．【解答】解：∴函数f（x）=，∴f（﹣1）=1+2=3，f（0）=1，∴f（﹣1）+f（0）=3+1=4，故选：B．【点评】本题考察了求函数值问题，考察分段函数，是一道基础题．9．函数f（x）=x﹣2+lnx的零点所在的一个区间是（）A．（0，1）B．（1，2）C．（2，3）D．（3，4）【考点】函数零点的判定定理；二分法求方程的近似解．【专题】计算题；函数的性质及应用．【分析】由题意，函数f（x）=x﹣2+lnx在定义域上单调递增，再求端点函数值即可【解答】解：函数f（x）=x﹣2+lnx在定义域上单调递增，f（1）=1﹣2＜0，f（2）=2+ln2﹣2＞0，故函数f（x）=x﹣2+lnx的零点所在区间是（1，2）；故选B．【点评】本题考查了函数的零点的判断，属于基础题．10．已知函数f（x）=（x﹣a）（x﹣b）（其中a＞b）的图象如图所示，则函数g（x）=a x+b 的图象是（）A．B．C．D．【考点】函数的图象．【专题】函数的性质及应用．【分析】先由函数f（x）的图象判断a，b的范围，再根据指数函数的图象和性质即可得到答案．【解答】解：由函数的图象可知，﹣1＜b＜0，a＞1，则g（x）=a x+b为增函数，当x=0时，y=1+b＞0，且过定点（0，1+b），故选：C【点评】本题考查了指数函数和二次函数的图象和性质，属于基础题．11．已知函数f（x）=e x﹣e﹣x，e为自然对数的底，则下列结论正确的是（）A．f（x）为奇函数，且在R上单调递增B．f（x）为偶函数，且在R上单调递增C．f（x）为奇函数，且在R上单调递减D．f（x）为偶函数，且在R上单调递减【考点】函数奇偶性的判断；函数单调性的判断与证明．【专题】函数思想；综合法；函数的性质及应用．【分析】可先得出f（x）的定义域为R，求f（﹣x）=﹣f（x），从而得出f（x）为奇函数，根据指数函数的单调性便可看出x增大时，f（x）增大，从而得到f（x）在R上单调递增，这样便可找出正确选项．【解答】解：f（x）的定义域为R；f（﹣x）=e﹣x﹣e x=﹣f（x）；∴f（x）为奇函数；x增加时，e﹣x减小，﹣e﹣x增加，且e x增加，∴f（x）增加；∴f（x）在R上单调递增．故选A．【点评】考查奇函数的定义，判断一个函数为奇函数的方法和过程，以及增函数的定义，指数函数的单调性．12．已知sinα=3cosα，则sinα•cosα的值为（）A．B．C．D．【考点】同角三角函数基本关系的运用．【专题】转化思想；综合法；三角函数的求值．【分析】由条件利用本题主要考查同角三角函数的基本关系，求得要求式子的值．【解答】解：∵sinα=3cosα，∴tanα=3，则sinα•cosα===，故选：B．【点评】本题主要考查同角三角函数的基本关系的应用，属于基础题．13．已知定义在R上的函数f（x）满足：对任意x1，x2∈R（x1≠x2），均有＞0，e为自然对数的底，则（）A．f（）＜f（）＜f（e） B．f（e）＜f（）＜f（） C．f（e）＜f（）＜f（）D．f（）＜f（）＜f（e）【考点】函数单调性的性质．【专题】函数思想；综合法；函数的性质及应用．【分析】根据条件及增函数的定义容易判断出f（x）在R上单调递增，从而比较这三个数的大小便可得出对应的函数值的大小，从而找出正确选项．【解答】解：∵；∴对任意的x1，x2∈R，x1＜x2时，会得到f（x1）＜f（x2）；∴f（x）在R上为增函数；又；∴．故选：A．【点评】考查增函数的定义，根据增函数的定义比较函数值大小的方法，清楚这三个数的大小关系．14．设＜α＜π，若sin（α+）=，则cos（+α）=（）A．﹣B．C．﹣D．【考点】运用诱导公式化简求值．【专题】计算题；转化思想；三角函数的求值．【分析】利用角的范围可确定三角函数值的符号，利用诱导公式即可求值．【解答】解：∵＜α＜π，＜α+＜，sin（α+）=＞0，∴＜α+＜π，可得：＜+α＜，∴cos（+α）=cos[（α+）+]=﹣sin（α+）=﹣．故选：C．【点评】本题主要考查了诱导公式的应用，属于基础题．15．在一块顶角为120°、腰长为2的等腰三角形钢板废料OAB中裁剪扇形，现有如图所示两种方案，则（）A．方案一中扇形的周长更长B．方案二中扇形的周长更长C．方案一中扇形的面积更大D．方案二中扇形的面积更大【考点】扇形面积公式．【专题】计算题；转化思想；数形结合法；三角函数的求值．【分析】由已知利用弧长公式，扇形面积公式求出值比较大小即可．【解答】解：∵△AOB为顶角为120°、腰长为2的等腰三角形，∴A=B=30°=，AM=AN=1，AD=2，∴方案一中扇形的周长=2=4+，方案二中扇形的周长=1+1+1×=2+，方案一中扇形的面积=2×=，方案二中扇形的周长==，故选：A．【点评】本题主要考查了弧长公式，扇形面积公式的应用，考查了计算能力，属于基础题．16．某种型号的电脑自投放市场以来，经过三次降价，单价由原来的5000元降到2560元，则平均每次降价的百分率是（）A．10% B．15% C．16% D．20%【考点】函数的值．【专题】计算题；函数思想；综合法；函数的性质及应用．【分析】设降价百分率为x%，由题意知5000（1﹣x%）2=2560，由此能够求出这种手机平均每次降价的百分率．【解答】解：设降价百分率为x%，∴5000（1﹣x%）3=2560，解得x=20．故选：D．【点评】本题考查数列的性质和应用，解题时要注意挖掘隐含条件，寻找数量关系，建立方程．17．已知函数f（x）=x|x|，若对任意的x≤1有f（x+m）+f（x）＜0恒成立，则实数m的取值范围是（）A．（﹣∞，﹣1） B．（﹣∞，﹣1] C．（﹣∞，﹣2） D．（﹣∞，﹣2]【考点】函数恒成立问题．【专题】函数思想；转化思想；函数的性质及应用．【分析】根据函数f（x）的解析式判断函数的奇偶性和单调性，利用函数奇偶性和单调性的关系将不等式进行转化，利用参数分离法转化为求函数的最值即可．【解答】解：f（x）=x|x|=，则函数f（x）在定义域为增函数，且f（﹣x）=﹣x|﹣x|=﹣x|x|=﹣f（x），则函数f（x）为奇函数，则若对任意的x≤1有f（x+m）+f（x）＜0恒成立，等价为若对任意的x≤1有f（x+m）＜﹣f（x）=f（﹣x），即x+m＜﹣x恒成立，即m＜﹣2x恒成立，∵x≤1，∴﹣2x≥﹣2，则m＜﹣2，故选：C【点评】本题主要考查不等式恒成立问题，根据条件判断函数的奇偶性和单调性是解决本题的关键．利用参数分离法是解决不等式恒成立问题的常用方法．18．存在函数f（x）满足：对任意x∈R都有（）A．f（|x|）=x B．f（|x|）=x2+2x C．f（|x+1|）=x D．f（|x+1|）=x2+2x【考点】函数的对应法则；函数的概念及其构成要素．【专题】计算题；转化思想；综合法；函数的性质及应用．【分析】在A、B中，分别取x=±1，由函数性质能排除选项A和B；令|x+1|=t，t≥0，则x2+2x=t2﹣1，求出f（x）=x2﹣1，能排除选项C．【解答】解：在A中，取x=1，则f（1）=1，取x=﹣1，则f（1）=﹣1，不成立；在B中，令|x|=t，t≥0，x=±t，取x=1，则f（1）=3，取x=﹣1，则f（1）=﹣1，不成立；在C中，令|x+1|=t，t≥0，则x2+2x=t2﹣1，∴f（t）=t2﹣1，即f（x）=x2﹣1，故C不成立，D成立．故选：D．【点评】本题考查抽象函数的性质，是中档题，解题时要认真审题，注意函数性质的合理运用．二、填空题（本大题共4个小题，每小题4分，共16分）19．计算：（log23）•（log34）= 2 ．【考点】对数的运算性质．【专题】计算题；函数思想；定义法；函数的性质及应用．【分析】根据换底公式计算即可．【解答】解：（log23）•（log34）=•=2，故答案为：2．【点评】本题考查了换底公式，属于基础题．20．函数f（x）=2的单调递增区间为[0，+∞）．【考点】复合函数的单调性．【专题】转化思想；综合法；函数的性质及应用．【分析】由题意可得，本题即求函数t=x2﹣1的增区间，再利用二次函数的性质可得结论．【解答】解：函数f（x）=2的单调递增区间，即函数t=x2﹣1的增区间，再利用二次函数的性质可得函数t=x2﹣1的增区间为[0，+∞），故答案为：[0，+∞）．【点评】本题主要考查指数函数、二次函数的性质，复合函数的单调性，属于中档题．21．对a，b∈R，记max{a，b}=，则函数f（x）=max{|x+1|，x+2}（x∈R）的最小值是．【考点】函数的最值及其几何意义．【专题】计算题；分类讨论；分析法；函数的性质及应用．【分析】讨论当|x+1|≥x+2，|x+1|＜x+2时，求出f（x）的解析式，由单调性可得最小值．【解答】解：当|x+1|≥x+2，即x+1≥x+2或x+1≤﹣x﹣2，解得x≤﹣时，f（x）=|x+1|，递减，则f（x）的最小值为f（﹣）=|﹣+1|=；当|x+1|＜x+2，可得x＞﹣时，f（x）=x+2，递增，即有f（x）＞，综上可得f（x）的最小值为．故答案为：．【点评】本题考查函数的最值的求法，考查绝对值不等式的解法，注意运用分类讨论的思想方法，以及函数的单调性，属于中档题．22．已知函数f（x）=log2（x+2）与g（x）=（x﹣a）2+1，若对任意的x1∈[2，6），都存在x2∈[0，2]，使得f（x1）=g（x2），则实数a的取值范围是[﹣1，2﹣]∪[，3] ．【考点】对数函数的图象与性质．【专题】函数思想；分类法；函数的性质及应用．【分析】分别求出f（x1）和g（x2）的值域，令f（x1）的值域为g（x2）的值域的子集列出不等式解出a．【解答】解：∵x1∈[2，6），∴f（2）≤f（x1）＜f（6），即2≤f（x1）＜3，∴f（x1）的值域为[2，3）．g（x）的图象开口向上，对称轴为x=a，（1）若a≤0，则g（x）在[0，2]上是增函数，∴g（0）≤g（x2）≤g（2），即g（x2）的值域为[a2+1，a2﹣4a+5]，∴，解得﹣1≤a≤0．（2）若a≥2，则g（x）在[0，2]上是减函数，∴g（2）≤g（x2）≤g（1），即g（x2）的值域为[a2﹣4a+5，a2+1]，∴，解得2≤a≤3．（3）若0＜a≤1，则g min（x）=g（a）=1，g max（x）=g（2）=a2﹣4a+5，∴g（x）的值域为[1，a2﹣4a+5]，∴，解得0．（4）若1＜a＜2，则g min（x）=g（a）=1，g max（x）=g（0）=a2+1，∴g（x）的值域为[1，a2+1]，∴，解得a＜2．综上，a的取值范围是[﹣1，0]∪[2，3]∪（0，2﹣）∪（，2）=[﹣1，2﹣]∪[，3]．故答案为[﹣1，2﹣]∪[，3]．【点评】本题考查了二次函数的值域，对数函数的单调性与值域，集合间的关系，分类讨论思想，属于中档题．三、解答题（本大题共3个小题，共30分．解答应写出文字说明、证明过程或演算步骤）23．设全集为实数集R，函数f（x）=lg（2x﹣1）的定义域为A，集合B={x||x|﹣a≤0}（a∈R）（Ⅰ）若a=2，求A∪B和A∩B（Ⅱ）若∁R A∪B=∁R A，求a的取值范围．【考点】交、并、补集的混合运算；并集及其运算；交集及其运算．【专题】计算题；集合思想；综合法；集合．【分析】（Ⅰ）先求出A=（），由a=2便可求出B=[﹣2，2]，然后进行并集、交集的运算即可；（Ⅱ）根据条件便有B⊆C R A，可求出，可讨论B是否为空集：B=∅时会得到a＜0；而B≠∅时得到a≥0，且B={x|﹣a≤x≤a}，这样便可得到，这两种情况下得到的a的范围求并集便可得出a的取值范围．【解答】解：（Ⅰ）A=；a=2时，B=[﹣2，2]；∴A∪B=[﹣2，+∞），；（Ⅱ）∵（C R A）∪B=C R A；∴B⊆C R A；；①当B=∅时，a＜0；②当B≠∅时，B={x|﹣a≤x≤a}（a≥0）；∴，且a≥0；∴；综上得，a的取值范围为．【点评】考查函数定义域的概念及求法，对数的真数大于0，绝对值不等式的解法，交集、并集的运算，以及子集、补集的概念，不要漏了B=∅的情况．24．已知△ABC的三个内角分别为A，B，C，且A≠．（Ⅰ）化简；（Ⅱ）若角A满足sinA+cosA=．（i）试判断△ABC是锐角三角形还是钝角三角形，并说明理由；（ii）求tanA的值．【考点】三角函数中的恒等变换应用；三角函数的化简求值．【专题】函数思想；综合法；三角函数的求值．【分析】（Ⅰ）由三角形内角和以及诱导公式化简可得原式=cosA；（Ⅱ）由sinA+cosA=和sin2A+cos2A=1，联立可解得sinA=，cosA=﹣，可得（i）△ABC 是钝角三角形；（ii） tanA==﹣【解答】解：（Ⅰ）由题意化简可得：==cosA；（Ⅱ）∵sinA+cosA=，又sin2A+cos2A=1，结合sinA应为正数，联立可解得sinA=，cosA=﹣，∴A为钝角，故可得（i）△ABC是钝角三角形；（ii） tanA==﹣【点评】本题考查三角函数恒等变换，涉及三角函数化简求值和同角三角函数基本关系，属基础题．25．已知定理：“实数m，n为常数，若函数h（x）满足h（m+x）+h（m﹣x）=2n，则函数y=h（x）的图象关于点（m，n）成中心对称”．（Ⅰ）已知函数f（x）=的图象关于点（1，b）成中心对称，求实数b的值；（Ⅱ）已知函数g（x）满足g（2+x）+g（﹣x）=4，当x∈[0，2]时，都有g（x）≤3成立，且当x∈[0，1]时，g（x）=2k（x﹣1）+1，求实数k的取值范围．【考点】抽象函数及其应用．【专题】综合题；新定义；分类讨论；分析法；函数的性质及应用；不等式的解法及应用．【分析】（Ⅰ）由对称性可得f（1+x）+f（1﹣x）=2b，化简整理，即可得到b=2；（Ⅱ）由g（2+x）+g（﹣x）=4可得g（x）的图象关于点（1，2）对称，且g（1）=2，对k讨论，当k=0，k＞0，k＜0，结合对称性和单调性，要使g（x）≤3，只需g（x）max≤3，运用单调性求得最大值，解不等式即可得到所求范围．【解答】解：（Ⅰ）函数f（x）=的图象关于点（1，b）成中心对称，可得f（1+x）+f（1﹣x）=2b，即有+=4=2b，解得b=2；（Ⅱ）由g（2+x）+g（﹣x）=4可得g（x）的图象关于点（1，2）对称，且g（1）=2，当k=0时，g（x）=2（0≤x≤1），又g（x）关于（1，2）对称，可得g（x）=2（0≤x≤2），显然g（x）≤3恒成立；当k＞0时，g（x）=2k（x﹣1）+1在[0，1]递增，又g（x）关于点（1，2）对称，可得g（x）在[0，2]递增，g（x）≤3，只需g（x）max=g（2）≤3，又g（2）+g（0）=4，则g（0）≥1即21﹣k≥1，即有0≤k≤1；当k＜0时，g（x）=2k（x﹣1）+1在[0，1]递减，又g（x）关于（1，2）对称，可得g（x）在[0，2]递减，要使g（x）≤3，只需g（x）max=g（0）≤3，即21﹣k≤3，解得1﹣log23≤k＜0．综上可得，1﹣log23≤k≤1．【点评】本题考查函数的对称性和运用，同时考查函数的单调性的运用，以及不等式恒成立问题的解法，考查运算能力，属于中档题．。

2019-2020学年浙江省温州市高一(上)期末数学试卷(a卷)

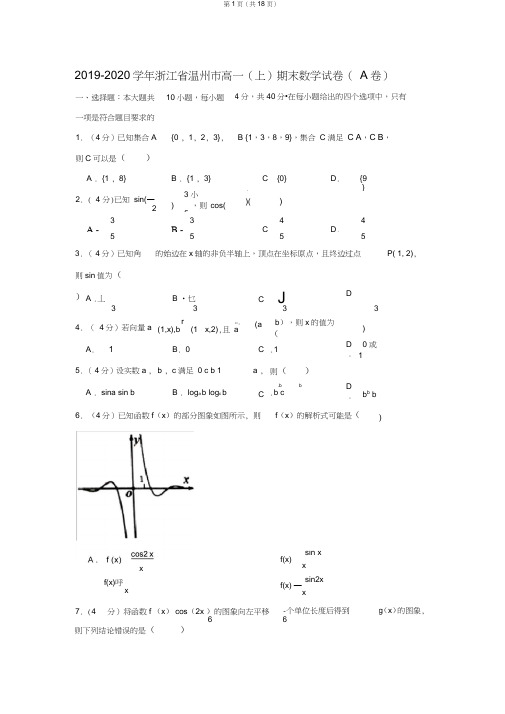
第1页（共18页）则下列结论错误的是（）2019-2020学年浙江省温州市高一（上）期末数学试卷（ A 卷）一、选择题：本大题共 10小题，每小题一项是符合题目要求的1. （4分）已知集合A {0 , 1, 2, 3},则C 可以是（）A . {1 , 8}B . {1 , 3} 2. ( 4 分)已知 sin (― 2 3 小) ，则 cos(5 33A.-B.-553. （ 4分）已知角 4分，共40分•在每小题给出的四个选项中，只有B {1，3，8，9}，集合C 满足 C A ，C B ，C . {0}D .{9})()44CD .55的始边在x 轴的非负半轴上，顶点在坐标原点，且终边过点 P( 1, 2),A .丄B •乜C JD . 3 3 33 4. （ 4分）若向量a r □ r (1,x),b (1 x,2),且 a (a b ），则x 的值为（) A . 1 B . 0 C .1D . 0或15. （ 4分）设实数a , b , c 满足 0 c b 1 a , 则（） A . sina sin b B . log a b log c b C .b b .b c D. b b b 则sin 值为（） f （x ）的解析式可能是（则)（4分）已知函数f （x ）的部分图象如图所示, 6. xf(x)呼xsin x f(x)x sin2xf(x) —x7. (4分）将函数f （x ） cos （2x ）的图象向左平移6-个单位长度后得到6g （x ）的图象,5B . g(x)的图象关于直线 x 对称 12C . g(x -)是奇函数6D . g(x)在(0,㊁)上单调递减F 列函数中一定有两个零点的是(10. (4分)已知平面向量a,b,c ，满足|b| 2,| a b | 1,c a个确定的向量a ,记|c|的最小值为m ，则当a 变化时，m 的最大值为C.-2二、填空题：本大题共 7小题，多空题每题 6分，单空题每题 4分，共36分.11. __________________________________________________________________ (6分)如果一扇形的圆心角为 60，半径等于3cm ，则该扇形的弧长为 _________________________ cm ，面积为 ___ cm 2.12. _________________________________________ (6 分)已知 a log 2 5 , 4b 9，则 2a b ,log s 3 _______________________________________ (用 a , b 表示).13. (6 分)已知 (0,)，且 sin( ) ，则 cos( ) ________________________ , tan _______ .4 10 4 14 . ( 6分)已知定义在R 上的奇函数f(x)满足对任意实数x ,都有 21f(x 1) f(x) 3x 3x 1 成立，则 fC) _________________ , f (3) ________ .215. (4分)某城市的电视发射搭建在市郊的一座小山上.如图所示，小山高 BC 为30米，在地平面上有一点 A ，测得A , C 两点间距离为50米，从点A 观测电视发射塔的视角&( 4分)已知函数f (x)2 x ,x-02x ,x,若对任意的 0 x R ，都有f(2x则实数a 的值为( C .9. (4分)已知函数f (x)x 2 bx c ,R , X ix 2是任意给定的两个不等的实数. 则A . y f(x) f(xjf(x) f(X 2)C. y f(x)f(X 1) f(X 2)f(x)21，若对每(CAD)为45，则这座电视发射塔的高度为_________ 米.rab夹角余弦值的最小值等于等于16. (4分)已知平面向a，b , c，满足山| 2 , |b| 3 , |C| 1，且(a C)詁C)217. (6分)已知函数f(x) |log2 | x || a(a 0)，其所有的零点依次记为石,x2,xX i(i N )，则xgx2 X i ____________________ .三、解答题：本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤18•已知函数f(x) Asin( x ),( A 0, 0,| | -)的部分图象如图所示.(1) 求函数f (x)的解析式，并求f (x)的对称中心;(2) 当x [0 , 4]时，求f(x)的值域._、x 319. 已知a 0，集合A {x| log2 x, 0} , B {x |a 4 a }.(1 )当a 2 时，求A U B ；(2)若(A U B) A，求实数a的取值范围.r 「厂、、/ r r20. 已知向量a (sin x,2sin x),b ( 3cosx,0)，设函数f (x) |a b |.(1 )解不等式f(x)….5 ;(2)是否存在实数t (3,)，使函数y f(x)在(3,t)内单调递增，若存在，求出t的取值范围；若不存在，请说明理由.uuu iur(1)证明：AM 2ODuuur uu求AEgCF 的取值范围. (1) 讨论f (x)的单调性；(2) 设h(x) |f(x)|，若h(x)的最大值为5，求a b 的取值范围.221.ABC 中，D 为BC 的中点,uur uuur uur O 为外心，点M 满足OA OB OCuuurOM . uuu uuu uur(2)若 | BA BC | | AC | 6，设AD 与OM 相交于点muiF 关于点P 对称，且|EF | 2 ,22.已知 0剟a 2 , b, 1 , 函数 f(x) ax 2 x 4ab 1 , x [ 2 , 2].。

(9份试卷汇总)2019-2020学年浙江省温州市数学高一(上)期末达标测试模拟试题

2019-2020学年高一数学上学期期末试卷一、选择题 1．已知向量(1,1)a =r ，(2,)b x =r ，若a b +r r 与42b a -r r平行，则实数x 的值为（）A ．2-B ．0C ．1D ．22．已知三棱锥P －ABC 的四个顶点在球O 的球面上，PA=PB=PC ，△ABC 是边长为2的正三角形，E ，F 分别是PA ，AB 的中点，∠CEF=90°.则球O 的体积为（）A ．86πB ．43πC ．6πD ．3π2 3．如图所示，在正方形ABCD 中，E 为AB 的中点，F 为CE 的中点，则AF =u u u rA.3144AB AD +u u u r u u u rB.1344AB AD +u u u r u u u r C.12AB AD +u u u r u u u r D.3142AB AD +u u u r u u u r 4．已知关于x 的不等式2680kx kx k -++≥对任意x ∈R 恒成立，则k 的取值范围是（）A ．01k ≤≤B ．01k <≤C ．k 0<或1k >D ．0k ≤或1k ³5．定义在上的偶函数满足：对任意的，，，有，且，则不等式的解集为 A ． B ．C ．D ．6．设()f x 为定义在R 上的偶函数，且()f x 在[0,)+∞上为增函数，则(2)f -，(π)f -，(3)f 的大小顺序是（）．A ．(π)(2)(3)f f f -<-<B ．(π)(3)(2)f f f ->>-C ．(π)(3)(2)f f f -<<-D ．(π)(2)(3)f f f ->->7．已知3x >，则函数()43f x x x =+-的最小值为（） A.1B.4C.7D.58．设等差数列{}n a 的前n 项和为S n ，a 2，a 5是方程2x 2－3x －2＝0的两个根，则S 6＝ A ．92B ．5C ．－92D ．－59．函数()af x x x=-（a R ∈）的图象不可能．．．是（） A. B. C. D.10．对于平面、β、γ和直线a 、b 、m 、n ,下列命题中真命题是( )A ．若,,,,a m a n m n αα⊥⊥⊂⊂,则a α⊥B ．若//,a b b α⊂,则//a αC ．若//,,,a b αβαγβγ==I I 则//a bD ．若,,//,//a b a b ββαα⊂⊂,则//βα11．某四棱锥的三视图如图所示，该四棱锥的表面积是A ．32B ．16+162 C ．48 D ．16322+12．如图，1111ABCD A B C D -为正方体，下面结论错误的是（）A ．//BD 平面11CB D B ．1AC BD ⊥ C ．1AC ⊥平面11CB DD ．异面直线AD 与1CB 所成的角为60︒ 二、填空题13．已知两条直线1y x =+, (1)y k x =-将圆221x y +=及其内部划分成三个部分, 则k 的取值范围是_______；若划分成的三个部分中有两部分的面积相等, 则k 的取值有_______种可能. 14．已知幂函数()f x x α=的部分对应值如下表，则不等式'(1)0,{'(3)0.g g <∴>的解集是__________.x 112 f （x ） 12215．设函数()20xf x x ⎧=⎨>⎩，，则满足1()()12f x f x +->的x 的取值范围是____________. 16．已知()0,θπ∈，且2sin()410πθ-=，则tan2θ=________．三、解答题17．已知数列{}n a 满足()2*12323n a a a na n n ++++=∈N L .（1）求数列{}n a 的通项公式；（2）若()*1n n b n na =∈N ，n T 为数列{}1n n b b +的前n 项和，求证：12n T < 18．已知()f x 是定义在R 上且满足()()2f x f x +=的函数．（1）如果0≤x＜2时，有()f x x =，求()3f 的值；（2）如果0≤x≤2时，有()()21f x f x =-，若﹣2≤a≤0，求()f a 的取值范围；（3）如果()()g x x f x =+在[0，2]上的值域为[3，8]，求()g x 在[﹣2，4]的值域．19．某镇在政府“精准扶贫”的政策指引下，充分利用自身资源，大力发展养殖业，以增加收入，政府计划共投入72万元，全部用于甲、乙两个合作社，每个合作社至少要投入15万元，其中甲合作社养鱼，乙合作社养鸡，在对市场进行调研分析发现养鱼的收益、养鸡的收益与投入（单位：万元）满足.设甲合作社的投入为（单位：万元）.两个合作社的总收益为（单位：万元）.（1）当甲合作社的投入为25万元时，求两个合作社的总收益；（2）试问如何安排甲、乙两个合作的投入，才能使总收益最大？20．已知函数()2121x x f x -=+．(1)若()322f a =-，求a 的值．(2)判断函数()f x 的奇偶性，并证明你的结论． (3)求不等式112024x x f f +⎛⎫⎛⎫+->⎪ ⎪⎝⎭⎝⎭的解集． 21．如图，三棱柱111ABC A B C -，1A A ⊥ 底面ABC ，且 ABC ∆为正三角形，D 为AC 中点．（1）求证：直线1//AB 平面1 BC D （2）求证：平面1BC D ⊥平面11 ACC A ；22．成都市海关对同时从A ，B ，C 三个不同地区进口的某种商品进行抽样检测，从各地区进口此种商品的数量（单位：件）如表所示．工作人员用分层抽样的方法从这些商品中共抽取6件样品进行检测．地区ABC数量50150100（2）若在这6件样品中随机抽取2件送往甲机构进行进一步检测，求这2件商品来自相同地区的概率．【参考答案】*** 一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 D D D A A B C A C C BD13．(,1][0,)-∞-+∞U 3 14．[]4,4- 15．1(,)4-+∞ 16．247-三、解答题 17．（1）21n n a n-=．（2）证明略 18．（1）1；（2）[]0,1；（3）[]1,10 19．（1）88.5万元（2）答案略.20．(1)12a =；(2)奇函数；(3)() 1,-+∞. 21．（1）略；（2）略 22．（1）三个地区的商品被选取的件数分别为1,3,2；（2）415．2019-2020学年高一数学上学期期末试卷一、选择题1．《九章算术》中有如下问题：今有蒲生一日，长三尺，莞生一日，长1尺．蒲生日自半，莞生日自倍．问几何日而长等？意思是：今有蒲第一天长高3尺，莞第一天长高1尺，以后蒲每天长高前一天的一半，莞每天长高前一天的2倍．若蒲、莞长度相等，则所需时间为（）（结果精确到0.1．参考数据：lg2＝0.3010，lg3＝0.4771．） A.2.6天 B.2.2天C.2.4天D.2.8天2．若实数满足不等式组，则的最大值为（）A.B. C. D. 3．f (x)＝－x 2＋4x ＋a ，x ∈[0,1]，若f (x)有最小值－2，则f (x)的最大值( ) A.－1B.0C.1D.24．在ABC ∆中，角,,A B C 的对边分别为,,a b c ，且面积为S .若cos cos sin b C c B a A +=，()22214S b a c =+-，则角B 等于（） A ．2π B ．3π C ．4π D ．6π 5．函数3cos 2cos 2sin cos cos510y x x x ππ=-的递增区间是（） A ．2[,]105k k ππππ-+（k Z ∈） B ．2[,]510k k ππππ-+ （k Z ∈） C ．3[,]510k k ππππ-- （k Z ∈） D ．37[,]2020k k ππππ-+ （k Z ∈） 6．如图，边长为2的正方形有一内切圆.向正方形内随机投入1000粒芝麻，假定这些芝麻全部落入该正方形中，发现有795粒芝麻落入圆内，则用随机模拟的方法得到圆周率π的近似值为( )A ．3.1B ．3.2C ．3.3D ．3.47．为了得到函数21lnx y e+=的图象，只需把函数ln y x =的图象上所有的点( ) A ．向左平移1个单位长度再向下平移2e 个单位长度 B ．向左平移1个单位长度再向下平移2个单位长度 C ．向右平移1个单位长度再向下平移2个单位长度 D ．向右平移1个单位长度再向下平移2e 个单位长度8．直线()2y k x =+被圆224x y +=截得的弦长为23 ）A ．6π B ．3π C ．6π或56π D ．3π或23π 9．已知函数()f x 在R 上是单调函数，且满足对任意x ∈R ，都有()34xf f x ⎡⎤-=⎣⎦，则()2f 的值是( )A.4B.8C.10D.1210．已知实数,x y 满足不等式组2324y x x y x y ≤⎧⎪+≤⎨⎪-≤⎩，则2z x y =-的最大值为（）A.5B.3C.1D.-411．函数sin()(0,)y A x A ωϕϕπ=+><在一个周期内的图像如图所示，则此函数的解析式为（）A.2sin(2)3y x π=+ B.2sin()23x y π=- C.2sin(2)3y x π=-D.22sin(2)3y x π=+12．设是两条不同直线，是两个不同的平面，下列命题正确的是（）A ．B ．，则C ．，则D ．，则二、填空题13．若函数()sin 2cos2f x x a x =+，x ∈R 的图像关于6x π=-对称，则a =________．14．若不等式20x mx m ++≥在[1,2]x ∈上恒成立，则实数m 的最小值为________15．某单位为了了解用电量y 度与气温x C o 之间的关系，随机统计了某4天的用电量与当天气温. 气温（℃） 14 12 8 6 用电量（度）22263438由表中数据得回归直线方程y b x a =+中2b ∧=-，据此预测当气温为5℃时，用电量的度数约为____.16．已知实数,x y 满足102801x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩，则3y x +的最大值为_______。

浙江省温州市2019-2020学年高一上学期期末数学试题(A)

2020年1月温州市高一期末教学质量统—检测数学试题卷（A ）本试卷分选择题和非选择题两部分，共4页，满分150分. 考试时间120分钟. 考生注意：1. 考生答题前，务必将自己的姓名、准考证号用黑色字迹的签字填写在答题卷上.2. 选择题的答案须用2B 铅笔将答题卷上对应题目的答案涂黑，如要改动，须将原填涂处用橡皮擦净.3. 非选择题的答案须用黑色字迹的签字笔或钢笔写在答题卷上相应区域内，答案写在本试题卷上无效.选择题部分一、选择题：本大题共10小题，每小题4分，共40分. 在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}{}0,1,2,3,1,3,8,9A B ==，集合C 满足,C A C B ⊆⊆，则C 可以是（）A. {}1,8B. {}1,3C. {}0D. {}9 2.已知sin -2πα⎛⎫⎪⎝⎭＝35 ，则cos (π＝α)的值为( ) A. 45 B. ＝45 C. 35 D. ＝353.已知角α始边在x轴的非负半轴上，顶点在坐标原点，且终边过点(P -，则sin α值为（）A. 3- B. 3C. 3D. 3-4.若向量(1,),(1,2)a x b x ==-r r ，且()a a b ⊥-r r r ，则x 的值为（）A. 1-B. 0C. 1D. 0或15.设实数,,a b c 满足01c b a <<<<，则（）A. sin sin a b >B. log log a c b b >C. b b b c >D. b c b b >的6.已知函数()f x 的部分图象如图所示，则()f x 的解析式可能是（）A. cos 2()x f x x= B. sin ()x f x x =C. 2cos ()x f x x =D. 2sin 2()x f x x = 7.将函数()cos 26f x x π⎛⎫=- ⎪⎝⎭的图象向左平移6π个单位长度后得到()y g x =的图象，则下列结论错误的是（）A. π-是()g x 的一个周期B. ()g x 的图象关于直线512x π=对称 C. 6g x π⎛⎫+⎪⎝⎭是奇函数 D. ()g x 在0,2π⎛⎫ ⎪⎝⎭上单调递减 8.已知函数22,0()22,0x x x x x f x x --⎧-≥=⎨-<⎩，若对任意的x ∈R ，都有(21)()f x f x a +≥-成立，则实数a 的值为（）A 12-B. 12C. 1-D. 1 9.已知函数2()f x x bx c =++，,b c R ∈，12,x x 是任意给定两个不等的实数. 则下列函数中一定有两个零点的是（）A. ()1()y f x f x =-B. ()2()y f x f x =+C. ()()12()2f x f x y f x +=-D. 12()2x x y f x f +⎛⎫=- ⎪⎝⎭10.已知平面向量,,a b c r r r ，满足||2,||1,b a b c a b λμ=+==+r r r r r r 且21λμ+=，若对每一个确定的向量a r，.记||c r 的最小值为m ，则当a r 变化时，m 的最大值为（） A. 14 B. 13 C. 12 D. 1非选择题部分二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分.11.如果一扇形的圆心角为60︒，半径等于3cm ，则该扇形的弧长为_________cm ，面积为_________2cm . 12.已知2log 5a =，49b =，则2a b +=_________，5log 3=_________ （用,a b 表示）.13.已知(0,)θπ∈，且sin 410πθ⎛⎫+= ⎪⎝⎭，则cos 4πθ⎛⎫-= ⎪⎝⎭_________，tan θ=_________ 14.已知定义在R 上奇函数()f x 满足对任意实数x ，都有2(1)()331f x f x x x +=+++成立，则12f ⎛⎫= ⎪⎝⎭_________，(3)f =_________.15.某城市的电视发射搭建在市郊的一座小山上. 如图所示，小山高BC 为30米，在地平面上有一点A ，测得,A C 两点间距离为50米，从点A 观测电视发射塔的视角（CAD ∠）为45︒，则这座电视发射塔的高度为_________米.16.已知平面向,,a b c r r r ，满足2,1a b c ===r r r ，且()()5a c b c -⋅-=r r r r ，a b -r r 与a b +r r 夹角余弦值的最小值等于_________.17.已知函数22()log ||(0)f x x a a x=-->，其所有的零点依次记为()*12,,,i x x x i N ⋯∈，则12i x x x ⋅=L _________.三、解答题：本大题共5小题，共74分. 解答应写出文字说明、证明过程或演算步骤..的18.已知函数()sin(),0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图像如图所示.（1）求函数()f x 的解析式，并求()f x 的对称中心；（2）当[0,4]x ∈时，求()f x 的值域.19.已知0a >，集合{}{}32|log 0,|4x A x x B x a a =≤=<<.（1）当2a =时，求A B U ；（2）若()A B A ⊆U ，求实数a 的取值范围.20.已知向量(sin ,2sin ),,0)a x x b x ==r r ，设函数()||f x a b =+r r .（1）解不等式()f x ≥（2）是否存在实数(3,)t ∈+∞，使函数()y f x =在(3,)t 内单调递增，若存在，求出t 的取值范围；若不存在，请说明理由.21.ABC ∆中，D 为BC 的中点，O 为外心，点M 满足OA OB OC OM ++=u u u r u u u r u u u r u u u u r.（1）证明：2AM OD =u u u u r u u u r ；（2）若||||6BA BC AC +==u u u r u u u r u u u r ，设AD 与OM 相交于点P ，,E F 关于点P 对称，且||2EF =u u u r ，求AE CF⋅u u u r u u u r 的取值范围.22.已知02,1a b ≤≤≤，函数2()41,[2,2]f x ax x a b x =--+-+∈-. （1）讨论()f x 的单调性；（2）设()|()|h x f x =，若()h x 的最大值为52，求+a b 的取值范围.。

温州市高一上学期数学期末考试模拟题(含答案) (3)

温州市高一上学期数学期末考试模拟题3一、选择题（本大题共12小题，共60.0分）1.满足{1}⊆A⊆{1，2，3}的集合A的个数是（）A. 2B. 3C. 4D. 82.已知幂函数f（x）=xα的图象过点（4，2），若f（m）=3，则实数m的值为（）A. B. C. ±9 D. 93.的值是（）A. B. C. D.4.已知直线l1：x+2y-1=0，l2：2x+ny+5=0，l3：mx+3y+1=0，若l1∥l2且l1⊥l3，则m+n的值为（）A. -10B. 10C. -2D. 25.已知，则=（）A. B. 1 C. D. 26.如图，正方体ABCD-A1B1C1D1中，异面直线AD1与A1C所成的角的大小是（）A. 30°B. 60°C. 90°D. 120°7.已知tanθ=2，则sin2θ+sinθcosθ-2cos2θ=（）A. -B.C. -D.8.设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是（）A. 若α⊥β，m⊂α，n⊂β，则m⊥nB. 若α∥β，m⊂α，n⊂β，则m∥nC. 若m⊥n，m⊂α，n⊂β，则α⊥βD. 若m⊥α，m∥n，n∥β，则α⊥β9.已知函数，则=（）A. 1B. lg2C. 2D. 010.若存在正数x使成立，则a的取值范围是（）A. （-∞，+∞）B. （-2，+∞）C. （0，+∞）D. （-1，+∞）11.如图，有一个水平放置的透明无盖的正方体容器，容器高4cm，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为3cm，如果不计容器的厚度，则球的体积为（）A.B.C.D.12.已知f（x）是定义在R上的单调函数，满足f[f（x）-e x]=1，且f（a）＜f（b）＜e，若，则a与b的关系是（）A. a=b3B. b=a3C. b=a4D. a=b4二、填空题（本大题共4小题，共20.0分）13.函数y=ln（1-x）的定义域为______．14.一个几何体的三视图如图所示（单位：m）则该几何体的体积为______．15.在平面直角坐标系xOy中，已知圆x2+y2=4有且仅有三个点到直线l：2x-5y+c=0的距离为1，则实数c的取值集合是______．16.已知函数，若a、b、c互不相等，且f（a）=f（b）=f（c），则abc的取值范围是______．三、解答题（本大题共6小题，共70.0分）17.已知点，，动点满足．（1）若点为曲线，求此曲线的方程；（2）已知直线在两坐标轴上的截距相等，且与（1）中的曲线只有一个公共点，求直线的方程．18.如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且PA=AB，点E是PD的中点．（Ⅰ）求证：AC⊥PB；（Ⅱ）求证：PB∥平面AEC．19.已知某公司生产某款手机的年固定成本为400万元，每生产1万部还需另投入160万元．设公司一年内共生产该款手机x（x≥40）万部且并全部销售完，每万部的收入为R（x）万元，且．（1）写出年利润W（万元）关于年产量x（万部的函数关系式；（2）当年产量为多少万部时，公司在该款手机的生产中所获得的利润最大？并求出最大利润．20.如图，正三棱柱ABC-A1B1C1的底面边长为3，侧棱AA1=3，D是CB延长线上一点，且BD=BC．（1）求二面角B1-AD-B的正切值；（2）求三棱锥C1-ABB1的体积．21.已知圆C过点P（2，2），且与圆M：（x+6）2+（y-6）2=r2（r＞0）关于直线x-y+6=0对称．（1）求圆C的方程；（2）过点P作两条相异直线分别与圆C相交于点A和点B，且直线PA和直线PB 的倾斜角互补，O为坐标原点，试判断直线OP和AB是否平行？请说明理由．22.已知f（x）=|x2-4|+x2+kx．（1）若k=2，求方程f（x）=0的解；（2）若关于x的方程f（x）=0在区间（0，4）上有两个不相等的实根x1、x2：①求实数k的取值范围；②证明：．答案和解析1.【答案】C【解析】【分析】本题考查子集的定义，元素与集合的关系，列举法的定义．属于基础题.根据条件{1}⊆A⊆{1，2，3}即可看出集合A必须含有元素1，可能含有元素2，3，由此即可求解．【解答】解：因为{1}⊆A⊆{1，2，3}，所以集合A必须含有元素1，可能含有元素2，3，故集合A可能为：{1}，{1，2}，{1，3}，{1，2，3}，共4个．故选：C．2.【答案】D【解析】解：∵幂函数f（x）=xα的图象过点（4，2），∴4a=2，解得a=，∴f（x）=，∵f（m）==3，∴m=9．故选：D．由函数f（x）=xα的图象过点（4，2），先求出幂函数f（x），再由f（m）=3，能求出m的值．本题考查幂函数的解析式的求法及应用，解题时要认真审题，注意待定系数法的灵活运用，是基础题．3.【答案】A【解析】解：原式=sin（π+）•cos（π-）•tan（-π-）=-sin•（-cos）•（-tan）=-×（-）×（-）=-．故选：A．原式三个因式中的角度变形后，利用诱导公式化简，计算即可得到结果．此题考查了诱导公式的作用，熟练掌握诱导公式是解本题的关键．4.【答案】C【解析】解：∵l1∥l2且l1⊥l3，∴n-4=0，m+6=0，解得n=4，m=-6．则m+n=4-6=-2．故选：C．由l1∥l2且l1⊥l3，可得n-4=0，m+6=0，解得n，m即可得出．本题考查了直线位置关系与斜率之间的关系，考查了推理能力与计算能力，属于基础题．5.【答案】D【解析】解：∵∴a lg2=b lg5=∴，∴=2lg2+2lg5=2lg10=2故选：D．先条件两边取常用对数，再利用对数的运算性质，即可求得结论．本题考查对数的运算，解题的关键是条件两边取常用对数，属于基础题．6.【答案】C【解析】【分析】本题考查异面直线所成的角的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．在正方体ABCD-A1B1C1D1中，推出AD1⊥平面A1DC，由此能求出结果．【解答】解：如图，在正方体ABCD-A1B1C1D1中，连结A1D，A1D⊥DC，A1D⊥AD1，∴AD1⊥平面A1DC，∴异面直线AD1与A1C所成的角的大小是90°．故选C．7.【答案】D【解析】【分析】本题主要考查了三角函数的恒等变换应用．本题利用了sin2θ+cos2θ=1巧妙的完成弦切互化．利用sin2θ+cos2θ=1，令原式除以sin2θ+cos2θ，从而把原式转化成关于tanθ的式子，把tanθ=2代入即可．【解答】解：sin2θ+sinθcosθ-2cos2θ====．故选：D．8.【答案】D【解析】解：选项A，若α⊥β，m⊂α，n⊂β，则可能m⊥n，m∥n，或m，n异面，故A错误；选项B，若α∥β，m⊂α，n⊂β，则m∥n，或m，n异面，故B错误；选项C，若m⊥n，m⊂α，n⊂β，则α与β可能相交，也可能平行，故C错误；选项D，若m⊥α，m∥n，则n⊥α，再由n∥β可得α⊥β，故D正确．故选：D．由α⊥β，m⊂α，n⊂β，可推得m⊥n，m∥n，或m，n异面；由α∥β，m⊂α，n⊂β，可得m∥n，或m，n异面；由m⊥n，m⊂α，n⊂β，可得α与β可能相交或平行；由m⊥α，m∥n，则n⊥α，再由n∥β可得α⊥β．本题考查命题真假的判断与应用，涉及空间中直线与平面的位置关系，属基础题．9.【答案】C【解析】解：∵函数，∴=ln（-lg2）+ln（）+2=ln（-lg2）+ln（+lg2）+2=ln1+2=2．故选：C．推导出=ln（-lg2）+ln（+lg2）+2=ln1+2，由此能求出结果．本题考查函数值的求法，考查函数性质等基础知识，考查运算求解能力，考查化归与转化思想、函数与方程思想，是基础题．10.【答案】D【解析】解：根据题意，⇒x-（）x＜a，设f（x）=x-（）x，其导数为f′（x）=1-（）x ln（）=1+（）x ln2＞0，则函数f（x）在R上为增函数，且f（0）=0-（）0=-1，则在（0，+∞）上，f（x）＞f（0）=-1恒成立；若存在正数x使成立，即x-（）x＜a有正实数解，必有a＞-1；即a的取值范围为（-1，+∞）；故选：D．根据题意，分析可得⇒x-（）x＜a，设f（x）=x-（）x，求出其导数，分析可得函数f（x）在R上为增函数以及f（0）的值，进而可得在（0，+∞）上，f（x）＞f （0）=-1恒成立；据此可得若存在正数x使成立，即x-（）x＜a有正实数解，分析可得a的取值范围，即可得答案．本题考查函数的单调性以及函数最值问题，涉及不等式有解问题，属于综合题．11.【答案】A【解析】解：设球的半径为R，设正方体上底面截球所得截面圆恰好为上底面正方形的内切圆，该圆的半径为r=2cm，且该截面圆圆心到水面的距离为1cm，球心到截面圆圆心的距离为（R-1）cm，由勾股定理可得R2=（R-1）2+22，解得，因此，球的体积为．故选：A．设球的半径为R，根据已知条件得出正方体上底面截球所得截面圆的半径为2cm，球心到截面圆圆心的距离为R-1，然后利用球体半径，截面圆半径和球心到截面圆圆心的距离形成勾股定理求出R的值，然后再利用球体体积公式可得出答案．本题考查球体体积的计算，解决本题的关键在于求出球体的半径，考查计算能力，属于中等题．12.【答案】A【解析】解：根据题意，f（x）是定义在R上的单调函数，满足f[f（x）-e x]=1，则f（x）-e x为常数，设f（x）-e x=t，则f（x）=e x+t，又由f[f（x）-e x]=1，即f（t）=1，则有e t+t=1，解可得t=0，则f（x）=e x，若f（a）＜f（b）＜e，即e a＜e b＜e1=e，则a＜b＜1，若，必有0＜a＜b，则有+=，又由0＜a＜b＜1，则＜1，解可得=，即lg a=3lg b，变形可得：a=b3，故选：A．根据题意，由函数单调性的性质可得f（x）-e x为常数，设f（x）-e x=t，则f（x）=e x+t，又由f[f（x）-e x]=1，即f（t）=1，则有e t+t=1，分析可得t的值，即可得函数的解析式，据此分析可得e a＜e b＜e1=e，即a＜b＜1，又由，则有+=，结合a、b的关系计算可得=，即lg a=3lg b，结合对数的运算性质分析可得答案．本题考查函数的单调性的应用以及对数的运算性质，涉及函数解析式的计算，属于基础题．13.【答案】[0，1）【解析】解：要使原函数有意义，则解得：0≤x＜1所以原函数的定义域[0，1）．故答案为[0，1）．根据偶次根式下大于等于0，对数函数的真数大于0建立不等式关系，然后解之即可求出函数的定义域．本题主要考查了对数函数的定义域及其求法，以及偶次根式的定义域，属于基础题．14.【答案】6+π【解析】解：由三视图还原原几何体如图，该几何体为组合体，下面为长方体，上面为圆锥，且长方体的长、宽、高分别为3、2、1，圆锥的底面半径为1，高为3，则该几何体的体积V=．故答案为：6+π．由三视图还原原几何体，可知原几何体是组合体，下面为长方体，上面为圆锥，且长方体的长、宽、高分别为3、2、1，圆锥的底面半径为1，高为3，代入体积公式求解．本题考查由三视图求面积和体积，关键是由三视图还原原几何体，是中档题．15.【答案】{}【解析】解：如图，由圆的方程x2+y2=4，可得圆心坐标为（0，0），圆半径r=2，由题意可知，原点到直线2x-5y+c=0的距离为1．由点到直线的距离公式可得：，∴c=±．故答案为：{±}．由题意画出图形，把圆x2+y2=5上有且仅有三个点到直线12x-5y+c=0的距离为1转化为原点到直线12x-5y+c=0的距离为1，再由点到直线的距离公式得答案．本题考查直线与圆的位置关系，考查点到直线距离公式的应用，是基础的计算题．16.【答案】（8，10）【解析】解：函数函数，图象如图所示：若a，b，c互不相等，且f（a）=f（b）=f（c），令a＜b＜c，则a•b=1，8＜c＜10，故8＜abc＜10，故答案为：（8，10）．画出函数的图象，根据a，b，c互不相等，且f（a）=f（b）=f（c），我们令a＜b＜c，我们易根据对数的运算性质，及c的取值范围得到abc的取值范围本题考查的知识点是对数函数图象与性质的综合应用，其中画出函数图象，利用图象的直观性，数形结合进行解答是解决此类问题的关键．17.【答案】解：（1）设P（x，y），∵点A（-4，0），B（2，0），动点P满足|PA|=2|PB|．∴=2，整理得：x2+y2-8x=0．∴曲线C方程为x2+y2-8x=0．（2）设直线l的横截距为a，则直线l的纵截距为a，当a=0时，直线l过（0，0），设直线方程为y=kx．把y=kx代入曲线C的方程x2+y2-8x=0，得：（k2+1）x2-8x=0，∵△=64-4（k2+1）×0=64，∴直线l与曲线C有两个公共点，与已知矛盾；当a≠0时，直线方程为x+y=a，把x+y=a代入曲线C的方程x2+y2-8x=0，得：2x2-（2a+8）x+a2=0，∵直线l与曲线C只有一个公共点，∴△=[-（2a+8）]2-8a2=0，解得a=4，∴直线l的方程为x+y-4+4=0或x+y-4-4=0．【解析】（1）设P（x，y），由点A（-4，0），B（2，0），动点P满足|PA|=2|PB|，列方程式求出曲线C的方程．（2）设直线l的横截距为a，则直线l的纵截距为a，当a=0时，直线l与曲线C有两个公共点，已知矛盾；当a≠0时，直线方程为x+y=a，把x+y=a代入曲线C的方程x2+y2-8x=0，得2x2-（2a+8）x+a2=0，由直线l与曲线C只有一个公共点，能求出直线l 的方程．本题考查点的轨迹方程的求法，考查直线方程的求法，考查圆、直线方程、根的判别式等基础知识，考查运算求解能力，考查化归与转化思想，是中档题．18.【答案】（Ⅰ）证明：∵在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，∴AC⊥AB，AC⊥PA，又AB∩PA=A，∴AC⊥平面PAB，∵PB⊂平面PAB，∴AC⊥PB．（Ⅱ）证明：连接BD，与AC相交于O，连接EO，∵ABCD是平行四边形，∴O是BD的中点，又E是PD的中点，∴EO∥PB，又PB不包含于平面AEC，EO⊂平面AEC，∴PB∥平面AEC．【解析】（Ⅰ）由已知得AC⊥AB，AC⊥PA，从而AC⊥平面PAB，由此能证明AC⊥PB．（Ⅱ）连接BD，与AC相交于O，连接EO，由已知得EO∥PB，由此能证明PB∥平面AEC．本题考查异面直线垂直的证明，考查直线与平面平行的证明，是中档题，解题时要注意空间思维能力的培养．19.【答案】解：（1）W=xR（x）-（160x+400）=x（-）-（160x+400）=74000--160x-400=73600--160x，（2）由（1）可得W=73600--160x≤73600-2=73600-16000=57600，当且仅当当且仅当=160，即x=50时取等号，所以当x=50时，y取得最大值57600万元．【解析】（1）当x≥100时，W=xR（x）-（400+160x），化简即可求出；（2）利用基本不等式即可求出．本题考查函数的解析式的求法，考查年利润的最大值的求法．属于中档题．20.【答案】解：（1）取BC中点O，B1C1中点E，连结OE，OA，∵正三棱柱ABC-A1B1C1的底面边长为3，侧棱AA1=3，D是CB延长线上一点，且BD=BC．∴以O为原点，OD为x轴，OE为y轴，OA为z轴，建立空间直角坐标系，B1（，3，0），A（0，0，），D（，0，0），B（，0，0），=（，0，-），=（，3，-），平面ABD的法向量=（0，1，0），设平面ADB1的法向量=（x，y，z），则，取z=，得=（1，1，），设二面角B1-AD-B的平面角为θ，则cosθ==，sinθ==，tanθ==2，∴二面角B1-AD-B的正切值为2．（2）三棱锥C1-ABB1的体积：====．【解析】（1）取BC中点O，B1C1中点E，连结OE，OA，以O为原点，OD为x轴，OE为y轴，OA为z轴，建立空间直角坐标系，利用向量法能求出二面角B1-AD-B的正切值．（2）三棱锥C1-ABB1的体积=，由此能求出结果．本题考查二面角的正切值的求法，考查三棱锥的体积的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，考查数形结合思想，是中档题．21.【答案】（1）解：由题意可得点C和点M（-6，6）关于直线x-y+6=0对称，且圆C和圆M的半径相等，都等于r，设C（m，n），由且，解得：m=0，n=0，故原C的方程为x2+y2=r2，再把点P（2，2）代入圆C的方程，求得r=，故圆的方程为：x2+y2=8；（2）证明：过点P作两条相异直线分别与圆C相交于A，B，且直线PA和直线PB的倾斜角互补，O为坐标原点，则得直线OP和AB平行，理由如下：由题意知，直线PA和直线PB的斜率存在，且互为相反数，故可设PA：y-2=k（x-2），PB：y-2=-k（x-2），由，得（1+k2）x2+4k（1-k）x+4（1-k）2-8=0，∵P的横坐标x=2一定是该方程的解，∴，同理，x B=，由于AB的斜率k AB====1=k OP（OP的斜率），∴直线AB和OP一定平行．【解析】本题考查的知识点是直线和圆的方程的应用，关于直线对称的圆的方程，其中根据已知条件求出圆C的方程是解答本题的关键，考查运算能力，属于中档题．（1）由已知中圆C过点P（2，2），且圆M：（x+6）2+（y-6）2=r2（r＞0）关于直线x-y+6=0对称，可以求出圆心坐标，即可求出圆C的方程；（2）由已知可得直线PA和直线PB的斜率存在，且互为相反数，设PA：y-2=k（x-2），PB：y-2=-k（x-2），求出A，B坐标后，代入斜率公式，判断直线OP和AB斜率是否相等，即可得到答案．22.【答案】解：（1）当k=2时，f（x）=|x2-4|+x2+2x，当|x|≥2时，f（x）=2x2+2x-4，由f（x）=2x2+2x-4=0，得x2+x-2=0，得x=1舍或x=-2；当|x|＜2时，f（x）=2x+4，由2x+4=0得x=-2（舍）；故当k=2时，方程f（x）=0的解是x=-2．（2）不妨设0＜x1＜x2＜4，∵f（x）=|x2-4|+x2+kx=，若x1、x2∈[2，4），与x1x2=-2矛盾，若x1、x2∈（0，2），与y=kx+4是单调函数矛盾则0＜x1＜2≤x2＜4；则kx1+4=0①，2x22+kx2-4=0 ②，由①，得：k=-＜-2，由②，得：k==-2x2+（-7，-2]；∴k的取值范围是（-7，-2）；联立①、②消去k得：2x22-•x2-4=0，即2x1x22-4x2-4x1=0，即x1x22=2x2+2x1，则+=，∵2≤x2＜4．∴＜2，即+＜2．【解析】（1）当k=2时，根据绝对值的应用，直接进行求解即可．（2）讨论两个根x1、x2的范围，结合一元二次方程根与系数之间的关系进行转化求解．本题主要考查函数与方程的应用，根据条件判断根的范围，以及利用一元二次方程与一次方程的性质进行转化是解决本题的关键．综合性较强，有一定的难度．。

浙江省温州市高一上学期数学期末测试卷

温州市高一数学第一学期期末试卷

浙江省温州市2022-2023学年高一上学期期末考试 数学(A卷)含答案

浙江省温州市高一数学上学期期末试卷(含解析)

浙江省温州市高一数学上学期期末试卷(含解析)

2019-2020学年浙江省温州市高一(上)期末数学试卷(a卷)

(9份试卷汇总)2019-2020学年浙江省温州市数学高一(上)期末达标测试模拟试题

浙江省温州市2019-2020学年高一上学期期末数学试题(A)

温州市高一上学期数学期末考试模拟题(含答案) (3)

浙江省温州市2022-2023学年高一上学期期末考试数学(A卷)含答案