安徽大学期末试卷09-10A(二)试题+答案.doc
安徽大学 2009--2010 高等数学 A(二)试题与答案

x 2+ y 2AA ⎩S S⎫ 安徽大学 2009--2010 高等数学 A(二)试题与答案一、填空题(2×5=10 分)1. 点(2,1,1) 到平面 x + y - z + 1 = 0⎛ 2. 极限 lim x 2 xy = 0. x →+∞x 2 + y 2 ⎪y →+∞⎝ ⎭ πsin x23. 交换积分次序⎰dx ⎰0 f (x , y )dy⎧ 2, - 1 < x < 04. 设 f (x ) 是周期为 2 的函数, 它在区间(-1,1] 上的定义为f (x ) = ⎨x 3 ,则 0 < x < 1f (x ) 的 Fourier 级数在x=1 5. 函数u=xyz 在点(1,1,1) 处沿方向(2,2,1) 的方向导数为二、选择题(2×5=10 分)6. 二元函数 f (x , y ) = 在点(0,0) 处 ( )A. 连续, 但偏导数不存在;B. 不连续; 且偏导数不存在;C. 不连续; 但偏导数存在;D. 连续, 且偏导数存在.7. 设第二类曲面积分 I 1 =⎰⎰ xyzdzdx , I 2 = ⎰⎰ xy 2 zdzdx ,其中 S 为 x 2 + y 2 + z 2= 1 的上半部分, 方向取上侧, 若S 1 为 S 在第一卦限部分, 且与 S 方向一致, 则( )A. I 1 = I 2 = 0 ;B. I 1 = 0, I 2 = 2⎰⎰Sxy 2 zdzdx ;C. I 1 = 2⎰⎰Sxyzdzdx , I 2 = 2⎰⎰S xy 2zdzdx D. I 1 = 2⎰⎰S xyzdzdx , I 2 = 08. 设Ω 为 R 3 中开区域,且Ω 内任意一条闭曲线总可以张成一片完全属于Ω 的曲面,函数 P,Q,R 在Ω 内连续可导,若曲线积分 ⎰LPdx + Qdy + Rdz 只依赖于曲线 L 的端点,而与积分路径无关,则下述命题不正确的是( D )A . 对Ω 内任意光滑闭曲线 C ,曲线积分 ⎰CPdx + Qdy + Rdz = 0 ;B . 存在Ω 上某个三元函数 u(x,y,z), 使得 du = Pdx + Qdy + Rdz ;∂P ∂Q ∂R ∂P ∂Q ∂RC . 等式 ∂y = ∂x , ∂x = ∂z , ∂z = ∂y在开区域Ω 内恒成立;1111A A yy 0 00 0 yy 0 0 0 0 yy 0 0 0 0 yy 0 0 0 0 解: 设 F (x , y , z ) = x 2 + y 2- z 则曲面 S 在点(1,1,2) 处的法向量为:( F x , F y , F z )(1,1,2) = (2x ,2 y ,-1)( 2,2,1) = (2,2,-1) 由题设可知平面∏通过法线L, 故:∂P ∂Q ∂RD . 等 式 ∂x + ∂y + ∂z= 0 在开区域Ω 内恒成立.9. 设函数 f (x , y ) 在开区域 D 内有二阶连续偏导数, 且 f x (x 0 , y 0 ) = f y (x 0 , y 0 ) =0. 则下列为 f (x , y ) 在点(x 0 , y 0 ) 处取极小值的充分条件的是( )A. f xx (x 0 , y 0 ) >0,B. f xx (x 0 , y 0 ) >0,C. f xx (x 0 , y 0 ) <0,D. f xx (x 0 , y 0 ) <0, f xx (x 0 , y 0 ) f xx (x 0 , y 0 ) f xx (x 0 , y 0 ) f xx (x 0 , y 0 ) f (x , y ) - f 2xy(x , y ) >0;f (x , y ) - f 2 xy (x , y ) <0; f (x , y ) - f 2 xy (x , y ) >0;f (x , y ) - f 2 xy (x , y ) <0. 10. 设函数u = f (x , y , z ) 具有二阶连续偏导数, 则div grad f = ( )A .f xx + f yy + f zz ; B. f x + f y + f z ; C. ( f x , f y , f z );D. ( f xx , f yy , f zz ).三、计算题(10×3+12×2=54 分)11. 设平面∏ : x + ay - z + b = 0 通过曲面 z = x 2 + y 2在点(1,1,2)处的法线 L,求 a , b 的值.12. 计算第二类曲线积分⎰Lydx - xdyx 2 + y 2, 其中 L 为正方形边界 x + y = 1 ,取顺时针方向.⎰⎰ 222n =013. 计算第一类曲面积分zdS ,其中∑为圆柱面 x 2 + y 2 = R 2 (R > 0) 介于平∑x + y + z面z = 0 与 z= h (h>0) 之间的部分.∞(-1)n14. 将函数 f (x ) = arctan x 展开成 x 的幂级数, 并求级数∑ 2n + 1 的和.15. 设函数 f (u ) 具有二阶连续导数, 且 z = f (e xsin y ) ,解法(一): 设x=Rcosu, y=Rsinu, z=v, 则∑对应于 D: 0 ≤ u ≤ 2π ,0 ≤ v ≤ h .v v v u u u 2x = -R sin u , y = R cos u , z = 0, x = 0, y = 0, z = 1故E = R ,F = 0,G = 1,∂ 2 z ∂ 2 z (1) 求 ∂x 2 , ∂y2 ;(2) 若函数 z = f (e xsin y ) 满足方程 ∂ 2 z ∂x 2 + ∂ 2 z ∂y 2= e 2 xz, 求函数 f (u )四、应用题(10×1+6×1=16 分)16. 将一根长为l 的铁丝分割成两段, 一段围成一个圆, 另一段围成一个长方形. 求使得圆面积与长方形面积之和最大的分割方法.17. 已知一条非均匀金属线 L 放置于平面 Oxy 上, 刚好为抛物线 y = x 2对应于0 ≤ x ≤ 1 的那一段, 且它在点(x,y) 处的线密度 ρ (x , y ) = x ,求该金属丝的质量.五、证明题(6×1+4×1=10 分)18. 证明级数∑(-1)n n =1lnn + 1 n 条件收敛. ∞ 解: 将(1) 中结果代入方程, 得 f ' (u )e2 x= e 2 x z 即: f ' (u ) - f (u ) = 0 这是一个二阶常 2 1特征根为λ = 1, λ = -1 2系数线性齐次微分方程, 相应的特征方程为λ - 1 = 0 1 22 1 故 f (u ) = C e u + C e -u,其中C , C 为任意常数。
安徽大学高数期末考试试卷及答案解析 (1)

安徽大学2009-2010学年第二学期《高等数学A (二)、B (二)》考试试卷(A 卷)参考答案与评分标准一、填空题(本大题共五小题,每小题2分,共10分)12、0;3、;4、1 /20 arcsin d (,y y f x y π∫∫)d x 32;5、53二、选择题(本大题共五小题,每小题2分,共10分)6、 A ;7、D ;8、D ;9、A ; 10、A.三、计算题(本大题共五小题,其中第11、12、13题每小题10分,第14、15题每小题12分,共54分)11.解. 设。
则曲面在点处的法向量为22(,,)F x y z x y z =+−S (1,1,2)(1,1,2)(1,1,2)(,,)(2,2,1)(2,2,1)x y z F F F x y =−=−由题设可知,平面Π通过法线L ,故12a b 0,+−+=(1,,1)(2,2,1)0a −⋅−=即,由此解得123a b a +=⎧⎨+=⎩035,.22a b =−=12.解:令222(,),(,)2y xP x y Q x y x y x y−==++,则d d L I P x Q y =+∫v ,当时,220x y +≠22222()Q x y Px x y y∂−==∂+∂∂2。
取一小圆周22:C x y εε+=,0ε>充分小,使得C ε完全位于L 所围成的区域内,取逆时针方向。
设D ε为由L 与C ε所围成的区域,则由Green 公式得d d (d L C D Q PP x Q y x y x yεε+∂∂+=−=∂∂∫∫∫0, 所以d d d d LC P x Q y P x Q yε+=−+∫∫22(sin )(sin )(cos )(cos )d πεθεθεθεθθε−−=−∫20d 2πθπ==∫13.解:设cos ,sin ,x R u y R u z ==v =,则Σ对应于:02,0D u v h π≤≤≤≤。
安徽大学期末试卷09-10年度第一学期《自动控制原理》考卷B卷答案
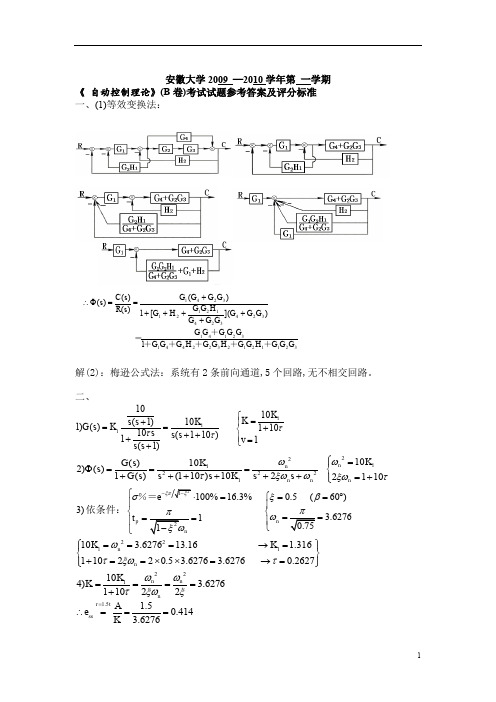
安徽大学2009 —2010学年第 一学期《 自动控制理论》(B 卷)考试试题参考答案及评分标准 一、(1)等效变换法:解(2):梅逊公式法:系统有2条前向通道,5个回路,无不相交回路。
二、111101010(1)1)() 11010(110)11(1)K K K s s G s K s s s v s s τττ⎧=+⎪==+⎨++⎪+=⎩+221122211010()2)() 1()(110)1022110n n n n n K K G s s G s s s K s s ωωτξωωξωτ⎧=⎪Φ===⎨++++++=+⎪⎩ 3)依条件:0.5 (60)100%16.3% 3.62761n p e t ξβσω-⎧==︒=⎧⎪⎪⎨⎨====⎪⎪⎩⎩%= 221110 3.627613.16 1.316110220.5 3.6276 3.6276 0.2627n n K K ωτξωτ⎧⎫===→=⎪⎪⎨⎬+==⨯⨯=→=⎪⎪⎩⎭221104) 3.627611022n n n K K ωωτξωξ====+1.5 1.50.4143.6276r t ss A e K =∴===3211212322441321413243241212132411)]([1)()()()(G G G H G G H G G H G G G G G G G G G G G G G G H G G H G G G G G s R s C s ++++++ =++++++==Φ∴三、(1)特征方程为()10(1)10(2)(1)10(2)(1)1(2)D s GH K s s s K s s s K s s s =+=-+=+-=+-=+换算成首一多项式,为:-根轨迹方程为: 由此可知,需要绘制零度根轨迹。
分离点的计算:12()()02.732,0.732dG sH s dss s ===- (2)由特征方程求取根轨迹与虚轴的交点,1,2s =±此时闭环系统临界稳定,出现等幅振荡,所对应的K =2。
安徽大学期末试卷MK09-10(1)高数A(三)答案.pdf

=λ
∑ 由此可知 λˆ
=
1 n
n i =1
xi 2
是λ
的无偏估计量。
五、证明题(本大题 8 分) 17. (本小题 8 分)证明:
(1)由 A2 + 2 AB − 2E = 0 得到
1 A( A + 2B) = E 2 故有 A + 2B 可逆。
(2)由(1)知 A + 2B 可逆,且逆矩阵为 1 A ,因而有 2
n i =1
xi 2
=0
得到 λ 的最大似然估计值为
∑ λˆ
=
1 n
n i =1
xi 2
∑ λ
的最大似然估计量为 λˆ
=
1 n
n i =1
Xi2
∫ (3)由于 EX 2 =
+∞
x2
i
2
−
xe
x2 λ
dx
=
λ
0
λ
∑ ∑ 因此 Eλˆ
=
E
⎛ ⎜⎝
1 n
n i =1
EX
i
2
⎞ ⎟⎠
=
1 n
n i =1
EX i2
0 0
−1 0
−2 0
−2 0
−6 0
−3⎟⎟ 0⎟
⎜ ⎝
0
0
0
0
0
0
⎟ ⎠
⎛1 0 −1 −1 −5 −2⎞
→
⎜ ⎜ ⎜
0 0
1 0
2 0
2 0
6 0
3⎟ ⎟Leabharlann 0⎟⎜ ⎝0
0
0
0
0
0
⎟ ⎠
对应的线性方程组为
安徽大学期末试卷离散数学期末试卷及答案.doc

一.判断题(共10小题,每题1分,共10分)在各题末尾的括号内画 表示正确,画 表示错误:1.设p、q为任意命题公式,则(p∧q)∨p ⇔ p ( )2.∀x(F(y)→G(x)) ⇔ F(y)→∃xG(x)。
( )3.初级回路一定是简单回路。
( )4.自然映射是双射。
( )5.对于给定的集合及其上的二元运算,可逆元素的逆元是唯一的。
( )6.群的运算是可交换的。
( )7.自然数集关于数的加法和乘法<N,+, >构成环。
( )8.若无向连通图G中有桥,则G的点连通度和边连通度皆为1。
( )9.设A={a,b,c},则A上的关系R={<a,b>,<a,c>}是传递的。
( )10.设A、B、C为任意集合,则A⨯(B⨯C)=(A⨯B)⨯C。
( )二、填空题(共10题,每题3分,共30分)11.设p:天气热。
q:他去游泳。
则命题“只有天气热,他才去游泳”可符号化为。
12.设M(x):x是人。
S(x):x到过月球。
则命题“有人到过月球”可符号化为。
13.p↔q的主合取范式是。
14.完全二部图K r,s(r < s)的边连通度等于。
15.设A={a,b},,则A上共有个不同的偏序关系。
16.模6加群<Z6,⊕>中,4是阶元。
17.设A={1,2,3,4,5}上的关系R={<1,3>,<1,5>,<2,5>,<3,3>,<4,5>},则R的传递闭包t(R) = 。
.18.已知有向图D的度数列为(2,3,2,3),出度列为(1,2,1,1),则有向图D的入度列为。
19.n阶无向简单连通图G的生成树有条边。
20.7阶圈的点色数是。
三、运算题(共5小题,每小题8分,共40分)21.求∃xF(x)→∃yG(x,y)的前束范式。
22.已知无向图G有11条边,2度和3度顶点各两个,其余为4度顶点,求G 的顶点数。
0910高等数学A(二)答案

0910高等数学A(二)答案第一篇:0910高等数学A(二)答案济南大学2009~2010学年第二学期课程考试试卷评分标准(含参考答案)A卷课程名称:高等数学A(二)任课教师:张苏梅等一、填空题(每小题3分,共18分)1.yzez-xy;2.y=2x3-x2;3.2xdx+2ydy;π∞(-1)n(2x)2n4.0;5.2;6..12(1-n∑=0(2n)!),(-∞,+∞)二、选择题(每小题3分,共18分)C;D;C;B;A;B.三、计算题(每小题8分,共32分)1.解:∂z∂x=1ycosxy;.....4分∂2z1xxx∂x∂y=-y2cosy+y3siny.....8分2.解:⎰⎰xydσ=⎰2dx⎰xxydy.....4分D0=12⎰20x3dx=2.....8分 3.解:dS=+x2x2+y+y2x2+ydxdy=2dxdy.....2分⎰⎰zdS=⎰⎰x2+y22dxdy.....5分∑Dxy=⎰2πdθ⎰2r2dr=π.....8分 4.解:⎰⎰(x2+y2+z2)dxdy=dxdy=πa4...........8分∑D⎰⎰axy四、应用题(每小题8分,共16分)1.解:由椭球的对称性,不妨设(x,y,z)是该椭球面上位于第Ⅰ卦限的任一点,内接长方体的相邻边长为2x,2y,2z(x,y,z>0),其体积为:V=8xyz构造拉格朗日函数F(x,y,z,λ)=8xyz-λ(x2y2a+b+z2c-1)......4分∂F∂x=8yz-λ2xa2=0令∂F2y∂y=8xz-λb2=0........6分∂F∂z=8xy-λ2zc2=0求得(x,y,z)=⎛a,b,c⎫⎪,V=8xyz=8abc......8分⎝33⎪⎭332.解:Iz=⎰⎰⎰(x2+y2)dv.........3分Ω=⎰2π2430dθ⎰0dr⎰r2rdz.........6分=2π⎰2r3(4-r2)dr=03π.........8分五、(8分)解:因为limana=limn=1,所以收敛半径为1.n→∞n+1n→∞n+1又x=±1时,级数均发散,故级数的收敛域为(-1,1).....3分n=1∑nx∞n=x∑nxn=1∞n-1=x(∑xn)'......6分 n=1∞xx=x()'=,x∈(-1,1).........8分 21-x(1-x)六、(8分)解:① 设u=x2+y2,则∂zx=f'(u);∂xu∂2zx21x2=()f''(u)+f'(u)-3f'(u)........2分 2uu∂xuy21y2同理,2=()f''(u)+f'(u)-3f'(u)uu∂yu由∂2z∂2z∂x2+∂2z∂y2=0⇒f''(u)+1f'(u)=0.....4分 u② 设f'(u)=p,f''(u)=dp,du则原方程化为:dp1dpdu+p=0⇒=-duupu积分得:p=CC,即f'(u)=,........6分 uu由f'(1)=1,得C=1.于是f(u)=ln|u|+C1代入f(1)=0得:C1=0.函数f(u)的表达式为:f(u)=ln|u|.......8分第二篇:1112高等数学B(二)答案济南大学2011~2012学年第二学期课程考试试卷评分标准(含参考答案)A卷课程名称:高等数学B(二)任课教师:一、填空题(每小题2分,共10分)1、2dx+dy,2、-5,3、1,4、⎰10dy⎰1yf(x,y)dx5、1二、选择题(每小题2分,共10分)1、A2、B3、C4、C5、D三、计算题(每小题8分,共40分)1、解:令F=x2+y2+z2-2z,则Fx=2x,Fz=2z-2.....2分∴∂zFx∂x=-xF=z.....4分z1-∂2z∂x(1-z)2+x2∴∂x2=∂x(1-z)=(1-z)3.....8分2、解:⎰⎰(x+6y)dxdy=⎰1dx5x76D0⎰x(x+6y)dy=3.....8分π3、解:⎰⎰+x2+y2dxdy=D⎰2dθ⎰1+r2rdr=π(22-1).....8分4、解:ux(2,1,3)=4,uy(2,1,3)=5,uz(2,1,3)=3 方向lϖ=(3,4,12)cosα=313,cosβ=413,cosγ=12 .....6分∂z∂l=uu68xcosα+ycosβ+uzcosγ=13.....8分5、解:收敛域为(0,2).....2分∞∞令S(x)=∑(n+1)(x-1)n=(1)n+1)'.....6分n=0∑(x-n=0S(x)=(x-12-x)'=1(2-x)2x∈(0,2).....8分四、解答题(每小11分,共33分)ϖ1、解:交线的方向向量为nϖiϖjkϖ=1-4=(-4,-3,-1).....8分2-1-5所求直线方程为x+3y-2z-54=3=1.....11分2、解:令f(x)=xx-1,则f'(x)=-1-x2x(x-1)<0x>1 所以un单调递减且limn→∞un=0∞所以级数∑(-1)nnn=2n-1.....6分n∞由于limn→∞=1,且∑1发散n=2nn∑∞(-1)n所以级数n.....11分n=2n-13、解:旋转曲面方程为z=x2+y2.....3分投影区域D:x2+y2≤1.....5分V=⎰⎰(1-x2-y2)dxdy=⎰2πdθ⎰1π(1-r)rdr=D.....11分五、证明题(每小题7分,共7分)ff(x,0)-f(0,0)x(0,0)=lim证:x→0x=0f(0,0)=limf(x,0)-f(0,0)xx→0x=0所以函数f(x,y)在(0,0)处可导.....3分lim∆z-fx(0,0)∆x-fy(0,0)∆yρ→0ρ=limf(∆x,∆y)∆x∆yρ→0∆x2+∆y2=limρ→0∆x2+∆y2取∆y=k∆x,得极限为k1+k,说明极限不存在所以函数f(x,y),在(0,0)点不可微.....7分第三篇:专升本高等数学(二)成人高考(专升本)高等数学二第一章极限和连续第一节极限[复习考试要求]1.了解极限的概念(对极限定义等形式的描述不作要求)。
2010-2011第二学期A卷参考答案及评分标准

安徽大学2010—2011学年第 2学期《 集成电路原理 》(A 卷)考试试题参考答案及评分标准一、简答题(每小题3分,共30分)1. 逻辑综合包括那几步?答:转换(1分)、逻辑优化(1分)和映射(1分)三步。
2. 等比例缩小有几类?答:恒定电场(CE )等比例缩小定律(1分)、恒定电压(CV )等比例缩小定律(1分)和准恒定电场(QCE )等比例缩小定律(1分)。
3. 什么是鸟嘴效应?答:在场区氧化过程中(1分),氧也会通过氮化硅边缘向有源区侵蚀,在有源区边缘形成氧化层,伸进有源区的这部分氧化层被形象地称为鸟嘴(1分),它使实际的有源区面积比版图设计的面积缩小(1分)。
4. 什么是闩锁效应?答:在CMOS 芯片中(1分),在电源VDD 和地线GND 之间由于寄生的PNP 和NPN 双极性BJT 相互影响而产生的一低阻抗通路(1分),它的存在会使VDD 和GND 之间产生大电流,从而破坏芯片或者引起系统错误(1分)。
5. CMOS 反相器的上升时间、下降时间和传输延迟时间的定义是什么?答:上升时间r t 是输出从DD V 1.0上升到DD V 9.0所需要的时间(1分);下降时间f t 是输出从DD V 9.0下降到DD V 1.0所需要的时间(1分);pHL t 表示从输入信号上升边的50%到输出信号下降边的50%所经过的延迟时间,也叫做输出从高向低转换的传输延迟时间,pLH t 表示从输入信号下降边的50%到输出信号上升边的50%所经过的延迟时间,也叫做输出从低向高转换的传输延迟时间(1分)。
6. 版图的检查包括哪些内容?版图的检查包括: 设计规则检查(Design Rule Check ,DRC )(1分); 版图和电路图的一致性检查(Layout Versus Schematic ,LVS )(1分);版图寄生参数提取(Layout Parasitic Extraction ,LPE )和 后仿真。
安徽大学2009-A卷-王发牛
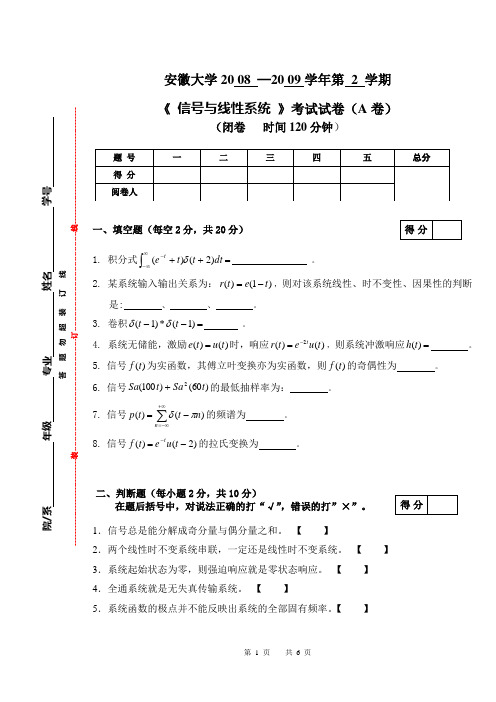
安徽大学20 08 —20 09学年第 2 学期《 信号与线性系统 》考试试卷(A 卷)(闭卷 时间120分钟)一、填空题(每空2分,共20分)1. 积分式=++⎰∞∞--dt t t e t )2()(δ 。
2. 某系统输入输出关系为:)1()(t e t r -=,则对该系统线性、时不变性、因果性的判断是: 、 、 。
3. 卷积=--)1(*)1(t t δδ 。
4. 系统无储能,激励)()(t u t e =时,响应)()(2t u e t r t -=,则系统冲激响应=)(t h 。
5. 信号)(t f 为实函数,其傅立叶变换亦为实函数,则)(t f 的奇偶性为 。
6. 信号)60()100(2t Sa t Sa +的最低抽样率为: 。
7. 信号∑+∞-∞=-=n n t t p )()(πδ的频谱为 。
8. 信号)2()(-=-t u e t f t 的拉氏变换为 。
二、判断题(每小题2分,共10分)在题后括号中,对说法正确的打“√”,错误的打”×”。
1.信号总是能分解成奇分量与偶分量之和。
【 】2.两个线性时不变系统串联,一定还是线性时不变系统。
【 】 3.系统起始状态为零,则强迫响应就是零状态响应。
【 】 4.全通系统就是无失真传输系统。
【 】5.系统函数的极点并不能反映出系统的全部固有频率。
【 】院/系 年级 专业 姓名 学号答 题 勿 超 装 订 线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------三、画图题(每小题5分,共20分)1.绘出函数)1()]1()([)(-+--=t u t u t u t t f 的波形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安徽大学2009--2010高等数学A(二)试题与答案
一、填空题(2×5=10分)
1. 点(2,1,1) 到平面01=+-+z y x
2. 极限=⎪⎪⎭⎫
⎝⎛++∞
→+∞→2
22
lim x y x y x xy 0.
3. 交换积分次序
⎰
⎰
dy y x f dx x
sin 0
2
),(π
4. 设)(x f 是周期为2的函数, 它在区间(-1,1] 上的定义为100
1,,2)(3
<<<<-⎩
⎨
⎧=x x x x f 则)(x f 的
Fourier 级数在x=15. 函数u=xyz 在点(1,1,1) 处沿方向(2,2,1) 二、选择题(2×5=10分) 6. 二元函数22),(y x y x f +=
在点(0,0) 处 ( A )
A. 连续, 但偏导数不存在;
B. 不连续; 且偏导数不存在;
C. 不连续; 但偏导数存在;
D. 连续, 且偏导数存在. 7. 设第二类曲面积分⎰⎰⎰⎰==
S
S
zdzdx xy I
xyzdzdx I 22
1,,其中S 为1222=++z y x 的上
半部分, 方向取上侧, 若S 1为S 在第一卦限部分, 且与S 方向一致, 则 ( A ) A. 021==I I ; B. ⎰⎰
==1
2212,0S zdzdx xy I I ;
C. ⎰⎰⎰⎰
==1
1
2212,2
S S zdzdx xy I xyzdzdx I D. 0,2211
==⎰⎰I xyzdzdx I S
8. 设Ω为R 3中开区域,且Ω内任意一条闭曲线总可以张成一片完全属于Ω的曲面,函数P,Q,R 在Ω内连续可导,若曲线积分
dz R Qdy Pdx L
⎰++只依赖于曲线L 的端点,而与积分
路径无关,则下述命题不正确的是 ( D ) A. 对Ω内任意光滑闭曲线C ,曲线积分
0=++⎰
dz R Qdy Pdx C
;
B. 存在Ω上某个三元函数u(x,y,z), 使得Rdz Qdy Pdx du ++=;
C. 等式
y
R z Q z P x R x Q y P ∂∂=∂∂∂∂=∂∂∂∂=∂∂,,在开区域Ω内恒成立;
D. 等式
0=∂∂+∂∂+∂∂z
R y Q x P 在开区域Ω内恒成立. 9. 设函数),(y x f 在开区域D 内有二阶连续偏导数, 且),(00y x f x =),(00y x f y =0. 则下列为),(y x f 在点),(00y x 处取极小值的充分条件的是 ( A ) A. ),(00y x f xx >0, ),(00y x f xx ),(00y x f yy -),(002y x f xy
>0; B. ),(00y x f xx >0, ),(00y x f xx ),(00y x f yy -),(002
y x f xy
<0; C. ),(00y x f xx <0, ),(00y x f xx ),(00y x f yy -),(002
y x f xy
>0; D. ),(00y x f xx <0, ),(00y x f xx ),(00y x f yy -),(002
y x f
xy
<0.
10. 设函数),,(z y x f u =具有二阶连续偏导数, 则div grad f = ( A ) A. +xx f yy f +zz f ; B. x f +y f +z f ; C. (x f ,y f ,z f ); D. (xx f ,yy f ,zz f ). 三、计算题(10×3+12×2=54分)
11. 设平面0:=+-+∏b z ay x 通过曲面2
2
y x z +=在点(1,1,2)处的法线L,求b a ,的值. 解: 设z y x z y x F -+=2
2
),,( 则曲面S 在点(1,1,2) 处的法向量为:
)1,2,2()1,2,2(),,()1,2,2()2,1,1(-=-=y x F F F z y x 由题设可知平面∏通过法线L, 故:
12. 计算第二类曲线积分
⎰
+-L
y x xdy
ydx 2
2 , 其中L 为正方形边界1=+y x ,取顺时针方向.
使得εC 完全位于L 所围成的区域内, 取逆时针方向。
设εD 为由L 与εC 所围成的区域,
13. 计算第一类曲面积分
dS z y x z ⎰⎰∑++2
22,其中∑为圆柱面)0(2
22>=+R R y x 介于平面z = 0与z = h (h>0) 之间的部分.
解法(一): 设x=Rcosu, y=Rsinu, z=v, 则∑对应于D:h v u ≤≤≤≤0,20π.
1,0,0,0,cos ,sin =====-=v v
v u u u z y x z u R y u R x 故,1,0,2===G F R E
14. 将函数x x f arctan )(=展开成x 的幂级数, 并求级数∑∞
=+-01
2)1(n n
n 的和.
15. 设函数)(u f 具有二阶连续导数, 且)sin (y e f z x
=,
(1) 求2222,y
z x z ∂∂∂∂ ;
(2) 若函数)sin (y e f z x
=满足方程z e y
z
x z x 22222=∂∂+∂∂ , 求函数)(u f
解: 将(1) 中结果代入方程, 得 z e e
u f x x
22)(='' 即:0)()(=-''u f u f 这是一个二阶常
系数线性齐次微分方程, 相应的特征方程为012
=-λ 特征根为1,121-==λλ 故u
u
e
C e C u f -+=21)(,其中21,C C 为任意常数。
四、应用题(10×1+6×1=16分)
16. 将一根长为l 的铁丝分割成两段, 一段围成一个圆, 另一段围成一个长方形. 求使得圆
面积与长方形面积之和最大的分割方法.
解: 设所围成的圆的半径为x, 长方形的长、宽分别为y, z 。
原问题转化为求函数
yz x S +=2π在条件l z y x =++)(22π下的最大值。
为此, 构造Lagrange 函数 )222(),,,(2l z y x yz x z y x L -++-+=πλπλ。
,022=-=πλπx L x
02=-=λz L y ,,02=-=λy L z 0)
(22=-++=l z y x L πλ。
得λλ2,===z y x ,
17. 已知一条非均匀金属线L 放置于平面Oxy 上, 刚好为抛物线2
x y =对应于10≤≤
x 的那一段, 且它在点(x,y) 处的线密度x y x =),(ρ,求该金属丝的质量.
五、证明题(6×1+4×1=10分)
18. 证明级数
∑∞
=+-1
1
ln
)
1(n n
n
n 条件收敛.
19. 设空间闭区域Ω可表示为{}y z x y x x z y x ≤≤≤≤≤≤,1,10/),,(.若)(t f 在[0,1] 上连续, 且)()()(),,(z f y f x f z y x F =.试证明:
⎰⎰⎰⎰Ω
=103
])([61),,(dt t f dxdydz z y x F 证明: 设⎰
=x
dt t f x F 0
)()(,则)()(x f x F ='。
