安徽大学高等数学期末试卷和答案
安徽大学高等数学期末考试试卷(含答案)

安徽大学高等数学期末考试试卷(含答案) 一、高等数学选择题
1.设函数,则.
A、正确
B、不正确
【答案】B
2.是微分方程.
A、正确
B、不正确
【答案】A
3.是偶函数.
A、正确
B、不正确
【答案】B
4.不定积分.
A、正确
B、不正确
【答案】B
5.极限.
A、正确
B、不正确
【答案】A
6.函数的单调减少区间是().
A、
B、
C、
D、
【答案】D
7.极限.
A、正确
B、不正确
【答案】A
8.是偶函数.
A、正确
B、不正确
【答案】B
9. ( ).
A、
B、
C、
D、
【答案】B
10.函数的图形如图示,则是函数的
( ).
A、最大值点
B、极大值点
C、极小值点也是最小值点
D、极小值点但非最小值点
【答案】C
11.().
A、
B、
C、
D、
【答案】B
12.曲线在点处切线的方程为().A、
B、
C、
D、
【答案】D
13.函数在点处连续.
A、正确
B、不正确
【答案】A
14.定积分.
A、正确
B、不正确
【答案】B
15.函数的导数.
A、正确
B、不正确
【答案】B。
安徽大学期末试卷MK09-10(1)高数A(三)答案.pdf

=λ
∑ 由此可知 λˆ
=
1 n
n i =1
xi 2
是λ
的无偏估计量。
五、证明题(本大题 8 分) 17. (本小题 8 分)证明:
(1)由 A2 + 2 AB − 2E = 0 得到
1 A( A + 2B) = E 2 故有 A + 2B 可逆。
(2)由(1)知 A + 2B 可逆,且逆矩阵为 1 A ,因而有 2
n i =1
xi 2
=0
得到 λ 的最大似然估计值为
∑ λˆ
=
1 n
n i =1
xi 2
∑ λ
的最大似然估计量为 λˆ
=
1 n
n i =1
Xi2
∫ (3)由于 EX 2 =
+∞
x2
i
2
−
xe
x2 λ
dx
=
λ
0
λ
∑ ∑ 因此 Eλˆ
=
E
⎛ ⎜⎝
1 n
n i =1
EX
i
2
⎞ ⎟⎠
=
1 n
n i =1
EX i2
0 0
−1 0
−2 0
−2 0
−6 0
−3⎟⎟ 0⎟
⎜ ⎝
0
0
0
0
0
0
⎟ ⎠
⎛1 0 −1 −1 −5 −2⎞
→
⎜ ⎜ ⎜
0 0
1 0
2 0
2 0
6 0
3⎟ ⎟Leabharlann 0⎟⎜ ⎝0
0
0
0
0
0
⎟ ⎠
对应的线性方程组为
安徽大学期末试卷离散数学期末试卷及答案.doc

一.判断题(共10小题,每题1分,共10分)在各题末尾的括号内画 表示正确,画 表示错误:1.设p、q为任意命题公式,则(p∧q)∨p ⇔ p ( )2.∀x(F(y)→G(x)) ⇔ F(y)→∃xG(x)。
( )3.初级回路一定是简单回路。
( )4.自然映射是双射。
( )5.对于给定的集合及其上的二元运算,可逆元素的逆元是唯一的。
( )6.群的运算是可交换的。
( )7.自然数集关于数的加法和乘法<N,+, >构成环。
( )8.若无向连通图G中有桥,则G的点连通度和边连通度皆为1。
( )9.设A={a,b,c},则A上的关系R={<a,b>,<a,c>}是传递的。
( )10.设A、B、C为任意集合,则A⨯(B⨯C)=(A⨯B)⨯C。
( )二、填空题(共10题,每题3分,共30分)11.设p:天气热。
q:他去游泳。
则命题“只有天气热,他才去游泳”可符号化为。
12.设M(x):x是人。
S(x):x到过月球。
则命题“有人到过月球”可符号化为。
13.p↔q的主合取范式是。
14.完全二部图K r,s(r < s)的边连通度等于。
15.设A={a,b},,则A上共有个不同的偏序关系。
16.模6加群<Z6,⊕>中,4是阶元。
17.设A={1,2,3,4,5}上的关系R={<1,3>,<1,5>,<2,5>,<3,3>,<4,5>},则R的传递闭包t(R) = 。
.18.已知有向图D的度数列为(2,3,2,3),出度列为(1,2,1,1),则有向图D的入度列为。
19.n阶无向简单连通图G的生成树有条边。
20.7阶圈的点色数是。
三、运算题(共5小题,每小题8分,共40分)21.求∃xF(x)→∃yG(x,y)的前束范式。
22.已知无向图G有11条边,2度和3度顶点各两个,其余为4度顶点,求G 的顶点数。
大一(第一学期)高数期末考试题及答案

页眉内容大一上学期高数期末考试一、单项选择题 (本大题有4小题, 每小题4分, 共16分) 1. )(0),sin (cos )( 处有则在设=+=x x x x x f .(A )(0)2f '= (B )(0)1f '=(C )(0)0f '= (D )()f x 不可导.2. )时( ,则当,设133)(11)(3→-=+-=x x x x xx βα.(A )()()x x αβ与是同阶无穷小,但不是等价无穷小; (B )()()x x αβ与是等价无穷小;(C )()x α是比()x β高阶的无穷小; (D )()x β是比()x α高阶的无穷小.3. 若()()()02xF x t x f t dt=-⎰,其中()f x 在区间上(1,1)-二阶可导且'>()0f x ,则( ).(A )函数()F x 必在0x =处取得极大值; (B )函数()F x 必在0x =处取得极小值;(C )函数()F x 在0x =处没有极值,但点(0,(0))F 为曲线()y F x =的拐点; (D )函数()F x 在0x =处没有极值,点(0,(0))F 也不是曲线()y F x =的拐点。
4.)()( , )(2)( )(1=+=⎰x f dt t f x x f x f 则是连续函数,且设(A )22x (B )222x +(C )1x - (D )2x +.二、填空题(本大题有4小题,每小题4分,共16分) 5. =+→xx x sin 2)31(l i m .6. ,)(cos 的一个原函数是已知x f xx=⋅⎰x xxx f d cos )(则.7.lim(cos cos cos )→∞-+++=22221n n nnnn ππππ .8. =-+⎰21212211arcsin -dx xx x .三、解答题(本大题有5小题,每小题8分,共40分)9. 设函数=()y y x 由方程sin()1x ye xy ++=确定,求'()y x 以及'(0)y . 10. .d )1(177x x x x ⎰+-求11. . 求,, 设⎰--⎪⎩⎪⎨⎧≤<-≤=1 32)(1020)(dx x f x x x x xe x f x12. 设函数)(x f 连续,=⎰10()()g x f xt dt,且→=0()limx f x A x ,A 为常数. 求'()g x 并讨论'()g x 在=0x 处的连续性.13. 求微分方程2ln xy y x x '+=满足=-1(1)9y 的解.四、 解答题(本大题10分)14. 已知上半平面内一曲线)0()(≥=x x y y ,过点(,)01,且曲线上任一点M x y (,)00处切线斜率数值上等于此曲线与x 轴、y 轴、直线x x =0所围成面积的2倍与该点纵坐标之和,求此曲线方程. 五、解答题(本大题10分)15. 过坐标原点作曲线x y ln =的切线,该切线与曲线x y ln =及x 轴围成平面图形D.(1) 求D 的面积A ;(2) 求D 绕直线x = e 旋转一周所得旋转体的体积V .六、证明题(本大题有2小题,每小题4分,共8分)16. 设函数)(x f 在[]0,1上连续且单调递减,证明对任意的[,]∈01q ,1()()≥⎰⎰qf x d x q f x dx.17. 设函数)(x f 在[]π,0上连续,且)(0=⎰πx d x f ,cos )(0=⎰πdx x x f .证明:在()π,0内至少存在两个不同的点21,ξξ,使.0)()(21==ξξf f (提示:设⎰=xdxx f x F 0)()()解答一、单项选择题(本大题有4小题, 每小题4分, 共16分) 1、D 2、A 3、C 4、C二、填空题(本大题有4小题,每小题4分,共16分)5. 6e . 6.c x x +2)cos (21 .7. 2π. 8.3π.三、解答题(本大题有5小题,每小题8分,共40分) 9. 解:方程两边求导(1)c o s ()()x ye y xy xy y +''+++= cos()()cos()x y x ye y xy y x e x xy +++'=-+0,0x y ==,(0)1y '=-10. 解:767u x x dx du == 1(1)112()7(1)71u du duu u u u -==-++⎰⎰原式 1(ln ||2ln |1|)7u u c =-++ 7712ln ||ln |1|77x x C =-++11. 解:101233()2x f x dx xe dx x x dx---=+-⎰⎰⎰123()1(1)xxd e x dx--=-+--⎰⎰00232cos (1sin )x x xe e d x πθθθ----⎡⎤=--+-=⎣⎦⎰ 令3214e π=--12. 解:由(0)0f =,知(0)0g =。
安徽大学期末试卷MKF学习学习文档高数09-10(1)高数A(三)试卷.pdf

答 题勿超装 订 线
------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------
专业
院/系
安徽大学期末试卷
二、填空题(每小题 2 分,共 10 分) 2 −3 1 5
6.方程 −4 6 x −10 = 0 的根为 1 24 7
x −1 −2 −4 −7
得分 。
7.设 3 阶矩阵 A 有 3 个特征值 1,2,3,且矩阵 B 与 A 相似,则| B + E |=
。
8. 设随机变量 X 的分布函数为
观察亩产量,得到 x = 500 kg,则总体均值 μ 的置信水平为 0.95 的置信区间为
。
( Φ(1.96) = 0.975, Φ(1.645) = 0.95 )
三、计算题(本大题 10 分) 11.计算下列行列式
an (a −1)n
(a − n)n
an−1 (a −1)n−1
(a − n)n−1
《高等数学 A(三) 》(A 卷) 第 4 页 共 7 页
安徽大学期末试卷
14.(本小题 10 分)设某人按如下原则决定某日的活动:如该天下雨则以 0.2 的概率外出 购物,以 0.8 的概率去探访朋友;如该天不下雨,则以 0.9 的概率外出购物,以 0.1 的概率 去探访朋友。已知该日下雨的概率为 0.3。 (1)试求那天他外出购物的概率; (2)若已知他那天外出购物,试求那天天下雨的概率。
安徽大学数学期末试卷汇编MK_2005下离散数学A参考答案

2005下离散数学(A)参考答案注:解答思路可能存在差异,描述方式也常常不唯一,下面仅仅给出典型的求解过程。
1.设E 为a,b,c,d 这4个字母的全排列集合,A 为出现ab 的排列集合,B 为出现cd 的排列集合。
由容斥原理,不允许出现ab 和cd 的排列个数为:| E |-|A ∪B|=4!-(3!+3!-2!)=102.(1)R 的关系矩阵是:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0100101100001001(2)R 不是自反的,不是反自反的,不是对称的,不是反对称的,不是传递的;(3)r(R)={(0,0),(0,3),(1,1),(2,0),(2,1),(2,2),(2,3),(3,2),(3,3)};s(R)={(0,0),(0,2),(0,3),(1,2),(2,0),(2,1),(2,3),(3,0),(3,2)};t(R)={(0,0),(0,1),(0,2),(0,3),(2,0),(2,1),(2,2),(2,3),(3,0),(3,1),(3,2),(3,3)}。
3. (1)对任意x ∈R,有3x x −=0,即(x,x)∈S,所以S 是自反的; (2)对任意x,y∈R,设(x,y)∈S,则3y x −为整数,那么3x y −也为整数,即(y,x)∈S,所以S 是对称的;(3)对任意x,y,z ∈R,设(x,y)∈S 且(y,z)∈S ,则3y x −,3z y −为整数,那么3y x −+3z y −=3z x −也为整数,即(x,z)∈S,所以S 是可传递的; 由(1)(2)(3)知S 是等价关系。
4.(1)可满足式 (2)可满足式 (3)可满足式(4)矛盾式 (5)重言式 (6)重言式5.(1)主析取范式:(P ∧¬Q)∨(P ∧Q) 主合取范式:(P ∨Q)∧(P ∨¬Q)(2)前束合取范式:∀x ∃z ∃u((¬P(x)∨¬Q(y)∨R(z))∧(¬P(x)∨¬Q(y)∨¬S(u)))6.令Q(x):x 是有理数 R(x):x 是实数 I(x):x 是整数 则整个命题符号化为:∀x(Q(x)→R(x)), ∃x(Q(x)∧I(x)) |- ∃x(R(x)∧I(x))证明:(1) ∃x(Q(x)∧I(x)) P(2) Q(a)∧I(a) ES(1)(3) Q(a) I(2)(4) I(a) I(2)(5) ∀x(Q(x)→R(x)) P(6) Q(a)→R(a) US(5)(7) R(a) I(3)(6)(8) R(a)∧I(a) I(4)(7)(9) ∃x(R(x)∧I(x)) EG(8)7. 要证明Vρh 与V’同构,需要证明如下几点:1)同型:Vρh 与V’同型?2)双射:定义映射f,并证明其为双射定义映射f:因为h是一个从S到S’的满射,S/ρh的可允许划分,所以对于每一个[x]ρh ∈S/ρh必存在某个x’∈S’,使得x’=h(x),于是可以如下定义函数:f: S/ρh →S’ ,使得f([x]ρh)=h(x)。
高数A(三)期末考试答案整理安徽大学

0
⎜⎝ 0
0 4k 0
⎜ 4k
0⎞ ⎜
0
⎟ ⎟
QT
=
⎜ ⎜
0
6k ⎟⎠
⎜ ⎜⎜⎝ 0
0 2k + 6k
2 −2k + 6k
2
0⎟
−2k
+
6k
⎟ ⎟
2⎟
2k + 6k 2
⎟ ⎟⎟⎠
13、解:二次型的矩阵为
各阶顺序主子式为
⎛ 2 2 −2⎞
⎜ ⎜
2
a
−4
⎟ ⎟
⎜⎝ −2 −4 5 ⎟⎠
2 2 −2 | 2 |= 2 , 2 2 = 2a − 4 , 2 a −4 = 2(3a −10) ,
。
10、从一批零件中,抽取 9 个零件,测得其直径(单位:毫米)为: 19.7,20.1,19.8,19.9,20.2,20.0,19.0,20.2,20.3
设零件直径服从正态分布 N (μ,σ 2 ) ,其中 μ 未知,σ = 0.21 (毫米), Φ(1.96) = 0.975 ,
则这批零件平均直径 μ 的对应于置信度为 0.95 的置信区间为
⎛ 0 −1 1 ⎞
7、
⎜ ⎜⎜⎝
0 1
2 0
−01⎟⎟⎟⎠
8、30
9、9
10、(19.77,20.05)
三、计算题(本大题共 4 小题,其中第 11 题和第 13 题各 10 分,第 12 题 14 分,第 14 题 12 分,共 46 分)
11、解:将第一行的-1 倍加到其余各行,得
x1
a2
a3
80
20
四、证明题(本大题共 2 小题,每题 12 分,共 24 分)
安徽大学《高等数学A(二)》2018-2019学年第二学期期末考试B卷
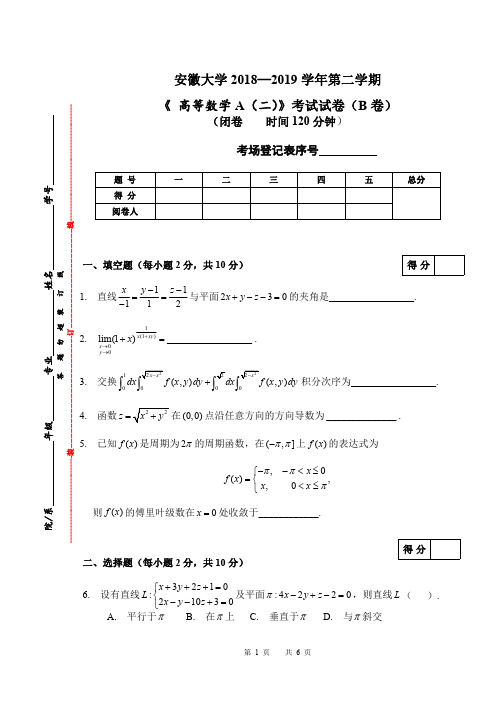
安徽大学2018—2019学年第二学期《高等数学A (二)》考试试卷(B 卷)(闭卷时间120分钟)考场登记表序号一、填空题(每小题2分,共10分)1.直线11112x y z --==-与平面230x y z +--=的夹角是_________________.2.1(1)00lim(1)x xy x y x +→→+=_________________.3.交换1(,)(,)dx f x y dy f x y dy +⎰积分次序为_________________.4.函数z =在(0,0)点沿任意方向的方向导数为______________.5.已知()f x 是周期为2π的周期函数,在(,]ππ-上()f x 的表达式为,0(),,0x f x x x πππ--<≤⎧=⎨<≤⎩则()f x 的傅里叶级数在0x =处收敛于____________.二、选择题(每小题2分,共10分)6.设有直线3210:21030x y z L x y z +++=⎧⎨--+=⎩及平面:4220x y z π-+-=,则直线L ().A.平行于πB.在π上C.垂直于πD.与π斜交题号一二三四五总分得分阅卷人得分院/年专业姓学答题勿超装订线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------得分7.设(),f x y 为连续函数,且(){}222,D x y xy t =+≤,则()+21lim ,t Df x y dxdy t π→=⎰⎰()A()0,0f B()0,0f -C()0,0f 'D 不存在8.设2222222,0,0,0x yx y z x yx y ⎧+≠⎪=+⎨⎪+=⎩则函数z 在点()0,0处().A 不连续B 连续,但偏导数不存在C 连续且偏导数都存在,但不可微D 可微9.常数0a >,则第一类曲面积分22222x y z a x dS ++==⎰⎰().A 443a πB243a πC 44a πD 24a π10.级数21sin n na n ∞=⎛- ⎝∑(a 为常数)().A 绝对收敛B 条件收敛C 发散D 收敛性与a 有关三、计算题(每小题6分,共60分)11.求曲面222328x yz y xz z +=-上点(1,2,1)-处的切平面和法线方程.得分12.设22(,)z f xy x y =+,求2zx y∂∂∂,其中(,)f u v 有二阶连续偏导数.13.计算曲线积分()()32522543sin xLxey x x dx x y dyx y++--++⎰,其中L 为从点()1,0A -沿曲线y =()1,0B 一段弧.答题勿超装订线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------14.计算曲面积分()()()323232Sxaz dydz y ax dzdx z ay dxdy +++++⎰⎰,其中S为上半球面z =.15.求幂级数11n n nx∞-=∑的和函数,并求级数12n n n∞=∑的和.16.将()2143f x x x =++展开成1x -的幂级数.四、应用题(每小题7分,共14分)17.已知一条非均匀金属丝L 放置于平面xOy 上,刚好为抛物线2y x =对应于01x ≤≤的那一段,且它在点(,)x y 处的线密度为(,)x y x ρ=,求该金属丝的质量.得分答题勿超装订线------------------------------装---------------------------------------------订----------------------------------------线----------------------------------------18.求二元函数2(,)(4)z f x y x y x y ==--在直线6x y +=,x 轴和y 轴所围成的区域D 上的最大值和最小值五、证明题(每小题6分,共6分)19.已知正项级数1n n u ∞=∑收敛,证明21n n u ∞=∑收敛.得分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安徽大学2011—2012 学年第一学期《高等数学A(三)》考试试卷(A 卷)(闭卷时间120 分钟)考场登记表序号题号一二三四五总分得分阅卷人一、选择题(每小题2 分,共10 分)得分1.设A为n阶可逆矩阵,则下列各式正确的是()。
(A)(2A)−1 =2A−1 ;(B)(2A−1)T=(2A T)−1 ;(C)((A−1)−1)T=((A T)−1)−1 ;(D)((A T)T)−1 =((A−1)−1)T。
2.若向量组1, 2 , , rααα可由另一向量组()。
βββ线性表示,则下列说法正确的是1, 2 , , sβββ线性表示,则下列说法正确的是(A)r≤s;(B)r≥s;(C)秩( 1, 2 , , r1, 2 , , s1, 2 , , rααα)≤秩(βββ);(D)秩(ααα)≥秩(βββ)。
1, 2 , , sβββ)。
3.设A, B为n阶矩阵,且A与B相似,E为n阶单位矩阵,则下列说法正确的是()。
(A)λE−A=λE−B;(B)A与B有相同的特征值和特征向量;(C)A与B都相似于一个对角矩阵;(D)对任意常数k,kE−A与kE−B相似。
4.设1, 2 , 3ααα为R3 的一组基,则下列向量组中,()可作为R3 的另一组基。
(A)1, 1 2 ,3 1 2 1, 2 ,2 1 2α+αα+αα+α。
αα−αα−α;(B)ααα+α;(C) 1 2 , 2 3, 1 3α+αα+αα−α;(D) 1 2 , 2 3, 1 35.设P(A) =0.8 ,P(B) =0.7 ,P(A| B) =0.8 ,则下列结论正确的是()。
(A)事件A与B互不相容;(B)A⊂B;(C)事件A与B互相独立;(D)P(A∪B) =P(A) +P(B) 。
第1 页共6 页二、填空题(每小题2分,共10分)得分6.设4 阶方阵A的秩为2,则其伴随矩阵A* 的秩为。
7.设λ=2 是非奇异矩阵A的一个特征值,则矩阵−1⎛1 ⎞A2⎜⎟⎝3 ⎠必有一个特征值等于。
8. 设离散型随机变量X的分布列为kP X=k=a⋅⎛⎜2 ⎞⎟( )⎝3 ⎠,k=0,1, 2, 3,则a=。
⎛−⎞1 0 19. 设离散型随机变量X的分布列为,若⎜⎟⎝⎠0.25 0.5 0.25Y=X2 ,则P(Y=1) =。
10.某车间生产的滚珠直径X服从N(μ,σ 2 ) ,现从产品中随机抽取 6 件,测得平均直径为x=,若已知方差σ 2 =0.06 ,则平均直径μ的置信度为95% 的置信区间14.95为。
(Φ(1.96) =0.975,Φ(1.645) =0.95)三、计算题(每小题9分,共9分)得分11.计算下列行列式a 1 1 111 a0 02D=1 0 a0n 31 0 0 an ,这里 2 3 n0a a a≠。
第2 页共6 页四、分析题(每小题13 分,共65 分)12.已知线性方程组AX=β有无穷多解,其中得分⎛a 1 1⎞⎜⎟A=⎜0 a−1 0⎟,⎜⎟1 1 a⎝⎠β⎛−⎞2⎜⎟=⎜1⎟。
⎜⎟1⎝⎠求:(1)a的值;(2)方程组AX=β的通解。
13.设二次型f(X) =2x2 +3x2 +3x2 +4x x,1 2 3 2 3(1)求正交变换X=QY,并写出f(X) 的标准形;(2)判定二次型f(X) 的正定性。
第3 页共6 页14.玻璃杯成箱出售,每箱8 只,假设每箱含0 只和1 只残次品的概率分别为0.8 和0.2。
一位顾客欲购一箱玻璃杯,在购买时,售货员随意取一箱,而顾客随机地查看2 只,若无残次品,则买下该箱玻璃杯,否则退回。
试求:(1)顾客买下该箱的概率;(2)在顾客买下的一箱中,确实没有残次品的概率。
第4 页共6 页15.设(X,Y) 服从以x轴、直线x=1以及y=x围成的三角区域上均匀分布,试判断X,Y的独立性和相关性。
16.假设总体X的密度函数为f(x;θ)⎧≥e x−(x−θ),θ−(x−θ),θe x=⎨⎩0 , x<θ其中,θ>0是未知参数,( , , )X X为取自X的样本,试求θ的矩估计量和最大似然估1 n计量。
第5 页共6 页得分五、证明题(每小题6 分,共6 分)17.若A为n阶方阵,且A3 =0,证明:A−E为可逆矩阵。
第6 页共6 页安徽大学2011—2012 学年第一学期《高等数学A(三)》(A 卷)考试试题参考答案及评分标准一、选择题(每小题2 分,共10 分)1、C;2、C;3、D;4、D;5、C。
二、填空题(每小题2 分,共10 分)6、0;7、3/4;8、27/65;9、0.5;10、(14.754,15.146) 。
三、计算题(每小题9 分,共9 分)111.解:将第j列乘上−均加到第1 列上(j=2, 3,",n),得到ajDn1 1 1a−−−− 1 1 1""1a a a2 3 n0 a0 0"=2(7 分)0 0 a0"3"""""0 0 0 a"n⎛⎞n 1∑"a. (9 分)=⎜a−⎟a a1 2 3 na⎝⎠j=2 j四、分析题(每小题13 分,共65 分)12. 解:(1)增广矩阵⎛a 1 1 −2⎞⎜⎟⎛1 1 a 1 ⎞⎜⎟→⎜0 a−1 0 1 ⎟⎜⎝−⎟⎠A=⎜a−⎟0 1 0 1⎜⎟1 1 a 1⎝⎠a 1 1 2⎛1 1 a 1 ⎞⎛1 1 a 1 ⎞⎜⎟⎜⎟→⎜−⎟→⎜−⎟0 a 1 0 1 0 a 1 0 1,⎜−−−−⎟⎜−−−⎟0 1 a 1 a 2 a0 0 1 a 1 a2 2⎝⎠⎝⎠因为线性方程组AX=β有无穷多解,故a=−1。
(6 分)(2)当a=−1时,⎛1 1 1 1⎞⎛1 0 1 3/ 2⎞⎛−⎞−− 1 0 1 3/ 2⎟⎜⎟,⎜⎟⎜A→⎜0 −2 0 1⎟→⎜0 −2 0 1 →⎜0 1 0 −1/ 2⎟⎟⎜⎟⎜⎟⎜⎟0 0 0 0 0 0 0 0 0 0 0 0⎝⎠⎝⎠⎝⎠故方程组的通解为第1 页共4 页X⎛3 ⎞⎛1⎞1 ⎜⎟⎜⎟=⎜−⎟+⎜⎟21 k0 (k为任意常数)。
(13 分)⎜⎟⎜⎟0 1⎝⎠⎝⎠⎛2 0 0⎞⎜⎟13.解:(1)二次型的矩阵为=⎜0 3 2⎟。
由A⎜⎟0 2 3 ⎝⎠λ−2 0 0λE−A=0 λ−3 −2 =(λ−2)(λ−5)( −λ1),0 −2 λ−3得A的特征值为λ1=2,λ2=5,λ3=1。
(4 分)当λ1=2 时, 解方程(2E−A)X=0,由⎛0 0 0 ⎞⎛0 1 2⎞⎜⎟⎜⎟2E−A=⎜0 −1 −2⎟→⎜0 01⎟⎜−−⎟⎜⎟0 2 1 0 0 0⎝⎠⎝⎠,得特征向量(1,0,0)T.取α=。
T1 (1, 0, 0)当λ2=5 时,解方程(5E−A)X=0 ,由⎛3 0 0 ⎞⎛1 0 0 ⎞⎜⎟⎜⎟5E−A=⎜0 2 −2⎟→⎜0 1 −1⎟⎜−⎟⎜⎟0 2 2 0 0 0⎝⎠⎝⎠,得特征向量(0,1,1)T.取α=。
T2 (0,1/ 2,1/ 2)当λ3=1 时,解方程(E−A)X=0,由⎛−1 0 0 ⎞⎛1 0 0⎞⎜⎟⎜⎟A−E=⎜−−⎟→⎜0 2 2 0 1 1,⎟⎜−−⎟⎜⎟0 2 2 0 0 0 ⎝⎠⎝⎠得特征向量(0,−1,1)T.取α=−−。
T3 (0, 1/ 2, 1/ 2)于是有正交矩阵Q=(α,α,α) 和正交变换X=QY,使1 2 3f=2y12+5y22+y32。
(10 分)(2) 因为该二次型的正惯性指数为3,故该二次型为正定二次型。
(13 分)14. 解:设A=“顾客买下该箱玻璃杯”,B=“该箱中恰有i个残次品”,i=0,1。
i(1)由全概率公式有P(A) =P(B)P(A| B) +P(B)P(A| B)0 0 1 1C C2 2=×8 +×7 =。
(7 分)0.8 0.2 0.95C C2 28 8第2 页共4 页(2)由贝叶斯公式有P(B)P(A| B)P(B| A) =0 00 +P(B)P(A| B) P(B)P(A| B)0 0 1 1=C220.8×8C8C C2 20.8×8+0.2×7C C2 28 8=0.842。
(13 分)15. 解:设(X,Y) 的联合概率密度函数为f(x, y)⎧∈2 (x, y) G =⎨0 (x, y)∉G ⎩⎧⎪≤≤x∫2dy, 0 x 1+∞∫f(x) =f(x, y)dy=⎨X−∞⎪0, 其他⎩⎧2x, 0 ≤x≤1 =⎨⎩0, 其他同理⎧≤≤1∫⎪2dx, 0 y 1+∞∫f(y) =f(x, y)dx=⎨yY−∞⎪⎩0,其他⎧2(1−y), 0 ≤y≤1=⎨⎩其他0,因为f(x, y) ≠f(x) f(y) ,所以X,Y不独立。
(7 分)X Y1 2 EX=∫x⋅xdx=⋅x=,1 3 12 2 |3 3 02 2 EY=∫y⋅−y dy=y−y=−=1 2 3 12 (1 ) ( ) | 13 30 13,EXY=∫∫xydxdy=∫∫xydy dx2 [ 2 ]1 x0 0G11 x 12 x =∫∫=∫⋅2x[ ydy]dx2x y| dx20 0 01 11 2 4 1 =∫⋅= =2x x dx x|2 414,1 2 1 1Cov(X,Y) =EXY−EXEY=−⋅=≠0 ,4 3 3 36故X,Y相关。
(13 分)16.解:先求θ的矩估计量μ1+∞−−+∞−=EX=∫xeθdx=eθ∫xedx(x) xθθ+∞−−+∞+∞=−eθ∫xd e=−eθxe−∫e d]( x) [ x| −x xθθθ=−eθ[0 −θe−θ+e−x|+∞] =−eθ[−θe−θ−e−θ]θ第3 页共4 页=eθθe−θ+e−θ=θ+1。
[ ]A=X。
1令μ 1 =A1 ,则有ˆX 1 θ=−,即为θ的矩估计量。
(7 分)再求θ的最大似然估计量。
似然函数为n∑n n nθ−xL(x, , x; ) f(x; ) e e",θθθ−x=∏=∏=ii i=11 n ii=1 i=1lnnL nθx =−∑,ii=1d ln Ldθ=n>0 ,即ln L为θ的递增函数,又因为对任意的i,有x≥θ,故θ的最大似然估计值为iˆminθ=x。
ii最大似然估计量为ˆminθ=X。
(13 分)ii五、证明题(每小题6分,共6分)17. 证明:由A3 =0得到A3 −E=−E,即(A−E)(A2 +A+E) =−E,(3 分)故(A−E)(−(A2 +A+E)) =E,因而A−E可逆。
(6 分)第4 页共4 页。
