2011一次函数单元测试卷
(完整)(一次函数单元测试题含答案),推荐文档

一次函数单元测试题(分数120分时间:120分钟)一、选择题(本大题共10小题,共30分)1.一次函数y=(k+2)x+k2−4的图象经过原点,则k的值为()A. 2B. −2C. 2或−2D. 32.已知一次函数y=kx+b−x的图象与x轴的正半轴相交,且函数值y随自变量x的增大而增大,则k,b的取值情况为( )A. k>1,b<0B. k>1,b>0C. k>0,b>0D. k>0,b<03.若直线y=kx+b经过第一、二、四象限,则直线y=bx+k的图象大致是()A. B. C. D.4.已知直线y=(m−3)x−3m+1不经过第一象限,则m的取值范围是()A. m≥13B. m≤13C. 13≤m<3 D. 13≤m≤35.下列函数关系式中:①y=2x+1;②y=1x ;③y=x+12−x;④s=60t;⑤y=100−25x,表示一次函数的有()A. 1个B. 2个C. 3个D. 4个6.如图,直线y=23x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,当PC+PD最小时,点P的坐标为()A. (−3,0)B. (−6,0)C. (−32,0) D. (−52,0)7.如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是()A. 乙前4秒行驶的路程为48米B. 在0到8秒内甲的速度每秒增加4米/秒C. 两车到第3秒时行驶的路程相等D. 在4至8秒内甲的速度都大于乙的速度8.如图,△ABC是等腰直角三角形,∠A=90∘,BC=4,点P是△ABC边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则下列能大致反映y与x函数关系的图象是( )A. B. C. D.9.小明、小华从学校出发到青少年宫参加书法比赛,小明步行一段时间后,小华骑自行车沿相同路线行进,两人均匀速前行.他们的路程差s(米)与小明出发时间t(分)之间的函数关系如图所示.下列说法:①小华先到达青少年宫;②小华的速度是小明速度的2.5倍;③a=24;④b=480.其中正确的是()A. ①②④B. ①②③C. ①③④D. ①②③④10.已知一次函数y=ax+4与y=bx−2的图象在x轴上相交于同一点,则ba的值是( )A. 4B. −2C. 12D. −12二、填空题(本大题共10小题,共30分)11.函数y=√x+2−√3−x中自变量x的取值范围是______.12.如果直线y=−2x+b与两坐标轴所围成的三角形面积是9,则b的值为______ .13.已知y−2与x成正比例,当x=1时,y=5,那么y与x的函数关系式是______ .14.正方形A1B1C1O,A2B2C2C1,A3B3C3C2…按如图所示放置,点A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,则A n的坐标是 .15.已知一次函数y=(−3a+1)x+a的图象经过一、二、三象限,不经过第四象限,则a的取值范围是______ .16.经过点(2,0)且与坐标轴围成的三角形面积为2的直线解析式是______ .17.如图,在平面直角坐标系中,直线y=−√52x+2√5与x轴,y轴分别交于点A,B,将△AOB沿过点A的直线折叠,使点B落在x轴的负半轴上,记作点C,折痕与y轴交于点D,则点D的坐标为______ 。
一次函数单元测试卷(含答案)

一次函数单元测试卷班级___________座号___________##___________评分___________一、选择题〔每小题5分,共25分〕1、下列函数〔1〕y =πx <2>y =2x -1 <3>y =错误! <4>y =2-1-3x <5>y =x 2-1中,是一次函数的有〔〕A 、4个B 、3个C 、2个D 、1个2、下列哪个点在一次函数43-=x y 上〔〕.A 、<2,3>B 、<-1,-1>C 、<0,-4>D 、<-4,0>3、若一次函数y =kx -4的图象经过点〔–2,4〕,则k 等于〔〕A 、–4B 、4C 、–2D 、24、点P 1〔x 1,y 1〕,点P 2〔x 2,y 2〕是一次函数y =-4x + 3 图象上的两个点,且x 1<x 2,则y 1与y 2的大小关系是〔〕.A 、y 1>y 2B 、y 1>y 2 >0C 、y 1<y 2D 、y 1=y 25、2012年"国际攀岩比赛"在重庆举行.小丽从家出发开车前去观看,途中发现忘了带门票,于是打 让妈妈马上从家里送来,同时小丽也往回开,遇到妈妈后聊了一会儿,接着继续开车前往比赛现场.设小丽从家出发后所用时间为t ,小丽与比赛现场的距离为S .下面能反映S 与t 的函数关系的大致图象是< >二、填空题〔每小题5分,共50分〕6、当k =________时,y =<k +1>x 2k +k 是一次函数;当m =_______时,y =<m -1>x 2m 是正比例函数.7、若一次函数y =<m -3>x +<m -1>的图像经过原点,则m =,此时y 随x 的增大而.8、一个函数的图象经过点〔1,2〕,且y 随x 的增大而增大,则这个函数的解析式是〔只需写一个〕9、一次函数y =-3x -1的图像经过点〔0,〕和〔,-7〕.10、一次函数y = -2x +4的图象与x 轴交点坐标是,与y 轴交点坐标是,图象与坐标轴所围成的三角形面积是.11、一次函数y =-2x +3的图像不经过的象限是_________12、若三点)1,0(),,2(),0,1(-P 在一条直线上,则P 的值为_________13、已知函数4-=+-=mx y m x y 与的图象的交点在x 轴的负半轴上,则=m ______.14、某市出租车的收费标准是:3千米以内〔包括3千米〕收费5元,超过3千米,每增加1千米加收1.2元,则路程x 〔x ≥3〕时,车费y 〔元〕与路程x 〔千米〕之间的关系式为:.15、我市某出租车公司收费标准如图所示,如果小明只有19元钱,那么他乘此出租车最远能到达公里处三、解答题〔每小题9分,共45分〕 16、某移动通讯公司开设两种业务."全球通":先缴50元月租费,然后每通话1分钟,再付0.4元,"神州行":不缴纳月租费,每通话1分钟,付话费0.6元.若设一个月内通话x 分钟,两种方式的费用分别为y 1和y 2元.〔1〕写出y 1、y 2与x 之间的函数关系式.〔2〕一个月内通话多少分钟,两种费用相同.〔3〕某人估计一个月内通话300分钟,应选择哪种合算?17、已知一次函数y =kx +b 的图象经过点<0, -3>,且与正比例函数y = 错误!x 的图象相交于点<2,a >, 求: <1>a 的值; <2> k ,b 的值;18、已知y 与z 成正比例,z +1与x 成正比例,且当x =1时,y =1;当x =0时,y =-3.求y 与x的函数关系式.19、已知一次函数434+-=x y .<1>求其图象与坐标轴围成的图形的面积;<2>求其图象与坐标轴的两个交点间的线段AB的长度;<3>求原点到该图象的垂线段OC的长度.20、在社会主义新农村建设中,衢州某乡镇决定对A,B两村之间的公路进行改造,并由甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y<米>与施工时间x<天>之间的函数图象,请根据图象所提供的信息解答下列问题:〔1〕乙工程队每天修公路多少米?〔2〕分别求甲、乙工程队修公路的长度y<米>与施工时间x<天>之间的函数关系式. 〔3〕若该工程由甲、乙两工程队一直合作施工,需几天完成?参考答案一、1、B 2、C 3、A 4、A 5、B二、6、1,-1 7、1,减小 8、y =2x 9、-1,-210、〔2,0 〕,〔0,4〕,4 11、第四象限 12、1 13、-214、y =1.2x +1.4 15、13三、16、 <1>y 1=50+0.4x ,y 2=0.6x<2>令y 1=y 2得:50+0.4x =0.6xx =250,即一个月通话250分钟时,费用相同.<3>当x =300时,y 1=170,y 2=180∴选择"全球通"合算.17、〔1〕将<2,a > 代入y = 错误!x 可解得:1=a ,〔2〕将<0, -3> ,<2,1>分别代入y =kx +b 可解得:3,2-==b k .18、解:设z +1=kx ,则z =kx -1,又设y =mz =m 〔kx -1〕=mkx -m .当x =1时,y =1,∴ 1=mk -m ,当x =0时,y =-3,∴ -3=0-m ,解得m =3.34k =, ∴ y =4x -3; 19、解:设一次函数434+-=x y 的图象与坐标轴交点为A 、B . 〔1〕分别将y =0,x =0代入434+-=x y ,得A 〔3,0〕,B 〔0,4〕 ∴3||=OA ,4||=OB .∴ 64321||||21=⨯⨯=⋅=∆OB OA S OAB . 〔2〕由勾股定理得543||22=+=AB .〔3〕∵ ||||21OC AB S AOB ⋅=∆,〔|OC |为原点到图象的垂线段长度〕,则 6||521=⋅⋅OC ,∴ 512||=OC . 20、[解析]〔1〕乙工程队一共修公路720米,总共修了<9-3>天;〔2〕观察图象,用待定系数法求修公路的长度y <米>与施工时间 x <天>之间的函数关系式. 〔3〕列出一元一次方程求解.解:〔1〕∵720÷<9-3>=120∴乙工程队每天修公路120米.〔2〕设y 乙=kx+b ,则309720k b k b +⎧⎨+⎩== ∴120360k b ⎧⎨-⎩==∴y 乙=120x -360 当x =6时,y 乙=360设y 甲=kx ,则360=6k ,k =60,∴y 甲=60x〔3〕当x =15时,y 甲=900,∴该公路总长为:720+900=1620<米>设需x 天完成,由题意得,<120+60>x =1620解得x =9答:需9天完成[点评]本题考查了函数的图象和一次函数的应用,培养学生观察图象的能力,分析解决问题的能力,要培养学生视图知信息的能力.解决此类题目最关键的地方是经过认真审题,从中整理出一次函数模型,用一次函数的知识解决此类问题.。
一次函数单元测试卷及答案

《一次函数》单元测验题班级:班级: 姓名:姓名: 座号:座号: 成绩:________一.选择题(每小题3分,共30分)1.在平面直角坐标系中,点(-1,-2)所在的象限是所在的象限是 ( ) A 、第一象限、第一象限 B 、第二象限、第二象限 C 、第三象限、第三象限 D 、第四象限、第四象限2. 2.函数函数1y x =-中,自变量x 的取值范围是的取值范围是 ( ) ( ) A . x < 1 B . x ≤ 1 C . x > 1 D . x ≥13. 3. 在函数在函数在函数 y y y==3x 3x--2,y =1xx +3,y =-=-2x 2x 2x,,y =-=-x x 2+7 7 是正比例函数的有是正比例函数的有( ) A . 0 . 0 个个 B . 1 . 1 个个 C . 2 . 2 个个 D . 3 . 3 个个4.点M (1,2)关于x 轴对称点的坐标为(轴对称点的坐标为( )A 、(-1,2)B 、(-1,-2)C 、(1,-2)D 、(2,-1)5. 如图,所示的象棋盘上,若○帅位于点(1,-2)上,○相 位于点(3,-2)上,则○炮位于点(位于点() A. (-1,1) B. (-1,2)C. (-2,1)D. (-2,2)6. 一次函数y=y=--2x+3的图像不经过的象限是(的图像不经过的象限是( )).A A 第一象限第一象限第一象限B B B 第二象限第二象限第二象限C C C 第三象限第三象限第三象限D D D 第四象限第四象限第四象限7.一天,小军和爸爸去登山,已知山脚到山顶的路程为300米.小军先走了一段路程,爸爸才开始出发.图中两条线段分别表示小军和爸爸离开山脚登山的路程S(米)与登山所用的时间t (分)的关系(从爸爸开始登山时计时).根据图象,下列说法错误的是( )A .爸爸登山时,小军已走了50米B .爸爸走了5分钟,小军仍在爸爸的前面分钟,小军仍在爸爸的前面 C .小军比爸爸晚到山顶.小军比爸爸晚到山顶D .爸爸前10分钟登山的速度比小军慢,10分钟后分钟后登山的速度比小军快登山的速度比小军快8.下列函数中,y 随x 的增大而减小的有(的增大而减小的有( )①12+-=x y ② x y -=6③ 31xy +-= ④x y )21(-=A.1个B.2个C.3个D.4个9.直线.直线 y=43 x +4与 x 轴交于轴交于 A,与y 轴交于B, O 为原点,则为原点,则图3相帅炮ab a k= ,b= .k= ,b= . 0 9 9 16 16 30 t /min S /km 40 12 19.(8分) 已知正比例函数x k y 1=的图像与一次函数92-=x k y 的图像交于点P (3,-6)。
珠厦中学2011-2012学年度第一学期《一次函数》单元测试卷3

班级:_____________ 姓名:____________ 座号:__________ 分数:______________一. 选择题(把正确答案填入表格内,每小题3分,共24分)题号 1 2 3 4 5 6 7 8 答案1.下列函数(1)y =πx ;(2)y =2x -1;(3)y =1x ;(4)y =x 2-1中,是一次函数的有( )A .4个B .3个C .2个D .1个 2.一次函数y=2x-3的图象不经过的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限 3.函数2y x =+中,自变量x 的取值范围是( )A .2x >-B .2x -≥C .2x ≠-D .2x -≤4.若正比例函数的图像经过点(-1,2),则这个图像必经过点( ) A .(1,2) B .(-1,-2) C .(2,-1) D .(1,-2) 5.下列各图给出了变量x 与y 之间的函数是:( )6.已知一次函数y=kx+b 的图象(如图),当y <0时,x 的取值范围是( )(A )x >0 (B )x <0 (C )x <1 (D )x >1 7.P 1(x 1,y 1),P 2(x 2,y 2)是正比例函数y= - x 图象上的两点,则下列判断正确的是( ) A .y 1>y 2 B .y 1<y 2 C .当x 1<x 2时,y 1>y 2 D .当x 1<x 2时,y 1<y 28.如图,乌鸦口渴到处找水喝,它看到了一个装有水的瓶子,但水位较低,且瓶口又小,乌鸦喝不着水,沉思一会后,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水。
在这则乌鸦喝水的故事中,从乌鸦看到瓶的那刻起开始计时并设时间为x ,瓶中水位的高度为y , 下列图象中最符合故事情景的是:二. 填空题(每题3分,共21分)9、已知函数:①y=0.2x+6;②y=-x-7;③y=4-2x ;④y=-x ;⑤y=4x ;⑥y=-(2-x),其中,y 的值随x 的增大而增大的函数是_____________;y 的值随x 的增大而减小的函数是________________10、已知正比例函数y =(m -1)25m x-的图象在第二、四象限,则m 的值为_________,此函数解析式为:________________-2 1 x yO (第6题) x y o A x y o B xy o D x y o Cxy 02311、函数y=1x -2自变量x 的取值范围是_________. 12、把直线y=-2x+1沿y 轴向上平移2个单位,所得直线的函数关系式为_____________ 13、一次函数y=-2x+4的图象与x 轴交点坐标是________,与y 轴交点坐标是________ 14、根据下图所示的程序计算函数值,若输入的x 值为23,则输出的结果为15、正方形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2,…按如图所示的方式放置.点A 1,A 2,A 3和点C 1,C 2,C 3,…分别在直线y kx b =+(k >0)和x 轴上,已知点B 1(1,1),B 2(3,2), 则B n 的坐标是______________. 第16题图三、解答题:(共55分)16、(本题6分)已知一次函数y=kx+b 的图像如上图所示,求其函数关系式?17、(本题6分)已知一次函数的图象与y= -21x 的图像平行,且与y 轴交点(0,-3),求此函数关系式?18、(本题9分)下图是北京春季某一天的气温随时间变化的图象,根据图象回答,在这一天:(1)8时、12时、20时的气温各是多少?(2)最高气温与最低气温各是多少?yxOC 1B 2A 2 C 3B 1 A 3B 3A 1 C 2(第15题图)输入x 值)12(2-≤≤-+=x x y)11(≤≤-=x x y )21(2≤≤+-=x x y 输出y 值(3)什么时间气温最高,什么时间气温最低?19、(本题10分)如图,一次函数138 55y x=-+和221y x=-相交于点A,(1) 求交点A的坐标?(2) 求两函数与y轴所围成的三角形的面积?20、(本题12分)一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.(1)农民自带的零钱是多少?(2)试求降价前y与x之间的关系式(3)由表达式你能求出降价前每千克的土豆价格是多少?(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?21、(本题12分)A市和B市分别库存某种机器12台和6台,现决定支援给C 市10台和D市8台.•已知从A市调运一台机器到C市和D市的运费分别为400元和800元;从B 市调运一台机器到C市和D市的运费分别为300元和500元.(1)设B市运往C市机器x台,•求总运费Y(元)关于x的函数关系式.(2)若要求总运费不超过9000元,问共有几种调运方案?(3)求出总运费最低的调运方案,最低运费是多少?。
一次函数单元测试题.docx

一次函数单元测试题一、选择题(每题2分,共20分)1. 一次函数的一般形式是()A. \( y = ax + b \)(\( a \neq 0 \))B. \( y = ax^2 + b \)C. \( y = a + bx \)D. \( y = b + ax \)2. 如果直线 \( y = 3x + 2 \) 与x轴相交于点(1,0),那么下列说法正确的是()A. \( a = 3 \),\( b = 2 \)B. 直线经过第一象限C. 直线不经过第二象限D. 直线经过原点3. 直线 \( y = -2x + 5 \) 的斜率是()A. 2B. -2C. 5D. 04. 一次函数 \( y = kx + b \) 经过点(2,5)和(-1,-1),则\( k \) 的值是()A. 2B. -2C. 3D. -35. 下列哪个方程不是一次函数的方程()A. \( y = 3x - 4 \)B. \( y = 2x + 1 \)C. \( y = x^2 \)D. \( y = -5x + 7 \)二、填空题(每题2分,共10分)6. 一次函数 \( y = 4x - 6 \) 与y轴的交点坐标是 _________ 。
7. 如果一次函数 \( y = kx + b \) 的图象过点(3,5)和(-2,-3),那么 \( b \) 的值是 _________ 。
8. 直线 \( y = -x + 3 \) 与直线 \( y = 2x - 4 \) 的交点坐标是_________ 。
9. 一次函数 \( y = 5x + 1 \) 的斜率是 _________ 。
10. 当 \( k > 0 \) 时,一次函数 \( y = kx + b \) 的图象是上升的,那么 \( b \) 的值可以是 _________ (填“正数”或“负数”或“零”)。
三、解答题(每题15分,共30分)11. 已知一次函数 \( y = kx + b \) 经过点(1,2)和(-1,0),求 \( k \) 和 \( b \) 的值,并写出函数的解析式。
一次函数单元测试卷(含答案)
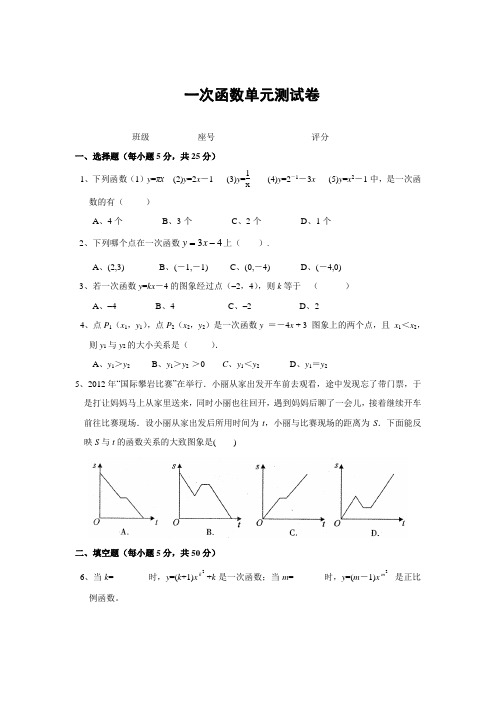
一次函数单元测试卷班级___________座号______________________评分___________一、选择题(每小题5分,共25分)1、下列函数(1)y =πx (2)y =2x -1 (3)y =1x(4)y =2-1-3x (5)y =x 2-1中,是一次函数的有( )A 、4个B 、3个C 、2个D 、1个2、下列哪个点在一次函数43-=x y 上( ).A 、(2,3)B 、(-1,-1)C 、(0,-4)D 、(-4,0)3、若一次函数y =kx -4的图象经过点(–2,4),则k 等于 ( )A 、–4B 、4C 、–2D 、24、点P 1(x 1,y 1),点P 2(x 2,y 2)是一次函数y =-4x + 3 图象上的两个点,且 x 1<x 2,则y 1与y 2的大小关系是( ).A 、y 1>y 2B 、y 1>y 2 >0C 、y 1<y 2D 、y 1=y 25、2012年“国际攀岩比赛”在举行.小丽从家出发开车前去观看,途中发现忘了带门票,于是打让妈妈马上从家里送来,同时小丽也往回开,遇到妈妈后聊了一会儿,接着继续开车前往比赛现场.设小丽从家出发后所用时间为t ,小丽与比赛现场的距离为S .下面能反映S 与t 的函数关系的大致图象是( )二、填空题(每小题5分,共50分)6、当k =________时,y =(k +1)x 2k +k 是一次函数;当m =_______时,y =(m -1)x 2m 是正比例函数。
7、若一次函数y =(m -3)x +(m -1)的图像经过原点,则m = ,此时y 随x 的增大而 .8、一个函数的图象经过点(1,2),且y 随x 的增大而增大,则这个函数的解析式是(只需写一个)9、一次函数y =-3x -1的图像经过点(0, )和( ,-7).10、一次函数y = -2x +4的图象与x 轴交点坐标是 ,与y 轴交点坐标是 , 图象与坐标轴所围成的三角形面积是 .11、一次函数y =-2x +3的图像不经过的象限是_________12、若三点)1,0(),,2(),0,1(-P 在一条直线上,则P 的值为_________13、已知函数4-=+-=mx y m x y 与的图象的交点在x 轴的负半轴上,则=m ______.14、某市出租车的收费标准是:3千米以(包括3千米)收费5元,超过3千米,每增加1千米加收1.2元,则路程x (x ≥3)时,车费y (元)与路程x (千米)之间的关系式为: .15、我市某出租车公司收费标准如图所示,如果小明只有19元钱,那么他乘此出租车最远能到达 公里处三、解答题(每小题9分,共45分)16、某移动通讯公司开设两种业务.“全球通”:先缴50元月租费,然后每通话1分钟,再付0.4元,“神州行”:不缴纳月租费,每通话1分钟,付话费0.6元。
一次函数单元测试题(含答案)

一次函数测试题一、选择题(每小题3分,共24分)1.下列函数中,自变量x 的取值范围是x ≥2的是( )A .y=2x -B .y=12x - C .y=24x - D .y=2x +·2x - 2.下列函数中,y 是x 的正比例函数的是( ) A .y=2x-1 B .y=3xC .y=2x 2D .y=-2x+1 3.一次函数y=-5x+3的图象经过的象限是( ) A .一、二、三 B .二、三、四 C .一、二、四 D .一、三、四4.若函数y=(2m+1)x 2+(1-2m )x (m 为常数)是正比例函数,则m 的值为( ) A .m>12 B .m=12 C .m<12 D .m=-125.若一次函数y=(3-k )x-k 的图象经过第二、三、四象限,则k 的取值范围是( ) A .k>3 B .0<k ≤3 C .0≤k<3 D .0<k<36.已知一次函数的图象与直线y=-x+1平行,且过点(8,2),那么此一次函数的解析式为( ) A .y=-x-2 B .y=-x-6 C .y=-x+10 D .y=-x-17.一次函数y=kx+b 的图象经过点(2,-1)和(0,3),•那么这个一次函数的解析式为( ) A .y=-2x+3 B .y=-3x+2 C .y=3x-2 D .y=12x-3 8.李老师骑自行车上班,最初以某一速度匀速行进,•中途由于自行车发生故障,停下修车耽误了几分钟,为了按时到校,李老师加快了速度,仍保持匀速行进,如果准时到校.在课堂上,李老师请学生画出他行进的路程y•(千米)与行进时间t (小时)的函数图象的示意图,同学们画出的图象如图所示,你认为正确的是( )二、填空题(每小题4分,共40分)9.已知自变量为x 的函数y=mx+2-m 是正比例函数,则m=________,•该函数的解析式为_________. 10.若点(1,3)在正比例函数y=kx 的图象上,则此函数的解析式为________.11.已知一次函数y=kx+b 的图象经过点A (1,3)和B (-1,-1),则此函数的解析式为_________. 12.若解方程x+2=3x-2得x=2,则当x_________时直线y=x+•2•上的点在直线y=3x-2上相应点的上方. 13.已知一次函数y=-x+a 与y=x+b 的图象相交于点(m ,8),则a+b=_________.14.若一次函数y=kx+b 交于y•轴的负半轴,•且y•的值随x•的增大而减少,•则k____0,b______0.(填“>”、“<”或“=”)15.已知直线y=x-3与y=2x+2的交点为(-5,-8),则方程组30220x y x y --=⎧⎨-+=⎩的解是________.16.已知一次函数y=-3x+1的图象经过点(a ,1)和点(-2,b ),则a=________,b=______.17.如果直线y=-2x+k 与两坐标轴所围成的三角形面积是9,则k 的值为_____.18.如图,一次函数y=kx+b 的图象经过A 、B 两点,与x 轴交于点C ,则此一次函数的解析式为__________,△AOC 的面积为_________. 三、应用题(共36分)23.(12分)一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:(1)农民自带的零钱是多少?(2)降价前他每千克土豆出售的价格是多少?(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?24.(12分)如图所示的折线ABC•表示从甲地向乙地打长途电话所需的电话费y (元)与通话时间t (分钟)之间的函数关系的图象.(1)写出y 与t•之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?25.(12分)已知雅美服装厂现有A 种布料70米,B 种布料52米,•现计划用这两种布料生产M 、N 两种型号的时装共80套.已知做一套M 型号的时装需用A 种布料1.•1米,B 种布料0.4米,可获利50元;做一套N 型号的时装需用A 种布料0.6米,B 种布料0.•9米,可获利45元.设生产M 型号的时装套数为x ,用这批布料生产两种型号的时装所获得的总利润为y 元. ①求y (元)与x (套)的函数关系式,并求出自变量的取值范围; ②当M 型号的时装为多少套时,能使该厂所获利润最大?最大利润是多?xy1234-2-1CA-14321O答案:411.D 2.D 3.B 4.C 5.D 6.A 7.C 8.B 9.C 10.A 11.2;y=2x 12.y=3x 13.y=2x+1 14.<2 15.1616.<;< 17.58xy=-⎧⎨=-⎩18.0;7 19.±6 20.y=x+2;421.①y=169x;②y=15x+7522.y=x-2;y=8;x=1423.①5元;②0.5元;③45千克24.①当0<t≤3时,y=2.4;当t>3时,y=t-0.6.②2.4元;6.4元25.①y=50x+45(80-x)=5x+3600.∵两种型号的时装共用A种布料[1.1x+0.•6(80-x)]米,共用B种布料[0.4x+0.9(80-x)]米,∴解之得40≤x≤44,而x为整数,∴x=40,41,42,43,44,∴y与x的函数关系式是y=5x+3600(x=40,41,42,43,44);②∵y随x的增大而增大,∴当x=44时,y最大=3820,即生产M型号的时装44套时,该厂所获利润最大,最大利润是3820元.。
一次函数_单元测试含答案

二、单选题:本大题共8小题,从第4小题到第5小题每题3.0分小计6.0分;从第6小题到第11小题每题4.0分小计24.0分;共计30.0分。
4、函数y=中,自变量x的取值范围是[]A.x>B.x<C.x≠D.x≠25、一列火车从青岛站出发,加速行驶一段时间后开始匀速行驶.过了一段时间,火车到达下一个车站,乘客上下车后,火车又加速,一段时间后再次开始匀速行驶.下面图________可以近似地刻画出火车在这段时间内的速度变化情况.[]A B C.D.6、正比例函数如图1所示,则这个函数的解析式为[]A.B.C.D.图1 图2 图37、下列函数中, 不是一次函数的是[ ]A.y=3xB.y=2-xC.y=x-D.y= -38、一次函数的图像不经过[]A.第一象限B.第二象限C.第三象限D.第四象限9、已知一次函数图像如图2所示,那么这个一次函数的解析式是[]A.B.C.D.11、弹簧的长度与所挂物体的质量的关系为一次函数,如图3所示,由此图可知不挂物体时弹簧的长度为[]A.7cm B.8 cm C.9 cm D.10 cm10、下列说法中正确的是[]A.用图象表示变量之间的关系时,用竖直方向上的点表示自变量;B.用图象表示变量之间的关系时,用水平方向上的点表示因变量;C.用图象表示变量关系用横轴上的点表示因变量;D.用图象表示变量关系用纵轴上的点表示因变量.三、填空题:本大题共6小题,从第12小题到第15小题每题3.0分小计12.0分;从第16小题到第17小题每题4.0分小计8.0分;共计20.0分。
12、一次函数y=kx+5的图象过点A(-2,-1),则k=________.13、正比例函数y=2x的图象经过第________象限.14、两港相距600千米,轮船以10千米/小时的速度航行,t小时后剩下的距离y与t的函数关系式________.15、已知一次函数的图象与y轴的交点的纵坐标为-2,且经过点(5,3),则此函数的表达式为________.16、当b为________时,直线与直线的交点在x轴上.17、已知函数y=的图象经过点B(m,),则m=________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第12、13章单元测试卷2011.10
班级 姓名 学号 成绩
一、选择题(每题3分,共30分)
1、下列各点中,在函数52+-=x y 的图象上的是 ( ) A 、(0,―5) B 、(2,9) C 、(–2,–9) D 、(4,―3)
2、下列函数①x y -=;②;112+=x y ③12++=x x y ;④x
y 1
=
中,一次函数的有( ) A 、4个 B 、3个 C 、2个 D 、1个
3、若函数m x m y 21)31(-+-=(m 为常数)是正比例函数,则m 的值为 ( ) A 、21>
m B 、21<m C 、21=m D 、2
1
-=m m
4、已知点P (x ,-4)不在..第三象限,则x 应满足的条件是 ( )
A 、0>x
B 、0≥x
C 、0<x
D 、0≤x
5、已知一次函数y =kx +b 的图象如右图所示,则k 、b 的符号是 ( )
A 、k >0,b >0
B 、k >0,b <0
C 、k <0,b >0
D 、k <0,b <0 6、若一次函数的图像与直线1+-=x y 平行,且过点(8,2),则此一次函
数的解析式为 ( ) A 、2--=x y B 、6--=x y C 、10+-=x y D 、1--=x y 7、如右图所示,一个蓄水桶,60min 可匀速将一满桶水放干.其中,水位h (cm )随着放水时间t (min )的变化而变化.h 与t 的函数的大致图像为 ( )
8、一次函数y ax b =+的图象(如左下图)经过A 、B 两点,则关于x 的不等式0<+b ax 的解集为 ( ) A 、2<x B 、0<x C 、2>x D 、0>x
9、弹簧的长度y cm 与所挂物体的质量x(kg)的关系是一次函数,图象如左下图所示,则弹簧不挂物体时的长度是 ( ) A 、9cm B 、10cm C 、10.5cm D 、11cm
10、小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜之后,余下的每千克降价0.4元,全部售完。
销售金额与卖瓜的千克数之间的关系如图所示,那么小李赚了 ( ) A 、32元 B 、36元 C 、38元 D 、44元 二、填空题(每题4分,共24分) 11、函数1
2
-=
x y 中,自变量x 的取值范围是 12、若点(1,3)在正比例函数kx y =的图像上,则此函数的解析式为 。
13、一次函数48+-=x y 的图象与x 轴交点坐标是_________,与y 轴交点坐标是___ ___ 图象与坐标轴所围成的三角形的面积是________________.
14、某人用充值50元的IC 卡从A 地向B 地打长途电话,按通话时间收费,3分钟内收费2.4元,以后每超过1分钟加收1元,若此人第一次通话t 分钟(3≤t ≤50),则IC 卡上所余的费用y (元)与t (分)之间的关系式是 。
15、如图,已知函数y ax b =+和y kx =的图象交于点P, 则根据图象可得,关于
y ax b
y kx =+⎧⎨
=⎩
的二元一次方程组的解是 16、已知A 地在B 地的正南方向3km 处,甲、乙两人同时分别从A ,B 两地向正北方向匀速直线前进,他们到A 地的距离s (km )与所用时间t (h )之间的函数关系的图象如图所示,当他们走了3h 的时候,则他们之间的距离是
三、解答题
17、(6分)已知3-y 与x 成正比,且当2=x 时,9=y
第10题图
第8题图 第9题图 第5题图 第6题图
(1)求y 与x 之间的函数关系式 (2)当3-=x 时,求y 的值 18、(6分)已知△ABC ,△ABC 中A 点平移到A 1(4,5),作出平移后的△A 1B 1C 1。
(1)写出B 1,C 1点的坐标。
(2)求出△ABC 的面积。
19、(8分)某种拖拉机的油箱可储油40L ,加满油并开始工作后,•油箱中的余油量y (L )与工作时间x (h )之间为一次函数关系,如图所示. (1)求y 与x 的函数解析式.
(2)一箱油可供拖位机工作几小时?
20、(8分)某化工厂现有甲种原料7吨,乙种原料5吨,现计划用这两种原料生产两种不同的化工产品A 和B 共
销售A B ,两种产品获得的利润分别为万元/吨、万元/吨.若设化工厂生产A 产品x 吨,且销售这两种产品所获得的总利润为y 万元. (1)求y 与x 的函数关系式 (2)求出x 的取值范围;
(3)问化工厂生产A 产品多少吨时,所获得的利润最大?最大利润是多少?
21、(8分)两张同样大小的矩形纸片相互重合,现将上面的一张纸向右平移(•如图),已
知矩形的一组邻边的长为30cm,10cm.
(1)求两张纸片重叠部分的面积y关于平移距离x•的函数关系式和自变量的取值范围;(2)若要使重叠部分的面积不超过100cm2,则至少要向右平移多少厘米?
22、(10分)我边防局接到情报,近海处有一可疑船只向正北方向行驶,边防局迅速派出
快艇B追击,如图l1,l2分别表示两船相对于海岸的距离S(海里)与追赶时间t(分)之
间的关系,根据图象,回答下列问题。
(1)求出两直线l1,l2 的函数关系式;
(2)快艇能否追上可疑船只?若能追上,大约需多少时间,离海岸多少海里?
附加题:(10分)已知:甲、乙两车分别从相距300千米的A B
,两地同时出发相向而行,甲到B地后立即返回,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)求出甲、乙两车离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数
关系式,并标明自变量x的取值范围;
(2
)。
