2014年全国高考理科数学试题-新课标2(word版)_2

合集下载

2014年全国高考理数真题试卷(新课标II卷)及解析

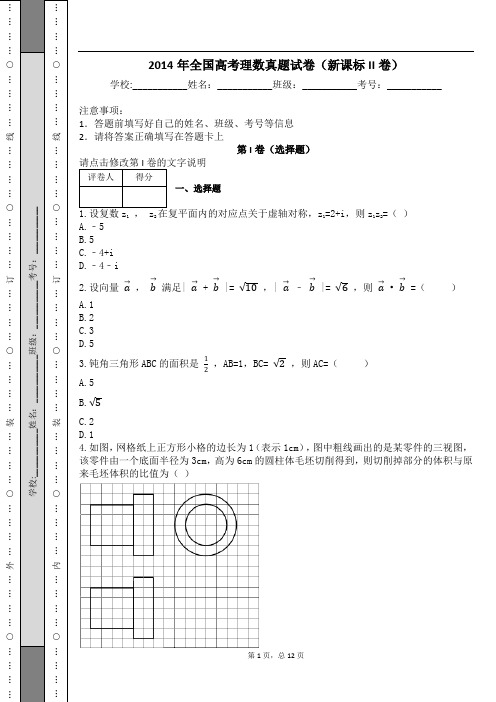
○…………外…………○…………学校:_________○…………内…………○…………2014年全国高考理数真题试卷（新课标II 卷）学校:___________姓名：___________班级：___________考号：___________注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题）一、选择题12z 1=2+i ，则z 1z 2=（） A.﹣5 B.5 C.﹣4+i D.﹣4﹣i2.设向量 a →， b →满足| a →+ b →|= √10 ，| a →﹣ b →|= √6 ，则 a →• b →=（） A.1 B.2 C.3 D.53.钝角三角形ABC 的面积是 12，AB=1，BC= √2 ，则AC=（） A.5 B.√5C.2D.1 4.如图，网格纸上正方形小格的边长为1（表示1cm ），图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（）答案第2页，总12页A.1727 B.59 C.1027 D.135.设F 为抛物线C ：y 2=3x 的焦点，过F 且倾斜角为30°的直线交C 于A ，B 两点，O 为坐标原点，则△OAB 的面积为（） A.3√34 B.9√38 C.6332 D.946.直三棱柱ABC ﹣A 1B 1C 1中，∠BCA=90°，M ，N 分别是A 1B 1 ， A 1C 1的中点，BC=CA=CC 1 ，则BM 与AN 所成角的余弦值为（） A.110 B.25 C.√3010 D.√227.设函数f （x ）= √3 sin πxm ，若存在f （x ）的极值点x 0满足x 02+[f （x 0）]2＜m 2 ，则m 的取值范围是（）A.（﹣∞，﹣6）∪（6，+∞）B.（﹣∞，﹣4）∪（4，+∞）C.（﹣∞，﹣2）∪（2，+∞）D.（﹣∞，﹣1）∪（1，+∞）第II 卷（非选择题）二、填空题（题型注释）（x+2φ）﹣2sinφcos（x+φ）的最大值为．9.已知偶函数f （x ）在[0，+∞）单调递减，f （2）=0，若f （x ﹣1）＞0，则x 的取值范围是．10.设点M （x 0 ， 1），若在圆O ：x 2+y 2=1上存在点N ，使得∠OMN=45°，则x 0的取值范围是．○…………外…………○………订…………○…………学校________考号：___________○…………内…………○………订…………○…………n 1n+1n （1）证明{a n + 12 }是等比数列，并求{a n }的通项公式；（2）证明： 1a 1+ 1a 2+…+ 1a n＜ 32 ．12.如图，四棱锥P ﹣ABCD 中，底面ABCD 为矩形，PA⊥平面ABCD ，E 为PD 的中点．（1）证明：PB∥平面AEC ；（2）设二面角D ﹣AE ﹣C 为60°，AP=1，AD= √3 ，求三棱锥E ﹣ACD 的体积．（1）求y 关于t 的线性回归方程；（2）利用（1）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入．附：回归直线的斜率和截距的最小二乘估计公式分别为： b ^=∑(t i −t ¯)(y i −y ¯)n i=1∑(t i −t ¯)2n i=1 ， a ^ = y ¯﹣b ^ t ¯．14.设F 1 ， F 2分别是C ： x 2a 2+y 2b 2=1 （a ＞b ＞0）的左，右焦点，M 是C 上一点且MF 2与x轴垂直，直线MF 1与C 的另一个交点为N ．答案第4页，总12页（1）若直线MN 的斜率为 34 ，求C 的离心率；（2）若直线MN 在y 轴上的截距为2，且|MN|=5|F 1N|，求a ，b ．15.在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，半圆C 的极坐标方程为ρ=2cosθ，θ∈[0， π2 ] （1）求C 的参数方程；（2）设点D 在半圆C 上，半圆C 在D 处的切线与直线l ：y= √3 x+2垂直，根据（1）中你得到的参数方程，求直线CD 的倾斜角及D 的坐标．○…………外…………○…………装………○…………线……学校:___________姓名__________○…………内…………○…………装………○…………线……参数答案1.A【解析】1.解：z 1=2+i 对应的点的坐标为（2，1）， ∵复数z 1 ， z 2在复平面内的对应点关于虚轴对称， ∴（2，1）关于虚轴对称的点的坐标为（﹣2，1），则对应的复数，z 2=﹣2+i ，则z 1z 2=（2+i ）（﹣2+i ）=i 2﹣4=﹣1﹣4=﹣5，故选：A【考点精析】本题主要考查了复数的乘法与除法的相关知识点，需要掌握设则；才能正确解答此题． 2.A【解析】2.解：∵| a →+ b →|= √10，| a →﹣ b →|= √6 ， ∴分别平方得 a →2+2 a →• b →+ b →2=10， a →2﹣2 a →• b →+ b →2=6，两式相减得4 a →• b →=10﹣6=4，即 a →• b →=1，故选：A ． 3.B【解析】3.解：∵钝角三角形ABC 的面积是 12 ，AB=c=1，BC=a= √2 ， ∴S= 12 acsinB= 12 ，即sinB= √22 ，当B 为钝角时，cosB=﹣ √1−sin 2B =﹣ √22 ，利用余弦定理得：AC 2=AB 2+BC 2﹣2AB•BC•cosB=1+2+2=5，即AC= √5 ，当B 为锐角时，cosB= √1−sin 2B = √22 ，利用余弦定理得：AC 2=AB 2+BC 2﹣2AB•BC•cosB=1+2﹣2=1，即AC=1，此时AB 2+AC 2=BC 2 ，即△ABC 为直角三角形，不合题意，舍去，则AC= √5 ．故选：B ．【考点精析】解答此题的关键在于理解余弦定理的定义的相关知识，掌握余弦定理:;;．答案第6页，总12页…………外………………○…………线………※※题※※…………内………………○…………线………4.C【解析】4.解：几何体是由两个圆柱组成，一个是底面半径为3高为2，一个是底面半径为2，高为4，组合体体积是：32π•2+22π•4=34π．底面半径为3cm ，高为6cm 的圆柱体毛坯的体积为：32π×6=54π 切削掉部分的体积与原来毛坯体积的比值为：54π−34π54π = 1027．故选：C ．【考点精析】通过灵活运用由三视图求面积、体积，掌握求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积即可以解答此题． 5.D【解析】5.解：由y 2=2px ，得2p=3，p= 32 ，则F （ 34 ，0）．∴过A ，B 的直线方程为y= √33 （x ﹣ 34 ），即x= √3 y+ 34 ．联立 {y 2=3x x =√3y +34，得4y 2﹣12 √3 y ﹣9=0．设A （x 1 ， y 1），B （x 2 ， y 2），则y 1+y 2=3 √3 ，y 1y 2=﹣ 94 ．∴S △OAB =S △OAF +S △OFB = 12 × 34 |y 1﹣y 2|= 38 √(y 1+y 2)2+4y 1y 2 = 38 × √(3√3)2+9 = 94 ．故选：D ．6.C【解析】6.解：直三棱柱ABC ﹣A 1B 1C 1中，∠BCA=90°，M ，N 分别是A 1B 1 ， A 1C 1的中点，如图：BC 的中点为O ，连结ON ，，则MN0B 是平行四边形，BM 与AN 所成角就是∠ANO，∵BC=CA=CC 1 ，设BC=CA=CC 1=2，∴CO=1，AO= √5 ，AN= √5 ，MB=== √6 ，…外…………○…………装订…………○…………线…………○…学校:___________姓考号：___________…内…………○…………装订…………○…………线…………○…在△ANO 中，由余弦定理可得：cos∠ANO= == √3010 ．故选：C ．【考点精析】本题主要考查了异面直线及其所成的角的相关知识点，需要掌握异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系才能正确解答此题． 7.C【解析】7.解：由题意可得，f （x 0）=± √3 ，且 πx0m =kπ+ π2 ，k∈z，即 x 0= 2k+12m ．再由x 02+[f （x 0）]2＜m 2 ，可得当m 2最小时，|x 0|最小，而|x 0|最小为 12 |m|， ∴m 2＞ 14m 2+3，∴m 2＞4．求得 m ＞2，或m ＜﹣2，故选：C ． 8.1【解析】8.解：函数f （x ）=sin （x+2φ）﹣2sinφcos （x+φ）=sin[（x+φ）+φ]﹣2sinφcos （x+φ） =sin （x+φ）cosφ+cos （x+φ）sinφ﹣2sinφcos （x+φ）=sin （x+φ）cosφ﹣cos （x+φ）sinφ=sin[（x+φ）﹣φ]=sinx，故函数f （x ）的最大值为1，所以答案是：1．【考点精析】关于本题考查的两角和与差的余弦公式和两角和与差的正弦公式，需要了解两角和与差的余弦公式：；两角和与差的正弦公式：才能得出正确答案．9.（﹣1，3）【解析】9.解：∵偶函数f （x ）在[0，+∞）单调递减，f （2）=0， ∴不等式f （x ﹣1）＞0等价为f （x ﹣1）＞f （2），答案第8页，总12页装…………○…………订…………○…※※要※※在※※装※※订※※线※※内※※答※※题※※装…………○…………订…………○…∴|x﹣1|＜2，解得﹣1＜x ＜3，所以答案是：（﹣1，3）【考点精析】本题主要考查了函数单调性的性质和函数奇偶性的性质的相关知识点，需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集；在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇才能正确解答此题． 10.[﹣1，1]【解析】10.解：由题意画出图形如图：点M （x 0 ， 1），要使圆O ：x 2+y 2=1上存在点N ，使得∠OMN=45°，则∠OMN 的最大值大于或等于45°时一定存在点N ，使得∠OMN=45°，而当MN 与圆相切时∠OMN 取得最大值，此时MN=1，图中只有M′到M″之间的区域满足MN≤1， ∴x 0的取值范围是[﹣1，1]．11.（1）证明：a n+1+12a n +12=3a n +1+12a n +12=3(a n +12)a n +12=3，∵ a 1+12=32 ≠0，∴数列{a n + 12 }是以首项为 32 ，公比为3的等比数列；∴a n + 12 = 32×3n−1= 3n2 ，即 a n=3n −12；（2）证明：由（1）知 1a n=23n −1 ，当n≥2时，∵3n ﹣1＞3n ﹣3n ﹣1，∴ 1a n=23n −1 ＜23n −3n−1 =13n−1，∴当n=1时， 1a 1=1＜32 成立，订…………○…………线__考号：___________订…………○…………线当n≥2时， 1a 1+ 1a 2+…+ 1a n＜1+ 13+132+ …+13n−1 =1−(13)n1−13= 32(1−13n ) ＜ 32 ．∴对n∈N +时， 1a 1+ 1a 2+…+ 1a n＜ 32 ．【解析】11.（1）根据等比数列的定义，后一项与前一项的比是常数，即b n+1b n=常数，又首项不为0，所以为等比数列；再根据等比数列的通项化式，求出{a n }的通项公式；（2）将 1a n进行放大，即将分母缩小，使得构成一个等比数列，从而求和，证明不等式．【考点精析】认真审题，首先需要了解数列的前n 项和(数列{a n }的前n 项和s n 与通项a n 的关系)，还要掌握等比数列的基本性质({a n}为等比数列，则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {a n}是各项不为零的常数列)的相关知识才是答题的关键． 12.（1）证明：连接BD 交AC 于O 点，连接EO ， ∵O 为BD 中点，E 为PD 中点， ∴EO∥PB，（2分）EO ⊂平面AEC ，PB ⊄平面AEC ，所以PB∥平面AEC ；（6分）（2）解：延长AE 至M 连结DM ，使得AM⊥DM，∵四棱锥P ﹣ABCD 中，底面ABCD 为矩形，PA⊥平面ABCD ， ∴CD⊥平面AMD ，∵二面角D ﹣AE ﹣C 为60°， ∴∠CMD=60°，∵AP=1，AD= √3 ，∠ADP=30°， ∴PD=2，E 为PD 的中点．AE=1， ∴DM= √32 ，CD= √32×tan600 = 32 ．三棱锥E ﹣ACD 的体积为： 13×12AD ⋅CD ⋅12PA = 13×12×√3×32×12×1 = √38 ．答案第10页，总12页…………○…………线…………○※※答※※题※※…………○…………线…………○【解析】12.（1）连接BD 交AC 于O 点，连接EO ，只要证明EO∥PB，即可证明PB∥平面AEC ；（2）延长AE 至M 连结DM ，使得AM⊥DM，说明∠CMD=60°，是二面角的平面角，求出CD ，即可三棱锥E ﹣ACD 的体积．【考点精析】通过灵活运用直线与平面平行的判定，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行即可以解答此题． 13.（1）解：由题意， t ¯= 17 ×（1+2+3+4+5+6+7）=4，y ¯= 17 ×（2.9+3.3+3.6+4.4+4.8+5.2+5.9）=4.3，∴ b ^=(−3)×(−1.4)+(−2)×(−1)+(−1)×(−0.7)+0.1+1×0.5+2×0.9+3×19+4+1+0+1+4+9 = 1428=0.5，a ^= y ¯ ﹣ b ^ t ¯=4.3﹣0.5×4=2.3．∴y 关于t 的线性回归方程为 y ^=0.5t+2.3；（2）解：由（1）知，b=0.5＞0，故2007年至2013年该地区农村居民家庭人均纯收入逐年增加，平均每年增加0.5千元．将2015年的年份代号t=9代入 y ^ =0.5t+2.3，得：y ^=0.5×9+2.3=6.8，故预测该地区2015年农村居民家庭人均纯收入为6.8千元第11页，总12页【解析】13.（1）根据所给的数据，利用最小二乘法可得横标和纵标的平均数，横标和纵标的积的和，与横标的平方和，代入公式求出b 的值，再求出a 的值，写出线性回归方程．（2）根据上一问做出的线性回归方程，代入所给的t 的值，预测该地区2015年农村居民家庭人均纯收入，这是一个估计值． 14.（1）解：∵M 是C 上一点且MF 2与x 轴垂直， ∴M 的横坐标为c ，当x=c 时，y= b 2a ，即M （c ，b 2a ），若直线MN 的斜率为 34 ，即tan∠MF 1F 2= b 2a2c =b 22ac=34 ，即b 2= 32ac =a 2﹣c 2，即c 2+ 32ac ﹣a 2=0，则 e 2+32e −1=0 ，即2e 2+3e ﹣2=0解得e= 12 或e=﹣2（舍去），即e= 12（2）解：由题意，原点O 是F 1F 2的中点，则直线MF 1与y 轴的交点D （0，2）是线段MF 1的中点，设M （c ，y ），（y ＞0），则 c 2a 2+y 2b 2=1 ，即 y 2=b 4a 2 ，解得y=b 2a ，∵OD 是△MF 1F 2的中位线，∴ b 2a =4，即b 2=4a ，由|MN|=5|F 1N|，则|MF 1|=4|F 1N|，解得|DF 1|=2|F 1N|，即 DF →1=2F 1N →设N （x 1，y 1），由题意知y 1＜0，则（﹣c ，﹣2）=2（x 1+c ，y 1）．即 {2(x 1+c)=−c 2y 1=−2 ，即 {x 1=−32cy 1=−1代入椭圆方程得 9c 24a 2+1b 2=1 ，将b 2=4a代入得 9(a 2−4a)4a 2+14a=1 ，答案第12页，总12页解得a=7，b= 2√7 ．【解析】14.（1）根据条件求出M 的坐标，利用直线MN 的斜率为 34 ，建立关于a ，c 的方程即可求C 的离心率；（2）根据直线MN 在y 轴上的截距为2，以及|MN|=5|F 1N|，建立方程组关系，求出N 的坐标，代入椭圆方程即可得到结论． 15.（1）解：由半圆C 的极坐标方程为ρ=2cosθ，θ∈[0， π2 ]，即ρ2=2ρcosθ，可得C 的普通方程为（x ﹣1）2+y 2=1（0≤y≤1）．可得C 的参数方程为 {x =1+costy =sint（t 为参数，0≤t≤π）．（2）解：设D （1+cos t ，sin t ），由（1）知C 是以C （1，0）为圆心，1为半径的上半圆，∵直线CD 的斜率与直线l 的斜率相等，∴tant= √3 ，t= π3 ．故D 的直角坐标为 (1+cos π3,sin π3) ，即（ 32 ， √32 ）【解析】15.（1）利用 {ρ2=x 2+y 2x =ρcosθ即可得出直角坐标方程，利用cos 2t+sin 2t=1进而得出参数方程．（2）利用半圆C 在D 处的切线与直线l ：y= √3垂直，则直线CD 的斜率与直线l 的斜率相等，即可得出直线CD 的倾斜角及D 的坐标．。

2014年新课标2卷高考理科数学试题及答案

2014理科（新课标卷二Ⅱ）三.解答题：17.已知数列{}n a 满足1a =1，131n n a a +=+. （Ⅰ）证明{}1n a +是等比数列，并求{}n a 的通项公式；（Ⅱ）证明：1231112n a a a ++<…+.18. 如图，四棱锥P-ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点. （Ⅰ）证明：PB ∥平面AEC ；（Ⅱ）设二面角D-AE-C 为60°，AP=1，E-ACD 的体积.（Ⅰ）求y 关于t 的线性回归方程；（Ⅱ）利用（Ⅰ）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.附：回归直线的斜率和截距的最小二乘法估计公式分别为：()()()121ni ii n i i t t y y b t t ∧==--=-∑∑，ˆˆay bt =-20. 设1F ,2F 分别是椭圆C:()222210y x a b a b+=>>的左,右焦点，M 是C 上一点且2MF 与x 轴垂直，直线1MF 与C 的另一个交点为N.（Ⅰ）若直线MN 的斜率为34，求C 的离心率；（Ⅱ）若直线MN 在y 轴上的截距为2，且15MN F N =，求a,b .21.已知函数()f x =2x x e e x ---zxxk（Ⅰ）讨论()f x 的单调性；（Ⅱ）设()()()24g x f x bf x =-，当0x >时，()0g x >,求b 的最大值；（Ⅲ）已知1.4142 1.4143<<，估计ln2的近似值（精确到0.001）23. 在直角坐标系xoy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，半圆C 的极坐标方程为2cos ρθ=，0,2πθ⎡⎤∈⎢⎥⎣⎦.（Ⅰ）求C 的参数方程；（Ⅱ）设点D 在C 上，C 在D处的切线与直线:2l y =+垂直，根据（Ⅰ）中你得到的参数方程，确定D 的坐标.参考答案三、解答题（17）解：（1）由131m m a a +=+得1113().22m m a a ++=+ 又113a 22+=，所以，{12m a + } 是首项为32，公比为3的等比数列。

2014年高考全国卷Ⅱ理科数学试题及答案

）
≤ 0 ，则 z x 3y 1 3x ≥0 5
D. 2
A. 10 【答案】【解析】 B
B. 8
画出区域，可知区域为三角形，经比较斜率，可知目标函数 z = 2x - y在两条直线 x - 3y + 1 = 0与 x + y - 7 = 0的交点 ( 5,2) 处 , 取得最大值 z = 8.故选 B.
C. 2 D. 3
y
2 x ，则 a
B. 1 D
x+1 ∴ f ( 0) = 0, 且 f ′ ( 0) = 2 .联立解得 a = 3 .故选 D .
f ( x) = ax - ln( x+ 1), ∴ f ′ ( x) = a -
1
.
x
9.设 x, y 满足约束条件
y y
C. 3
7≤ 0 2x y 的最大值为（
3 3 3 2 m = 2 ? + 3m, 2n = 2 ? - 3 n ，解得 m = ( 2 + 4 4 2 1 3 9 ∴SΔ OAB = ? ? ( m + n) = .故选 D . 2 4 4
11.直三棱柱点，
ABC A1 B1C1 中，
BCA
90 ， M , N 分别是 A1B1 ， AC 1 1 的中
1
∴ sin B =
2
,
【答案】
【解析】本题考查条件概率，记第一天空气质量优良为事件天的空气质量也为优良为事件
A ，随后一
B ，则 AB 表示连续两天空气质量都为优 P ( AB ) P( A) 0.6 0.75 0.8
良，则所求概率为
P( B | A)
6.如图，网格纸上正方形小格的边长为由一个底面半径为比值为（ A. ）

2014年新课标2卷高考理科数学试题及答案

2014年普通高等学校招生全国统一考试理科（新课标卷二Ⅱ）第Ⅰ卷一.选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合M=｛0,1,2｝，N={}2|320x x x -+≤，则M N ⋂=( ) A. ｛1｝B. ｛2｝C. ｛0，1｝D. ｛1，2｝2.设复数1z ，2z 在复平面内的对应点关于虚轴对称，12z i =+，则12z z =（） A. - 5 B. 5 C. - 4+ i D. - 4 - i3.设向量a,b 满足|a+b|a-ba ⋅b = ( ) A. 1 B. 2 C. 3 D. 54.钝角三角形ABC 的面积是12，AB=1，，则AC=( )A. 5C. 2D. 15.某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（）A. 0.8B. 0.75C. 0.6D. 0.456.如图，网格纸上正方形小格的边长为1（表示1cm ）,图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（）A. 1727B. 59C. 1027D. 137.执行右图程序框图，如果输入的x,t 均为2，则输出的S= （） A. 4 B. 5 C. 6 D. 78.设曲线y=a x-ln(x+1)在点(0,0)处的切线方程为y=2x ，则a = A. 0 B. 1 C. 2 D. 39.设x,y 满足约束条件70310350x y x y x y +-⎧⎪-+⎨⎪--⎩≤≤≥，则2z x y =-的最大值为（）A. 10B. 8C. 3D. 210.设F 为抛物线C:23y x =的焦点，过F 且倾斜角为30°的直线交C 于A,B 两点，O 为坐标原点，则△OAB 的面积为（）C. 6332D. 9411.直三棱柱ABC-A 1B 1C 1中，∠BCA=90°，M ，N 分别是A 1B 1，A 1C 1的中点，BC=CA=CC 1，则BM 与AN 所成的角的余弦值为（）A. 1B. 2512.设函数()x f x mπ=.若存在()f x 的极值点0x 满足()22200x f x m +<⎡⎤⎣⎦，则m 的取值范围是（）A. ()(),66,-∞-⋃∞B. ()(),44,-∞-⋃∞C. ()(),22,-∞-⋃∞D.()(),14,-∞-⋃∞本卷包括必考题和选考题两部分.第13题~第21题为必考题，每个试题考生必须做答.第22题~第24题为选考题，考生根据要求做答.本试题由整理二.填空题13.()10x a +的展开式中，7x 的系数为15，则a =________.(用数字填写答案)14.函数()()()sin 22sin cos f x x x ϕϕϕ=+-+的最大值为_________.15.已知偶函数()f x 在[)0,+∞单调递减，()20f =.若()10f x ->，则x 的取值范围是__________.16.设点M （0x ,1），若在圆O:221x y +=上存在点N ，使得zxxk ∠OMN=45°，则0x 的取值范围是________.三.解答题：解答应写出文字说明，证明过程或演算步骤.17.（本小题满分12分）已知数列{}n a 满足1a =1，131n n a a +=+.（Ⅰ）证明{}12n a +是等比数列，并求{}n a 的通项公式；（Ⅱ）证明：1231112n a a a ++<…+.18. （本小题满分12分）如图，四棱锥P-ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点. （Ⅰ）证明：PB ∥平面AEC ；（Ⅱ）设二面角D-AE-C 为60°，AP=1，E-ACD 的体积.19. （本小题满分12分）某地区2007年至2013年农村居民家庭纯收入y （单位：千元）的数据如下表：（Ⅰ）求y 关于t 的线性回归方程；（Ⅱ）利用（Ⅰ）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入. 附：回归直线的斜率和截距的最小二乘法估计公式分别为：()()()121niii ni i t t y y b t t ∧==--=-∑∑，ˆˆay bt =-20. （本小题满分12分）设1F ,2F 分别是椭圆C:()222210yx a b a b+=>>的左,右焦点，M 是C 上一点且2MF 与x 轴垂直，直线1MF 与C 的另一个交点为N.（Ⅰ）若直线MN 的斜率为34，求C 的离心率；（Ⅱ）若直线MN 在y 轴上的截距为2，且15MN F N =，求a,b .21. （本小题满分12分）已知函数()f x =2x x e e x ---zxxk （Ⅰ）讨论()f x 的单调性；（Ⅱ）设()()()24g x f x bf x =-，当0x >时，()0g x >,求b 的最大值；（Ⅲ）已知1.4142 1.4143<<，估计ln2的近似值（精确到0.001）请考生在第22、23、24题中任选一题做答，如果多做，有途高考网同按所做的第一题计分，做答时请写清题号.22.（本小题满分10）选修4—1：几何证明选讲如图，P 是 O 外一点，PA 是切线，A 为切点，割线PBC 与 O相交于点B ，C ，PC=2PA ，D 为PC 的中点，AD 的延长线交 O 于点E.证明：（Ⅰ）BE=EC ；（Ⅱ）AD ⋅DE=22PB23. （本小题满分10）选修4-4：坐标系与参数方程在直角坐标系xoy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，半圆C 的极坐标方程为2cos ρθ=，0,2πθ⎡⎤∈⎢⎥⎣⎦.zxxk （Ⅰ）求C 的参数方程；（Ⅱ）设点D 在C 上，C 在D 处的切线与直线:2l y =+垂直，根据（Ⅰ）中你得到的参数方程，确定D 的坐标.24. （本小题满分10）选修4-5：不等式选讲设函数()f x =1(0)x x a a a++->（Ⅰ）证明：()f x ≥2；（Ⅱ）若()35f <，求a 的取值范围.2014年普通高等学校招生全国统一考试理科数学试题参考答案一、选择题（1）D （2）A （3）A （4）B （5）A （6）C （7）D （ 8）D （9）B （10）D （11）C （12）C二、填空题（13）12（14）1 （15）（-1,3）（16）[-1，1]三、解答题（17）解：（1）由131m m a a +=+得1113().22m m a a ++=+ 又113a 22+=，所以，{12m a + } 是首项为32，公比为3的等比数列。

2014年高考理科数学试题及答案-全国卷2

2014年普通高等学校招生全国统一考试（全国卷2)理科数学第Ⅰ卷（共60分)一、选择题：本大题共12个小题,每小题5分,共60分。

在每小题给出的四个选项中,只有一项是符合题目要求的。

1. 已知全集,{|0},{|1}U R A x x B x x ==≤=≥,则集合()U C AB =( )A ．{|0}x x ≥B ．{|1}x x ≤C ．{|01}x x ≤≤D ．{|01}x x << 2. 设复数z 满足(2)(2)5z i i --=，则z =（）A ．23i +B ．23i -C ．32i +D ．32i - 3。

已知132a -=，21211log ,log 33b c ==，则（） A ．a b c >> B ．a c b >> C ．c a b >> D ．c b a >> 4. 已知m ，n 表示两条不同直线，α表示平面，下列说法正确的是（ )A ．若//,//,m n αα则//m nB ．若m α⊥，n α⊂，则m n ⊥C ．若m α⊥,m n ⊥，则//n αD ．若//m α，m n ⊥，则n α⊥5. 设,,a b c 是非零向量，学科网已知命题P ：若0a b •=,0b c •=,则0a c •=；命题q ：若//,//a b b c ，则//a c ，则下列命题中真命题是（ )A ．p q ∨B ．p q ∧C ．()()p q ⌝∧⌝D ．()p q ∨⌝ 6. 6把椅子摆成一排，3人随机就座,任何两人不相邻的做法种数为（）A ．144B ．120C ．72D ．24 7。

某几何体三视图如图所示，则该几何体的体积为（）A ．82π- B ．8π- C ．82π- D ．84π- 8. 设等差数列{}n a 的公差为d,若数列1{2}n a a为递减数列,则（ )A ．0d <B ．0d >C ．10a d <D ．10a d > 9。

2014年全国2卷理科数学解析版

2014年普通高等学校招生全国统一考试理科（新课标卷二Ⅱ）第Ⅰ卷一.选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设集合M=｛0,1,2｝，{}023|2≤+-=x x x N ，则N M I =( ){}1.A {}2.B {}1,0.C {}2,1.D2. 设复数1z ，2z 在复平面内的对应点关于虚轴对称，12z i =+，则12z z =( )5.-A 5.B i C +-4. i D --4.3. 设向量a ,b 满足|a +b 10|a -b 6，则a ⋅b =( )1.A2.B3.C 5.D4. 钝角三角形ABC 的面积是12，AB=1，2，则AC=( )5.A 5.B 2.C 1.D5. 某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是( ) A. 0.8 B. 0.75 C. 0.6 D. 0.456. 如图，网格纸上正方形小格的边长为1（表示1cm ）,图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为( )A. 1727B. 59C. 1027D. 137. 执行右图程序框图，如果输入的x,t 均为2，则输出的S=( ) A. 4 B. 5 C. 6 D. 78. 设曲线)1ln(+-=x ax y 在点(0,0)处的切线方程为x y 2=，则a = A. 0 B. 1 C. 2 D. 39. 设x,y 满足约束条件⎪⎩⎪⎨⎧≥--≤+-≤-+05301307y x y x y x ，则2z x y =-的最大值为( )A. 10B. 8C. 3D. 210. 设F 为抛物线C:23y x =的焦点，过F 且倾斜角为30°的直线交C 于A,B 两点，O 为坐标原点，则△OAB 的面积为( )A.33 B.93 C. 6332 D. 9411. 直三棱柱ABC-A 1B 1C 1中，∠BCA=90°，M ，N 分别是A 1B 1，A 1C 1的中点，BC=CA=CC 1，则BM 与AN 所成的角的余弦值为( ) A. 110 B. 25C.30 D.2 12. 设函数()3x f x mπ=.若存在()f x 的极值点0x 满足()22200x f x m +<⎡⎤⎣⎦，则m 的取值范围是( )A. ),6()6,(+∞--∞YB. ),4()4,(+∞--∞YC. ),2()2,(+∞--∞YD.),4()1,(+∞--∞Y第Ⅱ卷二.填空题13. ()10x a +的展开式中，7x 的系数为15，则a =________.(用数字填写答案) 14. 函数()()()sin 22sin cos f x x x ϕϕϕ=+-+的最大值为________.15. 已知偶函数()f x 在[)0,+∞单调递减，()20f =.若()10f x ->，则x 的取值范围是________. 16. 设点M （0x ,1），若在圆O:221x y +=上存在点N ，使得∠OMN=45°，则0x 的取值范围是________. 三.解答题：解答应写出文字说明，证明过程或演算步骤.17. （本小题满分12分）已知数列{}n a 满足1a =1，131n n a a +=+.（Ⅰ）证明{}12n a +是等比数列，并求{}n a 的通项公式；（Ⅱ）证明：1231112na a a ++<…+.18. （本小题满分12分）如图，四棱锥P-ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点. （Ⅰ）证明：PB ∥平面AEC ；（Ⅱ）设二面角D-AE-C 为60°，AP=1，3，求三棱锥E-ACD 的体积.19. （本小题满分12分）（Ⅰ）求y 关于t 的线性回归方程；（Ⅱ）利用（Ⅰ）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.附：回归直线的斜率和截距的最小二乘法估计公式分别为：()()()121niii ni i t t y y b t t ∧==--=-∑∑，ˆˆay bt =-20. （本小题满分12分）设1F ,2F 分别是椭圆C:()222210y x a b a b+=>>的左,右焦点，M 是C 上一点且2MF 与x 轴垂直，直线1MF 与C 的另一个交点为N.（Ⅰ）若直线MN 的斜率为34，求C 的离心率；（Ⅱ）若直线MN 在y 轴上的截距为2，且15MN F N =，求a,b .21. （本小题满分12分）已知函数()f x =2x x e e x --- （Ⅰ）讨论()f x 的单调性；（Ⅱ）设()()()24g x f x bf x =-，当0x >时，()0g x >,求b 的最大值；（Ⅲ）已知1.4142 1.4143<，估计ln2的近似值（精确到0.001）请考生在第22、23、24题中任选一题做答，如果多做，按所做的第一题计分，做答时请写清题号.22.（本小题满分10）选修4—1：几何证明选讲如图，P 是e O 外一点，PA 是切线，A 为切点，割线PBC 与e O 相交于点B ，C ，PC=2PA ，D 为PC 的中点，AD 的延长线交e O 于点E.证明：（Ⅰ）BE=EC ；（Ⅱ）AD ⋅DE=22PB23. （本小题满分10）选修4-4：坐标系与参数方程在直角坐标系xoy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，半圆C 的极坐标方程为2cos ρθ=，0,2πθ⎡⎤∈⎢⎥⎣⎦.（Ⅰ）求C 的参数方程；（Ⅱ）设点D 在C 上，C 在D 处的切线与直线:32l y x =+垂直，根据（Ⅰ）中你得到的参数方程，确定D 的坐标.24. （本小题满分10）选修4-5：不等式选讲设函数()f x =1(0)x x a a a++->（Ⅰ）证明：2)(≥x f ；（Ⅱ）若()35f <，求a 的取值范围.答案与详解一、选择题1~6 DAABAC 7~12 DDBDCC 二、填空题13、 0.5 14、 1 15、 (-1,3) 16、 [-1,1] 三、解答题17.（Ⅰ）证明：∵131+=+n n a a ，∴)21(3211+=++n n a a ∴321211=+++n n a a ，即数列⎭⎬⎫⎩⎨⎧+21n a 是等比数列。

2014年普通高等学校招生全国统一考试(全国新课标Ⅱ卷)数学试题(理科)解析版

2014年新课标II 卷数学试卷（理科）第I 卷一、选择题（本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一个选项是符合题目要求的） 1. 设集合M ={0,1,2}，20{|32}N x x x =-≤+，则M N ⋂=( )A. {1}B. {2}C. {0,1}D. {1,2} 【答案解析】D解析：把0，1，2代人2203x x +≥-验证，只有1，2满足不等式，故选D. 考点：考查集合与一元二次不等式的知识，简单题.2. 设复数12,z z 在复平面内的对应点关于虚轴对称，12z i =+，则12z z =（）A. -5B.5C.-4+iD.-4-i 【答案解析】A. 解析：12i z =+ 与2z 关于虚轴对称，∴2z =-2+i∴12(2i)(2i)5z z =+-+=- ，故选A. 考点：考查复数的基本知识，简单题. 3. 设向量,a b 满足10a b +=，6a b -=，则a b ∙=（）A. 1B.2C. 3D.5 【答案解析】A.解析：||10,6|4=41=+=-=∴+⋅+⋅+∴⋅∴⋅=-=2222a b a b a 2a b b a 2a b b a b a b 故选A.考点：考查平面向量的数量积，中等题. 4. 钝角三角形ABC 的面积是12，AB=1，BC =AC =（）A.5 【答案解析】B. 解析：∵△ABC 面积为12，1,AB BC ==∴111sin45,135222B B B⋅=⇒=⇒=︒︒当B=45°时，222cos451222111BCAAC AB BCCAB⋅︒=+-⋅=⇒=-=+此时，AC=AB=1,故A=90°，这与△ABC为钝角三角形矛盾.当B=135°时，222cos1351221225AC AB B BCC AACB=+-⋅︒=++⋅=⇒=故选B.考点：考查正余弦定理的应用，中等题.5. 某地区空气质量监测资料表明，一天的空气质量为优良的概率为0.75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（）A. 0.8B.0.75C. 0.6D.0.45【答案解析】A.解析：设第i天空气优良记着事件iA，则1(A)0.75,(A A)0.6(i1,2,)i i iP P+=== , ∴第1天空气优良，第2天空气也优良这个事件的概率为12211()0.60.8((|).75)0A APAAPP A===，故选A.考点：考查条件概率的概率，简单题.6. 如图，网格纸上正方形小格子的边长为1(表示1cm)，图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm，高为6cm的圆柱体毛胚切削而得到，则切削掉部分的体积与原来毛胚体积的比值为（）A.1727B.59C.1027D.13【答案解析】C.解析：毛胚的体积23654Vππ⋅⋅==制成品的体积221322434Vπππ⋅⋅+⋅⋅==∴切削掉的体积与毛胚体积之比为：13454101127VVππ-=-=，故选C.考点：考查三视图于空间几何体的体积，中等题.7. 执行右图的程序框图，如果输入的x ，t 均为2，则输出的S =( )A.4B.5C.6D.7 【答案解析】D.解析：第1次循环M=2,S=5,k=1 第2次循环，M=2,S=7,k=2 第3次循环k=3>2,故输出S=7考点：考查算法的基本知识，简单题.8. 设曲线y=ax -ln (x +1)在点(0,0)处的切线方程为y =2x ，则a =（）A.0B.1C.2D.3 【答案解析】D. 解析：0ln(121)1,1|x y ax x y a x y a ==-+∴'=-'=∴-+= 故a=3，选D.考点：考查导数的几何应用，中等题.9. 设x ，y 满足约束条件03103507x y x x y y ≤⎧⎪-+≤⎨⎪--≥-⎩+，则z =2x -y 的最大值为( )A.10B.8C.3D.2 【答案解析】B. 解析：作图即可.考点：考查二元一次不等式组的应用，中等题.10. 设F 为抛物线23C y x =：的焦点，过F 且倾斜角为30°的直线交C 于A ，B 两点，O 为坐标原点，则△OAB 的面积为（）C. 6332D.94【答案解析】D 解析：∵23y x =∴抛物线C 的焦点的坐标为：()3,04F 所以直线AB 的方程为：330an )t (4y x ︒-=故23)43x y y x ⎧==-⎪⎨⎪⎩从而2122161689012x x x x -+=+=⇒ ∴弦长12||=3122x x AB ++= 又∵O点到直线:430AB x --=的距离38d =∴13129428OAB S ⋅⋅==,故选D. 考点：综合考查抛物线的知识，弦长计算与分析直线和圆锥曲线位置关系的能力，难度为困难题.11. 直三棱柱111ABC A B C -中，∠BCA=90°，M ，N 分别是11A B ，11A C 的中点，1BC CA CC ==，则BM 与AN 的夹角的余弦值为( ) A.110 B. 25C. 10D.2【答案解析】C.解析：设AC =2，12BC CA CC ∴===(2,0,0),(1,0,2),(0,2,0),(1,1,2)A N B M ∴(1,1,2),(1,2,0)BM AN ∴=-=-cos ,||||6AN BM AN BM AN BM ⋅∴<>====⋅故选C. 考点：考查空间夹角问题.中等题.12. 设函数)n(f x xmπ，若存在f (x )的极值点0x 满足22200[()]x f x m +<，则m 的取值范围是（）A.,6()(6,)∞-⋃+∞-B. ,4()(4,)∞-⋃+∞-C. ,2()(2,)∞-⋃+∞-D.,1()(1,)∞-⋃+∞- 【答案解析】C.解析：()()cosxx f x f m m x mππ=⇒'=令()0cos0()2xxx k k Z mf mππππ'=⇒=⇒=+∈(21)2k m x +=∴ ，即f (x )的极值点0(2)1()2mx k k Z =+∈ ∵存在f (x )的极值点0x ，满足22200()f x x m +<∴ 2220(2)m 31sin []2x k m mπ+<+ 又∵222202sin )(21)m sin s s in in (222()1k k x k m m ππππππ===++⋅=+ ∴存在k Z ∈，使得221[]2(2)m 3k m ++< ∴存在k Z ∈,使得223(2)141k m +<-∴223(21)13[1]|m |24414max k m +<-=⇒->= ，故选C. 考点：考查导数与极值，三角函数，不等式的知识，为困难题.第II 卷二、填空题（本大题共4小题，每小题5分，共20分）13. 10()x a +的展开式中，7x 的系数为15，则a = .（用数字填写答案）【答案解析】12解析：1010110(0(),1,,10)r r rr T C x r x a a -+==+展开式的通项为∴10()x a +展开式中7x 的系数为31031125C a a ⇒==考点：考查二项展开式的通项公式，简单题.14. 函数()sin(2)2sin cos()x x f x ϕϕϕ=+-+的最大值为 .【答案解析】1．解析：()(2)2()cos()sin 2sin cos()cos()si ()sin()cos sin()cos n sin .f x sin x sin cos x x f x x x x x x ϕϕϕϕϕϕϕϕϕϕϕϕϕ=+-+∴++-++=-+==+故填写1.考点：本题考查和差角公式，为中等题.15. 已知偶函数f (x )在[0,+∞)上单调递减，f (2)=0,若f (x -1)>0,则x 的取值范围是 . 【答案解析】(-1,3).解析：作出函数f (x )的示意图，如图所示因为(1213)201x x f x ⇒-<-<⇒--<<> 考点：本题考查函数的单调性与奇偶性.简单题.16. 设点0(,1)M x ，若在园22:1O x y +=上存在点N ，使得∠OMN =45°，则0x 的取值范围是 . 【答案解析】[-1,1]解析：设N 点的坐标为,s (cos )in θθ （1）当00,1x ≠± 时 ∵0(,1)M x 点的坐标为 ∴OM ,MN 的斜率分别为：001s n c s ,i o 1OM MN k x k x θθ-==- ∵45OMN ∠=︒ ∴1tan 45()1MN OMMN OM MN OM MN OMk k k k k k k k -︒=±⇒=-++±即000011sin 1()11sin cos cos ()x x x x θθθθ--±-=--+⋅*取正号时，化简（*）式得：2000(1)sin 11()cos x x x θθ+-=++ 取负号化简（*）式得：2000(1)sin 1(1)cos x x x θθ++=+-200)1x θϕ+=+2400011||1x x x ≥+⇒≤⇒≤ 故0||<1x 且00x ≠（2）当00x =时，取(1,0)N ,此时满足题设. （3）当01x =±时，取(0,1)N ，此时也满足题设. 综上所述，011x -≤≤考点：考查应用斜率与倾斜角的概念，直线方程，园的方程,分析问题的能力.困难题. 三、解答题（本大题共8小题） 17. (12分)已知数列{}n a 满足111,31n n a a a +==+.(I)证明{12}n a +是等比数列，并求{}n a 的通项公式； (II)证明2111132n a a a +++<. 【答案解析】解析：(I)∵131n n a a +=+11331111)223(22n n n n a a a a ++∴⇒+=+++=+ 1112132a a =+⇒=∴{12}n a +是首项为32 ，公比为3的等比数列∴1*131333,2222n n n n n a a n N --⋅+==∈=⇒ (II)由(I)知，*13,2n n a n N -=∈，故 121213111111231(13)nn a a a +++=++-+-- 12110331112()3333n n --+-≤+-+ 12111()11131331(1()).133323213nn n --=++++==⋅-<-考点：考查等比数列的通项公式,求和公式，考查放缩法证明不等式的技巧.中等题. 18. (12分)如图，四棱锥P-ABCD 中，底面ABCD 为矩形，D A BC P A ⊥平面，E 为PD 中点. (I)证明:PB ||平面AEC ;(II)设二面角D-AE-C 为60°，AP =1，AD =E-ACD 的体积.【答案解析】解析：(I)连接EF ,因为四边形ABCD 是矩形，故F 为AC 中点，又因为E 为PD 中点，故EF 是△PBD 的中位线，从而||EF PB ,故||.PB AEC 面(II)建立坐标系如图所示.因为1,AP AD ==，E 为PD 中点，∴1(0,0,1),)0)2,P D E ，设||CD a = ，则(,0,0),(B a C a∴31(0,,),(,3,0)2AE AC a == ∵PA ABCD ⊥面，ABCD 平面是矩形∴(,0,0)PAD AB AB a ⊥⇒=面是平面ADE 的法向量设平面AEC 的法向量为=(,,)n xy z ，则31002n AE yz n AC ax ⎧⋅=+=⎪⎨⎪⋅=+=⎩令y =，得,33x a z =-=- ，故3(3)n a=-- ∵二面角D AE C --的大小为60° ∴||||cos60||n AB n AB ⋅︒===⋅解得32a =∵三棱锥E ACD -的高为111||1222PA =⋅=∴1111131(||||)(||)()32238222E ACDAD CD PV A-⋅⋅⋅⋅=⋅⋅==考点：考查空间线面关系，椎体的体积计算和向量法解决立体几何问题的技能，中等题.19. (12分)某地区2007年至2013年农村居民家庭人均纯收入y(单位：千元)的数据如下表：(I)求y关于t的线性回归方程；(II)利用(I)中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民人均纯收入.附：回归直线的斜率和截距的最小二乘估计公式分别为：2()()()ˆni iiniit ytt ybt=---∑∑，ˆˆa by t=-.【答案解析】解析：（I）7117221ˆ0.5.28ˆˆ 4.30.542()()14(.)3i iiiit t ybtty bya t==∑====∑=-=-⋅--=-∑∑∴回归方程为：0.5 2.3y t=+(II)由于ˆ0.50b=>，故y与t是正线性相关的，因此从2007年到2013年农村居民的人均纯收入是逐年上升的.当9t=时，9 2.3 6.80.5y⋅+==，即2015年农村居民的人均纯收入预测将达到6.8千元.考点：考查线性回归方程，线性相关的概念的应用.难度中等.20. (12分)设12,F F分别是椭圆22221(0):x yCaa bb+=>>的左右焦点，M是C上一点且2MF与x轴垂直，直线1MF 与C 的另一个交点是N . (I)若直线MN 的斜率为34，求C 的离心率; (II)若直线MN 在y 轴上的截距为2，且1|MN |5||F N =，求a ，b . 【答案解析】解析：（I ）∵2MF x ⊥轴（不妨设M 在x 轴的上方）∴M 的坐标满足方程组222221(,)x b M c a a y bx c⎧⎪⇒⎨⎪⎩=+= ∵MN 的斜率为34∴2234322b a ac cb =⇒= ∵222222()3ac a a c c b =-⇒-=又∵222(1)32320ce e e e e a⇒+-⇒-=== ∴椭圆离心率为12e = .(II)∵MN 在y 轴上的截距为2，O 为12,F F 的中点 ∴M 的坐标为(c ,4)(不妨设M 在x 轴的上方)由（I ）得24b a= (*) ∵1||5||MN NF = ∴11||4||MF NF = 作1NF x ⊥轴于T ,由于112~TF F N MF ,故有24,4M N Ny cy c x =--=- ∴321,14N M N y y c x =-=-=- ，即,3()12c N --把N 点的坐标代人椭圆方程得：2221419c a b+=∴2222222)111(9(9544**)4a b b a b a b +=⇒-=-把（*）与（**）联立得：7a b ==⎧⎪⎨⎪⎩考点：考查椭圆的几何性质以及直线与椭圆的位置关系，难题.21. (12分)已知函数()e 2x x f x e x -=--.(I)讨论f(x)的单调性;(II)设()(2)4()g x f x bf x =-，当0x >时，()0g x >，求b 的最大值;(III)已知1.4142 1.4143，估计ln2的近似值(精确到0.001).【答案解析】解析：(I)∵22()x e x f ex ---=∴2()2x x x f e e -'=≥+=-∴()f x 在R 上递增.（II ）()2x x e e f x x --=-224(2)x x x x f e e ---∴=22()(2)4()()4b(4)2x x x x g x f x bf x e x e x e e --∴=-=-----22()()4b()0((0,)4)2x x x x g x e e e x x e x ----∴=-->∀+∞-∈（注意这里用分离变量法处里恒成立无法进行下去!）∵22()0,(2)22420x x x x f e x e f x e e --'=≥'=++-≥-()(0)0,(2)(0)0f x f f x f ∴>=>=又∵22()2244(2)x x x x g e b e e x e --+--+-'=2()24(81(()))x x x x g x e e e b e b --+-++∴-'=2[()2(1[])2])(x x x x e b e e e --⋅=-+-+-令()02(11)x x x g e b x e e b -+=-=-'=⇒⇒（1）当1b ≤时2(10()0)x x e e b g x -≥⇒'+-≥-∴()(0)0g x g >= 成立,故1b ≤成立.(2)当12b <≤时),2(201b <-≤ 而2x x e e -+≥ ，此时22(1)x x b e e -≥≥-+∴()0()(0)0x x g g g '≥⇒>= 成立，故12b <≤（3）当2b >时2221((1)12)b b b b b b =-+>--⇒->2222(2)4422(2)22b b b b b b b b b -⇒--=-+<--<=-∴ 1ln(1001b b <⇒--<<又∵0112b b >⇒->-∴l 10n(b ->若x R ∈时， 2(1))0(0x x g e b x e -+-->⇔>'ln(1x b ⇔<- 或ln(1x b >-2(1))0(0x x g e b x e -+--<⇔<'ln(1ln(1b x b ⇔-<<-∴区间(ln(1)1b b --是()g x 的减区间∵(0)0g =∴ (ln(10g b -<即在区间ln(1)0(,b -上()0g x < 这与()g x 在区间(0,)+∞上大于0矛盾，故(2,)b ∈+∞/综上所述，(,2]b ∈-∞ ，故2max b = .(III)由（I ）得，当0x >时，()(0)0f x f >= ，由(II)得，当2b ≤时，(2)4()00()0f x b f x x g x >⇒->⇒> ，从而(2)8()0f x f x ->的近似值，该怎么取x 的值代人是显然的）令1l x =，则1111221111(2)8()48(2)x x x x f x f x x x e e e e -->-->--⇒∴132ln 2ln 2)ln 22212->⇒>-由（II ）的证明过程（3）知道，当b >2时，在区间ln(1]0[,b -上()0g x <.若ln(1ln 101b b ≤≤-+⇒≤≤，令1b =，由()0g x <，得2211)(()2l 0e g x e e e --=----<∴ln 2<=∴ln 2<<下面进行误差估计：∵1.4142 1.4143<1.414230.6928121288.316⋅->==∴1819.412828430.6934<= ∴符合精度要求的值为ln 20.693(0.001)≈精确到 .考点：本题考查利用导数研究函数性质的能力，考查分类讨论的能力及误差估计的思想，思路背景为常规思路，构建函数()g x 的图像即可，难度压轴题.22. (10分)选修4-1：几何证明选讲如图，P 是O 外一点，PA 是切线，A 为切点，割线PBC 与O 相交于点B ，C ，PC =2PA ，D 为PC 中点，AD 的延长线交O 于点E ，证明：(I) BE = EC(II) 22DE B AD P ⋅= 【答案解析】解析：(I)连接OA ,OD 交BC 于F ,设PAD α∠=，因PA 是O 的切线，则90-EAO OEA α∠=∠=︒∵2,2PC PA PC PD ==∴P A D P PD A ⇒=是等腰三角形∴ PDA EDF α∠=∠=∵(90)90EDF OEA αα∠+∠=+︒-=︒∴OE BC ⊥故OE 平分弧BC ,从而BE = EC.(II)∵2,2PC PC PA D PB P ⋅==∴22PA PB PD ⋅=由（I ）知PD PA =∴222PA PA PB PB PA ⋅⇒==∴()()DE BD DC BD PA PD PB PA A PA D PA PB ⋅=⋅=⋅=-⋅=-⋅ 2()PA PB PC PA PB PC PA PA PB PB ⋅=⋅-⋅=⋅-=-()PC PD PB DC PB PA PB ⋅-=⋅=⋅=把2PA PB =代人上式，得222PA PB B P PB P B ⋅=⋅=∴22DE B AD P ⋅= 考点：考查与园有关的角的知识和圆幂定理的应用.难度中等.23. (10分)选修4-4：坐标系与参数方程在直角坐标系xOy 中，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，半圆C 的极坐标方程为 2cos ,[0,]2πρθθ=∈.(I)求C 的参数方程(II)设点D 在C 上，C 在D 处的切线与直线2:l y =+垂直，根据(I)中你得到的参数方程，确定D 的坐标.【答案解析】解析：（I ）∵极坐标方程为2cos ,[0,]2πρθθ=∈∴22cos ρρθ=∴对应的普通方程为：220()02x y x y =≥+- ，即22(01)1()x y y -+=≥ ∴对应的参数方程为[0,]sin 1cos ,x y ϕϕπϕ⎧∈=+⎨=⎩(II)设半圆的圆心为A ，则A (1,0),又由（I ）知，可以设D 点坐标为(1cos n ),si ϕϕ+ ∴直线DA 的斜率tan k ϕ=∵切线与直线2y =+垂直∴tan 3([0,])πϕϕϕπ⇒=∈∴,sin 231cos 2ϕϕ==+ 即D点坐标为3(,22 考点：本题考查园的极坐标方程参数方程以及参数方程的简单应用，难度中等题.24. (10分)选修4-5：不等式选讲设函数()||||()10af x x x a a =++->. (I)证明：()2;f x ≥(II)若(3)5f <，求a 的取值范围.【答案解析】解析：（I ）∵()||||()10af x x x a a =++-> ∴1111,2x ,(12),a a a a x f x a a a x a x x a a ⎧⎪⎪⎪+-≤≤⎨-+-<-=⎪⎪-+>⎪⎩∴()f x 在递增(,)a +∞，在递减(-1)a ∞，-，在[]1,aa -上为常数 ∴()f x的最小值为()(11)2f a f a a a ≥-=+== ∴()2f x ≥（II ）（1）当3a ≥时，1(3)5f a a+<=∴2510a a a ⇒<<-+<∴3a ≤< （2）当03a <<时，2(3)61510f a a a a <⇒-+-->=∴a <或a >3a <<综上所述15(22a ++∈ 考点：考查带有绝对值的不等式的应用能力，考查函数与不等式的关系，中等题.。

2014年全国高考理科数学试题详解-(新课标2规范精校版)

2014年普通高等学校招生全国统一考试理科数学（新课标卷二Ⅱ）第Ⅰ卷一.选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合M=｛0,1,2｝，N={}2|320x x x -+≤，则M N ⋂=( ) A. ｛1｝ B. ｛2｝ C. ｛0，1｝ D. ｛1，2｝【答案】D解析：把},12,0{=M 中的数,代入不等式,023-2≤+x x 经检验x=1,2满足。

故选D.2.设复数1z ，2z 在复平面内的对应点关于虚轴对称，12z i =+，则12z z =（） A. - 5 B. 5 C. - 4+ i D. - 4 - i 【答案】A解析：∵i z +=21与2z 关于虚轴对称，∴i z +-=22，∴12z z =541-=--，故选A3.设向量，满足=+||b a =-||b a ，则=⋅ ( ) A. 1 B. 2 C. 3 D. 5 【答案】A解析：∵=+||b a =-||b a 10222=⋅++b a b a ，6222=⋅-+b a b a联立方程解得 =⋅b a 1，故选A4.钝角三角形ABC 的面积是1，AB=1，，则AC=( )A. 5B.C. 2D. 1【答案】B 解析：∵21sin 1221sin 21=⋅⋅⋅==∆B B ac S ABC ，∴22sin =B 4π=⇒B 或43π 当4π=B 时，经计算ABC ∆为等腰三角形，不符合题意，舍去。

当43π=B 时，由余弦定理，B ac c a b cos 2222-+=，解得5=b ，故选B5.某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（）A. 0.8B. 0.75C. 0.6D. 0.45【答案】 A解析：,p 优良的概率为则随后一个空气质量也设某天空气质量优良，.,8.0,75.06.0A p p 故选解得则据题有=∙=6.如图，网格纸上正方形小格的边长为1（表示1cm ）,图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（）A. 1727B. 59C. 1027D. 13【答案】 C 解析：..2710π54π34-π54π.342π944.2342π.546π96321C v v 故选积之比削掉部分的体积与原体体积，高为径为，右半部为大圆柱，半，高为小圆柱，半径加工后的零件，左半部体积，，高加工前的零件半径为==∴=⋅+⋅=∴=⋅=∴π7.执行右图程序框图，如果输入的t x ,均为2，则输出的S = （） A. 4 B. 5 C. 6 D. 7 【答案】 D由题意，当1=k 时，5,2==S M ，当2=k 时，7,2==S M ，当3=k 时输出7=S ，故选D8.设曲线)1ln(+-=x ax y 在点(0,0)处的切线方程为x y 2=，则=aA. 0B. 1C. 2D. 3 【答案】 D解析：.11-)(),1ln(-)(+='∴+=x a x f x ax x f .2)0(,0)0(='=∴f f 且联立方程解得.3=a 故选D9.设y x ,满足约束条件70310350x y x y x y +-⎧⎪-+⎨⎪--⎩≤≤≥，则2z x y =-的最大值为（）A. 10B. 8C. 3D. 2 【答案】 B解析：y x ,的约束条件如图所示，阴影部分为三角形其顶点坐标可求得 )1,2(、)2,5(、)4,3(，目标函数2z x y =-在两直线013-=+y x 与 07-=+y x 的交点)2,5(处取得最大值，2528z =⨯-=，故选B10.设F 为抛物线C:23y x =的焦点，过F 且倾斜角为30°的直线交C 于A,B 两点，O 为坐标原点，则△OAB 的面积为（）A.B.C. 6332D. 94【答案】 D解析：，则由抛物线的定义，分别在第一和第四象限、设点n BF m AF B A 2,2==和直角三角形知识可：，解得n n m m 3-4322,34322⋅=+⋅=： .6),3-2(23),32(23=+∴=+=n m n m ..49)(4321ΔOAB D n m S 故选=+∙∙=∴11.直三棱柱ABC-A 1B 1C 1中，∠BCA=90°，M ，N 分别是A 1B 1，A 1C 1的中点，BC=CA=CC 1，则BM 与AN 所成的角的余弦值为（）A. 110B. 25C.D.【答案】 C解析：轴，建立坐标系。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2014年普通高等学校招生全国统一考试理科数学新课标第二卷
第Ⅰ卷
一.选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，学科网只有一项是符合题目要求的.
1.设集合M=｛0,1,2｝，N={}2|320x x x -+≤，则M N ⋂=( ) A. ｛1｝
B. ｛2｝
C. ｛0，1｝
D. ｛1，2｝
2.设复数1z ，2z 在复平面内的对应点关于虚轴对称，12z i =+，则12z z =（） A. - 5
B. 5
C. - 4+ i
D. - 4 - i
3.设向量a,b 满足|a+b
|a-b
|=a ⋅b = ( ) A. 1
B. 2
C. 3
D. 5
4.钝角三角形ABC 的面积是12
，AB=1，
，则AC=( )
A. 5
B.
C. 2
D. 1
5.某地区空气质量监测资料表明，一天的空气质量为优良学科网的概率是0.75，连续两为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（）
A. 0.8
B. 0.75
C. 0.6
D. 0.45
6.如图，网格纸上正方形小格的边长为1（表示1cm ）,图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm ，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（） A. 1727 B. 59 C. 1027 D. 13
7.执行右图程序框图，如果输入的x,t 均为2，则输出的S= （） A. 4 B. 5 C. 6 D. 7
8.设曲线y=a x-ln(x+1)在点(0,0)处的切线方程为y=2x ，则a = A. 0 B. 1 C. 2 D. 3
9.设x,y 满足约束条件70
310350x y x y x y +-⎧⎪
-+⎨⎪--⎩
≤≤≥，则2z x y =-的最大值为
（）
A. 10
B. 8
C. 3
D. 2
10.设F 为抛物线C:23y x =的焦点，过F 且倾斜角为30°的直线交C 于A,B 两点，O 为坐标原点，则△OAB 的面积为（）
A.
B.
C. 6332
D. 94
11.直三棱柱ABC-A 1B 1C 1中，∠BCA=90°，M ，N 分别是A 1B 1，A 1C 1的中点，BC=CA=CC 1，则BM 与AN 所成的角的余弦值为（） A. 110 B. 25
C.
D.
12.设函数(
)x f x m
π=.若存在()f x 的极值点0x 满足()2
2200x f x m +<⎡⎤⎣⎦，则m 的取值范围是（） A.
()()
,66,-∞-⋃∞ B.
()()
,44,-∞-⋃∞ C.
()(),22,-∞-⋃∞
D.()(),14,-∞-⋃∞
第Ⅱ卷
本卷包括必考题和选考题两部分.第13题~第21题为必考题，学科网每个试题考生必须做答.第22题~第24题为选考题，考生根据要求做答. 二.填空题
13.()10
x a +的展开式中，7x 的系数为15，则a =________.(用数字填写答案) 14.函数()()()sin 22sin cos f x x x ϕϕϕ=+-+的最大值为_________.
15.已知偶函数()f x 在[)0,+∞单调递减，()20f =.若()10f x ->，则x 的取值范围是__________. 16.设点M （0x ,1），若在圆O:221x y +=上存在点N ，使得∠OMN=45°，则0x 的取值范围是________. 三.解答题：解答应写出文字说明，证明过程或演算步骤. 17.（本小题满分12分）
已知数列{}n a 满足1a =1，131n n a a +=+.
（Ⅰ）证明{
}
12
n a +是等比数列，并求{}n a 的通项公式；
（Ⅱ）证明：1231112
n
a a a ++<…+.
18. （本小题满分12分）
如图，四棱锥P-ABCD 中，底面ABCD 为矩形，PA ⊥平面ABCD ，E 为PD 的中点. （Ⅰ）证明：PB ∥平面AEC ；
（Ⅱ）设二面角D-AE-C 为60°，AP=1，
E-ACD 的体积.
19. （本小题满分12分）
某地区2007年至2013年农村居民家庭纯收入y （单位：千元）的数据如下表：
（Ⅰ）求y 关于t 的线性回归方程；
（Ⅱ）利用（Ⅰ）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
()()
()
1
2
1
n
i
i
i n
i i t t y y b t t ∧
==--=
-∑∑，ˆˆa
y bt =-
20. （本小题满分12分）
设1F ,2F 分别是椭圆()222210y x a b a b
+=>>的左右焦点，M 是C 上一点且2MF 与x 轴垂直，直线1MF 与C 的另一个交点为N.
（Ⅰ）若直线MN 的斜率为34
，求C 的离心率；
（Ⅱ）若直线MN 在y 轴上的截距为2，且15MN F N =，求a,b .
21. （本小题满分12分）已知函数()f x =2x x e e x ---
（Ⅰ）讨论()f x 的单调性；
（Ⅱ）设()()()24g x f x bf x =-，当0x >时，()0g x >,求b 的最大值；
（Ⅲ）已知1.4142 1.4143<
<，估计ln2的近似值（精确到0.001）
请考生在第22、23、24题中任选一题做答，如果多做，学科网同按所做的第一题计分，做答时请写清题号.
22.（本小题满分10）选修4—1：几何证明选讲如图，P 是
O 外一点，PA 是切线，A 为切点，割线PBC 与
O 相
交于点B ，C ，PC=2PA ，D 为PC 的中点，AD 的延长线交O 于点
E.证明：（Ⅰ）BE=EC ；（Ⅱ）AD ⋅DE=22PB
23. （本小题满分10）选修4-4：坐标系与参数方程
在直角坐标系xoy 中，以坐标原点为极点，x 轴为极轴建立极坐标系，半圆C 的极坐标方程为
2cos ρθ=，
0,2πθ⎡⎤∈⎢⎥
⎣⎦
. （Ⅰ）求C 的参数方程；
（Ⅱ）设点D 在C 上，C 在D 处的切线与直线:2l y =+垂直，根据（Ⅰ）中你得到的参数方程，确定D 的坐标.。