电工学-第3章交流电路
合集下载
2019年电工学-第3章-交流电路习题及答案.ppt
π 已知某正弦电流当其相位角为6
3.2.2 已知 A = 8 + j6 ， B 8 45 。求（1）A＋B ;（2） B A A－B；（3）A B ；（4） ；（5）j A＋B ；（6） 。 A j B
返回主页 下一页
第 3 章
交 流 电 路
3.3.1 在图3.6（教材图3.01）所示 电路中，已知R 100 , L 31.8 mH,C 318 F, 求电源的频率和电压分别为50 Hz、100 V 和1 000 Hz，100 V两种情况下，开关S 合向 a、b、c 位置时电流表的读数，并 计算各元件中的有功功率和无功功率。 3.4.1 在图3.7（教材图3.02）所示电路中，三个照明相同 ， R XC X L ,试问接于交流电源上时，照明灯的亮度有什么不 同？若该接到电压相同的直流电源上，稳定后，与接交流电 源时相比，各照明灯的亮度有什么变化？ 3.4.2 求串联交流电路中下列三种情况下电路中的 R 和 X 各为多少？指出电路的性质和电压对电流的相位差
图3.15
j10 , Z 2 (40 j 30) , I
I 2 和U 。 。求：I 1 、 5 30 A
图3.17
返 回 上一页 下一页
第 3 章
交 流 电 路
Байду номын сангаас
3.5.5
在图3.18（教材图3.09）所
示电路中，已知 R X C , U 220V 总电压U 与总电流 I 相位相同。
1 1 若T 10 m s,则 f Hz 100Hz 3 T 10 10
I 7.07 180 A 7.07 180 A 7.07 A
3.2.2 已知 A = 8 + j6 ， B 8 45 。求（1）A＋B ;（2） B A A－B；（3）A B ；（4） ；（5）j A＋B ；（6） 。 A j B
返回主页 下一页
第 3 章
交 流 电 路
3.3.1 在图3.6（教材图3.01）所示 电路中，已知R 100 , L 31.8 mH,C 318 F, 求电源的频率和电压分别为50 Hz、100 V 和1 000 Hz，100 V两种情况下，开关S 合向 a、b、c 位置时电流表的读数，并 计算各元件中的有功功率和无功功率。 3.4.1 在图3.7（教材图3.02）所示电路中，三个照明相同 ， R XC X L ,试问接于交流电源上时，照明灯的亮度有什么不 同？若该接到电压相同的直流电源上，稳定后，与接交流电 源时相比，各照明灯的亮度有什么变化？ 3.4.2 求串联交流电路中下列三种情况下电路中的 R 和 X 各为多少？指出电路的性质和电压对电流的相位差
图3.15
j10 , Z 2 (40 j 30) , I
I 2 和U 。 。求：I 1 、 5 30 A
图3.17
返 回 上一页 下一页
第 3 章
交 流 电 路
Байду номын сангаас
3.5.5
在图3.18（教材图3.09）所
示电路中，已知 R X C , U 220V 总电压U 与总电流 I 相位相同。
1 1 若T 10 m s,则 f Hz 100Hz 3 T 10 10
I 7.07 180 A 7.07 180 A 7.07 A
电工学课件--第三章 正弦交流电路
U • o I= U =U 0 ∠ R
• •
u =Um sinω t u Um i = = sinω = Im sinω t t R R
U =I R
U =I R
•
•
可见： 可见：电压与电流同相位 ui
i
u
•
IU
•
I
•
U
+−
2．功率关系
ui
i
⑴ 瞬时功率
•
u
IU
p=ui=UmImsin2ωt =UI(1-cos2ωt)
角频率ω: 单位时间里正弦量变化的角度 称为角频率。单位是弧度/秒 （rad/s）. ω=2π/T=2πf 周期，频率，角频率从不同角度描 述了正弦量变化的快慢。三者只要知 道其中之一便可以求出另外两时值， 瞬时值中最大的称为最大值。Ｉm、 Ｕ m 、Ｅ m 分别表示电流、电压和电动 势的最大值. 表示交流电的大小常用有效值的概 念。
单位是乏尔（Var） 单位是乏尔（Var）
第四节 RLC串联交流电路 串联交流电路 一.电压与电流关系
i R u L C
uR uL
u =uR +uL +uC
U =UR+UL+UC
• • • •
uC
以电流为参考相量， 以电流为参考相量， 相量图为： 相量图为：
•
UL UL+UC
φ
• • • •
•
U I
•
U
φ UR
UL-UC
UR
UC
2 可见： 可见： U = UR +(UL −UC)2
U L −UC X L − XC = arctg = arctg UR R
大连理工大学 电工学-第3章交流电路-1
U =U∠ψ =Uejψ =U(cosψ+ jsinψ) =Ucosψ+ j(Usinψ) U& m = 2U&
在相量图中，同频交流电在任何时刻它们的相对位
置不变，所以各矢量可不必旋转，固定在初始位置
在复平面上用来表示正弦交流电的矢量称为正 弦交流电的相量。
例题
[例1] 已知u1=141sin(ωt+45°)V， u2=310sin(ωt-15°)V，画出它们的有效值相量图。
=282.1+j13.8 =284∠2.8°V
即U=284 V ，ϕ =2.8°
U ≠ U1 + U2
参考相量
参考相量：在进行交流电路的分析和计算时，可令同 一电路的某一电流、电压或电动势的初相位为零。
i= Imsin(ωt +0 )
Im = Im∠ 0° = Im(cos0o + jsin0o ) = Im
电源电压
最大值 Um = 2 ⋅220V = 311V
该用电器最高耐压低于电源电压的最大值，所 以不能用。
电源插头
三、交流电的相位、初相位、相位差
i = 10 sin（1 000 t + 30°）A
u = 311sin（314 t－60°）V
相位: ωt + ψ
相位
初相位:ψi = 30° , ψu =－60°
= 100∠45o V
U& 2
=
310∠-15o 2
=
220∠-15o
V
+j U1
2.8°
U +1
U& =U&1 +U&2 =100∠45o + 220∠-15oV
电工学第三章三相电路
B
iA iN iB RC
RA
N
RB
iC
N I A I B I C 0 I
一、负载的星形联结 二、负载的三角形联结
交流电路中的用电设备，大体可分为两类： 一类是需要接在三相电源上才能正常工作
的叫做三相负载 ,如果每相负载的阻抗值和阻抗
角完全相等，则为对称负载，如三相电动机。
另一类是只需接单相电源的负载，它们可
以按照需要接在三相电源的任意一相相电压或 线电压上。对于电源来说它们也组成三相负载， 但各相的复阻抗一般不相等，所以不是三相对 称负载。如照明灯。
二、三相电源的连接
1、星形联结 把三相绕组的尾端 XYZ 接成一点。 而把首端 A、B、C 作为与外电路相联接的端点。 这种 联接方式称为电源的星形联结。
中性点 U A 或零点
+
–
N
– U C
+
– + U B
+ U A – – – U B +
+
U AB
–
A 相线（火线）
相电 压
一、三相对称正弦电动势
1.三相交流发电机主要组成部分： 电枢（是固定的，亦称定子）：定子铁心内圆周表面 有槽，放入三相电枢绕组。 A B C 磁极 （是转动的，亦称转子） A
Y
– + S
Z
n
+
B
绕 组
A
X
X Y Z
三相绕组
单相绕组
N
C
铁 心
+
+ X
三相绕组的三相电动势 幅值相等, 频率相同, 彼 此之间相位相差120°。
U C
+
iA iN iB RC
RA
N
RB
iC
N I A I B I C 0 I
一、负载的星形联结 二、负载的三角形联结
交流电路中的用电设备，大体可分为两类： 一类是需要接在三相电源上才能正常工作
的叫做三相负载 ,如果每相负载的阻抗值和阻抗
角完全相等，则为对称负载，如三相电动机。
另一类是只需接单相电源的负载，它们可
以按照需要接在三相电源的任意一相相电压或 线电压上。对于电源来说它们也组成三相负载， 但各相的复阻抗一般不相等，所以不是三相对 称负载。如照明灯。
二、三相电源的连接
1、星形联结 把三相绕组的尾端 XYZ 接成一点。 而把首端 A、B、C 作为与外电路相联接的端点。 这种 联接方式称为电源的星形联结。
中性点 U A 或零点
+
–
N
– U C
+
– + U B
+ U A – – – U B +
+
U AB
–
A 相线（火线）
相电 压
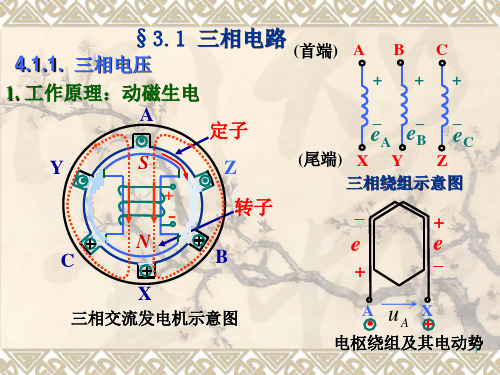
一、三相对称正弦电动势
1.三相交流发电机主要组成部分： 电枢（是固定的，亦称定子）：定子铁心内圆周表面 有槽，放入三相电枢绕组。 A B C 磁极 （是转动的，亦称转子） A
Y
– + S
Z
n
+
B
绕 组
A
X
X Y Z
三相绕组
单相绕组
N
C
铁 心
+
+ X
三相绕组的三相电动势 幅值相等, 频率相同, 彼 此之间相位相差120°。
U C
+
电工与电子技术之电工技术第三章课后题解
第3章 正弦交流电路的稳态分析本章的主要任务是学习正弦量、正弦交流电路和相量法的基本概念、正弦交流电路的稳态分析与计算、正弦交流电路功率的概念和计算。
在此基础上理解和掌握功率因数提高的意义，和谐振的概念。
本章基本要求(1) 正确理解正弦量和正弦交流电路概念； (2) 正确理解相量法引入的意义；(3) 正确理解有功功率和功率因数的概念； (4) 掌握相量法；(5) 掌握电路定律的相量形式和元件约束方程的相量形式； (6) 分析计算正弦稳态电路； (7) 了解功率因数提高的意义； (8) 了解谐振的概念。
本章习题解析3-1 已知正弦电压和电流的三角函数式，试用有效值相量表示它们，并画出它们的相量图。
（1）)20sin(210 +=t i ωA ，)60sin(2150 +=t u ωV （2）)20sin(28 -=t i ωA ，)45sin(2120 -=t u ωV （3）)30sin(25 +=t i ωA ，)90sin(2100 +=t u ωV解 (1)︒∠=2010IA ，︒∠=60150U V ，相量图如图3-1（a ）所示。
(2))20(10︒-∠=IA ，)45(120︒-∠=U V ，相量图如图3-1（b ）所示 (3)︒∠=305IA ，︒∠=90100U V ，相量图如图3-1（c ）所示3-2 已知电压、电流的相量表示式，试分别用三角函数式、波形图及相量1+j （a ）1+（b ）1+j（c ）图3-1图表示它们。
（1）4030j U+= V ，43j I += A （2）100=UV ，43j I -= A （3）V 10045 j e U=，A 44j I +=解 (1))13.53(504030︒∠=+=j U=︒+︒13.53sin 5013.53cos 50j ，V )13.53(543︒∠=+=j I=︒+︒13.53sin 513.53cos 5j ，A 波形图相量图如图3-2（a ）所示。
电工学第三章三相交流电ppt课件
结论：电源 Y形联结时, 线电压Ul 3UP, 且超 前相应的相电压 30 , 三相线电压也是对称的 。
6
3.1.2 三相电路中负载的联结方法
1. 三相负载
分类
三相负载：需三相电源同时供电
负载
三相电动机等
单相负载：只需一相电源供电
照明负载、家用电器
对称三相负载：ZA=ZB= ZC
三相负载
如三相电动机
此时负载中性点N´即为 A, 因此负载各相电压为 N
UA 0 , UA 0
B
UB UB A, UB 380 V UC UC A , UC 380 V C
+
U A
iA
iC
– –
N´
–
iB
+ U C U B +
此情况下，B相和C相的电灯组由于承受电压上所加 的电压都超过额定电压（220V) ，这是不允许的。
(2) 相UA电B=流UBC=UIIICABCABCA=UUUUZZZClCAABB=AABBCCUP
A
+–
U AB
– U CA
B U+ BC C–
+
IB IC
ICA
ZCA
IAB
ZBC ZAB
IBC
相电流： 线电流：
IIAA、B、IIB、BC、IC ICA
线电流不等于相电流
20
(3) 线电流
IA IAB ICA
16
(2) A相断路
A
1) 中性线未断
B、C相灯仍承受220V N
电压, 正常工作。
2) 中性线断开
B
变为单相电路，如图(b) C 所示, 由图可求得
I UBC 380 12 .7 A RB RC 10 20
6
3.1.2 三相电路中负载的联结方法
1. 三相负载
分类
三相负载：需三相电源同时供电
负载
三相电动机等
单相负载：只需一相电源供电
照明负载、家用电器
对称三相负载：ZA=ZB= ZC
三相负载
如三相电动机
此时负载中性点N´即为 A, 因此负载各相电压为 N
UA 0 , UA 0
B
UB UB A, UB 380 V UC UC A , UC 380 V C
+
U A
iA
iC
– –
N´
–
iB
+ U C U B +
此情况下，B相和C相的电灯组由于承受电压上所加 的电压都超过额定电压（220V) ，这是不允许的。
(2) 相UA电B=流UBC=UIIICABCABCA=UUUUZZZClCAABB=AABBCCUP
A
+–
U AB
– U CA
B U+ BC C–
+
IB IC
ICA
ZCA
IAB
ZBC ZAB
IBC
相电流： 线电流：
IIAA、B、IIB、BC、IC ICA
线电流不等于相电流
20
(3) 线电流
IA IAB ICA
16
(2) A相断路
A
1) 中性线未断
B、C相灯仍承受220V N
电压, 正常工作。
2) 中性线断开
B
变为单相电路，如图(b) C 所示, 由图可求得
I UBC 380 12 .7 A RB RC 10 20
电工学-交流电路A
t 起点改变时，它们的初相位 i1与i3反相 角改变，但初相角之差不变。
8
3.2 正弦交流电的相量表示法
第3章 3 2
正弦量的相量表示法就是用复数来表示正弦量
正弦量可用复平面中的旋转有向线段表示
y
A
i i= Imsin( t+)
•
A
• t1+
0
Im
x
0
t1 t
A
t1
有向线段长度是Im，t=0时，与横轴的夹角是，以角速度
•
I = Ia +j Ib
相
=I(cos +jsin )
量
有效
=Iej 有效值
=I
I•m= Ia m +j Ibm
初相位
=Im(cos +jsin )
=Imej
=Im
最大值
图 +j 值相量
•
最大
Ib
•
I
Im 值相量
0
Ia
+1
相量是表示正弦交流电的复数，正弦交流
电是时间的函数，所以二者之间并不相等。 11
第3章 3 3
–
u
波
形
图
0
i
+j U•
t
0
•
I
+1
电压超前电流90
电压与电流大小关系 电压与电流相量式
UU• ==I jXI•L
XL
相量图
25
2.功率
i +
u
L
波
ui
形
图
0
第3章 3 3
t
–
i = Imsin t u= Umsin( t+90)
电工学第3章交流电路2
U Z = I
+ i R L C − + − + uR uL
u
− + u − C
ϕ = ψ u −ψ i
结论： Ｚ 的模为电路总电压和总电流有效值之比， Ｚ 的幅角则为总电压和总电流的相位差。
3.4 串联交流电路
U = UR + UL + UC =[R + j ( XL－XC )]I U =ZI
3. 相量图
UL U C
由相量图可求得
U UX X UR 0＜ ϕ ＜ 90° 感性电路 I
│Z│
U = U R + (U L − U C )
2
2
2 2
ϕ
R UC
= I R + ( X L − XC ) =I R +X
2 2
R = Z cos ϕ X = Z sin ϕ
由阻抗三角形得
=I Z
Z = R 2 + ( X L − X C )2 X L − XC R
= Z e jϕ = Z ∠ϕ
− + u − C
阻抗 三角形
R2 + X2
阻抗模:│Z│=√
阻抗角: ϕ = arctan (X / R)
ϕ
|Z|
X
3.4 串联交流电路
U = UR + UL + UC =[R + j ( XL－XC )]I U =ZI 2. 阻抗 Z 由 U =Z I 可得： U = U∠ψ u = U ∠ψ −ψ = Z ∠ϕ Z= u i I∠ ψ i I I
二、纯电容电路
1. 电压、电流的关系
设 由 有 式中 容抗
i + u – C
+ i R L C − + − + uR uL
u
− + u − C
ϕ = ψ u −ψ i
结论： Ｚ 的模为电路总电压和总电流有效值之比， Ｚ 的幅角则为总电压和总电流的相位差。
3.4 串联交流电路
U = UR + UL + UC =[R + j ( XL－XC )]I U =ZI
3. 相量图
UL U C
由相量图可求得
U UX X UR 0＜ ϕ ＜ 90° 感性电路 I
│Z│
U = U R + (U L − U C )
2
2
2 2
ϕ
R UC
= I R + ( X L − XC ) =I R +X
2 2
R = Z cos ϕ X = Z sin ϕ
由阻抗三角形得
=I Z
Z = R 2 + ( X L − X C )2 X L − XC R
= Z e jϕ = Z ∠ϕ
− + u − C
阻抗 三角形
R2 + X2
阻抗模:│Z│=√
阻抗角: ϕ = arctan (X / R)
ϕ
|Z|
X
3.4 串联交流电路
U = UR + UL + UC =[R + j ( XL－XC )]I U =ZI 2. 阻抗 Z 由 U =Z I 可得： U = U∠ψ u = U ∠ψ −ψ = Z ∠ϕ Z= u i I∠ ψ i I I
二、纯电容电路
1. 电压、电流的关系
设 由 有 式中 容抗
i + u – C
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
7
第 3
章 三、交流电的相位、初相位、相位差
交
i = 10 sin（1 000 t + 30°）A
流 电
u = 311sin（314 t－60°）V
路
相位: ωt + ψ
初相位:ψi = 30° , ψu =－60°
相位 初相位
相位差: 同频率的正弦电量的初相位之差。
i = 100 sin（314 t + 30）A u = 311sin（314 t－60）V
三角式
= c e jψ
指数式
=c ψ
极坐标式
高等教育出版社
11
第 3
章 二、复数的运算方法
交 复数的运算：加、减、乘、除法。
流
电 路
设： A1 = a1＋j b1 = c1 ψ1 A2 = a2＋j b2 = c2 ψ2 ≠０
加、减法：A1±A2 = (a1±a2) + j (b1±b2)
乘法: 除法：
的有效值并画出相量图； (2) 总电压 u 与 u1 及 u2 的相位
差。
[解] (1) 选 u1为参考相量
ψ ψ2
1 =ψ –ψ1
U1
U1= 100 0 A U2 = 60 – 60 A U = U1 + U2
2 =ψ –ψ2
U2 ψ2 = 60
U
相量图
=（100 0 + 60 – 60 ）V = 140 – 21.79 V
i
交
流
电
路
O
ψ = 0°
i 0＜ψ＜180°
ωt
O
ψ
ωt
i －180°＜ψ ＜ 0°
i
ψ = ±180°
O ψ
ωt
O
ωt
高等教育出版社
4
第 3
章 一、交流电的周期、频率、角频率
i
交
流
2π
电
路
O
ωt
T
周期 T ：变化一周所需要的时间（s）。
频率 f ：1s 内变化的周数（Hz）。
f
=
1 T
角频率ω ： 正弦量 1s 内变化的弧度数。
电工技术
第 3 章 交流电路
3.1 正弦交流电的基本概念
3.2 正弦交流电的相量表示法 3.3 单一参数交流电路 3.4 串联交流电路 3.5 并联交流电路 3.6 交流电路的功率 3.7 电路的功率因数 * 3.8 电路中的谐振 3.9 非正弦周期信号电路 3.10 应用实例
返回主页 上一章1 下一章
[解]
(1) 采用相量运算
(2) 相量图
I1m = 20 60 A I2m = 10 – 45 A Im= I1m+ I2m
= 19.9 30.9 A i = Im sin(ωt +ψ)
= 19.9 sin(ωt + 30.9 ) A
+j
I1m
Im
60° 30.9°
O 45°
+1
I2m
高等教育出版社
+j
j I1
I
ψ1
O
+1
j I1
高等教育出版社
13
第
3
章
[例 3.2.1] 已知 i1 = 20 sin (ωt + 60º) A， i2 = 10 sin
交 流 电 路
(ωt－45º) A 。两者相加的总电流为i ，即i = i1 + i2 。
(1) 求 i 的数学表达式；(2) 画出相量图； (3) 说明 i 的 最大值是否等于 i1 和 i2 的最大值之和， i 的有效值是否 等于 i1 和 i2 的有效值之和，并说明为什么。
=ψu －ψi = －60－30 =－90
高等教育出版社
8
第
3
章
iu
0＜ ＜180°
iu
－180°＜ ＜ 0°
交
流
电 路
O
ωt
O
ωt
u 超前于 i
u 滞后于 i
iu
= 0°
iu
= ±180°
O
ωt
O
u 与 i 同相位
ωt
u 与 i 反相
高等教育出版社
9
第
3
章
3.2 正弦交流电的相量表示法
ωt
Um = R Im (3) 相量关系：U = R I
如 ：U = U 0 则：I=I 0
I
U
高等教育出版社
第 3
(2) 1 =ψ –ψ1= – 21.79 – 0 = – 21.79
2 =ψ –ψ2 = – 21.79 – ( – 60 ) = 38.21
高等教育出版社
16
第
3
章
3.3 单一参数交流电路
交 流
一、 纯电阻电路
电 路
1. 电压、电流的关系 (1) 波形图
ui
(2) 大小关系 U= R I
O
A1 A2 = c1 c2 ψ1＋ψ2
A1 A2
=
c1 c2
ψ1－ψ2
高等教育出版社
12
第 3
章 由于： e±j90 = 1 ±90 =±j
交则
流 电 路
j I = I e j90 = I ejψ ·ej90 = I e j(ψ + 90 ) －j I = I e j90 = I ejψ·e j90 = I ej(ψ 90 )
6
第
3 章
二、交流电瞬时值、最大值、有效值
交
e、i、u
流 电
Em、Im、Um
路
E、I、U
瞬时值 最大值 有效值
IR
i
R
Wd = RI2T
Wa T Ri2dt 0
如果热效应相当，Wd = Wa ，则 I 是 i 的有效值。
正弦电量的有效值：
I
=
Im √2
U =√2Um E =√2Em
高等教育出版社
ω = 2πf
=
2π T
(rad/s)
高等教育出版社
5
第
3
章
常见的频率值
交 流
各国电网频率：中国和欧洲国家 50 Hz，
电 路
美国 、日本 60 Hz
有线通信频率：300 ~ 5 000 Hz；
无线通信频率：30 kHz ~ 3×104 MHz ； 高频加热设备频率：200 ~ 300 kHz。
高等教育出版社
交 流
(a) 旋转矢量 +j
(b) 正弦交流电
电
ω
路
ωt1
ωt2
ψ
O
O
+1
ψ
ωt
正弦交流电可以用 一个固定矢量表示 最大值相量 Im
有效值相量 I
ωt1
ωt2 +j
Im
I ψ
+1 O
高等教育出版社
第
3 章
一、复数的表示方法
+j
交 流
b
p
电
路
ψ
模
O
a +1
10
辐角
Op = a + j b
代数式
= c (cosψ + j sinψ )
14
第
3
章
(3) 因为 i1 + i2 的初相位不同，故最大值和有效
值之间不能代数相加。
交 流 电 路
高等育出版社
15
第
3
章
[例 3.2.2] 已知 u1 和 u2 的有效值分别为U1 = 100 V，
交 流 电 路
U2 = 60 V，u1 超前于 u2 60º，求： (1) 总电压 u = u1 + u2
2
第
3
章
3.1 正弦交流电的基本概念
交
流 交流电: 大小和方向都周期性变化、在一个周期
电 路
上的函数平均值为零。 正弦交流电: 按正弦规律变化的交流电。
i
i = Imsin(ωt +ψ)
Im
瞬时值最大值
最大值
角频 率
初相位
O
ψ
角频率 正弦交流电的三要素
初相位
ωt
高等教育出版社
3
第 3
章 正弦交流电的波形: