电工学——正弦交流电路
电工学-正弦交流电路

O
f 而对直流所呈现的容抗趋于无穷大,故
XL 与 f 的关系 可视为开路。
2.3.3 电容元件的交流电路
1. 电压电流关系 i
+
u
C
–
i
u Um sint i Im sin( t 90 )
+j •
u
I
波 形O 图
电流超前电压 90 电压与电流大小关系 电压与电流相量式
t
U XCI U jXC I
2.1 正弦电压与电流 I, U
直流电路在稳定状态下电流、电压的大
小和方向是不随时间变化的,如图所示。
正弦电压和电流是按正弦规律周期性
变化的,其波形如图示。
O u, i
t
电路图上所标的方向是指它们的参考
方向,即代表正半周的方向。
负半周时,由于的参考方向与实际方
+
向相反,所以为负值。
实
i
O i
t
际 方
第 2 章 正弦交流电路
在生产和生活中普遍应用正弦交流电,特别是三相电路应 用更为广泛。
正弦交流电路是指含有正弦电源(激励)而且电路各部分所 产生的电压和电流(响应)均按正弦规律变化的电路。
本章将介绍交流电路的一些基本概念、基本理论和基本分 析方法,为后面学习交流电机、电器及电子技术打下基础。
本章还将讨论三相交流电路和非正弦周期电压和电流。 交流电路具有用直流电路的概念无法理解和无法分析的物 理现象,因此在学习时注意建立交流的概念,以免引起错误。
•
UL
为正
时电路 中电压 电流相 量图
•
• UL UC
•
U
•
UR
•
UC
的大小和正负由
电工学课件--第三章 正弦交流电路

U • o I= U =U 0 ∠ R
• •
u =Um sinω t u Um i = = sinω = Im sinω t t R R
U =I R
U =I R
•
•
可见: 可见:电压与电流同相位 ui
i
u
•
IU
•
I
•
U
+−
2.功率关系
ui
i
⑴ 瞬时功率
•
u
IU
p=ui=UmImsin2ωt =UI(1-cos2ωt)
角频率ω: 单位时间里正弦量变化的角度 称为角频率。单位是弧度/秒 (rad/s). ω=2π/T=2πf 周期,频率,角频率从不同角度描 述了正弦量变化的快慢。三者只要知 道其中之一便可以求出另外两时值, 瞬时值中最大的称为最大值。Im、 U m 、E m 分别表示电流、电压和电动 势的最大值. 表示交流电的大小常用有效值的概 念。
单位是乏尔(Var) 单位是乏尔(Var)
第四节 RLC串联交流电路 串联交流电路 一.电压与电流关系
i R u L C
uR uL
u =uR +uL +uC
U =UR+UL+UC
• • • •
uC
以电流为参考相量, 以电流为参考相量, 相量图为: 相量图为:
•
UL UL+UC
φ
• • • •
•
U I
•
U
φ UR
UL-UC
UR
UC
2 可见: 可见: U = UR +(UL −UC)2
U L −UC X L − XC = arctg = arctg UR R
《电工学》(秦曾煌主编第六版)第四章__正弦交流电路(完整版)

∴
,
,
, 4.5.8 解 求图 4.15 所示电路的阻抗 Zab。 对图 4.15(a)所示电路
对图 4.15(b)所示电路 ,
4.5.9 解
求图 4.16 两图中的电流 。
用分流比法求解。
对图 4.16(a)所示电路
对图 3.18(b)所示电路
4.5.10 解
计算上题中理想电流源两端的电压。
对图 4.16(a)所示电路
线圈电感 43.3 H,试求线圈电流及功率因数。 解
, 4.4.5 日光灯管与镇流器串联接到交流电压上,可看作为
1=280Ω
, 串联电路。
2=20Ω
如已知某灯管的等效电阻 =1.65H,电源电压
,镇流器的电阻和电感分别为
和
=220V,试求电路中的电流和灯管两端与镇流器上的电压。
这两个电压加起来是否等于 220V?电源频率为 50HZ。 解 日光灯电路的等效电路见图 T4.4.5。
根据题意画出等效电路图 T4.4.2
4.4.3
一个线圈接在
=120V 的直流电源上, =20A;若接在 f=50HZ, 及电感 。
=220V 的交流电源上,则 =28.2A。试求线圈的电阻 解 线圈加直流电源,电感 看作短路,电阻
。 。
线圈加交流电源,等效阻抗 感抗 ∴
4.4.4
有一 JZ7 型中间继电器,其线圈数据为 380V 50HZ,线圈电阻 2KΩ ,
,试求电容值。同上题比较,u2
画出相量图 T4.4.9 ,由相量图知 u2 滞后 u1
, u1 滞后 i
。
4.4.10
图 4.07 所示的是桥式移相电路。当改变电阻
时,可改变控制电
压 ug 与电源电压 u 之间的相位差 ,但电压 ug 的有效值是不变的,试证明之。 图中的 Tr 是一变压器。 证 ,设 ,则
电工学 正弦交流电

相量
复数表示法 复数运算
相量的复数表示—相量式
将复数 A 放到复平面上,可如下表示:
j
•
A
A a2 b2
bU
tan 1 b
+1
a
a
A a jb A c o s jA sin
•
A
b A
a
欧 拉
cos
e j e j 2
公 式
sin
e j
e j
2j
A a jb A(cos jsin )
t
i i 领先于
1
2
相 位
i1
落 后
2 1
i2
120 t i i1 落后于 2
三相交流电路:三种电压初相位各差120。
uA uB uC
t
可以证明同频率正弦波运算后,频率不变。
如: u1 2U 1sin t1 u2 2U 2sin t2
uu1u2
2U1sin t1 2U2sin t2 2Usin t 幅度、相位变化
复数
瞬时值
正误判断
已知: i1s0i n t4 ()5
? I 10 45 2
j45
有效值
? Im10e45
正误判断
已知: u2 1s0i(n t 1)5
则:
U10?15
? U 1 0ej15
正误判断
已知: I10 5 00
则: i 1
Im 2I102 0
代数式
A e j
指数式
A
极坐标形式
相量的复数运算
1. 加 、减运算 • 设: A 1 a 1 j b1 • A 2 a 2 jb2
则:
•• •
正弦交流电路定义 -回复

正弦交流电路定义-回复什么是正弦交流电路?正弦交流电路是指由正弦波形的电压或电流组成的电路系统。
正弦波形是一种周期性变化的波形,具有均匀而连续的变化特点,可以描述许多实际电源和负载所产生的电压和电流。
在正弦交流电路中,电压和电流的大小会随着时间的推移而不断变化,但其变化满足正弦函数的规律。
正弦函数是一种典型的周期函数,其图像呈现出一种重复模式,具有相同的幅值和频率。
正弦交流电路由多个元素组成,包括电源、负载以及连接电源和负载的导线。
电源可以是交流电源或直流电源,而负载可以是电阻、电感、电容或他们的组合。
在正弦交流电路中,电压和电流的变化遵循欧姆定律、基尔霍夫定律和电容、电感的特性等。
欧姆定律描述了电压、电流和电阻之间的关系,表明它们成正比关系;基尔霍夫定律描述了电流在闭合电路中的分配和电压在闭合电路中的合成;电容和电感则分别描述了电压和电流随时间的变化规律。
正弦交流电路在实际应用中具有广泛的用途。
例如,在家庭中,我们常常使用交流电路来为各种电器设备供电,如电视机、冰箱、空调等。
在工业生产中,正弦交流电路也是不可或缺的部分,被用于各种电机、照明设备、变压器、电子器件等的驱动和控制。
为了更好地分析和设计正弦交流电路,我们可以使用交流电路理论和相关工具。
交流电路理论包括复数分析法、相频特性、幅频特性、相频特性等方法和概念,可以帮助我们理解电压和电流在正弦交流电路中的行为。
此外,计算机软件也可以提供模拟和仿真工具,以帮助我们更好地理解和优化正弦交流电路的性能。
总而言之,正弦交流电路是由正弦波形的电压或电流组成的电路系统,具有周期性变化的特点。
它在日常生活和工业生产中广泛应用,通过交流电路理论和相关工具的应用,我们可以更好地分析和设计正弦交流电路。
正弦交流电知识点整理
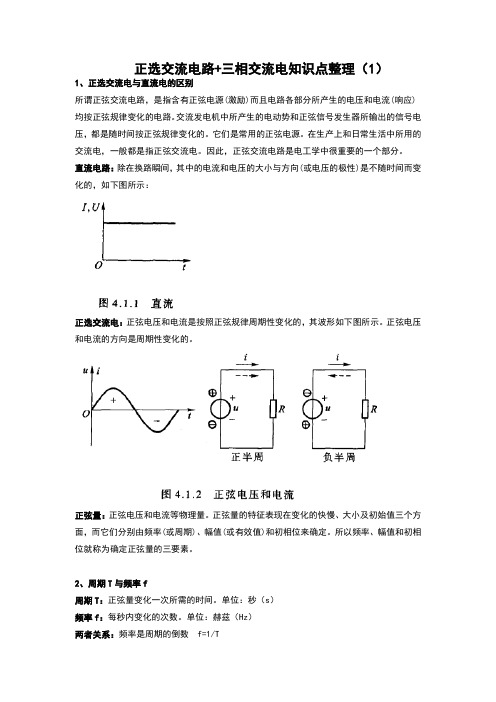
正选交流电路+三相交流电知识点整理(1)1、正选交流电与直流电的区别所谓正弦交流电路,是指含有正弦电源(激励)而且电路各部分所产生的电压和电流(响应)均按正弦规律变化的电路。
交流发电机中所产生的电动势和正弦信号发生器所输出的信号电压,都是随时间按正弦规律变化的。
它们是常用的正弦电源。
在生产上和日常生活中所用的交流电,一般都是指正弦交流电。
因此,正弦交流电路是电工学中很重要的一个部分。
直流电路:除在换路瞬间,其中的电流和电压的大小与方向(或电压的极性)是不随时间而变化的,如下图所示:正选交流电:正弦电压和电流是按照正弦规律周期性变化的,其波形如下图所示。
正弦电压和电流的方向是周期性变化的。
正弦量:正弦电压和电流等物理量。
正弦量的特征表现在变化的快慢、大小及初始值三个方面,而它们分别由频率(或周期)、幅值(或有效值)和初相位来确定。
所以频率、幅值和初相位就称为确定正弦量的三要素。
2、周期T与频率f周期T:正弦量变化一次所需的时间。
单位:秒(s)频率f:每秒内变化的次数。
单位:赫兹(Hz)两者关系:频率是周期的倒数 f=1/T高频炉的频率是200- 300kHz;中频炉的频率是500-8000Hz;高速电动机的频率是150-2000Hz; 通常收音机中波段的频率是530-1600kHz ,短波段是2.3-23MHz;移动通信的频率是900MHz和1800MHz; 在元线通信中使用的频率可高 300 GHz。
正弦量变化的其他表达方式:角频率正弦量变化的快慢除用周期和频率表示外,还可用角频率ω来表示。
因为一周期内经历了 2π弧度(图 4.1.3) ,所以角频率为:上式表示 T,f,ω三者之间的关系,只要知道其中之一,则其余均可求出。
3、幅值与有效值正弦量在任一瞬间的值称为瞬时值,用小写字母来表示,如 i , U 及 e 分别表示电流、电压及电动势的瞬时值。
瞬时值中最大的值称为幅值或最大值,用带下标 m 的大写字母来表示,如Im, Um 及 Em 分别表示电流、电压及电动势的幅值。
第三章:正弦交流电路
& =U & = − jI & X = − j 2 × 50∠45 o = 50 2∠ − 45 o V U ao C C C & =U & = jI & X = j 2 × 50∠ − 45o = 50 2∠45o V U bo L L L & & & U = U − U = 50 2∠ − 45o − 50 2∠45o =
2
& 与U & 之间的相位差 I R
ϕ = arctan
XC 1 = arctan R Rω C
第三章
正弦交流电路
31
& 与U & 之间的相位差 U θ = 2ϕ ab 由上式可知,当改变电阻 R 时,输出电压 Uab 是一个不变恒定的值,即有 U U ab = 2 20 本题中 U ab = = 10V 2 当电阻 R 由零变到无穷大时, ϕ 角由 90o 变到零, θ 角由 180o 变到零。当电阻 R & 的相位从 180o 减小到: 由零变到 1.5kΩ 时, U
& = jI &X = j4.4 × 40∠73o = 176∠163o V U L L & & U C = − jIX C = − j4.4 × 80∠73o = 352∠ − 17 o V 【例题 3.2】 图 3.2(a)为 RC 移相电路。已知电阻 R = 100 Ω ,输入电压 u1 的频率为
Z = R + j( X L − X C ) = 30 + j(40 − 80) = 30 − j40 = 50∠ − 53o Ω
28
电工学试题精选与答题技巧
o & & = U = 220∠20 = 4.4∠73o Α I Z 50∠ − 53o & =I &R = 4.4 × 30∠73o = 132∠73o V U R
正弦交流电路
幅值(最大值)、有效值:表示正弦量的大小 周期、频率、角频率:表示正弦量的变化速度 初相位:给出观察正弦量的起始点
目录
正弦交流电的基本概念 正弦量的向量表示法 单一参数的交流电路 RLC串联交流电路 阻抗的串并联
正弦量的相量表示法
●瞬时值表达式(三角函数表达式)
●波形图
i 2I sin(wt )
例
u1 4 2 sin wt 60
u2 3 2 sin wt 30
U2
ua u1 u2 ub u1 u2
U a U1 U 2 523
ua 5 2 sin wt 23
U b U1 U 2 597
ub 5 2 sin wt 97
Ub
5
U1
4
Ua
97 o
U
U
有效值相量图
用符号: I U E 表示。
包含大小与相位信息。
例
i1 8 2 sin wt 60 i2 6 2 sin wt 30
I1 860o A I2 6 30o A
相量式
有效值
I1 8
60 o
30 o
6
I2
初相位
相量图
正弦量的相量表示法
●同频率正弦量的运算
加减运算用相量图—平行四边形法则
有向线段表示正弦量 有向线段不等于正弦量
ω
u Um sinw t
Um
wt
正弦量的相量表示法
相量用复平面的有向线段表示,其长度(相量的模)表示正弦量的有效值;其与横轴 的夹角(相量的幅角)表示正弦量的初相位。
直角坐标式:
U a jb U cos j sin
指数式:
U Ue j
极坐标式:
正弦交流电路定义
正弦交流电路定义正弦交流电路是指由正弦波形式的电压或电流组成的电路。
在正弦交流电路中,电压或电流的变化遵循正弦函数的规律,其波形呈现出周期性的波动。
正弦交流电路广泛应用于电力系统、电子设备以及通信系统等各个领域。
正弦交流电路的特点是具有周期性、频率稳定以及幅度可调的特性。
在正弦交流电路中,电压或电流的周期性表示了波形的重复性,频率稳定性表示波形中重复的时间间隔保持恒定,而幅度的可调性意味着可以通过调节振幅来控制电路的输出。
正弦交流电路可以使用不同的元器件来实现,其中最常见的是电阻、电容和电感。
电阻用于限制电流的流动和控制电路中的能量损耗,电容用于储存和释放电荷以及滤波,而电感用于储存和释放磁能以及调节电流。
在正弦交流电路中,电压和电流可以通过几种不同的方式表示。
最常见的是峰值值(peak value)、峰峰值(peak-to-peak value)以及有效值(rms value)。
峰值值表示波形的最大值和最小值之间的差异,峰峰值表示波形最高点和最低点之间的差异,而有效值表示波形在一个周期内产生的平均功率与直流电平相同的值。
正弦交流电路的设计和分析需要考虑到电路元件的阻抗和相位差。
阻抗是指电路中电压和电流之间的比例关系,其单位是欧姆。
相位差表示两个正弦波的相对位置,可以是正值(在同一方向)、负值(在相反方向)或零值(同相位)。
正弦交流电路在实际应用中具有广泛的用途。
在电力系统中,交流电路通过变压器、发电机和输电线路进行传输和分配电能。
在电子设备中,交流电路通过放大器、滤波器和振荡器等电路模块进行信号处理和控制。
在通信系统中,交流电路通过调制、解调和放大等电路模块进行信息传递和信号增强。
总结而言,正弦交流电路是由正弦波形式的电压或电流组成的电路,具有周期性、频率稳定以及幅度可调的特性。
正弦交流电路的设计和分析需要考虑到电路元件的阻抗和相位差。
正弦交流电路在电力系统、电子设备以及通信系统等领域中起着重要的作用,为各种电路应用提供了稳定且可调的电源和信号处理功能。
电工学--正弦交流电1
三、相位、初相位、相位差(表示变化进程) 相位、初相位、相位差(表示变化进程)
时的相位,称为初相位角 初相位角或 : ϕ t = 0 时的相位,称为初相位角或初相位。 i
i = 2 I sin (ω t + ϕ ) :正弦量的相位角或相位 (ωt + ϕ) 正弦量的相位角或相位
ωt
U I
效值
当 i = I m sin
(ω t +ϕ )时, 可得
Im I = 2
瞬时值i可写为: 瞬时值 可写为: 可写为
i = 2I sin (ω t + ϕ )
可得
同理: 同理
u = Um sin (ω t + ϕ )
U = m U 2
瞬时值u可写为: 瞬时值 可写为: 可写为
u = 2U sin (ω t +ϕ )
南京航空航天大学
正弦量的相量表示法
ω
u = U m sin(ω t + ϕ )
Um
ϕ
ωt
ϕ
矢量长度 =
Um
矢量与横轴夹角 = 初相位
ϕ
矢量以角速度ω 按逆时针方向旋转
南京航空航天大学
正弦量的相量表示法
ω
u = U m sin(ω t + ϕ )
Um
ϕ
ωt
ϕ
正弦量在某时刻的瞬时值可以由旋转有向线段在该瞬 时在纵轴上的投影值来表示。 时在纵轴上的投影值来表示。 正弦量可用旋转有向线段表示, 正弦量可用旋转有向线段表示,而有向线段可用 复数表示,所以正弦量可用复数表示。 复数表示,所以正弦量可用复数表示。
南京航空航天大学
问题与讨论
的电器, 若购得一台耐压为 300V 的电器,是否可用于 220V 的线路上? ~ 220V
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
交流设备名牌标注的电压、电流均为有效值
4.1.3初相位与相位差
相位:t ψ
i i Imsin(ωt ψ)
反映正弦量变化的进程。 O
ωt
初相位: 表示正弦量在 t =0时的相角。
ψ ( t ) t 0
: 给出了观察正弦波的起点或参考点。
4.1.3 相位差 :
两同频率的正弦量之间的初相位之差。
4.1.2 幅值与有效值
幅值:Im、Um、Em
幅值必须大写, 下标加 m。
有效值:与交流热效应相等的直流定义为交流
电的有效值。
T
0
i2R dt
I 2RT
交流 直流
则有 I 1 T i 2dt
T0
有效值必
须大写
1 T
T 0
Im2 sin2
ωt
dt
Im 2
同理: U Um 2
E Em 2
注意: 交流电压、电流表测量数据为有效值
相量表示:
U Ue j ψ U ψ 相量的模=正弦量的有效值
相量辐角=正弦量的初相角
电压的有效值相量
或:
Um Umejψ Um ψ
相量的模=正弦量的最大值 相量辐角=正弦量的初相角
注意:
电压的幅值相量
(1)相量只是表示正弦量,而不等于正弦量。
? i Imsin(ω t ψ) = Ime jψ Im ψ
由欧拉公式:
ej ψ ej ψ
cos ψ
,
2
ej ψ ej ψ sin ψ
2j
可得: ej ψ cosψ jsin ψ
(3) 指数式 A r ej ψ (4) 极坐标式 A r ψ
A a jb r cos j r sin rejψ r ψ
相量: 表示正弦量的复数称相量
设正弦量:u Umsin( ωt ψ)
ui u i
O
ωt
90°
ψ1 ψ2 180
电压与电流反相
ui u i
O
ωt
注意:
(1) 两同频率的正弦量之间的相位差为常数, 与计时的选择起点无关。
i i1
i2
O
t
(2) 不同频率的正弦量比较无意义。
4.2 正弦量的相量表示法
1.正弦量的表示方法
u
波形图
O
ωt
瞬时值表达式 u Umsin( t )
• 实际应用中,模多采用有效值,符号: U 、I 如:已知 u 220 sin(ω t 45)V
则U m 220ej45V或 U 220 e j45V 2
⑥“j”的数学意义和物理意义
e 旋转 90因子: j90
ej90 cos 90 jsin90 j
A B
设相量 A rejψ
+j
如:u Umsin( ω t ψ1 )
i Imsin( ω t ψ2 )
( t 1 ) ( t 2 )
ψ1 ψ2
ui u i
若 ψ1 ψ2 0
O
电压超前电流
ωt
ψ1 ψ2 0 电流超前电压
ui i
u
O
ωt
电压与ψ电1 流ψ同2 相 0
ui u
i
O
ωt
ψ1 ψ2 90 电流超前电压90
4.1 正弦电压与电流
正弦量:
随时间按正弦规律做周期变化的量。
ui
i
i
+ _
t
_
+
_u
R
+
_u R
_
正弦交流电的优越性:
正半周
便于传输;易于变换
便于运算;
有利于电器设备的运行;
.....
负半周
4.1 正弦电压与电流
设正弦交流电流:
i
Im
i Im sin t
O
2
t
T
初相角:决定正弦量起始位置
第4章 正弦交流电路
4.1 正弦电压与电流 4.2 正弦量的相量表示法 4.3 单一参数的交流电路 4.4 电阻、电感与电容元件串联交流电路 4.5 阻抗的串联与并联 4.6 复杂正弦交流电路的分析与计算 4.7 交流电路的频率特性 4.8 功率因数的提高
4.9 非正弦周期交压和电流
第4章 正弦交流电路
角频率:决定正弦量变化快慢
幅值:决定正弦量的大小
幅值、角频率、初相角成为正弦量的三要素。
4.1.1 频率与周期
周期T:变化一周所需的时间 (s)
频率f:
f1 T
(Hz)
角频率: ω 2π 2πf (rad/s)
T
i
O
T
t
* 电网频率:我国 50 Hz ,美国 、日本 60 Hz
* 高频炉频率:200 ~ 300 kHz (中频炉500 ~ 8000 Hz) * 收音机中频段频率:530~1600 kHz * 移动通信频率:900MHz~1800 MHz * 无线通信频率: 高达 300GHz
• A
相量 A 乘以
将逆时针旋转
e90j90, ,得到
B
ψ
•A 将相顺量时针A 乘旋以转e9-0j9,0 得,到C
O
+1
C
正误判断
1.已知:
u 220 sin(ω t 45)V
•
U 220 45V
2
有效值
j45
Um 220 ? e45V
2.已知: I 10 60A
i 10 sin ( ω t 60)?A
(2)只有正弦量才能用相量表示, 非正弦量不能用相量表示。
(3)只有同频率的正弦量才能
(4)相量的两种表示形式
相量式: U Uejψ U ψ U( cos ψ jsin ψ)
相量图: 把相量表示在复平面的图形
可不画坐标轴
(5)相量的书写方式
• 模用最大值表示 ,则用符号:U m 、Im
本章要求 1. 理解正弦量的特征及其各种表示方法; 2. 理解电路基本定律的相量形式及阻抗;
熟练掌握计算正弦交流电路的相量分析法, 会画相量图; 3. 掌握有功功率和功率因数的计算,了解瞬时 功率、无功功率和视在功率的概念; 4.了解正弦交流电路的频率特性,串、并联谐 振的条件及特征; 5.了解提高功率因数的意义和方法。
相量 U Uψ
必须 小写
重点
前两种不便于运算,重点介绍相量表示法。
2.正弦量用旋转有向线段表示
设正弦量: y
u
Umsin(
t ψ)
u
u0ω
O
x
u1
U
O
m
ψ
ω t1
ωt
若:有向线段长度 = Um
有向线段与横轴夹角 =
初相位
有向线段以速度ω 按逆时针方向旋转
则:该旋转有向线段每一瞬时在纵轴上的投影即表示
最大值
3.已知:
I 4 e j30A 复数 4 2 sin (ω t 30 )A?
相应时刻正弦量的瞬时值。
3. 正弦量的相量表示
实质:用复数表示正弦量 复数表示形式
设A为复数: (1) 代数式A =a + jb
+j
b
r
0
A
a +1
式中: a r cos ψ b r sin ψ
(2) 三角式
r ψ
a2 b2 arctan
b
复数的模 复数的辐角
a
A r cos ψ j r sin ψ r (cos ψ jsin ψ)
