电工学 正弦交流电路
合集下载
电工学-正弦交流电路
O
f 而对直流所呈现的容抗趋于无穷大，故
XL 与 f 的关系 可视为开路。
2.3.3 电容元件的交流电路
1. 电压电流关系 i
+
u
C
–
i
u Um sint i Im sin( t 90 )
+j •
u
I
波 形O 图
电流超前电压 90 电压与电流大小关系 电压与电流相量式
t
U XCI U jXC I
2.1 正弦电压与电流 I, U
直流电路在稳定状态下电流、电压的大
小和方向是不随时间变化的，如图所示。
正弦电压和电流是按正弦规律周期性
变化的，其波形如图示。
O u, i
t
电路图上所标的方向是指它们的参考
方向，即代表正半周的方向。
负半周时，由于的参考方向与实际方
+
向相反，所以为负值。
实
i
O i
t
际 方
第 2 章 正弦交流电路
在生产和生活中普遍应用正弦交流电，特别是三相电路应 用更为广泛。
正弦交流电路是指含有正弦电源(激励)而且电路各部分所 产生的电压和电流(响应)均按正弦规律变化的电路。
本章将介绍交流电路的一些基本概念、基本理论和基本分 析方法，为后面学习交流电机、电器及电子技术打下基础。
本章还将讨论三相交流电路和非正弦周期电压和电流。 交流电路具有用直流电路的概念无法理解和无法分析的物 理现象，因此在学习时注意建立交流的概念，以免引起错误。
•
UL
为正
时电路 中电压 电流相 量图
•
• UL UC
•
U
•
UR
•
UC
的大小和正负由
电工学课件--第三章 正弦交流电路
U • o I= U =U 0 ∠ R
• •
u =Um sinω t u Um i = = sinω = Im sinω t t R R
U =I R
U =I R
•
•
可见： 可见：电压与电流同相位 ui
i
u
•
IU
•
I
•
U
+−
2．功率关系
ui
i
⑴ 瞬时功率
•
u
IU
p=ui=UmImsin2ωt =UI(1-cos2ωt)
角频率ω: 单位时间里正弦量变化的角度 称为角频率。单位是弧度/秒 （rad/s）. ω=2π/T=2πf 周期，频率，角频率从不同角度描 述了正弦量变化的快慢。三者只要知 道其中之一便可以求出另外两时值， 瞬时值中最大的称为最大值。Ｉm、 Ｕ m 、Ｅ m 分别表示电流、电压和电动 势的最大值. 表示交流电的大小常用有效值的概 念。
单位是乏尔（Var） 单位是乏尔（Var）
第四节 RLC串联交流电路 串联交流电路 一.电压与电流关系
i R u L C
uR uL
u =uR +uL +uC
U =UR+UL+UC
• • • •
uC
以电流为参考相量， 以电流为参考相量， 相量图为： 相量图为：
•
UL UL+UC
φ
• • • •
•
U I
•
U
φ UR
UL-UC
UR
UC
2 可见： 可见： U = UR +(UL −UC)2
U L −UC X L − XC = arctg = arctg UR R
《电工学》(秦曾煌主编第六版)第四章__正弦交流电路(完整版)
∴
，
，
， 4.5.8 解 求图 4.15 所示电路的阻抗 Zab。 对图 4.15（a）所示电路
对图 4.15（b）所示电路 ，
4.5.9 解
求图 4.16 两图中的电流 。
用分流比法求解。
对图 4.16（a）所示电路
对图 3.18（b）所示电路
4.5.10 解
计算上题中理想电流源两端的电压。
对图 4.16（a）所示电路
线圈电感 43.3 H，试求线圈电流及功率因数。 解
， 4.4.5 日光灯管与镇流器串联接到交流电压上，可看作为
1=280Ω
， 串联电路。
2=20Ω
如已知某灯管的等效电阻 =1.65H，电源电压
，镇流器的电阻和电感分别为
和
=220V，试求电路中的电流和灯管两端与镇流器上的电压。
这两个电压加起来是否等于 220V？电源频率为 50HZ。 解 日光灯电路的等效电路见图 T4.4.5。
根据题意画出等效电路图 T4.4.2
4.4.3
一个线圈接在
=120V 的直流电源上， =20A；若接在 f=50HZ， 及电感 。
=220V 的交流电源上，则 =28.2A。试求线圈的电阻 解 线圈加直流电源，电感 看作短路，电阻
。 。
线圈加交流电源，等效阻抗 感抗 ∴
4.4.4
有一 JZ7 型中间继电器，其线圈数据为 380V 50HZ，线圈电阻 2KΩ ，
，试求电容值。同上题比较，u2
画出相量图 T4.4.9 ，由相量图知 u2 滞后 u1
， u1 滞后 i
。
4.4.10
图 4.07 所示的是桥式移相电路。当改变电阻
时，可改变控制电
压 ug 与电源电压 u 之间的相位差 ，但电压 ug 的有效值是不变的，试证明之。 图中的 Tr 是一变压器。 证 ，设 ，则
电工学 正弦交流电
相量
复数表示法 复数运算
相量的复数表示—相量式
将复数 A 放到复平面上，可如下表示：
j
•
A
A a2 b2
bU
tan 1 b
+1
a
a
A a jb A c o s jA sin
•
A
b A
a
欧 拉
cos
e j e j 2
公 式
sin
e j
e j
2j
A a jb A(cos jsin )
t
i i 领先于
1
2
相 位
i1
落 后
2 1
i2
120 t i i1 落后于 2
三相交流电路：三种电压初相位各差120。
uA uB uC
t
可以证明同频率正弦波运算后，频率不变。
如： u1 2U 1sin t1 u2 2U 2sin t2
uu1u2
2U1sin t1 2U2sin t2 2Usin t 幅度、相位变化
复数
瞬时值
正误判断
已知： i1s0i n t4 ()5
？ I 10 45 2
j45
有效值
？ Im10e45
正误判断
已知： u2 1s0i(n t 1)5
则：
U10？15
？ U 1 0ej15
正误判断
已知： I10 5 00
则： i 1
Im 2I102 0
代数式
A e j
指数式
A
极坐标形式
相量的复数运算
1. 加 、减运算 • 设： A 1 a 1 j b1 • A 2 a 2 jb2
则：
•• •
正弦交流电知识点整理
正选交流电路+三相交流电知识点整理（1）1、正选交流电与直流电的区别所谓正弦交流电路，是指含有正弦电源(激励)而且电路各部分所产生的电压和电流(响应)均按正弦规律变化的电路。
交流发电机中所产生的电动势和正弦信号发生器所输出的信号电压，都是随时间按正弦规律变化的。
它们是常用的正弦电源。
在生产上和日常生活中所用的交流电，一般都是指正弦交流电。
因此，正弦交流电路是电工学中很重要的一个部分。
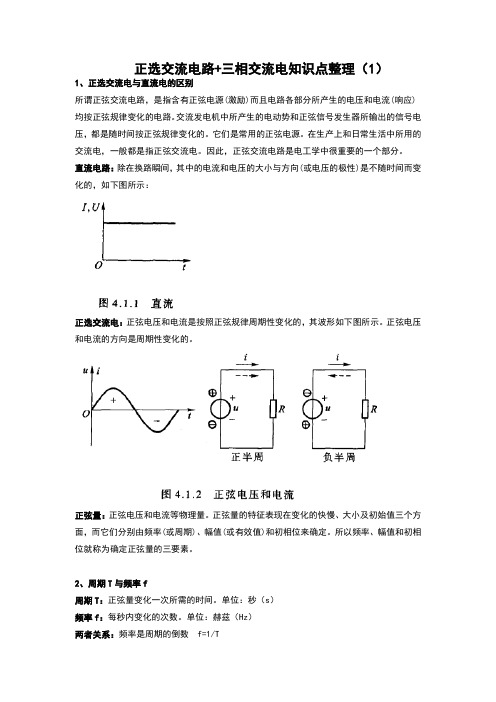
直流电路：除在换路瞬间，其中的电流和电压的大小与方向(或电压的极性)是不随时间而变化的，如下图所示：正选交流电：正弦电压和电流是按照正弦规律周期性变化的，其波形如下图所示。
正弦电压和电流的方向是周期性变化的。
正弦量：正弦电压和电流等物理量。
正弦量的特征表现在变化的快慢、大小及初始值三个方面，而它们分别由频率(或周期)、幅值(或有效值)和初相位来确定。
所以频率、幅值和初相位就称为确定正弦量的三要素。
2、周期T与频率f周期T：正弦量变化一次所需的时间。
单位：秒（s）频率f：每秒内变化的次数。
单位：赫兹（Hz）两者关系：频率是周期的倒数 f=1/T高频炉的频率是200- 300kHz；中频炉的频率是500-8000Hz；高速电动机的频率是150-2000Hz; 通常收音机中波段的频率是530-1600kHz ，短波段是2.3-23MHz；移动通信的频率是900MHz和1800MHz; 在元线通信中使用的频率可高 300 GHz。
正弦量变化的其他表达方式：角频率正弦量变化的快慢除用周期和频率表示外，还可用角频率ω来表示。
因为一周期内经历了 2π弧度(图 4.1.3) ，所以角频率为：上式表示 T，f,ω三者之间的关系，只要知道其中之一，则其余均可求出。
3、幅值与有效值正弦量在任一瞬间的值称为瞬时值，用小写字母来表示，如 i ， U 及 e 分别表示电流、电压及电动势的瞬时值。
瞬时值中最大的值称为幅值或最大值，用带下标 m 的大写字母来表示，如Im， Um 及 Em 分别表示电流、电压及电动势的幅值。
电工学第三章
3-1正弦交流电的基本概念 3-1-1 正弦交流电的三要素 正弦交流电: 大小和方向都随时间按正弦规律作周期性变化 的电量（电压、电流、电动势）。
i
设正弦交流电流：
Im
O
t
T
i I m sin t
初相角：决定正弦量起始位置 角频率：决定正弦量变化快慢 in( t 2 )
I I1 I 2
i i1 i 2
上节复习：
1、写出下列正弦量对应的相量，并作出相量图
i1 4 2 s in ( t 3 0 )
i2 1 0 2 c o s ( t 1 2 0 )
i3 1 4 .1 4 s in ( t 1 5 0 )
相量的模=正弦量的最大值
相量辐角=正弦量的初相角
U
U
u U m sin ( t )
电压的有效值相量
U
U
相量的模=正弦量的最大值
相量辐角=正弦量的初相角
例1：
u 10 sin( 314 t 60 )
写出其相量形式
U 5 2 60
U m 10 60
3-1-3 正弦交流电的参考方向
i
O
i I m sin t
ωt
i 0，实际方向与参考方向相 同
i 0，实际方向与参考方向 相反
3-2正弦交流电的相量表示法
１.正弦量的表示方法 波形图
O
u/i
ωt
瞬时值表达式
u U m sin ( t )
i I m s in
电工学第4章
i1 i i2
i1与i2 同相 i1与i2 反相
i1 ωt o ψ1 ψ2 ϕ i i2 ωt
ψ2 o ψ1
注意：不同频率的正弦量比较无意义。 注意：不同频率的正弦量比较无意义。
[例题] 正弦电流 =100sin(6280t − π)mA,指出它的周期 例题] i , 4 频率,角频率幅值 有效值初相位画出波形图 , , , , . 解：Im =100mA i 100(mA) Im = 100=70.7mA I= 2 2 ω=6280rad/s oπ f = ω = 6280=1000Hz =1kHz 4 2π 2π T= 1 = 1 =0.001s=1ms f 1000 ψ=− π 4
4.1.2 幅值与有效值
幅值： 幅值：Im、Um、Em 有效值： 有效值：与交流热效应相等的直流定义为交流电的 有效值。 有效值。
幅值必须大写, 幅值必须大写, 下标加 m。
= I 2 RT ∫0 i R dt
T 2
交流
直流
则有
I =
Im 1 T 2 2 有效值必 = Imsin ωt dt = 2 须大写 T ∫0 Um Em 同理： 同理： U = E= 2 2 注意：交流电压、电流表的刻度、 注意：交流电压、电流表的刻度、数据为有效值
r ψ
a
A = r cos ψ + j r sin ψ = r (cos ψ + jsin ψ)
jψ
由欧拉公式: 由欧拉公式 cos ψ = e 可得: 可得 (3)
= cos ψ + jsin ψ 指数式 A = r ej ψ e
jψ
+e 2
−j ψ
ej ψ − e− j ψ , sin ψ = 2j
i1与i2 同相 i1与i2 反相
i1 ωt o ψ1 ψ2 ϕ i i2 ωt
ψ2 o ψ1
注意：不同频率的正弦量比较无意义。 注意：不同频率的正弦量比较无意义。
[例题] 正弦电流 =100sin(6280t − π)mA,指出它的周期 例题] i , 4 频率,角频率幅值 有效值初相位画出波形图 , , , , . 解：Im =100mA i 100(mA) Im = 100=70.7mA I= 2 2 ω=6280rad/s oπ f = ω = 6280=1000Hz =1kHz 4 2π 2π T= 1 = 1 =0.001s=1ms f 1000 ψ=− π 4
4.1.2 幅值与有效值
幅值： 幅值：Im、Um、Em 有效值： 有效值：与交流热效应相等的直流定义为交流电的 有效值。 有效值。
幅值必须大写, 幅值必须大写, 下标加 m。
= I 2 RT ∫0 i R dt
T 2
交流
直流
则有
I =
Im 1 T 2 2 有效值必 = Imsin ωt dt = 2 须大写 T ∫0 Um Em 同理： 同理： U = E= 2 2 注意：交流电压、电流表的刻度、 注意：交流电压、电流表的刻度、数据为有效值
r ψ
a
A = r cos ψ + j r sin ψ = r (cos ψ + jsin ψ)
jψ
由欧拉公式: 由欧拉公式 cos ψ = e 可得: 可得 (3)
= cos ψ + jsin ψ 指数式 A = r ej ψ e
jψ
+e 2
−j ψ
ej ψ − e− j ψ , sin ψ = 2j
正弦交流电路
幅值（最大值）、有效值：表示正弦量的大小 周期、频率、角频率：表示正弦量的变化速度 初相位：给出观察正弦量的起始点
目录
正弦交流电的基本概念 正弦量的向量表示法 单一参数的交流电路 RLC串联交流电路 阻抗的串并联
正弦量的相量表示法
●瞬时值表达式（三角函数表达式）
●波形图
i 2I sin(wt )
例
u1 4 2 sin wt 60
u2 3 2 sin wt 30
U2
ua u1 u2 ub u1 u2
U a U1 U 2 523
ua 5 2 sin wt 23
U b U1 U 2 597
ub 5 2 sin wt 97
Ub
5
U1
4
Ua
97 o
U
U
有效值相量图
用符号: I U E 表示。
包含大小与相位信息。
例
i1 8 2 sin wt 60 i2 6 2 sin wt 30
I1 860o A I2 6 30o A
相量式
有效值
I1 8
60 o
30 o
6
I2
初相位
相量图
正弦量的相量表示法
●同频率正弦量的运算
加减运算用相量图—平行四边形法则
有向线段表示正弦量 有向线段不等于正弦量
ω
u Um sinw t
Um
wt
正弦量的相量表示法
相量用复平面的有向线段表示，其长度（相量的模）表示正弦量的有效值；其与横轴 的夹角（相量的幅角）表示正弦量的初相位。
直角坐标式：
U a jb U cos j sin
指数式：
U Ue j
极坐标式：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2001-02-10 南京航空航天大学
u U m sin(t u )V i I m sin(t i ) A
(t u ) (t i ) u i
①>0， u> i
称u在相位上超前i 角度，或i滞后u 角度。
②<0, u < I
第三章
正弦交流电路
交流电： 大小和方向随着时间作周期性交变且在一个周 期内的平均值为零的电流、电压和电动势总称 为交流电。
正弦交流电路： 含有正弦电动势的电路称为正弦电动势
（1）为什么要采用交流电输电？ 便于升、降压，高压输电有助于减少线路损耗。 （2）为什么要用正弦交流电？
因为正弦信号“+”、“-”、“求导”、“积分”后仍为正 弦信号。
u U m sin(t u )V
频率、幅值和初相位--------就称为正弦量的三要素。
i I m sin(t i ) A
其中：Um 、Im 为最大值
u、i为初相
为角频率
工频：我国工业用电频率为50Hz
2001-02-10
南京航空航天大学
正弦量的表达式中一般用角度或弧度来表示，因此常用 角频率来表示。 由于一个周期内经历了2弧度，所以：
2 2f T
单位：弧度/秒 （rad/s)
i I m sin(t i ) A
这里i 0
2001-02-10
南京航空航天大学
一、频率与周期
正弦量变化一次所需的时间（秒）称为周期T。 单位：秒（s） 每秒钟内变化的次数称为频率f。 三、幅值与有效值 单位：赫兹（Hz）
0
T T 0 2 2
2001-02-10 南京航空航天大学
所以
I
同理
U
Im 2
Um 2
0.707 I m
0.707U m
Em E 0.707 Em 2
正弦交流电的有效值等于它的最大值除以 而与其频率及初相无关。
一般用电磁式电工仪表所测得均为有效值。
2001-02-10 南京航空航天大学
2001-02-10
南京航空航天大学
对于正弦交流电流
i I m sin( t i ) A
因为
1 T 2 2 I I sin ( t ) dt m T 0
sin (t )dt
2 T 0 T 1 dt cos( 2t 2 )dt 0 2
T
称u在相位上滞后i 角度
2001-02-10
南京航空航天大学
③ =±
反相
④ =0
同相
⑤ =±/2
2001-02-10
正交
南京航空航天大学
2001-02-10 南京航空航天大学
§3-1 正弦电压与电流
直流电路中，其电压、电流的大小或极性是不随时间而 变化的恒定量 正弦电压和电流是按照正弦规律周期性变化的, 在图示 正方向下，其工作波形如图所示： i
u
+ + -
i
-
i
u 正半周
0
-
t
+
u 负半周
2001-02-10
南京航空航天大学
正弦量的特征：
有效值的定义
某周期电流i 通过电阻R在一个周期内产生的热量和另一个
直流I 通过同样大小的电阻在相等的时间内产生的热量相等，
那么这个周期性变化的电流I的有效值在数值上就等于这个直流 I。
2001-02-10
南京航空航天大学
设一交变电流i通过电阻R,在一个周期内该电阻 消耗的电能是:
W~ i Rdt R i dt
2
三、初相位
i I m sin(t i ) A
1.相位 (t+i) 称为正弦交流电的相位，也称相位角。
单位：弧度或度
不同时刻相位不同，并且正弦交流电的大小 和方向也不同。
2001-02-10
南京航空航天大学
2. 初相位
t=0时的相位角称为初相位，也称初相角
(t i ) t 0 i
① 正弦量在任一瞬间的值称为瞬时值，
用小写字母 i ，u，e 表示。
② 瞬时值中最大的值称为幅值或最大值，
用Im,Um,Em表示。
2001-02-10 南京航空航天大学
③ 由于最大值仅是某特定瞬间的数值，不能反映电流或电压 做功的效果,因此，在工程上，则以热效应的角度（或做功） 来衡量电压或电流的大 小，常用有效值来表示。
2 2 0 0
T
T
i
R
如果有一个直流电流I通过同一电阻R，在同一时 间T内所消耗的电能为：
W I 2 RT
I
பைடு நூலகம்
R
2001-02-10
南京航空航天大学
所以，当在一个周期的时间内，W～=W—时，有:
I T i dt
2 2 0
T
1 T 2 I i dt T 0
可见：交流电流的有效值就是与它的平均耗能 相等的直流电流值。 上式适用于任何周期性变化的量，不适用 于非周期性量。
i I m sin( 314 t ) A 2
初相位的确定： ①增长过零点 ②最大值的先后
2001-02-10 南京航空航天大学
3. 初始值
t=0时，正弦量的取值称为初始值
例： i 20 sin( 314 t
6
)A
t=0时,
i( t 0 ) 20 sin
6
10 A
同样，计算起点不同，正弦量的初值也不同。
2001-02-10
南京航空航天大学
4. 相位差
u U m sin(t u )V i I m sin(t i ) A
可见相位差与记时起点无关记时点变，仅改变初相位。 两个同频率正弦量的相位角之差，或初相位角之差—相位差
(t u ) (t i ) u i
例： i1=10sint 和 i2=20sin(t+/2) 它们的相位分别为t 和
t+/2，初相分别为1=0
和 2 = /2
南京航空航天大学
2001-02-10
注意：正弦量的初相位与记时起点有关，同一
正弦量，若记时起点不同，则初相位也不同，如下 图所示
i I m sin(314 t ) A 6
u U m sin(t u )V i I m sin(t i ) A
(t u ) (t i ) u i
①>0， u> i
称u在相位上超前i 角度，或i滞后u 角度。
②<0, u < I
第三章
正弦交流电路
交流电： 大小和方向随着时间作周期性交变且在一个周 期内的平均值为零的电流、电压和电动势总称 为交流电。
正弦交流电路： 含有正弦电动势的电路称为正弦电动势
（1）为什么要采用交流电输电？ 便于升、降压，高压输电有助于减少线路损耗。 （2）为什么要用正弦交流电？
因为正弦信号“+”、“-”、“求导”、“积分”后仍为正 弦信号。
u U m sin(t u )V
频率、幅值和初相位--------就称为正弦量的三要素。
i I m sin(t i ) A
其中：Um 、Im 为最大值
u、i为初相
为角频率
工频：我国工业用电频率为50Hz
2001-02-10
南京航空航天大学
正弦量的表达式中一般用角度或弧度来表示，因此常用 角频率来表示。 由于一个周期内经历了2弧度，所以：
2 2f T
单位：弧度/秒 （rad/s)
i I m sin(t i ) A
这里i 0
2001-02-10
南京航空航天大学
一、频率与周期
正弦量变化一次所需的时间（秒）称为周期T。 单位：秒（s） 每秒钟内变化的次数称为频率f。 三、幅值与有效值 单位：赫兹（Hz）
0
T T 0 2 2
2001-02-10 南京航空航天大学
所以
I
同理
U
Im 2
Um 2
0.707 I m
0.707U m
Em E 0.707 Em 2
正弦交流电的有效值等于它的最大值除以 而与其频率及初相无关。
一般用电磁式电工仪表所测得均为有效值。
2001-02-10 南京航空航天大学
2001-02-10
南京航空航天大学
对于正弦交流电流
i I m sin( t i ) A
因为
1 T 2 2 I I sin ( t ) dt m T 0
sin (t )dt
2 T 0 T 1 dt cos( 2t 2 )dt 0 2
T
称u在相位上滞后i 角度
2001-02-10
南京航空航天大学
③ =±
反相
④ =0
同相
⑤ =±/2
2001-02-10
正交
南京航空航天大学
2001-02-10 南京航空航天大学
§3-1 正弦电压与电流
直流电路中，其电压、电流的大小或极性是不随时间而 变化的恒定量 正弦电压和电流是按照正弦规律周期性变化的, 在图示 正方向下，其工作波形如图所示： i
u
+ + -
i
-
i
u 正半周
0
-
t
+
u 负半周
2001-02-10
南京航空航天大学
正弦量的特征：
有效值的定义
某周期电流i 通过电阻R在一个周期内产生的热量和另一个
直流I 通过同样大小的电阻在相等的时间内产生的热量相等，
那么这个周期性变化的电流I的有效值在数值上就等于这个直流 I。
2001-02-10
南京航空航天大学
设一交变电流i通过电阻R,在一个周期内该电阻 消耗的电能是:
W~ i Rdt R i dt
2
三、初相位
i I m sin(t i ) A
1.相位 (t+i) 称为正弦交流电的相位，也称相位角。
单位：弧度或度
不同时刻相位不同，并且正弦交流电的大小 和方向也不同。
2001-02-10
南京航空航天大学
2. 初相位
t=0时的相位角称为初相位，也称初相角
(t i ) t 0 i
① 正弦量在任一瞬间的值称为瞬时值，
用小写字母 i ，u，e 表示。
② 瞬时值中最大的值称为幅值或最大值，
用Im,Um,Em表示。
2001-02-10 南京航空航天大学
③ 由于最大值仅是某特定瞬间的数值，不能反映电流或电压 做功的效果,因此，在工程上，则以热效应的角度（或做功） 来衡量电压或电流的大 小，常用有效值来表示。
2 2 0 0
T
T
i
R
如果有一个直流电流I通过同一电阻R，在同一时 间T内所消耗的电能为：
W I 2 RT
I
பைடு நூலகம்
R
2001-02-10
南京航空航天大学
所以，当在一个周期的时间内，W～=W—时，有:
I T i dt
2 2 0
T
1 T 2 I i dt T 0
可见：交流电流的有效值就是与它的平均耗能 相等的直流电流值。 上式适用于任何周期性变化的量，不适用 于非周期性量。
i I m sin( 314 t ) A 2
初相位的确定： ①增长过零点 ②最大值的先后
2001-02-10 南京航空航天大学
3. 初始值
t=0时，正弦量的取值称为初始值
例： i 20 sin( 314 t
6
)A
t=0时,
i( t 0 ) 20 sin
6
10 A
同样，计算起点不同，正弦量的初值也不同。
2001-02-10
南京航空航天大学
4. 相位差
u U m sin(t u )V i I m sin(t i ) A
可见相位差与记时起点无关记时点变，仅改变初相位。 两个同频率正弦量的相位角之差，或初相位角之差—相位差
(t u ) (t i ) u i
例： i1=10sint 和 i2=20sin(t+/2) 它们的相位分别为t 和
t+/2，初相分别为1=0
和 2 = /2
南京航空航天大学
2001-02-10
注意：正弦量的初相位与记时起点有关，同一
正弦量，若记时起点不同，则初相位也不同，如下 图所示
i I m sin(314 t ) A 6