8.6 椭 圆
地球椭球及高斯投影(测量工培训材料之二)

过P点的 椭球法线
P H
的中的表示法为: (L,B,H)
X O B
Y
L 参考椭球
3
三、高斯投影
X
中央子午线
P(x,y)
Y
特点:中央子午线上的长度和方向无变形,其他区域 的变形随偏离中央子午线距离的增大而增大。
4
四、投影分带
带号 12 13 14 15 16 17 18 19 20 21 22 23
B0 (50221746 (293622 (2350 22 cos2 ) cos2 ) cos2 ) 1010 sin cos N 0 6399698902 (21562267 (108.973 0.612cos2 B0 ) cos2 B0 ) cos2 B0 . . Z y /( N 0 cos B0 ) b2 (0.5 0.003369 2 B0 ) sin B0 cos B0 cos b3 0.333333 (0.166667 0.001123 2 B0 ) cos2 B0 cos b4 0.25 (0.16161 0.00562cos2 B0 ) cos2 B0 b5 0.2 (0.1667 0.0088cos2 B0 ) cos2 B0
y (1 ( a3 a5l 2 )l 2 )lN cos B
式中:
N 6399698902 (21562267 (108.973 (0.612 0.004cos2 B) . . cos2 B ) cos2 B ) cos2 B a0 321404048 (135.3303 (0.7092 0.0041cos2 B ) cos2 B ) cos2 B . a3 0.1666667 (0.3333333 0.001123 2 B) cos2 B cos a4 0.04167 (0.25 0.00253cos2 B) cos2 B a5 0.00833 (0.1667 (0.1967 0.0040cos2 B ) cos2 B ) cos2 B a6 (0.083 0.167cos2 B ) cos2 B l ( L L0 ) /
2022版新教材高考数学一轮复习第八章平面解析几何8.6双曲线学案新人教A版202105192134
8.6双曲线必备知识预案自诊知识梳理1.双曲线的定义平面内与两个定点F1,F2的等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.这两个定点叫做,两焦点间的距离叫做.集合P={M|||MF1|-|MF2||=2a},|F1F2|=2c,其中a>0,c>0,且a,c为常数.(1)若a c,则点M的轨迹是双曲线;(2)若a c,则点M的轨迹是两条射线;(3)若a c,则点M不存在.2.标准方程(1)中心在坐标原点,焦点在x轴上的双曲线的标准方程为x2a2−y2b2=1(a>0,b>0);(2)中心在坐标原点,焦点在y轴上的双曲线的标准方程为y2a2−x2b2=1(a>0,b>0).3.双曲线的性质图形续表2 2−y2b2=1(a>0,b>0)y2a2−x2b2=1(a>0,b>1.过双曲线x2a 2−y 2b 2=1(a>0,b>0)上一点M (x 0,y 0)的切线方程为x 0xa 2−y 0y b 2=1.2.双曲线x 2a 2−y 2b 2=1(a>0,b>0)的左、右焦点分别为F 1,F 2,点P (x 0,y 0)为双曲线上任意一点,且不与点F 1,F 2共线,∠F 1PF 2=θ,则△F 1PF 2的面积为b 2tanθ2.3.若点P (x 0,y 0)在双曲线x 2a2−y 2b 2=1(a>0,b>0)内,则被点P 所平分的中点弦的方程为x 0x a 2−y 0y b 2=x 02a 2−y 02b 2.4.双曲线中点弦的斜率公式设点M (x 0,y 0)为双曲线x 2a 2−y 2b2=1(a>0,b>0)的弦AB (不平行y 轴)的中点,则k AB ·k OM =b 2a2,即k AB =b 2x0a 2y 0.5.双曲线的焦半径公式双曲线x 2a 2−y 2b 2=1(a>0,b>0)的焦点为F 1(-c ,0),F 2(c ,0),当点M (x 0,y 0)在双曲线右支上时,|MF 1|=ex 0+a ,|MF 2|=ex 0-a ;当点M (x 0,y 0)在双曲线左支上时,|MF 1|=-ex 0-a ,|MF 2|=-ex 0+a.6.若P 是双曲线右支上一点,F 1,F 2分别为双曲线的左、右焦点,则|PF 1|min =a+c ,|PF 2|min =c-a.7.双曲线的同支的焦点弦中最短的为通径(过焦点且垂直于实轴所在直线的弦),其长为2b 2a;异支的弦中最短的为实轴,其长为2a.考点自诊1.判断下列结论是否正确,正确的画“√”,错误的画“×”.(1)平面内到点F1(0,4),F2(0,-4)距离之差的绝对值等于8的点的轨迹是双曲线.()(2)双曲线x2m2−y2n2=λ(m>0,n>0,λ≠0)的渐近线方程是x2m2−y2n2=0,即xm±yn=0.()(3)关于x,y的方程x2m −y2n=1(mn>0)表示焦点在x轴上的双曲线.()(4)与双曲线x2m −y2n=1(其中mn>0)共渐近线的双曲线方程可设为x2m−y2n=λ(λ≠0).()(5)若双曲线x2a2−y2b2=1(a>0,b>0)与x2b2−y2a2=1(a>0,b>0)的离心率分别是e1,e2,则1e12+1e22=1.()2.“m>0”是“方程x2m −y2m+2=1表示双曲线”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.已知双曲线C:x2a2−y2b2=1(a>0,b>0)过点(√2,√3),且实轴的两个端点与虚轴的一个端点组成一个等边三角形,则双曲线C的标准方程为()A.x212-y2=1 B.x29−y23=1C.x2-y23=1 D.x223−y232=14.(2019北京,5)已知双曲线x2a2-y2=1(a>0)的离心率是√5,则a=() A.√6 B.4C.2D.125.若双曲线x2a2−y2b2=1(a>0,b>0)的一条渐近线经过点(3,-4),则此双曲线的离心率为.关键能力学案突破考点双曲线的定义【例1】(1)已知点F2为双曲线C:x2a2−y2b2=1(a>0,b>0)的右焦点,直线y=kx交双曲线C于A,B两点,若∠AF2B=2π3,S△AF2B=2√3,则双曲线C的虚轴长为.(2)已知双曲线E :x 2a 2−y 2b 2=1(a>0,b>0)的左、右焦点分别为F 1,F 2,过点F 1的直线l 与双曲线的左、右两支分别交于A ,B 两点.若△ABF 2的内切圆与边AB ,BF 2,AF 2分别相切于点M ,N ,P ,且|AP|=4,则a 的值为 .解题心得双曲线定义的应用主要有两个方面:一是判定平面内动点轨迹是否为双曲线,进而求出曲线方程;二是在“焦点三角形”中,常利用正弦定理、余弦定理,结合||PF 1|-|PF 2||=2a ,运用平方的方法,建立与|PF 1|·|PF 2|的联系.对点训练1(1)(2020河南非凡联盟4月联考)已知双曲线C :x 2a 2−y 29=1(a>0)的左、右焦点分别为F 1,F 2,一条渐近线与直线4x+3y=0垂直,点M 在双曲线C 上,且|MF 2|=6,则|MF 1|=( )A.2或14B.2C.14D.2或10(2)(2020河北廊坊省级示范学校联考)设F 1,F 2分别为双曲线C :x 2a 2−y 2b 2=1(a>0,b>0)的左、右焦点,过点F 1的直线交双曲线C 的左支于A ,B 两点,且|AF 2|=3,|BF 2|=5,|AB|=4,则△BF 1F 2的面积为 .考点双曲线的标准方程【例2】(1)已知动圆M 与圆C 1:(x+4)2+y 2=2外切,与圆C 2:(x-4)2+y 2=2内切,则动圆圆心M 的轨迹方程为( )A.x 22−y 214=1(x ≥√2) B.x 22−y 214=1(x ≤-√2) C.x 22+y 214=1(x ≥√2) D.x 22+y 214=1(x ≤-√2)(2)在平面直角坐标系中,经过点P (2√2,-√2),渐近线方程为y=±√2x 的双曲线的标准方程为( )A.x 24−y 22=1 B.x 27−y 214=1C.x 23−y 26=1D.y 214−x 27=1(3)已知双曲线x 2a 2−y 2b 2=1(a>0,b>0)的左、右焦点分别为F 1,F 2,过点F 2且斜率为247的直线与双曲线在第一象限的交点为A ,若(F 2F 1⃗⃗⃗⃗⃗⃗⃗⃗ +F 2A ⃗⃗⃗⃗⃗⃗⃗ )·F 1A ⃗⃗⃗⃗⃗⃗⃗ =0,则双曲线的标准方程可能为( ) A.x 24−y 23=1B.x 23−y 24=1C.x 216−y 29=1D.x 29−y 216=1解题心得1.求双曲线标准方程的答题模板2.利用待定系数法求双曲线方程的常用方法 (1)与双曲线x 2a 2−y 2b 2=1共渐近线的方程可设为x 2a 2−y 2b 2=λ(λ≠0);(2)若双曲线的渐近线方程为y=±bax ,则双曲线的方程可设为x 2a2−y 2b 2=λ(λ≠0);(3)若双曲线过两个已知点,则双曲线的方程可设为x 2m +y 2n=1(mn<0)或mx 2+ny 2=1(mn<0).对点训练2(1)(2020河南安阳模拟)过双曲线x 2a 2−y 2b 2=1(a>0,b>0)的右焦点F (c ,0)作其渐近线y=√32x 的垂线,垂足为M ,若S △OMF =4√3(O 为坐标原点),则双曲线的标准方程为( )A.x 24−y 23=1 B.x 28−y 26=1 C.x 216−y 212=1D.x 232−y 224=1(2)过双曲线C :x 2a 2−y 2b 2=1的右顶点作x 轴的垂线,与双曲线C 的一条渐近线相交于点A.若以双曲线C 的右焦点F 为圆心,4为半径的圆经过A ,O 两点(O 为坐标原点),则双曲线C 的方程为( )A.x 24−y 212=1 B.x 27−y 29=1 C.x 28−y 28=1 D.x 212−y 24=1(3)经过点P (3,2√7),Q (-6√2,7)的双曲线的标准方程为 .考点双曲线的几何性质(多考向探究)考向1 求双曲线的渐近线方程【例3】(2020福建厦门一模)已知双曲线C :x 2a 2−y 2b 2=1(a>0,b>0)的一个焦点为F ,点A ,B 是双曲线C 的一条渐近线上关于原点对称的两点,以AB 为直径的圆过点F 且交双曲线C 的左支于M ,N 两点,若|MN|=2,△ABF 的面积为8,则双曲线C 的渐近线方程为( )A.y=±√3xB.y=±√33x C.y=±2xD.y=±12x解题心得求双曲线的渐近线方程的方法依据题设条件,求出双曲线方程x 2a 2−y 2b 2=1(a>0,b>0)中a ,b 的值或a 与b 的比值,进而得出双曲线的渐近线方程.对点训练3(2020山东德州高三第二次模拟)已知椭圆x 2a 2+y 2b 2=1(a>b>0)与双曲线x 2a 2−y 2b 2=12的焦点相同,则双曲线渐近线方程为( )A.y=±√33x B.y=±√3x C.y=±√22xD.y=±√2x考向2 求双曲线的离心率【例4】(2020广东汕尾一模)已知双曲线C :x 2a 2−y 2b 2=1(a>0,b>0),F 为双曲线C 的右焦点,A 为双曲线C 的右顶点,过点F 作x 轴的垂线,交双曲线C 于M ,N 两点.若tan ∠MAN=-34,则双曲线C 的离心率为( )A.3B.2C.43D.√2解题心得求双曲线离心率的值或取值范围的方法 (1)求a ,b ,c 的值,由e=ca =√1+b 2a 2直接求出e.(2)列出含有a ,b ,c 的齐次方程(或不等式),借助b 2=c 2-a 2消去b ,然后转化为关于e 的方程(或不等式)求解.对点训练4(2019全国2,理11)设F 为双曲线C :x 2a 2−y 2b 2=1(a>0,b>0)的右焦点,O 为坐标原点,以OF 为直径的圆与圆x 2+y 2=a 2交于P ,Q 两点.若|PQ|=|OF|,则C 的离心率为( )A.√2B.√3C.2D.√5考向3 与双曲线有关的取值范围问题【例5】已知M (x 0,y 0)是双曲线C :x 22-y 2=1上的一点,F 1,F 2是双曲线C 的两个焦点,若MF 1⃗⃗⃗⃗⃗⃗⃗⃗ ·MF 2⃗⃗⃗⃗⃗⃗⃗⃗ <0,则y 0的取值范围是( )A.(-√33,√33) B.(-√36,√36) C.(-2√23,2√23) D.(-2√33,2√33)解题心得与双曲线有关的取值范围问题的解题思路(1)若条件中存在不等关系,则借助此关系直接转化为不等式求解.(2)若条件中没有明显的不等关系,则要善于发现隐含的不等关系来解决. 对点训练5已知焦点在x 轴上的双曲线x 28-m+y 24-m=1,它的焦点到渐近线的距离的取值范围是 .考点双曲线与圆的综合问题【例6】已知点P 为双曲线C :x 2a 2−y 2b 2=1(a>0,b>0)上一点,F 1,F 2为双曲线C 的左、右焦点,若|PF 1|=|F 1F 2|,且直线PF 2与以双曲线C 的实轴为直径的圆相切,则双曲线C 的渐近线方程为( )A.y=±43x B.y=±34xC.y=±35xD.y=±53x对点训练6过双曲线x 2a 2−y 2b 2=1(a>0,b>0)的左焦点F 作圆O :x 2+y 2=a 2的两条切线,切点为A ,B ,双曲线的左顶点为C ,若∠ACB=120°,则双曲线的渐近线方程为( )A.y=±√3xB.y=±√33x C.y=±√2x D.y=±√22x8.6 双曲线 必备知识·预案自诊知识梳理1.距离的差的绝对值 双曲线的焦点 双曲线的焦距 (1)< (2)= (3)> 3.坐标轴 原点 (-a ,0) (a ,0) (0,-a )(0,a)a2+b22a2b考点自诊1.(1)×(2)√(3)×(4)√(5)√2.A由“方程x2m −y2m+2=1表示双曲线”得m(m+2)>0,即m>0或m<-2,又“m>0”是“m>0或m<-2”的充分不必要条件,故“m>0”是“方程x 2m −y2m+2=1表示双曲线”的充分不必要条件.故选A.3.C由双曲线C:x2a2−y2b2=1(a>0,b>0)过点(√2,√3),且实轴的两个端点与虚轴的一个端点组成一个等边三角形,可得{2a2-3b2=1,b a =√3,解得{a=1,b=√3.故双曲线C的标准方程为x2-y23=1.4.D∵双曲线的离心率e=ca =√5,c=√a2+b2,∴√a2+1a=√5,解得a=12.故选D.5.5 3由题意知直线y=-bax过点(3,-4),所以3ba=4,即ba=43,所以e=ca=√1+b2a2=√1+169=53.关键能力·学案突破例1(1)2√2(2)2(1)设双曲线C的左焦点为F1,连接AF1,BF1,由对称性可知四边形AF1BF2为平行四边形,因为∠AF2B=2π3,S△AF2B=2√3,所以S△AF1F2=2√3,∠F1AF2=π3.设|AF1|=r1,|AF2|=r2,则4c2=r12+r22-2r1r2cosπ3,又|r1-r2|=2a,故r1r2=4b2.又S△AF1F2=12r1r2sinπ3=2√3,所以b2=2,所以该双曲线的虚轴长为2√2.(2)由题意知|BM|=|BN|,|PF2|=|NF2|,|AM|=|AP|=4.根据双曲线的定义,知|BF1|-|BF2|=|MF1|-|NF2|=2a,|AF2|-|AF1|=2a,则|AF1|=|AF2|-2a,所以|BF1|-|BF2|=|AM|+|AF1|-|NF2|=|AM|+|AP|+|PF2|-2a-|NF2|=8-2a=2a,所以a=2.对点训练1(1)C(2)92(1)由题意知3a=34,故a=4,则c=5.由|MF2|=6<a+c=9,知点M在双曲线C的右支上.由双曲线的定义知|MF1|-|MF2|=2a=8,所以|MF1|=14.(2)因为|AF2|=3,|BF2|=5,|AF2|-|AF1|=2a,|BF2|-|BF1|=2a,所以|AF2|+|BF2|-|AB|=3+5-4=4=4a,所以a=1,所以|BF1|=3.又|AF2|2+|AB|2=|BF2|2,所以∠F2AB=90°,所以S△BF1F2=12|BF1||AF2|=12×3×3=92.例2(1)A(2)B(3)D(1)设动圆M的半径为r,由题意可得|MC1|=r+√2,|MC2|=r-√2,|C1C2|=8,所以|MC1|-|MC2|=2√2<|C1C2|,所以由双曲线的定义可知动点M在以C1(-4,0),C2(4,0)为焦点,实轴长为2√2的双曲线的右支上,所以a=√2,c=4,所以b2=16-2=14,故动圆圆心M的轨迹方程为x22−y214=1(x≥√2).(2)因为双曲线的渐近线方程为y=±√2x ,所以可设所求双曲线的方程为2x 2-y 2=k (k ≠0).又点P (2√2,-√2)在双曲线上,所以k=16-2=14,所以双曲线的方程为2x 2-y 2=14,所以双曲线的标准方程为x 27−y 214=1.故选B .(3)由(F 2F 1⃗⃗⃗⃗⃗⃗⃗⃗ +F 2A ⃗⃗⃗⃗⃗⃗⃗ )·F 1A ⃗⃗⃗⃗⃗⃗⃗ =0,可知(F 2F 1⃗⃗⃗⃗⃗⃗⃗⃗ +F 2A ⃗⃗⃗⃗⃗⃗⃗ )·(F 2A ⃗⃗⃗⃗⃗⃗⃗ −F 2F 1⃗⃗⃗⃗⃗⃗⃗⃗ )=0,即|F 2A ⃗⃗⃗⃗⃗⃗⃗ |2-|F 2F 1⃗⃗⃗⃗⃗⃗⃗⃗⃗⃗ |2=0,所以|F 2A|=|F 1F 2|=2c.又AF 2的斜率为247,所以cos ∠AF 2F 1=-725.在△AF 1F 2中,由余弦定理得|AF 1|=165c.由双曲线的定义得165c-2c=2a ,即c a=53,所以a ∶b=3∶4.所以此双曲线的标准方程可能为x 29−y 216=1.故选D .对点训练2(1)C (2)A (3)y 225−x 275=1(1)由题意易得|FM|=b ,又|OF|=c ,FM ⊥OM ,所以|OM|=√|OF |2-|FM |2=a.联立{ba =√32,12ab =4√3,解得{a =4,b =2√3, 所以双曲线的标准方程为x 216−y 212=1.故选C .(2)不妨设渐近线y=ba x 与直线x=a 交于点A ,则点A (a ,b ).依题意,c=4,√(4-a )2+b 2=4,a 2+b 2=c 2=16,解得a 2=4,b 2=12,故双曲线的标准方程为F 24−y 212=1.(3)设双曲线的方程为mx 2+ny 2=1(mn<0).因为所求双曲线经过点P (3,2√7),Q (-6√2,7), 所以{9m +28n =1,72m +49n =1,解得{m =-175,n =125.故所求双曲线的方程为y 225−x 275=1.例3B 不妨设点A ,B 在直线y=b a x 上,点F (c ,0),则设点A (x 0,b a x 0),B -x 0,-bax 0.因为以AB 为直径的圆过点F ,所以AF ⃗⃗⃗⃗⃗ ⊥BF ⃗⃗⃗⃗⃗ ,所以AF ⃗⃗⃗⃗⃗ ·BF ⃗⃗⃗⃗⃗ =c 2-x 02−b 2a2x 02=c 2-c 2a2x 02=0,所以x 0=±a.所以S △ABF =12·c·|2bax 0|=bc=8.由{x 2+y 2=c 2,x 2a 2-y 2b 2=1,得y=±b 2c ,则|MN|=2b 2F=2,即b 2=c.所以b=2,c=4,所以a=√c 2-b 2=2√3.所以双曲线C 的渐近线方程为y=±√33x.故选B .对点训练3A 由椭圆x 2a 2+y 2b 2=1(a>b>0)与双曲线x 2a 2−y 2b 2=12,即x 2a 22−y 2b 22=1的焦点相同,可得a 2-b 2=a 22+b 22,即a 2=3b 2,所以ba =√33.所以双曲线的渐近线方程为y=±√33x.故选A .例4B 由题意可知tan ∠MAN=2tan∠MAF1-tan 2∠MAF =-34,解得tan ∠MAF=3.令x=c ,则y=±b 2a , 可得tan ∠MAF=b 2ac -a =c 2-a 2ac -a=c+a a=3,则e=ca =2.故选B .对点训练4A 如图,设PQ 与x 轴交于点A ,由对称性可知PQ ⊥x 轴.∵|PQ|=|OF|=c ,∴|PA|=c2.∴PA 为以OF 为直径的圆的半径,A 为圆心,∴|OA|=c2. ∴Pc 2,c 2.又点P 在圆x 2+y 2=a 2上,∴c24+c 24=a 2,即c22=a 2,∴e 2=c2a 2=2,∴e=√2.故选A .例5A 因为点F 1(-√3,0),F 2(√3,0),x 022−y 02=1,所以MF 1⃗⃗⃗⃗⃗⃗⃗⃗ ·MF 2⃗⃗⃗⃗⃗⃗⃗⃗ =(-√3-x 0,-y 0)·(√3-x 0,-y 0)=x 02+y 02-3<0,即3y 02-1<0,解得-√33<y 0<√33.对点训练5(0,2) 因为双曲线x 28-m+y 24-m =1的焦点在x 轴上,所以{8-m >0,4-m <0,解得4<m<8.所以焦点到渐近线的距离d=√m -4∈(0,2).例6A 如图.由已知得|PF1|=|F1F2|=2c.因为直线PF2与以双曲线C的实轴为直径的圆相切,设切点为M,所以|OM|=a,OM⊥PF2,所以|MF2|=√c2-a2=b.由双曲线的定义可得|PF2|-|PF1|=2a,所以|PF2|=2a+2c,所以cos∠OF2M=bc =(2c)2+(2a+2c)2-(2c)22×2c×(2a+2c),整理得c=2b-a.又c2=a2+b2,解得ba=43.所以双曲线C的渐近线方程为y=±43x.故选A.对点训练6A如图,连接OA,OB.设双曲线x 2a2−y2b2=1(a>0,b>0)的焦距为2c(c>0),则点C(-a,0),F(-c,0).由双曲线和圆的对称性,可知点A与点B关于x轴对称,则∠ACO=∠BCO=12∠ACB=12×120°=60°.因为|OA|=|OC|=a,所以△ACO为等边三角形,所以∠AOC=60°.因为FA与圆O相切于点A,所以OA⊥FA.在Rt△AOF中,因为∠AOC=60°,所以|OF|=2|OA|,即c=2a,所以b=√c2-a2=√(2a)2-a2=√3a.所以双曲线x 2a2−y2b2=1(a>0,b>0)的渐近线方程为y=±√3x.。
八、工地渣土运输及车辆出门清洗保障措施(8.6)
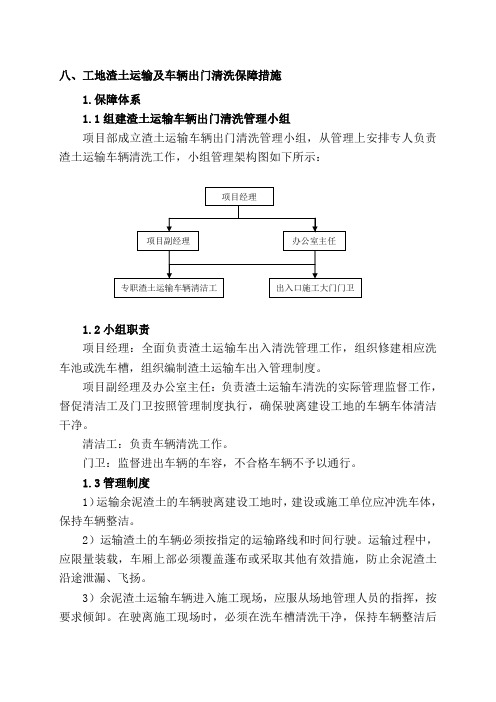
八、工地渣土运输及车辆出门清洗保障措施1.保障体系1.1组建渣土运输车辆出门清洗管理小组项目部成立渣土运输车辆出门清洗管理小组,从管理上安排专人负责渣土运输车辆清洗工作,小组管理架构图如下所示:1.2小组职责项目经理:全面负责渣土运输车出入清洗管理工作,组织修建相应洗车池或洗车槽,组织编制渣土运输车出入管理制度。
项目副经理及办公室主任:负责渣土运输车清洗的实际管理监督工作,督促清洁工及门卫按照管理制度执行,确保驶离建设工地的车辆车体清洁干净。
清洁工:负责车辆清洗工作。
门卫:监督进出车辆的车容,不合格车辆不予以通行。
1.3管理制度1)运输余泥渣土的车辆驶离建设工地时,建设或施工单位应冲洗车体,保持车辆整洁。
2)运输渣土的车辆必须按指定的运输路线和时间行驶。
运输过程中,应限量装载,车厢上部必须覆盖蓬布或采取其他有效措施,防止余泥渣土沿途泄漏、飞扬。
3)余泥渣土运输车辆进入施工现场,应服从场地管理人员的指挥,按要求倾卸。
在驶离施工现场时,必须在洗车槽清洗干净,保持车辆整洁后方可放行。
4)未经许可,外来车辆不准进入工地,进入工地的车辆在驶出工地前,应按规定,将车辆冲洗干净,严禁带土上路。
5)如有进入施工现场车辆未经冲洗,驶出工地上路,影响市容市貌者,给予处罚。
6)对于未按指定路线行驶的车辆或未清洗干净的车辆,门卫应予以阻止,否则酌情对门卫及车辆驾驶员予以处罚。
2.保证措施1)根据贵阳市文明施工要求,在施工现场入门处或物料车辆必经之处设置宽≥4m的洗车槽并配备高压冲洗设备。
做法详见下图,图中尺寸单位为毫米,具体结构尺寸满足贵阳市文明施工标准化图集要求。
车辆冲洗设施平面示意图车辆冲洗设施剖面示意图2)如因场地条件限制不能按上图设置,向轨道公司土建工程部提交申请,经市住房和城乡建设局备案同意后按照冲洗平台示意图Ⅰ、Ⅱ设置。
冲洗平台示意图Ⅰ冲洗平台示意图Ⅱ自动洗车台自动洗车台3)洗车池两侧设置挡水墙,两端设置截水沟,以便对洗车用水进行回收,经三级沉淀后再次利用。
地球椭球体

当制图区域比较小时,由于地图投影的变 形较小,地图上各方向长度缩小的比例近 似相等。地图比例尺是指图上长度与相应 地面之间的长度比例,即d/D=1/M。
比例尺赋予地图可量测计算的性质,为地 图使用者提供了明确的空间尺度概念。
3.2地球椭球体基本要素 3.2.2地图比例尺
高差:某两点的高程之差。
3.2地球椭球体基本要素 3.2.3高程
如图所示, P0P’0为大地水准面,地面点A 和点B到 的垂直距离HA和HB分别为A、B两点 的高度。地面点到任一水准面的高程称为相 对高程。在图中,A、B两点至任一水准面 的 垂直距离 和P1P’1 即为A、B两点的相对高程。
6378206.40 6377397.16
Flattening f
1/298.26 1/298.26 1/298.257 1/298.30 1/297 1/293.47
1/294.98 1/299.15
Use
Newly Adopted Newly Adopted China Russia, China Much of World France, Most of Africa North America Mid Europe, Indonisia
2
3.2.1地球椭球体
WGS [world geodetic system] 84 ellipsoid:
WGS-84坐标系 a = 6 378 137m (世界大地坐标系), b = 6 356 752.3m –它是美国国防局 equatorial diameter–=为1进2 7行56G.3PkSm导航定位 polar diameter = 12–7于131.59k84m年建立的 equatorial circumfer–e地nc心e 坐= 4标0 系07,5.1km surface area = 510 0–614958050年km投2入使用。
椭球基本知识

控制测量计算理论
六、地面观察值归算至椭球面
3、地面观察方向归算至椭球面 归算旳基本要求 地面观察方向归算至椭球面上有3个基本内容: 1) 将测站点铅垂线为基准旳地面观察方向换算成椭球面上以 法线方向为准旳观察方向; 2) 将照准点沿法线投影至椭球面,换算成椭球面上两点间旳 法截线方向; 3) 将椭球面上旳法截线方向换算成大地线方向。
H H正常 (高程异常)
H H正 N (大地水准面差距)
控制测量计算理论
一、常用旳四种坐标系
2、空间直角坐标系 以椭球中心O为原点,起始子午面与赤道面交线为X轴, 在赤道面上与X轴正交旳方向为Y轴,椭球体旳旋转轴为Z 轴,构成右手坐标系O-XYZ,在该坐标系中,P点旳位置 用X、Y、Z表达 。 空间直角坐标系旳坐标原点位于地球 质心(地心坐标系)或参照椭球中心(参 心坐标系),Z 轴指向地球北极,x 轴指 向起始子午面与地球赤道旳交点,y 轴垂 直于XOZ 面并构成右手坐标系。
4、平均曲率半径
在实际际工程应用中,根据测量工作旳精度要求,在一定范围内,把
椭球面当成具有合适半径旳球面。取过地面某点旳全部方向 RA 旳平均值
来作为这个球体旳半径是合适旳。这个球面旳半径——平均曲率半径R:
R MN 或
R b c N a (1 e2 ) W2 V2 V W2
所以,R等于该点子午圈曲率半径M和卯酉圈曲率半径N旳几何
控制测量计算理论
三、地球椭球及其定位
1、椭球旳几何参数及其关系
e2
a2 b2 a2
e'2
a2 b2 b2
1 e2
b2 a2
1 e2
80坐标系椭球参数

80坐标系椭球参数
首先,长半轴a是指椭球体的长轴长度,它是椭球体的主要参数之一,用于确定地球形状的大小。
在80坐标系中,长半轴a的数值为6378137米。
其次,扁率f是描述椭球体扁平程度的参数,它表示椭球体短轴与长轴之比。
在80坐标系中,扁率f的数值为1/298.257。
最后,偏心率是描述椭球体形状的参数,它表示椭球体中心到焦点的距离与长轴长度之比。
在80坐标系中,偏心率的数值为
0.08181919。
这些参数对于地图投影、测量和导航等领域具有重要意义,它们提供了地球形状和大小的基本参考,帮助人们进行精准的地理定位和测量工作。
同时,这些参数也为各种地理信息系统和卫星定位系统的设计和运行提供了重要的基础数据。
总的来说,80坐标系椭球参数是地球测量和地图绘制领域中不可或缺的重要参数,对于相关领域的研究和实践具有重要意义。
测量基础--椭球和投影.

1.地球椭球的几何特性我们知道,地球是一个两极稍扁,赤道略鼓的球体。
为了满足大地测量归算的需要,应选取一个与大地体十分接近且在数学上又能简单表示的表面作为计算的根据面。
通常选择的体形是由.一个椭圆绕其短轴旋转而形成的旋转椭球体,简称参考椭球体。
............................1.1. 地球椭球的基本元素我们设想,地球是一个椭圆绕其短轴旋转而形成的旋转椭球体。
这个椭圆也叫做子午椭圆。
椭球的基本元素就是由椭圆的基本元素来决定的。
决定椭球的大小和形状,一般有下列五大元素:.....................在以上各元素中,只要已知其中两个,就可以确定椭圆的大小和形状,但是其中一个必须是长度元素(a或b)。
一般常用长半......轴.a.和扁率...............α.来确定椭圆的大小和形状。
在以上各元素中,存在一下关系:1.a与b的关系b/a = √1-e2a/b = √1-e’22.e2与e’2的关系e’2 = e2/(1- e2); e2= e’2/(1+ e’2)(1- e2)(1+ e’2) = 13.α与e2的关系α = 1-√1- e2e2= 2α-α24.一些辅助量c = a2/bη = e’cosBV = √1+e’2COS2B = √1+η2W = √1-e2sin2BN = a/W根据上面的公式,可以导出c与偏心率的关系,实际上c就是椭圆两极点处的曲率半径。
5.中国海洋石油公司使用的坐标系统现在中国海洋石油总公司统一使用WGS84椭球,各元素数值如下:a = 6,378,137.0 mb = 6,356,752.3142 mα = 1/298.257223563e2 = 0.00669 43799 9013e’2= 0.00673 94967 42227 以前曾使用过WGS72椭球:a = 6,378,135.0 mb = 6,356,750.52 mα = 1/298.26e2 = 0.00669 43178e’2= 0.00673 94337和WGS54(克拉索夫斯基)椭球:a = 6,378,245.0 mb = 6,356,863.01877 mα = 1/298.3e2 = 0.00669 34216 2297e’2= 0.00673 85254 14681.2. 椭球面上的各种坐标系及其相互之间的关系1.2.1空间直角坐标系与子午面上的直角坐标系空间直角坐标系的原点..2.-.1)..,.z.轴...O.与椭球的中心相合........(.见图与椭球的短轴相合,.................y.轴..........x.轴与赤道面和起始子午面的交线相合,与.xz..平面正交,指向东方.........。
几种主要的椭球公式

§6.3 几种主要的椭球公式过椭球面上任意一点可作一条垂直于椭球面的法线,包含这条法线的平面叫做法截面,法截面同椭球面交线叫法截线(或法截弧)。
包含椭球面一点的法线,可作无数多个法截面,相应有无数多个法截线。
椭球面上的法截线曲率半径不同于球面上的法截线曲率半径都等于圆球的半径,而是不同方向的法截弧的曲率半径都不相同。
6.3.1子午圈曲率半径子午椭圆的一部分上取一微分弧长ds DK =,相应地有坐标增量dx ,点n 是微分弧dS 的曲率中心,于是线段Dn 及Kn 便是子午圈曲率半径M 。
任意平面曲线的曲率半径的定义公式为:dBdS M = 子午圈曲率半径公式为:32)1(W e a M -= 3V c M = 或 2V N M = M 与纬度B 有关.它随B 的增大而增大,变化规律如下表所示:6.3.2卯酉圈曲率半径过椭球面上一点的法线,可作无限个法截面,其中一个与该点子午面相垂直的法截面同椭球面相截形成的闭合的圈称为卯酉圈。
在图中E PE '即为过P 点的卯酉圈。
卯酉圈的曲率半径用N 表示。
为了推导N 的表达计算式,过P 点作以O '为中心的平行圈PHK 的切线PT ,该切线位于垂直于子午面的平行圈平面内。
因卯酉圈也垂直于子午面,故PT 也是卯酉圈在P 点处的切线。
即PT 垂直于Pn 。
所以PT 是平行圈PHK 及卯酉圈E PE '在P 点处的公切线。
卯酉圈曲率半径可用下列两式表示:W a N = Vc N = 6.3.3 任意法截弧的曲率半径子午法截弧是南北方向,其方位角为0°或180°。
卯酉法截弧是东西方向,其方位角为90°或270°。
现在来讨论方位角为A 的任意法截弧的曲率半径A R 的计算公式。
任意方向A 的法截弧的曲率半径的计算公式如下:AB e N A N R A 22222cos cos 1cos 1'+=+=η (7-87)6.3.4 平均曲率半径在实际际工程应用中,根据测量工作的精度要求,在一定范围内,把椭球面当成具有适当半径的球面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.真题小试
感悟考题
试一试
2 2 x y (1)(2014·大纲版全国卷)已知椭圆C: 1(a>b>0)的左、右 a 2 b2 焦点为F1,F2,离心率为 3 , 过F2的直线l交C于A,B两点,若△AF1B的 3
周长为 4 3,则C的方程为(
x 2 y2 x2 A. 1B. y 2 1 3 2 3 x 2 y2 x 2 y2 C. 1D. 1 12 8 12 4
图
形
标准方程 范围
x 2 y2 2 1 2 a b __________(a>b>0)
y2 x 2 2 1 2 __________(a>b>0) a b
性 质
-a a ___≤x≤__ b -b ___≤y≤__
对称性
-b b ___≤x≤__ a -a ___≤y≤__ 坐标轴 对称轴:_______ 原点 对称中心:_____
2c 3 5 x2 c ② c x2 4 3 2 y12 c b 2 1, 2 2 y2 又点A,B在椭圆上,所以 x 2 2 1, b c 2 1 b 2, 3y 2 2 2 2 与①②联立解得 b . 所以椭圆方程为 x 1. 2 3
3.必用技法
核心总结
看一看
(1)常用方法:待定系数法、定义法、点差法. (2)数学思想:数形结合思想、分类讨论思想与方程思想.
【小题快练】
1.思考辨析 静心思考 判一判
(1)平面内与两个定点F1,F2的距离之和等于常数的点的轨迹是椭
圆.( )
(2)椭圆上一点P与两焦点F1,F2构成△PF1F2的周长为2a+2c(其中a为椭 圆的长半轴长,c为椭圆的半焦距).( (3)椭圆的离心率e越大,椭圆就越圆.( ) ) )
2a 长轴A1A2的长为___ 2b 短轴B1B2的长为___ 2c |F1F2|=___
c (0,1) e= a ∈______
b2+c2 a2=_____
2.必备结论
教材提炼
记一记
x 2 y2 (1)设椭圆 2 2 =1(a>b>0)上任意一点P(x,y),则当x=0时,|OP|有最 a b
(2)(选修2-1P49T5(3)改编)已知椭圆的一个焦点为F(1,0),离心率
为 1 ,则椭圆的标准方程为_______.
x 2 y2 【解析】设椭圆的标准方程为 2 2 =1(a>b>0). a b 1 因为椭圆的一个焦点为F(1,0),离心率 e , 2 c 1, c 1 a 2c 2, 所以 解得 2 , b 3, a 2 2 2 2 a b c , 2 2 x y 故椭圆的标准方程为 1. 4 3 2 2 x y 答案: 1 4 3
(4)椭圆既是轴对称图形,又是中心对称图形.(
【解析】(1)错误.由椭圆的定义知,当该常数大于|F1F2|时,其轨迹才 是椭圆,而常数等于|F1F2|时,其轨迹为线段F1F2,常数小于|F1F2|时, 不存在图形. (2)正确.由椭圆的定义得,|PF1|+|PF2|=2a, 又|F1F2|=2c,所以|PF1|+|PF2|+|F1F2|=2a+2c.
b 这时,P在短轴端点处;当x=±a时,|OP|有最大值__, a 这时,P在 小值__, 长轴端点处. (2)椭圆的一个焦点、中心和短轴的一个端点构成直角三角形,其中a 是斜边长,a2=b2+c2.
4a (3)已知过焦点F1的弦AB,则△ABF2的周长为___.
(4)若P为椭圆上任一点,F为其焦点,则a-c≤|PF|≤a+c.
)
【解析】选A.由椭圆的定义可知,|AF1|+|AF2|=2a,
|BF1|+|BF2|=2a,
又因为|AF1|+|AF2|+|BF1|+|BF2|= 4 3,
即4a= 4 3,解得 a 3. 又 c 3,
a 3
则c=1,b2=a2-c2=2,
2 2 x y 所以椭圆的方程为 1. 3 2
第六节
椭
圆
【知识梳理】
1.必会知识 教材回扣 填一填
(1)椭圆的定义
条 件 结论1 结论2
平面内的动点M与平面内 的两个定点F1,F2 |MF1|+|MF2|=2a 2a>|F1F2|
F1,F2 _____ 为椭圆的焦点
M点的轨迹 为椭圆 |F1F2| ______ 为椭圆的焦距
பைடு நூலகம்
(2)椭圆的标准方程和几何性质
(2)(2014·安徽高考)设F1,F2
分别是椭圆E:x2+
y 2 =1(0<b<1)的左、 b2
右焦点,过点F1的直线交椭圆E于A,B两点,若|AF1|=3|F1B|,AF2⊥x轴, 则椭圆E的方程为 .
【解析】如图所示,设A(c,y1),B(x2,y2),作BC∥F1F2,
则
y1 3 y1 3y 2 ① y2 1
焦距为4,则m等于( A.8 B.7
) C.6 D.5
2 2 x y 【解析】选A.因为椭圆 =1的焦点在x轴上. m 2 10 m 10 m 0, 所以 解得6<m<10. m 2 0, m 2 10 m,
因为焦距为4,
所以c2=m-2-10+m=4, 解得m=8.
2 2 c a b b 2 所以e越大,则 b 越小,椭圆 (3)错误.因为 e 1 ( ) , a a a a
就越扁. (4)正确.由椭圆的对称性知,其关于原点中心对称,也关于两坐标轴对 称. 答案:(1)× (2)√ (3)× (4)√
2.教材改编
链接教材
练一练
2 2 x y (1)(选修2-1P49T2(1)改编)已知椭圆 =1的焦点在x轴上, m 2 10 m
顶点
(-a,0) 2______ (a,0) A1_______,A
(0,-b) 2______ (0,b) B1_______,B
(0,-a) 2______ (0,a) A1_______,A
(-b,0) 2______ (b,0) B1_______,B
性 质
轴 焦距 离心率 a,b,c 的关系
