DSP第三章3.2 DFT定义

合集下载

数字信号处理

2《Digital Signal Processing—A Computer Approach Third Edition》 Mitra
3《Digital Signal Processing》A.V.Oppenheim 4…….
4
第一章数字信号处理概述
1.1 数字信号处理技术 1.2 数字信号与连续时间信号的关系 1.3 数字信号处理的分析方法 1.4 A/D、D/A原理 1.5 模拟信号的数字滤波
12
1.4 A/D、D/A原理
1.4.1 A/D原理与抽样定理
模拟信号的抽样抽样信号的频谱无失真抽样条件前置预滤波器的作用 A/D变换的指标
.4.2 D/A原理和重构定理
重构定理一种D/A变换器原理
13
1.4.1 A/D原理与抽样定理
A/D 将模拟信号转变为数字信号
s
Ya (
j)

FT

ya (t) X a ( j)G(
ya (t) xa (t)
j)

Xa(
j) (*)
X a ( j)
19
讨论
1、（*）式成立的条件：
s 2m
s
1
T
k
Xa(
j
jks )
Xˆ a ( j) s
当m s / 2
Xˆ a ( j)
18
m s / 2
时信号的提取
xˆa (t)
G( j)
Xˆ a ( j)
ya (t)
G(
j)

T , 0,

1 2
s

1 2
s

DSP-chapter3

(n)]

X
p
(k
)
DFS[xp
(n)]

X
p
(k)
（2）序列实部和虚部的对称性
DFS{Re[ x p (n)]} X pe (k ) DFS { j Im[ xp (n)]} X po (k )
若 x p (n) Re[ x p (n)]
X p (k) | X p (k) | e j(k)
即令则：
N 1
j 2 kn
X p (k) x p (n)e N
n0
WN e j2 / N

xp (n)
1 N
N 1
X p (k )WNkn
k 0 N 1

IDFS[ X p (k )]

X P (K ) xp (n)WNkn DFS[xp (n)]
一、周期序列的傅立叶级数表示
设 x p n 是周期为N的周期序列，可用一系列正弦或
复指数序列来表示

j 2 kn
xp n X p k e N
k
由于：
j 2 (k 2rN )n
j 2 kn
eN
e N
基频：
ej2 Nn故：序列的离散傅立叶级数的谐波成分只有N个是独立的成分（k=0,1,2,…,N-1)，所以，序列可展成离散傅立叶级数：
则 DFS [x p (n)] X p (k ) X pe (k )
| X p (k) || X p (k) |
(k) (k)
（3）周期序列的共轭对称部分的傅立叶级数和共轭反对称部分的傅立叶级数：
DFS [ X pe (n)] Re[ X p (k )] DFS [ X po (n)] j Im[ X p (k )]

DSP工作原理

DSP工作原理DSP（Digital Signal Processing，数字信号处理）是一种通过数学算法和计算机技术对信号进行处理的技术。

它在现代通信、音频处理、图像处理等领域得到了广泛应用。

本文将深入探讨DSP的工作原理。

引言概述DSP是一种数字信号处理技术，通过数学算法和计算机技术对信号进行处理。

它可以对信号进行滤波、变换、编码、解码等操作，广泛应用于通信、音频处理、图像处理等领域。

下面将从信号采样、数学算法、计算机实现、信号重构和应用领域五个方面详细介绍DSP的工作原理。

一、信号采样1.1 采样定理：根据奈奎斯特采样定理，信号的采样频率必须是信号最高频率的两倍以上，才能够准确还原原始信号。

1.2 采样过程：采样过程将连续时间域信号转换为离散时间域信号，通过模数转换器将模拟信号转换为数字信号。

1.3 采样率选择：采样率的选择取决于信号的频率成分，通常选择高于信号最高频率两倍的采样率，以确保信号的还原质量。

二、数学算法2.1 离散傅里叶变换（DFT）：DFT是DSP中最基本的变换之一，将离散时间域信号转换为离散频率域信号，用于频谱分析和滤波等操作。

2.2 快速傅里叶变换（FFT）：FFT是DFT的一种高效算法，通过减少计算量和复杂度，实现了快速的频域分析和滤波操作。

2.3 滤波算法：滤波是DSP中常用的操作之一，包括低通滤波、高通滤波、带通滤波等，通过滤波算法可以去除噪声、改善信号质量。

三、计算机实现3.1 固定点数表示：计算机中常用的表示方式是固定点数表示，将实数转换为二进制表示，通过定点运算实现DSP算法。

3.2 浮点数表示：浮点数表示可以更精确地表示实数，但计算复杂度较高，对于精度要求较高的应用，可以使用浮点数表示。

3.3 指令集优化：为了提高DSP算法的执行效率，可以针对特定的DSP芯片进行指令集优化，利用硬件加速器提高计算速度。

四、信号重构4.1 逆变换：通过逆变换，将离散频率域信号转换为离散时间域信号，实现信号的重构和还原。

常用DSP算法

长度为NL，序列Lh(n)的K长度为1K。
为了利用DFT计算线性卷积，必须选择满足上式的DFT长度N，并对 x(n)至少补K-1个零，对h(列卷积的DFT实现方法
• 在大多数实际情况中，长序列对应于系统输入，短序列对应于系统冲激响应。 • 将长序列分割成长度为N的序列块，计算每一块与短序列的卷积。 • 每一个序列块的卷积必须适当地合并，以得到长序列和短序列卷积的最后结果。 • 有两种合并的方法，分别是重叠相加法和重叠保留法。
DFT的一些重要结论
• N越大，则它的DFT与傅里叶变换越近似，因为在区间[0，2π）的取样数增加了。 • N的取值通常需要根据实际应用中允许的运算复杂度决定，因为补零个数越多，则DFT计算所需要的运
算和存储器件越多。
DFT实现数字滤波器
• 线性和圆周卷积 • 重叠相加法 • 重叠保留法
线性和圆周（循环）卷积
• 时不变系统可以实现输入信号与系统冲激响应之间的线性卷积。 • 两个序列卷积的傅里叶变换等于它们的傅里叶变换相乘，即可在频域计算卷积。 • 频域取样导致信号时域周期重复，理论上利用DFT只能计算圆周（循环）卷积，而不能实现线性卷积。
圆周卷积等价于线性卷积的条件
其中，N为DFT的长度，序列x(n)的
取x(k)的共轭，得x*(k)；求x*(k)的FFT；再求共轭，乘以1/N，即得。
基-2算法：序列长度N为2的整数幂，即N=2L，
其精确复乘次数为（考虑省去非乘法的次数）：
N
3
2 log2 N 2 N 不 2同基的 F F T 算法
83其N基精l-o4确g算2复N法乘：次N序数列1为长（度考N虑为省4的去整非数乘幂法，的即次N数=）22L：，基-4算法比基-2算法更高效。

数字信号处理DSP第三章3.2 DFT定义

⎛ 2π j⎜ ⎝ N ⎞ ⎟k ⎠
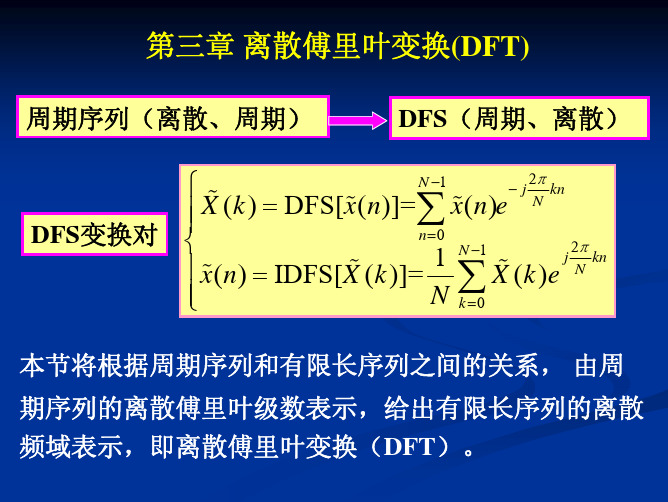
易知，DFT的变换区间长度N不同，表示对X(ejω)在区间［0, 2π］上的采样间隔和采样点数不同，所以DFT 的变换结果也不同。
jIm(z)
−2 WN −1 WN 0 WN k ＝0 − ( N −2 ) WN
X (ejω)
X (k )
o
Re[z] o π
W
− ( N −3) N
ω
DFT与序列傅里叶变换、Z变换的关系
例1 已知序列x(n)=δ(n)，求它的N点DFT。解
nk 0 X (k ) = ∑ δ (n)WN = WN =1 n=0 N −1
k=0, 1, …, N-1
对序列δ(n)，不论对它进行多少点的DFT，所得结果都是一个离散矩形序列。
本节将根据周期序列和有限长序列之间的关系，由周期序列的离散傅里叶级数表示，给出有限长序列的离散频域表示，即离散傅里叶变换（DFT）。
一、预备知识 1、余数运算表达式如果n=n1+mN， m为整数；则有
((n))N=n1, 0≤n1≤N-1
运算符(( ))N表示n被N除，商为m，余数为n1。 n1是((n))N的解, 或称作取余数，或说n对N取模值，简称取模值，n模N，(n mod N) 。
周期延拓
长度为M的有限长序列x(n)的N点DFT，是有限长序
~
x(n)
N
~ x (n)
DFS
DFS[ ~ x (n) ]
~ X (k )
% (k ) R (k ) 取主值 X N
DFT[x(n)]N
注：以上定义中N长度没有限制！
有限长序列x(n)的N点DFT—即DFT正变换公式
X (k ) = DFT[ x(n)]N = ∑ xN (n)W ， 0 ≤ k ≤ N − 1

第三章离散傅里叶变换及其快速计算方法(DFT、FFT)

X (e jw )
（2）Z 变换 -- 提供任意序列的 z 域表示。
n

x( n)e jnw
X (z)
n

x ( n) z n
这两种变换有两个共同特征：
（1）变换适合于无限长序列（2）它们是连续变量 ω 或 z 的函数
华北电力大学自动化系
3
3.1 问题的提出：可计算性
X (z)
而对于
n

x ( n) z n
n

x ( n) z n
找不到衰减因子使它绝对可和（收敛）。为此，定义新函数，其 Z 变换：
华北电力大学自动化系
15
DFS 定义：正变换
X ( z)
n
x ( n) z n ~ ( n ) z n x
华北电力大学自动化系
6
3.1 问题的提出：傅里叶变换的四种形式（3）
2. 周期连续时间信号：傅里叶级数 FS
~ (t ) x X (n 0 )
t T

时域周期频域离散
0
2 T
x(t)
~
n -
X(n 0 )e jn0t

时域连续函数造成频域是非周期的谱。频域的离散对应时域是周期函数。
X (e jT )

T T
X (e jT )e jnT d
取样定理
n

x(nT )e jnT
1 X ( 0 ) T n
时域的离散化造成频域的周期延拓时域的非周期对应于频域的连续
华北电力大学自动化系
8

数字信号处理DSP第三章3.3 DFT性质

y ( n ) = x (( n + m )) N R N ( n )
① 若 (( m )) N = n0 ② 先求出
⎧ 左移 n0 则⎨ ⎩ 右移 n0
m>0 m<0
y (0) = x((m)) N
再依次相继循环写出其他的y(n)。例: 已知x(n)(0≤n≤2), y(n)=x((n+m))5R5(n)，当m=-16时，求y(3)=？。 y(3)=x(2)。
y(n) = x1 (n)* x2 (n) =
=
m=−∞
∞
∑ x (m) x (n − m)
1 2
2 1
∞
m=−∞
∑ x (m) x (n − m)
线性卷积结果非零区间? 线性卷积结果长度？
循环卷积计算过程： 1）根据卷积长度补零,使得作卷积的两序列长度相同； 2）循环翻转(求其中一个序列的循环翻转序列)； 3）将循环翻转序列右循环移位(n=0,1,2, …，N-1)； 4）相乘相加。 5）对下一个n，重复上述4步。
R7 (m )
0
x2
m
((3 −
m
) )7
R7 (m )
0
m
y(0) = [∑x1 (m)x2 ((0 − m))7 ]R7 (m) = 1×1+1×1+1× 0 + 0 × 0 + 0 × 0 + 0 ×1+ 0 ×1 = 2
m=0 6
6
y(1) = [∑x1 (m)x2 ((1− m))7 ]R7 (m) = 1×1+1×1+1×1+ 0× 0 + 0× 0 + 0× 0 + 0 ×1 = 3

DFT的定义和性质

4 DFT 总结DFT 的定义是针对任意的离散序列)(nTs x 中的有限个离散抽样)0(N n <≤的，它并不要求该序列具有周期性。

由DFT 求出的离散谱)()(Z k NT k H H k H S k ∈⎪⎪⎭⎫⎝⎛==∆是离散的周期函数，周期为s s s f T NT N T N Nf ====1/00、离散间隔为0011f T N f NT s s ===。

离散谱关于变元k 的周期为N 。

如果称离散谱经过IDFT 所得到的序列为重建信号，))(('Z n nTs x ∈，则重建信号是离散的周期函数，周期为001f T NT s ==(对应离散谱的离散间隔的倒数)、离散间隔为001/Nf N T N NT T s s ===(对应离散谱周期的倒数)。

经IDFT 重建信号的基频就是频域的离散间隔，或时域周期的倒数，为S NT T f 1100==。

实序列的离散谱关于原点和2N (如果N 是偶数)是共轭对称和幅度对称的。

因此，真正有用的频谱信息可以从0~12-N 范围获得，从低频到高频。

在时域和频域N ~0范围内的N 点分别是各自的主值区间或主值周期。

5 DFT 性质线性性：对任意常数m a (M m ≤≤1)，有[]∑∑==⇔⎥⎥⎦⎤⎢⎢⎣⎡M m m m M m m m n x DFT a n x a DFT 11)()( 奇偶虚实性：DFT 的反褶、平移：先把有限长序列周期延拓，再作相应反褶或平移，最后取主值区间的序列作为最终结果。

DFT 有如下的奇偶虚实特性：奇⇔奇；偶⇔偶；实偶⇔实偶；实奇⇔虚奇；实 ⇔(实偶) + j(实奇)；实 ⇔(实偶)·EXP(实奇)。

反褶和共轭性：对偶性：)()(k Nx n X -⇔把离散谱序列当成时域序列进行DFT ，结果是原时域序列反褶的N 倍；如果原序列具有偶对称性，则DFT 结果是原时域序列的N 倍。

时移性：km N W k X m n x )()(⇔-。

32 dft的基本性质

无限长序列x(n)的共轭反对称性（共轭反对称序列）：
xo (n) = −xo*(−n), −∞ ≤ n ≤ +∞
有限长序列x(n)的共轭反对称性（共轭反对称序列）：
xop (n) = −xo*p (N − n), 0 ≤ n ≤ N −1
无限长序列： x(n) = xe (n) + xo (n)
有限长序列也可以表示为共轭对称部分和共轭反对称部分之和：
5、DFT的共轭对称性
DTFT的对称性
x(n)无限长
DFT的对称性
x(n)有限长
关于原点的对称性关于N/2点的对称性
无限长序列x(n)的共轭对称性（共轭对称序列）：
xe (n) = xe*(−n), −∞ ≤ n ≤ +∞
有限长序列x(n)的共轭对称性（共轭对称序列）：
xep (n) = xe*p (N − n), 0 ≤ n ≤ N −1 xep (n) 隐含周期性，把 xe*p (−n)右移一个周期使之在0～N-1的主值区间内。
n′=0
= WN−km X (k )
循环时移：
N −1+m
∑ Y (k) =
x((n′))NWNk (n′−m)
n′=m
N −1+m
∑ = WN−km
x((n′))
W kn′
NN
n′=m
x((n
±
m)) N
RN
(n)
↔
W ∓ km N
X
(k)
线性时移：
x(n ± n0 ) ↔ e± jωn0 X (e jω )
~
x(n)
移位
~
x(n
+
m)
取主值

DSP-离散傅里叶变换(DFT)

由于：
N1
N 1 W k0
k(mn) N
{1 0
mnM N,MM为整数
mnM N,M
所以，在变换区间上满足下式：
IDFT[X(k)]=x(n),
0≤n≤N-1
离散傅里叶逆变换是唯一的。
3.1 离散傅里叶变换的定义
[例]
解:
序(1)列设x变(n换)=区R4间(nN) ，=8求，x(则n)：的X (8k点) 和n1760 点x(DnF)WT 8。kn
设序列x(n)的长度为N，其Z变换和DFT分别为：
N1
X(z)ZT[x(n)] x(n)zn
n0
N1
X(k)DFT[x(n)] x(n)WNkn
n0
比较上面二式可得关系式
0kN-1
X(k) XXX(((kkkX )))(XXX(z(z(z)z)))zzezej2jN 2Njk2ke ,k,j,2N k00,0kkkNN--N 11-10((33k ..1(1.3.33. )1).3)N ze N
离散傅里叶变换(DFT)
本章主要内容
▪ 离散傅里叶变换的定义 ▪ 离散傅里叶变换的基本性质 ▪ 频率域采样 ▪ 离散傅里叶变换的应用举例
离散傅里叶变换(DFT)
DFT变换的实质：有限长序列的傅里叶变换的有限点离散采
样(时域和频域都是离散化的有限点长的序列)。
DFT变换的意义：
▪ 开辟了频域离散化的道路，使数字信号处理可以在频域中进行处理，增加了数字信号处理的灵活性。 ▪ DFT具有多种快速算法(FFT)，实现了信号的实时处理和设备的简化。
3 N 0
j 2 kn
e8
XX(k(k)
77
)
n n0 0

第三章_DSP DFT

第三章离散傅氏变换(DFT)•离散信号在Z域及频域的表示•频域DTFT（绝对可加序列）•Z域ZT（任意序列的频域表示）–适用于无限长序列，是ω及z的连续函数–不适合用数值计算•为进行数值计算，新的变换方法–对DTFT在频域上进行抽样•DFS（周期序列）－＞DFT（有限长序列）－＞FFT（DFT快速算法）的频谱密度函数，dt4、离散时间、离散频率--DFT–时域、频域上都离散--适合数值计算⎪⎪⎩⎪⎪⎨⎧−≤≤==−≤≤==∑∑−=−−=101010,)(1)()()(10,)()()()(N k nk n N N n nk N n N k W k X N n G n x n x N k W n x k G k X k X3.2 周期序列的离散傅氏级数-DFS1、DFS 变换对–设周期为N 的周期序列–周期序列的ZT 不存在（不绝对可和），取其中一个周期，序列的FT)(~n x 为任意整数r )(~)(~rN n x n x +=∑−=−=10)()(N n nj j e n x e X ωω∑−=−===1022)(~)(~)(~)(~N n kn Nj k N j j en x k X e X e X ππω2、MatLab 实现–Function dfs(xn,N)–Function idfs(Xk,N)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡×=−−−−)1)(1(11111111)*(*N N N N N N N N N N W W W W N N W W x X x X 的矩阵为为矩阵相乘代表序列的行向量及n k)()(~)(~)](~[110m n i W W i x W m n x m n x DFS m N m i mk Nki N nk N N n +==+=+∑∑+−=−−=)(~)(~rN i x i x +=ki NkNi N W W =)(~)(~)](~[10k X W W i x W m n x DFS mk N N i ki N mk N −−=−==+∑由于周期性，有：所以：3、调制特性4、周期卷积)(~)](~[lnl k X n x W DFS N+=)(~)(~)(~)](~[10)(10ln ln l k X W n x W n x W n x W DFS N n n k l N N n kn N N N +===∑∑−=+−=)(~)(~)(~21k X k X k Y ⋅=∑∑−=−=−=−==10121021)()()(~)(~)](~[)(~N m N m m n x m x m n x m x k Y IDFS n y周期N ＝6的周期卷积图示3.4 从DFS 到DFT1、主值区间–求主值区间即为n 对N 的求余运算∑∞−∞=+==⎩⎨⎧−≤≤=r N rN n x n x n R n x n x others N n n x n x )()(~ ),()(~)(010)(~)(Nn x ))(()4()5(~)7()25(~4))5((,49)1(5,7))25((,792255,25,999x x x x n n n n N =−==−+×−=−==+×==−===，　的主值求例：–MatLab实现•rem(n,N)函数用来确定n除以N的余数,但n<0时要修正•Function m=mod(n,N)–实际工作中常用到非周期序列•有限长序列(N点)•无限长序列—用矩形窗截断(N点)–序列的FT变换(DTFT)，但DTFT在频域上连续(n)–x(n)周期化形成xs–求DFS，然后取其中一个周期X(k)–X(k)将是序列的DTFT的近似表示3.5DFT 性质1、线性–x 1(n)与x 2(n)均为N 点，则线性运算也为N 点–x 1(n)与x 2(n)点数不等，N ＝Max(N 1,N 2))()()]()([2121k bX k aX n bx n ax DFT +=+N＝6圆周移位3、共轭对称性（奇偶虚实特性）–序列FT （DTFT ）的对称性)()]}(Im[{)()]}({Re[ωωj o j e e X n x j DTFT e X n x DTFT ==)](Im[)]([)](Re[)]([ωωj o j e e X j n x DTFT e X n x DTFT ==实部偶对称，虚部奇对称•奇序列•偶序列)()()(n N x n x n x −−=−−=)()()()()()(10)(1))((10))((10k X W m x W n N x W n N x W n x k X N m k m N N n k n N N N n k n N N n nk N −−=−=−−=−−==∑∑∑∑−=−=−−−=−−−=其DFT 依然为奇对称其DFT 依然为偶对称}14,9,12,15{)()(14}0,4,6,4{}]1,2,3,4{}0,2,2,1[{))0(()(9}0,2,4,3{}]4,1,2,3{}0,2,2,1[{))2(()(12}0,8,2,2{}]3,4,1,2{}0,2,2,1[{))1(()(15}0,6,8,1{}]2,3,4,1{}0,2,2,1[{))0(()())(()()()(403)(2130303042130303042130303042130303042130421211=⊗∴==⋅=−==⋅=−==⋅=−==⋅=−−=⊗∑∑∑∑∑∑∑∑∑∑∑∑∑=============n x n x m x m x m x m x m x m x m x m x m n x m x n x n x n x m m m m m m m m m m m m m 点至点，补序列为6、有限长序列的线卷积与圆卷积–时域上圆卷积－－两序列的DFT 相乘（FFT ），但在实际问题中要处理线性卷积圆卷积线性卷积关系222111N 10)(N ,10)(，列长为列长为−≤≤−−−−−≤≤−−−−N n n x N n n x–线性卷积11121201122121212()()()()()():01():0102()1():3():5()7N m m y n x m x n m x m x n m x m m N x n m n m N n N N y n N N x n x n y n −∞=−∞==−=−≤≤−−≤−≤−∴≤≤+−∴+−∑∑ 的列长为例如：点，点，为点。

数字信号处理：第3章离散傅里叶变换(DFT)

N 1
X (k mN ) x(n)WN(kmN )n
n0
N 1
x(n)WNkn X (k)
n0
同理可证明(3.1.2)式中
x(n+mN)=x(n)
~
实际上，任何周期为N的周期序列 x 都可以看
作长度为N的有限长序列x(n)的周期延拓序列，而x(n)
则是
~
x
的一个周期，即
~
x(n) x(n mN )
式和(3.2.10)式代入得到
x*(N-n)=x*ep(N-n)+x*op(N-n) =xep(n)-xop(n)
xep(n)=1/2［x(n)+x*(N-n)］ xop(n)=1/2［x(n)-x*(N-n)］
(3.2.12) (3.2.13) (3.2.14)
2. DFT的共轭对称性 (1) 如果x(n)=xr(n)+jxi(n) 其中 xr=Re［x(n)］=1/2［x(n)+x*(n)］ jxi(n)=jIm［x(n)］=1/2［x(n)-x*(n)］由(3.2.7)式和(3.2.13)式可得 DFT［xr(n)］=1/2DFT［x(n)+x*(n)］
n0
X(k)的离散傅里叶逆变换为
X (k) DFT[x(n)]
1 N
N 1 n0
X (n)WNkn ,
k=0, 1, &, N-1
(3.1.2)
式中，
j 2
eN
， N称为DFT变换区间长度N≥M，
通常称(3.1.1)式和(3.1.2)式为离散傅里叶变换对。下面
证明IDFT［X(k)］的唯一性。
则 ((n))N=n1
~
例如， N 5, x(n) x(n)5,

dsp3_Q

3.2周期序列的离散傅里叶级数(DFS)及性质
1.周期序列的离散傅里叶级数
若离散时间序列x(n)为周期序列，则 x(n)=x(n+rN)
其中N（正整数)为信号的周期，该周期序列记作：
~
x
(
n
)
周期序列可以用傅里叶级数(DFS)来表示，其定义公式为：
x ~(n)1N 1X ~(k)ej2 N nkID F S[X ~(k)]n0,1,..N ..,1
2 n e v e n
n
例3-3 若序列h(n)是实因果序列，其傅里叶变换的实部为
HR(ej)1cos，求序列h(n)及其傅里叶变换 H ( e j )
解：由题意知：
比较两式得：由于h(n)是实因果序列，根据共轭对称性得：
因此 H (ej)h e(n )ejn 1 ej2 ej 2co s n
第3章离散时间系统的频域分析——傅里叶变换
3.1 非周期序列的傅里叶变换及性质 3.2 周期序列的离散傅里叶级数(DFS)及性质 3.3 有限长序列的离散傅里叶变换(DFT) 3.4 频率抽样理论 3.5 利用DFT对连续时间信号处理时应注意的问题
3.1 非周期序列的傅里叶变换及性质
3.1.1 非周期序列傅里叶变换
5.时间反转
设 D TFT[x(n)]X(ej)
则 D TF T[x(n)]X(ej)
6.尺度变换 DTFT[anx(n)]X(1ej) a
7.频域微分
DTFT[nx(n)]jdX(ej)
d
3.1.2 非周期序列傅里叶变换的性质
8.共轭性
设 D TFT[x(n)]X(ej) 则 D TF T[x*(n)]X*(ej)
5

DSP实验有限长序列,频谱,DFT的性质

课程名称：数字信号处理实验名称：有限长序列、频谱、DFT 的性质一、实验目的和要求设计通过演示实验，建立对典型信号及其频谱的直观认识，理解DFT 的物理意义、主要性质。

二、实验内容和步骤2-1用MATLAB ，计算得到五种共9个序列：2-1-1实指数序列⎩⎨⎧-≤≤=otherwiselength n a n x n10)( 例如，a=0.5, length=10 a=0.9, length=10 a=0.9, length=202-1-2复指数序列⎩⎨⎧-≤≤+=otherwiselength n jb a n x n10)()(例如，a=0.5, b=0.8, length=102-1-3从正弦信号x (t )=sin(2πft +delta)抽样得到的正弦序列x (n )=sin(2πfnT +delta)。

如，信号频率f =1Hz ，初始相位delta=0，抽样间隔T=0.1秒，序列长length=10。

2-1-4从余弦信号x (t )=cos(2πft + delta)抽样得到的余弦序列x (n )=cos(2πfnT + delta)。

如，信号频率f =1Hz ，初相位delta=0，抽样间隔T=0.1秒，序列长length=10。

2-1-5含两个频率分量的复合函数序列x (n )=sin(2πf 1nT )+delta ×sin(2πf 2nT +phi)。

如，2-2 用MATLAB ，对上述各个序列，重复下列过程。

2-2-1画出一个序列的实部、虚部、模、相角；观察并记录实部、虚部、模、相角的特征。

2-2-2 计算该序列的幅度谱、频谱实部、频谱虚部；观察和并记录它们的特征，给予解释。

2-2-3 观察同种序列取不同参数时的频谱，发现它们的差异，给予解释。

三、主要仪器设备MATLAB 编程。

四、操作方法和实验步骤（参见“二、实验内容和步骤”）五、实验数据记录和处理1. 实指数序列⎩⎨⎧-≤≤=otherwiselength n a n x n10)(1-1. a=0.5, length=10 clc;clf;clear;%清除 n=0:9;%设置自变量区间 xn=0.5.^n;%计算相应的x(n) k=0:9;%设置DFT 采样长度 xw=dftmtx(10)*xn';%DFT 变换figure(1);%画出原序列的实部、虚部、模、相角subplot(2,2,1);stem(n,real(xn),'filled');xlabel('x');ylabel('real(xn)');title('xn 实部'); subplot(2,2,2);stem(n,imag(xn),'filled');xlabel('x');ylabel('imag(xn)');title('xn 虚部'); subplot(2,2,3);stem(n,abs(xn),'filled');xlabel('x');ylabel('abs(xn)');title('xn 模'); subplot(2,2,4);stem(n,angle(xn),'filled');xlabel('x');ylabel('angle(xn)');title('xn 相角'); figure(2);%画出频谱的幅度谱、频谱实部、频谱虚部subplot(3,1,1);stem(k,abs(xw),'filled');xlabel('k');ylabel('abs(xw)');title('幅度谱'); subplot(3,1,2);stem(k,real(xw),'filled');xlabel('k');ylabel('real(xw)');title('频谱实部'); subplot(3,1,3);stem(k,imag(xw),'filled');xlabel('k');ylabel('imag(xw)');title('频谱虚部');1-2. a=0.9, length=10 clc;clf;clear;%清除 n=0:9;%设置自变量区间 xn=(0.9).^n;%计算相应的x(n) k=0:9;%设置DFT 采样长度 xw=dftmtx(10)*xn';%DFT 变换figure(1);%画出原序列的实部、虚部、模、相角subplot(2,2,1);stem(n,real(xn),'filled');xlabel('n');ylabel('real(xn)');title('xn 实部'); subplot(2,2,2);stem(n,imag(xn),'filled');xlabel('n');ylabel('imag(xn)');title('xn 虚部');subplot(2,2,3);stem(n,abs(xn),'filled');xlabel('n');ylabel('abs(xn)');title('xn 模'); subplot(2,2,4);stem(n,angle(xn),'filled');xlabel('n');ylabel('angle(xn)');title('xn 相角'); figure(2);%画出频谱的幅度谱、频谱实部、频谱虚部subplot(3,1,1);stem(k,abs(xw),'filled');xlabel('k');ylabel('abs(xw)');title('幅度谱'); subplot(3,1,2);stem(k,real(xw),'filled');xlabel('k');ylabel('real(xw)');title('频谱实部'); subplot(3,1,3);stem(k,imag(xw),'filled');xlabel('k');ylabel('imag(xw)');title('频谱虚部');1-3. a=0.9, length=20 clc;clf;clear;%清除 n=0:19;%设置自变量区间 xn=(0.9).^n;%计算相应的x(n) k=0:19;%设置DFT 的采样长度 xw=dftmtx(20)*xn';%DFT 变换figure(1);%画出原序列的实部、虚部、模、相角subplot(2,2,1);stem(n,real(xn),'filled');xlabel('n');ylabel('real(xn)');title('xn 实部'); subplot(2,2,2);stem(n,imag(xn),'filled');xlabel('n');ylabel('imag(xn)');title('xn 虚部'); subplot(2,2,3);stem(n,abs(xn),'filled');xlabel('n');ylabel('abs(xn)');title('xn 模'); subplot(2,2,4);stem(n,angle(xn),'filled');xlabel('n');ylabel('angle(xn)');title('xn 相角'); figure(2);%画出频谱的幅度谱、频谱实部、频谱虚部subplot(3,1,1);stem(k,abs(xw),'filled');xlabel('k');ylabel('abs(xw)');title('幅度谱'); subplot(3,1,2);stem(k,real(xw),'filled');xlabel('k');ylabel('real(xw)');title('频谱实部'); subplot(3,1,3);stem(k,imag(xw),'filled');xlabel('k');ylabel('imag(xw)');title('频谱虚部');2.复指数序列⎩⎨⎧-≤≤+=otherwiselength n jb a n x n10)()(a=0.5, b=0.8, length=10clc;clf;clear;%清除 n=0:9;%设置自变量区间xn=(0.5+1j*0.8).^n;% 计算相应的x(n) k=0:9;%设置DFT 的采样长度 xw=dftmtx(10)*xn';% DFT 变换figure(1);%画出原序列的实部、虚部、模、相角subplot(2,2,1);stem(n,real(xn),'filled');xlabel('n');ylabel('real(xn)');title('xn 实部');subplot(2,2,3);stem(n,abs(xn),'filled');xlabel('n');ylabel('abs(xn)');title('xn模');subplot(2,2,4);stem(n,angle(xn),'filled');xlabel('n');ylabel('angle(xn)');title('xn相角');figure(2);%画出频谱的幅度谱、频谱实部、频谱虚部subplot(3,1,1);stem(k,abs(xw),'filled');xlabel('k');ylabel('abs(xw)');title('幅度谱');subplot(3,1,2);stem(k,real(xw),'filled');xlabel('k');ylabel('real(xw)');title('频谱实部');subplot(3,1,3);stem(k,imag(xw),'filled');xlabel('k');ylabel('imag(xw)');title('频谱虚部');3. 从正弦信号x(t)=sin(2πft+delta)抽样得到的正弦序列x(n)=sin(2πfnT+delta)。

数字信号处理中的离散傅里叶变换

数字信号处理中的离散傅里叶变换数字信号处理（Digital Signal Processing，简称DSP）是在数字计算机或数字信号处理器上对信号进行处理和分析的一种技术。

离散傅里叶变换（Discrete Fourier Transform，简称DFT）作为DSP中的重要方法之一，在信号处理的各个领域都发挥着重要的作用。

一、离散傅里叶变换的定义和原理离散傅里叶变换是将离散的时间域信号转换为频域信号的一种方法，它可以将信号从时域转换到频域进行分析。

DFT的定义如下：$X[k] = \sum_{n=0}^{N-1}x[n]e^{-j\frac{2\pi}{N}nk}$其中，$x[n]$为离散时间域信号，$X[k]$为离散频域信号，$N$为信号的长度，$k$为频域的索引。

离散傅里叶变换可以看作是对信号进行一系列的乘法和求和操作，它使用复指数函数作为基函数来表示信号。

通过将信号与不同频率的正弦波进行内积操作，可以得到信号在不同频率上的幅度和相位信息，从而实现频谱的分析。

二、离散傅里叶变换的性质离散傅里叶变换具有一些重要的性质，这些性质对于信号处理和频域分析非常有用。

以下是几个常见的性质：1. 线性性质：DFT是线性变换，即对两个信号的和进行DFT等于分别对这两个信号进行DFT后再求和。

2. 周期性：若信号的长度为$N$，则DFT系数$X[k]$具有周期性，周期为$N$。

3. 对称性：若信号的长度为$N$，则当$k$取$N-k$时，$X[k]$与$X[N-k]$相等。

4. 移位性质：对于一个时域序列$x[n]$，将其向右移动$m$个位置得到新的序列$x[n-m]$，则对应的DFT系数$X[k]$只需将原始的$X[k]$循环右移$m$个位置得到。

三、离散傅里叶变换的应用离散傅里叶变换在数字信号处理中有着广泛的应用，以下列举几个典型的应用场景：1. 信号分析：通过DFT可以将信号从时域转换到频域，得到信号在不同频率上的能量分布情况。

DSP知识点

DSP知识点第二章知识点1、系统的线性、时不变性、因果性、稳定性的判断2、线性卷积的计算3、系统的差分方程与单位取样响应的关系4、时域抽样定律第三章知识点1、Z 变换及收敛域的求解2、逆Z 变换求解（长除法和部分分式法）3、利用系统函数求解零、极点，判断系统的因果性和稳定性第四章知识点 1、周期卷积的计算 2、DFT 计算第五章知识点1、按时间抽取的基2 FFT 算法流图2、按频率抽取的基2 FFT 算法流图第六章知识点1、IIR 滤波器的直接型、级连型、并联型结构实现2、FIR 滤波器的横截型、级连型结构实现第七章知识点1、冲激响应不变法设计数字滤波器2、双线性变换法设计数字滤波器复习题集： 1、设x(n)和y(n)分别表示一个系统的输入和输出，试确定下列系统是否为（1）稳定系统（2）因果系统（3）线性系统（4）时不变系统：（1）y(n)=2x(n)+3 （2）y(n)=x(n)sin(wn) （3）y(n)=x 2(n) （4）y(n)=n 2x(n)2、图1中，)(n x 和)(n h 分别是线性时不变系统的输入和单位脉冲响应，试以图解法求解输出信号)(n y ，给出详细求解图形。

h (n ) x (n ) 0n-121 0.51 2 图 13 常系数差分方程)1(21)()(-+=n y n x n y（1）初始条件为n <0时，y (n )=0，求其单位脉冲响应；（2）初始条件为n ≥0时，y (n )=0，求其单位脉冲响应。

4、一个理想采样系统，采样间隔为25.0=T ，采样后经理想低通滤波器)(Ωj H 还原。

其中Ω≥Ω<Ω=Ω4||,04||,4/1)(πj H今有两个输入t t x a π2cos )(1=和t t x a π5cos )(2=，问输出信号)(1t y a ，)(2t y a 有没有失真？为什么？5、求出以下序列的Z 变换及收敛域。

（1）)(2n u n- （2）)1(2----n u n（3）)(2n u n-- （4）)(n δ（5）)1(-n δ （6）)]10()([2---n u n u n6、已知：112122113)(---+-=zz X求出对应)(z X 的各种可能的序列表达式。

DSP原理及应用第三章

直接寻址指令
15~8 7 6~0
操作码
I=0
dmad
堆栈指针SP
16位堆栈指针SP
SP+dmad
16位数据存储器地址 16位SP+dmad 高 9位
dmad
低 7位
15
DP地址的范围是从0~511(29-1)，将存储器分成 512页。 7 位 dmad 范围是从 0~127 ，每页有 128 个可以访问的单元。以DP为基准的直接寻址是由DP 值确定是 512 页中的哪一页，由dmad确定是该页中的哪一个单元。 SP 可以指向存储器中的任意一个地址。 dmad 可以指向当前页中具体的单元，从而允许访问存储器任意基地址中的连续的128个单元
循环寻址的有效地址计算
循环缓冲区的参数主要包括：长度寄存器（BK）、有效基地址（EFB）、尾地址（EOB）。 N>32, 则N=6。例如：缓冲区长度 R=32 , 若 2 BK:定义了循环缓冲区的大小R。大小为R的循环缓冲缓冲区开始的地址： xxxx xxxx xx00 0000 B 器其地址要始于最低 N位为零的地址。并且 R要满足下缓冲区长度 N>R 装入循环缓冲长度寄存器BK中。面的条件： 2R=32 EFB：循环缓冲器的有效基地址（EFB）就是用户选定的辅助寄存器（ARx）的低N位置 0后所得到的值。 EOB：是通过用BK的低N位代替ARx的低N位得到。
LD
*（BUFFER），A
9
绝对寻址总结
16位地址表示形式： ① 地址符号，如：TABLE； ② 16位数值，如：89AB、1234。特点：指令中包含一个固定的16位地址，能寻址所有数据、程序和I/O存储空间，但运行速度慢，需要较大的存储空间。用途：用于对速度要求较低的场合。

第3章1DFT的定义

定义为：
N 1
X (k) DFT[ x(n)] x(n) WNkn ,
n0
x(n)
IDFT[
X (k)]
1 N
N 1
X (k ) WNkn ,
k 0
式中：
WN
j2
e N
k 0,1,,N 1 n 0,1,,N 1
Ｎ是DFT变换区间长度；
3.1 离散傅立叶变换的定义
一、DFT的定义
2、说明
三、DFT的隐含周期性
1、周期延拓序列和主值序列
任意周期为N的周期序列 ~x(n) 都可以看作
长度为N的有限长序列 x(n) 的周期延拓序列，
而 x(n) 则是 ~x(n) 的一个周期，即：
~x (n)
x(n mN )
m
周期延拓序列
x(n) ~x (n) RN (n)
主值序列
3.1 离散傅立叶变换的定义
二、DFT的物理意义
比较可见：
X (k) X (e j ) 2k , k 0,1, , N 1 N
X (k) X (z) j2 k , k 0,1, , N 1 ze N
DFT的物理意义： ➢ 对有限长序列x(n)的N点DFT，相当于是对
X (e j )在(0~2π)区间上的N点等间隔采样； ➢ 对有限长序列x(n)的N点DFT，相当于是对
3.1 离散傅立叶变换的定义
三、DFT的隐含周期性
2、隐含周期性
➢ 由 WNkn的周期性得出
WNkn
W (kmN)n N
W k(nmN) N
N 1
N 1
X (k mN )
x(n)WN(k mN)n
x(n)W
kn N