图像平滑与锐化算法的分析与实现
数字图像处理- 图像平滑与锐化
数字图像处理
7
数字图像处理
8
巴特沃斯滤波器
通带波动下的切比雪夫滤波器
阻带波动下的切比雪夫滤波器
数字图像处理
椭圆函数滤波器
9
数字图像处理
10
数字图像处理
11
数字图像处理
12
数字图像处理
13
涉及4种图像初始、中间或最终结果，和三个主要 处理步骤。
图像结果包括原始图像、原始变换域、滤波后的变换域 和滤波后的图像； 处理步骤包括傅里叶正变换、低通滤波和傅lt; complex > CImageProcessing::Low_pass_filter( CTArray< complex > original_signal ) { long dimension = original_signal.GetDimension(); double threshold = 0; for( int index = 0; index < dimension; index ++ ) { double magnitude = sqrt( original_signal[ index ].m_re * original_signal[ index ].m_re + original_signal[ index ].m_im * original_signal[ index ].m_im ); if( magnitude > threshold ) threshold = magnitude; } threshold /= 100; for( int index = 0; index < dimension; index ++ ) { double magnitude = sqrt( original_signal[ index ].m_re * original_signal[ index ].m_re + original_signal[ index ].m_im * original_signal[ index ].m_im ); double eplon = 1.0 / sqrt( 1 + ( threshold / magnitude ) * ( threshold / magnitude ) ); original_signal[ index ].m_re *= eplon; original_signal[ index ].m_im *= eplon; } return original_signal; } 21 数字图像处理
图像锐化算法实现
算法原理：通过将图像分解成多个频带，对每个频带进行滤波处理，再合并处理后的频带得到 锐化图像。
算法特点：能够更好地保留图像细节，提高图像清晰度，适用于各种类型的图像。
算法步骤：频带分解、滤波处理、频带合并、锐化图像。
算法应用：广泛应用于图像处理领域，如医学影像、遥感图像、安全监控等。
算法原理：根据图像局部特性自适 应调整滤波器系数，以提高图像边 缘清晰度
优点：对噪声具有较好的鲁棒性， 能够自适应地处理不同场景下的图 像锐化
添加标题
添加标题
常用实现方法：Laplacian、 Unsharp Masking等
添加标题
添加标题
适用场景：适用于各种类型的图像， 尤其适用于存在噪声和模糊的图像
图像锐化的实现步 骤
将彩色图像转换为灰度图像 增强图像对比度 突出图像边缘信息 减少图像数据量，加速处理速度
边缘检测是图像 锐化的重要步骤， 通过检测图像中 的边缘信息，可 以对图像进行清 晰化处理。
常见的边缘检测 算法包括Sobel、 Prewitt、Canny 等，这些算法通 过不同的方式检 测图像中的边缘 信息。
在边缘检测之后， 通常需要进行阈 值处理，将边缘 信息与阈值进行 比较，保留重要 的边缘信息，去 除不必要的噪声。
经过边缘检测和 阈值处理后，可 以对图像进行锐 化处理，使其更 加清晰。
对图像进行滤波处理，去除噪声和干扰 选择合适的滤波器，如高斯滤波器、中值滤波器等 对滤波后的图像进行锐化处理，增强边缘和细节 可根据实际需求选择不同的滤波器和参数，以达到最佳效果
对图像进行滤波处理，去除噪声 对图像进行边缘检测，突出边缘信息 对图像进行对比度增强，提高图像的清晰度 对图像进行细节增强，增强图像的纹理和细节信息
《数字图像处理》课程教学大纲
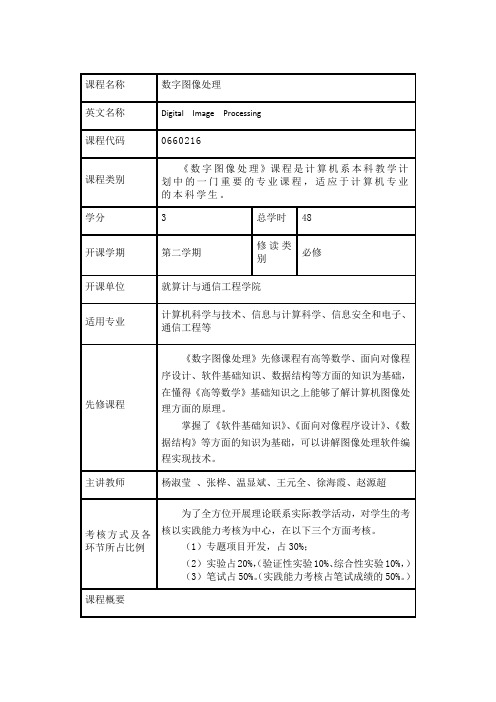
二、课程章节主要内容及学时分配第一章、数字图像处理方法概述讲课3课时了解本课程研究的对象、内容及其在培养软件编程高级人才中的地位、作用和任务；了解数字图像处理的应用；了解数字图像的基本概念、与设备相关的位图(DDB)、与设备无关的位图(DIB)；了解调色板的基本概念和应用；了解CDIB类与程序框架结构介绍；了解位图图像处理技术。
重点：CDIB类与程序框架结构介绍。
难点：调色板的基本概念和应用。
第二章、图像的特效显示讲课3课时、实验2学时了解扫描、移动、百叶窗、栅条、马赛克、渐显与渐隐、浮雕化特效显示。
重点：渐显与渐隐。
难点：马赛克。
第三章、图像的几何变换讲课2课时了解图像的缩放、平移、镜像变换、转置、旋转。
重点：镜像变换。
难点：旋转。
第四章、图像灰度变换讲课3课时、实验2学时了解非0元素取1法、固定阈值法、双固定阈值法的图像灰度变换；了解灰度的线性变换、窗口灰度变换处理、灰度拉伸、灰度直方图、灰度分布均衡化。
重点：灰度直方图。
难点：灰度分布均衡化。
第五章、图像的平滑处理讲课3课时了解二值图像的黑白点噪声滤波、消除孤立黑像素点、3*3均值滤波、N*N 均值滤波器、有选择的局部平均化、N*N中值滤波器、十字型中值滤波器、N*N最大值滤波器、产生噪声。
重点：消除孤立黑像素点、中值滤波器。
难点：有选择的局部平均化。
第六章、图像锐化处理及边缘检测讲课3课时、实验2学时了解梯度锐化、纵向微分运算、横向微分运算、双方向一次微分运算、二次微分运算、Roberts边缘检测算子、Sobel边缘检测算子、Krisch边缘检测、高斯-拉普拉斯算子。
重点：Roberts边缘检测算子、高斯-拉普拉斯算子。
难点：梯度锐化。
第七章、图像分割及测量讲课4课时了解图像域值分割、轮廓提取、轮廓跟踪、图像的测量。
重点：轮廓提取、轮廓跟踪。
难点：图像的测量。
包括：图像的区域标记、图像的面积测量及图像的周长测量。
第八章、图像的形态学处理讲课3课时了解图像腐蚀、图像的膨胀、图像开启与闭合、图像的细化、图像的粗化、中轴变化。
图像平滑与锐化处理
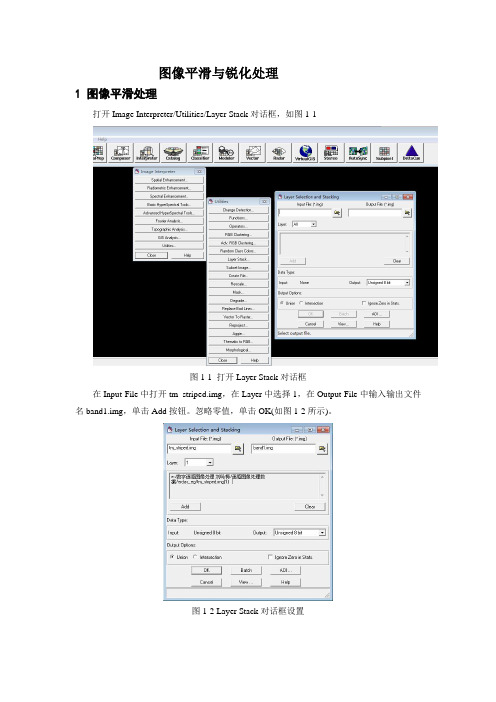
图像平滑与锐化处理1 图像平滑处理打开Image Interpreter/Utilities/Layer Stack对话框，如图1-1图1-1 打开Layer Stack对话框在Input File中打开tm_striped.img，在Layer中选择1，在Output File中输入输出文件名band1.img，单击Add按钮。
忽略零值，单击OK(如图1-2所示)。
图1-2 Layer Stack对话框设置打开Interpreter>Spatial Enhancement>Convolution对话框。
如图1-3图1-3 打开Convolution对话框在Input File中选择band1.img。
在Output File中选择输出的处理图像，命名为lowpass.img。
在Kernel中选择7*7Low Pass，忽略零值。
单击OK完成图像的增强处理（如图1-4所示）。
图1-4 卷积增强对话框（Convolution）平滑后的图像去掉噪音的同时造成了图像模糊，特别是对图像的边缘和细节消弱很多。
而且随着邻域范围的扩大，在去噪能力增强的同时模糊程度越严重（如图1-5）。
图1-5 处理前后的对比为了保留图像的边缘和细节信息，可对上述算法进行改进，引入阈值T，将原有图像灰度值f（i，j）,和平均值g（i，j）之差的绝对值与选定的阈值进行比较，根据比较结果决定像元（i，j）的最后灰度值G（i，j）。
当差小于阈值的时候取原值；差大于阈值的时候取平均值。
这里通过查询得T取4，其表达式为下：g（i，j），当| f（i，j）-g（i，j）|>4G（i，j）=f（i，j），当| f（i，j）-g（i，j）|<=4具体操作步骤：在图标控制面板工具栏中点击空间建模Modeler>Model Maker选项。
先放置对象图形，依次连接每个对象图形，然后定义对象，最后定义函数并运行模型（如图1-6，1-7,1-8,1-9,1-10,1-11所示）。
浅谈图像平滑滤波和锐化的区别及用途总结
浅谈图像平滑滤波和锐化的区别及⽤途总结空域滤波技术根据功能主要分为与滤波。
能减弱或消除图像中的⾼频率分量⽽不影响低频分量，⾼频分量对应图像中的区域边缘等值具有较⼤变化的部分，可将这些分量滤去减少局部起伏，使图像变得⽐较平滑。
也可⽤于消除噪声，或在提取较⼤⽬标前去除太⼩的细节或将⽬标的⼩间断连接起来。
滤波正好相反，滤波常⽤于增强被模糊的细节或⽬标的边缘，强化图像的细节。
⼀、基本的灰度变换函数1.1.图像反转适⽤场景：增强嵌⼊在⼀幅图像的暗区域中的⽩⾊或灰⾊细节，特别是当⿊⾊的⾯积在尺⼨上占主导地位的时候。
1.2.对数变换（反对数变换与其相反）过程：将输⼊中范围较窄的低灰度值映射为输出中较宽范围的灰度值。
⽤处：⽤来扩展图像中暗像素的值，同时压缩更⾼灰度级的值。
特征：压缩像素值变化较⼤的图像的动态范围。
举例：处理傅⾥叶频谱，频谱中的低值往往观察不到，对数变换之后细节更加丰富。
1.3.幂律变换（⼜名：伽马变换）过程：将窄范围的暗⾊输⼊值映射为较宽范围的输出值。
⽤处：伽马校正可以校正幂律响应现象，常⽤于在计算机屏幕上精确地显⽰图像，可进⾏对⽐度和可辨细节的加强。
1.4.分段线性变换函数缺点：技术说明需要⽤户输⼊。
优点：形式可以是任意复杂的。
1.4.1.对⽐度拉伸：扩展图像的动态范围。
1.4.2.灰度级分层：可以产⽣⼆值图像，研究造影剂的流动。
1.4.3.⽐特平⾯分层：原图像中任意⼀个像素的值，都可以类似的由这些⽐特平⾯对应的⼆进制像素值来重建，可⽤于压缩图⽚。
1.5.直⽅图处理1.5.1直⽅图均衡：增强对⽐度，补偿图像在视觉上难以区分灰度级的差别。
作为⾃适应对⽐度增强⼯具，功能强⼤。
1.5.2直⽅图匹配（直⽅图规定化）：希望处理后的图像具有规定的直⽅图形状。
在直⽅图均衡的基础上规定化，有利于解决像素集中于灰度级暗端的图像。
1.5.3局部直⽅图处理：⽤于增强⼩区域的细节，⽅法是以图像中的每个像素邻域中的灰度分布为基础设计变换函数，可⽤于显⽰全局直⽅图均衡化不⾜以影响的细节的显⽰。
数字图像处理图像变换实验报告
实验报告实验名称:图像处理姓名:刘强班级:电信1102学号:1404110128实验一图像变换实验——图像点运算、几何变换及正交变换一、实验条件PC机数字图像处理实验教学软件大量样图二、实验目的1、学习使用“数字图像处理实验教学软件系统”,能够进行图像处理方面的简单操作;2、熟悉图像点运算、几何变换及正交变换的基本原理,了解编程实现的具体步骤;3、观察图像的灰度直方图,明确直方图的作用与意义;4、观察图像点运算与几何变换的结果,比较不同参数条件下的变换效果;5、观察图像正交变换的结果,明确图像的空间频率分布情况。
三、实验原理1、图像灰度直方图、点运算与几何变换的基本原理及编程实现步骤图像灰度直方图就是数字图像处理中一个最简单、最有用的工具,它描述了一幅图像的灰度分布情况,为图像的相关处理操作提供了基本信息。
图像点运算就是一种简单而重要的处理技术,它能让用户改变图像数据占据的灰度范围。
点运算可以瞧作就是“从象素到象素”的复制操作,而这种复制操作就是通过灰度变换函数实现的。
如果输入图像为A(x,y),输出图像为B(x,y),则点运算可以表示为:B(x,y)＝f[A(x,y)]其中f(x)被称为灰度变换(Gray Scale Transformation,GST)函数,它描述了输入灰度值与输出灰度值之间的转换关系。
一旦灰度变换函数确定,该点运算就完全确定下来了。
另外,点运算处理将改变图像的灰度直方图分布。
点运算又被称为对比度增强、对比度拉伸或灰度变换。
点运算一般包括灰度的线性变换、阈值变换、窗口变换、灰度拉伸与均衡等。
图像几何变换就是图像的一种基本变换,通常包括图像镜像变换、图像转置、图像平移、图像缩放与图像旋转等,其理论基础主要就是一些矩阵运算,详细原理可以参考有关书籍。
实验系统提供了图像灰度直方图、点运算与几何变换相关内容的文字说明,用户在操作过程中可以参考。
下面以图像点运算中的阈值变换为例给出编程实现的程序流程图,如下:2、图像正交变换的基本原理及编程实现步骤数字图像的处理方法主要有空域法与频域法,点运算与几何变换属于空域法。
数字图像处理[图像锐化]
![数字图像处理[图像锐化]](https://img.taocdn.com/s3/m/e9eb2348df80d4d8d15abe23482fb4daa48d1d54.png)
上机参考程序2
I=imread('cameraman.tif'); subplot(2,2,1);imshow(I);title('original'); K=fspecial('laplacian',0.7);K1=filter2(K,I)/100; subplot(2,2,2);imshow(K1);title('laplacian'); L=fspecial('sobel');L1=filter2(L,I)/200; subplot(2,2,3);imshow(L1);title('sobel'); M=fspecial('prewitt');M1=filter2(M,I)/200; subplot(2,2,4);imshow(L1);title('prewitt');
灰度截面 一阶微分
二阶微分
(a) 阶跃形
(b) 细线形
(c) 斜坡渐变形
二阶微分锐化
—— 景物细节对应关系
1）对于突变形的细节，通过一阶微分的极大 值点，二阶微分的过0点均可以检测出来。
二阶微分锐化
—— 景物细节对应关系
2）对于细线形的细节，通过一阶微分的过0 点，二阶微分的极小值点均可以检测出来。
0
0
1 2 1
1*1+2*2+1*3-1*3-2*0-1*8=-3
12321 21262 30876 12786 23269
00 0 0 0 0 -3 -13 -20 0 0 -6 -13 -13 0 0 1 12 5 0 00 0 00
问题：计算结果中出现了小于零的像素值
7种锐化方法原理与实现
7种锐化方法原理与实现
1. Laplacian锐化：该方法是通过对图像进行二阶微分操作来
增强图像的高频信息。
具体实现可以通过先计算图像的拉普拉斯算子，然后将其与原始图像进行加权叠加得到锐化后的图像。
2. 高斯锐化：该方法是通过将原始图像与经过高斯滤波的图像相减得到锐化后的图像。
高斯滤波可以减少图像的高频噪声，相减操作可以增强图像的边缘信息。
3. Unsharp Masking锐化：该方法是通过先对原始图像进行模
糊操作，然后将模糊后的图像与原始图像进行相减得到细节信息。
最后将细节信息与原始图像进行加权叠加得到锐化后的图像。
4. 锐化滤波器：该方法是通过设计特定的锐化滤波器来增强图像的边缘信息。
常用的锐化滤波器有Sobel、Prewitt、Robert 等，它们通过计算图像的梯度来增强边缘信息。
5. 平滑锐化：该方法是通过先对原始图像进行平滑操作，然后将平滑后的图像与原始图像进行相减或相加得到锐化后的图像。
平滑操作可以减少图像的噪声，相减或相加操作可以增强图像的边缘信息。
6. 均值锐化：该方法是通过先对原始图像进行均值滤波操作，然后将滤波后的图像与原始图像进行相减得到锐化后的图像。
均值滤波会模糊图像的细节信息，相减操作可以增强图像的边缘信息。
7. 锐化掩模：该方法是通过设计特定的锐化掩模来增强图像的边缘信息。
锐化掩模可以通过卷积操作实现，它将图像的像素值与周围像素值进行计算，从而增强边缘信息。
数字图像处理实验三图像滤波实验(模板运算)
实验三图像滤波实验（模板运算）一．实验目的：模板运算是空间域图象增强的方法，也叫模板卷积。
（1）平滑：平滑的目的是模糊和消除噪声。
平滑是用低通滤波器来完成，在空域中全是正值。
（2）锐化：锐化的目的是增强被模糊的细节。
锐化是用高通滤波器来完成，在空域中，接近原点处为正，在远离原点处为负。
二．实验内容：（1）利用线性空间滤波（均值滤波）对一幅图象进行平滑，验证模板尺寸和滤波参数对图象的模糊效果的影响。
（2）利用非线性空间滤波器（中值滤波）对一幅噪声图象（椒盐噪声）进行平滑去噪，同时检验两种滤波模板（分别使用一个5×5的线性邻域平均模板和一个非线性模板：3×3中值滤波器）对噪声的滤波效果。
（3）利用线性空间滤波器，对灰度图象分别利用二阶标准Laplacian算子和对角线Laplacian算子对其进行锐化操作，增强图像边缘，验证检测效果。
三．实验原理：1．用31×31均值滤波模板，并分别采用参数boundary_options默认值和‘replicate’对图像test_pattern进行平滑处理；用3×3，5×5，7×7均值滤波模板对图像lena平滑处理，观察不同参数、不同模板尺寸对滤波效果的影响。
1．线性空间滤波函数imfilter来实现线性空间滤波，语法为：g = imfilter(f, w, filtering_mode, boundary_options, size_options)其中，f是输入图像，w为滤波模板，g为滤波结果，filtering_mode用于指定在滤波过程中是使用相关运算(‘corr’)还是卷积运算(‘conv’)，相关就是按模板在图像上逐步移动运算的过程，卷积则是先将模板旋转180度，再在图像上逐步移动的过程，显然，若模板中心对称，则相关和卷积运算是相同操作，默认为相关运算；boundary_options用于处理边界充零问题，默认为赋零，若该参数为’replicate’表示输出图像边界通过复制原图像边界的值来扩展；size_options可以是’full’或’same’，默认为’same’，表示输出图像与输入图像的大小相同。
数字图像处理复习资料
一、填空题（每空1分，共10分）填空题主要是一些常见知识。
三、论述题（每小题8分，共40分）下面的内容包括简答和论述题的部分1.简述线性位移不变系统逆滤波恢复图像原理。
答：设退化图象为g(x,y)，其傅立叶变换为G(u,v),若已知逆滤波器为1/H(u,v)则对G(u,v)作逆滤波得F(u,v)=G(u,v)/H(u,v) （2分）对上式作逆傅立叶变换得逆滤波恢复图象f(x,y)f(x,y)=IDFT[F(u,v)]以上就是逆滤波恢复图象的原理。
（2分）若存在噪声，为避免H(u,v)=0,可采用两种方法处理。
（0.5分）①在H(u,v)=0时,人为设置1/H(u,v)的值；②使1/H(u,v)具有低同性质。
即H-1(u,v)=1/H(u,v) 当D≤DH-1(u,v)=0 当D>D(0.5分)2.直方图均衡化。
如果对一幅图像已经用直方图均衡化方法进行了处理，那么对处理后的图像再次应用直方图均衡化，处理结果会不会更好？答：1. 直方图均衡化的基本思想是对原始图像中的像素灰度图做某种映射变换，使变换后图像灰度的概率密度是均匀分布的，即变换后图像是一幅灰度级均匀分布的图像，这意味着图像灰度的动态范围得到了增加，从而可提高图像的对比度。
2.处理结果与处理前结果大致相同,没有太大的变化,只是平均值稍有所变。
3. 图像锐化与图像平滑有何区别与联系？答：区别：图象锐化是用于增强边缘，导致高频分量增强，会使图象清晰；（2分）图象平滑用于去噪，对图象高频分量即图象边缘会有影响。
（2分）联系：都属于图象增强，改善图象效果。
（1分）4.什么是中值滤波，有何特点？答：中值滤波法是一种非线性平滑技术，它将每一象素点的灰度值设置为该点某邻域窗口内的所有象素点灰度值的中值.中值滤波是非线性的处理方法，在去噪的同时可以兼顾到边界信息的保留。
中值滤波首先选一个含有奇数点的窗口W，将这个窗口在图像上扫描，把该窗口中所含的像素点按灰度级的升（或降）序排列，取位于中间的灰度值，来代替该点的灰度值。
图像平滑与图像锐化
图像平滑与图像锐化邻域运算,一阶微分算子,二阶拉普拉斯算子,卷积模板,,3某3的模板,均值滤波,高斯噪声,椒盐噪声,中值滤波程序,均值滤波,模板尺寸邻域运算一、实验目的1.巩固对图像增强的认识，明确图像空域处理的类型2.理解图像平滑与图像锐化的概念3.掌握图像模板卷积运算的实现方法4.锻炼编程开发图像处理算法的能力二、实验准备1.了解图像处理点运算和邻域运算的区别2.学习利用模板卷积的方法进行图像邻域运算3.复习均值滤波和中值滤波的原理4.列出常用的模板形式，思考中值滤波要用到的简单排序方法5.分析对比图像平滑和图像锐化模板的差异三、实验内容与步骤1.列出常用的卷积模板2.基于3某3的模板，编写均值滤波的处理程序，处理含有加性高斯噪声和椒盐噪声的图像，观察处理结果3.编写中值滤波程序，处理相同的图像与均值滤波进行比较；改变模板尺寸观察处理结果4.编程实现利用一阶微分算子和二阶拉普拉斯算子进行图像锐化的程序5.对比不同的邻域运算结果，体会图像锐化与图像平滑的区别四、实验报告与思考题1.总结实验内容及步骤方法完成实验报告，报告中要求有关键代码的注释说明及程序运行和图像处理结果2.实验报告中回答以下问题(1)均值滤波和中值滤波分别适用于处理哪类图像？(2)图像平滑和图像锐化所采用的模板有什么不同？(3)邻域运算的模板尺寸对处理结果有什么影响？邻域运算,一阶微分算子,二阶拉普拉斯算子,卷积模板,,3某3的模板,均值滤波,高斯噪声,椒盐噪声,中值滤波程序,均值滤波,模板尺寸实验4邻域运算,一阶微分算子,二阶拉普拉斯算子,卷积模板,,3某3的模板,均值滤波,高斯噪声,椒盐噪声,中值滤波程序,均值滤波,模板尺寸。
图像的锐化与平滑同一检查的多序列图像同步对比
第四部分：MR 工作站软件操作系统（4 套）技术要求 支持 DICOM 3.0 和 HL7 标准。 提供所投产品的 DICOM 及 IHE Conformance Statement. 遵循 IHE 规范 兼容放射科内所有影像检查的信息录入、查询管理 支持与医院所有 DICOM 和非 DICOM 影像设备的连接，包括 CT、MR、CR、DR、RF、DSA、 PET、US、ES 等所有医疗影像设备 支持 DICOM 存储服务 Storage Commitment SCU/SCP，确保影像资料传送的正确性与完整性 支持 DICOM 传送与接收 支持 DICOM RAW DATA、DICOM Part 10、DICOM JPEG‐Lossless、DICOM JPEG‐Lossy、BMP、JPG 等影像类型 对于非 DICOM 标准的影像可以通过 DICOM GATEWAY 的方式，进行图像格式的转换 可直接导入所有符合 DICOM3.0 标准的影像数据 支持纠正病人的相关信息 同一病人影像合并归档 支持采用集中式数据库及独立影像储存管理机制， 记录所有影像的储存位置， 支持影像的分 级存储和在线扩容 可根据用户的需求，设置存储设备的影像删除策略。在删除影像前需要确认影像已经备份， 影像删除恢复功能 *支持双显示器、三显示器 可以方便查看当前的工作状况 窗宽窗位的调整；预设值窗宽窗位值，并可自定义设置；快捷键调窗 双击放大显示，再次双击还原 多平面重建 可以复制已打开的图像进行对比显示 具有平铺显示、堆叠显示、MPR 显示等多种图像显示模式 支持多种图像选择模式：行选、列选、同一检查、同一序列、同一图像；支持通过键盘 Shift、 Ctrl 进行多选； 支持多种显示格式。可以设置默认的显示格式，并可以自定义显示格式； 支持多种对比格式。可以设置默认的对比格式，并可以自定义对比格式； 支持多种图像导航模式：上一检查、下一检查、 上一页、下一页、滚轮、键盘翻页键、滚 动条 图像还原：还原全部、还原位置、还原镜像、还原窗值、还原旋转 图像处理：无级缩放、漫游、放大镜、左右镜像、上下镜像、旋转 180 度、顺时针旋转、逆 时针旋转 标准测量：文字、直线、箭头、自由曲线、矩形、圆形、多边形 支持添加删除定位线，可以按序列添加； 电影回放：播放控制、播放速度、播放模式：正向，逆向，循环，震荡 伪彩：添加伪彩；还原为灰度显示；支持多套伪彩编码 *ROI 分析：对矩形、圆形、任意多边形区域进行分析：最大值、最小值、平均值、标准方 差、面积、周长等 心胸比值测量 *角度、COBB 角测量 *GAMMA 校正
(完整版)实验-灰度图像的锐化处理
实验五灰度图像的锐化处理一、实验目的1．了解图像锐化的基本原理；2．掌握图像空域锐化处理的方法；3．利用VC编写图像空域锐化处理的程序；4．在微机上调试程序。
二、实验原理图像平滑处理可以减弱噪声的影响，但窗口增大后将会产生图像边缘不清的问题。
图像在传输和转换过程中，一般来讲，质量都会降低，除了噪声的因素之外，图像一般都要变得模糊一些，这主要因为图像的传输或转换系统的传递函数对高频成分的衰减作用，造成图像的细节轮廓不清晰。
图像锐化的作用就是补偿图像的轮廓，增强图像的边缘级灰度跳变部分，使图像较清晰。
图像锐化是一种能加强图像轮廓的处理方法，因此，从增强的目的来看它是与图像平滑相反的一类处理，图像锐化同样也可分为频域和空域处理两类实现方法。
本实验要求完成空域中图像的锐化处理。
1．图像空域锐化处理的方法微分处理可加强高频成分，例如对正弦信号sin(Nx)，其微分为余弦函数Ncos(Nx)，经微分处理后，信号的频率不变，幅度增大N倍，且频率越高，增幅越大。
对图像进行微分处理后：∆f/∆xG[(x,y)]=∆f/∆yG[(x,y)]是点(x,y)的梯度，其方向指向f(x,y)最大变化方向。
对连续图像：G[(x,y)]=[（∆f/∆x）2+（∆f/∆y）2]1/2对离散图像：G[(x,y)]常采用下列几种算法：（1）典型的差分算法G[(x,y)]=[[f(x,y)-f(x+1,y)]2+[f(x,y)-f(x,y+1)]2]1/2（2）罗伯茨算法G[(x,y)]=[[f(x,y)-f(x+1,y+1)]2+[f(x+1,y)-f(x,y+1)]2]1/2（3）绝对差算法相对于典型的差分算法和罗伯茨算法有：G[(x,y)]=|f(x,y)-f(x+1,y)|+|f(x,y)-f(x,y+1)|G[(x,y)]=|f(x,y)-f(x+1,y+1)|+|f(x+1,y)-f(x,y+1)|在实际处理一幅图像时，最后一行（列）梯度的值一般可以用前一行（列）的梯度的值来代替。
锐化滤波和平滑滤波
锐化滤波和平滑滤波锐化滤波和平滑滤波是数字图像处理中常用的两种滤波方法。
它们可以用来提高图像质量、减少噪声或者改变图像外观。
本文将详细介绍这两种滤波方法的原理和应用。
一、锐化滤波锐化滤波是一种增强图像细节和边缘的方法。
它是通过加强图像的高频部分来实现的。
在数字图像中，高频部分指的是像素值变化幅度较大的区域，也就是图像中的边缘和细节。
我们可以使用一些特定的算子来实现锐化滤波。
这些算子一般被称为锐化滤波器或者边缘增强算子。
常见的锐化滤波器包括拉普拉斯算子、索贝尔算子、普瑞瓦特算子等。
这些算子可以通过卷积运算来实现。
卷积运算是指将一个算子和图像中的每一个像素做乘积，并将相邻像素的乘积相加。
具体来说，假设我们需要使用一个3x3的拉普拉斯算子：0 101 -4 10 10对一个灰度图像进行锐化滤波。
我们需要将该算子与图像中的每一个像素进行卷积运算。
运算公式为：f(x,y) = ∑g(i,j)h(x-i,y-j)其中，f(x,y)表示卷积运算后的像素值，g(i,j)表示图像中位置为(i,j)的像素值，h(i,j)表示拉普拉斯算子中位置为(i,j)的元素值。
在运用锐化滤波器时需要注意，过强的锐化可能会使图像出现噪点。
此外，图像中一些边缘和细节可能会被误认为噪声而被消除，从而使图像质量降低。
二、平滑滤波平滑滤波又称为模糊滤波，是一种减少图像噪声和平滑图像细节的方法。
它是通过对图像进行低频滤波来实现的。
低频部分指的是像素值变化比较缓慢或者连续性比较强的区域，也就是图像中的平滑区域或者背景。
我们可以使用一些特定的算子来实现平滑滤波。
这些算子一般被称为平滑滤波器或者模糊滤波器。
常见的平滑滤波器包括均值滤波器、中值滤波器、高斯滤波器等。
这些滤波器也可以通过卷积运算来实现。
均值滤波器就是最简单的平滑滤波器之一。
它是将像素周围的值取平均数，用平均值来代替该像素的值。
假设我们需要使用一个3x3的均值滤波器：1 1 11 1 11 1 1对一个灰度图像进行平滑滤波。
图像的拉普拉斯锐化方法及讨论
图像的拉普拉斯锐化方法及讨论摘要：本文讲述了空域锐化中常用的二阶微分算法——拉普拉斯算子法。
全文首先对拉普拉斯运算做了简单的描述，并简明地分析了其原理：通常是将原图像和对他实施拉式算子后的结果组合后产生一个锐化图像。
然后对其在数字图像处理方面进行举例分析，并编程实现锐化效果。
最后对实验结果进行分析与讨论，说明其在图像处理应用方面，特别是用来改善因扩散效应的模糊方面特别有效。
关键字：图像处理二阶微分锐化拉普拉斯锐化1.引言图象在传输和转换过程中，一般情况下质量都要降低，除了加入了噪声的因素之外，图象还要变得模糊一些。
这主要因为图象的传输或转换系统的传递函数对高频成分的衰减作用，造成图象的细节和轮廓不清晰。
图象锐化就是加强图象中景物的细节和轮廓，使图象变得较清晰。
在数字图象中，细节和轮廓就是灰度突变的地方。
我们知道，灰度突变在频城中代表了一种高频分量，如果使图象信号经历一个使高频分量得以加强的滤波器，就可以达到减少图象中的模糊，加强图象的细节和轮廓的目的。
可以看出，锐化恰好是一个与平滑相反的过程。
我们使用对象素及其邻域进行加权平均，也就是用积分的方法实现了图象的平滑；反过来，应当可以利用微分来锐化一个图象。
2.理论和方法拉式算子是一个刻画图像灰度的二阶商算子，它是点、线、边界提取算子，亦称为边界提取算子。
通常图像和对他实施拉式算子后的结果组合后产生一个锐化图像。
拉式算子用来改善因扩散效应的模糊特别有效，因为它符合降制模型。
扩散效应是成像过程中经常发生的现象。
拉普拉斯算子也是最简单的各向同性微分算子，具有旋转不变性。
一个二维图像函数的拉普拉斯变换是各向同性的二阶导数，定义为：[),(4,()1,(),1(),1(),(2)1,()1,(),(),(2),1(),1(),(2222222222y x f y x f y x f y x f y x f f y x f y x f y x f yy x f y x f y x f y x f xy x f y f x f f --+++-++=∇--++=∂∂--++=∂∂∂∂+∂∂=∇为了更适合于数字图像处理，将拉式算子表示为离散形式：另外，拉普拉斯算子还可以表示成模板的形式，如下图(1)所示，为离散拉普拉斯算子的模板，图(2)表示其扩展模板。
实验三图像的平滑与锐化
实验三 图像的平滑与锐化一．实验目的1.掌握图像滤波的基本定义及目的；2.理解空域滤波的基本原理及方法；3.掌握进行图像的空域滤波的方法。
二．实验基本原理图像噪声从统计特性可分为平稳噪声和非平稳噪声两种。
统计特性不随时间变化的噪声称为平稳噪声；统计特性随时间变化的噪声称为非平稳噪声。
另外，按噪声和信号之间的关系可分为加性噪声和乘性噪声。
假定信号为S (t )，噪声为n (t )，如果混合叠加波形是S (t )+n (t )形式，则称其为加性噪声；如果叠加波形为S (t )［1+n (t )］形式， 则称其为乘性噪声。
为了分析处理方便，往往将乘性噪声近似认为加性噪声，而且总是假定信号和噪声是互相独立的。
1.均值滤波均值滤波是在空间域对图像进行平滑处理的一种方法，易于实现，效果也挺好。
设噪声η(m,n)是加性噪声，其均值为0，方差（噪声功率）为2σ，而且噪声与图像f(m,n)不相关。
除了对噪声有上述假定之外，该算法还基于这样一种假设：图像是由许多灰度值相近的小块组成。
这个假设大体上反映了许多图像的结构特征。
∑∈=s j i j i f M y x g ),(),(1),( (3-1)式(2-1)表达的算法是由某像素领域内各点灰度值的平均值来代替该像素原来的灰度值。
可用模块反映领域平均算法的特征。
对模板沿水平和垂直两个方向逐点移动，相当于用这样一个模块与图像进行卷积运算，从而平滑了整幅图像。
模版内各系数和为1，用这样的模板处理常数图像时，图像没有变化；对一般图像处理后，整幅图像灰度的平均值可不变。
(a) 原始图像 (b) 邻域平均后的结果图3-1 图像的领域平均法2.中值滤波中值滤波是一种非线性处理技术，能抑制图像中的噪声。
它是基于图像的这样一种特性：噪声往往以孤立的点的形式出现，这些点对应的象素很少，而图像则是由像素数较多、面积较大的小块构成。
在一维的情况下，中值滤波器是一个含有奇数个像素的窗口。
数字图像处理简答题及答案.
数字图像处理简答题及答案简答题1、数字图像处理的主要研究内容包含很多方面，请列出并简述其中的4种。
2、什么是图像识别与理解？3、简述数字图像处理的至少3种主要研究内容。
4、简述数字图像处理的至少4种应用。
5、简述图像几何变换与图像变换的区别。
6、图像的数字化包含哪些步骤？简述这些步骤。
7、图像量化时，如果量化级比较小会出现什么现象？为什么？8、简述二值图像与彩色图像的区别。
9、简述二值图像与灰度图像的区别。
10、简述灰度图像与彩色图像的区别。
11、简述直角坐标系中图像旋转的过程。
12、如何解决直角坐标系中图像旋转过程中产生的图像空穴问题？13、举例说明使用邻近行插值法进行空穴填充的过程。
14、举例说明使用均值插值法进行空穴填充的过程。
15、均值滤波器对高斯噪声的滤波效果如何？试分析其中的原因。
16、简述均值滤波器对椒盐噪声的滤波原理，并进行效果分析。
17、中值滤波器对椒盐噪声的滤波效果如何？试分析其中的原因。
18、使用中值滤波器对高斯噪声和椒盐噪声的滤波结果相同吗？为什么会出现这种现象？19、使用均值滤波器对高斯噪声和椒盐噪声的滤波结果相同吗？为什么会出现这种现象？20、写出腐蚀运算的处理过程。
21、写出膨胀运算的处理过程。
22、为什么YUV表色系适用于彩色电视的颜色表示？23、简述白平衡方法的主要原理。
24、YUV表色系的优点是什么？25、请简述快速傅里叶变换的原理。
26、傅里叶变换在图像处理中有着广泛的应用，请简述其在图像的高通滤波中的应用原理。
27、傅里叶变换在图像处理中有着广泛的应用，请简述其在图像的低通滤波中的应用原理。
28、小波变换在图像处理中有着广泛的应用，请简述其在图像的压缩中的应用原理。
29、什么是图像的无损压缩？给出2种无损压缩算法。
2、对于扫描结果：aaaabbbccdeeeeefffffff，若对其进行霍夫曼编码之后的结果是：f=01e=11 a=10 b=001 c=0001 d=0000。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
目录第一章引言 (1)1.1 课题研究的目的 (1)1.2 课题研究的可行性分析 (1)第二章基本理论 (2)2.1 傅立叶变换 (2)2.1.1 二维的傅立叶变换基本原理 (2)2.1.2 离散的傅立叶变换 (2)2.1.3 快速傅立叶变换 (2)2.2 卷积定理 (4)2.2.1 卷积定理的基本理论 (4)2.2.2 卷积定理与二维的傅立叶变换 (4)第三章图像 (5)3.1 图像类型 (5)3.2 图像噪声 (5)第四章图像平滑 (7)4.1 图像平滑的基本概述 (7)4.2 图像平滑的基本方法 (7)4.2.1 线性滤波（领域平均法） (7)4.2.2 中值滤波 (8)第五章图像锐化 (9)5.1 图像锐化的基本概述 (9)5.2 图像锐化的基本方法 (9)5.2.1 微分算子法 (9)5.2.2 拉氏算子 (9)第六章图像平滑和锐化的实现 (12)6.1 图像处理程序设计的思路 (12)6.2 图像处理程序设计的图形界面 (12)6.3 图像处理程序设计的实现 (13)结论 (15)致谢 (16)参考文献： (17)附录： (18)图像平滑与锐化算法的分析与实现宋卫，数学计算机科学学院摘要：随着互联网技术和多媒体技术的发展，越来越多的可视化信息的应用得到了人们的重视。
图像作为一个信息载体中最基础的一部分，在数据结构、互联网应用、数据压缩、通信工程等领域得到广泛的应用。
然而，在采集、传递、分析和数据挖掘中往往会因为分析或者应用的需要对其进行加工性的处理。
由于在处理图像时存在着主观因素而导致的差异性需求，图像的处理方式多种多样。
在众多的处理方法中，图像平滑和图像锐化是最常使用的处理方法。
关键词：图像处理算法；图像平滑；图像锐化；MA TLABAnalysis and Realization of Algorithm of Image Smoothing andSharpeningSong Wei, School of Mathematics and Computer ScienceAbstract：With the development of internet technology and multimedia technology, more and more visual information of the application of the attention. Image as the most basic part of an information carrier, data structures, internet applications, data compression, communications engineering and other fields has been widely used. However, often in the collection, transmission, analysis and data mining, application or analysis needs its processing and handling. Differences in demand caused by the existence of subjective factors in the image processing, image processing a variety of ways. Processing method, image smoothing and image sharpening to any of the most commonly used approach.Key words：image processing algorithm; image smoothing; image sharpening; MATLAB第一章引言1.1 课题研究的目的由于现阶段，随着科技的发展，计算机技术的应用已经渗透到社会的方方面面，而与图像有关的通信、网络、传媒、多媒体等已经给人们的生活带来巨大的变化。
放观长远，图像技术将在未来的很长一段时间内，影响着计算机应用的各个领域。
因此，探究图像处理技术对今后计算机图像处理的发展有着很好的前瞻作用，也为图像处理的技术创新在以后提供理论上的支持。
图像平滑和图像锐化作为图像处理中比较基础且尤为重要的基本方式，在今后的数字化的信息时代中仍然会有广泛的用处。
作为基本的图像处理，在数字技术应用的许多方面都有需要的地方，无论是计算机，还是微电子、通信工程、嵌入式系统、传感技术都有着十分重要的地位。
1.2 课题研究的可行性分析首先，图像处理的平滑算法和锐化算法在理论上是可行的。
而且目前两种图像处理的常用方法有很多。
就图像平滑处理而言，常见的算法邻域平均法，加权平均法，中值滤波，掩膜平滑法等。
而图像锐化的目的主要是加强图像中的目标边界和图像的细节，以增强图像的质量。
常见的算法有微分算子方法，索贝尔（Sobel）算子，空间高通滤波等。
再者，两种算法在技术上实现是可行的，MATLAB本身是一款数学专业者使用的软件，其本身自带了许多的数学函数，大大减缓的程序设计的压力。
同时，MATLAB在使用的时候，本身的语言比较简单，而且程序设计语言语法十分通俗，对于计算机专业的本科生来说，用起来应该是得心应手的。
在使用MATLAB 的时候，很多在VC和Java环境下需要复杂构写的数学函数，被MATLAB自带的函数库给取代了，大幅度简化的程序设计的时间以及对程序的测试和修改。
最后，图像处理可以在MATLAB这个有着完整界面化程序设计的软件下完成，其被设计的程序拥有比较良好的图形界面和人机交互功能，在这个良好的前提下，算法的实现将会比其他的编程软件好用的多。
第二章 基本理论2.1 傅立叶变换2.1.1 二维的傅立叶变换基本原理傅立叶变化的定义如下：()()mj mj n m een m f F 2121,,ωωωω--∞-∞=∞-∞=∑∑= (2.1)式中，1ω和2ω为变频变量，其单位为弧度每采样单元。
通常函数()21,ωωF 称为函数()n m f ,的频域表征。
()21,ωωF 是复变函数，其变量1ω和2ω的周期均为π2。
因为这种周期性的存在，所以通常在图像显示时，这两个变量额取值范围为πωωπ≤≤-21,。
反傅立叶逆变换的定义如下： ()()⎰⎰--=ππωωππωωωωπ212121,41,d d eeF n m f mj mj (2.2)该方程说明()n m f ,可以表示为无限多项不同频率的复指函数之和。
而不同的频率点()21,ωω所做的贡献由()21,ωωF 所决定。
2.1.2 离散的傅立叶变换离散傅立叶变换(Discrete Fourier Transform,DFT)是计算机中通常采用的一种傅立叶变换方法，其原因是由于计算机内的DFT 的输入和输出均为离散值。
2.1.3 快速傅立叶变换快速傅立叶变换(Fast Fourier Transform,FFT)是一种DFT 。
FFT 的设计思想是：将原函数分为奇数项和偶数项，通过不断将一个奇数项和一个偶数项相加（减），得到需要的结果。
FFT 通过计算两个单点的DFT ，来计算两个双点的DFT 。
通过计算两个双点的DFT ，来计算四个点的DFT ，…，以此类推。
对于任何N=2m 的DFT 的计算，通过计算两个N/2点额DFT ，来计算N 个点的DFT 。
快速傅立叶变换的主要推导过程如下： 令⎪⎭⎫ ⎝⎛-=N x j WXNπμμ2exp(2.3)则有 ()()w XNN x x f NF μμ∑-==11()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++=∑∑-=-=+1201211221222221N x Nx x Nx Nw wx f Nx f Nμμ()()⎥⎦⎤⎢⎣⎡++=∑∑-=-=1111212121M x M x NxMxNw w wx f Mx f Mμμμ()()[]μμμ021F F w Ne+=(2.4)上式在计算时分成了奇数项和偶数项 同理 ()()()[]M F M F M F W MNe+++=++μμμμ021()()[]μμμ021F F w MNe++= (2.5)又⎪⎭⎫ ⎝⎛-⋅=⋅=+N M j ww w wNMN NMNπμμμ2e x p()w wNNj μμπ-=-⋅=exp (2.6)∴ ()()()[]μμμμ021F F M F wNe-=+ (2.7)由以上两式推导可得到FFT 的定义式为()()eN y Mx j N M F y x F ⎪⎭⎫ ⎝⎛+-=-=∑∑=νμπνμνμ211,, (2.8),1,0=μ…1,-M ,1,0=ν…1,-NFFT 的逆变换为()()∑∑-=⎪⎭⎫ ⎝⎛+-==1021,1,M N y Mx j N eF MNy x F μνμπννμ (2.9),1,0=μ…1,-M ,1,0=ν…1,-N 2.2 卷积定理2.2.1 卷积定理的基本理论二个二维连续函数在空间域中的卷积可求其相应的二个傅立叶变换乘积的反变换而得。
反之，在频域中的卷积可用的在空间域中乘积的傅立叶变换而得。
即 ()()()g F f F g f F ⋅=⨯ (2.10) 其中()f F 表示f 的傅立叶变换。
借由傅立叶逆变换，1-F ，也可以写成 ()()()g F f F F g f ⋅=⨯-1(2.11)以上的写法只对特定形式定义的变换正确，变换可能由其它方式正规化，使得上面的关系式中出现其它的常数因子。
利用卷积定理可以简化卷积的运算量。
对于长度为n 的序列，按照卷积的定义进行计算，需要做12-n 组对位乘法，其计算复杂度为()2n O ；而利用傅立叶变换将序列变换到频域上后，只需要一组对位乘法，利用傅快速的不理也变换之后，总的计算复杂度为()n n O log 。
2.2.2 卷积定理与二维的傅立叶变换假设A 是N M ⨯的矩阵，B 是Q P ⨯的矩阵，则A 和B 的卷积可以通过一下步骤实现：①对A 和B 补0，使其都为()()11++⨯++Q N P M②用式 (2.8) 对矩阵A 和B 进行二维的FFT 变换。
③将两个FFT 结果相乘，然后利用式 (2.9) 对其乘积进行傅立叶逆变换第三章图像3.1 图像类型数字化图像按照记录方式可以分为两种：矢量图像和位图图像。
(1)矢量图像。
矢量图像是用数学的矢量方式来记录图像内容，以线条和色块为主。
例如，一条线段的数据只需记录两个端点的坐标、线段的粗细和色彩等，因此其文件占有的容量较小，也可很容易地进行放大、缩小和旋转等操作，并不会失真，精确度较高，并可以制作3D图像。