长方体和正方体——完全浸没、不完全浸没问题
长方体和正方体——完全浸没、不完全浸没问题

2021/5/18
例2.如图,在长、宽、高分别为10cm,10cm,6cm的长方体容 器中盛有深4cm的水,若向容器中放入一个棱长为5cm的正方体铁 块,那么水深变为多少厘米? 上升的水的体积:5×5×5=125(立方厘米) 水的底面积:10×10=100(平方厘米) 放入铁块之后水增加高度:125÷100=1.25(厘米)
2021/5/18
例2.如图,在长、宽、高分别为10cm,10cm,6cm的长方体容器 中盛有深4cm的水,若向容器中放入一个棱长为5cm的正方体铁块, 那么水深变为多少厘米?
先判断铁块是否 完全浸没在水中。
方法:抓不变量。
放入铁块前、后水的体积不变。
2021/5/18
例2.如图,在长、宽、高分别为10cm,10cm,6cm的长方体容器 中盛有深4cm的水,若向容器中放入一个棱长为5cm正方体铁块, 那么水深变为多少厘米? 水的体积:10×10×4=400(立方厘米) 放入铁块之后水的底面积:10×10-5×5=75(平方厘米)
放入铁块之后水深:4+1.25=.25(厘米)
答:水深变为5.25厘米。
2021/5/18
二、不完全浸没问题 例3.一个长方体玻璃缸,从里面量长8分米,宽6分米,高5分米, 水深2分米。如果投入一块棱长是4分米的正方体铁块(如图), 缸里水上升多少分米? 水的体积:8×6×2=96(立方分米) 放入铁块之后水底面积:8×6-4×4=32(平方分米)
长方体和正方体
完全浸没、不完全浸没
2021/5/18
一、完全浸没问题 例1.在一个长50厘米,宽40厘米,高30厘米的长方体玻璃缸中,盛有 19.5厘米深的水,如放入一块棱长为10厘米正方体铁块,玻璃缸中水面 高度是多少厘米?
思维拓展训练:长方体和正方体-数学五年级下册
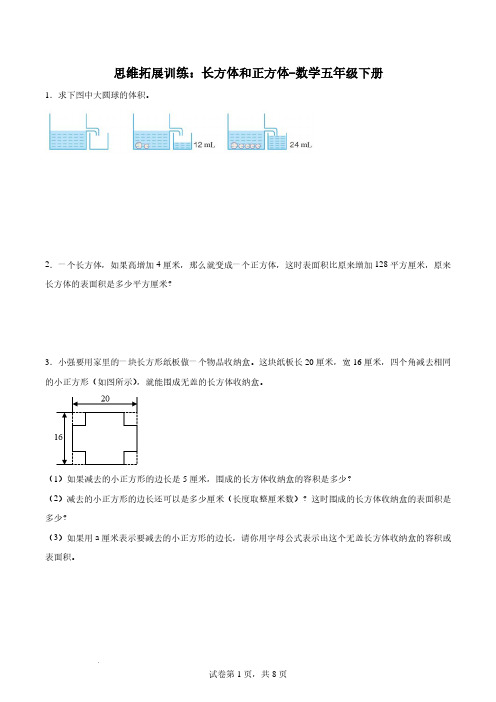
思维拓展训练:长方体和正方体-数学五年级下册1.求下图中大圆球的体积。
2.一个长方体,如果高增加4厘米,那么就变成一个正方体,这时表面积比原来增加128平方厘米,原来长方体的表面积是多少平方厘米?3.小强要用家里的一块长方形纸板做一个物品收纳盒。
这块纸板长20厘米,宽16厘米,四个角减去相同的小正方形(如图所示),就能围成无盖的长方体收纳盒。
(1)如果减去的小正方形的边长是5厘米,围成的长方体收纳盒的容积是多少?(2)减去的小正方形的边长还可以是多少厘米(长度取整厘米数)?这时围成的长方体收纳盒的表面积是多少?(3)如果用a厘米表示要减去的小正方形的边长,请你用字母公式表示出这个无盖长方体收纳盒的容积或表面积。
4.下图是李师傅为小明做的一个底面为正方形,内高是20厘米的无盖玻璃容器。
(1)把1升水倒入玻璃容器,水深10厘米,再把一个苹果沉入容器(苹果被水全部淹没),结果水面上升了3厘米,这个苹果的体积是多少立方厘米?(2)制作这个玻璃容器至少需要玻璃多少平方厘米?5.如下图,一个长、宽、高分别为30厘米、16厘米、21厘米的长方体容器中水位高度是10厘米,如果将另一个长方体(长、宽、高分别为16厘米、10厘米、36厘米的铁块竖直)放入左边的容器中(贴底面齐平),那么这个容器中的水会溢出吗?如果不溢出,那么容器中水位将上升至多少高度?如果溢出,那会溢出多少立方厘米的水量?6.笑笑家有甲、乙两个不同规格的带盖收纳盒,她想把家里散落的小包纸巾分别放入这两个收纳盒中(纸巾不能超过收纳盒的上沿且不能挤压)。
一小包纸巾的长、宽、高和收纳盒内部的长、宽、高如下图所示。
(单位:厘米)(1)甲收纳盒中最多可以放置多少包纸巾?(2)尽可能多地往乙收纳盒中放纸巾,你可以放置多少包?结合生活实际想一想,我()笑笑的想法。
(填“同意”或“不同意”)如果同意,请你写出理由;如果不同意,尽可能多地往乙收纳盒中放纸巾,你可以放置多少包?写出你的思考过程,可以写一写,画一画。
(苏教版)六上《长方体和正方体》课后练习题

长方体和正方体第1课时一、填空题。
1.长方体有个顶点,有条棱,有个面,一般情况下面的面积相等。
正方体是的长方体。
2.一个正方体的棱长是8分米,它的棱长总和是分米。
3. 我们在画长方体时一般只画出三个面,这是因为长方体最多看到个面。
4. 用一根长铁丝正好做一个长6厘米、宽5厘米、高3厘米的长方体框架。
5. 一个长方体长6厘米、宽2厘米、高1.5厘米,它的棱长总和是。
6.用36厘米的铁丝折一个正方体框架,这个正方体棱长是。
7. 一个长方体的棱长总和是48厘米,长是5厘米,宽是4厘米,它的高是。
8.一个正方体的棱长是4米,它的棱长总和是,每个面的面积是。
9.一根80分米长的铁条,剪断后刚好可焊接成一个长8分米,宽5.5分米的长方体框架。
这个长方体的高是分米。
二、判断题(对的打“√”,错的打“×”)。
1.所有的长方体都有六个面。
………………………………()2.长方体中对面的面积是相等的。
…………………………()3.长方体的表面中不可能有正方形。
………………………()4.正方体的表面中有可能有长方形。
………………………()5.长方体的六个面中有可能有四个面的面积相等。
………()三、解决实际问题。
1.用三个棱长2分米的正方体拼成一个长方体,这个长方体的棱长总和是多少分米?2.一根铁丝长84厘米,围成长方体相交于一个顶点的两条棱长为15厘米、4厘米,那么这个顶点的第三条棱长为多少厘米?这个长方体的前面面积是多少平方厘米?3.一个长方体长、宽、高为三个连续的自然数,且他们的和是24,这个长方体的棱长总和是多少?4.王师傅有2根一样长的铁丝,一根围成了长8分米、宽6分米、高为4分米的长方体框架,另一根围成另一个正方体框架。
这个正方体框架的棱长是多少?30 10 6 长方体和正方体第2课时1.下面哪些图形折叠后能围成正方体? (能围成正方体的画“√”,不能围成正方体的画“×”)( ) ( ) ( ) ( ) ( ) ( )2.下面哪些图形沿虚线折叠后能围成一个长方体?(能围成长方体的画“√”,不能围成长方体的画“×”)( ) ( ) ( ) ( ) ( ) ( )3.如图,是一个正方体的展开图,其中与1号面相对的是( )号面,与2与2号面相对的是( )号面,与3号面相对的是( )号面。
物体浸没问题 非常完整版

水中浸物问题1、完全浸没:物体的体积=水上升的体积例:把一个铝球浸没在一个底面半径是8分米的水桶中,水面的高度由4分米上升至4.2分米,这个铝球的体积是多少立方分米?解析:铝球完全浸没,物体的体积=水上升的体积水上升的体积=底面积×高=底面积×上升的高度=3.14×8×8×(4.2-4)=40.192(立方分米)所以铝球的体积也是40.192立方分米1、不完全浸没:抓住水的体积不变例:一只装有水的圆柱形玻璃杯,底面积是80平方厘米,水深8厘米,现在将一个底面积是16平方厘米的长方体铁块竖直放入水中后,仍有一部分铁块露在外面,现在水深是多少厘米?解析:铁块没有完全浸没,抓住水的体积不变来解题水的体积=容器底面积×水深=80×8=640(立方厘米)后来水的底面积变成一个环状的底面积=容器底面积-铁块底面积=80-16=64(平方厘米)此时水深:640÷64=10(厘米)【针对性练习】1、一个无盖观赏鱼缸,里面放有一块高为21cm,体积为4200cm3的假山石。
如果水管以每分钟12dm3的流量向鱼缸内注水,至少要多长时间才能使假山石完全淹没?2、一个长方体水族箱从里面量长32cm、宽25cm。
如果每条金鱼的体积是640cm3,向水族箱中放入3条金鱼(水没有溢出)后,水族箱中的水位上升了多少厘米?3、算一算,铁块的高是多少厘米?4、一个底面长和宽都是2dm的长方体玻璃容器里面有5.6L水。
若将一个苹果浸没在水中,水深1.5dm,这个苹果的体积是多少立方分米?(玻璃厚度忽略不计)5、下图是一个长方体容器,里面水深5.6dm。
把一个南瓜放入(南瓜全部浸没在水中)后,从容器里溢出4L水。
这个南瓜的体积是多少?6、观察量杯中水的变化,计算出大正方体的体积。
7、将棱长是1.6dm的正方体石块浸没到一个长方体水槽中,水面上升了0.8dm。
小学数学中的浸没问题完整版

小学数学中的浸没问题 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】立体图形提高题——浸没问题专题简析:(底面接触、完全浸没、非完全浸没)抓住浸没问题的关键:水面上升(下降)的体积=物体浸没部分的体积即:容器底面积×水面上升(下降)的高度=物体底面积×高以此关系利用方程解决较为简便。
例1.在一个底面直径是20cm的装有水的圆柱形容器中,浸没着一个底面直径12cm,高10cm的圆锥形铅锤,把铅锤从水中取出时,水面高度下降了多少cm?举一反三:1.一个底面半径9cm,高15cm的圆锥形铁块完全浸没在底面直径是20cm的装有水的圆柱形容器中,取出铁块后,水面高度下降了多少cm?2.把一个底面半径6cm的圆锥形零件完全浸没在棱长12cm的正方体容器中,水面比原来上升了3.14cm,这个圆锥形零件的高是多少cm?3.一个从里面量长15cm、宽12cm、高20cm的长方体容器内装有10cm高的水,当把一个底面半径5cm的圆锥形零件完全浸没在长方体容器中时,水面上升到11.57cm,这个圆锥形零件的高是多少cm?例2.一个底面积是72cm2的圆柱形容器中装有高2.5cm深的水,当把棱长6cm的正方体铁块放入容器中,并没有完全浸没,现在水深多少cm?举一反三:1.一个底面半径10cm,高20cm的圆柱形容器内装有8cm深的水,放入长8cm、宽8cm、高15cm的长方体铁块,使它与容器底面接触,现在水深多少cm?2.一个从里面量底面半径是9cm、高50cm的圆柱体容器内装有20cm高的水,当把一个底面直径是2cm、高30cm的圆柱形铁棒垂直放入容器中时,并没有完全浸没,现在水深多少cm?3.一个从里面量底面半径是5cm、高20cm的圆柱体容器内装有15cm高的水,当把一个底面直径是2cm、高18cm的圆柱形铁棒垂直放入容器中时,并没有完全浸没,现在水深多少cm?扩展与提高:1. 有一个高8cm 、容积64ml 的圆柱形容器中装满了水,把一个长40cm 的圆柱形小棒垂直插入水中,直至容器底部,这时有一部分水溢出。
新人教版五年级数学下册《 长方体和正方体 解决问题(不规则物体的体积)》公开课教案_20

《不规则物体的体积》教学设计教学内容:人教版小学数学五年级下册第三单元“长方体和正方体”第39页例6及练习九相关的练习。
教材分析:体积对学生来说是一个新的概念,从理解平面图形到理解立体图形是学生空间观点的一次发展。
而不规则物体的体积这个内容是在学习了长方体和正方体体积计算后安排的,是长方体和正方体体积计算的拓展。
设计理念:新课标强调,教学中的“做”比“知道”更重要。
数学活动课要把握好实践活动的时机,凡是能让学生自己设计的,就让自己亲自去发挥;凡是能让学生自己去做的,就让学生亲自去动手。
通过数学实践活动,让学生把在课堂上学到的知识应用到实际生活中去。
在活动过程中,教师在学生独立思考和合作交流的基础上实行有针对性的指导,让学生有较大的自主发展的空间,激发学生的学习兴趣,培养学生自主发现问题,自主提出问题,自主解决问题的水平,感受数学与生活的联系。
教学目标:1、通过试验,探索生活中一些不规则物体体积的测量及计算方法,加深对已学知识的理解和深化。
2、感受数学知识之间的相互联系,树立转化的数学思想,体会解决问题的方法的多样性。
3、通过活动培养学生观察思考的水平,并培养小组合作精神和解决问题水平。
教学重点:探索并掌握不规则物体体积的计算方法。
教学难点:在理解“上升或下降部分水的体积就是浸入水中物体的体积”的基础上,感悟“转化”的数学思想。
活动准备:魔方、正方体透明容器、量杯、水槽、尺子、橡皮泥、梨和水等。
教学方法:实验、探究、发现、练习等教学方法相结合。
教学过程:(一)“魔方”引旧知,揭示新“课题”。
教师拿出学生们常玩的“魔方”,学生的学习兴趣立即调动起来。
师:从数学图形方面来讲,“魔方”是一个——正方体(学生抢答)。
你能求出它的体积吗?生:正方体的体积是棱长×棱长×棱长师:这个魔方的棱长大约是5厘米,它的体积是多少?(学生 :125立方厘米)师:你还会求哪些立体图形的体积?师:像我们刚才提到的长方体、正方体,还有以后会学到的圆柱、圆锥、球等能够通过公式直接求出体积的物体(课件出示:规则物体图),我们一般称为规则物体。
数学人教版五年级下册浸没问题

2、一个长50cm宽24cm高20cm长方体的 金鱼缸中,放有一个棱长为10cm的正方体 铁块,如果水管以每分钟4立方分米的流量向 空金鱼缸中注水,那么至少需要多长时间能 完全浸没这个铁块?
练习题
在一个长20cm宽20cm高15cm的长方体玻璃缸 中,水深8cm,现在要放入长和宽都是8cm、 高为15cm的一个铁块。 (1)如果把铁块横放入水中,水面上升多少厘米? (2)如果把铁块竖放入水中,水面上升多少厘米?
(1)(8*8*15)÷(20*20)=2.4(厘米)
(2)(20*20*8)÷(20*20—8*8)=9.52(厘米) 9.52---8=1.52(厘米)
浸没问题
青山区钢城第十二小学
李 敬 东
阿基米德皇冠故事
1 2
结核概述
学校结核病பைடு நூலகம்情现状
3 学校结核病防控职责 4
学校结核病疫情监测 学校结核病疫情处置
几何中的浸没问题
1、完全浸没 思考关键: 浸没物体的体积=上升的水面体积
2、不完全浸没 思考关键:水的体积没有变,底面积变小
1、一个长方体的玻璃缸,长15dm,宽 12dm,水深10dm。如果投入一块棱长为 3dm的正方体铁块,这时缸里的水深多少分 米?
铁块的体积 3*3*3=27(立方厘米) 水槽的底面积 27÷0.3=90(平方厘米) 铁球的体积 90*0.5=45(立方厘米)
长方体与正方体三视图、浸没、染色问题

8、在长、宽、高分别是10cm、10cm、6cm的 长方体的容器中盛有深4cm的水,在向容器中 放入棱长5cm的正方体铁块,则水深变为多少 厘米?(5.25厘米)
9、一个长方体容器,里面长12分米、宽10 分米、水深10.5分米,容器中浸没着一个小 铁块,当铁块从水中取出后,水面下降了 0.4分米,这个小铁块的体积是__48____立 方分米.
3、18个边长为2厘米的小正方体堆成如图的形 状,求它的表面积。(208平方厘米)
4、右图是由16个棱长2厘米的小正方体重叠而 成的,求这个立体图形的表面积。(184平方 厘米)
例3、下图是一个棱长为3厘米的正方体,一只 蚂蚁从A点沿表面爬向B点。请画出蚂蚁爬行 的最短路线。这样的路线共有几条?
10、一个长方体容器的底面是底面积是一个边 长60厘米的正方形,容器里直立着一个高1米、 底面边长15厘米的长方形铁块。这时容器里 的 水深0.5米。如果把铁块取出,容器里的水 深多少厘米?(46.875厘米) 11、在一个底面是边长为60厘米的正方形的长 方体容器中,直立着一个厂1米,底面边长为15 厘米的正方形的长方体铁棍。这时容器里水深 50厘米,现在把铁棍轻轻向上提起24厘米,求 露出水面的长方体铁棍浸湿部分长多少厘米? (25.6厘米)
分析:根据切的表面积变化特点: 每切一次,增加两个切开面的面 积。题中一共切了9次,总共增 加18个面的面积。
(2+3+4)×2×1×1+60×1×1=78(平方 米)
1、把27块棱长是1厘米的小正方体堆成一个大 正方体,这个正方体的表面积比原来所有的小 正方体的面积之和少多少平方厘米?(108平 方米厘米) 2、把24个棱长是1厘米的小正方体摆成一个 长方体,这个长方体的表面积至少是多少平 方厘米?(52平方厘米)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.33厘米>5厘米,此题属于完全浸没问题。
例2.如图所示,在长、宽、高分别为10cm,10cm,6cm的长方 体容器中盛有深4cm的水,若向容器中放入一个棱长为5cm的正方 体铁块,那么水深变为多少厘米? 上升的水的体积:5×5×5=125(立方厘米) 水的底面积:10×10=100(平方厘米) 放入铁块之后水增加的高度:125÷100=1.25(厘米)
例2.如图所示,在长、宽、高分别为10cm,10cm,6cm的长方体 容器中盛有深4cm的水,若向容器中放入一个棱长为5cm的正方体 铁块,那么水深变为多少厘米?
先判断铁块是否 完全浸没在水中。
方法:抓不变量。
放入铁块前、后水的体积不变。
例2.如图所示,在长、宽、高分别为10cm,10cm,6cm的长方体 容器中盛有深4cm的水,若向容器中放入一个棱长为5cm的正方体 铁块,那么水深变为多少厘米? 水的体积:10×10×4=400(立方厘米) 放入铁块之后水的底面积:10×10-5×5=75(平方厘米)
完全浸没、不完全浸没
一、完全浸没问题 例1.在一个长50厘米,宽40厘米,高30厘米的长方体玻璃缸中,盛有 19.5厘米深的水,如果放入一块棱长为10厘米的正方体铁块,玻璃缸中 水面高度是多少厘米?
上升的水的体积=放入物体的体积 正方体铁块的体积:10×10×10=1000(立方厘米) 水的底面积:50×40=2000(平方厘米) 水上升的高度:1000÷2000=0.5(厘米) 现在水面的高度:19.5+0.5=20(厘米) 答:玻璃缸中水面高度是20厘米。
放入铁块之后水的高度:96÷32=3(分米) 3分米<4分米,此题属于不完全浸没问题。 3-2=1(分米)
答:缸里的水上升1分米。
1.完全浸没(水没有溢出): 上升的水的体积=放入物体的体积。
2.不完全浸没: 放入物体后水的高度=水原来的体积÷(容器底面积-放入物体的底面积)
放铁块之后水深:4+1.25=5.25(厘米)
答:水深变为5.25厘米。
二、不完全浸没问题 例3.一个长方体玻璃缸,从里面量长8分米,宽6分米,高5分米, 水深2分米。如果投入一块棱长是4分米的正方体铁块(如图), 缸里的水上升多少分米? 水的体积:8×6×2=96(立方分米) 放入铁块之后水的底面积:8×6-4×4=32(平方分米)
