小球沿哪个曲面下降最快
光滑圆弧面下滑。求小球在任一位置时的速度和对圆弧面的

2l
1
1
例5 一质量 m ,半径 r 的球体在水中静止释 放沉入水底.已知阻力 Fr 6πrv , 为粘滞系数, 求 v(t ) . FB 为浮力 解 取坐标如图 mg FB 6πrv ma FB Fr b 6πr 令 F0 mg FB dv dv F0 b F0 bv m (v ) dt dt m b v v t dv b dt 0 v ( F0 b) m 0 P b ln[v ( F0 b)] ln[ F0 b] t y m v - ( F0 b) F0 e ( b / m ) t v [ e (b / m )t] 1 F0 b b
例1 .质量为m的小球最初位于A点,然后沿半径为R 的光滑圆弧面下滑。求小球在任一位置时的速度和 对圆弧面的作用力。 2 dv v 解: mg cos mat m N mg sin man m dt R
dv dvds dv v dt dsdt Rd dv mg cos mv Rd vdv Rg cos d
F0 b
v
o
v0
t
m
dt
bv
v
0
v v0 e
(b / m)t
v
0 dt m
v
t
o
例6 一升降机内有一光滑斜面,斜面固定在升降机的 地板上,其倾角为,如图所示,当升降机以匀加速度 a1上升时,物体m从斜面的顶点沿斜面下滑,求物体m 相对于斜面的加速度以及相对于地面的加速度。 y 解: 已知斜面对地面的加速度为 a1 设物体对斜面的加速度为a 2 物体对地面的加速度为 a
例4.密度为1的液体,上方悬一长为l,密度为2的 均质细棒AB,棒的B端刚好和液面接触。今剪断绳, 并设棒只在重力和浮力作用下下沉,求: A (1)棒刚好全部浸入液体时的速度。 (2)若2<1/2,棒浸入液体的最大深度。 B o (3)棒下落过程中能达到的最大速度。 x 解: (1) mg F ma dv dv 2lsg 1 xsg 2 sl 2lsv x dt dx v x 1 x 1 x ) gdx vdv (1 ) gdx 0 vdv 0 (1 2l 2l
小球沿哪个曲面下降最快

如图所示为一个曲面。
曲面的两端固定。
小球自由滑落,无摩擦。
问:曲面设计成什么形状时,小球滑落下来的时间最短?
这个问题很简单,也很有趣。
设小球在垂直方向的位移达到了y 。
此时,小球的速度为v 。
根据能量守恒,有:
212
mv mgy =
故v 。
y ∆为垂直方向上的一小段。
要走完y ∆,需要的时间为:
s t v ∆∆==; 把垂直方向的总位移b 分成n 段,即i b y y n
∆≡∆=;走完全程需要的总时间为:
1
n i i T t ==∆=∑
约束条件是:1
n i i x a =∆=∑。
a 为水平方向的总位移。
事实上问题转化为求i x ∆变化时T 的极大值。
采用哈密尔顿算法。
令:
11()n n
i i i T x a λ===-∆-∑
则有:0i i T x x λ∂=∆=∂∆. 化简,得:22212[()()]i i gy x y λ∆+∆=;考虑到()i yi yi b x y x x n
''∆=∆=;有: 2(1)i yi y x K const '+=≡。
K 为待定系数。
推而广之:对于所有的,x y ;有:
2(1)y y x K '+=
变形;得:
d x y =; 这是个很简单的微分方程;
解之,得:x K =即为斜面的形状。
呈一个摆线。
当10a b ==时,15K =可以满足边界条件。
这时用仿真软件可以画出曲面的形状。
PROE最速曲线设计方程

Proe最速曲线设计
最速曲线:两点之间一小球滚下,不是直线的连线下降最快,而是小球在最速曲线上滚下最快。
在一个斜面上,摆两条轨道,一条是直线,一条是曲线,起点高度以及终点高度都相同。
两个质量、大小一样的小球同时从起点向下滑落,曲线的小球反而先到终点。
这是由于曲线轨道上的小球先达到最高速度,所以先到达。
然而,两点之间的直线只有一条,曲线却有无数条,那么,哪一条才是最快的呢?伽利略与1630年提出了这个问题,当时他认为这条线应该是一条直线,
/* 为笛卡儿坐标系输入参数方程
/*根据t (将从0变到1) 对x, y和z
/* 例如:对在x-y平面的一个圆,中心在原点
/* 半径= 4,参数方程将是:
/* x = 4 * cos ( t * 360 )
/* y = 4 * sin ( t * 360 )
/* z = 0
/*------------------------------------------------------------------- theta=180*t
alh=PI*t
x=101*(alh-sin(theta))
y=101*(1-cos(theta))
z=0。
小球最速曲线原理

小球最速曲线原理小球最速曲线原理是一项非常有趣的物理学原理,它解释了为什么在相同高度下,小球在凹凸不平的曲线上滚动的速度最快。
这一原理我们可以在生活中的各个方面都看到运用,如过山车和雪橇等。
接下来,我们将详细介绍这一原理。
首先,让我们了解一下小球的普通滚动和滚动能量的概念。
在平面上,小球的滚动通常被称作“匀速滚动”。
这是因为小球的速度是由其滚动的半径和角速度(旋转速度)决定的。
它们之间的比例关系是小球速度=滚动半径*角速度。
当小球在非平面的曲面上滚动时,情况就有所不同了。
曲面的凹凸不平使得小球沿着不同的半径滚动,这些半径的角速度不同。
根据动能定理,小球的总能量等于其动能和势能之和。
匀速滚动时,小球的所有势能都转换成了动能,滚动速度恒定。
当小球在曲面上滚动时,其速度会因为势能的变化而发生变化,这称为“动能和势能的等效转化”。
当小球沿着一段曲面上较高的凸起(高点)滚动时,它首先具有一种高势能,这种势能随着小球的下滚而转换为动能,由此使小球加速。
当小球到达曲面的底部(低点)时,其动能被完全转化为势能,这会使小球減速。
当小球滚过底部,爬升另一边的凸起时,同样的原理又会帮助小球加速。
当小球再次滚动回中心位置时,它又会减速。
这激发了小球在沿着曲面上滚动时进行更快的操作,从而实现了最速曲线的效果。
最后,小球最速曲线原理的应用有很多,其中最经典的例子就是过山车。
过山车的轨道设计就是基于小球最速曲线原理,以使车辆在曲线上滑行时具有最大速度,为乘客提供最激动人心的的体验。
雪橇和滑板等也运用了这一原理以最大限度地提高体验的激情和速度。
小球最速曲线原理是一项非常重要的物理学原理,它对我们的生活有着深刻的影响。
理解这个原理将帮助我们设计和制造更高效的运动设备。
自由落体运动的规律及经典例题及答案

自由落体运动的规律【知识讲解】自由落体运动一、定义物体只在重力作用下从静止开始下落的运动,叫自由落体运动。
在没有空气阻力时,物体下落的快慢跟物体的重力无关。
1971年美国宇航员斯科特在月球上让一把锤子和一根羽毛同时下落,观察到它们同时落到月球表面。
此实验说明:①在月球上无大气层。
②自由落体运动的快慢与物体的质量无关。
自由落体运动在地球大气层里是一种理想运动,但掌握了这种理想运动的规律,也就为研究实际运动打下了基础。
当空气阻力不太大,与重力相比较可以忽略时,实际的落体运动可以近似地当作自由落体运动.对自由落体运动的再研究:为了纪念伽利略的伟大贡献,1993年4月8日来自世界各地的一些科学家,用精密自动投卸仪把不同材料制成的木球、铝球、塑料球等许多小球从比萨斜塔上44米高处同时投下,用精密电子仪器和摄像机记录,结果发现所有小球同时以同一速度落地.所以,一般情况下,物体在空气中下落,可以忽略空气的影响,近似地认为是自由落体运动。
二、自由落体运动的条件1、从静止开始下落,初速为零。
2、只受重力,或其它力可忽略不计.(这是一种近似,忽略了次要因素,抓住了主要因素,这是一种理想化研究方法)三、自由落体运动的性质伽利略不但巧妙地揭示了亚里士多德观点的内部矛盾,还对自由落体运动的性质做了许多研究。
他的研究方法是提出假设-—数学推理——实验验证――合理外推.伽利略所处的年代还没有钟表,计时仪器也较差,自由落体运动又很快,伽利略为了研究落体运动,利用当时的实验条件做了在斜面上从静止开始下滑的直线运动(目的是为了“冲淡重力),证明了在阻力很小的情况下小球在斜面上的运动是匀变速直线运动,用逻辑推理外推到斜面倾角增大到90°的情况,小球将自由下落,成为自由落体,他认为这时小球仍然会保持匀变速直线运动的性质,多么巧妙啊!正确与否需要用实验来验证,如图是处理课本中的自由落体纸带运动轨迹.猜想:自由落体是匀变速直线运动则由给定的公式v t=,因数据相邻点时间t=0.02s得v A=0v B==0。
最速降线问题
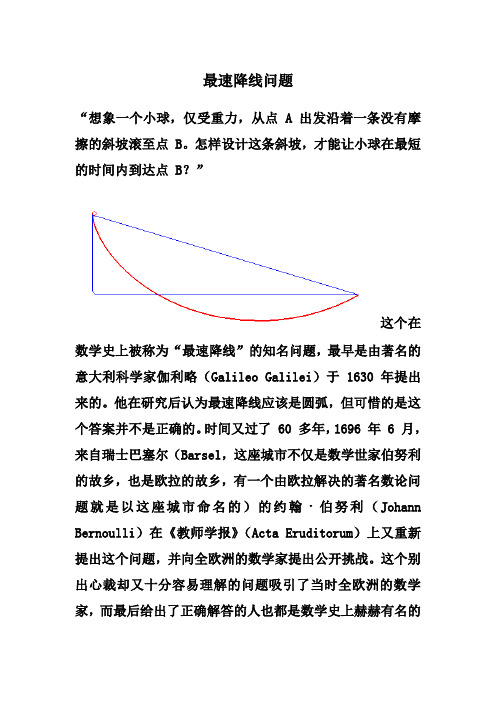
最速降线问题“想象一个小球,仅受重力,从点 A 出发沿着一条没有摩擦的斜坡滚至点 B。
怎样设计这条斜坡,才能让小球在最短的时间内到达点 B?”这个在数学史上被称为“最速降线”的知名问题,最早是由著名的意大利科学家伽利略(Galileo Galilei)于 1630 年提出来的。
他在研究后认为最速降线应该是圆弧,但可惜的是这个答案并不是正确的。
时间又过了 60 多年,1696 年 6 月,来自瑞士巴塞尔(Barsel,这座城市不仅是数学世家伯努利的故乡,也是欧拉的故乡,有一个由欧拉解决的著名数论问题就是以这座城市命名的)的约翰・伯努利(Johann Bernoulli)在《教师学报》(Acta Eruditorum)上又重新提出这个问题,并向全欧洲的数学家提出公开挑战。
这个别出心裁却又十分容易理解的问题吸引了当时全欧洲的数学家,而最后给出了正确解答的人也都是数学史上赫赫有名的巨人。
这也让这次挑战成为了数学史上最激动人心的一场公开挑战。
数学家之间公开挑战的传统要追溯到 16 世纪在意大利的博洛尼亚(Bologna)。
16 世纪初的博洛尼亚曾是欧洲数学思想的大熔炉,全欧洲的学生都会来到博洛尼亚大学。
他们甚至还“发明”了一项新的观赏运动——数学比赛。
这听起来有些匪夷所思,但在当时确实有大批的观众从各地涌来,围观数学家们互相之间用数学斗法。
其中最有名的一次,是在塔塔里亚(Tartaglia)和费奥(Fior)间上演的,是一场关于求出一元三次方程通解的世纪智力大战。
言归正传,在约翰・伯努利发出挑战后的半年里,他收到的唯一一份答案来自《教师学报》的主编,他的老师莱布尼茨(Gottfriend Wilhelm Leibniz)。
在莱布尼茨的要求下,他将接受答案的最后期限推迟到 1697 年的复活节,以便有更多的数学家能参与到这场挑战中来。
我们都知道,过两点的直线段是两点间的最短路径。
但使质点的运动时间最短的运动轨迹,却不是那么的显而易见。
小球下落时间最短曲线

小球下落时间最短曲线
我们要找出小球下落时间最短的曲线。
首先,我们需要理解小球下落的基本物理原理。
假设小球从高度 h 处自由下落,其下落的时间 t 可以用以下公式表示:
t = sqrt(2h/g)
其中 g 是重力加速度,约为 m/s^2。
为了使小球的下落时间最短,我们需要找到一个曲线,使得小球在相同的高度下落时,其下落的时间最短。
由于小球下落的轨迹是一个抛物线,我们可以使用抛物线的标准方程 y = ax^2 + bx + c 来表示。
但是,为了简化问题,我们可以假设小球沿着一条直线下落,并使用上述公式计算其下落时间。
当小球沿着直线以高度 h=0 下落时,其下落的时间最短,为 0 秒。
最速下降问题

最速下降演示实验清华大学物理系 路峻岭如图,三个相同的球沿三个不同的轨道——斜线、圆弧、旋轮线轨道滚动,结果是沿旋轮线轨道滚动最快,用时最短。
1.球沿轨道作纯滚动与纯滑动的比较以斜线轨道为例进行讨论。
如下图,设斜线轨道的倾角为θ,匀质实心球质量为M ,半径R ,滚动半径r ,绕过质心轴的转动惯量225MR 。
球体受到3个力作用:重力、弹力和静摩擦力。
若静摩擦力足够大,球体可以保持纯滚动。
以,,,c c a v βω为变量,则有()()2sin 25000c c c Mg f Ma fr MR a r v R θββω−=⎧⎪⎪=⎪⎨⎪=⎪==⎪⎩ (1) 解得:22222sin ,,,25sin sin 2255c c c g v a t t R r r rg r g a R R r r rθβωβθθ===+==++ (2) 如果球在光滑的轨道上只滑动不滚动,则sin c a g θ=,即球的纯滚动与纯滑动的质心加速度仅相差一个与仪器结构有关的因子。
对上面三个轨道,结构因子相同。
这样球在三个轨道下落快慢的问题,可以等效地用球光滑滑动(质点)替代实际的球纯滚动(刚体)进行讨论,所得结论不变。
2.最速下降问题最速下降是个古老的问题,又称捷线问题。
有关泛函或变分法的书多采用此例引入相关概念。
其问题是:在空间高低两点之间寻找一条连接两点的光滑轨道,使质点沿轨道从高点下滑到低点用时最短。
如右图,过高低两点作一铅直平面,在此平面内建立直角坐标系。
以高点为原点,水平方向为x 轴,竖直向下为y 轴,设低点E的坐标为000(,)(0)x y y >。
现在的问题就是寻找过O 点和E 点的众多平面曲线()y y x =中使得质点下滑用时最少者。
设轨道()y y x =连续光滑,易得到质点由静止开始沿轨道由O 点到E 点所用时间为:()00x t y x =⎡⎤⎣⎦∫ (3)()t y x ⎡⎤⎣⎦表示t 是函数()y x 的函数,ds dy dx dx y =+=′+222)()(1为质点下落()y x 后的速度大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图所示为一个曲面。
曲面的两端固定。
小球自由滑落,无摩擦。
问:曲面设计成什么形状时,小球滑落下来的时间最短?
这个问题很简单,也很有趣。
设小球在垂直方向的位移达到了y 。
此时,小球的速度为v 。
根据能量守恒,有:
212
mv mgy =
故v 。
y ∆为垂直方向上的一小段。
要走完y ∆,需要的时间为:
s t v ∆∆==; 把垂直方向的总位移b 分成n 段,即i b y y n
∆≡∆=;走完全程需要的总时间为:
1
n i i T t ==∆=∑
约束条件是:1
n i i x a =∆=∑。
a 为水平方向的总位移。
事实上问题转化为求i x ∆变化时T 的极大值。
采用哈密尔顿算法。
令:
11()n n
i i i T x a λ===-∆-∑
则有:0i i T x x λ∂=∆=∂∆. 化简,得:22212[()()]i i gy x y λ∆+∆=;考虑到()i yi yi b x y x x n
''∆=∆=;有: 2(1)i yi y x K const '+=≡。
K 为待定系数。
推而广之:对于所有的,x y ;有:
2(1)y y x K '+=
变形;得:
d x y =; 这是个很简单的微分方程;
解之,得:x K =即为斜面的形状。
呈一个摆线。
当10a b ==时,15K =可以满足边界条件。
这时用仿真软件可以画出曲面的形状。
