11.第十单元检测卷
天津耀华嘉诚中学初中化学九年级上册第十单元《酸和碱》检测题(含答案解析)

一、选择题1.(0分)[ID:133940]进行化学实验时非常容易出事故,所以我们在操作过程中都有严格的操作要求。
下列实验操作不正确的是()A.检查气密性B.倾倒液体C.闻气体的气味D.稀释浓硫酸2.(0分)[ID:133933]化学与生产、生活息息相关,以下对应物质及用途不正确的是()A.可用pH试纸测得食醋的pH=2.9B.可用熟石灰改良酸性土壤C.可利用洗洁精的乳化作用去除油污D.可用氢氧化铝治疗胃酸过多3.(0分)[ID:133930]将稀盐酸分别滴入NaOH溶液和NaCl溶液中,充分混合后均无明显现象。
混合后相关变化的微观示意图如下,下列说法正确的是A.物质间均未发生化学反应B.变化中都有新物质产生C.混合后溶液酸碱性都不变D.图甲可表示酸碱反应的实质4.(0分)[ID:133929]下列关于硫酸(或浓硫酸)的认识,正确的是()SO 的数目相同A.组成:硫酸溶液中H+和24B.性质:能与CO2、SO2等非金属氧化物反应C.稀释:将浓硫酸沿器壁缓慢倒入到水中,并不断用玻璃棒搅拌D.生产:含硫酸废水用CaCl2处理后直接排放5.(0分)[ID :133910]下列四个图象分别对应四个变化过程,其中正确的是A .一定量的饱和石灰水中加入氧化钙B .常温下,相同质量的锌和铁分别与足量的溶质质量分数相同的稀硫酸反应C .等体积、等浓度的双氧水制取氧气D .服用胃舒平[主要成分Al(OH)3]治疗胃酸过多,胃液pH 的变化6.(0分)[ID :133905]归纳总结是学习化学的重要方法之一。
下列排序正确的是A .金属活动性顺序:K Mg Cu Ag−−−−−−→、、、由强到弱B .溶液的pH:HCl NaCl NaOH−−−−−−→、、由大到小 C .地壳中的元素含量: O Si Fe Al−−−−−→由高到低、、、 D .气体的密度:222CO H O−−−−→、由大到小7.(0分)[ID :133889]下列各组物质反应,所得溶液能使酚酞试液变红的是( ) ①一定量的稀盐酸与适量的氢氧化钠溶液恰好完全反应 ②相同质量,相同溶质质量分数的氢氧化钾溶液与盐酸相混合 ③将硫酸钾溶液滴入氢氧化钡溶液中恰好完全反应 ④将二氧化碳气体通入氢氧化钠溶液中得到碳酸钠溶液 A .②④B .③④C .①②③D .②③④8.(0分)[ID :133888]下列实验方法一定能达到实验目的的是选实验目的实验方法项A检验一瓶气体是否为CO2将燃着的木条伸入瓶中B除去CO中混有的CO2将混合气体通过灼热的氧化铜C鉴别石灰水和NaOH溶液加入适量的稀盐酸D除去氢气中的HCl依次通过氢氧化钠溶液和浓硫酸溶液A.A B.B C.C D.D9.(0分)[ID:133870]某同学记录下的下列实验现象或操作都正确的是A.铁丝在空气中剧烈燃烧,火星四射、产生黑色固体B.CO还原Fe2O3实验开始时,要先点燃酒精喷灯再通入COC.向软水中滴加少许肥皂水,振荡,静置,出现大量垢状物且无泡沫D.稀释浓硫酸时,要把浓硫酸缓缓注入盛有水的烧杯中,用玻璃棒引流并搅拌10.(0分)[ID:133865]下列鉴别物质的方法中,能够达到目的的是()A.用燃着的木条鉴别二氧化碳和氮气B.用水鉴别氢氧化钠固体和硝酸铵固体C.用酚酞溶液鉴别氯化钠溶液和稀盐酸D.用稀盐酸鉴别银饰品和铂(白金)饰品11.(0分)[ID:133854]实验小组将未打磨的铝片和稀盐酸放入密闭容器中,用传感器探究反应过程中温度和压强的变化,结果如图所示。
苏教版小学一年级数学上册20以内的进位加法第10单元过关检测卷

第十单元过关检测卷二、我会做。
(1、3题每题8分,2、4题每题6分,共28分)1. 先圈出10个,再填一填2. 在二里填上“〉”“ v ”或、算——算 ■算(18 分)9 + 5= 8 + 8= 12 — 2 = 4 + 8 = 7 + 6= 2 + 9 = 5 + 7 = 6 + 6 = 8 + 5=9 + 7=19— 10 =5 + 6=4+6+6= 3+9-2= 4+2+8=9 + 4— 10= 3 + 6+ 3=7+ 8— 5=4.在中填上合适的数。
=14+ 4= 12+ 6= 123.在16 1314 里填上6= 15 3= 611'-2+ 9三、按要求解决问题。
(1题8分,2题6分,共14分)2.选一选。
(在正确答案下面的—里画“)(1)下面的算式中得数比7+ 6小的是哪组?10+ 3 9+ 5 8 + 4(2)4 + ( )<12,( )里最大可以填几?7 8 9四、看图列式计算。
(每题3分,共12分)=17 9+ =15 =11五、填表。
(8分)2.4+。
颗(颗)1.从16、6、7、9中选三个数写出四道算式。
第一组第二组男生有 5人 4人 女生有 8人 7人 一共有()人()人原有 9辆 16辆 开走 4辆 6辆 还剩()辆()辆六、解决问题。
(1、2题每题4分,3、4题每题6分,共20分)1.现在一共有多少辆车?2.—共捐了多少本书?我描了 8本书」我捐的和你同样多計匚CEL 乂开来9辆。
(1)打篮球的和打乒乓球的一共有多少人 ?CQ(2)打乒乓球的和游泳的一共有多少人?□0C 匸4.玩具大促销,价格如下图所示。
欢欢想买两个不同的玩具,最多花多少元?最少呢?馋的元粋最多:=—I最少: __________ =_() 9元8元(元答案、14 16 10 12 13 11 12 12 13 16 911 16 10 14 3 12 10、1.圈10个略2. < > > >3. + + + + —+ + —4. 9 8 6 9 6 4三、1.16 00=02.四、1.00口=回①2.□G&回㈤3.4. 003s回倔)1610 10五、13 11 5 104.最埶 9 Q R * 17(元)2. 3.⑴ (2133习=回UG&回4(本)最外IZKDIXk回(元)。
2023年安徽中考生物一轮专题复习:命题点11 第三单元诊断检测卷

2023年安徽中考生物一轮专题复习命题点11第三单元诊断检测卷总分:50一、单项选择题(本大题共20小题,每小题1分,共20分)1.紫菜营养丰富、味道鲜美,富含蛋白质、维生素和矿物质等营养物质。
下列植物中,与紫菜同属于藻类植物的是()A.葫芦藓B.马尾松C.贯众D.衣藻2.2022年4月,中国国家植物园在北京正式揭牌,其标志中包含了我国特有珍稀裸子植物银杏和水杉等元素(如图)。
这两种植物的基本特征是()A.具有假根、茎和叶的分化B.不具有输导组织C.种子裸露,无果皮包被D.生活在阴湿环境3.“花生玉米排骨汤”是人们喜爱的一道美食。
花生和玉米种子中贮存营养物质的结构分别是()A.子叶、子叶B.子叶、胚乳C.胚芽、胚乳D.子叶、胚芽4.选取相同的绿豆种子40粒,清水浸泡10小时,平均分成4组。
对每组种子的子叶进行不同处理后,放在相同且适宜的条件下培养10天,测量植株的高度,每组取平均值,具体如下表。
下列相关叙述错误的是()A.实验变量是“子叶完整程度”B.实验设计了甲组与其他三组对照C.实验结果是“子叶越完整植株越高”D.实验结论是“子叶贮存营养物质”5.4月中下旬是贵德梨花盛开的季节,如遇到阴雨连绵的天气会使梨树减产,造成该现象的原因最可能是阴雨天影响了梨树的()A.传粉过程B.蒸腾作用C.呼吸作用D.吸收作用6.冬瓜多蔓生,花呈黄色,大多为单性花,雌花和雄花的结构如图所示,下列叙述错误的是()A.冬瓜可以异花传粉,传粉媒介主要是昆虫B.雄蕊由含花粉的花药和含花粉管的花丝组成C.精子到达胚珠与卵细胞结合形成受精卵D.一个冬瓜中有许多种子,是因为子房中有许多胚珠7.荒漠的生态条件极为严酷,夏季炎热干旱,土壤贫瘠。
荒漠的植物种类十分贫乏,植被稀疏,根系一般很发达,非常耐旱。
下列关于植物根的描述,错误的是()A.发达的根系可以有效地固定植物体、吸收水分等物质B.在植物根尖的结构中,吸收水分的主要部位是成熟区C.根尖伸长区细胞比分生区细胞的体积大、长,这是细胞分化的结果D.植物的根尖之所以具有分裂能力,这是因为根尖具有分生组织8.某种植物可以通过输导组织向叶片输送有毒物质防止昆虫啃食。
单元滚动检测卷(七)
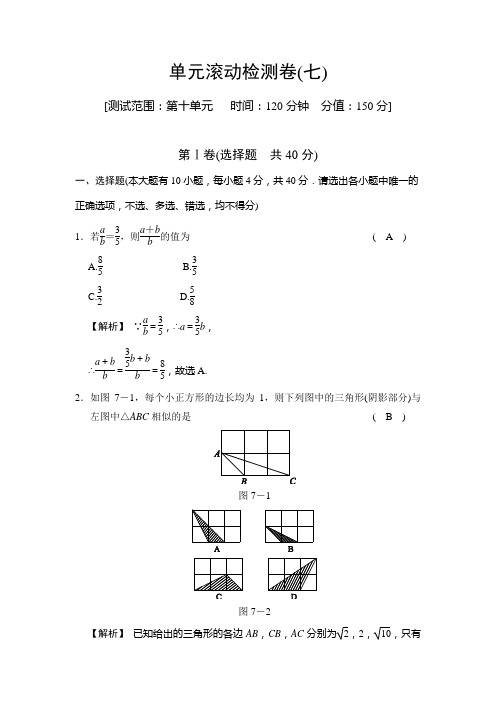
单元滚动检测卷(七)[测试范围:第十单元 时间:120分钟 分值:150分]第Ⅰ卷(选择题 共40分)一、选择题(本大题有10小题,每小题4分,共40分.请选出各小题中唯一的 正确选项,不选、多选、错选,均不得分) 1.若a b =35,则a +b b 的值为( A )A.85B.35C.32D.58【解析】 ∵a b =35,∴a =35b , ∴a +b b =35b +bb =85,故选A.2.如图7-1,每个小正方形的边长均为1,则下列图中的三角形(阴影部分)与左图中△ABC 相似的是( B)图7-1图7-2【解析】 已知给出的三角形的各边AB ,CB ,AC 分别为2,2,10,只有选项B 的各边分别为1,2,5与它的各边对应成比例.故选B.3.如图7-3所示,给出下列条件:①∠B=∠ACD;②∠ADC=∠ACB;③AC CD=ABBC;④AC2=AD·AB.其中单独能够判定△ABC∽△ACD的个数为(C)A.1 B.2C.3 D.4【解析】有3个.①∠B=∠ACD,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定.②∠ADC=∠ACB,再加上∠A为公共角,可以根据有两组角对应相等的两个三角形相似来判定.③中两组对应边的比相等,∠A不是对应边的夹角,故不正确.④可以根据两组对应边的比相等且相应的夹角相等的两个三角形相似来判定,故选C.图7-3图7-44.如图7-4是小明设计用手电来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C 处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是(B) A.6米B.8米C.18米D.24米【解析】∵△ABP∽△CDP,∴ABCD=BPPD,∴CD=1.2×121.8=8(米).故选B.5.手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边,其中每个图案花边的宽度都相等,那么,每个图案中花边的内外边缘所围成的几何图形不相似的是(D)图7-5【解析】虽然矩形的四个角相等,但每条边长减去同一个常数后,对应边不一定成比例,故选D.6.若△ABC∽△DEF,△ABC与△DEF的相似比为1∶2,则△ABC与△DEF 的周长比为(B) A.1∶4 B.1∶2C.2∶1 D.1∶ 2【解析】相似三角形的周长比等于相似比,故选B.7.如图7-6,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,若AD∶AB =3∶4,AE=6,则AC等于(D)图7-6A.3 B.4C.6 D.8【解析】∵DE∥BC,∴ADAB=AEAC,∴34=6AC,解得AC=8.8.如图7-7,P AB,PCD为⊙O的两条割线,AD,BC相交于点E,则图中相似三角形共有(C)图7-7A .0对B .1对C .2对D .3对【解析】 ∵∠BEA =∠DEC ,∠B =∠D , ∴△ABE ∽△CDE .∵∠B =∠D ,∠P =∠P ,∴△PBC ∽△PDA , ∴共有两对相似三角形.9.如图7-8,直角梯形ABCD 中,AB ∥CD ,∠C =90°,∠BDA =90°,AB =a ,BD =b ,CD =c ,BC =d ,AD =e ,则下列等式成立的是( A )图7-8A .b 2=acB .b 2=ceC .be =acD .bd =ae【解析】 ∵CD ∥AB ,∴∠CDB =∠DBA ,又∵∠C =∠BDA =90°, ∴△CDB ∽△DBA ,∴CD DB =BC AD =BDAB , 即c b =d e =b a , ∴b 2=ac ,故选A.10.如图7-9,在平行四边形ABCD 中,AC 与BD 交于点O ,E 为OD 的中点,连结AE 并延长交DC 于点F ,则DF ∶FC =( D )图7-9A.1∶4 B.1∶3C.2∶3 D.1∶2第Ⅱ卷(非选择题共110分)二、填空题(本大题有6小题,每小题5分,共30分)11.如图7-10,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上,则球拍击球的高度h为__1.5__m.图7-1012.如图7-11所示,DE是△ABC的中位线,则△ADE与△ABC的面积比为__1∶4__.图7-1113.如图7-12,在▱ABCD中,∠ABC的平分线BE交AD边于点E,交对角线AC于点F,若ABBC=35,则AFAC=__38__.图7-12【解析】∵四边形ABCD是平行四边形,∴AD∥BC,∴∠EBC=∠AEB.∵BE 是∠ABC 的角平分线, ∴∠EBC =∠AEB =∠ABE , ∴AB =AE .∵AB BC =35,∴AE BC =35.∵AD ∥BC ,∴△AFE ∽△CFB ,∴AE BC =AF FC =35,∴AFAC =AF AF +FC =33+5=38.14.如图7-13所示,⊙O 的两弦AB ,CD 交于点P ,连结AC ,BD ,得S △ACP ∶S △DBP =16∶9,则AC ∶BD =__4∶3__.图7-13【解析】 相似三角形对应边的比等于面积比的算术平方根.由同弧所对的圆周角相等,易知∠B =∠C ,∠D =∠A , ∴△ACP ∽△DBP , ∴⎝ ⎛⎭⎪⎫AC BD 2=S △ACP S △DBP =169, ∴AC BD =169=43.15.如图7-14,△ABC 中,点D 在边AB 上,满足∠ACD =∠ABC ,若AC =2,AD =1,则DB =__3__.【解析】 由于∠ACD =∠ABC ,∠BAC =∠CAD ,所以△ADC ∽△ACB ,所以AC AB =AD AC ,即AB ·AD =AC 2,则AB =AC 2AD=4,所以BD =AB -AD =3.图7-14图7-1516.如图7-15,已知△ABC,AB=AC=1,∠A=36°,∠ABC的平分线BD交AC于点D,则AD的长是2,cos A的值是4结果保留根号).【解析】∵△ABC中,AB=AC=1,∠A=36°,∴∠ABC=∠ACB=180°-∠A2=72°.∵BD是∠ABC的平分线,∴∠ABD=∠DBC=12∠ABC=36°,∴∠A=∠ABD=∠DBC=36°,∠BDC=∠C=72°.又∵∠C=∠C,∴△ABC∽△BDC,∴ACBC=BCCD.设AD=x,则BD=BC=AD=x,则1x=x1-x,解得x=-5-12(舍去)或x=5-12,故x=5-1 2.过点D作DE⊥AB于点E,∵AD=BD,∴E为AB的中点,即AE=12AB=12.在Rt△AED中,cos A=AEAD=125-12=5+14.三、解答题(本大题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)17.已知x2=y3=z4,(1)求x-2yz的值;(2)若x+3=z-y,求x的值.解:由x2=y3=z4,设x=2k,y=3k,z=4k,则(1)x-2yz=2k-6k4k=-1.(2)x+3=z-y可化为2k+3=k,∴2k+3=k2,即k2-2k-3=0,∴k=3或k=-1,经检验,k=-1不符合题意,∴k=3,从而x=2k=6,即x=6.18.如图7-16,△ABC∽△DAB,AB=8,BC=12,求AD的长.图7-16解:∵△ABC∽△DAB,∴BCAB=ABAD.∵AB=8,BC=12,∴128=8AD,∴AD=16 3.19.如图7-17,四边形ABCD是平行四边形,点F在BA的延长线上,连结CF交AD于点E.(1)求证:△CDE∽△F AE;(2)当E是AD的中点,且BC=2CD时,求证:∠F=∠BCF.图7-17证明:(1)∵四边形ABCD是平行四边形,∴CD∥AB,即CD∥F A,∴△CDE∽△F AE;(2)∵△CDE∽△F AE,DE=EA,∴△CDE≌△F AE,∴CD=AF,∴BF=2CD.∵BC=2CD,∴BF=BC,∴∠F=∠BCF.20.已知:如图7-18,在△ABC中,∠C=90°,点D,E分别在边AB,AC 上,DE∥BC,DE=3,BC=9.(1)求ADAB的值;(2)若BD=10,求sin A的值.图7-18 解:(1)∵DE∥BC,∴△ADE∽△ABC,∴ADAB=DEBC.又∵DE=3,BC=9,∴ADAB=39=13.(2)根据(1)中ADAB=DEBC得ADAD+BD=DEBC.∵BD=10,DE=3,BC=9,∴ADAD+10=3 9,∴AD=5,∴AB=3AD=15,∴sin A=BCAB=915=35.21.如图7-19,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD 相似,已知AB=4.(1)求AD的长;(2)求矩形DMNC与矩形ABCD的相似比.图7-19解:(1)由已知得MN=AB,MD=12AD=12BC,∵矩形DMNC与矩形ABCD相似,∴DMAB=MNBC.∵MN=AB,DM=12AD,BC=AD,∴12AD2=AB2,∴由AB=4,得AD=42;(2)矩形DMNC与矩形ABCD的相似比为DMAB=224=22.22.已知如图7-20,在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连结BD,AE⊥BD,垂足为E.(1)求证:△ABE∽△DBC;(2)求线段AE的长.图7-20解:(1)证明:∵AB=AD=25,∴∠ABD=∠ADB.∵AD∥BC,∴∠ADB=∠DBC,∴∠ABD=∠DBC.∵AE⊥BD,∴∠AEB=∠C=90°,∴△ABE∽△DBC.(2)∵AB=AD,又AE⊥BD,∴BE=DE,∴BD=2BE.由△ABE∽△DBC,得ABBD=BEBC.∵AB=AD=25,BC=32,∴252BE=BE32,∴BE=20,∴AE=AB2-BE2=252-202=15.23.如图7-21,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB =12,BC=5,BE⊥DC交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求DE的长;图7-21 解:(1)∵AB=DB,∴∠BDA=∠BAD.又∵∠BDA和∠BCA是弧AB所对的圆周角,∴∠BDA=∠BCA.∴∠BCA=∠BAD.(2)∵在Rt△ABC中,AB=12,BC=5,∴AC=AB2+BC2=13.又∵∠BAC和∠BDC是弧BC所对的圆周角,∴∠BAC=∠BDC.∵∠ABC=∠DEB=90°,∠BAC=∠BDC,∴△ACB∽△DBE.∴ABDE=ACBD.∴DE=AB·BDAC=12×1213=14413.24.如图7-22,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别与边AB,BC所在的直线相交,交点分别为E,F.图7-22(1)当PE⊥AB,PF⊥BC时,如图(1),则PEPF的值为________;(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图(2),求PEPF的值;(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP∶PC=1∶2时,如图(3),PEPF的值是否有变化?证明你的结论.解:(1)3(2)如图(1),过点P作PH⊥AB,PG⊥BC,垂足分别为H,G,则∠PHE=∠PGB =∠PGF=90°.由(1)得PHPG= 3.第24题答图(1)又∵∠ABC=90°,∴四边形PHBG为矩形,∴∠HPG=90°,∴∠HPE+∠EPG=90°,又∵∠EPF=∠EPG+∠GPF=90°,∴∠HPE=∠GPE=α,又∵∠EHP=∠PGF=90°,∴Rt△PHE∽Rt△PGF,∴PEPF=PHPG,∴PEPF= 3.(3)PEPF的值有变化.证明:如图(2),过点P作PH⊥AB,PG⊥BC,垂足分别为H,G,第24题答图(2)(3)则∠AHP=∠ABC=∠PGC=90°,∴HP∥BC,∴∠APH=∠PCG,∴△APH∽△PCG,∴PHCG=APPC=12.在Rt△PCG中,∠PCG=30°,tan∠PCG=PGCG,∴PGCG=3 3,∴CG=3PG,∴PH3PG=12,∴PHPG=3 2.同(2)中可证得PEPF=PHPG=32.。
牛津版小学三年级下册英语第十单元检测

1.听录音并判断,相符的打√,不相符的打×。(12分)
2.听录音,判断图片与录音是否相符,相符的画“ ”,不相符的画“ ”。(8分)
(1) (2)
(3)(4)
3.听录音,根据所听内容标上序号。(10分)
belt shoes tie nice would
( ) () ( )( )( )
参考答案
1.× × √ × √ √
【解析】volleyball (2)baseball (3)basketball (4)accordion (5)football (6) piano
2.(1) (2) (3) (4)
【解析】(1)Do you play the piano? No, I don’t. I play the violin.
( ) (2)What do you play? B. Thank you.
( )(3)What would you like? C. No, I don’t.
( )(4)Let’s go and play volleyball. D. Great. Let’s go.
( ) (5)Here you are. E. I play the piano.
5.听录音,判断下列句子与所听内容是否相符,相符的打√,不相符的打×。(10分)
( )(1)Do you play baseball? No, I don’t.
( )(2)What do you play?
( )(3)I play basketball.
( )(4)What about the red one?
(3) Can I play the guitar?
(4) I’d like a hat.
人教版八年级数学上册 第11章 三角形单元测试卷(含答案) (4)

单元检测试卷第十一单元三角形考试时间:120分钟;满分:150分学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共10小题,每小题4分,共40分)1.如图,在△ABC中,∠ACB=90°,∠ADC=90°,则△ABC斜边AB上的高为()A.CD B.AC C.BC D.BD第1题第2题第4题第5题2.如图AD⊥BC于点D,那么图中以AD为高的三角形有()个A.3B.4C.5D.63.已知三角形的三边长分别为2、x、10,若x为正整数,则这样的三角形个数为()A.1B.2C.3D.44.如图,在△ABC中,点D是∠ABC和∠ACB角平分线的交点,若∠BDC=110°,那么∠A=()A.40°B.50°C.60°D.70°5.如图在△ABC中,D是AB上一点,E是AC上一点,BE,CD相交于点F,∠A=70°,∠ACD=20°,∠ABE=32°,则∠CFE的度数为()A.68°B.58°C.52°D.48°6.如图,顺次连结同一平面内A,B,C,D四点,已知∠A=40°,∠C=20°,∠ADC =120°,若∠ABC的平分线BE经过点D,则∠ABE的度数()A.20°B.30°C.40°D.60°第6题第9题第10题7.直角三角形的一个锐角∠A是另一个锐角∠B的3倍,那么∠B的度数是()A.22.5°B.45°C.67.5°D.135°8.一个多边形截去一角后,变成一个八边形则这个多边形原来的边数是()A.8或9B.2或8C.7或8或9D.8或9或10 9.如图,∠1,∠2,∠3是五边形ABCDE的3个外角,若∠A+∠B=220°,则∠1+∠2+∠3=()A.140°B.180°C.220°D.320°10.把一副直角三角板按如图所示的方式摆放在一起,其中∠C=90°,∠F=90°,∠D =30°,∠A=45°,则∠1+∠2等于()A.270°B.210°C.180°D.150°二、填空题(本大题共4小题,每小题5分,共20分)11.如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD 与BE交于H,则∠CHD=.12.如图,在△ABC中,∠B=60°,AD平分∠BAC,点E在AD延长线上,且EC⊥AC.若∠E=50°,则∠ADC的度数是.13.如图,把三角形纸片ABC折叠,使得点B,点C都与点A重合,折痕分别为DE,MN,若∠BAC=110°,则∠DAM=度.14.一个正多边形的每个内角都是150°,则它是正边形.三、解答题(本大题共9小题,满分90分,其中第15,16,17,18题每题8分,19,20题每题10分,21,22题每题12分,23题14分)15.若a,b,c是△ABC的三边,化简:|a﹣b+c|+|c﹣a﹣b|﹣|a+b+c|.16.如图,五边形ABCDE的内角都相等,且AB=BC,AC=AD,求∠CAD的度数.17.(1)已知三角形三个内角的度数比为1:2:3,求这个三角形三个外角的度数.(2)一个正多边形的内角和为1800°,求这个多边形的边数.18.如图,△ABC中,A1,A2,A3,…,A n为AC边上不同的n个点,首先连接BA1,图中出现了3个不同的三角形,再连接BA2,图中便有6个不同的三角形…(1)完成下表:(2)若出现了45个三角形,则共连接了多少个点?(3)若一直连接到A n,则图中共有个三角形.19.如图,点P是△ABC内任意一点,求证:PA+PB+PC>AB+BC+AC.20.如图,在Rt△ABC中,∠ACB=90°,∠A=40°,△ABC的外角∠CBD的平分线BE 交AC的延长线于点E,点F为AC延长线上的一点,连接DF.(1)求∠CBE的度数;(2)若∠F=25°,求证:BE∥DF.21.如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:(1)∠BAE的度数;(2)∠DAE的度数;(3)探究:小明认为如果条件∠B=70°,∠C=30°改成∠B﹣∠C=40°,也能得出∠DAE的度数?若能,请你写出求解过程;若不能,请说明理由.22.我们定义:在一个三角形中,如果一个角的度数是另一个角度数的3倍,那么这样的三角形我们称之为“和谐三角形”.如:三个内角分别为105°,40°,35°的三角形是“和谐三角形”概念理解:如图1,∠MON=60°,在射线OM上找一点A,过点A作AB⊥OM交ON于点B,以A为端点作射线AD,交线段OB于点C(点C不与O,B重合)(1)∠ABO的度数为,△AOB(填“是”或“不是”)“和谐三角形”;(2)若∠ACB=80°,求证:△AOC是“和谐三角形”.应用拓展:如图2,点D在△ABC的边AB上,连接DC,作∠ADC的平分线交AC于点E,在DC 上取点F,使∠EFC+∠BDC=180°,∠DEF=∠B.若△BCD是“和谐三角形”,求∠B的度数.23.【问题背景】(1)如图1的图形我们把它称为“8字形”,请说理证明∠A+∠B=∠C+∠D【简单应用】(2)如图2,AP、CP分别平分∠BAD、∠BCD,若∠ABC=20°,∠ADC=26°,求∠P的度数(可直接使用问题(1)中的结论)【问题探究】(3)如图3,直线AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,若∠ABC=36°,∠ADC=16°,猜想∠P的度数为【拓展延伸】(4)在图4中,若设∠C=x,∠B=y,∠CAP=∠CAB,∠CDP=∠CDB,试问∠P与∠C、∠B之间的数量关系为(用x、y表示∠P)(5)在图5中,AP平分∠BAD,CP平分∠BCD的外角∠BCE,猜想∠P与∠B、∠D 的关系,直接写出结论.参考答案与试题解析一.选择题(共10小题)1.解:∵∠ADC=90°,∴CD⊥AB,∴CD是△ABC斜边上的高,故选:A.2.解:∵AD⊥BC于D,而图中有一边在直线CB上,且以A为顶点的三角形有6个,∴以AD为高的三角形有6个.故选:D.3.解:∵10﹣2=8,10+2=12,∴8<x<12,∵若x为正整数,∴x的可能取值是9,10,11,故这样的三角形共有3个.故选:C.4.解:∵∠BDC=110°,∴∠DBC+∠DCB=70°,∵点D是∠ABC和∠ACB角平分线的交点,∴∠ABC+∠ACB=2(∠DBC+∠DCB)=140°,∴∠A=180°﹣140°=40°,故选:A.5.解:∵∠A=70°,∠ACD=20°,∴∠BDF=∠A+∠ACD=70°+20°=90°,在△BDF中,∠BFD=180°﹣∠BDF﹣∠ABE=180°﹣90°﹣32°=58°,∴∠CFE=∠BFD=58°.故选:B.6.解:∵∠ADE=∠ABD+∠A,∠EDC﹣∠DBC+∠C,∴∠ADC=∠ADE+∠EDC=∠A+∠C+∠ABC,∴120°=40°+20°+∠ABC,∴∠ABC=60°,∵BE平分∠ABC,∴∠ABE=∠ABC=30°,故选:B.7.解:设∠B=x°,则∠A=3x°,由直角三角形的性质可得∠A+∠B=90°,∴x+3x=90,解得x=22.5,∴∠B=22.5°,故选:A.8.解:∵截去一个角后边数可以增加1,不变,减少1,∴原多边形的边数是7或8或9.故选:C.9.解:根据∠A+∠B=220°,可知∠A的一个邻补角与∠B的一个邻补角的和为360°﹣220°=140°.根据多边形外角和为360°,可知∠1+∠2+∠3=360°﹣140°=220°.故选:C.10.解:如图:∵∠1=∠D+∠DOA,∠2=∠F+∠FPB,∵∠DOA=∠COP,∠EPB=∠CPO,∴∠1+∠2=∠D+∠F+∠COP+∠CPO=∠D+∠F+180°﹣∠C=30°+90°+180°﹣90°=210°.故选:B.二.填空题(共4小题)11.解:在△ABC中,三边的高交于一点,所以CF⊥AB,∵∠BAC=75°,且CF⊥AB,∴∠ACF=15°,∵∠ACB=60°,∴∠BCF=45°在△CDH中,三内角之和为180°,∴∠CHD=45°,故答案为∠CHD=45°.12.解:∵EC⊥AC.∠E=50°,∴∠DAC=40°,∵AD平分∠BAC,∴∠BAD=40°,∵∠B=60°,∴∠ADC=40°+60°=100°,故答案为:100°.13.解:∵∠BAC=110°,∴∠B+∠C=180°﹣∠BAC=70°,∵把三角形纸片ABC折叠,使得点B,点C都与点A重合,∴∠BAD=∠B,∠CAM=∠C,∴∠BAD+∠CAM=∠B+∠C=70°,∴∠DAM=∠BAC﹣∠BAD﹣∠CAM=110°﹣70°=40°,故答案为:40.14.解:∵一个正多边形的每个内角为150°,∴它的外角为30°,360°÷30°=12,故答案为:十二.三.解答题(共9小题)15.解:∵a、b、c是△ABC的三边,∴a﹣b+c>0,c﹣a﹣b<0,a+b+c>0,∴原式=a﹣b+c++a+b﹣c﹣a﹣b﹣c=a﹣b﹣c.16.证明:∵五边形ABCDE的内角都相等,∴∠BAE=∠B=∠BCD=∠CDE=∠E=(5﹣2)×180°÷5=108°,∵AB=AC,∴∠1=∠2=(180°﹣108°)÷2=36°,∴∠ACD=∠BCD﹣∠2=72°,∵AC=AD,∴∠ADC=∠ACD=72°,∴∠CAD=180°﹣∠ACD﹣∠ADC=36°.17.解:(1)设此三角形三个内角的比为x,2x,3x,则x+2x+3x=180,6x=180,x=30,则三个内角分别为30°、60°、90°,相应的三个外角分别为150°、120°、90°.(2)设这个多边形的边数是n,则(n﹣2)•180°=1800°,解得n=12.故这个多边形的边数为12.18.解:(1)(2)8个点;(3)1+2+3+…+(n+1)=[1+2+3+…+(n+1)+1+2+3+…+(n+1)]=(n+1)(n+2).故答案为(n+1)(n+2).19.证明:∵PA+PB>AB,PB+PC>BC,PC+PA>AC.∴把它们相加,再除以2,得PA+PB+PC>AB+BC+AC.20.解:(1)∵在Rt△ABC中,∠ACB=90°,∠A=40°,∴∠ABC=90°﹣∠A=50°,∴∠CBD=130°.∵BE是∠CBD的平分线,∴∠CBE=∠CBD=65°;(2)∵∠ACB=90°,∠CBE=65°,∴∠CEB=90°﹣65°=25°.又∵∠F=25°,∴∠F=∠CEB=25°,∵DF∥BE.21.解:(1)∵∠B+∠C+∠BAC=180°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣70°﹣30°=80°,∵AE平分∠BAC,∴∠BAE=∠BAC=40°;(2)∵AD⊥BC,∴∠ADE=90°,而∠ADE=∠B+∠BAD,∴∠BAD=90°﹣∠B=90°﹣70°=20°,∴∠DAE=∠BAE﹣∠BAD=40°﹣20°=20°;(3)能.∵∠B+∠C+∠BAC=180°,∴∠BAC=180°﹣∠B﹣∠C,∵AE平分∠BAC,∴∠BAE=∠BAC=(180°﹣∠B﹣∠C)=90°﹣(∠B+∠C),∵AD⊥BC,∴∠ADE=90°,而∠ADE=∠B+∠BAD,∴∠BAD=90°﹣∠B,∴∠DAE=∠BAE﹣∠BAD=90°﹣(∠B+∠C)﹣(90°﹣∠B)=(∠B﹣∠C),∵∠B﹣∠C=40°,∴∠DAE=×40°=20°.22.解:(1)∵AB⊥OM,∴∠OAB=90°,∴∠ABO=90°﹣∠MON=30°,∵∠OAB=3∠ABO,∴△AOB为“和谐三角形”,故答案为:30;是;(2)证明:∵∠MON=60°,∠ACB=80°,∵∠ACB=∠OAC+∠MON,∴∠OAC=80°﹣60°=20°,∵∠AOB=60°=3×20°=3∠OAC,∴△AOC是“和谐三角形”;应用拓展:∵∠EFC+∠BDC=180°,∠ADC+∠BDC=180°,∴∠EFC=∠ADC,∴AD∥EF,∴∠DEF=∠ADE,∵∠DEF=∠B,∴∠B=∠ADE,∴DE∥BC,∴∠CDE=∠BCD,∵AE平分∠ADC,∴∠ADE=∠CDE,∴∠B=∠BCD,∵△BCD是“和谐三角形”,∴∠BDC=3∠B,或∠B=3∠BDC,∵∠BDC+∠BCD+∠B=180°,∴∠B=36°或∠B=.23.(1)证明:在△AOB中,∠A+∠B+∠AOB=180°,在△COD中,∠C+∠D+∠COD=180°,∵∠AOB=∠COD,∴∠A+∠B=∠C+∠D;(2)解:如图2,∵AP、CP分别平分∠BAD,∠BCD,∴∠1=∠2,∠3=∠4,由(1)的结论得:,①+②,得2∠P+∠2+∠3=∠1+∠4+∠B+∠D,∴∠P=(∠B+∠D)=23°;(3)解:如图3,∵AP平分∠BAD的外角∠FAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4,∴∠PAD=180°﹣∠2,∠PCD=180°﹣∠3,∵∠P+(180°﹣∠1)=∠D+(180°﹣∠3),∠P+∠1=∠B+∠4,∴2∠P=∠B+∠D,∴∠P=(∠B+∠D)=×(36°+16°)=26°;故答案为:26°;【拓展延伸】(4)同法可得:∠P=x+y;故答案为:∠P=x+y,(5)同法可得:∠P=.故答案为:∠P=.。
2020年最新青岛版一年级数学下册单元测试题及答案大全套

(2)小丽比小娟少拍了多少下? □ □=□(下)
(3)小勇再拍多少下就和小娟拍的一样多了? □ 2.小康遇到了几个小朋友?
□= □ (下 )
2020年最新
□ □=□(个) 3.捉迷藏。
4.谁起得最早?
附加题: (10 分) 小丽今年 11 岁,小明今年 4 岁。 3 年后,小丽比小明大多少岁? □ □=□(岁)
2020年最新
答案
一、 8 8 8 2 13 7 7 5 9 12 二、 8 7
三、 四、= < < > = < = < > < < > 五、 7 2 2 5 六、 3 5 9 6 4 5 七、 7 9 16 8 八、 11-3=8(块) 13-6=7(个) 14-5=9(个) 8+5=13(个) 13-5=8(个) 13-8=5(个)
1.青蛙妈妈捉了多少条虫子?
( )个 7个 6个
= (条)
2. ( 1)两组一共做了多少朵花?
= (朵)
( 2)二组再做几朵就和一组做的一样多了?
= (朵)
2020年最新
3.原来有 12 件衣服。卖出去多少件?
= (件)
4. ( 1)每个小朋友吃一个苹果,还剩几个苹果?
= (个) ( 2)你还能提出什么问题?并解答。
1.
2.
=
(块 )
=
(只 )
2020年最新
七、完成表格。 (9 分)
原有 12 台
( )辆
15 块 八、解决问题。 (共 28 分) 1.房子里还剩下几只小鸡? (6 分)
卖出 5台
还剩 ( )台
9辆
9 (6 分)
=
(只 )
=
(个)
3. (1)小白比小黑多几个松果? (5 分)
2020-2021学年沪科版八年级物理全一册第十一章 小粒子与大宇宙单元检测卷(含答案)

2020-2021学年下学期八年级物理单元检测第十一单元小粒子与大宇宙考试时间:45分钟班级:______姓名:_______座号:_______一、单选题(每小题2分,共32分)1.在原子中,带负电的是()A.电子B.质子C.中子D.原子2.端午情浓,粽叶飘香.端午节那天,小明家里弥漫着粽子的清香.这一现象表明()A.分子间存在引力 B.分子间存在斥力C.温度越高分子运动越慢 D.分子在不停地做无规则的运动3.下列现象中用分子动理论解释的是()A.春天,柳絮飞舞B.夏天,茉莉花飘香C.秋天,黄沙扑面D.冬天,雪花飘飘4.通过可直接感知的现象,推测无法直接感知的物理规律,这是物理学中常用的探究方法,下列根据所列现象进行的推测既合理义符合事实的是()A.现象:空气中沙尘飞舞;推测:分子在做无规则运动B.现象:用手捏海绵,海绵的体积变小了;推测:分子之间有空隙C.现象:破镜不能重圆;推测:分子之间存在排斥力D.现象:将两块表面平滑的的铅块压紧后,它们会粘在一起,推测:分子间存在吸引力5.关于原子核式结构模型看法,下列说法正确的是()A.原子是由原子核和核外质子组成B.原子核是由带正电的质子和不带电的中子组成C.组成原子核的质子带负电,中子不带电D.夸克是由比其更小的质子与中子组成6.关于粒子和宇宙,下列说法正确的是()A.物质是由分子组成的,分子是不可再分的B.宇宙是一个有层次的天体系统,太阳是宇宙的中心C.汤姆生建立了类似于行星绕日的原子核式结构模型D.银河系、地球、分子、原子核是按照尺度由大到小的顺序排列的7.下列各项排列中,按照尺度的数量级由大到小排列的是()A.银河系、太阳系、地球、生物体、分子、原子核、电子B.太阳系、银河系、地球、生物体、原子核、分子、电子C.银河系、太阳系、地球、生物体、原子核、分子、电子D.太阳系、银河系、地球、生物体、分子、原子核、电子8.科学探究需要进行实验,在取得数据和事实后,再进行分析和推理,因此,在科学探究中我们需要区分事实与推论。
