北师大版2021年中考数学总复习《整式的乘除》(含答案)
新版北师大七年级数学下册第一章《整式的乘除运算》知识点总结及习题

第一章整式的乘除知识点总结一、单项式:数字与字母的乘积组成的代数式叫做单项式。
单独的一个数或一个字母也是单项式。
一个单项式中,数字因数叫做这个单项式的系数,所有字母的指数和叫做这个单项式的次数。
注意:π是数字,而不是字母,它的系数是π,次数是0. 二、多项式几个单项式的代数和叫做多项式。
其中每个单项式叫做这个多项式的项。
多项式中不含字母的项叫做常数项。
多项式中次数最高的项的次数,叫做这个多项式的次数。
三、整式:单项式和多项式统称为整式。
四、整式的加减法:整式加减法的一般步骤:(1)去括号;(2)合并同类项。
五、幂的运算性质:1、同底数幂的乘法:),(都是正整数n m aa a nm nm+=∙2、幂的乘方:),(都是正整数)(n m a a mnn m =3、积的乘方:)()(都是正整数n b a ab nnn= 4、同底数幂的除法:)0,,(≠=÷-a n m a a a nm nm都是正整数六、零指数幂和负整数指数幂: 1、零指数幂:);0(10≠=a a 2、负整数指数幂:),0(1是正整数p a aa p p≠=- 七、整式的乘除法:1、单项式乘以单项式:法则:单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,其余的字母连同它的指数不变,作为积的因式。
2、单项式乘以多项式:法则:单项式与多项式相乘,就是根据分配律用单项式去乘多项式的每一项,再把所得的积相加。
3、多项式乘以多项式:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。
4、单项式除以单项式:单项式相除,把系数、同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的一个因式。
5、多项式除以单项式:多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加。
八、整式乘法公式:1、平方差公式: 22))((b a b a b a -=-+2、完全平方公式: 2222)(b ab a b a ++=+ 2222)(b ab a b a +-=-七年级数学(下)第一章《整式的运算》一、 知识点:1、都是数与字母的乘积的代数式叫做单项式(单独的一个数或一个字母也是单项式);几个单项式的和叫做多项式;单项式和多项式统称整式。
完整word版北师大版七年级下册数学第一章整式的乘除附答案
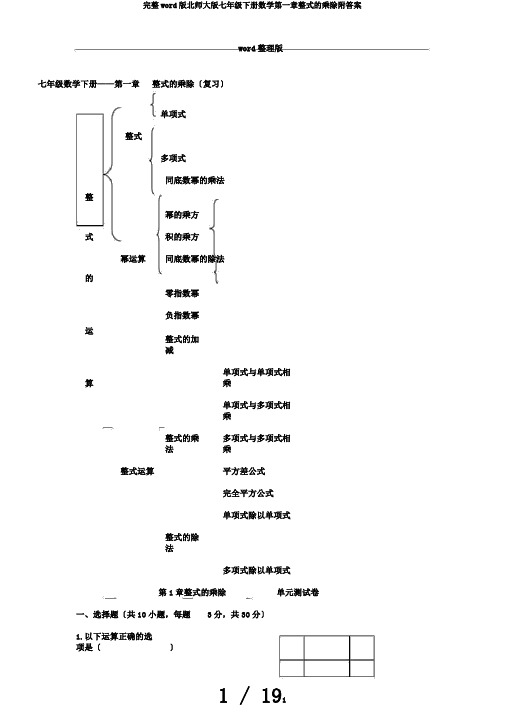
word整理版七年级数学下册——第一章整式的乘除〔复习〕单项式整式多项式整同底数幂的乘法幂的乘方式积的乘方的幂运算同底数幂的除法零指数幂运负指数幂整式的加减算单项式与单项式相乘单项式与多项式相乘整式的乘法多项式与多项式相乘整式运算平方差公式完全平方公式单项式除以单项式整式的除法多项式除以单项式第1章整式的乘除单元测试卷一、选择题〔共10小题,每题3分,共30分〕1.以下运算正确的选项是〔〕A.a4a5a9B.a3a3a33a3C.2a43a56a9D.a34a720213202 12.52〔〕135A.1B.1C.0D.19973.设5a3b25a3b2A,那么A=〔〕A.30abB.60abC.15abD.12ab4.x y5,xy3,那么x2y2〔〕A.25.B25C19D、195.x a3,x b 5,那么x3a2b〔〕A、27B、9C、3D、52251056..如图,甲、乙、丙、丁四位同学给出了四a b a种表示该长方形面积的多项式:m学习参考资料nword 整理版①(2a+b)(m+n); ②2a(m+n)+b(m+n); ③m(2a+b)+n(2a+b); ④2am+2an+bm+bn ,你认为其中正确的有A 、①②B 、③④C 、①②③D 、①②③④〔 〕7.如(x+m)与(x+3) 的乘积中不含 x 的一次项,那么m 的值为〔〕A 、–3B 、3C 、0D 、12128..(a+b)=9,ab=-12,那么a2+b 的值等于〔〕A 、84B、78C 、12D 、62 244〕9.计算〔a -b 〕〔a+b 〕〔a+b 〕〔a -b 〕的结果是〔A .a 8+2a 4b 4+b 8B .a 8-2a 4b 4+b 8C .a 8+b 8D .a 8-b 810. P7 m 1,Qm 28m 〔m 为任意实数〕,那么P 、Q 的大小关系为15 15〔〕A 、PQB 、P QC 、PQD、不能确定二、填空题〔共 6小题,每题4分,共 24分〕11. 设4 x 2mx 121 是一个完全平方式,那么m=_______。
专题1.2 整式的乘法-重难点题型(举一反三)(北师大版)(解析版)

专题1.2 整式的乘法-重难点题型【北师大版】【题型1 整式乘法中的求值问题】【例1】(2021•开平区一模)已知等式(x+p)(x+q)=x2+mx+36(p,q为正整数),则m的值不可能是( )A.37B.13C.20D.36【分析】利用多项式乘多项式的法则,把等式的左边进行运算,再根据条件进行分析即可.【解答】解:(x+p)(x+q)=x2+(p+q)x+pq,∵(x+p)(x+q)=x2+mx+36,∴p+q=m,pq=36,∵36=4×9,则p+q=13,36=1×36,则p+q=37,36=2×18,则p+q=20,36=3×12,则p+q=15,36=6×6,则p+q=12,∴p+q不可能为36,即m不可能为36.故选:D.【变式1-1】(2021春•潍坊期末)若(x+a)(x﹣5)=x2+bx﹣10,则ab﹣a+b的值是( )A.﹣11B.﹣7C.﹣6D.﹣55【分析】先利用多项式乘多项式法则计算等式的左边,根据等式得到a、b的值,代入计算出代数式ab﹣a+b的值.【解答】解:∵(x+a)(x﹣5)=x2+(a﹣5)x﹣5a,又∵(x+a)(x﹣5)=x2+bx﹣10,∴x2+(a﹣5)x﹣5a=x2+bx﹣10.∴a﹣5=b,﹣5a=﹣10.∴a=2,b=﹣3.∴ab﹣a+b=2×(﹣3)﹣2﹣3=﹣11.故选:A.【变式1-2】(2020秋•播州区期末)若x+y=2,xy=﹣1,则(1﹣2x)(1﹣2y)的值是 .【分析】根据多项式乘以多项式的法则展开,整理后整体带入求值即可.【解答】解:(1﹣2x)(1﹣2y)=1﹣2y﹣2x+4xy=1﹣2(x+y)+4xy,当x+y=2,xy=﹣1时原式=1﹣2×2+4×(﹣1)=﹣7.故答案为:﹣7.【变式1-3】(2021春•江都区期中)在计算(2x+a)(x+b)时,甲错把b看成了6,得到结果是:2x2+8x﹣24;乙错把a看成了﹣a,得到结果:2x2+14x+20.(1)求出a,b的值;(2)在(1)的条件下,计算(2x+a)(x+b)的结果.【分析】(1)根据题意得出(2x+a)(x+6)=2x2+(12+a)x+6a=2x2+8x﹣24,(2x﹣a)(x+b)=2x2+(﹣a+2b)x﹣ab=2x2+14x+20,得出12+a=8,﹣a+2b=14,求出a、b即可;(2)把a、b的值代入,再根据多项式乘以多项式法则求出即可.【解答】解:(1)甲错把b看成了6,(2x+a)(x+6)=2x2+12x+ax+6a=2x2+(12+a)x+6a=2x2+8x﹣24,∴12+a=8,解得:a=﹣4;乙错把a看成了﹣a,(2x﹣a)(x+b)=2x2+2bx﹣ax﹣ab=2x2+(﹣a+2b)x﹣ab=2x2+14x+20,∴2b﹣a=14,把a=﹣4代入,得b=5;(2)当a=﹣4,b=5时,(2x+a)(x+b)=(2x﹣4)(x+5)=2x2+10x﹣4x﹣20=2x2+6x﹣20.【题型2 整式乘法中的不含某项问题】【例2】(2021春•蜀山区校级期中)关于x的代数式(mx﹣2)(2x+1)+x2+n化简后不含有x2项和常数项.(1)分别求m,n的值.(2)求m2020n2021的值.【分析】(1)先展开整理原式,再根据题意建立关于m、n的等式,分别求解即可得出结论.(2)同底数幂乘法的逆运算,使n2021变为n2020•n,再利用积的乘方逆运算即可求出原式的值.【解答】解:(1)原式=2mx2+mx﹣4x﹣2+x2+n,=(2m+1)x2+mx﹣4x+n﹣2,由题意2m+1=0,n﹣2=0,∴m=―12,n=2.(2)原式=m2020•n2020•n,=(m•n)2020•n,由(1)得m=―12,n=2,原式=(―12×2)2020×2,=2.【变式2-1】(2021春•通川区校级月考)若多项式x2+mx﹣8和x2﹣3x+n的的乘积中不含x2和x3的项,求m+n的值.【分析】利用多项式的乘法法则将两个多项式的乘积展开,令x2项和x3项的系数为0,结论可得.【解答】解:由题意:(x2+mx﹣8)(x2﹣3x+n)=x4﹣3x3+nx2+mx3﹣3mx2+mnx﹣8x2+24x﹣8n=x4+(m﹣3)x3+(n﹣3m﹣8)x2+(mn+24)x﹣8n.∵乘积中不含x2和x3的项,∴m﹣3=0,n﹣3m﹣8=0.∴m=3,n=17.∴m+n=20.【变式2-2】(2021春•金牛区校级月考)已知(x3+mx+n)(x2﹣3x+4)展开式中不含x3和x2项.(1)求m、n的值;(2)当m、n取第(1)小题的值时,求(m+n)(m2﹣mn+n2)的值.【分析】(1)利用多项式乘以多项式法则计算得到结果,根据展开式中不含x2和x3项列出关于m与n 的方程组,求出方程组的解即可得到m与n的值;(2)先利用多项式乘以多项式的法则将(m+n)(m2﹣mn+n2)展开,再合并同类项化为最简形式,然后将(1)中所求m、n的值代入计算即可.【解答】解:(1)(x3+mx+n)(x2﹣3x+4)=x5﹣3x4+(m+4)x3+(n﹣3m)x2+(4m﹣3n)x+4n,根据展开式中不含x2和x3项得:m+4=0 n―3m=0,解得:m=―4n=―12.即m=﹣4,n=﹣12;(2)∵(m+n)(m2﹣mn+n2)=m3﹣m2n+mn2+m2n﹣mn2+n3=m3+n3,当m=﹣4,n=﹣12时,原式=(﹣4)3+(﹣12)3=﹣64﹣1728=﹣1792.【变式2-3】(2021春•太湖县期末)【知识回顾】七年级学习代数式求值时,遇到这样一类题“代数式ax﹣y+6+3x﹣5y﹣1的值与x的取值无关,求a的值”,通常的解题方法是:把x、y看作字母,a看作系数合并同类项,因为代数式的值与x的取值无关,所以含x项的系数为0,即原式=(a+3)x﹣6y+5,所以a+3=0,则a=﹣3.【理解应用】(1)若关于x的多项式(2x﹣3)m+2m2﹣3x的值与x的取值无关,求m值;(2)已知A=(2x+1)(x﹣1)﹣x(1﹣3y),B=﹣x2+xy﹣1,且3A+6B的值与x无关,求y的值;【能力提升】(3)7张如图1的小长方形,长为a,宽为b,按照图2方式不重叠地放在大长方形ABCD内,大长方形中未被覆盖的两个部分(图中阴影部分),设右上角的面积为S1,左下角的面积为S2,当AB的长变化时,S1﹣S2的值始终保持不变,求a与b的等量关系.【分析】(1)由题可知代数式的值与x的取值无关,所以含x项的系数为0,故将多项式整理为(2m﹣3)x﹣3m+2m2,令x系数为0,即可求出m;(2)根据整式的混合运算顺序和法则化简3A+6B可得3x(5y﹣2)﹣9,根据其值与x无关得出5y﹣2=0,即可得出答案;(3)设AB=x,由图可知S1=a(x﹣3b),S2=2b(x﹣2a),即可得到S1﹣S2关于x的代数式,根据取值与x可得a=2b.【解答】解:(1)(2x﹣3)m+2m2﹣3x=2mx﹣3m+2m2﹣3x∵其值与x的取值无关,∴2m﹣3=0,解得,m=3 2,答:当m=32时,多项式(2x﹣3)m+2m2﹣3x的值与x的取值无关;(2)∵A=(2x+1)(x﹣1)﹣x(1﹣3y),B=﹣x2+xy﹣1,∴3A+6B=3[(2x+1)(x﹣1)﹣x(1﹣3y)]+6(﹣x2+xy﹣1)=3(2x2﹣2x+x﹣1﹣x+3xy]﹣6x2+6xy﹣6=6x2﹣6x+3x﹣3﹣3x+9xy﹣6x2+6xy﹣6=15xy﹣6x﹣9=3x(5y﹣2)﹣9,∵3A+6B的值与x无关,∴5y﹣2=0,即y=2 5;(3)设AB=x,由图可知S1=a(x﹣3b),S2=2b(x﹣2a),∴S1﹣S2=a(x﹣3b)﹣2b(x﹣2a)=(a﹣2b)x+ab,∵当AB的长变化时,S1﹣S2的值始终保持不变.∴S1﹣S2取值与x无关,∴a﹣2b=0∴a=2b.【题型3 整式乘法的计算】【例3】(2020秋•河北区期末)计算:(1)―12x2y⋅(13x3y2―34x2y+16)(2)(x﹣1)(2x+1)﹣2(x﹣5)(x+2)【分析】(1)根据单项式与多项式相乘的法则计算即可;(2)根据多项式与多项式相乘的法则计算即可.【解答】解:(1)―12x2y⋅(13x3y2―34x2y+16)=―12x2y⋅13x3y2+12x2y⋅34x2y―12x2y⋅16(2)(x﹣1)(2x+1)﹣2(x﹣5)(x+2)=2x2+x﹣2x﹣1﹣2(x2+2x﹣5x﹣10)=2x2﹣x﹣1﹣2x2+6x+20=5x+19.【变式3-1】(2021春•九龙坡区校级期中)计算:(1)2x2y(x―12y+1);(2)(x﹣2y)(y﹣x).【分析】(1)单项式与多项式相乘的运算法则:单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.(2)多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加.【解答】解:(1)原式=2x3y﹣x2y2+2x2y;(2)原式=xy﹣x2﹣2y2+2xy=3xy﹣x2﹣2y2.【变式3-2】(2021春•海陵区校级月考)计算:(1)﹣3x2(2x﹣4y)+2x(x2﹣xy).(2)(3x+2y)(2x﹣3y)﹣3x(3x﹣2y).【分析】(1)根据多项式乘多项式,多项式乘单项式进行计算即可;(2)根据多项式乘多项式,多项式乘单项式进行计算即可.【解答】解:(1)原式=﹣6x3+12x2y+2x3﹣2x2y=﹣4x3+10x2y;(2)原式=6x2﹣9xy+4xy﹣6y2﹣9x2+6xy=﹣3x2+xy﹣6y2.【变式3-3】(2021春•未央区月考)小奇计算一道整式的混合运算的题:(x﹣a)(4x+3)﹣2x,由于小奇将第一个多项式中的“﹣a”抄成“+a”,得到的结果为4x2+13x+9.(1)求a的值.(2)请计算出这道题的正确结果.【分析】(1)根据题意列出关系式,根据多项式相等的条件即可求出a的值;(2)列出正确的算式,计算即可得到结果.【解答】解:(1)根据题意得:(x+a)(4x+3)﹣2x=4x2+(3+4a﹣2)x+3a=4x2+13x+9;∴1+4a=13,解得:a=3;(2)正确的算式为(x﹣3)(4x+3)﹣2x=4x2﹣9x﹣9﹣2x=4x2﹣11x﹣9.【题型4 整式乘法的应用】【例4】(2021春•铁西区期中)有一电脑程序:每按一次按键,屏幕的A区就会自动减去a,同时B区就会自动加上3a,且均显示化简后的结果.已知A,B两区初始显示的分别是25和﹣16(如图所示).例如:第一次按键后,A,B两区分别显示:25﹣a,﹣16+3a.(1)那么第二次按键后,A区显示的结果为 ,B区显示的结果为 .(2)计算(1)中A、B两区显示的代数式的乘积,并求当a=2时,代数式乘积的值.【分析】(1)根据题意列出代数式即可;(2)利用多项式乘多项式法则进行计算,然后将a=2代入求值.【解答】解:(1)A区显示的结果为:25﹣a﹣a=﹣2a+25;B区显示的结果为:﹣16+3a+3a=6a﹣16;(2)(﹣2a+25)(6a﹣16)=﹣12a2+32a+150a﹣400=﹣12a2+182a﹣400,当a=2时,原式=﹣12×22+182×2﹣400=﹣84.【变式4-1】(2021春•碑林区校级期中)为迎接十四运,某小区修建一个长为(3a﹣b)米,宽为(a+2b)米的长方形休闲场所ABCD.长方形内筑一个正方形活动区EFGH和连接活动区到矩形四边的四条笔直小路(如图),正方形活动区的边长为(a﹣b)米,小路的宽均为2米.活动区与小路铺设鹅卵石,其它地方铺设草坪.(1)求铺设草坪的面积是多少平方米;(2)当a=10,b=4时,需要铺设草坪的面积是多少?【分析】(1)用大长方形的面积减去小正方形的面积和四个长方形的面积即可;(2)将a=10,b=4代入(1)中结果计算可得答案.【解答】解:(1)草坪的面积为:(3a﹣b)(a+2b)﹣(a﹣b)2﹣[3a﹣b﹣(a﹣b)]×2﹣[a+2b﹣(a﹣b)]×2=3a2+5ab﹣2b2﹣a2﹣b2+2ab﹣2a×2﹣3b×2=2a2+7ab﹣3b2﹣4a﹣6b(平方米);(2)当a=10,b=4时,草坪的面积为:2×102+7×10×4﹣3×42﹣4×10﹣6×4=368(平方米).【变式4-2】(2021春•成都期末)(1)如图是小颖家新房的户型图,小颖的爸爸打算把两个卧室以外的部分都铺上地砖,至少需要多少平方米的地砖?如果某种地砖的价格为每平方米a元,那么购买地砖至少需要多少元?(2)如果房屋的高度是h米,现在需要在客厅和两个卧室四周的墙上贴墙纸,那么至少需要多少平方米的墙纸?如果某种墙纸的价格为每平方米b元,那么购买所需的墙纸至少要多少元?(计算时不扣除门、窗所占的面积,忽略墙的厚度)【分析】(1)求出卫生间,厨房,以及客厅的面积之和即可得到需要地砖的面积;根据每平方米地砖的价格是a元钱,求出需要的钱数即可;(2)求出客厅与卧室的面积,乘以高h,即可得到需要的壁纸数;根据壁纸的价格是b元/平方米,求出需要的钱数即可.【解答】解:(1)由题意知,两个卧室以外的部分面积为:3y•y+2y•(3x﹣x﹣y)=3y2+4xy﹣2y2=y2+4xy(平方米).∴购买地砖所需的费用为:(y2+4xy)a=ay2+4axy(元).(2)客厅贴墙纸的面积为:(2y+6y)h=8yh,两个卧室贴墙纸的面积为:(4x+6y)h=4xh+6yh,∴贴墙纸的总面积为:8yh+4xh+6yh=14yh+4xh(平方米),∴购买墙纸所需的费用为:(14yh+4xh)b=14yhb+4xhb(元).【变式4-3】(2021春•莲湖区期末)已知有甲、乙两个长方形,它们的边长如图所示,面积分别为S1,S2.(1)S1与S2的大小关系为:S1 S2.(2)若一个正方形的周长与甲的周长相等.①求该正方形的边长(用含m的代数式表示).②若该正方形的面积为S3,试探究:S3与S2的差(即S3﹣S2)是否为常数?若为常数,求出这个常数,如果不是,请说明理由.【分析】(1)根据长方形的面积公式列式,然后根据整式的混合运算法则进行计算求解;(2)①根据正方形和长方形的周长公式计算求解;②根据正方形和长方形的面积公式列式,然后利用整式的混合运算法则进行计算求解.【解答】解:(1)由题意:S1=(m+2)(m+6)=m2+6m+2m+12=m2+8m+12,S2=(m+5)(m+3)=m2+5m+3m+15=m2+8m+15,∵S1﹣S2=(m2+8m+12)﹣(m2+8m+15)=m2+8m+12﹣m2﹣8m﹣15=﹣3<0,∴S1<S2,故答案为:<,(2)①甲的周长为2(m+2+m+6)=4m+16,∵正方形的周长与甲的周长相等,∴正方形的边长为4m164=m+4,②由①可得,正方形的面积S3=(m+4)2,∴S3﹣S2=(m+4)2﹣(m2+8m+15)=m2+8m+16﹣m2﹣8m﹣15=1,∴S3与S2的差(即S3﹣S2)是常数,这个常数是1.【题型5 整式除法的应用】【例5】(2021春•上城区期末)一个长方形的面积是15x3y5﹣10x4y4+20x3y2,一边长是5x3y2,则它的另一边长是( )A.2y3﹣3xy2+4B.3y3﹣2xy2+4C.3y3+2xy2+4D.2xy2﹣3y3+4【分析】利用长方形的面积公式,列出相应的式子,结合整式的除法法则进行运算即可.【解答】解:(15x3y5﹣10x4y4+20x3y2)÷(5x3y2)=15x3y5÷(5x3y2)﹣10x4y4÷(5x3y2)+20x3y2÷(5x3y2)=3y3﹣2xy2+4.故选:B.【变式5-1】(2020•台湾)计算2x2﹣3除以x+1后,得商式和余式分别为何?( )A.商式为2,余式为﹣5B.商式为2x﹣5,余式为5C.商式为2x+2,余式为﹣1D.商式为2x﹣2,余式为﹣1【分析】先将被除式2x2﹣3补0,再列竖式计算即可.【解答】解:∵被除式2x2﹣3缺项,∴补0后变为2x2+0x﹣3,长除法计算为:故选:D.【变式5-2】(2020秋•袁州区校级期中)已知一个长方形的面积是6a2﹣4ab+2a,且它的一条边长为2a,则长方形的周长为 .【分析】直接利用整式的除法运算法则分别计算得出答案.【解答】解:∵一个长方形的面积是6a2﹣4ab+2a,且它的一条边长为2a,∴长方形的另一边长为:(6a2﹣4ab+2a)÷2a=3a﹣2b+1,故长方形的周长为:2(3a﹣2b+1+2a)=10a﹣4b+2.故答案为:10a﹣4b+2.【变式5-3】(2021春•潍坊期末)若多项式A除以2x2﹣3,得到的商式为3x﹣4,余式为5x+2,则A = .【分析】根据题意列出关系式,计算即可得到结果.【解答】解:∵多项式A除以2x2﹣3,得到的商为3x﹣4,余式为5x+2,∴A=(2x2﹣3)(3x﹣4)+5x+2=6x3﹣8x2﹣9x+12+5x+2=6x3﹣8x2﹣4x+14.故答案为:6x3﹣8x2﹣4x+14.【题型6 整式乘法中的规律探究】【例6】(2020秋•邹城市期末)观察下列各式(x﹣1)(x+1)=x2﹣1(x﹣1)(x2+x+1)=x3﹣1(x﹣1)(x3+x2+x+1)=x4﹣1…(1)分解因式:x5﹣1= ;(2)根据规律可得(x﹣1)(x n﹣1+…+x+1)= (其中n为正整数);(3)计算:(3﹣1)(350+349+348+…+32+3+1).【分析】(1)观察各式,得到因式结果即可;(2)利用得出的规律计算即可;(3)利用得出的规律计算即可得到结果.【解答】解:(1)原式=(x﹣1)(x4+x3+x2+x+1);(2)(x﹣1)(x n﹣1+…+x+1)=x n﹣1;(3)原式=351﹣1.故答案为:(1)(x﹣1)(x4+x3+x2+x+1);(2)x n﹣1【变式6-1】(2021春•包河区期末)探究规律,解决问题:(1)化简:(m﹣1)(m+1)= ,(m﹣1)(m2+m+1)= .(2)化简:(m﹣1)(m3+m2+m+1),写出化简过程.(3)化简:(m﹣1)(m n+m n﹣1+m n﹣2+…+1)= .(n为正整数,m n+m n﹣1+m n﹣2+…+1为n+1项多项式)(4)利用以上结果,计算1+3+32+33+…+3100的值.【分析】(1)(2)根据多项式乘多项式的运算法则进行计算即可;(3)根据(1)(2)得出的规律可直接得出答案;(4)根据(3)的出的规律可直接代数进行计算即可.【解答】解:(1)(m﹣1)(m+1)=m2﹣1;(m﹣1)(m2+m+1)=m3﹣1;故答案为:m2﹣1;m3﹣1;(2)(m﹣1)(m3+m2+m+1)=m4+m3+m2+m﹣m3﹣m2﹣m﹣1=m4﹣1;(3)(m﹣1)(m n﹣1+m n﹣2+…m2+m+1)=m n+1﹣1;故答案为:m n+1﹣1;(4)根据(3)得出的规律可得:1+3+32+33+…+3100=31011 31,=310112.【变式6-2】(2021春•合肥期中)观察以下等式:(x+1)(x2﹣x+1)=x3+1(x+3)(x2﹣3x+9)=x3+27(x+6)(x2﹣6x+36)=x3+216…(1)按以上等式的规律,填空:(a+b)( )=a3+b3(2)利用多项式的乘法法则,证明(1)中的等式成立.(3)利用(1)中的公式化简:(x+y)(x2﹣xy+y2)﹣(x﹣y)(x2+xy+y2)【分析】(1)根据所给等式可直接得到答案(a+b)(a2﹣ab+b2)=a3+b3;(2)利用多项式与多项式相乘的法则:多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加进行计算即可得到答案;(3)根据题目所给的例子,找出公式后直接运用即可.【解答】解:(1)(a+b)(a2﹣ab+b2)=a3+b3;故答案为:a2﹣ab+b2;(2)(a+b)(a2﹣ab+b2)=a3﹣a2b+ab2+a2b﹣ab2+b3=a3+b3;(3)(x+y)(x2﹣xy+y2)﹣(x﹣y)(x2+xy+y2)=x3+y3﹣(x3﹣y3)=2y3.【变式6-3】(2020秋•石狮市校级月考)探究应用:(1)计算:(x﹣1)(x2+x+1)= ;(2x﹣y)(4x2+2xy+y2)= .(2)上面的乘法计算结果很简洁,你发现了什么规律(公式)?用含字母a、b的等式表示该公式为: .(3)下列各式能用第(2)题的公式计算的是 .A.(m+2)(m2+2m+4)B.(m﹣2n)(m2+2mn+2n2)C.(3﹣n)(9+3n+n2)D.(m﹣n)(m2+2mn+n2)(4)设A=109﹣1,利用上述规律,说明A能被37整除.【分析】(1)用多项式乘以多项式的法则计算即可;(2)观察第(1)问的计算,找出规律,用字母表示即可;(3)判断各选项是否符合公式的特点;(4)公式的逆用,求得A中有37的因数即可.【解答】解:(1)(x﹣1)(x2+x+1)=x3+x2+x﹣x2﹣x﹣1=x3﹣1;(2x﹣y)(4x2+2xy+y2)=8x3+4x2y+2xy2﹣4x2y﹣2xy2﹣y3=8x3﹣y3;故答案为:x3﹣1;8x3﹣y3;(2)从第(1)问发现的规律是:(a﹣b)(a2+ab+b2)=a3﹣b3,故答案为:(a﹣b)(a2+ab+b2)=a3﹣b3;(3)A.第一个多项式不是减法,不符合题意;B.最后一项应该是4n2,不符合题意;C.符合题意;D.第二个多项式的第二项应该为mn,不符合题意.故选:C.(4)A=109﹣1=(103)3﹣1=(103﹣1)(106+103+12)=999×1001001=3×3×3×37×1001001,∴A能被37整除.。
整式的乘除综合复习(二)(北师版)(含答案)

学生做题前请先回答以下问题问题1:整式混合运算处理方法:①观察结构划部分;②有序操作依法则;③每步推进一点点.其中,在合并同类项时,要________,同类项画相同的线.请利用上述方法计算:.问题2:计算.你是怎么思考的?用到的公式是什么?问题3:计算.你是怎么思考的?问题4:计算.你是怎么思考的?问题5:计算.你是怎么思考的?整式的乘除综合复习(二)(北师版)一、单选题(共10道,每道10分)1.计算的结果是( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:完全平方公式2.计算的结果是( )A.2B.C.-2D.6答案:D解题思路:故选D.试题难度:三颗星知识点:幂的乘方3.计算的结果是( )A. B.C. D.答案:B解题思路:故选B.试题难度:三颗星知识点:整式的乘除4.计算的结果是( )A. B.C. D.答案:B解题思路:故选B.试题难度:三颗星知识点:整式的乘除5.计算的结果是( )A. B.C. D.答案:C解题思路:故选C.试题难度:三颗星知识点:平方差公式6.计算的结果是( )A. B.C. D.答案:C解题思路:故选C.试题难度:三颗星知识点:整式的乘除混合运算7.计算的结果是( )A. B.C. D.答案:A解题思路:试题难度:三颗星知识点:整式的乘除混合运算8.计算的结果是( )A. B.C. D.答案:A解题思路:故选A.试题难度:三颗星知识点:整式的乘除混合运算9.当,时,代数式的值为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:化简求值10.计算结果的个位数字是( )A.1B.3C.7D.9答案:A解题思路:试题难度:三颗星知识点:整式的乘法。
专题03 整式的乘除法-2021年七年级数学下册(北师大版)(解析版)

整式的乘除法一、单选题(共30分)1.(本题3分)23a b ⋅的计算结果是( )A .6aB .6bC .5abD .6ab【答案】D【分析】根据单项式相乘法则计算求解判断即可.【详解】解:23a b ⋅6ab =. 故选:D .【点睛】此题考查了单项式乘以单项式,熟练掌握单项式相乘法则是解题的基础.2.(本题3分)下列运算结果是4a 的是( )A .()6222a a -÷-B .22a a +C .D .()22a -【答案】A【分析】根据整式运算法则逐项计算验证即可.【详解】A 、()62422a a a -÷-=,符合题意,故正确; B 、2222a a a +=,不符合题意,故错误;C 、,不符合题意,故错误;D 、,不符合题意,故错误;故选:A .【点睛】本题考查整式的运算,掌握相关运算法则是解题关键.3.(本题3分)若多项式2x mx n -+可分解为(3)(5)x x -+,则m n +的值为( )A .13-B .17-C .17D .23【答案】B【分析】根据多项式乘以多项式和恒等式变形即可求解.【详解】解:∵(x -3)(x +5)=x 2-mx +n ,∴x 2+2x -15=x 2-mx +n ,∴m =-2,n =-15,∴m +n =-17.故选:B .【点睛】本题考查了多项式乘以多项式,解决本题的关键是理解运用恒等关系.4.(本题3分)已知多项式x a +与21x x +-的乘积中不含x 项.则常数a 的值是( )A .B .1-C .1D .2 【答案】C【分析】将多项式乘以多项式展开,合并同类项,因为不含x 项,让这项的系数等于0即可.【详解】解:(x +a )(x 2+x -1)=x 3+x 2-x +ax 2+ax -a=x 3+(1+a )x 2+(a -1)x -a ,因为不含x 项,所以a -1=0,所以a =1.故选:C .【点睛】本题考查了多项式乘以多项式,不含某一项就让这一项的系数等于0是解题的关键.5.(本题3分)已知()232(2)224x x mx n x x x -+-=-+-,则m ,n 的值分别为( )A .0,2m n ==B .0,2m n ==-C .4,2m n ==D .2,2m n ==- 【答案】B【分析】利用多项式乘多项式法则计算,再根据同类项的系数相同得到m 和n 的值.【详解】解:∵()2(2)x x mx n -+- ===∴m -2=-2,-(n +2m )=2,∴m =0,n =-2,故选B .【点睛】本题考查了多项式乘多项式法则,合并同类项时要注意项中的指数及字母是否相同.6.(本题3分)下列运算正确的是( )A .236a a a ⋅=B .()325328a b a b -=-C .22242212362ab ab a a b a b ⎛⎫⨯-+=-+ ⎪⎝⎭ D .325235a a a += 【答案】C【分析】逐一进行判断即可.【详解】A. 2356a a a a ⋅=≠,故该选项错误;B. ,故该选项错误;C. 22242212362ab ab a a b a b ⎛⎫⨯-+=-+ ⎪⎝⎭,故该选项正确;D. 322,3a a 不能合并,故该选项错误;故选:C .【点睛】本题主要考查整式的运算,掌握同底数幂的乘法法则,积的乘方,单项式乘多项式的法则,合并同类项的法则是关键.7.(本题3分)计算的结果是( )A .26a b -B .24a b -C .D .24a b +【答案】B【分析】根据多项式除以单项式法则计算.【详解】解:=24a b -故选B .【点睛】本题考查了多项式除以单项式,解题的关键是掌握运算法则. 8.(本题3分)将每边长是a 厘米的正方形纸片,正中间挖了一个正方形的洞,成为一个四边宽b 厘米的方框.把五个这样的方框放在桌面上,成为一个这样的图案,如图所示,则桌面上被这些方框盖住的部分面积是( )A .22020ab b -B .22028ab b -C .21013ab b -D .21018ab b -【答案】B【分析】首先求得一个方框的面积,再求出五个方框的重合部分的面积,然后用5个这样的方框的面积减去五个方框的重合部分的面积,即可得出答案.【详解】解:一个方框的面积是:a 2-(a -2b )2=4ab -4b 2,五个方框的重合部分的面积=8b 2.则方框盖住的部分面积是:(4ab -4b 2)×5-8b 2=20ab -28b 2.故选:B .【点睛】本题考查列代数式,用到的知识点是图形面积的计算,正确计算一个方框的面积和重合部分的面积是解决本题的关键.9.(本题3分)生活在海洋中的蓝鯨,又叫长须鲸或剃刀鲸,它的体重达到150吨,它体重的万亿分之一用科学记数法可表示为( )A .1.5×1010-吨B .1.5×1110-吨C .15×1210-吨D .1.5×910-吨【答案】A【分析】解答时,分两步走,把150写成1.5×210吨;把1万亿写成4812101010⨯=,根据题意,列式计算即可.【详解】∵150=1.5×210吨;1万亿=4812101010⨯=,∴它体重的万亿分之一为=2121.510-⨯=1.5×1010-(吨),故选A .【点睛】本题考查了科学记数法的综合计算,同底数幂的除法,熟练掌握科学记数法和同底数幂的除法法则是解题的关键.10.(本题3分)下面是用黑色棋子摆成的美丽图案,按照这样的规律摆下去,第10个这样的图案需要黑色棋子的个数为( )A .148B .152C .168D .174【答案】D【分析】 根据摆成各个图形所需棋子数量的变化,可找出变化规律,然后写成第n 个图案的通式,再取n =10进行计算即可求解.【详解】解:根据图形,第1个图案有1+2+3+3+2+1=43⨯=12枚棋子,第2个图案有1+2+3+4+4+3+2+1+2=542⨯+=22枚棋子,第3个图案有1+2+3+4++5+5+4+3+2+1+4=654⨯+=34枚棋子,第4个图案有1+2++3+4+5+6+6+5+4+3+2+1+4=766⨯+=34枚棋子,…第n 个图案有(n +3)(n +2)+2(n -1)=n 2+7n +4枚棋子,故第10个这样的图案需要黑色棋子的个数为102+7×10+4=100+70+4=174(枚).故选:D .【点睛】本题考查了规律型:图形的变化类,根据摆成各个图形所需棋子数量的变化,找出变化规律是解题的关键.二、填空题(共15分)11.(本题3分)若,则常数m 的值为__________.【答案】-3【分析】根据多项式乘以多项式后利用恒等关系即可求解.【详解】解:(x +2)(x -5)=x 2-3x -10=x 2+mx -10,所以m =-3.故答案为:-3.【点睛】本题考查了多项式乘以多项式,解决本题的关键是理解恒等式.12.(本题3分)现规定一种运算:m n m n m n *=+-,其中m ,n 为有理数,则()m n n m n *+-*等于______.【答案】2n n -根据新运算展开,再化简,即可得出答案.【详解】原式=故答案为:2n n -【点睛】本题考查的是新定义,认真审题、理清题目意思是解决本题的关键.13.(本题3分)化简()()253624423(2)(2)a b a b a b a b a b a b +-÷--+-=________. 【答案】【分析】先利用幂的乘方和积的乘方运算,再根据多项式除以单项式和多项式乘多项式法则计算,最后合并.【详解】解:()()253624423(2)(2)a b a b a b a b a b a b +-÷--+- ==22223242ab a b a ab ab b +--+-+=故答案为:.【点睛】此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.14.(本题3分)如图,一块直径为+a b 的圆形钢板,从中挖去直径分别为a 与b 的两个圆,则剩余阴影部分面积为______.【答案】【分析】由大圆面积减去两个小圆面积求出阴影部分面积即可.【详解】解:根据题意得:S 阴影= .故答案为:.此题考查了圆的面积和整式的混合运算,弄清题意是解本题的关键.15.(本题3分)有若干张如图所示的正方形A 类、B 类卡片和长方形C 类卡片(已知2a b ≠),若要拼成个长为,宽为(2)a b +的大长方形,则需要C 类卡片________张.【答案】7【分析】计算出长为(3a +b ),宽为(a +2b )的大长方形的面积,再分别得出A 、B 、C 卡片的面积,即可看出应当需要各类卡片多少张.【详解】解:长为(3a +b ),宽为(a +2b )的大长方形的面积为:(3a +b )(a +2b )=3a 2+2b 2+7ab ;A 卡片的面积为:a ×a =a 2;B 卡片的面积为:b ×b =b 2;C 卡片的面积为:a ×b =ab ;因此可知,拼成一个长为(3a +b ),宽为(a +2b )的大长方形,需要3块A 卡片,2块B 卡片和7块C 卡片.故答案为:7.【点睛】本题考查了多项式乘法,此题的立意较新颖,注意对此类问题的深入理解.三、解答题(共55分)16.(本题8分)计算:(1)()2733()x x x ⋅-÷- (2)22(3)33x x x ⎛⎫-⋅-+ ⎪⎝⎭【答案】(1);(2)3229x x -【分析】(1)先根据幂的乘方法则计算,再利用同底数幂的乘除法则计算;(2)将括号展开,再计算.【详解】解:(1)()2733()x x x ⋅-÷-=736()x x x ⋅-÷=;(2)22(3)33x x x ⎛⎫-⋅-+ ⎪⎝⎭ =3229x x -【点睛】本题考查了整式的混合运算,解题的关键是掌握运算法则.17.(本题10分)先化简,再求值:,其中12x =-,1y =. 【答案】32324y xy -++,0【分析】利用多项式除以单项式法则计算,再将x 和y 值代入计算.【详解】解:=32324y xy -++ 将12x =-,1y =代入, 原式=321312142⎛⎫-⨯+⨯-⨯+ ⎪⎝⎭=0. 【点睛】本题主要考查了整式的混合运算-化简求值,熟练掌握整式的=运算法则进行计算是解决本题的关键.18.(本题13分)若()2(2)x x ax b -++的积中不含x 的二次项和一次项,求2(32)2a b ab -+的值. 【答案】20【分析】原式利用多项式乘多项式法则计算,由积中不含x 的二次项和一次项,求出a 与b 的值,再把a 、b 的值代入计算可得.【详解】解:(x -2)(x 2+ax +b )=x 3+ax 2+bx -2x 2-2ax -2b =x 3+(a -2)x 2+(b -2a )x -2b ,∵(x -2)(x 2+ax +b )的积中不含x 的二次项和一次项,∴a -2=0且b -2a =0,解得:a =2、b =4,将a =2、b =4代入2(32)2a b ab -+=2(3224)224⨯-⨯+⨯⨯=4+16=20.【点睛】本题主要考查整式的化简求值,解题的关键是熟练掌握整式的混合运算顺序和运算法则.19.(本题12分)己知矩形纸片甲,其边长如图所示(m >0),面积为S 甲.(1)用含m 的代数式表示S 甲=_____________.(2)若一个正方形纸片的周长与甲的周长相等,其面积设为S 正.①求该正方形边长.(用含m 的代数式表示);②小方同学发现,“S 正与S 甲的差是定值”请判断小方同学的发现是否正确,并通过计算说明理由.【答案】(1); (2)①5m +;②正确,见解析;【分析】(1)根据矩形的面积公式计算即可;(2)①根据矩形和正方形的周长公式即可得到结论;②根据矩形和正方形的面积公式即可得到结论.【详解】(1)S 甲=,故答案为:;(2)①由题意得:甲的周长为:()246420m m m +++=+,∵该正方形纸片的周长与乙的周长相等,∴该正方形边长为:42054m m +=+; ②正确,理由如下:22(5)(1024)S S m m m -=+-++甲正22=(m 1025)(m 1024)m m ++-++=1∴S S -甲正的差等于1,是定值.【点睛】BatchDoc-Word 文档批量处理工具BatchDoc-Word 文档批量处理工具 本题主要考查列代数式,整式的混合运算,解题的关键是掌握多项式乘多项式、矩形的性质、正方形的性质等知识.20.(本题12分)如图,某市有一块长为米,宽为米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为米的道路.(0,0a b >>).(1)试用含a ,b 的代数式表示绿化的面积是多少平方米?(2)若30,20a b ==,请求出绿化面积.【答案】(1)(3a 2+3ab )平方米;(2)4500平方米【分析】(1)根据图形可得长方形的面积减去中间正方形的面积减去两个小长方形的面积即可得结果; (2)把a =30,b =20代入(1)所得整式,即可得结果.【详解】解:(1)由题意可得:(3a +b )(2a +b )-(a +b )2-a (3a +b -a -b )=6a 2+5ab +b 2-a 2-2ab -b 2-2a 2=(3a 2+3ab )平方米;答:绿化的面积是(3a 2+3ab )平方米;(2)当a =30,b =20,绿化面积是3a 2+3ab =3×900+3×30×20=4500平方米.【点睛】本题考查了多项式乘多项式,看懂题图掌握多项式乘多项式法则是解决本题的关键.。
(2021年整理)北师大版七年级下册数学总复习一整式的乘除

(完整版)北师大版七年级下册数学总复习一整式的乘除编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((完整版)北师大版七年级下册数学总复习一整式的乘除)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(完整版)北师大版七年级下册数学总复习一整式的乘除的全部内容。
(完整版)北师大版七年级下册数学总复习一整式的乘除编辑整理:张嬗雒老师尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布到文库,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是我们任然希望(完整版)北师大版七年级下册数学总复习一整式的乘除这篇文档能够给您的工作和学习带来便利。
同时我们也真诚的希望收到您的建议和反馈到下面的留言区,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请下载收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为〈(完整版)北师大版七年级下册数学总复习一整式的乘除> 这篇文档的全部内容。
知识要点一、概念 1、代数式:2、单项式:由数字与字母的乘积的代数式叫做单项式。
单项式不含加减运算,分母中不含字母。
3、多项式:几个单项式的和叫做多项式。
多项式含加减运算。
4、整式:单项式和多项式统称为整式。
二、公式、法则:(1)同底数幂的乘法:a m﹒a n=a m+n(同底,幂乘,指加)逆用: a m+n=a m﹒a n(指加,幂乘,同底)(2)同底数幂的除法:a m÷a n=a m-n(a ≠0).(同底,幂除,指减)逆用:am —n= a m ÷a n(a ≠0)(指减,幂除,同底)(3)幂的乘方:(a m)n=a mn(底数不变,指数相乘)逆用:a mn=(a m )n(4)积的乘方:(ab )n=a n b n推广:逆用, a n b n=(ab )n(当ab=1或-1时常逆用)(5)零指数幂:a 0=1(注意考底数范围a ≠0)。
北师大版2021年七年级数学下册单元复习卷第一章《整式的乘除》【含答案】

(2)设 aa 1 a2 b 2 ,求 a2 b2 ab 的值. 2
20、(6 分) 如图所示,边长为 a 的大正方形中有一个边长为 b 的小正方形.
(1)请用字母 a 和 b 表示出图甲阴影部分的面积; (2)将阴影部分还能拼成一个长方形,如图乙这个长方形的长和宽分别是多少? 表示出阴影部分的面积;
3
(3)比较(1)和(2)的结果,可以验证什么公式。请给予解答.
21、(6 分)若 (x2 px q)(x2 2x 3) 展开后不含 x2 , x3 项,求 p ,q 的值。
22、(6 分)已知一个三角形的面积是 4a3b 6a2b2 12ab2 ,一边长为 4ab,求该边上的高.
答案
1-10:CBCCB BBDBC
A、 a 1,b 2 B、 a 1,b 2
C、 a 1,b 2
D、 a 1,b 2
6、若(x-2y)2=(x+2y)2+m,则 m 等于( ).
A、4xy
B、-4xy C、8xy D、-8xy
7、可以运用平方差公式运算的有( )个
①
②
③
A、1
B、2
C、3
8、若 (x 4)(x 2) x2 px q ,则 p、q 的值是(
C、 (4x 1)2 16x2 8x 1
D、 (x 3)2 x2 9
4、 (x 4 y)(x 5y) 的结果是( )
A、 x2 9xy 20 y2
B、 x2 xy 20 y2
C、 x2 xy 20 y2
D、 x2 20 y2
5、 如果 (ax b)(x 2) x2 4 ,那么( )
(完整word版)北师大版七年级下册数学总复习一整式的乘除

知识要点一、看法1、代数式:2、单项式 : 由数字与字母的乘积的代数式叫做单项式。
单项式不含加减运算,分母中不含字母。
3、多项式 : 几个单项式的和叫做多项式。
多项式含加减运算。
4、整式 : 单项式和多项式统称为整式。
二、公式、法规:(1)同底数幂的乘法: a m﹒ a n=a m+n(同底,幂乘,指加)逆用: a m+n =a m﹒ a n(指加,幂乘,同底)(2)同底数幂的除法: a m÷ a n=a m-n( a≠ 0)。
(同底,幂除,指减)逆用: a m-n = a m÷ a n( a≠0)(指减,幂除,同底)(3)幂的乘方:( a m)n =a mn(底数不变,指数相乘)逆用: a mn = ( a m)nnn n( 4)积的乘方:( ab) =a b实行:逆用, a n b n = ( ab)n(当 ab=1 或-1 常常逆用)( 5)零指数幂: a =1(注意考底数范围a≠ 0)。
( 1 )p1p (a0)( 底倒,指反 )(6)负指数幂: a pa a(7)单项式与多项式相乘: m(a+b+c)=ma+mb+mc。
(8)多项式与多项式相乘: (m+n)(a+b)=ma+mb+na+nb 。
( 9 )平方差公式:(a+b)(a-b)=a2-b2公式特点:(有一项完满相同,另一项只有符号不相同,结果= (相同)2(不相同)2实行(项数变化):连用变化:( 10)完满平方公式:(a b)2a22ab b2 ,( a b) 2a22ab b2 ,逆用: a 22ab b2( a b) 2 , a 22ab b2( a b)2 .完满平方公式变形(知二求一):a2b2(a b)22ab a2b2(a b)22aba2b221 [( a b)2(a b)2 ]a2b2(a b) 22ab (a b) 22ab21 [( a b)2( a b)2 ](a b)2(a b)24ab ab41 [( a b)2(a b)2 ]完满平方和公式中间项 =完满平方差公式中间项 =完满平方公式中间项 =比方: 9x2 +mxy+4y2是一个完满平方和公式,则m=;是一个完满平方差公式,则=;是一个完满平方公式,则=;m m( 11)多项式除以单项式的法规: ( a b c)m a m b m c m.( 12)常用变形:( x2 n=(y-x)2n,( x2 n 1=-(y-x)2n+1 y)y)练习。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北师大版2021年中考数学总复习
《整式的乘除》
一、选择题
1.计算a•a2的结果是( )
A.a3 B.a2 C.3a D.2a2
2.已知x+y﹣4=0,则2y•2x的值是( )
A.16
B.﹣16
C.
D.8
3.计算(-2a2)3的结果是( )
A.-6a2
B.-8a5
C.8a5
D.-8a6
4.计算(﹣2m)2•(﹣m•m2+3m3)的结果是( )
A.8m5 B.﹣8m5 C.8m6 D.﹣4m4+12m5
5.要使多项式(x2+px+2)(x-q)不含x的二次项,则p与q的关系是( )
A.相等
B.互为相反数
C.互为倒数
D.乘积为-1 已知a-b=3,ab=2,则a2+b2的值为()
A.13
B.7
C.5
D.11
6.若9a2+kab+16a2是一个完全平方式,那么k的值是( )
A.2
B.12
C.±12
D.±24
7.已知a=96,b=314,c=275,则a、b、c的大小关系是( )
A.a>b>c
B.a>c>b
C.c>b>a
D.b>c>a
二、填空题
8.若 a x=3,a y=2,则 a x+2y= .
9.若2×8n×16n=222,则n=_______
10.已知(x﹣y)2﹣2x+2y+1=0,则x﹣y= .
11.已知x2+y2+10=2x+6y,则x21+21y的值为__
三、解答题
12.化简:3a(2a2-9a+3)-4a(2a-1)
13.化简:(x+1)2+x(x-2)-(x+1)(x-1).
14.已知a+b=7,ab=12.求:(1)a2+b2;(2)(a-b)2的值.
15.从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方
形(如图2).
(1)图1中阴影部分面积为,图2中阴影部分面积为,对照两个图形的面
积可以验证公式(填公式名称)请写出这个乘法公式.
(2)应用(1)中的公式,完成下列各题:
①已知x2﹣4y2=15,x+2y=3,求x﹣2y的值;
②计算:(2+1)(22+1)(24+1)(28+1)……(264+1)+1.
参考答案
1.答案为:A.
2.A;
3.D.
4.答案为:A.
5.答案为:A;
6.A
7.答案为:D;
8.C
9.答案为:12;
10.答案为:3
11.答案为:1.
12.答案为:64.
13.原式=6a3-35a2+13a
14.解:原式=x2+2x+1+x2-2x-x2+1=x2+2.
15.解:(1)a2+b2=(a+b)2-2ab=72-2×12=49-24=25;
(2)(a-b)2=(a+b)2-4ab=72-4×12=49-48=1.
16.解:(1)图1中阴影部分面积为a2﹣b2,图2中阴影部分面积为(a+b)(a﹣b),
对照两个图形的面积可以验证平方差公式:a2﹣b2=(a+b)(a﹣b).
故答案为:a2﹣b2,(a+b)(a﹣b),平方差,a2﹣b2=(a+b)(a﹣b).
(2)①∵x2﹣4y2=(x+2y)(x﹣2y),∴15=3(x﹣2y),∴x﹣2y=5;
②(2+1)(22+1)(24+1)(28+1)……(264+1)+1
=(2﹣1)(2+1)(22+1)(24+1)(28+1)……(264+1)+1
=(22﹣1)(22+1)(24+1)(28+1)……(264+1)+1
=(24﹣1)(24+1)(28+1)……(264+1)+1
=(28﹣1)(28+1)……(264+1)+1
=(264﹣1)(264+1)+1
=2128﹣1+1
=2128.。
