初中九年级学业水平考试数学专题复习七——全等三角形的相关证明及计算
专题7:全等三角形的证明(答案版)

初中数学学科教师辅导讲义四、例题例1:AB=AC ,DB=DC ,F 是AD 的延长线上的一点。
求证:BF=CF在△ABD 与△ACD 中,AB=ACBD=DCAD=AD∴△ABD ≌△ACD ∴∠ADB=∠ADC ∴∠BDF=∠FDC在△BDF 与△FDC 中BD=DC ∠BDF=∠FDCDF=DF∴△FBD ≌△FCD ∴BF=FC例2:已知AB ∥DE ,BC ∥EF ,D ,C 在AF 上,且AD =CF ,求证:△ABC ≌△DEF .证明:∵AD=DF ∴AC=DF ∵AB //DE ∴∠A=∠EDF又∵BC //EF ∴∠F=∠BCA ∴△ABC ≌△DEF (ASA )F DCB A课堂作业一、选择题1、如果一个角的补角是150°,那么这个角的余角的度数是()A 30°B 60°C 90°D 120°2、下列各组的两个图形属于全等图形的是()A. B. C. D.3、如图所示,点E在AC的延长线上,下列条件中能判断AB∥CD的是()A.∠3=∠4 B.∠D=∠DCEC.∠1=∠2 D.∠D+∠ACD=180°4、如图,,=30°,则的度数为()A.20° B.30° C.35° D.40°5、下列说法中,正确的有()①正方形都是全等形;②等边三角形都是全等形;③形状相同的图形是全等形;④能够完全重合的图形是全等形.A.1个 B.2个 C.3个 D.4个个6、如图,△ABC≌△DEF,∠A=50°,∠C=30°,则∠E的度数为()A.30° B.50° C.60° D.100°7、如图12.1-10,△ABC≌△FED,则下列结论错误的是()A. EC=BDB. EF∥ABC. DF=BDD. AC∥FD8、等腰三角形的一个角是50°,则它的底角是()A.50° B.50°或65° C.80° D.65°9、如图,ΔABC中,AB=AC,BD=CE,BE=CF,若∠A=50°,则∠DEF的度数是()A.75° B.70° C.65° D.60°10、如图1—102所示.在ABC中,AC=BC,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E.若AB=6 cm,则DEB的周长为()A.12 cm B.8 cm C.6 cm D.4 cm二、填空题11、如图,直线AB和CD相交于点O,OE平分∠DOB,∠AOC=40°,则∠DOE= _________ 度.12、如图,已知AB∥CD,∠C=65°,∠E=25°,则∠A的度数为.13、如图,AB∥CD,∠C=35°,∠E=25°,则∠A= °;14、如图,把长方形ABCD沿EF对折,若∠1=500,则∠AEF的度数等于.15、如图,将边长为的等边△沿边向右平移得到△,则四边形的周长为.16、如图,已知△AB C≌△ADE,若AB=7,AC=3,则BE的长为.三、简答题17、已知:如图,∠B=42°,∠A+10°=∠1,∠ACD=64°求证:AB∥CD。
初中数学知识归纳三角形的全等性质与计算

初中数学知识归纳三角形的全等性质与计算三角形是初中数学中重要的概念之一,对于理解三角形的性质以及进行计算至关重要。
本文将对三角形的全等性质进行归纳,并介绍一些相关的计算方法。
一、全等性质的概念与判定全等是指两个事物在形状、大小、性质等方面完全相同。
在三角形中,当两个三角形的对应边和对应角完全相等时,我们可以判断这两个三角形是全等的。
1. 全等三角形的判定条件全等三角形的判定条件有五种,分别是:(1)SSS判定法:如果两个三角形的三条边相等,则这两个三角形是全等的。
(2)SAS判定法:如果两个三角形的一条边和该边上的两个夹角分别与另外一个三角形的一条边和该边上的两个夹角相等,则这两个三角形是全等的。
(3)ASA判定法:如果两个三角形的两个角和这两个角所夹的边分别与另外一个三角形的两个角和这两个角所夹的边相等,则这两个三角形是全等的。
(4)AAS判定法:如果两个三角形的两个角和一个非夹角的对应边分别与另外一个三角形的两个角和一个非夹角的对应边相等,则这两个三角形是全等的。
(5)HL判定法:如果两个三角形的一条直角边和斜边分别与另外一个三角形的一条直角边和斜边相等,则这两个三角形是全等的。
通过以上的判定法则,我们可以准确地判断两个三角形是否全等,这对于后续计算和推理非常重要。
二、全等性质的应用1. 三角形全等导致的性质(1)对应顶点性质:两个全等三角形的对应顶点是相等的。
即,如果三角形ABC与三角形DEF全等,则∠A=∠D,∠B=∠E,∠C=∠F。
(2)对应边性质:两个全等三角形的对应边是相等的。
即,如果三角形ABC与三角形DEF全等,则AB=DE,BC=EF,AC=DF。
(3)对应角性质:两个全等三角形的对应角是相等的。
即,如果三角形ABC与三角形DEF全等,则∠ABC=∠DEF,∠BCA=∠EFD,∠CAB=∠FDE。
2. 利用全等性质进行计算根据全等性质,我们可以利用已知的边长或角度来计算其他未知的边长或角度。
九年级数学中考复习课件:全等三角形

∴S△ECD=1 3
53
45 5
.
2
2
16
模型四 一线三等角模型
一般通过一线三等角找等角或进行角度转换,证三角形全等时必须还有一组边 相等这个条件. 常见基本图形如下: 1.两个三角形在直线同侧,点P在线段AB上,已知:∠1=∠2=∠3,AP=BD.
锐角一线三等角
钝角一线三等角
结论:△CAP≌△PBD.
则△ACD是等腰直角三角形.
12
基本图形2 如图③,已知:AB⊥BC,AE⊥BD,CD⊥BD,AB=BC.
图③
图④
图③结论:①∠A=∠DBC,∠ABE=∠C;②DE=AE-CD.
13
模型应用 4. 如图,BA⊥AC,CD∥AB,BC=ED,且BC⊥DE,若AB=5, CD=8,则AE=___3_____.
15
模型应用
(2)若AD=3,AB=9,求△ECD的面积.
(2)解:由△ADE≌△BEC得∠AED=∠BCE,AD=BE.
∴∠AED+∠BEC=∠BCE+∠BEC=90°.
∴∠DEC=9Βιβλιοθήκη °.又∵AD=3,AB=9,
∴BE=AD=3,AE=9-3=6.
∵∠1=∠2,
∴ED=EC= AE 2 AD2 62 32 3 5,
20
模型应用 7. 如图,在△ABC中,AB=AC,点D,E分别在AC及其延长线上, 点B,F分别在AE两侧,连接CF,已知AD=EC,BC=FD, BC∥DF. (1)求证:△ABC≌△EFD;
证明三角形全等的关键:(1)加(减)共线部分CE,得BC=EF; 解题思路
(2)利用平行线性质找对应角相等
7
模型应用
1. 如图,点B、C、E、F在同一直线上,BC=EF,AC⊥BC于点 C,DF⊥EF于点F,AC=DF.求证:AB∥DE.
初三数学总复习——全等三角形

题(2)是题(1)的拓展、升华,三角形的三条高相交于一点, 受题(1)的启发,我们能够作出△ABC的三条高的交点P, 再作射线PC与AB交于点D,则CD就是所求作的AB边上的高.
宝典●能力提升
P73页
13.(13.江西)如图,AB是半圆的直径,图1中,点C在半圆外, 图2中,点C在半圆内,请仅用无刻度的直尺按要求画图 (1)在图1中,画出△ABC的三条高的交点 (2)在题2中,画出△ABC中AB边上的高
∵在Rt△ACD和Rt△AED中 ∴Rt△ACD≌Rt△AED(HL); (2)解: ∵DC=DE=1,DE⊥AB, ∴∠DEB=90°, ∵∠B=30°, ∴BD=2DE=2.
作业
完成宝典P75~76页的能力提升
∴△DOF≌△BOE(SAS), ∴FD=BE.
宝典●能力提升
P73页
16.(13.温州)如图,在△ABC中, ∠C=90º,AD平分∠CAB, 交CB于点D,过点D作DE⊥AB于点E (1)求证: △ACD≌ △AED (2)若∠B=30º,CD=1,求BD的长 (1)证明: ∵AD平分∠CAB,DE⊥AB,∠C=90°, ∴CD=ED,∠DEA=∠C=90°,
1.一般三角形全等的判定 (1)如果两个三角形的三条边分别对应相等,那么这两个三角形全等,简记为(SSS); (2) 如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等,简记为 (SAS); (3) 如果两个三角形的两角及其夹边分别对应相等,那么这两个三角形全等,简记为 (ASA); (4)如果三角形的两角及其中一角的对边分别对应相等,那么这两个三角形全等,简记为 (AAS). 2.直角三角形全等的判定 (1)两直角边对应相等的两个直角三角形全等; (2)一边一锐角对应相等的两个直角三角形全等; (3)如果两个直角三角形的斜边及一条直角边分别对应相等,那么这两个直角三角形全 等.简记为(HL).
(完整版)初中数学全等三角形的证明题含答案

1. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCBD=DC∴△ACD ≌△BDE∴AC=BE=2∵在△ABE 中AB-BE <AE <AB+BE∵AB=4即4-2<2AD <4+21<AD <3∴AD=22. 已知:D 是AB 中点,∠ACB=90°,求证:12CD AB延长CD 与P ,使D 为CP 中点。
连接AP,BP∵DP=DC,DA=DB∴ACBP 为平行四边形又∠ACB=90∴平行四边形ACBP 为矩形∴AB=CP=1/2AB3. 已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2AD BC证明:连接BF 和EF∵ BC=ED,CF=DF,∠BCF=∠EDF∴ 三角形BCF 全等于三角形EDF(边角边)∴ BF=EF,∠CBF=∠DEF连接BE在三角形BEF 中,BF=EF∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在三角形ABF 和三角形AEF 中AB=AE,BF=EF,∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF∴ 三角形ABF 和三角形AEF 全等。
∴ ∠BAF=∠EAF (∠1=∠2)。
4. 已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG ∥EF 交AD 的延长线于点GCG ∥EF ,可得,∠EFD =CGDDE =DC∠FDE =∠GDC (对顶角)∴△EFD ≌△CGDEF =CGB ACDF21 E∠CGD=∠EFD又,EF∥AB∴,∠EFD=∠1∠1=∠2∴∠CGD=∠2∴△AGC为等腰三角形,AC=CG又EF=CG∴EF=AC5.已知:AD平分∠BAC,AC=AB+BD,求证:∠B=2∠CA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C6.已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE 上取F ,使EF =EB ,连接CF∵CE ⊥AB∴∠CEB =∠CEF =90°∵EB =EF ,CE =CE ,∴△CEB ≌△CEF∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180°∴∠D =∠CFA∵AC 平分∠BAD∴∠DAC =∠FAC∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE7. 已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE∠BDE=∠ADCAD BCBD=DC∴△ACD≌△BDE∴AC=BE=2∵在△ABE中AB-BE<AE<AB+BE ∵AB=4即4-2<2AD<4+21<AD<3∴AD=28.已知:D是AB中点,∠ACB=90°,求证:12 CD AB9.已知:BC=DE,∠B=∠E,∠C=∠D,F是CD中点,求证:∠1=∠2证明:连接BF 和EF 。
中考数学复习 全等三角形精品课件

北师大版数学九年级中考复习第四章第四节
二、全等三角形的判定
【例2】 (2018·安顺)如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,
已知AB=AC,现添加以下的哪个条件仍不能判定△ABE≌△ACD( )
A.∠B=∠C
B.AD=AE
C.BD=CE
D.BE=CD
【解析】 ∵AB=AC,∠A为公共角.如添加∠B=∠C,利用 ASA可证明△ABE≌△ACD;如添加AD=AE,利用SAS可证明 △ABE≌△ACD;如添加BD=CE,由等量关系可得AD=AE,利 用SAS可证明△ABE≌△ACD;如添加BE=CD,因为SSA,不一 定能证明△ABE≌△ACD.
(2)全等三角形的对应高、对应中线、对应角平分线________.
第四节 全等三角形
●考点二 全等三角形的判定
已知条件 三边
两角 两角夹边 一边 两角对边
图形
北师大版数学九年级中考复习第四章第四节
是否全等 是
形成结论 __S_S__S___
是
ASA
是
AAS
第四节 全等三角形
已知条件 两边
两边夹角 一角
【解析】 由△ABO≌△ADO,得AB=AD,∠AOB=∠AOD=90°,∠BAC
=∠DAC,又AC=AC,所以△ABC≌△ADC,所以CB=CD.根据已知条 件,推证不出DA=DC.
【答案】 ①②③
【点拨】 明晰全等三角形的对应元素,才能准确得到“对应的线段相等和 对应的角相等”.
第四节 全等三角形
第四节 全等三角形
北师大版数学九年级中考复习第四章第四节
如图,在Rt△ABC与Rt△DCB中,已知∠A=∠D=90°,请你添加一
(完整版)初中数学全等三角形的证明题含答案
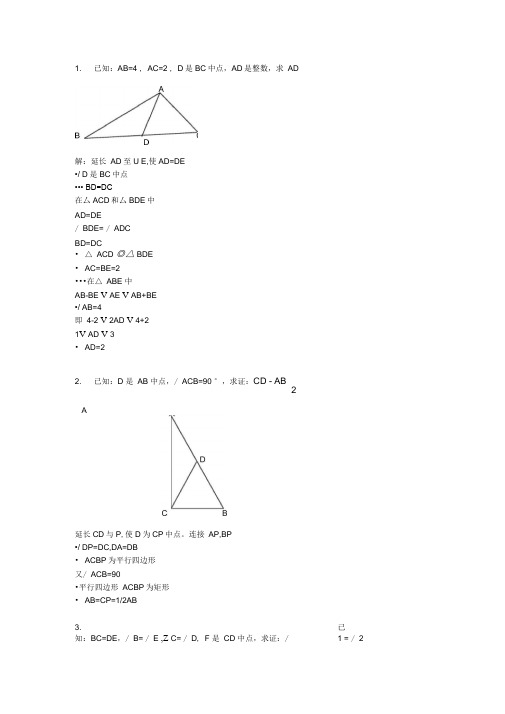
1. 已知:AB=4 , AC=2 , D是BC中点,AD是整数,求 AD 解:延长 AD至U E,使AD=DE •/ D是BC中点 ••• BD=DC 在厶ACD和厶BDE中 AD=DE / BDE= / ADC BD=DC • △ ACD ◎△ BDE
• AC=BE=2 •••在△ ABE 中 AB-BE V AE V AB+BE •/ AB=4 即 4-2 V 2AD V 4+2 1V AD V 3 • AD=2
2. 已知:D 是 AB 中点,/ ACB=90 °,求证:CD - AB 2
A
延长CD与P,使D为CP中点。连接 AP,BP •/ DP=DC,DA=DB • ACBP为平行四边形 又/ ACB=90 •平行四边形 ACBP为矩形 • AB=CP=1/2AB
3. 已知:BC=DE,/ B= / E ,Z C= / D, F 是 CD 中点,求证:/ 1 = / 2 证明:连接BF和EF •/ BC=ED,CF=DF, / BCF= / EDF •••三角形BCF全等于三角形 EDF(边角边) ••• BF=EF, / CBF= / DEF 连接BE 在三角形BEF中,BF=EF • / EBF= / BEF。 •/ / ABC= / AED。 • / ABE= / AEB。 AB=AE 。 在三角形ABF和三角形 AEF中 AB=AE,BF=EF, / ABF= / ABE+ / EBF= / AEB+ / BEF= / AEF •三角形ABF和三角形AEF全等。 • / BAF= / EAF ( / 1 = / 2)。
4. 已知:/ 仁/2, CD=DE , EF//AB,求证:
CG// EF,可得,/ EFD= CGD DE= DC / FDE=Z GDC (对顶角) • △ EFD^A CGD
EF= CG
过C作CG // EF交AD的延长线于点 G
EF=AC / CGD=Z EFD
中考专题复习之全等三角形

B.1
C.1.5
D.2
图20-8
基
础
知
识
巩
固
高
频
考
向
探
究
2.如图20-9,已知在△ABC和△DEF中,∠B=∠E,BF=CE,点B,F,C,E在同一条直线上,
若使△ABC≌△DEF,则还需添加的一个条件是 AB=DE(或∠A=∠D等) .(只填一
个即可)
图20-9
基
础
知
识
巩
固
高
频
考
向
探
固
(2)完成下面的证明.
高
频
考
向
探
究
又在Rt△ABC中,有∠BAC+∠ABC=90°,∠DCA+∠DCB=90°,
证明:连接PA,PC,QA,QC,DC.
∵PA=PC,QA=
, ∴PQ是AC的垂直平分线(
)(填推理的
依据). ∴E为AC中点,AD=DC.∴∠DAC=∠DCA.
∴∠ABC=∠DCB(
)(填推理的依据). ∴DB=DC.∴AD=DC=BD.
,两弧在∠AOB内相交于点P; (3)作射线OP,OP即为所求
基
础
知
识
巩
固
高
频
考
向
探
究
(续表)
步骤:
4. 作 线 段 的 垂 直
(1)分别以点 A,B 为圆心, 大于AB 长为半径向
平分线
线段两侧作弧,两弧分别交于点 M,N; (2)过点 M,N
作直线,所得直线 MN 即为所求
步骤:
5. 过 直 线 上 一 点
基
础
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
彩云中学2015——2016学年九年级学业水平考试数学专题复习资料
第1页 共八页(九年级数学专题复习七) 第2页 共八页(九年级数学专题复习七)
复习专题七:全等三角形的相关证明及计算
1.(本题满分6分)如图,∠AOB=90°,OA=OB,直线L经过点O,分别过A、B两点作AC⊥L交L于点C,BD⊥L交L于点D. 求证:AC=OD 2.(5分)(2014•北京)如图,点B在线段AD上,BC∥DE,AB=ED,BC=DB.求证:∠A=∠E. 3.(6分)(2014•黄冈)已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF. 4.(9分)如图,AB是半圆O的直径,点P是半圆上不与点A,B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD,PO. (1)求证:△CDP≌△POB;
(2)填空:①若AB=4,则四边形AOPD的最大面积为_________________;
②连接OD,当∠PBA的度数为________时,四边形BPDO是菱形.
5.(本小题5分)如图,BD,请添加一个条件(不得添加辅助线),
使得△ABC≌△ADC,并说明理由.
l
O
D
B
C
A
A
B D
C
彩云中学2015——2016学年九年级学业水平考试数学专题复习资料
第3页 共八页(九年级数学专题复习七) 第4页 共八页(九年级数学专题复习七)
6.(10分)(2014•怀化)如图,在平行四边形ABCD中,∠B=∠AFE,EA是∠BEF的角
平分线.求证:
(1)△ABE≌△AFE;
(2)∠FAD=∠CDE.
7.(本小题5分)如图,点B、E、C、F在同一条直线
上,∠A=∠D,∠B=∠DEF,BE=CF。
求证:AC=DF
8、(本小题5分)已知:如图,点A、B、C、D在同一
条直线上,AB=CD,AE∥CF,且AE=CF.
求证:∠E=∠F
9.(本小题5分)已知:如图,AD、BC相交于点O,OA=OD,AB∥CD.求证:AB=CD.
10.(10分)(2013•曲靖)如图,点E在正方形ABCD的边AB上,连接DE,过点C作
CF⊥DE于F,过点A作AG∥CF交DE于点G.
(1)求证:△DCF≌△ADG.
(2)若点E是AB的中点,设∠DCF=α,求sinα的值.
第16题图
F
E
DCB
A
