余角和补角习题练习
七年级数学初一下(余角与补角练习题)(精.选)

ACBD余角和补角【基础训练】1、如果两个锐角的和是_________ (即______°),则这两个角互为余角; 如果两个角的和是________ (即______°),则这两个角互为补角。
2、⑴∵1∠和2∠互余,∴=∠+∠21_____(或2_____1∠-=∠) ⑵∵1∠和2∠互补,∴=∠+∠21_____(或2_____1∠-=∠)3、若∠α=50º,则它的余角是 ,它的补角是 。
4、7150'︒=∠α,则它的余角等于________;β∠的补角是2183102'''︒,则β∠=_______5、如果∠α='3931︒,∠α的余角∠β =_________,∠α的补角∠γ=_________,∠γ-∠β=________.一个角的补角比余角大 .6、若∠β=110º,则它的补角是 ,它的补角的余角是 。
7. 已知∠1=200,∠2=300,∠3=600,∠4=1500,则∠2是__ __的余角,___ __是∠4的补角. 8. 若∠1+∠2=90°,∠3+∠2=90°,∠1=40°,则∠3=__ __°, 依据是___ ____。
9、如图,∠ACB=∠CDB=90º,图中∠ACD 的余角有 个。
10、若∠1与∠2互余,∠3和∠2互补,且∠3=120º,那么∠1= 。
余角与补角的性质11、如果∠1+∠2=90 º,∠2+∠3=90 º,则∠1与∠3的关系为________,其理由是_____________________. 如果∠1+∠2=180 º,∠2+∠3=180 º,则∠1与∠3的关系为________,其理由是___________________. 如果∠1+∠2=90 º,∠2=∠3,∠3+∠4=90 º,则∠1与∠3的关系为_______,其理由是______________. 如果∠1+∠2=180 º,∠2=∠3,∠3+∠4=180 º,则∠1与∠3的关系为_______,其理由是____________. 对顶角的定义: . 对顶角的性质: . 12、如右图,其中共有________对对顶角。
(完整版)余角、补角、对顶角的概念和习题答案

余角和补角和对顶角余角:如果两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角。
ZA + /C=90 °/A= 90 ° ZC , ZC 的余角=90 ° ZC 即:/A 的余角=90 ° ZA补角:如果两个角的和是一个平角,那么这两个角叫互为补角.其中一个角叫做另一个角的补角ZA + /C=180 °Z A= 180 ° ZC , ZC 的补角=180 ° ZC 即:Z A 的补角=180 ° Z A对顶角: 一个角的两边分别是另一个角的反向延长线,这两个角是对顶角。
两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角。
两条直线相交,构成两对对顶角。
对顶角相等•对顶角与对顶角相等•对顶角是对两个具有特殊位置的角的名称;对顶角相等反映的是两个角间的大小关系。
补角的性质:同角的补角相等。
比如:Z A+ ZB=180 °Z A+ ZC=180 :则:Z C= Z。
等角的补角相等。
比如:Z A+ ZB=180 °/D+ ZC=180 °,ZA= ZD 贝U:Z C= /B。
余角的性质:同角的余角相等。
比如:Z A+ ZB=90 °,ZA+ ZC=90。
,则:Z C= /B。
A+ ZB=90 °,ZD+ ZC=90 °,ZA= ZD 贝U:Z C= Z B。
等角的余角相等。
比如:Z注意:①钝角没有余角;②互为余角、补角是两个角之间的关系。
如Z A+ ZB+ ZC=90 °,不能说ZA、/B、/C互余;同样:如Z A+ ZB+ZC=180 °,不能说ZA、Z B、Z C互为补角;③互为余角、补角只与角的度数相关,与角的位置无关。
只要它们的度数之和等于90 ° 或180 °,就一定互为余角或补角。
七年级数学余角和补角练习题精选

七年级数学余角和补角练习题精选本文档为七年级数学余角和补角的练题精选,旨在帮助学生提高对余角和补角的理解和运用能力。
以下是一些精选练题,供学生们进行练和复。
问题1已知角A的度数为50°,求角A的余角和补角。
解答:角A的余角等于90°减去角A的度数,即90° - 50° = 40°。
角A的补角等于180°减去角A的度数,即180° - 50° = 130°。
问题2已知角B的度数为120°,求角B的余角和补角。
解答:角B的余角等于90°减去角B的度数,即90° - 120° = -30°。
角B的补角等于180°减去角B的度数,即180° - 120° = 60°。
问题3已知角C的余角为70°,求角C的度数和补角。
解答:角C的度数等于90°减去角C的余角,即90° - 70° = 20°。
角C的补角等于180°减去角C的度数,即180° - 20° = 160°。
问题4已知角D的补角为80°,求角D的度数和余角。
解答:角D的度数等于180°减去角D的补角,即180° - 80° = 100°。
角D的余角等于90°减去角D的度数,即90° - 100° = -10°。
以上为七年级数学余角和补角的练习题精选。
同学们可以根据题目要求进行计算,加深对余角和补角的理解。
希望能对大家的数学学习有所帮助。
余角与补角练习题一

====Word 行业资料分享--可编辑版本--双击可删====
源-于-网-络-收-集 《余角和补角》基础练习1
1.一个锐角的补角比这个角的余角大 .
2.若一个角的余角是这个角的4
1,则这个角是 ,这个角的补角是 . 3.一个角的补角加上10°后等于这个角的余角的3倍,求这个角的度数.
4.如图OA 的方向是北偏东15°,OB 的方向是北偏西40°.
(1)若∠AOC =∠AOB ,则OC 的方向是 ;
(2)OD 是OB 的反向延长线,则OD 的方向是 ;
(3)∠BOD 可看作是OB 绕点O 逆时针方向旋转至OD ,作∠BOD 的平分线OE ,OE 的方向
是 ;
(4)在(1)、(2)、(3)的条件下,∠COE = .
参考答案
1. 90°
2.72°;108°
3.设这个角为x ,则180°-x +10°=3(90°-x ),解得x =40°.
4.(1)北偏东70° (2)南偏东40°
(3)南偏西50° (4)160°。
余角和补角练习题大全与答案
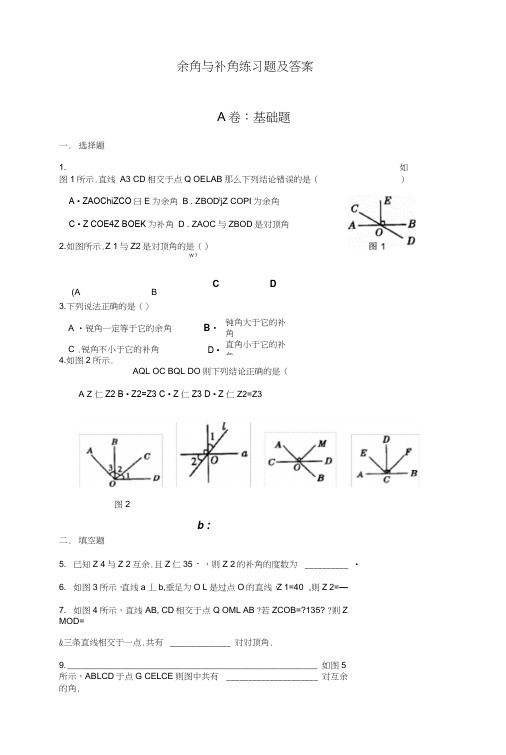
余角与补角练习题及答案A卷:基础题一.选择題1. 如图1所示.直线A3 CD相交于点Q OELAB那么下列结论错误的是()A • ZAOChiZCO曰E为余角B . ZBOD l jZ COPI为余角C • Z COE4Z BOEK为补角D . ZAOC与ZBOD是对顶角2.如图所示.Z 1与Z2是对顶角的是()(A B W 7C D3.下列说法正确的是(〉A •锐角一定等于它的余角B・钝角大于它的补角C .锐角不小于它的补角D •直角小于它的补角4.如图2所示.AQL OC BQL DO则下列结论正确的是(A Z 仁Z2B • Z2=Z3C • Z 仁Z3D • Z 仁Z2=Z3b :二.填空题5. 已知Z 4与Z 2互余.且Z仁35・,则Z 2的补角的度数为__________ •6. 如图3所示,直线a丄b,垂足为O L是过点O的直线,Z 1=40° ,则Z 2=—7. 如图4所示,直线AB, CD相交于点Q OML AB ?若ZCOB=?135? ?则Z MOD=&三条直线相交于一点.共有______________ 对对顶角.9. ____________________________________________________ 如图5所示,ABLCD于点G CELCE则图中共有 _____________________ 对互余的角.图2三.解答題10. 如图所示,直线AB CD相交于点Q Z BOE-90・若Z COE=55 • ?求Z BODfi勺度数.11. 如图所示.直线AB与CD相交于点O 0E平分Z AOD Z AOC=?120?.求ZBOD z AOSTJ度数.B卷:提高题一.七彩题1. (一題乡解遼)如图所示.三条直线AB CD EF相交于点Q Z AOF=3/ FOBZA0090 •求Z EOCfi<J度数.二、知识交叉题2. (科内交叉题)一个角的补角与这个角的余角的和比平角少3. (科外交叉题)如图所示,十光线从空气射入水中时,光线的传播方向发生了改变.这就是光的折射现象.若Z 1=42- • Z 2=?28?°•则光的传播方向改变了_______________ 度. AB 、10°•求这个B三. 实际应用题4.如图所示是一个经过改造的台球桌面的示意图.图中4个角上的阴影部分分别表示 4个 入球袋.如果一个球按图中所示的方向被击岀 (?假设用足够的力气击出,使球可以经过多次反射)•那么该球最后落入哪个球袋?在图上Hi 出被击的球所走路程.四、经典中考题5. (2007,济南,4分)已知:如图所示,AB 丄CD 垂足为点 O EF 为过点O 湖一条直线, 则Z1与Z 2的关系一定成立的是( )A 相等B •互余C •互补D .互为对顶角参考答案A 卷■1. C 点拨:因为Z COE 与ZDO 包为补角,所以 C 错误,故选C.2. D 3 ・ B4. C 点拨:因为 AQLOC BQL DO所以Z AOC=9C ・ Z BOD=90 ,即Z 3*Z 2=90° ・ Z 2+Z 仁90° ,根据同角的余角相等可得z 1=Z3-故选C.6. (2008.南通. 3分)已知Z A=40°•则Z A 的余2号球袋5. 125°点拨:因为Z 1与Z2互余.所以Z 1*Z2=90° ,又因为Z 仁35° , ?所以Z 2=90° -35=55 °・所以180°・Z2=180°・55・=125-,即Z 2?的补侑的度数是125-・6. 50* 点拨:由已知可得Z 1+Z2=180°・90・=90°・2 2=90°・Z 仁9CF ・?40° =50° .7. 45°点拨:因为OMLAB所以Z MOD艺BOD=90 .所以N MOD-90 - ZBOD又因为Z BOD=180 ・ ZCOB=180 -135* =45° ,所以Z MOD=90 -45 ° =45°・8. 6 点拨:如图所示,直线AB. CD EF相交于点Q ZAOD与ZBOC Z AOE与Z BOF? ZDOE*JZ COE ZDOB»jZ COA ZEOB'jZ FOA ZEOC'jZFOD韵分别构成对顶角. 共有6对对顶角.9. 4 点拨:由ABr CD可得Z ACE与N ECD互余,Z DCF与Z FCB互余.由CE±CF,可得Z ECD与ZDCF互余,又由于Z ACB为平角,所以Z ACE与ZBCF互余,共有4对.10. 解:因为Z BOE1 JZ AOE5补,Z BOE=9Q .所以Z A0E=18CT ・ ZBOE=?180 ・90 ° =90°・即/ COE-teT COA=90 ,又Z COE=55,所以Z COA=90 ・ ZCOE=90 -?55 ° =35° ,闵为直线AB, CD相交于点Q 所以Z BOD^COA=35・11. W:因为直线AB与CD相交于点O所以Z BODNA00120 ,因为Z AOC+?/ AOD=180 ・所以Z AOD=180 -120° =60°・因为OE平分Z AOD所以Z Z AOD丄X 60° =30° .2 2点拨:由Z BOD与ZAOC是对顶角,可得Z BOD的度数.由Z AOC与ZAOD互补,?可得ZAOD 的度数.又由 OE 平分Z AOD 可得Z AO 日为度数. B 卷 一 % 1.解法一:因为Z FOB 幺AOF=180・ZAOF=MFOB (已知)・ 所以Z FOB+3?ZFOB=18a (等虽代换),所以Z FOB=45・ 所以Z AOE^T FOB=45 (对顶角相等),因为Z AOC=90 , 所以Z EOC^T AOC^ AOE=90 -45 ° =45° ・ 解法二:因为Z FOBt/ AOF=180 ・ Z AOF=3^ FOB 所以N FOB+3/ FOB^180 , ?所以N FOB-45 , 所以Z AOF=3/ FOB=^< 45° =135° ・ 所以Z BOE=^AOF=135 •又因为Z AOC=90 , 所以Z BOC=180 ・ ZAOC=180 ・90 ° =90° , 所以Z E0CNB0E2B0C=?135 ・90° =45° . 2. 解:设这个角为 x,则其补角为180° -x,余角为90* -x , 根据题意,得(?480° -x) + (90- -x ) =180° ・10・,解得 x=50° , 所以这个角的度数为 50°・ 点拨:本题是互余.互补及平角的槪念的一个交叉综合题,要理清各种关系, 列出方程.3. 14点拨:本題是对顶角的性质在物理学中的应用.4. 解:落入2号球袋,如图所示.点拨:此趙应与实际相联系• 球被击中后在桌面上迟的路线与台球桌面的边缘构成的角 等于反弹后走的路线与台球桌面的边缘构成的角. 5. B 点拨:因为AB1 CD 于点Q 所以Z BOC=90 •又CD 与EF 相交于点 a ?所以Z COEN 2,所以Z 1 + Z2=Z1+ZCOE^BOC=90 ,即Z 1 与Z2 互余,故选 B.才能正确 1蚪球袋 2号球袋!6. 50°点拨^ Z A的余角为90° - ZA=90° -40° =50° .。
余角、补角、对顶角的概念和习题答案

余角和补角和对顶角令狐采学余角:如果两个角的和是一个直角,那么称这两个角互为余角,简称互余,也可以说其中一个角是另一个角的余角。
∠A +∠C=90°,∠A= 90°-∠C ,∠C的余角=90°-∠C 即:∠A的余角=90°-∠A补角:如果两个角的和是一个平角,那么这两个角叫互为补角.其中一个角叫做另一个角的补角∠A +∠C=180°,∠A= 180°-∠C ,∠C的补角=180°-∠C 即:∠A 的补角=180°-∠A对顶角:一个角的两边分别是另一个角的反向延长线,这两个角是对顶角。
两条直线相交后所得的只有一个公共顶点且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角。
两条直线相交,构成两对对顶角。
对顶角相等.对顶角与对顶角相等.对顶角是对两个具有特殊位置的角的名称;对顶角相等反映的是两个角间的大小关系。
补角的性质:同角的补角相等。
比如:∠A+∠B=180°,∠A+∠C=180°,则:∠C=∠B。
等角的补角相等。
比如:∠A+∠B=180°,∠D+∠C=180°,∠A=∠D则:∠C=∠B。
余角的性质:同角的余角相等。
比如:∠A+∠B=90°,∠A+∠C=90°,则:∠C=∠B。
等角的余角相等。
比如:∠A+∠B=90°,∠D+∠C=90°,∠A=∠D则:∠C=∠B。
注意:①钝角没有余角;②互为余角、补角是两个角之间的关系。
如∠A+∠B+∠C=90°,不能说∠A、∠B、∠C互余;同样:如∠A+∠B+∠C=180°,不能说∠A、∠B、∠C互为补角;③互为余角、补角只与角的度数相关,与角的位置无关。
只要它们的度数之和等于90°或180°,就一定互为余角或补角。
余角与补角概念认识提示:(1)定义中的“互为”一词如何理解?如果∠1与∠2互余,那么∠1的余角是∠2 ,同样∠2的余角是∠1 ;如果∠1与∠2互补,那么∠1的补角是∠2 ,同样∠2的补角是∠1。
苏科版(2024)七年级数学上册第六章习题练课件:6.2.2 补角、余角
3.若一个角比它的余角大30°,则这个角等于 ( B )
A.30°
B.60°
C.105°
D.120°
解析 设这个角的度数为x,则x-(90°-x)=30°,
解得x=60°,故选B.
4.(2022江苏连云港中考)已知∠A的补角为60°,则∠A= 120 °. 解析 ∠A=180°-60°=120°.
第6章 平面图形的初步认识 6.2.2 补角、余角
基础过关全练
知识点4 补角、余角的概念
1.(2021甘肃兰州中考)若∠A=40°,则∠A的补角为(D )
A.40°
B.50°
C.60°
D.140°
解析 互补的两个角的度数和为180°, 所以∠A的补角为180°-∠A=140°.
2.(2023江苏南通通州月考)一副三角板按如图所示的方式摆 放,若∠1的度数是∠2的3倍,则∠1的度数为 D( ) A.20° B.22.5° C.25° D.67.5° 解析 根据题图可知∠1+∠2=180°-90°=90°, 因为∠1的度数是∠2的3倍,所以∠1=3∠2, 所以4∠2=90°,所以∠2=22.5°, 所以∠1=90°-∠2=67.5°.
7.如图所示,点O在直线AB上,且∠AOC=∠BOC=∠EOF=90°, 试判断∠AOE与∠BOF的关系以及∠COE与∠BOF的关系.
解析 由题意得,∠AOE+∠BOF=180°-∠EOF=90°,所以 ∠AOE与∠BOF互余,根据同角的余角相等可得∠COE= ∠BOF.
能力提升全练
8.(2024江苏泰州姜堰期末,6,★★☆)如图,点O在直线AB上, ∠1=∠2,∠3=∠4,则图中互余的角共有 B( ) A.5对 B.4对 C.3对 D.2对
完整版余角、补角、对顶角概念及习题
余角和补角和对顶角余角:若是两个角的和是一个直角 ,那么称这两个角互为余角 ,简称互余 ,也能够说其中一个角是另一个角的余角。
∠A+ ∠C=90 °,∠A= 90 °-∠C ,∠C 的余角 =90 °-∠C 即 :∠A 的余角 =90 °-∠A补角:若是两个角的和是一个平角,那么这两个角叫互为补角.其中一个角叫做另一个角的补角∠A + ∠C=180 °,∠A= 180°-∠C ,∠C的补角=180°-∠C即:∠A的补角=180°-∠A对顶角:一个角的两边分别是另一个角的反向延长线,这两个角是对顶角。
两条直线订交后所得的只有一个公共极点且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角。
两条直线订交,构成两对对顶角。
对顶角相等.对顶角与对顶角相等.对顶角是对两个拥有特别地址的角的名称;对顶角相等反响的是两个角间的大小关系。
补角的性质:同角的补角相等。
比方:∠A+ ∠B=180 °,∠A+ ∠C=180 °,则:∠ C= ∠B。
等角的补角相等。
比方:∠A+ ∠B=180 °,∠D+ ∠C=180 °,∠A= ∠D 则:∠C= ∠B。
余角的性质:同角的余角相等。
比方:∠A+ ∠B=90 °,∠A+ ∠C=90 °,则:∠C= ∠B。
等角的余角相等。
比方:∠A+ ∠B=90 °,∠D+ ∠C=90 °,∠A= ∠D 则:∠C= ∠B。
注意:①钝角没有余角;②互为余角、补角是两个角之间的关系。
如∠ A+ ∠B+ ∠C=90 °,不能够说∠A 、∠B、∠C 互余;同样:如∠ A+∠B+ ∠C=180 °,不能够说∠A 、∠B、∠C 互为补角;③互为余角、补角只与角的度数相关,与角的地址没关。
只要它们的度数之和等于90 °或180 °,就必然互为余角或补角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《余角和补角》典例精析
1
【例1】已知一个角的补角是这个角的余角的4倍,求这个角的度数.
【 解析】设这个角的度数为 度,利用题目中的等量关系得:
,
解得: .
【 答案】 .
【 点评】注意利用方程思想解决图形问题,使数和形有机的结合.
【例2】如图∠AOC= ∠BOC=∠DOE=90°,则
图中与∠3互余的角是_________,
图中与∠4互余的角是_________,
图中有与∠3互补的角吗?是_________.
【 解析】假设∠3= 根据已知条件推得∠4= .
, 然后根据角度判断相关角.
【 答案】 、∠4 ;∠3 、 ;.
【 点评】利用特值法,可以使复杂的问题变简单.
