六(下)奥数第5讲~平面几何之曲线图形
小学奥数几何知识点讲解

小学奥数几何知识点讲解几何是数学的一个重要分支,主要研究空间形状、大小、相对位置等概念及其性质和关系。
在小学奥数竞赛中,几何是一个常见的考察内容。
下面我将为大家讲解一些小学奥数几何知识点,希望能够帮助大家更好地应对几何题目。
1.点、线、面的概念在几何中,点是没有大小和形状的,只有位置的概念。
线是由无数个点组成的,没有宽度、长度、厚度等,可以用箭头表示方向。
面是由无数个点和线组成的,是平面上的一个二维图形。
2.正方形、长方形、三角形正方形是一种四条边都相等且角都是直角的四边形,它拥有四条对称轴。
长方形是一种拥有两组相等的对边和四个直角的四边形,它有两条对称轴。
三角形是一种由三条边和三个角组成的图形。
3.圆和半圆圆是由等距离圆心的所有点组成的集合,圆心到圆上任意一点的距离都相等。
半圆是圆的一半,由圆周上的一个弧和两条半径组成。
4.平行线和垂直线平行线是在同一个平面内永远不会相交的两条直线。
垂直线是与另一条线段相交时,两条线段之间的角度为90度的线。
5.直角、锐角和钝角直角是一个角度为90度的角,锐角是小于90度的角,钝角是大于90度小于180度的角。
6.对称和中心对称对称是指两个物体在一些轴线上镜像重合的关系,中心对称是指一个图形可以通过一些点进行旋转180度后重合。
7.面积和周长面积是指一个二维图形所占的空间大小,通常用平方单位表示,如平方厘米、平方米等。
周长是指一个图形的边缘长度。
8.直角三角形和勾股定理直角三角形是一种其中一个角为90度的三角形。
勾股定理是指在直角三角形中,直角边的平方之和等于斜边的平方,即a²+b²=c²。
9.分数、比例和相似分数是表示一个整体被分成几等份的表达方式。
比例是指两个或多个数之间的等比关系。
相似是指两个图形有相同的形状,但是可能有不同的大小。
10.正多边形和不规则图形正多边形是指所有边和角都相等的多边形。
不规则图形是指边和角都不相等的图形。
六年级下册奥数知识点梳理:几何图形
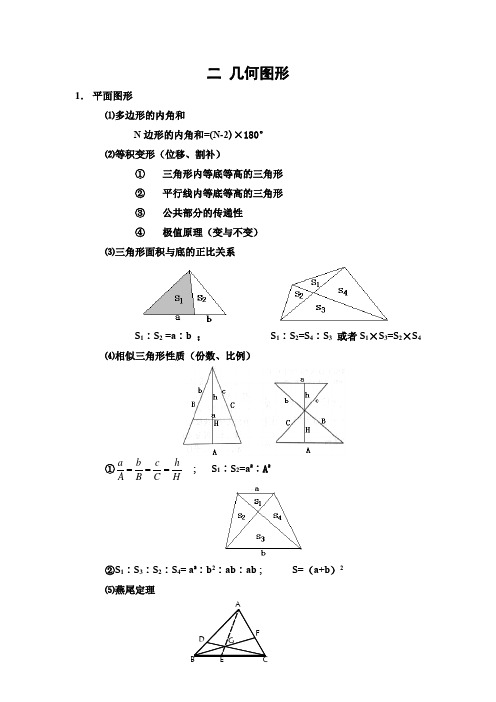
二 几何图形
1. 平面图形
⑴多边形的内角和
N 边形的内角和=(N -2)×180°
⑵等积变形(位移、割补)
①
三角形内等底等高的三角形 ②
平行线内等底等高的三角形 ③
公共部分的传递性 ④ 极值原理(变与不变)
⑶三角形面积与底的正比关系
S 1︰S 2 =a ︰b ; S 1︰S 2=S 4︰S 3 或者S 1×S 3=S 2×S 4 ⑷相似三角形性质(份数、比例)
①a b c h A B C H === ; S 1︰S 2=a 2︰A 2
②S 1︰S 3︰S 2︰S 4= a 2︰b 2︰ab ︰ab ; S=(a+b )2 ⑸燕尾定理
S△ABG:S△AGC=S△BGE:S△GEC=BE:EC;
S△BGA:S△BGC=S△AGF:S△GFC=AF:FC;
S△AGC:S△BCG=S△ADG:S△DGB=AD:DB;
⑹差不变原理
知5-2=3,则圆点比方点多3。
⑺隐含条件的等价代换
例如弦图中长短边长的关系。
⑻组合图形的思考方法
①化整为零
②先补后去
③正反结合
2.立体图形
⑴规则立体图形的表面积和体积公式
⑵不规则立体图形的表面积
整体观照法
⑶体积的等积变形
①水中浸放物体:V升水=V物
②测啤酒瓶容积:V=V空气+V水
⑷三视图与展开图
最短线路与展开图形状问题
⑸染色问题
几面染色的块数与“芯”、棱长、顶点、面数的关系。
六年级奥数几何-平面部分.学生版

平面几何部分知识点拨一、等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如右图12::S S a b =③夹在一组平行线之间的等积变形,如右图ACDBCD S S =△△;反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形); ⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上), 则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCB A图⑴ 图⑵三、蝴蝶定理任意四边形中的比例关系(“蝴蝶定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系. 梯形中比例关系(“梯形蝴蝶定理”): ①2213::S S a b = ②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.baS 2S 1DC BA S 4S 3S 2S 1O DCB A A BC D Ob aS 3S 2S 1S 4四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AFAB AC BC AG===; ②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半.相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形. 五、燕尾定理在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=. 上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.典型例题【例 1】 如图,正方形ABCD 的边长为6,AE =1.5,CF =2.长方形EFGH 的面积为 .【巩固】如图所示,正方形ABCD 的边长为8厘米,长方形EBGF 的长BG 为10厘米,那么长方形的宽为几厘米?_ H_G_F_E_D_C_B_ A _A_B_C_D_E_ F_G_H_ A _ B_ G_ C _ E _ F_ D_ A _ B_ G_ C_ E_ F_ DO F ED C B A【例 2】长方形ABCD的面积为362cm,E、F、G为各边中点,H为AD边上任意一点,问阴影部分面积是多少?E【巩固】在边长为6厘米的正方形ABCD内任取一点P,将正方形的一组对边二等分,另一组对边三等分,分别与P点连接,求阴影部分面积.【例 3】如图所示,长方形ABCD内的阴影部分的面积之和为70,8AD=,四边形EFGO的面积AB=,15为.B【巩固】如图,长方形ABCD的面积是36,E是AD的三等分点,2=,则阴影部分的面积为.AE EDB【例 4】 已知ABC 为等边三角形,面积为400,D 、E 、F 分别为三边的中点,已知甲、乙、丙面积和为143,求阴影五边形的面积.(丙是三角形HBC)B【例 5】 如图,已知5CD =,7DE =,15EF =,6FG =,线段AB 将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG 的面积是 .GFE DC BA【例 6】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBA【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?EDCBA【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E D CBA【例 7】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDA【例 8】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EF【例 9】 如图所示的四边形的面积等于多少?DCB13131212【例 10】 如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC ∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【例 11】 如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.【例 12】 如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米?FEABDC【例 13】 如图,三角形ABC 的面积是1,E 是AC 的中点,点D 在BC 上,且:1:2BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于 .FED CBA【巩固】如图,长方形ABCD 的面积是2平方厘米,2EC DE =,F 是DG 的中点.阴影部分的面积是多少平方厘米?x y y x ABCD E FGE D CBA【例 14】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形ABD 的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍.ABC DO【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知, 求:⑴三角形BGC 的面积;⑵:AG GC =?B【例 15】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGFEDCBA【例 16】 如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长方形ABCD 的面积.ABCD EF G【例 17】如图,正方形ABCD面积为3平方厘米,M是AD边上的中点.求图中阴影部分的面积.CBA【巩固】在下图的正方形ABCD中,E是BC边的中点,AE与BD相交于F点,三角形BEF的面积为1平方厘米,那么正方形ABCD面积是平方厘米.AB CDEF【例 18】已知ABCD是平行四边形,:3:2BC CE ,三角形ODE的面积为6平方厘米.则阴影部分的面积是平方厘米.B【巩固】右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是平方厘米.【巩固】右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.B【例 19】 如图,长方形ABCD 被CE 、DF 分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为___________平方厘米.?852O A BCDEF【例 20】 如图,ABC ∆是等腰直角三角形,DEFG 是正方形,线段AB 与CD 相交于K 点.已知正方形DEFG 的面积48,:1:3AK KB =,则BKD ∆的面积是多少?B【例 21】 下图中,四边形ABCD 都是边长为1的正方形,E 、F 、G 、H 分别是AB ,BC ,CD ,DA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数mn,那么,()m n +的值等于 .BEE【例 22】 如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==,则::ADEDEGF FGCB S S S =△四边形四边形 .EGF A D CB【巩固】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.A ED CB【巩固】如图, ABC △中,DE ,FG ,MN ,PQ ,BC 互相平行,AD DF FM MP PB ====,则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形 .【例 23】 如图,已知正方形ABCD 的边长为4,F 是BC 边的中点,E 是DC 边上的点,且:1:3DE EC =,AF与BE 相交于点G ,求ABG S △GFAEDCB【例 24】 如图所示,已知平行四边形ABCD 的面积是1,E 、F 是AB 、AD 的中点, BF 交EC 于M ,求BMG∆的面积.MHGF E D CBAQ E GNMF P A D C B【例 25】如图,ABCD为正方形,1cmAM NB DE FC====且2cmMN=,请问四边形PQRS的面积为多少?CA【例 26】如右图,三角形ABC中,:4:9BD DC=,:4:3CE EA=,求:AF FB.OFED CBA【巩固】如右图,三角形ABC中,:3:4BD DC=,:5:6AE CE=,求:AF FB.OFED CBA【巩固】如右图,三角形ABC中,:2:3BD DC=,:5:4EA CE=,求:AF FB.OFED CBA【例 27】如右图,三角形ABC中,:::3:2AF FB BD DC CE AE===,且三角形ABC的面积是1,则三角形ABE 的面积为______,三角形AGE的面积为________,三角形GHI的面积为______.IHGFED CBA【巩固】 如右图,三角形ABC 中,:::3:2AF FB BD DC CE AE ===,且三角形GHI 的面积是1,求三角形ABC的面积.IH G FEDCBA【巩固】如图,ABC ∆中2BD DA =,2CE EB =,2AF FC =,那么ABC ∆的面积是阴影三角形面积的倍.B【巩固】如图在ABC △中,12DC EA FB DB EC FA ===,求GHI ABC △的面积△的面积的值. IHG FEDCBA【例 28】 如图,三角形ABC 的面积是1,BD DE EC ==,CF FG GA ==,三角形ABC 被分成9部分,请写出这9部分的面积各是多少?GFE D CBA【巩固】如图,ABC 的面积为1,点D 、E 是BC 边的三等分点,点F 、G 是AC 边的三等分点,那么四边形JKIH 的面积是多少?K JI HABC D EF G【例 29】 右图,ABC △中,G 是AC 的中点,D 、E 、F 是BC 边上的四等分点,AD 与BG 交于M ,AF 与BG 交于N ,已知ABM △的面积比四边形FCGN 的面积大7.2平方厘米,则ABC △的面积是多少平方厘米?N M GA BCD EF【例 30】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求阴影部分面积.GCBA【例 31】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求中心六边形面积.GCBA。
小学奥数平面几何五大定律及应用PPT文档36页

36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好 。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
40、人类法律,事物有规律,这富 ❖ 丰富你的人生
71、既然我已经踏上这条道路,那么,任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远,吾将上下而求索。——屈原 75、内外相应,言行相称。——韩非
奥数平面几何之曲线图形 (附答案)

平面几何之曲线图形基本模型:【例1】如图,阴影部分的面积是多少?例1图【举一反三】计算图中阴影部分的面积(单位:分米)。
举一反三图【例2】如图,大圆半径为小圆的直径,已知图中阴影部分面积为S1,空白部分面积为S2,那么这两个部分的面积之比是多少?(圆周率取3.14)例2图【例3】(第四届走美决赛试题)如图,边长为3的两个正方形BDKE、正方形DCFK并排放置,以BC为边向内侧作等边三角形,分别以B、C为圆心,BK、CK为半径画弧。
求阴影部分面积。
(π取3.14)例3图【例4】(奥林匹克决赛试题)在桌面上放置3个两两重叠、形状相同的圆形纸片。
它们的面积都是100平方厘米,盖住桌面的总面积是144平方厘米,3张纸片共同重叠的面积是42平方厘米。
那么图中3个阴影部分的面积的和______是平方厘米。
例4图【例5】三角形ABC是直角三角形,阴影Ι的面积比阴影Π的面积小25cm2,AB=8cm,求BC的长度。
(π 取3.14 )例5图【例6】在直角边为3与4的直角三角形各边上向外分别作正方形,三个正方形顶点顺次连接成如图所示的六边ABCDEF。
求这个六边形的面积是多少?例6图【巩固】如图所示,直角三角形PQR的直角边为5厘米,9厘米。
问图中3个正方形面积之和比4个三角形面积之和大多少?巩固图【例7】传说古老的天竺国有一座钟楼,钟楼上有一座大钟,这座大钟的钟面有10平方米。
每当太阳西下,钟面就会出现奇妙的阴影(如右图)。
那么,阴影部分的面积是_____平方米。
例7图【例8】草场上有一个长20米、宽10米的关闭着的羊圈,在羊圈的一角用长30米的绳子拴着一只羊(见下图)。
问:这只羊能够活动的范围有多大?例8图【例9】如图,ABCD是一个长为4,宽为3的长方形,围绕C点按顺时针方向旋转90°,分别求出四边扫过图形的面积。
例9图练习:1、求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)2、正方形面积是7平方厘米,求阴影部分的面积。
六年级奥数 几何;第5讲;几何综合_二_;教师版
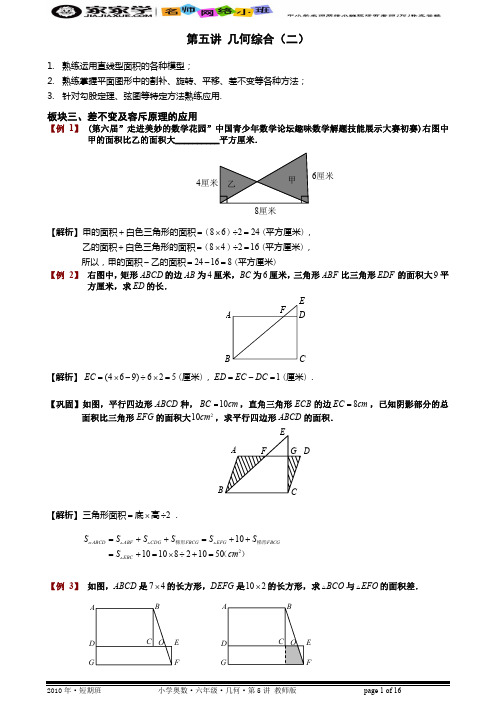
方法二:连接正方形 A 对角线(如右上图),将 40 平方厘米的图形分成面积相等的两个梯形,而梯
形的上下底之和恰好是 20 厘米,所以梯形的高为 20 × 2 ÷ 20 = 2 (厘米),即两个正方形的边长差,
由此可求出乙正方形的边长为(20 − 2)÷ 2 = 9 (厘米),从而乙正方形的面积为 9 × 9 = 81(厘米 2).
A
甲乙 D I JF
M
N H丙
B
E
C
【解析】因为 D 、 E 、 F 分别为三边的中点,所以 DE 、 DF 、 EF 是三角形 ABC 的中位线,也就与对应 的边平行,根据面积比例模型,三角形 ABN 和三角形 AMC 的面积都等于三角形 ABC 的一半, 即为 200. 根据图形的容斥关系,有 SΔABC − S丙 = SΔABN + SΔAMC − SAMHN ,即 400 − S丙 = 200 + 200 − SAMHN ,所 以 S丙 = SAMHN .
【例 8】 从一块正方形的玻璃板上锯下宽为 0.5 米的一个长方形玻璃条后,剩下的长方形的面积为 5 平方 米,请问锯下的长方形玻璃条的面积等于多少?
0.5
5 5
5
0.5
0.5
5 5
2010 年·短期班
图a
图b
小学奥数·六年级·几何·第 5 讲 教师版
page 3 of 16
【解析】我们先按题目中的条件画出示意图(如图 a ),我们先看图中剩下的长方形,已知它的面积为 5 平 方米,它的长和宽相差 0.5 米,我们可以将这样形状的四个长方形拼成一个弦图(如图 b ). 图 b 是一个大正方形,它的边长等于长方形的长和宽之和, 中间的那个小正方形的边长,等于长方形的长和宽之差, 即 0.5 米.所以中间的小正方形的面积为 0.5 × 0.5 = 0.25 平 方米,那么大正方形的面积为 5 × 4 + 0.25 = 20.25 平方米. 因为 4.5 × 4.5 = 20.25 ,所以大正方形的边长等于 4.5 米.所 以原题中剩下的长方形的长与宽的和为 4.5 米,而长与宽 的差为 0.5 米,所以剩下的长方形的长为: (4.5 + 0.5) ÷ 2 = 2.5 米,即原正方形的边长为 2.5 米.又知锯下的长方形玻璃条的宽为 0.5 米,于是 可得锯下的长方形玻璃条的面积为 2.5 × 0.5 = 1.25 平方米.
【小升初培优专题】六年级下册数学-平面几何综合训练—曲线型(解析版)

【小升初培优专题】六年级下册数学-平面几何综合训练—曲线型(解析版)一、知识点1、圆周长:C=πd=2πr扩倍问题(1):若圆的半径扩大到n倍,则直径扩大到n倍,周长扩大到n倍,面积扩大到n²倍扩倍问题(2):若两个圆的半径比为n:m,则它们的直径比为n:m,周长比为n:m,面积比则为n²:m²构造圆在长方形中画一个最大的圆在长方形中画最大的半圆技巧:长的一半与宽比较,谁小谁是半径。
2、半圆周长:C=πr+d面积:πr²÷23、圆环=大圆面积-小圆面积=πR²-πr²圆环面积:S环4、扇形弧长:r nl π2360⨯=面积:2360r nS π=5、组合图形方中圆:正方形与圆面积之比为4:π圆中方:圆与正方形面积之比为π:2方中圆中方:大正方形面积是小正方形面积的2倍圆中方中圆:大圆面积是小圆面积的2倍割补法:重叠问题:整体减空白一、填空题。
(每道小题5分,共 40分)1. (1)一个圆的半经扩大到3倍,直径扩大到 倍;周长扩大到 倍;面积扩大到 倍。
【解答】3,3,9。
(2)大圆和小圆的半径比是3:2,它们的直径比是 ,他们的周长比是 ,它们的面积比是 。
【解答】3:2,3:2,9:4。
2. 在一个长10厘米、宽4厘米的长方形内画圆,圆的直径最大是 厘米,能画 个这样的圆且互不重叠。
【解答】如下图,4:2。
3. 如图,以B 、C 为圆心的两个半圆的直径都是3厘米,图中阴影部分的周长是 厘米。
【解答】如下图,半径为3÷2=1.5(厘米),连接BP 与CP ,因为BC 、CP 、PB 均为半径,所以△BCP 是等边三角形,那么∠PBC =∠PCB =60(度),弧长PB =60=弧长PC =36060×3.14×3=1.57(厘米),阴影部分的周长为1.57+1.57+1.5=4.64(厘米)。
六年级下册数学人教版奥数专讲:平面图形 课件(共17张PPT)

例题二
有4根直径都是4分米的圆柱形木头,现用绳 子分别在两端把它们捆在一起,至少需要绳子多 少分米?(接头处不计)
圆弧长: 3.14×4=12.56(分米)
线段长: 4×4=16(分米)
总长: 12.56+16=28.56(分米)
答:至少需要绳子28.56分米。
等高的三角形面积之比 等于底之比!
AE=EF=FC
3×(1+2+2+4)=27(平方厘米)
2S△ADE=S△DEC=S△ABE 2S△DEC=S△EBC 答:梯形ABCD的面积是27平方厘米。
4S△ADE=S△EBC
例题四
求下图阴影部分的面积。(单位:厘米)
4×4÷2=8(平方厘米) 答:阴影部分面积是8平方厘米。
课程结束
奥数六年级下册春季课程
当b大于0.5a时,半圆的直径等于a; 当b等于0.5a时,半圆的直径等于a,半径等于b; 当b小于0.5a时,半圆的半径等于b。
2.半圆的周长: C r d
3.用绳子把多根相同直径的圆柱捆绑在一起, 一周的圆弧部分长度和等于一个以圆柱直径 为直径的圆的周长。
例题三
如图,平行四边形ABCD的对角线AC被E、F 两点三等分,已知三角形ABE的面积是5平方厘米, 求平行四边形ABCD的面积。
练习五
如图,两个扇形的半径都是2厘米,求阴影 部分的面积。
(90÷360)×3.14×22 =3.14(平方厘米) 答:阴影部分的面积是3.14平方厘米。
小结
1. 等底等高的三角形面积相等 。 2. 高(底)相等的三角形的面积之比等于
底(高)之比 。
3. 求组合图形面积的常用方法—— 翻折法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级下册奥数 第5讲~平面几何之曲线图形
重点、难点
1、圆与扇形的周长、面积求法
2、弓形、谷子、弯角的面积求法 教学内容
【本讲说明】本讲内容属于几何专题中的必考题型,在历年升学考试中所占比例已达到30%-40%,在16年大桥,15年外国语,16年辅仁等试题中均有出现,主要以大题和操作题的形式考察。
每题的分值在8-10分左右。
本讲主要属于综合复习,对学生的综合要求以及几何思维能力要求较高,课前先复习一下知识点
【课堂目标】本讲主要包含两大部分:1、掌握圆和扇形周长的相关题型;2、掌握圆和扇形面积的相关题型。
3、重点掌握圆和扇形与容斥定理相结合的题型。
知识点一:基本公式
圆的周长 r C π2= 扇形的弧长3602N r l ⨯
=π 扇形的周长l r C +=2 圆的面积2r S π= 扇形的面积3602N r S ⨯=π 知识点二:基本模型
1、圆环的面积:()22r R -π
2、 弓形:222
141r r ππ-
3、谷子(也叫柳叶):2221r r -π
4、弯角形(也叫弯月):224
1r r π-
5、方中圆、圆中方模型
圆=2a π 圆=2a π 方=2422a a a =⨯ 方=()22
222a a =÷ 方:圆=4:π 方:圆=2:π
6、方圆套中套:大方是小方的2倍,大圆是中圆的2倍,中圆是小圆的2倍。
知识点三:圆和扇形周长的运用
例1、如图所示的图形由1个大的半圆弧和6个小的半圆弧围成,已知最大的半圆弧的直径为1,则这个
图形的周长是多少?(圆周率用π表示)
练1、如图所示,已知米米,70120==BC AB ,从A 到C 有3条不同的半圆弧线路可走,请你判断走
哪一条半圆弧线路的距离最短。
知识点四:圆和扇形面积
例2、如图,ABC是等腰三角形,D是半圆周的中点,BC是半圆的直径。
已知10
AB,那么阴
=
=BC 影部分的面积是多少?(圆周率取3.14)
练2、如图所示,正方形ABCD和正方形CEFG并排放置,cm
12=
BC15
=,,图中阴影部分的面
cm
CE
积是多少?(保留π)
例3、三角形ABC是直角三角形,阴影Ⅰ的面积比阴影Ⅱ的面积小252
cm,cm
=,求BC的长度。
(π
AB8
取3.14)
练3、下图(1)是一个半径为3厘米的半圆,AB是直径,如图(2)所示,让A点不动,把整个半圆逆时针转30°,此时B点移动到C点,请问:图中阴影部分的面积是多少平方厘米?
例4、【2016大桥】下图中,ABCD是一个长方形,长AD为4厘米,宽AB为3厘米,以长方形的
边AB 和AD 为半径作两个扇形,与长方形有重叠部分。
(保留π)
(1)图中阴影部分面积为多少?
(2)连接DF ,图中I 部分的面积为多少?
练4、【2015年外国语】求下图中阴影部分的面积(长度单位:厘米)(保留π)
自我挑战:
1、【2018天一】如图,大圆半径为小圆的直径,已知图中阴影部分面积为1S ,空白部分面积为2S ,那么
这两个部分的面积之比是多少?( 取3)
2、【2013年迎春杯】如图,分别以正八边形的四个顶点A 、B 、C 、D 为圆心,以正八边形边长为半径画
圆。
圆弧的焦点分别为E 、F 、G 、H 。
如果正八边形的边长为100厘米,那么,阴影部分的周长是多少厘米?(π取3.14)
3、
【大桥思训题】下图中的圆是以O 为圆心点,半径是10cm 的圆,求阴影部分
面积。
4、【2014大桥】如图,ABCD是边长为10厘米的正方形,且AB是半圆的直径,则阴影部分的面积是多
少平方厘米?(保留π)
你的作业,请认真完成哦!
1、如图,阴影部分的面积是多少?
2、如图,分别以一个边长为2厘米的等边三角形的三个顶点为圆心,以2厘米为半径画弧,求阴影图形的周长是多少厘米?
3、【2008年辅仁】如图,长方形ABCD中,cm
6=
=,做扇形ABE,交AD延长线于E,做
,
AB4
cm
BC
扇形CBF,交CD于F,求阴影部分的面积。
(保留π)
4、如图,图中空白部分为长方形,求阴影部分的面积。
(π取3.14)
5、如图,一只狗用皮带系在边长是10的正方形狗窝的一角上,皮带长为14,在狗窝外面狗能活动的范
围是多少?画出图形并计算。
(狗的大小忽略不计,π取3,长度单位:分米)
6、下图中,O为圆心,OC垂直于AB,三角形ABC的面积为45平方厘米,求阴影部分的面积。
