北航数理统计回归分析大作业
北航数值分析大作业二(纯原创,高分版)
(R_5 ,I_5 )=(-1.493147080915e+000, 0.000000000000e+000)
(R_6 ,I_6 )=(-9.891143464723e-001, 1.084758631502e-001)
-0.8945216982
-0.0993313649
-1.0998317589
0.9132565113
-0.6407977009
0.1946733679
-2.3478783624
2.3720579216
1.8279985523
-1.2630152661
0.6790694668
-0.4672150886
6.220134985374e-001
-1.119962139645e-001
-2.521344456568e+000
-1.306189420531e+000
-3.809101150714e+000
8.132800093357e+000
-1.230295627285e+000
-6.753086301215e-001
而其本质就是
1.令 以及最大迭代步数L；
2.若m≤0，则结束计算，已求出A的全部特征值，判断 或 或m≤2是否成立，成立则转3，否则转4；
3.若 ，则得一个特征值 ，m=m-1，降阶；若 ，则计算矩阵：
的特征值得矩阵A的两个特征值，m=m-2，降阶，转2.；
4.若k≤L，成立则令
k=k+1，转2，否则结束计算，为计算出矩阵A的全部特征值；
北航数理统计第一次大作业
数理统计第一次课程论文广州恒大队在２0１5赛季亚冠的进球数的多元线性回归模型学号： SＹ15272０5姓名：郭谢有摘要本赛季亚洲冠军联赛，来自中国的球队广州恒大淘宝队最终在决赛中力克阿联酋的迪拜阿赫利队，三年之内第二次夺得亚冠冠军。
为了研究恒大的夺冠过程，本文选取了恒大该赛季亚冠总共15场比赛中的进球数为因变量,对可能影响进球数的射门数、射正数等7个自变量进行统计,并进一步利用统计软件SPSS对以上数据进行了多元逐步线性回归。
最终确定了进球数与各因素之间关系的“最优”回归方程。
关键词：多元线性回归,逐步回归法，广州恒大,SPSS目录摘要 (1)1.引言 (3)2.符号说明 (3)3.数据的采集和整理 (3)3.1数据的采集 (3)3.2建模 (4)4.数据分析及计算 (4)4.结论 (9)参考文献 (10)致谢 (10)1.引言一场足球比赛的进球数说明了一支球队攻击力的强弱，也是决定比赛胜负的至关因素,综合反映出这支球队的实际水平。
而作为竞技体育,足球场上影响进球数的因素很多,为了研究本赛季恒大在亚冠夺冠过程中的14场比赛中进球数与其他一些因素的关系,本论文从搜达足球和新浪体育数据库中查找了进球数和其他7个主要影响因素的数据,包括射门次数、射正次数、传球次数、传中次数、角球次数、抢断次数。
并进一步采用多元逐步回归分析方法对以上因素进行了显著性分析，从而确定了关于恒大在本赛季亚冠中进球数的最优多元线型回归方程。
２.符号说明3.数据的采集和整理３.1数据的采集本文统计数据时，查阅了搜达足球数据库，确定恒大在亚冠1４场比赛中的进球数为因变量,并初步选取这14场比赛中的射门次数、射正次数、传球次数、传中次数、角球次数、抢断次数7因素为自变量，具体数据见下表1。
3.２建模本文选取了恒大在亚冠比赛中的进球数作为因变量y，并选取可能对进球数造成影响的因素为自变量,其中对应关系在符号说明中已经列举。
这里构建模型如下：7⋅X i+εy=β0+∑βii=1其中,其中ε为随机误差项，β0为常数项，βi为待估计的参数。
北航应用数理统计大作业多元线性回归
多元线性回归分析摘要：本文查找2011年《中国统计年鉴》，取我国31个省市自治区直辖市2010年的数据，利用SPSS软件对影响居民消费的因素进行讨论构造线性回归模型。
并对模型的回归显著性、拟合度、正态分布等分别进行检验，最终得到最优线性回归模型，寻找影响居民消费的各个因素。
关键字：回归分析；线性；相关系数；正态分布1. 引言变量与变量之间的关系分为确定性关系和非确定性关系，函数表达确定性关系。
研究变量间的非确定性关系，构造变量间经验公式的数理统计方法称为回归分析。
回归分析是指通过提供变量之间的数学表达式来定量描述变量间相关关系的数学过程，这一数学表达式通常称为经验公式。
一方面，研究者可以利用概率统计知识，对这个经验公式的有效性进行判定；另一方面，研究者可以利用经验公式，根据自变量的取值预测因变量的取值。
如果是多个因素作为自变量的时候，还可以通过因素分析，找出哪些自变量对因变量的影响是显著的，哪些是不显著的。
回归分析目前在生物统计、医学统计、经济分析、数据挖掘中得到了广泛的应用。
通过对训练数据进行回归分析得出经验公式，利用经验公式就可以在已知自变量的情况下预测因变量的取值。
实际问题的控制中往往是根据预测结果来进行的，如在商品流通领域，通常用回归分析商品价和与商品需求之间的关系，以便对商品的价格和需求量进行控制。
本文查找2011年《中国统计年鉴》，取我国31个省市自治区直辖市2010年的数据，利用SPSS软件对影响居民消费的因素进行讨论构造多元线性线性回归模型。
以探求影响居民消费水平的各个因素，得到最优线性回归模型。
随后，我们对模型的回归显著性、拟合度、正态分布等分别进行检验，以考察线性回归模型的可信度。
本文将分为5章进行论述。
在第2章，我们介绍多元线性回归模型的概念。
第3章，我们进行模型的建立与数据的收集和整理。
我们在第4章对数据进行处理，得出多元线性回归模型，并对其进行检验。
在第5章，我们进行总结。
北航数理统计答案
北航数理统计答案【篇一：北航数理统计考试题】术部2011年12月2007-2008学年第一学期期末试卷一、（6分，a班不做）设x1，x2，…，xn是来自正态总体n(?,?2)的样本，令t?x?x)，试证明t服从t-分布t（2）二、（6分，b班不做）统计量f-f(n,m)分布，证明1f的?（0?1）的分位点x?是1f1??(n,m)。
三、（8分）设总体x的密度函数为?(1??)x?,0?x?1p(x;?)??0,其他?其中???1，是位置参数。
x1，x2，…，xn是来自总体试求参数?的矩估计和极大似然估计。
四、（12分）设总体x的密度函数为?1?x???exp???，x???p(x;?)??????，??0,其它其中???????,?已知，??0,?是未知参数。
x1，x2，…，xn是来自总?体x的简单样本。
（1）试求参数?的一致最小方差无偏估计?；（2）?是否为?的有效估计？证明你的结论。
五、（6分，a班不做）设x1，x2，…，xn是来自正态总体n(?简单样本，y1，y2，…，yn是来自正态总体n(?两样本相互独立，其中?设h0:?1??2,h1:?1??2,1221?,?1)2的,?2)的简单样本，且21,?1,?2,?222是未知参数，???22。
为检验假可令zi?xi?yi, i?1,2,...,n ,???1??2 ,则上述假设检验问题等价于h0:?1?0,h1:?1?0,这样双样本检验问题就变为单检验问题。
基于变换后样本z1，z2，…，zn，在显著性水平?下，试构造检验上述问题的t-检验统计量及相应的拒绝域。
六、（6分，b班不做）设x1，x2，…，xn是来自正态总体n(?简单样本，?0已知，?2未知，试求假设检验问题h0:?2,?)02的??0,h1:?22??02的水平为?的umpt。
七、（6分）根据大作业情况，试简述你在应用线性回归分析解决实际问题时应该注意哪些方面？八、（6分）设方差分析模型为?xij????i??j??ij?2??ij服从正态总体分布n(0,?)且?ij相互独立??i?1,2,...,p;j?1,...,q?pq??和?满足??i?0,??j?0.j?ii?1j?1?总离差平方和pst?sa?sb?se中sa?q?(xi??x),x?i?1x??pqi?1j?11pqij,xi??1qijx?qj?1,且e(se)=(p-1)(q-1)?.?...??p?0的拒绝2试求e(sa)，并根据直观分析给出检验假设h0:?1??2域形式。
北航数值分析大作业三
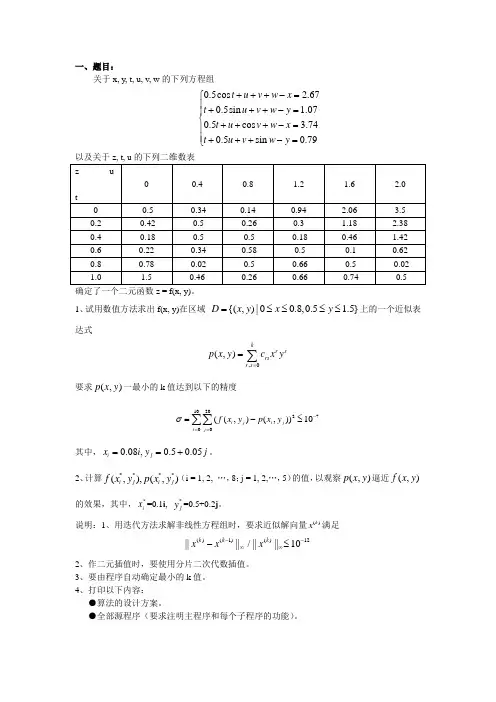
一、题目：关于x, y, t, u, v, w 的下列方程组0.5cos 2.670.5sin 1.070.5cos 3.740.5sin 0.79t u v w x t u v w y t u v w x t u v w y +++-=⎧⎪+++-=⎪⎨+++-=⎪⎪+++-=⎩1、试用数值方法求出f(x, y)在区域 {(,)|00.8,0.5 1.5}D x y x y =≤≤≤≤上的一个近似表达式,0(,)kr s rsr s p x y cx y ==∑要求(,)p x y 一最小的k 值达到以下的精度10202700((,)(,))10i j i j i j f x y p x y σ-===-≤∑∑其中，0.08,0.50.05i j x i y j ==+。
2、计算****(,),(,)i j i j f x y p x y （i = 1, 2, …，8；j = 1, 2,…，5）的值，以观察(,)p x y 逼近(,)f x y 的效果，其中，*i x =0.1i , *j y =0.5+0.2j 。
说明：1、用迭代方法求解非线性方程组时，要求近似解向量()k x 满足()(1)()12||||/||||10k k k x x x --∞∞-≤2、作二元插值时，要使用分片二次代数插值。
3、要由程序自动确定最小的k 值。
4、打印以下内容：●算法的设计方案。
●全部源程序（要求注明主程序和每个子程序的功能）。
●数表：,,i j x y (,)i j f x y （i = 0,1,2,…,10；j = 0,1,2,…,20）。
●选择过程的,k σ值。
●达到精度要求时的,k σ值以及(,)p x y 中的系数rs c （r = 0,1,…,k;s = 0,1,…,k ）。
●数表：**,,i j x y ****(,),(,)i j i j f x y p x y （i = 1, 2, ...,8；j = 1, 2, (5)。
数理统计 北航 大作业
北京市财政收入的逐步回归模型研究摘要：财政收入水平高低是反映一国经济实力的重要标志，关系着一个国家经济的发展和社会的进步。
本文根据北京市2012年度统计年鉴，选取了农林牧渔业总产值、工业总产值、建筑业总产值、常驻总人口数、社会消费品零售总额、入境旅游人数、客运量、货运量、全社会固定资产投资以及第三产业总产值，共10个指标，对北京市财政收入及其可能的影响因素进行了研究。
文中运用逐步线性回归方法建立了多元线性回归模型，分析各因素对该地区财政收入的影响；利用SPSS软件进行求解。
通过分析SPSS软件计算的数据，从相关性检验、多重共线性检验、方差分析以及残差分析四个角度，分别对模型合理性进行了验证。
结果表明，北京市财政收入与建筑业总产值和农林牧渔也总产值呈显著线性关系。
其中与建筑业正相关，与农林牧渔业负相关。
关键字：财政收入，多元，逐步线性回归，SPSS1. 引言财政收入是指政府为履行其职能、实施公共政策和提供公共物品与服务需要而集中的一切资金的综合，包括税收、企事业收入、能源交通重点建设基金收入、债务收入、规费收入、罚没收入等[1]。
财政收入水平高低是反映一国经济实力的重要标志，关系着一个国家经济的发展和社会的进步。
因此，研究财政收入的增长及就显得尤为必要[2]。
一个地区的财政收入可能受到诸多因素的影响，如工业总产值、农业总产值、建筑业总产值、人口数等。
本文以北京市为例，以财政收入为因变量，选取农林牧渔业总产值、工业总产值、建筑业总产值、常驻总人口数、社会消费品零售总额、入境旅游人数、客运量、货运量、全社会固定资产投资以及第三产业总产值这10个指标为自变量，利用SPSS统计软件进行回归分析，建立财政收入影响因素模型，分析影响财政收入的主要因素及其影响程度。
2. 理论概述2.1 多元线性回归[3]在许多实际问题中，影响一个事物的因素常常不止一个，采用多元线性回归分析方法可以找出这些因素与事物之间的数量关系。
北航数值分析大作业第一题幂法与反幂法
《数值分析》计算实习题目第一题：1. 算法设计方案（1）1λ，501λ和s λ的值。
1)首先通过幂法求出按模最大的特征值λt1，然后根据λt1进行原点平移求出另一特征值λt2，比较两值大小，数值小的为所求最小特征值λ1，数值大的为是所求最大特征值λ501。
2)使用反幂法求λs ，其中需要解线性方程组。
因为A 为带状线性方程组，此处采用LU 分解法解带状方程组。
（2）与140k λλμλ-5011=+k 最接近的特征值λik 。
通过带有原点平移的反幂法求出与数k μ最接近的特征值 λik 。
（3）2cond(A)和det A 。
1）1=nλλ2cond(A)，其中1λ和n λ分别是按模最大和最小特征值。
2）利用步骤（1）中分解矩阵A 得出的LU 矩阵，L 为单位下三角阵,U 为上三角阵，其中U 矩阵的主对角线元素之积即为det A 。
由于A 的元素零元素较多，为节省储存量，将A 的元素存为6×501的数组中，程序中采用get_an_element()函数来从小数组中取出A 中的元素。
2.全部源程序#include <stdio.h>#include <math.h>void init_a();//初始化Adouble get_an_element(int,int);//取A 中的元素函数double powermethod(double);//原点平移的幂法double inversepowermethod(double);//原点平移的反幂法int presolve(double);//三角LU 分解int solve(double [],double []);//解方程组int max(int,int);int min(int,int);double (*u)[502]=new double[502][502];//上三角U 数组double (*l)[502]=new double[502][502];//单位下三角L 数组double a[6][502];//矩阵Aint main(){int i,k;double lambdat1,lambdat2,lambda1,lambda501,lambdas,mu[40],det;init_a();//初始化Alambdat1=powermethod(0);lambdat2=powermethod(lambdat1);lambda1=lambdat1<lambdat2?lambdat1:lambdat2;lambda501=lambdat1>lambdat2?lambdat1:lambdat2;presolve(0);lambdas=inversepowermethod(0);det=1;for(i=1;i<=501;i++)det=det*u[i][i];for (k=1;k<=39;k++){mu[k]=lambda1+k*(lambda501-lambda1)/40;presolve(mu[k]);lambda[k]=inversepowermethod(mu[k]);}printf("------------所有特征值如下------------\n");printf("λ=%1.11e λ=%1.11e\n",lambda1,lambda501);printf("λs=%1.11e\n",lambdas);printf("cond(A)=%1.11e\n",fabs(lambdat1/lambdas));printf("detA=%1.11e \n",det);for (k=1;k<=39;k++){printf("λi%d=%1.11e ",k,lambda[k]);if(k % 3==0) printf("\n");} delete []u;delete []l;//释放堆内存return 0;}void init_a()//初始化A{int i;for (i=3;i<=501;i++) a[1][i]=a[5][502-i]=-0.064;for (i=2;i<=501;i++) a[2][i]=a[4][502-i]=0.16;for (i=1;i<=501;i++) a[3][i]=(1.64-0.024*i)*sin(0.2*i)-0.64*exp(0.1/i); }double get_an_element(int i,int j)//从A中节省存储量的提取元素方法{if (fabs(i-j)<=2) return a[i-j+3][j];else return 0;}double powermethod(double offset)//幂法{int i,x1;double beta=0,prebeta=-1000,yita=0;for (i=1;i<=501;i++)u[i]=1,y[i]=0;//设置初始向量u[]for (int k=1;k<=10000;k++){yita=0;for (i=1;i<=501;i++) yita=sqrt(yita*yita+u[i]*u[i]);for (i=1;i<=501;i++) y[i]=u[i]/yita;for (x1=1;x1<=501;x1++){u[x1]=0;for (int x2=1;x2<=501;x2++)u[x1]=u[x1]+((x1==x2)?(get_an_element(x1,x2)-offset):get_an_element(x1,x2))*y[x2];} prebeta=beta;beta=0;for (i=1;i<=501;i++) beta=beta+ y[i]*u[i];if (fabs((prebeta-beta)/beta)<=1e-12) {printf("offset=%f lambda=%f err=%e k=%d\n",offset,(beta+offset),fabs((prebeta-beta)/beta),k);break;};//输出中间过程,包括偏移量,误差,迭代次数}return (beta+offset);}double inversepowermethod(double offset)//反幂法{int i;double u[502],y[502];double beta=0,prebeta=0,yita=0;for (i=1;i<=501;i++)u[i]=1,y[i]=0; //设置初始向量u[]for (int k=1;k<=10000;k++){yita=0;for (i=1;i<=501;i++) yita=sqrt(yita*yita+u[i]*u[i]);for (i=1;i<=501;i++) y[i]=u[i]/yita;solve(u,y);prebeta=beta;beta=0;for (i=1;i<=501;i++) beta=beta+ y[i]*u[i];beta=1/beta;if (fabs((prebeta-beta)/beta)<=1e-12) {printf("offset=%f lambda=%f err=%e k=%d\n",offset,(beta+offset),fabs((prebeta-beta)/beta),k);break;};//输出中间过程,包括偏移量,误差,迭代次数}return (beta+offset);}int presolve(double offset)//三角LU分解{int i,k,j,t;double sum;for (k=1;k<=501;k++)for (j=1;j<=501;j++){u[k][j]=l[k][j]=0;if (k==j) l[k][j]=1;} //初始化LU矩阵for (k=1;k<=501;k++){for (j=k;j<=min(k+2,501);j++){sum=0;for (t=max(1,max(k-2,j-2)) ; t<=(k-1) ; t++)sum=sum+l[k][t]*u[t][j];u[k][j]=((k==j)?(get_an_element(k,j)-offset):get_an_element(k,j))-sum;}if (k==501) continue;for (i=k+1;i<=min(k+2,501);i++){sum=0;for (t=max(1,max(i-2,k-2));t<=(k-1);t++)sum=sum+l[i][t]*u[t][k];l[i][k]=(((i==k)?(get_an_element(i,k)-offset):get_an_element(i,k))-sum)/u[k][k];}}return 0;}int solve(double x[],double b[])//解方程组{int i,t;double y[502];double sum;y[1]=b[1];for (i=2;i<=501;i++){sum=0;for (t=max(1,i-2);t<=i-1;t++)sum=sum+l[i][t]*y[t];y[i]=b[i]-sum;}x[501]=y[501]/u[501][501];for (i=500;i>=1;i--){sum=0;for (t=i+1;t<=min(i+2,501);t++)sum=sum+u[i][t]*x[t];x[i]=(y[i]-sum)/u[i][i];}return 0;}int max(int x,int y){return (x>y?x:y);}int min(int x,int y){return (x<y?x:y);}3.计算结果结果如下图所示:部分中间结果：给出了偏移量(offset)，误差(err)，迭代次数(k)4.讨论迭代初始向量的选取对计算结果的影响,并说明原因使用u[i]=1（i=1,2,...,501）作为初始向量进行迭代，可得出以上结果。
数理统计第一次大作业——回归分析
北京市农业经济总产值的逐步回归分析姓名：学号：摘要：农业生产和农村经济是国民经济的基础，影响农村经济总产值的因素有多种，主要包括农林牧渔业。
本文以北京市农业生产和农村经济总产值为对象，首先分析了各种因素的线性相关性，建立回归模型，再利用逐步回归法进行回归分析，得到最符合实际情况的回归模型。
以SPSS 17.0为分析工具，给出了实验结果，并用预测值验证了结论的正确性。
关键词：农业生产和农村经济，线性回归模型，逐步回归分析，SPSS1.引言农林牧渔业统计范围包括辖区内全部农林牧渔业生产单位、非农行业单位附属的农林牧渔业生产活动单位以及农户的农业生产活动。
军委系统的农林牧渔业生产（除军马外）也应包括在内，但不包括农业科学试验机构进行的农业生产。
在近几年中国经济快速增长的带动下，各地区农林牧渔业也得到了突飞猛进的发展。
以北京地区为例，2005年的农业总产值为1993年的6倍。
因此用统计方法研究分析农业总产值对指导国民经济生产，合理有效的进行产业布局，提高生产力等有着重要意义。
表1 北京市农业经济产值及各产品产量统计数据本文以北京市农生产为对象，分析了农业经济总产值与粮食产量、棉花产量、油料产量、蔬菜产量、干鲜果品产量、猪牛羊肉产量、禽蛋产量、水产品产量的关系，并建立农业经济总产值的回归模型。
表1中列出了1999年至2008年间的统计数据（数据来源于北京统计信息网）。
2.线性回归模型的建立2.1 线性回归模型的假设为了研究农业经济总产值与各种农生产量的关系，必须要建立二者之间的数学模型。
数学模型可以有多种形式，比如线性模型，二次模型，指数模型，对数模型等等。
而实际生活中，影响农业经济总产值的因素很多，并且这些因素的影响不能简单的用某一种模型来描述，所以要建立农业经济总产值的数学模型往往是很难的。
但是为了便于研究，我们可以先假定一些前提条件，然后在这些条件下得到简化后的近似模型。
以下我们假定两个前提条件：1) 农产品的价格是不变的。
北航数值分析大作业一
北京航空航天大学数值分析大作业一学院名称自动化专业方向控制工程学号ZY*******学生姓名许阳教师孙玉泉日期2021 年11月26 日设有501501⨯的实对称矩阵A ，⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=5011A a b c b c c b c b a其中，064.0,16.0),501,,2,1(64.0)2.0sin()024.064.1(1.0-==⋅⋅⋅=--=c b i e i i a ii 。
矩阵A 的特征值为)501,,2,1(⋅⋅⋅=i i λ，并且有||min ||,501150121i i s λλλλλ≤≤=≤⋅⋅⋅≤≤1λ，501λ和s λ的值。
A 的与数4015011λλλμ-+=kk 最接近的特征值)39,,2,1(⋅⋅⋅=k k i λ。
A 的(谱范数)条件数2)A (cond 和行列式detA 。
一 方案设计1 求1λ，501λ和s λ的值。
s λ为按模最小特征值，||min ||5011i i s λλ≤≤=。
可使用反幂法求得。
1λ，501λ分别为最大特征值及最小特征值。
可使用幂法求出按模最大特征值，如结果为正，即为501λ，结果为负，那么为1λ。
使用位移的方式求得另一特征值即可。
2 求A 的与数4015011λλλμ-+=kk 最接近的特征值)39,...,2,1(=k k i λ。
题目可看成求以k μ为偏移量后，按模最小的特征值。
即以k μ为偏移量做位移，使用反幂法求出按模最小特征值后，加上k μ，即为所求。
3 求A 的(谱范数)条件数2)(A cond 和行列式detA 。
矩阵A 为非奇异对称矩阵，可知，||)(min max2λλ=A cond(1-1)其中m ax λ为按模最大特征值，min λ为按模最小特征值。
detA 可由LU 分解得到。
因LU 均为三角阵，那么其主对角线乘积即为A 的行列式。
二 算法实现1 幂法使用如下迭代格式：⎪⎪⎩⎪⎪⎨⎧⋅===⋅⋅⋅=------||max |)|sgn(max ||max /),,(111111)0()0(10k k k k k k k k Tn u u Ay u u u y u u u β任取非零向量 (2-1)终止迭代的控制理论使用εβββ≤--||/||1k k k ， 实际使用εβββ≤--||/||||||1k k k(2-2)由于不保存A 矩阵中的零元素，只保存主对角元素a[501]及b,c 值。
北航数理统计第二次数理统计大作业 判别分析
数理统计大作业（二）全国各省发展程度的聚类分析及判别分析指导教师院系名称材料科学与工程院学号学生姓名2015 年 12 月21 日目录全国各省发展程度的聚类分析及判别分析 (1)摘要： (1)引言 (1)1实验方案 (2)1.1数据统计 (2)1.2聚类分析 (3)1.3判别分析 (4)2结果分析与讨论 (5)2.1聚类分析结果 (5)2.2聚类分析结果分析： (8)2.3判别分析结果 (9)2.4 Fisher判别结果分析： (11)参考文献： (16)全国各省发展程度的聚类分析及判别分析摘要：利用SPSS软件对全国31个省、直辖市、自治区(浙江、安徽、甘肃除外)的主要经济指标进行多种聚类分析，分析选择最佳聚类类数，并对浙江、湖南、甘肃进行类型判别分析。
通过这两个方法对全国各省进行发展分类。
本文选取了7项社会发展指标作为决定发展程度的影响因素，其中经济因素为主要因素，同时评估城镇化率和人口素质因素。
各项数据均来自2014年国家统计年鉴。
分析结果表明：北京市和上海市和天津市为同一类；江苏省和山东省和广东省为同一类型；河北、湖北、河南、湖南、四川、辽宁为同一类；其余的为另一类。
关键词：聚类分析、判别分析、发展引言聚类分析是根据研究对象的特征对研究对象进行分类的多元统计分析技术的总称。
它直接比较各事物之间的性质，将性质相近的归为一类，将性质差别较大的归入不同的类。
系统聚类分析又称集群分析，是聚类分析中应用最广的一种方法，它根据样本的多指标（变量）、多个观察数据，定量地确定样品、指标之间存在的相似性或亲疏关系，并据此连结这些样品或指标，归成大小类群，构成分类树状图或冰柱图。
判别分析是根据多种因素(指标)对事物的影响来实现对事物的分类，从而对事物进行判别分类的统计方法。
判别分析适用于已经掌握了历史上分类的每一个类别的若干样品，希望根据这些历史的经验（样品），总结出分类的规律性（判别函数）来指导未来的分类。
北航数分大作业一
《数值分析》计算实习题第一题姓名：学号：一、 算法的设计方案 ⒈矩阵A 的存储由于A[501][501]是带状矩阵，并且阶数远大于带宽5，为节省内存空间，设置一个二维数组C[5][501]用于存放A 的带内元素。
A 中元素与C 数组中元素的对应关系，即A 的检索方式为： A 的元素ij a =C 中的元素1,i j s j C -++ 2.求解特征值λ1，λ501，λs①由于λ1‹λ2‹…‹λ501，所以在以所有特征值建立的数轴上，λ1、λ50⒊1位于数轴的两端，两者之一必为按模最大。
利用幂法，可以求出来按模最大的特征值λM ，即为λ1和λ501中一个；然后将原矩阵平移λM,再利用幂法求一次平移后矩阵的按模最大的特征值λM ′。
比较λM 和λM+λM ′大小，大者为λ501，小的为λ1。
②利用反幂法，求矩阵A 的按模最小的特征值λs 。
但是反幂法中要用到线性方程组的求解，而原矩阵A 又是带状矩阵，采用LU 分解。
所以在这之前要定义一个LU 分解子程序，将A 矩阵分解为单位下三角矩阵L 和上三角矩阵U 的乘积。
⒊求解A 的与数μk =λ1+k （λ501-λ1）/40的最接近的特征值λik（k=1,2，…，39）。
先使k 从1到39循环，求出μk 的值，然后使用带原点平移的反幂法，令平移量p=μk 。
计算过程需调用LU 分解子程序对A-u k I 矩阵进行LU 分解。
最终反幂法求出的值加上μk 即为与μk 最接近的特征值λik4.求解A的（谱范数）条件数cond（A）2和行列式detAcond（A）2=|λ1/λn|，其中λ1和λn分别是矩阵A的模最大和最小特征值，上边已经求出，可直接调用。
detA等于对A记性LU分解以后U的所有对角线上元素的乘积。
二、全部源程序#include<stdio.h>#include <math.h>/***全局变量、函数申明***/#define N 501#define EMS 1.0e-12double U[N],Y[N];double c[5][N] ;double fuzhi(); /*对A进行压缩存储*/ void DLU(double C[5][N]); /*对矩阵A进行LU分解*/ double pingyi(double C[5][N],double b); /*求矩阵的平移矩阵*/ double mifa(double c[5][N]); /*幂法计算矩阵A按模最大的特征值*/ double fmifa(double c[5][N],double b); /*反幂法求矩阵A按模最小的特征值*/void main(){double lamuda_m1,lamuda_m2,lamuda_max,lamuda_min,lamuda_sum,lamuda_s;fuzhi();lamuda_m1=mifa(c);pingyi(c, lamuda_m1);lamuda_m2 =mifa(c);lamuda_sum= lamuda_m1+ lamuda_m2;if (lamuda_m1>lamuda_sum){lamuda_max=lamuda_m1;lamuda_min=lamuda_sum;}else{lamuda_max=lamuda_sum;lamuda_min=lamuda_m1;}printf("矩阵的最大特征值为：\n lamuda_501=%.11e\n",lamuda_max); printf("矩阵的最小特征值为：\n lamuda_1=%.11e\n",lamuda_min); int i;double conda,u[39];for(i=1;i<40;i++)u[i]=lamuda_min+(lamuda_max-lamuda_min)*i/40;lamuda_s=fmifa(c,0);printf("矩阵的按模最小特征值为：\n lamuda_s=%.11e\n", lamuda_s); printf("与uk最接近的特征值如下：\n");/*求与uk接近的特征值*/for(i=1;i<40;i++)printf("u[%2d]=%.11e 与其最接近的特征值为lamuda_%2d=%.11e\n",i,u[i],i,fmifa(c,u[i]));/*求矩阵A的条件数*/conda=fabs(lamuda_m1/lamuda_s);printf("矩阵A的(谱范数)条件数为:\n cond（A）=%.11e\n", conda); /*求矩阵A的行列式*/fuzhi();double detA=1.0;DLU(c);for(i=0;i<N;i++)detA*=c[2][i];printf("矩阵A的行列式为：\n detA=%.11e\n", detA);}/*建立矩阵A的压缩存储二维数组，并对其赋值*/double fuzhi(){int i;c[0][0]=0;c[0][1]=0;c[1][0]=0;c[3][500]=0;c[4][499]=0;c[4][500]=0;for(i=2;i<N;i++)c[0][i]=-0.064;for(i=1;i<N;i++)c[1][i]=0.16;for(i=1;i<N+1;i++)c[2][i-1]=(1.64-0.024*i)*sin(0.2*i)-0.64*exp(0.1/i); for(i=0;i<N-1;i++)c[3][i]=0.16;for(i=0;i<N-2;i++)c[4][i]=-0.064;return (c[5][N]);}/*求最大值*/int max(int a,int b){if(a>b) return a;else return b;}/*求最小值*/int min(int a,int b){if(a<b) return a;else return b;}/*向量乘以向量*/double xiangliangji(double G[N],double H[N]) {int i;double sum;sum=0;for(i=0;i<N;i++)sum+=G[i]*H[i];return sum;}/*向量除数*/void xlcs (double G[N],double yita){int i;for(i=0;i<N;i++)Y[i]=G[i]/yita;}/*矩阵乘向量*/void juchengxiang(double c[N][N],double G[N])int i,j;double m;for(i=0;i<N;i++)U[i]=0;for(i=0;i<N;i++){m=max(0,i-2);for(j=min(i+2,N-1);j>=m;j--)U[i]+=c[i+2-j][j]*G[j];}}/*矩阵的主对角线元素平移*/ double pingyi(double C[5][N],double b) {int i;for(i=0;i<N;i++)C[2][i]=C[2][i]-b;return C[5][N];}/*幂法求按模最大特征值*/double mifa(double c[5][N])int i,q;double sum,yita,beita,beita1,cancha; beita=0;for(i=0;i<N;i++)U[i]=1;for (q=1;;q++){beita1=beita;sum= xiangliangji(U,U);yita=sqrt(sum);xlcs (U,yita);juchengxiang (c,Y);beita=xiangliangji(Y,U);cancha=fabs((beita1-beita)/beita); if (cancha<EMS) break;}return beita;}/*矩阵的Doolittle分解*/void DLU(double C[5][N]){ int k,i,j,t;int m,l;for(k=0;k<N;k++){m=min(k+2,N-1);for(j=k;j<=m;j++){double sum=0;l=max(max(0,k-2),j-2);for(t=l;t<=k-1;t++)sum+=C[k-t+2][t]*C[t-j+2][j];C[k-j+2][j]=C[k-j+2][j]-sum;}if(k<N-1){m=min(k+2,N-1);for(i=k+1;i<=m;i++){double sum=0;l=max(max(0,i-2),k-2);for(t=l;t<=k-1;t++)sum+=C[i-t+2][t]*C[t-k+2][k];C[i-k+2][k]=(C[i-k+2][k]-sum)/C[2][k];}}}}/*反幂法求按模最小特征值*/double fmifa(double c[5][N],double b){int i,q;int m,t,p;double sum,yita,beita,beita1,cancha,lamuda;double G[N];beita=0;for(i=0;i<N;i++) /*设置初始向量U0*/{U[i]=1;}for (q=1;;q++){beita1=beita;sum=xiangliangji (U,U);yita=sqrt(sum);xlcs (U,yita);fuzhi();pingyi(c,b);DLU(c);for(i=0;i<N;i++)G[i]=Y[i];for(i=1;i<N;i++){double sum=0;m=max(0,i-2);for(t=m;t<=i-1;t++)sum+=c[i-t+2][t]*G[t];G[i]=G[i]-sum;}U[N-1]=G[N-1]/c[2][N-1]; for(i=N-2;i>=0;i--){double sum=0;p=min(i+2,N-1);for(t=i+1;t<=p;t++)sum+=c[i-t+2][t]*U[t];U[i]=(G[i]-sum)/c[2][i]; }beita=xiangliangji(Y,U);lamuda=1/beita+b;cancha=fabs((beita1-beita)/beita);if (cancha<1.0e-12) break;}printf("迭代次数%d\n",q);return lamuda;}三、计算结果矩阵的最大特征值为：lamuda_501=9.72463409878e+000矩阵的最小特征值为：lamuda_1=-1.07001136150e+001迭代次数70, 矩阵的按模最小特征值为：lamuda_s=-5.55791079423e-003与uk最接近的特征值如下：迭代次数7, u[ 1]=-1.01894949222e+001lamuda_1=-1.01829340331e+001 迭代次数226, u[ 2]=-9.67887622933e+000lamuda_ 2=-9.58570742507e+000迭代次数7, u[ 3]=-9.16825753648e+000lamuda_ 3=-9.17267242393e+000迭代次数8, u[ 4]=-8.65763884364e+000lamuda_ 4=-8.65228400790e+000迭代次数118, u[ 5]=-8.14702015079e+000lamuda_ 5=-8.0934*******e+000迭代次数16, u[ 6]=-7.63640145795e+000lamuda_ 6=-7.65940540769e+000迭代次数15, u[ 7]=-7.12578276510e+000lamuda_ 7=-7.11968464869e+000迭代次数19, u[ 8]=-6.61516407226e+000lamuda_ 8=-6.61176433940e+000迭代次数28, u[ 9]=-6.10454537941e+000lamuda_ 9=-6.0661*******e+000迭代次数21, u[10]=-5.59392668657e+000lamuda_10=-5.58510105263e+000lamuda_11=-5.11408352981e+000迭代次数13, u[12]=-4.57268930088e+000 lamuda_12=-4.57887217687e+000迭代次数290, u[13]=-4.06207060803e+000 lamuda_13=-4.09647092626e+000迭代次数13, u[14]=-3.55145191519e+000 lamuda_14=-3.55421121575e+000迭代次数6, u[15]=-3.04083322234e+000 lamuda_15=-3.0410*******e+000迭代次数1606, u[16]=-2.53021452950e+000 lamuda_16=-2.53397031113e+000迭代次数72, u[17]=-2.01959583665e+000 lamuda_17=-2.00323076956e+000迭代次数19, u[18]=-1.50897714381e+000 lamuda_18=-1.50355761123e+000迭代次数17, u[19]=-9.98358450965e-001 lamuda_19=-9.93558606008e-001迭代次数11, u[20]=-4.87739758120e-001 lamuda_20=-4.87042673885e-001迭代次数10, u[21]=2.28789347246e-002 lamuda_21=2.23173624957e-002迭代次数13, u[22]=5.33497627570e-001 lamuda_22=5.32417474207e-001迭代次数15, u[23]=1.04411632041e+000 lamuda_23=1.05289896269e+000迭代次数29, u[24]=1.55473501326e+000 lamuda_24=1.58944588188e+000迭代次数81, u[25]=2.06535370610e+000 lamuda_25=2.06033046027e+000迭代次数40, u[26]=2.57597239895e+000 lamuda_26=2.55807559707e+000迭代次数13, u[27]=3.08659109179e+000 lamuda_27=3.08024050931e+000迭代次数23, u[28]=3.59720978464e+000 lamuda_28=3.61362086769e+000迭代次数16, u[29]=4.10782847748e+000 lamuda_29=4.0913*******e+000迭代次数23, u[30]=4.61844717033e+000 lamuda_30=4.60303537828e+000迭代次数12, u[31]=5.12906586317e+000 lamuda_31=5.132********e+000迭代次数30, u[32]=5.63968455602e+000 lamuda_32=5.59490634808e+000lamuda_33=6.08093385703e+000迭代次数18, u[34]=6.66092194171e+000lamuda_34=6.68035409211e+000迭代次数74, u[35]=7.17154063455e+000lamuda_35=7.29387744813e+000迭代次数30, u[36]=7.68215932740e+000lamuda_36=7.71711171424e+000迭代次数11, u[37]=8.19277802024e+000lamuda_37=8.22522001405e+000迭代次数38, u[38]=8.70339671309e+000lamuda_38=8.64866606519e+000迭代次数10, u[39]=9.21401540593e+000lamuda_39=9.25420034458e+000矩阵A的(谱范数)条件数为:cond（A）=1.92520427390e+003矩阵A的行列式为：detA=2.77278614175e+118四、讨论迭代初始向量的选取对于计算结果的影响：1.影响迭代速度。
北航数值分析报告大作业第二题精解
实用文档目标：使用带双步位移的QR 分解法求矩阵10*10[]ij A a =的全部特征值，并对其中的每一个实特征值求相应的特征向量。
已知：sin(0.50.2)()1.5cos( 1.2)(){i j i j ij i j i j a +≠+== (i,j=1,2, (10)算法：以上是程序运作的逻辑，其中具体的函数的算法，大部分都是数值分析课本上的逻辑，在这里特别写出矩阵A 的实特征值对应的一个特征向量的求法：()[]()()[]()[]()111111I 00000i n n n B A I gause i n Q A I u Bu u λλ-⨯-⨯-=-⨯-⎛⎫ ⎪-=−−−−→=−−−−−−→= ⎪⎝⎭选主元的消元检查知无重特征值由于=0i A I λ-，因此在经过选主元的高斯消元以后，i A I λ-即B 的最后一行必然为零，左上方变为n-1阶单位矩阵[]()()11I n n -⨯-，右上方变为n-1阶向量[]()11n Q ⨯-，然后令n u 1=-，则()1,2,,1j j u Q j n ==⋅⋅⋅-。
这样即求出所有A 所有实特征值对应的一个特征向量。
#include<stdio.h>#include<math.h>#include<conio.h>#define N 10#define E 1.0e-12#define MAX 10000//以下是符号函数double sgn(double a){double z;if (a>E) z=1;else z=-1;return z;}//以下是矩阵的拟三角分解void nishangsanjiaodiv(double A[N][N]){int i,j,k;int m=0;double d,c,h,t;double u[N],p[N],q[N],w[N];for (i=0;i<N-2;i++){for (j=i+2;j<N;j++) if (A[j][i]<=E) m=m+1;if (m==(N-2-i)) continue ;for (j=i+1,d=0;j<N;j++) d=d+A[j][i]*A[j][i];d=sqrt(d);c=-1*sgn(A[i+1][i])*d;h=c*c-c*A[i+1][i];for (j=i+2;j<N;j++) u[j]=A[j][i];for (j=0;j<i+2;j++) u[j]=0;u[i+1]=A[i+1][i]-c;for (j=0;j<N;j++){for (k=i+1,p[j]=0;k<N;k++) p[j]=A[k][j]*u[k]+p[j];p[j]=p[j]/h;}for(j=0;j<N;j++){for(k=i+1,q[j]=0;k<N;k++) q[j]=A[j][k]*u[k]+q[j];q[j]=q[j]/h;}for(j=0,t=0;j<N;j++) t=t+p[j]*u[j];t=t/h;for(j=0;j<N;j++) w[j]=q[j]-t*u[j];for(j=0;j<N;j++){for(k=0;k<N;k++) A[j][k]=A[j][k]-w[j]*u[k]-u[j]*p[k];}}}//以下是矩阵的QR分解void qrdiv(double A[N][N],double Q[N][N],double R[N][N]){int i,j,k;//int m=0;double d,c,h;double u[N],w[N],p[N];for(i=0;i<N;i++){for(j=0;j<N;j++) {if (i==j) Q[i][j]=1; else Q[i][j]=0;}}for(i=0;i<N;i++){for(j=0;j<N;j++) R[i][j]=A[i][j];}for(i=0;i<N-1;i++){//for(j=i+1;j<N;j++) if(R[j][i]<=E) m=m+1;//if(m==(N-1-i)) continue;for(j=i,d=0;j<N;j++) d=d+R[j][i]*R[j][i];d=sqrt(d);c=-1*sgn(R[i][i])*d;h=c*c-c*R[i][i];for(j=i+1;j<N;j++) u[j]=R[j][i];for(j=0;j<i;j++) u[j]=0;u[i]=R[i][i]-c;for(j=0;j<N;j++) {for(k=0,w[j]=0;k<N;k++) w[j]=Q[j][k]*u[k]+w[j];} for(j=0;j<N;j++) {for(k=0;k<N;k++) Q[j][k]=Q[j][k]-w[j]*u[k]/h;}for(j=0;j<N;j++){for(k=i,p[j]=0;k<N;k++) p[j]=R[k][j]*u[k]+p[j];p[j]=p[j]/h;}for(j=0;j<N;j++){for(k=0;k<N;k++) R[j][k]=R[j][k]-u[j]*p[k];}}}//矩阵的QR分解//以下是二次多项式求根double root(double b,double c){double m;m=b*b-4*c;return m;} //二次多项式求根//以下是求解矩阵的所有特征值void characteristic(double A[N][N],double chaR[N],double chaI[N]){int k=0,m=N-1;int i,j;int L;double s,t,x;double M[N][N],B[N][N];int f=0;double d,c,h;double u[N],w[N],p[N];double Q[N][N],R[N][N];for(L=0;L<MAX;L++){next: if (m==0) {chaR[0]=A[0][0];chaI[0]=0;break;}if(fabs(A[m][m-1])<=E){chaR[m]=A[m][m];chaI[m]=0;m--;goto next;}s=A[m-1][m-1]+A[m][m];t=A[m-1][m-1]*A[m][m]-A[m][m-1]*A[m-1][m];if(m==1){x=root(s,t);if(x>=E){x=sqrt(x);chaR[m]=s/2+x/2;chaR[m-1]=s/2-x/2;chaI[m]=0;chaI[m-1]=0;}else{x=sqrt(fabs(x));chaR[m]=s/2;chaR[m-1]=s/2;chaI[m]=x/2;chaI[m-1]=-x/2;}break;}if(fabs(A[m-1][m-2])<=E){x=root(s,t);if(x>=E){x=sqrt(x);chaR[m]=s/2+x/2;chaR[m-1]=s/2-x/2;chaI[m]=0;chaI[m-1]=0;}else{x=sqrt(fabs(x));chaR[m]=s/2;chaR[m-1]=s/2;chaI[m]=x/2;chaI[m-1]=-x/2;} m=m-2;goto next;}for(i=0;i<=m;i++){for(j=0;j<=m;j++){if(i==j){for(k=0,M[i][j]=0;k<=m;k++) M[i][j]=A[i][k]*A[k][j]+M[i][j];M[i][j]=M[i][j]-s*A[i][j]+t;}else{for(k=0,M[i][j]=0;k<=m;k++) M[i][j]=A[i][k]*A[k][j]+M[i][j];M[i][j]=M[i][j]-s*A[i][j];}}}// 以下是M的QR分解for(i=0;i<=m;i++){for(j=0;j<=m;j++) {if (i==j) Q[i][j]=1; else Q[i][j]=0;}}for(i=0;i<=m;i++){for(j=0;j<=m;j++) R[i][j]=M[i][j];}for(i=0;i<m;i++){for(j=i+1;j<=m;j++) if(R[j][i]<=E) f=f+1;if(f==(m-i)) continue;for(j=i,d=0;j<=m;j++) d=d+R[j][i]*R[j][i];d=sqrt(d);c=-1*sgn(R[i][i])*d;h=c*c-c*R[i][i];for(j=i+1;j<=m;j++) u[j]=R[j][i];for(j=0;j<i;j++) u[j]=0;u[i]=R[i][i]-c;for(j=0;j<=m;j++){for(k=0,w[j]=0;k<=m;k++) w[j]=Q[j][k]*u[k]+w[j];}for(j=0;j<=m;j++){for(k=0;k<=m;k++) Q[j][k]=Q[j][k]-w[j]*u[k]/h;}for(j=0;j<=m;j++){for(k=i,p[j]=0;k<=m;k++) p[j]=R[k][j]*u[k]+p[j];p[j]=p[j]/h;}for(j=0;j<=m;j++){for(k=0;k<=m;k++) R[j][k]=R[j][k]-u[j]*p[k];}}for(j=0;j<=m;j++){for(k=0;k<=m;k++) M[j][k]=Q[j][k];}// 以上是M的QR分解for(i=0;i<=m;i++){for(j=0;j<=m;j++){for(k=0,B[i][j]=0;k<=m;k++) B[i][j]=M[k][i]*A[k][j]+B[i][j];} }for(i=0;i<=m;i++){for(j=0;j<=m;j++){for(k=0,A[i][j]=0;k<=m;k++) A[i][j]=B[i][k]*M[k][j]+A[i][j];} }}}//以下是求矩阵的所有特征值的特征向量void eigenvector(double V[N][N],double T[N]){double A[N][N],baoz[N][N],guod[N];double c;int i,j,k,m,t;int W=0;for(i=0;i<N;i++) for(j=0;j<N;j++) baoz[i][j]=V[i][j];for(t=0;t<6;t++){for(i=0;i<N;i++) for(j=0;j<N;j++) A[i][j]=baoz[i][j];for(i=0;i<N;i++) A[i][i]=A[i][i]-T[t];for(i=0;i<N-1;i++){for(j=i;j<N;j++) if(fabs(A[j][i])>E) {k=j;break; }for(j=i;j<N;j++) {guod[j]=A[i][j];A[i][j]=A[k][j];A[k][j]=guod[j];}for(j=i;j<N;j++){c=A[j][i];if(fabs(c)>E) for(m=i;m<N;m++) A[j][m]=A[j][m]/c;}for(j=0;j<N;j++){c=A[j][i];if(j!=i) {for(m=i;m<N;m++) A[j][m]=A[j][m]-A[i][m]*c;}}}V[t][N-1]=-1;for(i=N-2;i>=0;i--){V[t][i]=A[i][N-1];}}}//以下是主函数void main(){double a[N][N],b[N][N],chaR[N],chaI[N];double q[N][N],r[N][N],qr[N][N];double shiyan[N];double f,g;int i,j,k;for(i=0;i<N;i++){for(j=0;j<N;j++){if(i!=j) a[i][j]=sin(0.5*(i+1)+0.2*(j+1));else a[i][j]=1.5*cos((i+1)+1.2*(j+1));}}nishangsanjiaodiv(a);printf("矩阵A的拟上三角分解：\n");for(i=0;i<N;i++){for(j=0;j<N-5;j++) {if (fabs(a[i][j])<E) a[i][j]=0; printf("%22.11e",a[i][j]);} printf("\n");}printf("\n");for(i=0;i<N;i++){for(j=N-5;j<N;j++) {if (fabs(a[i][j])<E) a[i][j]=0; printf("%22.11e",a[i][j]);} printf("\n");}printf("\n");qrdiv(a,q,r); printf("\n");printf("\n");printf("\n");printf("拟上三角矩阵A的QR分解：\n");printf("上三角矩阵R：\n");for(i=0;i<N;i++){for(j=0;j<N-5;j++) {if (fabs(r[i][j])<E) r[i][j]=0;printf("%22.12e",r[i][j]);}printf("\n");} printf("\n");for(i=0;i<N;i++){for(j=N-5;j<N;j++) {if (fabs(r[i][j])<E) r[i][j]=0;printf("%22.12e",r[i][j]);}printf("\n");} printf("\n");printf("正交矩阵Q：\n");for(i=0;i<N;i++){for(j=0;j<N-5;j++) {if (fabs(q[i][j])<E) q[i][j]=0;printf("%22.12e",q[i][j]);} printf("\n");} printf("\n");for(i=0;i<N;i++){for(j=N-5;j<N;j++) {if (fabs(q[i][j])<E) q[i][j]=0;printf("%22.12e",q[i][j]);} printf("\n");} printf("\n");for(i=0;i<N;i++){for(j=0;j<N;j++) for(k=0,qr[i][j]=0;k<N;k++) qr[i][j]=qr[i][j]+r[i][k]*q[k][j];} printf("\n");printf("\n");printf("\n");printf("R*Q：\n");for(i=0;i<N;i++){for(j=0;j<N-5;j++) {if (fabs(qr[i][j])<E)qr[i][j]=0;printf("%22.12e",qr[i][j]);}printf("\n");} printf("\n");printf("\n");printf("\n");for(i=0;i<N;i++){for(j=N-5;j<N;j++) {if (fabs(qr[i][j])<E)qr[i][j]=0;printf("%22.12e",qr[i][j]);}printf("\n");} printf("\n");printf("\n");printf("\n");characteristic(a,chaR,chaI);for(i=1;i<N;i++){if (i<3){f=chaR[i];g=chaI[i];chaR[i]=chaR[7+i];chaI[i]=chaI[7+i];chaR[7+i]=f;chaI[7+i]=g;} if (i==5){f=chaR[i];g=chaI[i];chaR[i]=chaR[7];chaI[i]=chaI[7];chaR[7]=f;chaI[7]=g;}}printf("矩阵A所有特征值：\n");for(j=0;j<N;j++){if(fabs(chaI[j])<=E) printf("λ%2d =%19.11e\n",j+1,chaR[j]);else if(chaI[j]>E) printf("λ%2d =%18.11e +%18.11ei\n",j+1,chaR[j],chaI[j]);else printf("λ%2d =%19.11e %19.11ei\n",j+1,chaR[j],chaI[j]);}printf("\n");printf("\n");printf("\n");for(i=0;i<N;i++){for(j=0;j<N;j++){if(i!=j) a[i][j]=sin(0.5*(i+1)+0.2*(j+1));else a[i][j]=1.5*cos((i+1)+1.2*(j+1));}}//重新输入矩阵Aeigenvector(a,chaR);printf("相应实特征值对应的特征向量：\n");for(i=0;i<6;i++){printf("λ%d的一个特征向量为：\n ",(i+1));for(j=0;j<N-5;j++) printf("%22.11e",a[i][j]);printf("\n ");for(j=N-5;j<N;j++) printf("%22.11e",a[i][j]);printf("\n");}getch();}。
数理统计大作业(北航)2014版
应用数理统计大作业一学院：XXXXXXX学号：XXXXXXX姓名：XXX指导老师：XXX2014年12月21日国民生产总值增量的多元线性回归模型摘要：国民生产总值一直是衡量国家综合经济水平的重要指标，本文要讨论研究的是国民生产总值的增量趋势与各产业增值趋势间的多元线性关系[1]。
本论文搜集了我国从1998至2012年15年的国民生产与各产业增量指标，拟定数个自变量，代入统计软件SPSS 19.0[2]对各影响因素进行了统计分析，综合分析结果模拟多元线性回归函数。
模型建立之后，又将2013年数据作为测试集测试模型的拟合精确度，得到的结果达到预期值，得出模型建立较为成功。
关键词：逐步回归法，国民生产总值增量，线性拟合一引言国民生产总值（Gross Domestic Product）是在一定时期中，一个国家地区经济生产出的全部最终产品和劳务的价值，被公认为衡量国家经济状况的较佳指标。
它不仅仅反映了一定的经济表现，还可以反映国家的综合国力与经济发展前景，作为经济政策的制定依据，研究我国的国民生产总值的制约因素成为了学者们的热点问题。
下文就以1998年至2012年的统计数据为标准，利用SPSS软件作出了多元线性回归分析。
二统计分析2.1变量说明因变量——国民生产总值增值（亿元）；自变量——第一产业增加值（亿元）自变量——第二产业增加值（亿元）自变量——第三产业增加值（亿元）自变量——工业增加值（亿元）自变量——建筑业增加值（亿元）2.2统计数据2000年9537.5 14944.72 45555.88 38713.95 40033.59 5522.29 1999年5274.77 14770.03 41033.58 33873.44 35861.48 5172.1 1998年5429.25 14817.63 39004.19 30580.47 34018.43 4985.76 表格2-11998~2012年训练集数据测试组国民生产总值增值(亿元)第一产业增加值(亿元)第二产业增加值(亿元)第三产业增加值(亿元)工业增加值(亿元)建筑业增加值(亿元)2013年49375.11 56957 249684.4 262203.8 210689.4 38995表格2-22013年测试集数据以上数据来自《中国统计年鉴2013》[3]中收录的近15年全国国民生产总值增值数据，考察与各产业间增量趋势变化中关系密切并且直观上有线性关系的因素，因此选取了第一产业增值、第二产业增值、第三产业增值、工业总产值增值、建筑业增值五大因素为自变量。
(完整word版)北航数理统计大作业1-线性回归分析
应用数理统计作业一学号:姓名：电话：二〇一四年十二月国内生产总值的多元线性回归模型摘要：本文首先选取了选取我国自1978至2012年间的国内生产总值为因变量,并选取了7个主要影响因素，进一步利用统计软件SPSS对以上数据进行了多元逐步线性回归。
从而找到了能反映国内生产总值与各因素之间关系的“最优”回归方程.然后利用多重线性的诊断找出存在共线性的自变量，剔除缺失值较多的因子.再次进行主成份线性回归分析,找出最优回归方程。
所得结论与我国当前形势相印证。
关键词:多元线性回归，逐步回归法，多重共线性诊断，主成份分析目录0符号说明 (1)1 介绍 (2)2 统计分析步骤 (3)2。
1 数据的采集和整理 (3)2。
2采用多重逐步回归分析 (7)2.3进行共线性诊断 (17)2。
4进行主成分分析确定所需主成份 (24)2。
5进行主成分逐步回归分析 (27)3 结论 (30)参考文献 (31)致谢 (32)0符号说明1 介绍文中主要应用逐步回归的主成份分析方法,对数据进行分析处理，最终得出能够反映各个因素对国内生产总值影响的最“优”模型及线性回归方程.国内生产总值是指在一定时期内（一个季度或一年)，一个国家或地区的经济中所生产出的全部最终产品和劳务的价值,常被公认为衡量国家经济状况的最佳指标.它不但可反映一个国家的经济表现，还可以反映一国的国力与财富。
2012年1月，国家统计局公布2011年重要经济数据，其中GDP增长9.2％，基本符合预期。
2012年10月18日,统计显示,2012年前三季度国内生产总值353480亿元，同比增长7.7%；其中，一季度增长8.1%，二季度增长7。
6％，三季度增长7.4％，三季度增幅创下2009年二季度以来14个季度新低。
中国的GDP核算历史不长，上世纪90年代之前通常用“社会总产值”来衡量经济发展情况。
上世纪80年代初中国开始研究联合国国民经济核算体系的国内生产总值（GDP）指标。
北航-数理统计大作业
对中国各地财政收入情况的聚类分析和判别分析应用数理统计第二次大作业学院名称学号学生姓名摘要我国幅员辽阔，由于人才、地理位置、自然资源等条件的不同，各地区的财政收入类型各自呈现出不一样的发展趋势，通过准确定位中国各地区财政收入情况对于正确认识我国财政收入具有重要的意义。
本文以中国各地财政收入情况为研究对象，从《中国统计年鉴》中选取2011年期间中国各地财政收入情况为因变量，选取国内增值税、营业税、企业所得税、个人所得税、城市维护建设税、土地增值税、契税、专项收入、行政事业性收费收入、国有资本经营收入和国有资源（资产）有偿使用收入11个可能影响中国各地财政收入的因素为自变量，利用统计软件SPSS，对27个地区的财政收入进行了聚类分析，并对另外4个地区的财政收入进行了判别分析，并最终确定了中国各地区根据财政收入类型的分类情况。
关键词：聚类分析，判别分析，SPSS，中国各地财政收入类型1、引言财政收入，是指政府为履行其职能、实施公共政策和提供公共物品与服务需要而筹集的一切资金的总和。
财政收入表现为政府部门在一定时期内（一般为一个财政年度）所取得的货币收入。
财政收入是衡量一国政府财力的重要指标，政府在社会经济活动中提供公共物品和服务的范围和数量，在很大程度上决定于财政收入的充裕状况。
通过准确定位中国各地区财政收入情况对于正确认识我国财政收入具有重要的意义。
本文利用统计软件SPSS，根据各地区的财政收入情况，对北京、天津、河北等27个地区进行聚类分析，并对青海、重庆、四川、贵州4个省市进行判别分析，判断属于聚类分析结果中的哪种财政收入类型。
1.1 聚类分析聚类分析是根据研究对象的特征对研究对象进行分类的多元统计分析技术的总称，它直接比较各事物之间的性质，将性质相近的归为一类，将性质差别较大的归入不同的类。
本文采用的是系统聚类分析，它又称集群分析，是聚类分析中应用最广的一种方法，其基本思想是：首先将每个聚类对象看作一类，然后根据对象间的相似程度，将相似程度最高的两类进行合并，并计算合并后的类与其他类之间的距离，再选择相近者进行合并，每合并一次减少一类，直至所有的对象都并为一类为止。
北航数理统计大作业(逐步回归)
北京航空航天大事BEIHANG UNIVERSITY应用数理统计第一次大作业学号：______姓名：______________班级： __________20 15年12月民航客运量得多元线性回归分析摘要：本文为建立以民航客运量为因变量得多元线性回归模型，选取了199 6年至2013年得统计数据，包含国民生产总值，民航航线里程，过夜入境旅游人数，城镇居民可支配收入等因素，利用统计•软件SPSS对各因素进行了筛选分析，采用逐步回归法得到最优多元线性回归模型，并对模型得回归显著性、拟合度以及随机误差得正态性进行了检验，并采用201 4年得数据进行检验，得到得结果达到预期，证明该模型建立就是较为成功得.关键词：多元线性回归，逐步回归法，民航客运量0、符号说明变量符号民用航空客运量Y国民生产总值X,民航航线里程X3城镇居民人均可支配收入X51、引言随着社会得进步，人民生活水平得提高，如何获得更快捷方便得交通成为人们日益关注得问题•因为航空得安全性，快速且价格水平越来越倾向大众，越来越多得人们选择航空这种交通方式。
近年来，我国得航空客运量已经进入世界前列，为掌握航空客运得动态，合理安排班机数量•科学地对我国民航客运量得影响因素得分析，并得出其回归方程，进而能够估计航空客运量就是非常有必要得。
本文收集整理了与我国航空客运量相关得历年数据，运用SPSS软件对数据进行分析，研究199 6年起至20 13年我国民航客运量y（万人）与国民生产总值Xi（亿元）、铁路客运量X2（万人）、民航航线里程X3 （万公里）、入境过夜旅游人数X4 （万人）、城镇居民人均可支配 收入X5 （元）得关系。
采用逐步回归法建立线 性模型，选出较优得线性回归模型。
2、数据得统计与分析本文在进行统计时，查阅《中国统计摘要》，《中国统计年鉴2 0 14》以及中国 知网数据查询中得数据，收集了 19 96年至201 3年各个自变量因素得数据，分析它们 之间得联系。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
应用数理统计第一次大作业学号：姓名：班级：2013年12月国家财政收入的多元线性回归模型摘 要本文以多元线性回归为出发点，选取我国自1990至2008年连续19年的财政收入为因变量，初步选取了7个影响因素,并利用统计软件PASW Statistics 17.0对各影响因素进行了筛选，最终确定了能反映财政收入与各因素之间关系的“最优”回归方程：46ˆ578.4790.1990.733yx x =++ 从而得出了结论，最后我们用2009年的数据进行了验证，得出的结果在误差范围内，表明这个模型可以正确反映影响财政收入的各因素的情况。
关键词：多元线性回归，逐步回归法，财政收入，SPSS0符号说明变 量 符号 财政收入 Y 工 业 X 1 农 业 X 2 受灾面积 X 3 建 筑 业 X 4 人 口 X 5 商品销售额X 6进出口总额X71 引言中国作为世界第一大发展中国家，要实现中华民族的伟大复兴，必须把发展放在第一位。
近年来，随着国家经济水平的飞速进步，人民生活水平日益提高，综合国力日渐强大。
经济上的飞速发展并带动了国家财政收入的飞速增加，国家财政的状况对整个社会的发展影响巨大。
政府有了强有力的财政保证才能够对全局进行把握和调控，对于整个国家和社会的健康快速发展有着重要的意义。
所以对国家财政的收入状况进行研究是十分必要的。
国家财政收入的增长，宏观上必然与整个国家的经济有着必然的关系，但是具体到各个方面的影响因素又有着十分复杂的相关原因。
为了研究影响国家财政收入的因素，我们就很有必要对其财政收入和影响财政收入的因素作必要的认识，如果能对他们之间的关系作一下回归，并利用我们所知道的数据建立起回归模型这对我们很有作用。
而影响财政收入的因素有很多，如人口状况、引进的外资总额，第一产业的发展情况，第二产业的发展情况，第三产业的发展情况等等。
本文从国家统计信息网上选取了1990-2009年这20年间的年度财政收入及主要影响因素的数据，包括工业，农业，建筑业，批发和零售贸易餐饮业，人口总数等。
文中主要应用逐步回归的统计方法，对数据进行分析处理，最终得出能够反映各个因素对财政收入影响的最“优”模型。
2解决问题的方法和计算结果2.1 样本数据的选取与整理本文在进行统计时，查阅《中国统计年鉴2010》中收录的1990年至2009年连续20年的全国财政收入为因变量，考虑一些与能源消耗关系密切并且直观上有线性关系的因素，初步选取这十九年的国内总产值、工业总产值、人口总数、建筑业、农业、受灾面积和商品零售总额等因素为自变量，分析它们之间的联系。
根据选择的指标，从《中国统计年鉴2010》查选数据，整理如表2-1所示。
表2-1 1990-2009年财政收入及其影响因素统计表工业（亿元）农业（亿元）受灾面积（千公顷）建筑业（亿元）人口（万人）社会商品零售总额（亿元）财政收入（亿元）国民生产总值（亿元）199018689.227662.13847413451143338300.12937.118718.3 199122088.688157554721564.31158239415.63149.4821826.2 199227724.219084.7513332174.411717110993.73483.3726937.3 19933969310995.5488293253.511851714270.44348.9535260.0 199451353.0315750.5550434653.311985018622.95218.148108.5 199554946.8620340.9458215793.812112123613.86242.259810.5 199662740.1622353.7469898282.212238928360.27407.9970142.5 199768352.6823788.4534299126.512362631252.98651.1478060.8 199867737.1424541.9501451006212476133378.19875.9583024.3 199972707.0424519.14998111152.912578635647.911444.0888479.2 200085673.6624915.85468812497.612674339105.713395.2398000.5 200195448.9826179.65221515361.512762743055.416386.04108068.2 2002110776.4827390.847119.118527.112845348135.918903.64119095.7 2003142271.2229691.854506.323083.812922752516.321715.25135174.0 2004201722.193623937106.25627745.31299885950126396.47159586.7 2005251619.539450.938818.22534552.013075667176.631649.29185808.6 2006316588.9640810.841091.4141557.11314487641038760.2217522.7 2007405177.1348892.935972.2351043.71321298921051321.78267763.7 2008130260.233702.056234.2618743.213280************.35316228.8 2009135239.935226.050223.5122398.81334741489468518.30343464.72.2 模型的建立与分析将数据录入统计软件excel，建立统计数据库，先建立财政收入与各变量的散点图，如图2-1至图2-7所示。
图2-1 财政收入与工业总产值的散点图图2-2 财政收入与农业总产值的散点图图2-3 财政收入与受灾面积的散点图图2-4 财政收入与建筑业的散点图图2-5 财政收入与人口总数的散点图图2-6 财政收入与商品零售总额的散点图图2-7 财政收入与国内总产值的散点图从散点图中看出，国内生产总值、工业生产总值、农业、建筑业、商品零售总额这四个变量与财政收入总量基本呈线性分布；而人口总数虽然也与财政收入存在正比的关系，但是从直观上看线性关系不显著，并且人口因素呈现指数关系。
受灾面积与财政收入总量的关系不明显。
因此为使得到的模型有显著的线性关系，在选取进入回归模型的自变量时，就要进行筛选。
下面给出筛选过程。
（1）将国内生产总值、农业、工业生产总值、建筑业和商品零售总额纳入自变量，逐步回归法，输出结果如图2-8(a)(b)所示。
从结果可以看出，该回归的F值为1600.595，查表得0.95(1,2)18.5F ，显而易见，回归的显著性很好；但是由于在这里我们要分析的是影响财政收入的具体产业，而该结果只说明了财政收入与国民生产总值的相关性很好，并不能说明问题的根本所在。
所以在下面的分析中我们将剔除国民生产总值这个因素做进一步的分析。
Anova b模型平方和df均方F Sig.1回归7.506E917.506E91600.595.000a 残差8.441E7184689341.382图2-8(a)(b) 输出结果（2）将工业生产总值、农工、建筑业和商品零售总额纳入自变量，逐步回归法，输出结果如图2-9(a)(b)(c)所示。
图2-9(a)(b)(c) 输出结果从结果可以看出，该回归的F 值为30.215，查表得0.95(1,3)10.1F =，显而易见，回归的显著性很好；但是对回归系数的显著性来说，从直方图中可以看出，采用以上三个变量作为自变量得到的线性模型仍不是很好。
这个模型也不是理想中的模型，所以下面我们试图根据我们的判断对样本数据进行筛选，力求得出比较理想的模型。
（3）下面我将农业这个变量暂且剔除，只采用工业、建筑业和商品零售总额作为自变量，采用逐步回归法，输出结果如图2-10(a)(b)所示。
从结果可以看出，该回归的F 值为20.219，查表得0.95(1,2)18.5F =，显而易见，回归的显著性很好；但是对回归系数的显著性来说，建筑业的t 检验值为0.0002，查表得3646.2)7(975.0=t ，显然回归系数的显著性不好。
以上检验得到的与利用P 值法（图中的Sig 值）得到的检验结果相符。
因此，采用以上三个变量作为自变量得到的线性模型仍不是很好。
同时可以看出，只对建筑业做回归分析时，F 值为20.19，查表得到0.95(1,7) 5.59F ，这证明一元回归模型和回归系数的显著性都很好。
图2-10(a)(b) 输出结果（4）只将工业和商品零售总额纳入自变量，输出结果如图2-11(a)(b)所示。
图2-11(a)(b) 输出结果从上图结果中可以看出，对这两个变量做回归分析时，F 值为15.39，证明一元回归模型和回归系数的显著性都很好。
2.3 分析结果由以上筛选和分析过程可以看出，财政收入Y 分别对X 7国内总产值、X 1工业总产值、X 4建筑业及商品零售总额X 6进行一元回归分析时，其回归的显著性都很好，但是综合为一个多元回归模型时，则出现了某些系数不显著的现象。
综合比较选取的几个多元模型，将X 4建筑业和X 6商品零售总额纳入自变量时得到的模型效果最为显著，回归方程如下：46ˆ578.479 5.199 4.733yx x =++ 其中10.99F =，20.564R =。
3 结论本次大作业，根据查阅中国统计年鉴，列举了影响财政收入的7个因素。
从直观上考虑，人口总量与受灾面积与财政收入存在线性关系，所以特意把这两个变量列到其中，但是散点图和回归效果显示这2个因素并没有进入逐步回归模型中，由此看来，这两项因素与财政收入存在的关系可能不是严格线性的，或者这种线性关系是长期的线性关系。
另外，在对进入模型的5个因素进行回归时发现，因变量对单独变量的回归性很显著，但是整合成多元回归出现了某些回归系数不显著的现象，具体原因可能是由于数据选取的太少，未能体现出长期线性这一特点。
虽然得到的几个模型系数都不是很显著，但经综合比较，选取了一个较为显著的模型作为最“优”解。
对得到的最“优”回归模型做预测，置信度为95%。
查阅中国统计年鉴，得到2009年的X 4建筑业为22398.8（亿元），X 6商品零售总额为14894（亿元），Y 财政收入为68518.30（亿元），将自变量带入回归方程：46ˆ578.479 1.199 2.733578.479 1.19922398.8 2.7331489468103.9902yx x =++=+⨯+⨯=（亿元）预测区间为))(ˆ),(ˆ(o o o x y x yδδ+-，其中0.975() 2.36462674.56()o x t δ===亿元。