人教版九年级数学《圆》复习测试题[附答案]

合集下载

人教版九年级数学上册第24章《圆》单元测试卷(含答案解析)

第24章《圆》单元测试卷一．选择题（共10小题）1．已知⊙O的半径为4，点O到直线m的距离为3，则直线m与⊙O公共点的个数为（）A．0个B．1个C．2个D．3个2．如图，AB是⊙O的直径，AB⊥CD于E，AB=10，CD=8，则BE为（）A．2B．3C．4D．3.53．正六边形内接于圆，它的边所对的圆周角是（）A．60°B．120°C．60°或120°D．30°或150°4．⊙O的半径r=5cm，直线l到圆心O的距离d=4，则直线l与圆的位置关系（）A．相离B．相切C．相交D．重合5．如图，AB是⊙O的直径，点C是⊙O上一点，点D在BA的延长线上，CD与⊙O交于另一点E，DE=OB=2，∠D=20°，则的长度为（）A．πB．πC．πD．π6．如图，⊙O是△ABC 的外接圆，BC 是直径，D在圆上，连接AD、CD，若∠ADC=35°，则∠ACB=（）A．70°B．55°C．40°D．45°7．如图，在△ABC中，AB=AC，∠ABC=45°，以AB为直径的⊙O交BC于点D，若BC=4，则图中阴影部分的面积为（）A．π+1B．π+2C．2π+2D．4π+18．如图，△ABC是⊙O的内接三角形，∠C=30°，⊙O的半径为5，若点P是⊙O 上的一点，在△ABP中，PB=AB，则PA的长为（）A．5B．C．5D．59．如图是某公园的一角，∠AOB=90°，弧AB的半径OA长是6m，C是OA的中点，点D在弧AB上，CD∥OB，则图中休闲区（阴影部分）的面积是（）A．B．C．D．10．如图，AB是⊙O的直径，弦CD⊥AB，过点C作⊙O的切线与AB的延长线交于点P．若∠BCD=32°，则∠CPD的度数是（）A．64°B．62°C．58°D．52°二．填空题（共8小题）11．如图，AB是⊙O的直径，点C、D在⊙O上，若∠ACD=25°，则∠BOD的度数为．12．如图，⊙O是△ABC的外接圆，BC为直径，BC=4，点E是△ABC的内心，连接AE并延长交⊙O于点D，则DE= ．13．如图所示，点A在半径为20的圆O上，以OA为一条对角线作矩形OBAC，设直线BC交圆O于D、E两点，若OC=12，则线段CE、BD的长度差是．14．如图，半径为2的⊙O与含有30°角的直角三角板ABC的AC边切于点A，将直角三角板沿CA边所在的直线向左平移，当平移到AB与⊙O相切时，该直角三角板平移的距离为．15．如图，PA、PB切⊙O于A、B，点C在上，DE切⊙O于C，交PA、PB于D、E，已知PO=13cm，⊙O的半径为5cm，则△PDE的周长是．16．△ABC中，AB=CB，AC=10，S=60，E为AB上一动点，连结CE，过A作AF△ABC⊥CE于F，连结BF，则BF的最小值是．17．如图，等边三角形△ABC内接于半径为1的⊙O，则图中阴影部分的面积是．18．如图，已知线段AB=6，C为线段AB上的一个动点（不与A、B重合），将线段AC绕点A逆时针旋转120°得到AD，将线段BC绕点B顺时针旋转120°得到BE，⊙O外接于△CDE，则⊙O的半径最小值为．三．解答题（共7小题）19．十一期间，小明一家一起去旅游，如图是小明设计的某旅游景点的图纸（网格是由相同的小正方形组成的，且小正方形的边长代表实际长度100m，在该图纸上可看到两个标志性景点A，B．若建立适当的平面直角坐标系，则点A （﹣3，1），B（﹣3，﹣3），第三个景点C（1，3）的位置已破损．（1）请在图中画出平面直角坐标系，并标出景点C的位置；（2）平面直角坐标系的坐标原点为点O，△ACO是直角三角形吗？请判断并说明理由．20．如图，AB是⊙O的直径，BD是⊙O的弦，延长BD到点C，使DC=BD，连结AC交⊙O于点F．（1）AB与AC的大小有什么关系？请说明理由；（2）若AB=8，∠BAC=45°，求：图中阴影部分的面积．21．已知AB是⊙O的直径，AP是⊙O的切线，A是切点，BP与⊙O交于点C．（1）如图①，若∠P=35°，求∠ABP的度数；（2）如图②，若D为AP的中点，求证：直线CD是⊙O的切线．22．如图，已知锐角△ABC内接于⊙O，连接AO并延长交BC于点D．（1）求证：∠ACB+∠BAD=90°；（2）过点D作DE⊥AB于E，若∠ADC=2∠ACB，AC=4，求DE的长．23．如图，点I是△ABC的内心，AI的延长线和△ABC的外接圆相交于点D，与BC相交于点E．（1）求证：DI=DB；（2）若AE=6cm，ED=4cm，求线段DI的长．24．如图，已知扇形AOB的圆心角为直角，正方形OCDE内接于扇形AOB．点C、E、D分别在OA、OB、弧AB上，过点A作AF⊥DE交ED的延长线于F，如果正方形的边长为1，求阴影部分M、N的面积和．25．如图：△A BC是圆的内接三角形，∠BAC与∠ABC的角平分线AE、BE相交于点E，延长AE交圆于点D，连接BD、DC，且∠BCA=60°．（1）求证：△BED为等边三角形；（2）若∠ADC=30°，⊙O的半径为，求BD长．参考答案一．选择题（共10小题）1．【解答】解：∵d=3＜半径=4∴直线与圆相交∴直线m与⊙O公共点的个数为2个故选：C．2．【解答】解：连接OC．∵AB是⊙O的直径，AB=10，∴OC=OB=AB=5；又∵AB⊥CD于E，CD=8，∴CE=CD=4（垂径定理）；在Rt△COE中，OE=3（勾股定理），∴BE=OB﹣OE=5﹣3=2，即BE=2；故选：A．3．【解答】解：圆内接正六边形的边所对的圆心角=360°÷6=60°，根据圆周角等于同弧所对圆心角的一半，边所对的圆周角的度数是60×=30°或180°﹣30°=150°．故选：D．4．【解答】解：∴⊙O的半径为5cm，如果圆心O到直线l的距离为4cm，∴5＞4，即d＜r，∴直线l与⊙O的位置关系是相交，故选：C．5．【解答】解：连接OE、OC，如图，∵DE=OB=OE，∴∠D=∠EOD=20°，∴∠CEO=∠D+∠EOD=40°，∵OE=OC，∴∠C=∠CEO=40°，∴∠BOC=∠C+∠D=60°，∴的长度==π，故选：A．6．【解答】解：∵BC是⊙O的直径，∴∠BAC=90°，∵∠B=∠D=35°，∴∠ACB=55°，故选：B．7．【解答】解：连接OD、AD，∵在△ABC中，AB=AC，∠ABC=45°，∴∠C=45°，∴∠BAC=90°，∴△ABC是Rt△BAC，∵BC=4，∴AC=AB=4，∵AB为直径，∴∠ADB=90°，BO=DO=2，∵OD=OB，∠B=45°，∴∠B=∠BDO=45°，∴∠DOA=∠BOD=90°，∴阴影部分的面积S=S△BOD +S扇形DOA=+=π+2．故选：B．8．【解答】解：连接OA、OB、OP，∵∠C=30°，∴∠APB=∠C=30°，∵PB=AB，∴∠PAB=∠APB=30°∴∠ABP=120°，∵PB=AB，∴OB⊥AP，AD=PD，∴∠OBP=∠OBA=60°，∵OB=OA，∴△AOB是等边三角形，∴AB=OA=5，则Rt△PBD中，PD=cos30°•PB=×5=，∴AP=2PD=5，故选：D．9．【解答】解：连接OD，∵弧AB的半径OA长是6米，C是OA的中点，∴OC=OA=×6=3米，∵∠AOB=90°，CD∥OB，∴CD⊥OA，在Rt△OCD中，∵OD=6，OC=3，∴CD===3米，∵sin∠DOC===，∴∠DOC=60°，∴S阴影=S扇形AOD﹣S△DOC=﹣×3×3 =（6π﹣）平方米．故选：A．10．【解答】解：连接OC，∵CD⊥AB，∠BCD=32°，∴∠OBC=58°，∵OC=OB，∴∠OCB=∠OBC=58°，∴∠COP=64°，∵PC是⊙O的切线，∴∠OCP=90°，∴∠CPO=26°，∵AB⊥CD，∴AB垂直平分CD，∴PC=PD，∴∠CPD=2∠CPO=52°故选：D．二．填空题（共8小题）11．【解答】解：由圆周角定理得，∠AOD=2∠ACD=50°，∴∠BOD=180°﹣50°=130°，故答案为：130°．12．【解答】解：如图，连接BD，CD，EC．∵点E是△ABC的内心，∴∠DAB=∠DAC，∠ECA=∠ECD，∵∠DCB=∠DAB，∠DEC=∠EAC+∠ECA，∠ECD=∠ECB+∠DCB，∴∠DEC=∠DCE，∴DE=DC，∵BC是直径，∴∠BDC=90°，∵∠DAB=∠DAC，∴=，∴BD=DC，∵BC=4，∴DC=DB=2，∴DE=2，故答案为2．13．【解答】解：如图，设DE的中点为M，连接OM，则OM⊥DE．∵在Rt△AOB中，OA=20，AB=OC=12，∴OB===16，∴OM===，在Rt△OCM中，CM===，∵BM=BC﹣CM=20﹣=，∴CE﹣BD=（EM﹣CM）﹣（DM﹣BM）=BM﹣CM=﹣=．故答案为：．14．【解答】解：根据题意画出平移后的图形，如图所示：设平移后的△A′B′C′与圆O相切于点D，连接OD，OA，AD，过O作OE⊥AD，可得E为AD的中点，∵平移前圆O与AC相切于A点，∴OA⊥A′C，即∠OAA′=90°，∵平移前圆O与AC相切于A点，平移后圆O与A′B′相切于D点，即A′D与A′A为圆O的两条切线，∴A′D=A′A，又∠B′A′C′=60°，∴△A′AD为等边三角形，∴∠DAA′=60°，AD=AA′=A′D，∴∠OAE=∠OAA′﹣∠DAA′=30°，在Rt△AOE中，∠OAE=30°，AO=2，∴AE=AO•cos30°=，∴AD=2AE=2，∴AA′=2，则该直角三角板平移的距离为2．故答案为：2．15．【解答】解：连接OA、OB，如下图所示：∵PA、PB为圆的两条切线，∴由切线长定理可得：PA=PB，同理可知：DA=DC，EC=EB；∵OA⊥PA，OA=5，PO=13，∴由勾股定理得：PA=12，∴PA=PB=12；∵△PDE的周长=PD+DC+CE+PE，DA=DC，EC=EB；∴△PDE的周长=PD+DA+PE+EB=PA+PB=24，故此题应该填24cm．16．【解答】解：过B作BD⊥AC于D，∵AB=BC，∴AD=CD=AC=5，∵S=60，△ABC∴，即，BD=12，∵AF⊥CE，∴∠AFC=90°，∴F在以AC为直径的圆上，∵BF+DF＞BD，且DF=DF'，∴当F在BD上时，BF的值最小，此时BF'=12﹣5=7，则BF的最小值是7，故答案为：7．17．【解答】解：连接OB、OC，连接A O并延长交BC于H，则AH⊥BC，BH=CH．∵△ABC是等边三角形，OB=OA=1，∴BH=OB，∴BH=CH=，∴BC=，=•（）2=，∴S△ABC∴S=π•12﹣=π﹣，阴故答案为π﹣．18．【解答】解：如图，连接OD、OA、OC、OB、OE．∵OA=OA，OD=OC，AD=AC，∴△OAD≌△OAC，∴∠OAC=∠OAD=∠CAD=60°，同法可证：∠OBC=∠OBE=∠ABE=60°，∴△AOB是等边三角形，∴当OC⊥AB时，OC的长最短，此时OC=OA•sin60°=3，故答案为3．三．解答题（共7小题）19．【解答】解：（1）如图；（2）△ACO是直角三角．理由如下：∵A（﹣3，1），C（1，3），∴OA==，OC==，AC==2，∵OA2+OC2=AC2，∴△AOC是直角三角形，∠AOC=90°．20．【解答】解：（1）AB=AC．理由是：连接AD．∵AB是⊙O的直径，∴∠ADB=90°，即AD⊥BC，又∵DC=BD，∴AB=AC；（2）连接OD、过D作DH⊥AB．∵AB=8，∠BAC=45°，∴∠BOD=45°，OB=OD=4，∴DH=2∴△OBD 的面积=扇形OBD的面积=，阴影部分面积=．21．【解答】（1）解：∵AB是⊙O的直径，AP是⊙O的切线，∴AB⊥AP，∴∠BAP=90°；又∵∠P=35°，∴∠AB=90°﹣35°=55°．（2）证明：如图，连接OC，OD、AC．∵AB是⊙O的直径，∴∠ACB=90°（直径所对的圆周角是直角），∴∠ACP=90°；又∵D为AP的中点，∴AD=CD（直角三角形斜边上的中线等于斜边的一半）；在△OAD和△OCD中，，∴△OAD≌△OCD（SSS），∴∠OAD=∠OCD（全等三角形的对应角相等）；又∵AP是⊙O的切线，A是切点，∴AB⊥AP，∴∠OAD=90°，∴∠OCD=90°，即直线CD是⊙O的切线．22．【解答】（1）证明：延长AD交⊙O于点F，连接BF．∵AF为⊙O的直径，∴∠ABF=90°，∴∠AFB+∠BAD=90°，∵∠AFB=∠ACB，∴∠ACB+∠BAD=90°．（2）证明：如图2中，过点O作OH⊥AC于H，连接BO．∵∠AOB=2∠ACB，∠ADC=2∠ACB，∴∠AOB=∠ADC，∴∠BOD=∠BDO，∴BD=BO，∴BD=OA，∵∠BED=∠AHO，∠ABD=∠AOH，∴△BDE≌△AOH，（AAS），∴DE=AH，∵OH⊥AC，∴AH=CH=AC，∴AC=2DE=4，∴DE=2．23．【解答】（1）证明：连接BI．∵点I是△ABC的内心，∴∠BAI=∠CAI，∠ABI=∠CBI．又∵∠DBI=∠CBI+∠DBC，∠DIB=∠ABI+∠BAI，∠DBC=∠DAC=∠BAI，∴∠DBI=∠DIB，∴DI=DB．（2）∵∠DBC=∠DAC=∠BAI，∠ADB=∠BDA，∴△BDE∽△ABD，∴，即BD2=D E•AD=DE•（AE+DE）=4×（6+4）=40，DI=BD=（cm）．24．【解答】解：连接OD，∵正方形的边长为1，即OC=CD=1，∴OD=，∴AC=OA﹣OC=﹣1，∵DE=DC，BE=AC，弧BD=弧AD=长方形ACDF的面积=AC•CD=﹣1．∴S阴25．【解答】（1）证明：∵∠BAC与∠ABC的角平分线AE、BE相交于点E，∴∠EAB=∠CAB，∠EBA=∠CBA，∴∠AEB=180°﹣（∠EAB+∠EBA）=180°﹣（∠CAB+∠CBA）=180°﹣（180°﹣∠BCA）=120°，∴∠DEB=60°，由圆周角定理得，∠BDA=∠BCA=60°，∴△BED为等边三角形；（2）∵∠ADC=30°，∠BDA=60°，∴∠BDC=90°，∴BC是⊙O的直径，即BC=4，∵AE平分∠BAC，∴=，∴BD=DC=4．。

人教版初三数学圆的测试题附详细标准答案

九年级圆测试题一、选择题（每题3分，共30分）1．如图，直角三角形ABC 中，∠C ＝90°，AC ＝2，AB ＝4，分别以AC 、BC 为直径作半圆，则图中阴影地面积为（）A 2π－3B 4π－43C 5π－4D 2π－232．半径相等地圆内接正三角形、正方形、正六边形地边长之比为（） A 1∶2∶3 B 1∶2∶3 C3∶2∶1 D 3∶2∶13．在直角坐标系中,以O(0，0)为圆心,以5为半径画圆,则点A(3-,4)地位置在（）A ⊙O 内B ⊙O 上C ⊙O 外D 不能确定4．如图，两个等圆⊙O 和⊙O ′外切，过O 作⊙O ′地两条切线OA 、OB ，A 、B 是切点，则∠AOB 等于（）A.30° B.45° C.60° D.90°5．在Rt △ABC 中，已知AB ＝6，AC ＝8，∠A ＝90°，如果把此直角三角形绕直线AC 旋转一周得到一个圆锥，其表面积为S 1；把此直角三角形绕直线AB 旋转一周得到另一个圆锥，其表面积为S 2，那么S 1∶S 2等于（）A 2∶3 B 3∶4 C 4∶9 D 5∶126．若圆锥地底面半径为 3，母线长为5，则它地侧面展开图地圆心角等于（） A ． 108° B ． 144° C ． 180° D ． 216°7．已知两圆地圆心距d = 3 cm ，两圆地半径分别为方程0352=+-x x地两根，则两圆地位置关系是（）A 相交 B 相离 C 相切 D 内含8．四边形中，有内切圆地是（）A 平行四边形 B 菱形 C 矩形 D 以上答案都不对OO'AB 第4题图9．如图，以等腰三角形地腰为直径作圆，交底边于D ，连结AD ，那么（）A ∠BAD +∠CAD= 90° B ∠BAD >∠CAD C ∠BAD =∠CAD D ∠BAD <∠CAD.10．下面命题中，是真命题地有（）①平分弦地直径垂直于弦；②如果两个三角形地周长之比为3∶2，则其面积之比为3∶4；③圆地半径垂直于这个圆地切线；④在同一圆中，等弧所对地圆心角相等；⑤过三点有且只有一个圆.A 1个 B 2个 C 3个 D 4个二、填空题（每题3分，共24分）11．一个正多边形地内角和是720°，则这个多边形是正边形；12．现用总长为m 80地建筑材料，围成一个扇形花坛，当扇形半径为_______时，可使花坛地面积最大；13．如图是一个徽章，圆圈中间是一个矩形，矩形中间是一个菱形，菱形地边长是 1 cm ，那么徽章地直径是；14．如图，弦AB 地长等于⊙O 地半径，如果C 是AmC 上任意一点，则sinC =；15．一条弦分圆成2∶3两部分，过这条弦地一个端点引远地切线，则所成地两弦切角为；16．如图，⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离，它们地半径都为1. 顺次连接五个圆心得到五边形ABCDE ，则图中五个阴影部分地面积之和是；17．如图：这是某机械传动部分地示意图，已知两轮地O·mBABCDAO外沿直径分别为2分米和8分米，轴心距为6分米，那么两轮上地外公切线长为分米.18．如图，ABC 是圆内接三角形，BC 是圆地直径，∠B=35°，MN 是过A 点地切线，那么∠C=________；∠CAM=________； ∠BAM=________；三、解答题19．求证：菱形地各边地中点在同一个圆上．已知：如图所示，菱形ABCD 地对角线AC 、BD 相交于O ，E 、F 、G 、H 分别是AB 、BC 、CD 、DA 地中点．求证：E 、F 、G 、H 在同一个圆上．20.已知：如图，AB 是⊙O 地直径，C 是⊙O 上一点，AD 和⊙O 在点C 地切线相垂直，垂足为D ，延长AD 和BC 地延长线交于点E ，求证：AB=AE ．★•第50题图 20题图21.如图，⊙O 以等腰三角形ABC 一腰AB 为直径，它交另一腰 AC 于 E ，交 BC 于D ．求证：BC=2DE22．如图，过圆心O 地割线PAB 交⊙O 于A 、B ，PC 切⊙O 于C ，弦CD ⊥AB 于点H ，点H分AB 所成地两条线段AH 、HB 地长分别为2和8．求PA 地长．23．已知：⊙O 1、⊙O 2地半径分别为2cm 和7cm ，圆心O 1O 2=13cm ，AB 是⊙O 1、⊙O 2地外公切线，切点分别是A 、B.求：公切线地长AB.圆测试题题答案一、选择题1． D.提示：设两个半圆交点为D.连接CD,CD ⊥AB.阴影地面积为两个半圆地面积减去直角三角形地面积2242 3.则CD=3,AD=1,BD=3.2．C ．提示：设圆地半径为R,则三角形边长为3R,正方形边长为2R,正六边形地边长为R.3．B.提示：用勾股定理可以求出点A到圆心地距离为5.4．C.提示：连接O’A,O’B.O’O.O’A⊥OA,O’B⊥OB.则OO’=2R,sin2A B∠=2RR,∠AOB=60°.5．A.提示：绕直线AC旋转一周时,底面边长6,高为8.表面积S1=π(r2+r l)=96π. 绕直线AB旋转一周时,底面边长8,高为6.表面积S1=π(r2+r l)=144π.6．D.提示：2πr=2360lπα︒.侧面展开图地圆心角等于216°.7．D.提示：设两圆地半径r1,r2.r1+r2=22ba=ba=5.r1-r21-r2.两圆内含.8．B.提示：从圆地圆心引两条相交直径，再过直径端点作切线，可以得到菱形.9．C．提示：AB是直径，所以AD垂直BD.ABC是等腰三角形.AB=AC,∠BAD =∠CAD. . 10．A.提示：④正确.①错在两条直径平分但不互相垂直.②面积之比为3∶2.③直径垂直于过直径端点地切线.⑤这三点可能在同一直线上.二、填空题11．6．提示：根据多边形地内角和公式，180°(n-2)=720°,n=6.12．20.提示：设半径为r,则弧长为(80-2r),S=1(802)2r r-=r(40-r)=-r2+40r=-(r-20)2+400,r=20时，S取得最大值.13．2.设矩形长为a,宽为b，则有22a b+=4r2,解得a2+b2=r2.菱形地边长22()()22a b+=1.r=1.14．12.提示：连接OA,OB,则△OAB是正三角形．∠AOB=60°.AB=60°,∠C=30°.15．72°.提示：如图.劣弧AB=144°，∠AOB=144°,∠OBA=18°,∠ABC=72°,OCBA16．32π,五边形ABCDE地内角和为540°，五个阴影部分地扇形地圆心角为540°,540°地扇形相当于32个圆.图中五个阴影部分地面积之和是32π.17．提示：将两圆圆心与切点连接起来，并将两圆地圆心联结起来，两圆地半径差是3，可抽象出如下地图形.过O作OC⊥O’B,OO’=6,O’C=CBAO'O18．55°,35°,125°.提示：∠C与∠B互余，∠C=55°，∠CAM是弦切角，∠CAM=∠B.∠BAM=90°+35°=125°.三、解答题19．证明：连结OE、OF、OG、OH．∵AC、BD是菱形地对角线，∴AC⊥BD于O．∴△AOB、△BOC、△COD、△DOA都是直角三角形．又OE、OF、OG、OH都是各直角三角形斜边上地中线，∴OE=12AB,OF=12BC,OG=12CD,OH=12AD∵AB＝BC＝CD＝DA，∴OE＝OF＝OG＝OH．∴E、F、G、H都在以O为圆心，OE为半径地圆上．应当指出地是：由于我们是在平面几何中研究地平面图形，所以在圆地定义中略去了“平面内”一词．更准确而严格地定义应是，圆是平面内到定点地距离等于定长地点地集合．证明四点共圆地另一种方法是证明这四个点所构成地四边形对角互补.20.提示：AB与AC位于同一个三角形中，所以只需证明∠B=∠E.圆中有直径地，通常要将圆上地一点与直径地端点连接起来，构造直角三角形.我们发现∠ACD是弦切角，∠ACD =∠B.∠ACD与∠CAD互余.在△ACE中，∠CAD与∠E互余,所以∠B=∠E.证明：连结AC．∵CD是⊙O地切线，∴∠ACD=∠B．又∵AB是⊙O地直径，∴∠ACB=∠ACE=90°，∴∠CAB+∠B=90°，∠CAE+∠E=90°．又∵CD⊥AE于D，∴∠ADC=90°．∴∠ACD+∠CAE=90°，∴∠ACD=∠E，∴∠B=∠E，∴AB=AE．21.提示：由等腰三角形地性质可得∠B=∠C，由圆内接四边形性质可得∠B=∠DEC，所以∠C=∠DEC，所以DE=CD，连结AD，可得AD⊥BC，利用等腰三角形“三线合一”性质得BC=2CD，即BC=2DE．证明：连结AD∵AB是⊙O直径∴AD⊥BC∵AB=AC∴BC=2CD，∠B=∠C∵⊙O内接四边形ABDE∴∠B=∠DEC(四点共圆地一个内角等于对角地外角)∴∠C＝∠DEC∴DE=DC∴BC=2DE22．提示：圆中既有切线也有割线，考虑使用切割线定理.PC2=PA•PB=PA(PA+PB)=PA2+10PA.又有相交弦，故也考虑用相交弦定理,AH•BH=CH2解：∵PC为O地切线，∴PC2=PA•PB=PA(PA+AB)=PA2+10PA又∵AB⊥CD,∴CH2=AH•BH=16PC2=CH2+PH2=16+(PA+2)2=PA2+4PA+20∴PA2+10PA=PA2+4PA+20∴PA=10 323．提示：因为切线垂直于过切点地半径，为求公切线地长AB，首先应连结O1A、O2B，得直角梯形O1ABO2.这样，问题就转化为在直角梯形中，已知上、下底和一腰，求另一腰地问题了.解：连结O1A、O2B，则O1A⊥AB，O2B⊥AB.过O1作O1C⊥O2B，垂足为C，则四边形O1ABC为矩形，于是有O 1C ⊥CO 2,O 1C=AB,O 1A=CB. 在Rt △O 1CO 2中， O 1O 2=13， O 2C=O 2B-O 1A=5， ∴O 1C=1251322=-(cm). ∴AB=12cm.由圆地对称性可知，图中有两条外公切线，并且这两条外公切线地长相等.版权申明本文部分内容，包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.83lcP 。

人教版九年级数学下册第二十四章《圆》检测卷(含答案)

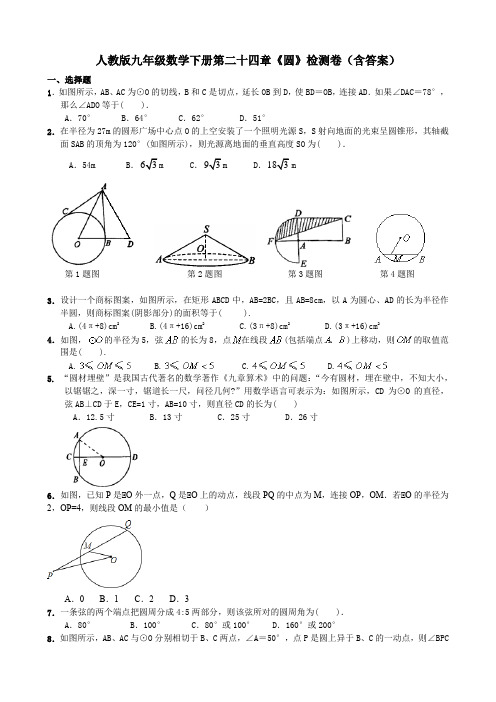
人教版九年级数学下册第二十四章《圆》检测卷（含答案）一、选择题 1．如图所示，AB 、AC 为⊙O 的切线，B 和C 是切点，延长OB 到D ，使BD ＝OB ，连接AD ．如果∠DAC ＝78°，那么∠ADO 等于( )．A ．70°B ．64°C ．62°D ．51°2．在半径为27m 的圆形广场中心点O 的上空安装了一个照明光源S ，S 射向地面的光束呈圆锥形，其轴截面SAB 的顶角为120°(如图所示)，则光源离地面的垂直高度SO 为( )． A ．54m B ．．m D ．m第1题图第2题图第3题图第4题图3．设计一个商标图案，如图所示，在矩形ABCD中，AB=2BC，且AB=8cm ，以A 为圆心、AD 的长为半径作半圆，则商标图案(阴影部分)的面积等于( ).A.(4π+8)cm 2B.(4π+16)cm 2C.(3π+8)cm 2D.(3π+16)cm 24．如图，的半径为5，弦的长为8，点在线段(包括端点)上移动，则的取值范围是( ). A. B. C. D. 5. “圆材埋壁”是我国古代著名的数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何?”用数学语言可表示为：如图所示，CD 为⊙O 的直径，弦AB ⊥CD 于E ，CE=1寸，AB=10寸，则直径CD 的长为( )A ．12.5寸B ．13寸C ．25寸D ．26寸6．如图，已知P 是⊙O 外一点，Q 是⊙O 上的动点，线段PQ 的中点为M ，连接OP ，OM ．若⊙O 的半径为2，OP=4，则线段OM 的最小值是（）A ．0B ．1C ．2D ．37．一条弦的两个端点把圆周分成4:5两部分，则该弦所对的圆周角为( )． A ．80° B ．100° C ．80°或100° D ．160°或200°的度数是( )．A ．65°B ．115°C ．65°或115°D ．130°或50°二、填空题 9．如下左图，是的内接三角形，，点P 在上移动(点P 不与点A 、C 重合)，则的变化范围是__ ________.第9题图第10题图10．如图所示，EB 、EC 是⊙O是两条切线，B 、C 是切点，A 、D 是⊙O 上两点，如果∠E=46°，∠DCF=32°，那么∠A 的度数是________________. 11．已知⊙O 1与⊙O 2的半径、分别是方程的两实根，若⊙O 1与⊙O 2的圆心距=5．则⊙O 1与⊙O 2的位置关系是 __ __ .12．如图，AB 为⊙O 的直径，AB=AC ，BC 交⊙O 于点D ，AC 交⊙O 于点E ，⊙BAC=45°，给出以下五个结论：①⊙EBC=22.5°；②BD=DC ；③AE=2EC ；④劣弧是劣弧的2倍；⑤AE=BC ，其中正确的序号是．13.两个圆内切，其中一个圆的半径为5，两圆的圆心距为2，则另一个圆的半径是_______ ________. 14.已知正方形ABCD ，截去四个角成一正八边形，则这个正八边形EFGHIJLK 的边长为____ ____，面积为_____ ___．15．如图(1)(2)…(m)是边长均大于2的三角形、四边形、……、凸n 边形，分别以它们的各顶点为圆心，以l 为半径画弧与两邻边相交，得到3条弧，4条弧，……1r 2r 2680x x -+=d(1)图(1)中3条弧的弧长的和为___ _____，图(2)中4条弧的弧长的和为_____ ___；(2)求图(m)中n条弧的弧长的和为____ ____(用n表示)．16．如图所示，蒙古包可以近似地看做由圆锥和圆柱组成，如果想用毛毡搭建20个底面积为9πm2，高为3.5m，外围高4 m的蒙古包，至少要____ ____m2的毛毡．三、解答题17. 如图，⊙O是△ABC的外接圆，FH是⊙O 的切线，切点为F，FH∥BC，连结AF交BC于E，∠ABC的平分线BD交AF于D，连结BF．（1）证明：AF平分∠BAC；（2）证明：BF＝FD.18.如图，四边形ABCD是⊙O的内接四边形，BC的延长线与AD的延长线交于点E，且DC=DE．（1）求证：⊙A=⊙AEB；（2）连接OE，交CD于点F，OE⊙CD，求证：⊙ABE是等边三角形．19．如图，相交两圆的公共弦长为120cm，它分别是一圆内接正六边形的边和另一圆内接正方形的边.求两圆相交弧间阴影部分的面积.20.问题背景：课外学习小组在一次学习研讨中，得到了如下两个命题：①如图(1)，在正△ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON＝60°，则BM＝CN；②如图(2)，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON＝90°，则BM＝CN．然后运用类似的思想提出了如下命题：③如图(3)，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON＝108°，则BM＝CN．任务要求：(1)请你从①②③三个命题中选择一个进行证明；(2)请你继续完成下面的探索；①在正n(n≥3)边形ABCDEF…中，M、N分别是CD、DE上的点，BM与CN相交于点O，试问当∠BON等于多少度时，结论BM＝CN成立(不要求证明)；②如图(4)，在正五边形ABCDE中，M、N分别是DE、AE上的点，BM与CN相交于点O，∠BON＝108°时，试问结论BM＝CN是否成立．若成立，请给予证明；若不成立，请说明理由．参考答案一、选择题 1．【答案】B ；【解析】由AB 为⊙O 的切线，则AB ⊥OD ．又BD ＝OB ，则AB 垂直平分OD ，AO ＝AD ，∠DAB ＝∠BAO ．由AB 、AC 为⊙O 的切线，则∠CAO ＝∠BAO ＝∠DAB ．所以，∠DAB ＝∠DAC ＝26°． ∠ADO ＝90°-26°＝64°．本题涉及切线性质定理、切线长定理、垂直平分线的性质、等腰三角形的性质等．2．【答案】C ；【解析】圆锥的高、底面半径与母线组成直角三角形．由题意，SO ⊥AB 于O ，∴ ∠SOA ＝∠SOB ＝90°．又SA ＝SB ，∠ASB ＝120°，∴ ∠SAB ＝∠SBA ＝，设SO ＝x m ，则AS ＝2x m ．∵ AO ＝27，由勾股定理，得(2x)2-x 2＝272，解得(m)．3．【答案】A.；【解析】对图中阴影部分进行分析，可看做扇形、矩形、三角形的面积和差关系. ∵ 矩形ABCD 中，AB=2BC ，AB=8cm ， ∴ AD=BC=4cm ，∠DAF=90°，，，又AF=AD=4cm ， ∴，∴ .4.【答案】A ；【解析】OM 最长是半径5；最短是OM ⊥AB 时，此时OM=3，故选A. 5．【答案】D ；【解析】因为直径CD 垂直于弦AB ，所以可通过连接OA(或OB)，求出半径即可. 根据“垂直于弦的直径平分弦，并且平分弦所对的两条弧”，知(寸)，在Rt △AOE 中，，即，解得OA=13，进而求得CD=26(寸).故选D. 6．【答案】B.【解析】设OP 与⊙O 交于点N ，连结MN ，OQ ，如图，⊙OP=4，ON=2， ⊙N 是OP 的中点， ⊙M 为PQ 的中点，⊙MN 为⊙POQ 的中位线，180120302=°-?°93x =⊙MN=OQ=×2=1，⊙点M 在以N 为圆心，1为半径的圆上，当点M 在ON 上时，OM 最小，最小值为1， ⊙线段OM 的最小值为1．故选B ． 7．【答案】C ；【解析】圆周角的顶点在劣弧上时，圆周角为；圆周角的顶点在优弧上时，圆周角为．注意分情况讨论． 8．【答案】C ；【解析】连接OC 、OB ，则∠BOC ＝360°-90°-90°-50°＝130°．点P 在优弧上时，∠BPC ＝∠BOC ＝65°；点P 在劣弧上时，∠BPC ＝180°-65°＝115°．主要应用了切线的性质定理、圆周角定理和多边形内角和定理．二、填空题 9．【答案】； 10．【答案】99°；【解析】由EB=EC ，∠E=46°知，∠ECB= 67°，从而∠BCD=180°-67°-32°=81°，在⊙O 中，∠BCD 与∠A 互补，所以∠A=180°-81°=99°. 11．【答案】相交；【解析】求出方程的两实根、分别是4、2，则-<<+,所以两圆相交.12.【答案】①①①；【解析】连接AD ，AB 是直径，则AD ⊙BC ，又⊙⊙ABC 是等腰三角形，故点D 是BC 的中点，即BD=CD ，故②正确； ⊙AD 是⊙BAC 的平分线，由圆周角定理知，⊙EBC=⊙DAC=⊙BAC=22.5°，故①正确；⊙⊙ABE=90°﹣⊙EBC ﹣⊙BAD=45°=2⊙CAD ，故④正确； ⊙⊙EBC=22.5°，2EC ≠BE ，AE=BE ，⊙AE ≠2CE ，③不正确； ⊙AE=BE ，BE 是直角边，BC 是斜边，肯定不等，故⑤错误．综上所述，正确的结论是：①②④．13.【答案】7或3；【解析】两圆有三种位置关系：相交、相切(外切、内切)和相离(外离、内含).两圆内切时，圆心距，题中一圆半径为5，而d=2，所以有，解得r=7或r=3，即另一圆半径为7或 3.5136010092⨯⨯=°°413608092⨯⨯=°°122680x x -+=1r 2r 1r 2r d 1r 2r14.【答案】；；【解析】正方形ABCD 外接圆的直径就是它的对角线，由此求得正方形边长为a ．如图所示，设正八边形的边长为x ．在Rt △AEL 中，LE ＝x ，AE ＝AL，∴ ，，即正八边形的边长为．．15.【答案】(1)π； 2π； (2)(n-2)π；【解析】∵ n 边形内角和为(n-2)180°，前n 条弧的弧长的和为个以某定点为圆心，以1为半径的圆周长，∴ n 条弧的弧长的和为．本题还有其他解法，比如：设各个扇形的圆心角依次为，，…，，则， ∴n 条弧长的和为．16.【答案】720π；【解析】∵ S ＝πr 2，∴ 9π＝πr 2，∴ r ＝3．∴ h 1＝4，∴ ，∴，．所求面积包括圆锥的侧面积和圆柱的侧面积，不包括底面积．1)a 22)a x 2x x a +=1)x a =1)a 2222241)]2)AEL S S S a x a a a =-=-=-=△正方形正八边形(2)1801(2)3602n n -=-121(2)(2)2n n ππ⨯⨯-=-1α2αn α12(2)180n n ααα+++=-…°1212111()180180180180n n απαπαππααα⨯+⨯++⨯=+++……(2)180(2)180n n ππ=-⨯=-5l ==223523 3.5152136S S S rl rh πππππππ=+=+=⨯⨯+⨯⨯=+=锥柱2036720S ππ=⨯=总17.【答案与解析】（1）连结OF∵FH 是⊙O 的切线 ∴OF⊥FH ∵FH∥BC ，∴OF 垂直平分BC∴∴AF 平分∠BAC .（2）由（1）及题设条件可知∠1=∠2，∠4=∠3，∠5=∠2 ∴∠1+∠4=∠2+∠3 ∴∠1+∠4=∠5+∠3 ∠FDB =∠FBD ∴BF =FD.18．【答案与解析】证明：（1）⊙四边形ABCD 是⊙O 的内接四边形， ⊙⊙A+⊙BCD=180°， ⊙⊙DCE+⊙BCD=180°， ⊙⊙A=⊙DCE ， ⊙DC=DE ，⊙⊙DCE=⊙AEB ， ⊙⊙A=⊙AEB ；（2）⊙⊙A=⊙AEB ， ⊙⊙ABE 是等腰三角形， ⊙EO ⊙CD ， ⊙CF=DF ，⊙EO 是CD 的垂直平分线， ⊙ED=EC ， ⊙DC=DE ， ⊙DC=DE=EC ，⊙⊙DCE 是等边三角形， ⊙⊙AEB=60°，⊙⊙ABE 是等边三角形．19.【答案与解析】解：∵公共弦AB ＝120 ∴==a R 46120r R a 6624222212060603=-⎛⎝ ⎫⎭⎪=-=2BF FC =A BCDE FO12345HA BCD EFO 12H()∴=-⎛⎝ ⎫⎭⎪=-==r R a O o 442422222602606090，∠S S S R a r AmB AO B AO B弓形扇形=-=-=-229036012180036004244∆ππS S S R a r AnB AO B AO B弓形扇形=-=-=-1160360122400360036266∆ππ()∴=+=-+S S S AmB AnB 阴影弓形弓形4200360013π()[]∴-+两圆相交弧间阴影部分的面积为42003600132πcm .20. 【答案与解析】 (1)如选命题①．证明：在图(1)中，∵ ∠BON ＝60°，∴ ∠1+∠2＝60°． ∵ ∠3+∠2＝60°，∴ ∠1＝∠3．又∵ BC ＝CA ，∠BCM ＝∠CAN ＝60°， ∴ △BCM ≌△CAN ，∴ BM ＝CM ．如选命题②．证明：在图(2)中，∵ ∠BON ＝90°，∴ ∠1+∠2＝90°． ∵ ∠3+∠2＝90°，∴ ∠1＝∠3．又∵ BC ＝CD ，∠BCM ＝∠CDN ＝90°， ∴ △BCM ≌△CDN ，∴ BM ＝CN ．如选命题③．证明：在图(3)中，∵ ∠BON ＝108°，∴ ∠1+∠2＝108°． ∵ ∠2+∠3＝108°，∴ ∠1＝∠3．又∵ BC ＝CD ，∠BCM ＝∠CDN ＝108°， ∴ △BCM ≌△CDN ，∴ BM ＝CN ． (2)①答：当∠BON ＝时结论BM ＝CN 成立．②答：当∠BON ＝108°时．BM ＝CN 还成立．证明：如图(4)，连接BD 、CE 在△BCD 和△CDE 中，∵ BC ＝CD ，∠BCD ＝∠CDE ＝108°，CD ＝DE ， ∴ △BCD ≌△CDE ．∴ BD ＝CE ，∠BDC ＝∠CED ，∠DBC ＝∠ECD ． ∵ ∠CDE ＝∠DEN ＝108°， ∴ ∠BDM ＝∠CEM ．∵ ∠OBC+∠OCB ＝108°，∠OCB+∠OCD ＝108°． (2)180n n-°又∵∠DBC＝∠ECD＝36°，∴∠DBM＝∠ECM．∴△BDM≌△CEN，∴ BM＝CN．。

人教版九年级数学中考复习圆(含答案)

人教版九年级数学中考复习圆一、选择题(本大题共10小题,每小题4分,满分40分)1.如图,四边形ABCD是☉O的内接正方形,P是CD上不同于点C的任意一点,则∠BPC的大小是（）A.22.5°B.30°C.45°D.50°2.如图,AB为☉O的直径,AB=30,点C在☉O上,∠A=24°,则AC的长为（）A.9πB.10πC.11πD.12π3.如图,已知☉O为四边形ABCD的外接圆,O为圆心.若∠BCD=120°,AB=AD=2,则☉O的半径长为（）A.3√22B.√62C.32D.2√334.在平面直角坐标系中,圆心为坐标原点,☉O的半径为10,则点P(-8,6)与☉O的位置关系为（）A.点P在☉O上B.点P在☉O外C.点P在☉O内D.无法确定5.如图,点A,B,C在半径为6的☉O上,AB的长为2π,则∠ACB的大小是（）A.20°B.30°C.45°D.60°6.在平面直角坐标系内,以原点O 为圆心,1为半径作圆,点P 在直线y =√3x +2√3上运动,过点P 作该圆的一条切线,切点为A ,则PA 的最小值为（） A.3 B.2 C.√3 D.√27.如图,正六边形ABCDEF 的边长为2,分别以点A ,D 为圆心,以AB ,DC 为半径作扇形ABF ,扇形DCE.则图中阴影部分的面积是（）A.6√3-43πB.6√3-83πC.12√3-43πD.12√3-83π8.如图,半圆O 的直径AB =10 cm,弦AC =6 cm,D 是BC的中点,则弦AD 的长为（）A.4 cmB.3√5 cmC.4√5 cmD.5√5 cm9.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是（） A.√28B.√34C.√24D.√3810.如图,AB 是☉O 的直径,C ,D 是☉O 上的点,且O C∥BD,A D 分别与BC ,OC 相交于点E ,F ,则下列结论:①AD ⊥BD ;②∠AOC =∠AEC ;③CB 平分∠ABD ;④AF =DF ;⑤BD =2OF ;⑥△CEF ≌△BED.其中结论一定成立的是（） A.②④⑤⑥ B.①③⑤⑥ C.②③④⑥D.①③④⑤二、填空题(本大题共4小题,每小题5分,满分20分)11.如图,AB 为☉O 的直径,点C 在☉O 上,且OC ⊥AB ,过点C 的弦CD 与线段OB 相交于点E ,满足∠AEC =65°,连接AD ,则∠BAD = °.x-3交x轴于点A,交y轴于点B,P是x轴上一动点,以点P为圆心,以1个12.如图,直线y=-34单位长度为半径作☉P,当☉P与直线AB相切时,点P的坐标是.13.如图,在Rt△OAB中,∠AOB=45°,AB=2,将Rt△OAB绕点O顺时针旋转90°得到Rt△OCD,则AB扫过的阴影部分的面积为.14.如图,在一个圆柱形铁桶内底面的点A处有一只飞虫,在其上边沿的点B处有一面包残渣.cm,铁桶的底面直径为40 cm,桶高已知C是点B正下方的桶内底面上一点,劣弧AC的长为40π360 cm,则该飞虫从点A到达点B的最短路径为 cm.三、(本大题共2小题,每小题8分,满分16分)15.如图,AB,CD是☉O的直径,弦CE∥AB,CE所对的圆心角的度数为50°,求∠AOC的度数.16.如图,已知AB是☉O的直径,点C,D在☉O上,∠D=60°且AB=6,过点O作OE⊥AC,垂足为E.(1)求OE的长;(2)若OE的延长线交☉O于点F,求阴影部分的面积S.四、(本大题共2小题,每小题8分,满分16分)17.如图,四边形ABCD是☉O的内接四边形,DB平分∠ADC,连接OC,OC⊥BD.(1)求证:AB=CD;(2)若∠A等于66°,求∠ADB的度数.18.如图,☉O为△ABC的内切圆,∠ACB=90°,AO的延长线交BC于点D,AC=4,CD=2,求☉O的半径.五、(本大题共2小题,每小题10分,满分20分)19.如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作☉O,分别与AC,BC相交于点M,N.(1)过点N作☉O的切线NE与AB相交于点E,求证:NE⊥AB;(2)连接MD,求证:MD=NB.20.已知☉O是△ABC的外接圆,∠CAD=∠ABC.(1)如图1,试判断直线AD与☉O的位置关系,并说明理由;(2)如图2,将直线AD沿直线AC翻折后交☉O于点E,连接OA,OE,CE.若∠ABC=30°,求证:四边形ACEO是菱形.六、(本题满分12分)21.如图,已知平面直角坐标系中一条圆弧经过正方形网格的格点A,B,C.(1)用直尺画出该圆弧所在圆的圆心M的位置;(2)若点A的坐标为(0,4),点D的坐标为(7,0),试验证点D是否在经过点A,B,C的圆上;(3)在(2)的条件下,求证:直线CD是☉M的切线.七、(本题满分12分)22.如图,已知点A,B,C,D均在☉O上,AD∥BC,BD平分∠ABC,∠BAD=120°,四边形ABCD的周长为15.(1)求☉O的半径;(2)求图中阴影部分的面积.八、(本题满分14分)23.小平所在的学习小组发现,车辆转弯时,能否顺利通过直角弯道的标准是车辆是否可以行驶到和路的边界夹角是45°的位置(如图1中的位置).例如,图2是某巷子的俯视图,巷子路面宽4 m,转弯处为直角,车辆的车身为矩形ABCD,CD与DE,CE的夹角都是45°时,连接EF,交CD 于点G,若GF的长度至少能达到车身宽度,则车辆能通过.(1)小平认为长8 m、宽3 m的消防车不能通过该直角转弯,请你帮他说明理由;(2)小平提出将拐弯处改为圆弧(MM'和NN'是以O为圆心,分别以OM和ON为半径的弧),长8 m、宽3 m的消防车就可以通过该弯道了,具体方案如图3,其中OM⊥OM',你能帮小平算出,ON 至少为多少时,这种消防车可以通过该巷子?答案一、选择题(本大题共10小题,每小题4分,满分40分)3.如图,四边形ABCD是☉O的内接正方形,P是CD上不同于点C的任意一点,则∠BPC的大小是A.22.5°B.30°C.45°D.50°4.如图,AB为☉O的直径,AB=30,点C在☉O上,∠A=24°,则AC的长为A.9πB.10πC.11πD.12π3.如图,已知☉O为四边形ABCD的外接圆,O为圆心.若∠BCD=120°,AB=AD=2,则☉O的半径长为A.3√22B.√62C.32D.2√334.在平面直角坐标系中,圆心为坐标原点,☉O的半径为10,则点P(-8,6)与☉O的位置关系为A.点P在☉O上B.点P在☉O外C.点P在☉O内D.无法确定5.如图,点A,B,C在半径为6的☉O上,AB的长为2π,则∠ACB的大小是A.20°B.30°C.45°D.60°6.在平面直角坐标系内,以原点O 为圆心,1为半径作圆,点P 在直线y =√3x +2√3上运动,过点P 作该圆的一条切线,切点为A ,则PA 的最小值为 A.3 B.2 C.√3 D.√27.如图,正六边形ABCDEF 的边长为2,分别以点A ,D 为圆心,以AB ,DC 为半径作扇形ABF ,扇形DCE.则图中阴影部分的面积是A.6√3-43πB.6√3-83πC.12√3-43πD.12√3-83π8.如图,半圆O 的直径AB =10 cm,弦AC =6 cm,D 是BC的中点,则弦AD 的长为A.4 cmB.3√5 cmC.4√5 cmD.5√5 cm提示:连接OC ,OD ,作DE ⊥AB 于点E ,OF ⊥AC 于点F.∴∠AFO =∠DEO =90°.∵CD=BD ,∴∠DOB =∠OAC =2∠BAD.∵OA =OD ,∴△AOF ≌△ODE (AAS),∴OE =AF =12AC =3 cm .在Rt△DOE 中,DE =√OD 2−OE 2=4 cm,在Rt△ADE 中,AD =√DE 2+AE 2=4√5 cm . 9.以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是 A.√28B.√34C.√24D.√3810.如图,AB是☉O的直径,C,D是☉O上的点,且O C∥BD,A D分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED.其中结论一定成立的是A.②④⑤⑥B.①③⑤⑥C.②③④⑥D.①③④⑤二、填空题(本大题共4小题,每小题5分,满分20分)11.如图,AB为☉O的直径,点C在☉O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD=20°.x-3交x轴于点A,交y轴于点B,P是x轴上一动点,以点P为圆心,以1个12.如图,直线y=-34,0).单位长度为半径作☉P,当☉P与直线AB相切时,点P的坐标是(−7313.如图,在Rt△OAB中,∠AOB=45°,AB=2,将Rt△OAB绕点O顺时针旋转90°得到Rt△OCD,则AB扫过的阴影部分的面积为π.14.如图,在一个圆柱形铁桶内底面的点A处有一只飞虫,在其上边沿的点B处有一面包残渣.cm,铁桶的底面直径为40 cm,桶高已知C是点B正下方的桶内底面上一点,劣弧AC的长为40π360 cm,则该飞虫从点A到达点B的最短路径为40√3 cm.提示:如图,连接AB,OC,OA,AC,作OH⊥AC于点H.设∠AOC=n°.∵AC的长=40π3,∴nπ·20180=40π3,∴n=120.∵OA=OC,OH⊥AC,∴∠COH=∠AOH=60°,CH=AH,∴AC=2CH=2·OC·sin 60°=2×20×√32=20√3(cm).在Rt△ABC中,AB=√BC2+AC2=√602+(20√3)2=40√3(cm),∴该飞虫从点A到达点B的最短路径为40√3 cm.三、(本大题共2小题,每小题8分,满分16分)15.如图,AB,CD是☉O的直径,弦CE∥AB,CE所对的圆心角的度数为50°,求∠AOC的度数.解:连接OE.由已知可得∠COE=50°.∵OC=OE,∴∠OCE=∠OEC=12(180°-50°)=65°.∵CE∥AB,∴∠AOC=∠OCE=65°.16.如图,已知AB是☉O的直径,点C,D在☉O上,∠D=60°且AB=6,过点O作OE⊥AC,垂足为E.(1)求OE的长;(2)若OE的延长线交☉O于点F,求阴影部分的面积S.解:(1)∵∠D =60°,∴∠B =60°.∵AB 是☉O 的直径,∴∠ACB =90°,∠CAB =30°. 又∵AB =6,∴OA =3. ∵OE ⊥AC ,∴OE =12OA =32.(2)连接OC.易得△COE ≌△AFE ,∠COF =60°, ∴阴影部分的面积S =S 扇形FOC =60π×32360=32π.四、(本大题共2小题,每小题8分,满分16分)17.如图,四边形ABCD 是☉O 的内接四边形,DB 平分∠ADC ,连接OC ,OC ⊥BD. (1)求证:AB =CD ;(2)若∠A 等于66°,求∠ADB 的度数.解:(1)∵DB 平分∠ADC ,∴AB =BC . ∵OC ⊥BD ,∴BC =CD . ∴AB=CD ,∴AB =CD. (2)∵四边形ABCD 是☉O 的内接四边形, ∴∠BCD =180°-∠A =114°. ∵BC=CD ,∴BC =CD , ∴∠BDC =12×(180°-114°)=33°. ∵DB 平分∠ADC , ∴∠ADB =∠BDC =33°.18.如图,☉O为△ABC的内切圆,∠ACB=90°,AO的延长线交BC于点D,AC=4,CD=2,求☉O的半径.解:设☉O与AC的切点为M,圆的半径为r.连接OM.∵OM⊥AC,∠ACB=90°,∴OM∥DC,∴∠MOC=∠DCO.又∵∠MCO=∠DCO,∴∠MOC=∠MCO,∴CM=OM=r,由条件易得△AOM∽△ADC,∴OMCD =AMAC,即r2=4−r4,解得r=43.∴☉O的半径是43.五、(本大题共2小题,每小题10分,满分20分)19.如图,在Rt△ABC中,∠ACB=90°,以斜边AB上的中线CD为直径作☉O,分别与AC,BC相交于点M,N.(1)过点N作☉O的切线NE与AB相交于点E,求证:NE⊥AB;(2)连接MD,求证:MD=NB.证明:(1)连接ON.∵CD是Rt△ABC的斜边AB上的中线,∴AD=CD=DB,∴∠DCB=∠DBC.又∵OC=ON,∴∠DCB=∠ONC,∴∠ONC=∠DBC,∴ON∥AB.∵NE是☉O的切线,ON是☉O的半径,∴∠ONE=90°,∴∠NEB=90°,即NE⊥AB.(2)由(1)可知ON∥AB.BC.又∵OC=OD,∴CN=NB=12∵CD是☉O的直径,∴∠CMD=90°.又∵∠ACB=90°,∴MD∥BC.BC,∵D是AB的中点,∴MD=12∴MD=NB.20.已知☉O是△ABC的外接圆,∠CAD=∠ABC.(1)如图1,试判断直线AD与☉O的位置关系,并说明理由;(2)如图2,将直线AD沿直线AC翻折后交☉O于点E,连接OA,OE,CE.若∠ABC=30°,求证:四边形ACEO是菱形.解:(1)直线AD与☉O相切.理由:作直径AP,连接CP.∵∠APC=∠ABC,∠CAD=∠ABC,∴∠CAD=∠APC.∵AP是☉O的直径,∴∠ACP=90°,∴∠CAP+∠APC=90°,∴∠CAP+∠CAD=90°,即∠DAP=90°,∴AD⊥AP,∴直线AD与☉O相切.(2)连接OC.∵∠ABC=30°,∴∠CAE=∠CAD=∠ABC=30°,∴∠AOC=2∠ABC=60°,∠COE=2∠CAE=60°.∵OA=OC=OE,∴△AOC,△COE都是等边三角形,∴OA=AC=OC,OC=CE=EO,∴OA=AC=CE=EO,∴四边形ACEO是菱形.六、(本题满分12分)21.如图,已知平面直角坐标系中一条圆弧经过正方形网格的格点A,B,C.(1)用直尺画出该圆弧所在圆的圆心M的位置;(2)若点A的坐标为(0,4),点D的坐标为(7,0),试验证点D是否在经过点A,B,C的圆上;(3)在(2)的条件下,求证:直线CD是☉M的切线.解:(1)图略.(2)由点A(0,4),可得小正方形的边长为1,从而点B(4,4),C(6,2),M(2,0),则圆弧所在圆的半径为√22+42=2√5,点D到点M的距离为7-2=5>2√5,所以点D不在经过点A,B,C的圆上.(3)设过点C与x轴垂直的直线与x轴的交点为E,连接MC,作直线CD.由(2)知小正方形的边长为1,所以CE=2,ME=4,ED=1,MD=5.在Rt△CEM中,MC2=ME2+CE2=42+22=20,在Rt△CED中,CD2=ED2+CE2=12+22=5,所以MD2=MC2+CD2,所以∠MCD=90°.因为MC为☉M的半径,所以直线CD是☉M的切线.七、(本题满分12分)22.如图,已知点A,B,C,D均在☉O上,AD∥BC,BD平分∠ABC,∠BAD=120°,四边形ABCD的周长为15.(1)求☉O的半径;(2)求图中阴影部分的面积.解:(1)∵AD∥BC,∠BAD=120°,∴∠ABC=60°.又∵BD 平分∠ABC ,AD ∥BC , ∴∠ABD =∠DBC =∠ADB =30°, ∴AB=AD =CD ,∴AB =AD =CD. ∵四边形ABCD 的周长为15,∴BC +3CD =15. 又∵在Rt△BDC 中,BC =2CD ,∴BC +32BC =15,∴BC =6, ∴☉O 的半径为3.(2)连接OA ,OD ,过点O 作OE ⊥AD 于点E. 在Rt△AOE 中,∠AOE =30°, ∴OE =OA ·cos 30°=3√32, ∴S △AOD =12AD ·OE =12×3×3√32=9√34, ∴S 阴影=S扇形AOD -S △AOD =60π×32360-9√34=6π−9√34. 八、(本题满分14分)23.小平所在的学习小组发现,车辆转弯时,能否顺利通过直角弯道的标准是车辆是否可以行驶到和路的边界夹角是45°的位置(如图1中的位置).例如,图2是某巷子的俯视图,巷子路面宽4 m,转弯处为直角,车辆的车身为矩形ABCD ,CD 与DE ,CE 的夹角都是45°时,连接EF ,交CD 于点G ,若GF 的长度至少能达到车身宽度,则车辆能通过.(1)小平认为长8 m 、宽3 m 的消防车不能通过该直角转弯,请你帮他说明理由;(2)小平提出将拐弯处改为圆弧(MM'和NN '是以O 为圆心,分别以OM 和ON 为半径的弧),长8 m 、宽3 m 的消防车就可以通过该弯道了,具体方案如图3,其中OM ⊥OM',你能帮小平算出,ON 至少为多少时,这种消防车可以通过该巷子?解:(1)作FH ⊥EC ,垂足为H.∵FH =EH =4,∴EF =4√2,且∠GEC =45°. ∵GC =4,∴GE =GC =4,∴GF=4√2-4<3,即GF的长度未达到车身宽度,∴消防车不能通过该直角转弯.(2)若点C,D分别与点M',M重合,则△OGM为等腰直角三角形,如图所示.∴OG=4,OM=4√2,∴OF=ON=OM-MN=4√2-4,∴FG=8-4√2<3,∴点C,D在MM'上.设ON=x,连接OC.在Rt△OCG中,OG=x+3,OC=x+4,CG=4,由勾股定理,得OG2+CG2=OC2,即(x+3)2+42=(x+4)2,解得x=4.5.答:ON至少为4.5 m时,这种消防车可以通过该巷子.。

人教版初三圆测试题及答案

人教版初三圆测试题及答案一、选择题（每题2分，共10分）1. 半径为2的圆的面积是多少？A. 4πB. 6πC. 8πD. 12π2. 圆的周长公式是：A. C = πrB. C = 2πrC. C = 4πrD. C = 8πr3. 若圆的半径是3，圆心角为60°，那么这个弧长是多少？A. πB. 3πC. 6πD. 9π4. 点P到圆心O的距离是5，圆的半径是3，那么点P与圆的位置关系是：A. 在圆上B. 在圆内C. 在圆外D. 无法确定5. 圆的切线与半径垂直，且切点到圆心的距离等于：A. 半径B. 直径C. 周长的一半D. 面积的平方根二、填空题（每题2分，共10分）6. 半径为4的圆的面积是_________。

7. 若圆的周长为12π，那么圆的半径是_________。

8. 圆心角为120°的弧所对的圆心角是_________。

9. 点P到圆心O的距离是2，圆的半径是4，点P与圆的位置关系是_________。

10. 圆的切线与半径垂直，切点到圆心的距离是_________。

三、计算题（每题5分，共20分）11. 已知圆的半径为5，求圆的周长和面积。

12. 已知圆的周长为16π，求圆的半径。

13. 若圆的半径为7，圆心角为45°，求该弧长。

14. 已知点P到圆心O的距离为10，圆的半径为8，求点P与圆的位置关系。

四、解答题（每题10分，共20分）15. 某圆的半径为6，圆心角为30°，求该弧所对的圆心角和弧长。

16. 已知圆的切线在点M处与圆相切，OM=6，半径为4，求切线PM的长度。

五、综合题（15分）17. 某工厂需要在一块半径为10米的圆形场地上安装一个直径为4米的圆形水池，水池的中心与场地的中心重合。

求水池的半径占场地半径的比例，以及水池的面积占整个场地面积的比例。

六、结束语本测试题覆盖了圆的基本概念、公式和计算方法，旨在帮助学生巩固和检验对圆的相关知识的掌握。

人教版初三圆试题及答案

人教版初三圆试题及答案一、选择题1. 已知圆的半径为5，圆心到直线的距离为3，那么直线与圆的位置关系是什么？A. 相交B. 相切B. 相离D. 无法确定2. 圆的周长是圆的直径的几倍？A. π倍B. 2倍C. 3倍D. 4倍3. 已知点A到圆心O的距离为6，点B到圆心O的距离为4，那么点A 和点B在圆上的位置关系是什么？A. 都在圆上B. 点A在圆外，点B在圆内C. 点A在圆内，点B在圆上D. 点A和点B都不在圆上二、填空题1. 圆的面积公式为__________。

2. 已知圆的半径为r，圆的直径为d，则d=__________。

3. 圆的切线与半径垂直，且切线的长度等于__________。

三、解答题1. 已知圆的半径为7，求圆的周长和面积。

解：圆的周长公式为C=2πr，代入r=7，得C=2×π×7=14π。

圆的面积公式为A=πr²，代入r=7，得A=π×7²=49π。

2. 已知点P在圆O上，OP=10，PA=6，求圆O的半径。

解：根据勾股定理，PA²+r²=OP²，即6²+r²=10²，解得r²=10²-6²=64，所以r=8。

四、应用题1. 某圆形花坛的周长为628厘米，求花坛的直径。

解：根据圆的周长公式C=πd，代入C=628，得d=628/π。

2. 一个圆的半径为8厘米，求这个圆的面积。

解：根据圆的面积公式A=πr²，代入r=8，得A=π×8²=64π。

结束语：本次试题涵盖了圆的基本性质和公式，通过选择题、填空题、解答题和应用题的形式，全面考察了学生对圆的理解和应用能力。

希望同学们能够通过练习，加深对圆的理解和掌握，提高解题技巧。

人教版九年级数学上册第24章《圆》测试卷1(附答案)

人教版九年级数学上册第24章《圆》测试卷1（附答案）时间：100分钟总分：120分一、选择题（每小题3分，共30分）1.已知⊙O与点P在同一平面内，如果⊙O的半径为5，线段OP的长为4，则点P( )A.在⊙O上B.在⊙O内C.在⊙O外D.以上答案都不正确2.若半径为5c m的一段弧长等于半径为2c m的圆的周长，则这段弧所对的圆心角为( )A.144°B.132°C.126°D.108°3.如图，一个直角三角尺的30°角的顶点P落在⊙O上，两边分别交⊙O于A，B两点，若⊙O的直径为4，则弦AB长为( )A.2B.3C.√2D.√3第3题图第4题图第5题图第6题图4.如图，CD是⊙O的直径，弦AB⊥CD于点G，直线EF与⊙O相切于点D，则下列结论中不一定正确的是( )A.AG=BGB.AD//BCC.AB//EFD. ∠ABC= ∠ADC5.某盏路灯照射的空间可以看成如图所示的圆锥，它的高AO=8m，底面半径OB=6m，则圆锥的侧面积是( )A.60πm²B.50π m²C.47.5π m²D.45.5π m²6. 如图，四边形ABCD内接于⊙O，若四边形ABCO是平行四边形，则∠ADC的大小为( )A.45°B.50°C.60°D.75°7. 已知⊙A与⊙B外切，⊙C与⊙A，⊙B都内切，且AB=5，AC=6，BC=7，那么⊙C的半径长是( )A.11B.10C.9D.88.如图，⊙P与x轴交于点A（-5，0），B（1，0），与y轴的正半轴交于点C.若∠ACB=60°，则点P的坐标为( )A.(-3, √3)B.(-2, √3,)C.(-3, 3√3)D.(-2, 3√3)第8题图第9题图第10题图9.如图，用6个小正方形构造如图所示的网格图（每个小正方形的边长均为2），设经过图中M，P，H三点的圆弧与AH交于点R，则图中阴影部分的面积为( )A.3π-2B.2π-5C.5π2--5 D. 5π4-5210. 如图，⊙O的半径为5，点A是⊙O上一定点，点B在⊙O上运动，且∠ABM =30°，AC⊥BM于点C，连接OC，则OC的最小值是( )A. 3−√32B.√32C. √33D.5√32−52二、填空题（每小题3分，共15分）11.已知某个正六边形的周长为6，则这个正六边形的边心距是__________.12.如图所示，在“世界杯”足球比赛中，甲带球向对方球门PQ进攻，当他带球冲到点A时，同伴乙已经成功冲到点B，现在有两种射门方式：第一种是甲直接射门；第二种是甲将球传给乙，由乙射门.仅从射门角度大小考虑，应选择第______种射门方式.第12题图第13题图第14题图第15题图13.用等分圆的方法，在半径为OA的圆中，画出了如图所示的四叶幸运草，若OA = 2，则四叶幸运草的周长是________.14. 如图，一条公路的转弯处是一段圆弧AB，点O是这段弧所在圆的圆心，AB=40m，C是弧AB的中点，且CD=10m，则这段弯路所在圆的半径为_________ m.15. 如图，在扇形OAB中，∠AOB=60°，OA = 4，射线AM⊥OA，E为弧AB上的一个动点，过点E作EF⊥AM于点F，连接AE，当AE－EF的值最大时，图中阴影部分的面积为______.三、解答题（本大题共8个小题，满分75分）16.（8分）如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于点D，且CO=CD，求∠PCA的度数.17.（9分）如图，矩形ABCD中，AB=2BC，以AB为直径作⊙O.（1）求证CD是OO的切线.（2）若BC=3，连接BD，求阴影部分的面积.（结果保留π）18.（9分）下面是小东设计的“过圆外一点作这个圆的两条切线”的尺规作图过程..已知：⊙O及⊙O外一点P.求作：直线P A和直线PB，使P A切⊙O于点A，PB切⊙O于点B.作法：如图.OP的长为半径作弧，两弧分别交于点M，N；①连接OP.分别以点O和点P为圆心，大于12②连接MN，交OP于点Q，再以点Q为圆心，OQ的长为半径作弧，交⊙O于点A和点B；③作直线P A和直线PB.所以直线P A和PB就是所求作的直线.根据小东设计的尺规作图过程解答下列问题：（1）使用直尺和圆规，补全图形（保留作图痕迹）（2）完成下面的证明.证明：连接OA，OB . ∵OP是⊙Q的直径，∴∠OAP=∠OBP =______°( ) (填推理的依据).∴P A⊥OA , PB⊥OB .∵OA，OB为⊙O的半径，∴P A，PB是⊙O的切线.̂上，连19.（9分）如图，在⊙O的内接四边形ABCD中，AB=AD，∠BCD=120°，点E在AD接AE，DE.（1）求∠AED的度数；（2）连接OA，OD，OE，当∠DOE=90°时，AE恰好为⊙O的内接正n边形的一边，求n的值.̂=BĈ= AĈ，点E是BC上的一点，20.（9分）如图，已知△ABC是⊙O的内接三角形，AB连接AE，过点B作BD//AE交⊙O于点D，连接CD交AB于点F.（1）求证：AF=BE.（2）若∠CAE=15°，请仅用无刻度的直尺在图中作出一个⊙O的内接等腰直角三角形（保留作图痕迹，不写作法）.̂的中点，N是AĈ的中点，弦MN分别交21.（10分）如图，AB，AC是⊙O的两条弦，M是ABAB，AC于点P，D.（1）求证AP=AD.（2）连接PO，若AP=3，OP=√10，⊙O的半径为5，求MP的长.22.（10分）如图，AB是⊙O的直径，点C是⊙O上一点（点C不与A，B重合），连接CA，CB，∠ACB的平分线CD与⊙O交于点D.（1）求∠ACD的度数；（2）探究CA，CB，CD三者之间的等量关系，并证明；（3）E为⊙O外一点，满足ED=BD，AB=5，AE =3，若P为AE中点，求PO的长.23.（11分）如图，AB是⊙O的直径，PC切⊙O于点P，过点A作直线AC⊥PC交⊙O于另一点D，连接P A,PB,PO.（1）求证：AP平分∠CAB；（2）若P是直径AB上方半圆弧上一动点。

2020 人教版九年级圆专题复习(有答案)

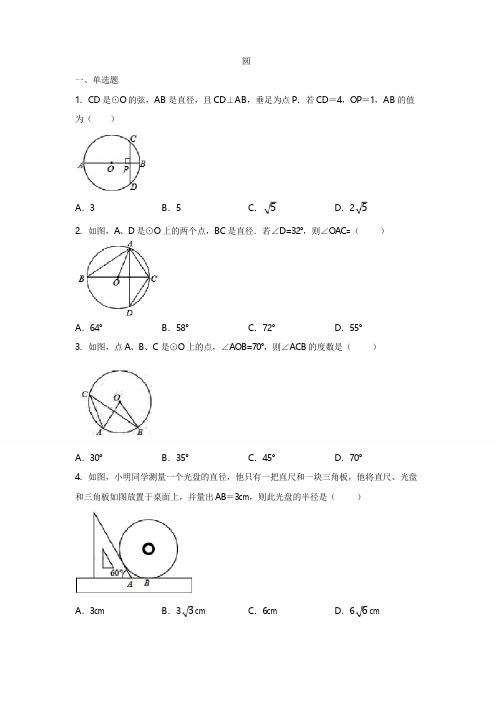
圆一、单选题1．CD是⊙O的弦，AB是直径，且CD⊥AB，垂足为点P．若CD＝4，OP＝1，AB的值为（）A．3B．5C．5D．252．如图，A、D是⊙O上的两个点，BC是直径．若∠D=32°，则∠OAC=（）A．64°B．58°C．72°D．55°3．如图，点A、B、C是⊙O上的点，∠AOB=70°，则∠ACB的度数是（）A．30°B．35°C．45°D．70°4．如图，小明同学测量一个光盘的直径，他只有一把直尺和一块三角板，他将直尺、光盘和三角板如图放置于桌面上，并量出AB＝3cm，则此光盘的半径是（）A．3cm B．33cm C．6cm D．66cm2D．34B．3A．2-π24C．2-8D．35．如图，A，B，P是⊙O上三点，若∠P＝110°，则∠AOB的度数为（）A．70°B．110°C．125°D．140°6．如图，△ABC中，∠A=30°，点O是边AB上一点，以点O为圆心，以OB为半径作圆，⊙O恰好与AC相切于点D，连接BD．若BD平分∠ABC，AD=23，则线段CD的长是（）A．2B．3C．3237．已知圆内接正三角形的面积为3，则该圆的内接正六边形的边心距是（）A．2B．1C．3D．32 8．如图，矩形ABCD的边AB=1，BE平分∠ABC，交AD于点E，若点E是AD的中点，以点B为圆心，BE长为半径画弧，交BC于点F，则图中阴影部分的面积是（）-πππ-249．如图，⊙O的半径为5△，ABC是⊙O的内接三角形，过点C作CD垂直AB于点D．若CD＝3，AC＝6，则BC长为（）»»¼②∠MAN=90°；③¼AM=BM；④∠ACM+∠ANM=∠MOB；⑤AE=A．3B．5C．32D．610．如图，AB是半圆O的直径，D，E是半圆上任意两点，连接AD，DE，AE与BD相交于点C，要使△ADC△与ABD相似，可以添加一个条件．下列添加的条件错误的是()A．∠ACD＝∠DABC．AD2＝BD·C DB．AD＝DED．CD·A B＝AC·B D11．若⊙A的半径为5，圆心A的坐标是（1，2），点P的坐标是（5，2），那么点P的位置为（）A．在⊙A内B．在⊙A上C．在⊙A外D．不能确定12．如图所示，MN是⊙O的直径，作AB⊥MN，垂足为点D，连接AM，AN，点C为AN 上一点，且AC=AM，连接CM，交AB于点E，交AN于点F，现给出以下结论：①AD=BD；¼其中正确结论的个数是（）12MF．A．2B．3C．4D．5二、填空题13．如图，在⊙O中，弦CD垂直于直径AB于点E，若∠BAD=30°，且BE=2，则CD=．14．若用一张直径为20cm的半圆形铁片做一个圆锥的侧面，接缝忽略不计，则所得圆锥的高为_____．15．如图，AB为⊙O的直径，弦CD⊥AB于点E，若CD=8，OE=3，则⊙O的半径为_______．16．如图，⊙O△是ABC的外接圆，⊙O的直径BD＝8，∠A＝60°，则BC的长度为_____.17．如图，AC是⊙O的直径，弦BD⊥AO，垂足为点E，连接BC，过点O作OF⊥BC，垂足为F，若BD＝8cm，AE＝2cm，则OF的长度是_____cm．18．如图，△Rt ABC的内切圆⊙O与两直角边AB，BC分别相切于点D，E，过弧DE(不包括端点D，E)上任一点P作⊙O的切线MN与AB，BC分别交于点M，N，若⊙O的半径为r，则△Rt MBN的周长为_______．19．工程上常用钢珠来测量零件上小圆孔的宽口，假设钢珠的直径是10mm，测得钢珠顶端离零件表面的距离为8mm，如图所示，则这个小圆孔的宽口AB的长度为____mm．20．如图，已知⊙P的半径为1，圆心P在抛物线y=x2-2上运动，当⊙P与x轴相切时，圆心P的坐标是___________________．三、解答题21．计算：如图，半径为3的⊙A经过原点O和点C(0，2)，B是y轴左侧⊙A优弧上一点，求tan∠OBC的值．22．如图，已知三角形ABC的边AB是0的切线，切点为B．AC经过圆心0并与圆相交于点D，C，过C作直线CE丄AB，交AB的延长线于点E,(1)求证：CB平分∠ACE；(2)若BE=3，CE=4，求O的半径.23．如图，△ABC中，AB＝AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，过点D作DF⊥AC于点F．（1）证明：DF是⊙O的切线；（2）若AC＝3AE，FC＝6，求AF的长．24．在如图所示的网格中，每个小正方形的边长为1，每个小正方形的顶点叫做格点．三角形ABC的三个顶点均在格点上，以点A为圆心的弧EF与BC相切于格点D，分别交AB，AC于点E，F．（1）直接写出三角形ABC边长AB＝；AC＝；BC＝．（2）求图中由线段EB，BC，CF及弧FE所围成的阴影部分的面积．（结果保留π）25．如图，DC是⊙O的直径，点B在圆上，直线AB交CD延长线于点A，且∠ABD=∠C．（1）求证：AB是⊙O的切线；（2）若AB=4cm，AD=2cm，求tanA的值和DB的长．26．如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作EF⊥AC 于点E，交AB延长线于点F．（1）判断直线EF与⊙O的位置关系，并说明理由；（2）若⊙O半径为5，CD＝6，求DE的长；（3）求证：BC2＝4CE•AB．参考答案1．D2．B3．B4．B5．D6．B7．B8．B9．B10．D11．A12．D13．4314．53cm15．516．4317．518．2r19．825．（1）证明略；（2）tanA=320．(3,1)或(-3,1)或(1,-1)或(-1,-1)21．2 422．（1）证明略；（2）258.23．（1）略；（2）AF＝3．24．（1）210，210，45；（2）20﹣5π6；DB的长为455．24 26．（1）EF与⊙O相切；（2）DE＝5；（3）略。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

人教版九年级数学（3份）第二十四章圆复习测试题班级姓名分数一、精心选一选(每小题5分,共25分)1.如图1,圆．和圆．的位置关系是( )(A)外离. (B)相切. (C)相交. (D)内含.2.如图2,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为( )(A)10. (B)8. (C)6. (D)4.3.一个扇形的圆心角为120°,它的面积为3πcm2,那么这个扇形的半径是( )(B)3cm. (C)6cm. (D)9cm.4.如图3,圆柱的高线长为10cm,轴截面的面积为240cm2,则圆柱的侧面积是( )(A)240cm2. (B)240πcm2. (C)480cm2. (D)480πcm2.5.下列说法正确的是( )(A)正五边形的中心角是108°. (B)正十边形的每个外角是18°.(C)正五边形是中心对称图形. (D)正五边形的每个外角是72°.二、耐心填一填(每小题5分,共25分)6.如图4,⊙O的半径OD为5cm,直线l⊥OD,垂足为O,则直线l沿射线OD方向平移______cm时与⊙O相切.7.如图5,∠C是⊙O的圆周角,∠C=38°,∠OAB=______度.8.两圆的半径分别为3cm和4cm,圆心距为5cm,则两圆的位置关系为______.9.如图6,A、B是⊙O上的两点,AC是过A点的一条直线,如果∠AOB=120°,那么当∠CAB的度数等于______时,AC才能成为⊙O的切线.10.如图7,某传送带的一个转动轮的半径为20cm,当物体从A传送20cm至B时,那么这个转动轮转了______度(π取3.14,结果保留四个有效数字)三、用心想一想(每题10分,共50分)11.如图8是不倒翁的正视图,不倒翁的圆形脸恰好与帽子边沿P A、PB分别相切于点A、B,不倒翁的鼻尖正好是圆心O,若∠OAB=25°,求∠APB的度数.(用尺规作图, 12.如图9,是一个破损的机器部件,它的残留边缘是圆弧,请作图找出圆心保留作图痕迹,写出作法,不用证明).13.如图10,在⊙O中,弦AB与DC相交于点E,AB=CD.求证:△AEC≌△DEB.14.如图11,有圆锥形粮堆,其主视图是边长为6m的正三角形ABC,母线AC的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠.(1)求圆锥侧面展开图的圆心角的度数;(2)小猫经过的最短路程是多少m(结果不取近似值)?15如图12①,直线AM⊥AN,⊙O分别与AM、AN相切于B、C两点,连结OC、BC,则有∠ACB=∠OCB;(请思考:为什么?)若将图12①中直线AN向右平移,与⊙O相交于C1、C2两点,⊙O与AM的切点仍记为B,如图12②.(1)请你写出与平移前相应的结论,并将图12②补充完整;(2)判断此结论是否成立,并说明理由.第二十四章复习测试题参考答案1.A2.C3.B4.B5.D6.57.528.两圆相交9.60°10.约57.23(提示:轮子转过的角度所对的弧长与线段AB的长相等) 11.50 12.略13.略14.(1)180°;(2)315.(1)图②中相应结论为∠AC1B=∠OC1B和∠AC2B=∠OC2B.(2)以前者为例进行证明:连接OB、OC1,∵AM与⊙O相切于B,∴OB⊥AM.∵AN⊥AM,∴OB∥AN.∴∠AC1B=∠OBC1.∵OB=OC1,∴∠OBC1=∠OC1B.故∠AC1B=∠OC1B.同理可证∠AC2B=∠OC2B.九年级圆复习(1)一、选择题（每小题4分，共40分）1.过⊙O 内一点M 的最长弦长为10cm ，最短弦长为8cm ，那么OM 的长为 ( ) A ．3 cm B ．6 cm C. 9 cm D ． √41 cm2.如图,△ABC 内接于⊙O ，若∠A=40°，则∠OBC 的度数为（）A ．20°B ．40°C ．50°D ．70°3.一条弦分圆为1∶5两部分，则这条弦所对的圆周角的度数为（）A ．300B ．1500C ．300或1500D ．不能确定 4.⊙O 的半径为R ，圆心到点A 的距离为d ，且R 、d 分别是方程 x 2－6x ＋8＝0的两根，则点A 与⊙O 的位置关系是（） A ．点A 在⊙O 内部 B ．点A 在⊙O 上 C ．点A 在⊙O 外部 D ．点A 不在⊙O 上5.已知:P (x ，y )是以坐标原点为圆心，5为半径的圆周上的点，若x 、y 都是整数，猜想这样的P 点一共有（） A.4个 B.8个 C.12个 D.16个6.两枚大小相同的硬币，一枚固定不动，另一枚绕其边缘滚动(无滑动)，当运动硬币滚动到原来位置(第一次重合)时，运动硬币自转了______圈.A.1B.2C.3D.47.若⊙O 1、⊙O 2的半径分别为1和3，⊙O 1和⊙O 2外切，则平面上的半径为4，且与⊙O 1、⊙O 2都相切的圆有 ( ) A.2个 B.3个 C.4个 D.5个8.已知△ABC 中，∠C =90°，AB =5，周长等于12，则它的内切圆的半径为 ( )A.1B.2C.2.5D.3.59.如图12，每张方格纸上都画有一个圆，只用不带刻度的直尺就能确定圆心位置的是（）A B DC10.如图9，点P 是半径为5的⊙O 内一点，且OP =4，在过P 点的所有⊙O 的弦中，你认为弦长为整数的弦的条数为（）A.6条B.5条C.4条D.2条二、填空题(每小题3分,共30分)11.⊙O 的圆心到直线l 的距离为d ，⊙O 的半径为r ，当d 、r 是关于x 的方程x 2－4x +m =0的两根，且直线l 与⊙O 相切时，则m 的值为_____.12.如图5，已知PA 切⊙O 于点A ，PO 交⊙O 于点B ，若PA ＝6，BP ＝4，则⊙O的半径为 .13.已知⊙O 的半径为2，点P 为⊙O 外一点，OP 长为3，那么以P 为圆心且与⊙O 相切的圆的半径为 . 14.在半径为1的⊙O 中，弦AB 、AC 分别是2、3，则∠BAC 的度数为____________.B15.若相交两圆的半径分别为5和4,公共弦长为6,则圆心距为_____________________. 16.两圆相切，圆心距为9 cm ，已知其中一圆半径为5 cm ，另一圆半径为____________.17.如图，这是一个滚珠轴承的平面示意图，若该滚珠轴承的内、外圆周的半径分别为2 和6，则在两圆周之间所放滚珠最大半径为_____，这样的滚珠最多能放______颗.18.⊙O 1和⊙O 2内切，它们的半径分别为3和1，过O 1作⊙O 2的切线，切点为A ，则O 1A 的长是_______________.19.如图，点A 、B 、C 在⊙O 上，AO ∥BC ，∠OAC=20°，则∠AOB 的度数是______________.20.已知，如图：AB 为⊙O 的直径，AB ＝AC ，BC 交⊙O 于点D ，AC 交⊙O 于点E ，∠BAC＝450。

给出以下五个结论：①∠EBC＝22.50，；②BD＝DC ；③AE＝2EC ；④劣弧⋂AE 是劣弧⋂DE 的2倍；⑤AE ＝BC 。

其中正确结论的序号是 . 三、解答题(每小题10分,共80分)21．如图，AB 是⊙O 的直径，BC 是弦，OD ⊥BC 于E ，交弧BC于D 。

（1）请写出四个不同类型的正确结论；（2）若BC=38，∠CBD=30°，求⊙O 的半径.22. 已知：△ABC 内接于⊙O ，过点A 作直线EF.（1）如图1，AB 为直径，要使EF 为⊙O 的切线，还需添加的条件是（只需写出三种情况）：① ；② ；③ .（2）如图2，AB 是非直径的弦，∠CAE=∠B ，求证：EF 是⊙O 的切线.23.如图，在平面直角坐标系中，⊙C 与y 轴相切，且C 点坐标为（1，0），直线l 过点A （—1，0），与⊙C 相切于点D ，求直线l 的解析式.图1 图2ACDB OE∙EDCBAO 20 题图第19题图第18题图第17题图24.如图所示,有一座拱桥是圆弧形,它的跨度为60米,拱高18米, 当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PN=4米时是否要采取紧急措施?25.如图,已知在Rt △ABC 中，∠B=90°，AC=13,AB=5,O 是AB 上的点,以O 为圆心,OB 为半径作⊙O.(1)当OB=2.5米时，⊙O 交AC 于D 点，求CD 的长.(2)当OB=2.4米时,AC 与⊙O 的位置关系如何? 试说明你的理由.26.已知:如图,AB 是⊙O 的直径,BE 是⊙O 的切线,切点为B,点C 为射线BE 上一动点.(点C 与点B 不重合),且弦AD 平行于OC.(1)求证:CD 是⊙O 的切线. (2)设⊙O 的半径为r,试问:当动点C 在射线BE 上运动到什么位置时,有AD=2r?请回答并证明你的结论.27.如图，公路MN 和公路PQ 在点P 处交汇，且∠QPN=30°，点A 处有一所中学，AP=160米，假设拖拉机行驶时，周围100米以内会受到噪声的影响，那么拖拉机在公路MN 上沿PN 方向行驶时，学校是否会受到噪声影响？请说明理由；如果受到影响，已知拖拉机的速度为18千米/时，那么学校受影响的时间为多少？BC BC E AMN P Q28.如图,在矩形ABCD中,AB=3,BC=4,P是边AD上一点(除端点A),过点A、B、P作⊙O.(1)指出圆心O的位置.(2)当AP=3时,判断CD与⊙O的位置关系.(3)当CD与⊙O相切时,求BC被⊙O截得的弦长.C第24章二单元和圆有关的位置关系二、经典例题举例[例1]如图所示，AB是⊙O的直径，C为⊙O上的一点，AD⊥CD，AC平分∠BAD，请问CD与⊙O相切吗？试说明理由。

[例2] 如图所示，在△ABC中，AB=AC=10，BC=12，试求△ABC的内切圆的半径。

[例3] 10、小明家的锅盖坏了，为了配一个锅盖，需要测量锅的直径（锅沿所形成的圆的直径），而小明家只有一把长20cm的直尺，根本不够长，怎么办呢？小明想了想，采取了以下办法：如图所示，首先把锅平放在墙根，锅沿刚好靠到两墙，用直尺紧贴墙面量得MA的长，即可求出直径，请你说出他这样做的道理。

三、A组练习（一）选择题1.在⊙O中，半径为3cm，圆心到一点M的距离为4cm，则点M（）A . 在⊙O上 B. 在⊙O外C .在⊙O内 D. 可能在⊙O内也可能在⊙O外2.已知AP是⊙O的切线，切点为A，AP=3，∠APO=30°，那么OP长为（）A.2/3B.23C. 63 D .233.半径为6cm和4cm的两圆相切，则它们的圆心距为（）A.2cmB. 5cm C .2cm或5cm D.2cm或10cm4直角三角形边长分别为3cm和4cm，则其外接圆的半径为（)A. 5cmB. 1cm C .2.4cm D. 7cm5.三角形的外心具有的性质是（)A .到三边的距离相等 B. 到三个顶点的距离相等C. 外心在三角形外D. 外心在三角形内6.已知⊙O的半径为3cm直线l上有点B到圆心O的距离等于3cm，则直线l与⊙O的位置关系是（）A .相离 B.相切 C.相交 D.相交或相切(二)填空题：7. 半径为15、18的两圆相切，则这两个圆的圆心距为8. ⊙O的半径为3，OP长为2，则P在⊙O的9. ⊙O的半径为5，圆心O到直线L上，且OP=5，则直线L与⊙O的位置关系为10.如图所示，以O为圆心的两个同心圆中，大圆的弦AB是小圆的切线，若大圆半径为10cm，小圆半径为6cm，则弦AB长为cm11.两圆外切，圆心距为16cm，且两圆半径之比为5:3,那么较小圆的半径是12.⊙O切△ABC三边AB、BC、AC于点D、E、F，∠B=45°，∠C=60°，则∠DEF=13.如图所示，两圆轮叠靠在墙边，已知两圆轮半径分别为4和1，则它们与墙的切点A、B之间的距离为（三）解答题14．如图所示，直线AB经过⊙O上的一点C，并且OA=OB，CA=CB，证明：AB是⊙O的切线。