2021年中考数学压轴题冲刺提升专题正确分析函数图象(原卷版)

合集下载

函数综合-2021届中考数学压轴大题专项训练(原卷版)

专题13 函数综合 2021届中考数学压轴大题专项训练（原卷版） 1．如图，在平面直角坐标系中，点(6,0)A 、(0,12)B 分别在x 轴、y 轴上，点C 是直线2y x =与直线AB的交点，点D 在线段OC 上，OD =（1）求直线AB 的解析式及点C 的坐标；（2）求点D 的坐标及直线AD 的解析式．2．如图，反比例函数y 1＝k x与一次函数y 2＝mx+n 相交于A （﹣1，2），B （4，a ）两点，AE⊥y 轴于点E ，则：（1）求反比例函数与一次函数的解析式；（2）若y 1≤y 2则直接写出x 的取值范围；（3）若M 为反比例函数上第四象限内的一个动点，若满足S ⊥ABM ＝S ⊥AOB ，则求点M 的坐标．3．小哲的姑妈经营一家花店，随着越来越多的人喜爱“多肉植物”，姑妈也打算销售“多肉植物”，小哲帮助姑妈针对某种“多肉植物”做了市场调查后，绘制了以下两张图：（1）如果在3月份出售这种植物，单株获利__________元；（2）单株售价1y 与月份x 之间的关系式为___________；单株成本2y 与月份x 之间的关系式为__________．（3）请你运用所学知识，帮助小哲的姑妈求出在哪个月销售这种“多肉植物”，单株获利最大（提示：单株获利=单株售价-单株成本）．4．如图，直线y mx n =+与双曲线k y x=相交于()1,2,(2,)A B b -两点，与x 轴交于点E ，与y 轴相交于点C ．（1）求m n ，的值；（2）若点D 与点C 关于x 轴对称，求ABD ∆的面积；（3）在坐标轴上是否存在异于D 点的点,P 使得PAB DAB S S ∆∆=?若存在，直接写出Р点坐标；若不存在，说明理由．5．如图，直角坐标系xOy 中，一次函数152y x =-+的图像1l 分别与x ，y 轴交于A ，B 两点，正比例函数的图像2l 与1l 交于点C (,4)m ．（1）求m 的值及2l 的解析式；（2）求⊥AOC 的面积；。

2021年中考数学压轴题提升训练图形规律探索题含解析

图形规律探索题【例1】如图,在平面直角坐标系中,等腰直角三角形OA 1A 2的直角边OA 1在y 轴的正半轴上,且OA 1=A 1A 2=1,以OA 2为直角边作第二个等腰直角三角形OA 2A 3,以OA 3为直角边作第三个等腰直角三角形OA 3A 4,…,依此规律,得到等腰直角三角形OA 2017A 2018,则点A 2017的坐标为【答案】（0,2）.【解析】解：由题意知：A 1(0,1),A 2(1,1),OA 2=A 2A 3,OA 3=2,∴A 3(2,0),同理,A 4(2,－2),A 5(0,－4),A 6(－4,－4),A 7(－8,0),A 8(－8,8),A 9(0,16)……每隔8个点恰好处于同一坐标系或象限内,2017÷8=252……1,即点A 2017在y 轴正半轴上,横坐标为0,各点纵坐标的绝对值为：20,20,21,21,22,22,23,23,……2017÷2=1008……1,可得点A 2017的纵坐标为：21008, 故答案为（0,21008）.【变式1-1】如图,在一个单位为 1 的方格纸上,△A 1A 2A 3,△A 3A 4A 5,△A 5A 6A 7,…,是斜边在 x 轴上、斜边长分别为 2,4,6,…的等腰直角三角形．若△A 1A 2A 3的顶点坐标分别为A 1(2,0),A 2(1,-1),A 3(0,0),则依图中所示规律,A 2019的横坐标为（）A ．-1008B ．2C ．1D ．1011【答案】A.【解析】解：观察图形可知,奇数点在x轴上,偶数点在象限内,所以A2019在x轴上,A1,A5,A9,A13……,A4n－3在x正半轴,4n－3=2019,n=505.5,所以A2019不在x正半轴上；A3（0,0）,A7（－2,0）,A11（－4,0）,A15（－8,0）……,3=4×0+3,7=4×1+3,11=4×2+3,15=4×3+3,……,2019=4×504+3,∴－2×504=－1008,即A2019的坐标为（－1008,0）,故答案为：A.【变式1-2】如图,在平面直角坐标系中,将正方形O ABC绕点O逆时针旋转45°后得到正方形OA1B1C1,称为一次旋转,依此方式,……,绕点O连续旋转 2 019 次得到正方形O A2 019B2 019C2 019,如果点A的坐标为(1,0),那么点B2 019 的坐标为.【答案】,0）.【解析】由旋转及正方形性质可得：B(1,1),B1(0, ),B2(－1, 1),B3(－,0),B4(－1, －1),B5(0, －),B6(1, －1),B7(, 0),B8(1, 1),……∴360÷45=8,2019÷8=252……3,∴点B2019落在x轴负半轴上,即B2019(,0),故答案为：,0）.【例2】如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A（53,0）,B（0,4）,则点B2016的横坐标为（）A．5 B．12 C．10070 D．10080 【答案】D．【解析】解：由图象可知点B2016在第一象限,∵OA=53,OB=4,∠AOB=90°,在Rt△BOA中,由勾股定理得：AB=133,可得：B2（10,4）,B4（20,4）,B6（30,4）,…∴点B2016横坐标为10080．故答案为：D．【变式2-1】我们将如图所示的两种排列形式的点的个数分别称作“三角形数”（如1,3,6,10…）和“正方形数”（如1,4,9,16…）,在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n 的值为（）A．33 B．301 C．386 D．571 【答案】C．【解析】解：由图形知：第n个三角形数为1+2+3+…+n＝()12n n+,第n个正方形数为n2,当n＝19时,()12n n+＝190＜200,当n＝20时,()12n n+＝210＞200,所以最大的三角形数：m＝190；当n＝14时,n2＝196＜200,当n＝15时,n2＝225＞200,所以最大的正方形数：n＝196,则m+n＝386,所以答案为：C．1.如图,边长为1的菱形ABCD中,∠DAB=60°．连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°；连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°；…,按此规律所作的第n个菱形的边长为．【答案】1n -．【解析】解：∵四边形ABCD 是菱形,∠DAB =60°,∴AB =BC =1,∠ACB =∠CAB =30°,∴AC ,同理可得：AC 1=2,AC 213,……第n 个菱形的边长为：1n -,故答案为：1n -．2.如图,在平面直角坐标系中,∠AOB =30°,点A 的坐标为（2,0）,过点A 作AA 1⊥OB ,垂足为点A 1,过A 1作A 1A 2⊥x 轴,垂足为点A 2；再过点A 2作A 2A 3⊥OB ,垂足为点A 3；再过点A 3作A 3A 4⊥x 轴,垂足为点A 4…；这样一直作下去,则A 2017的横坐标为（）A ．32 ）2015B ．32 ）2016C ．32 ）2017D ．32）2018 【答案】B ．【解析】解：∵∠AOB =30°,点A 坐标为（2,0）,∴OA =2,∴OA 1OA OA 2OA 1=2×2⎝⎭,OA 3OA 2=2×3⎝⎭…,∴OA n =）n OA =2）n ．∴OA 2018）2018=32）2016故答案为：B．3.如图,函数()()()4022824x x xyx x--≤<⎧=⎨-+≤<⎩的图象记为C1,它与x轴交于点O和点A1,将C1绕点A1选择180°得C2,交x轴于点A2……,如此进行下去,若点P(103,m)在图象上,则m的值是（）A. -2B. 2C. -3D. 4【答案】A．【解析】解：由图可知：横坐标每间隔8个单位,函数值相同,即函数图象重复周期为8,103÷8=12……5,当x=5时,y=－2,即m=－2,故答案为：A.4.如图,弹性小球从点P(0,1)出发,沿所示方向运动,每当小球碰到正方形DABC 的边时反弹,反弹时反射角等于入射角,当小球第 1 次碰到正方形的边时的点为P1(-2,0),第 2 次碰到正方形的边时的点为P2,……,第n 次碰到正方形的边时的点为Pn,则点P2 019的坐标是（）A．(0,1) B．(-4,1) C．(-2,0) D．(0,3)【答案】D．【解析】解：根据图象可得：P1(-2,0),P2(-4,1),P3(0,3),P4(-2,4),P5(-4,0),P6(0,1),P7（－2,0）……2019÷6=336……3,即P2019（0,3）,故答案为：D.5.如图,在坐标系中放置一菱形 OABC ,已知∠ABC =60°,点 B 在 y 轴上,OA =1,先将菱形 OABC 沿 x 轴的正方向无滑动翻转,每次翻转 60°,连续翻转2019次,点 B 的落点依次为 B 1,B 2,B 3,…,则 B 2 019 的坐标为（）A . (1010,0)B .(1310.5, 2)C . (1345, 2)D . (1346,0)【答案】D .【解析】解：连接AC ,如图所示．∵四边形OABC 是菱形,∴OA =AB =BC =OC ．∵∠ABC =60°,∴△ABC 是等边三角形．∴AC =AB ．∴AC =OA ．∵OA =1,∴AC =1．由图可知：每翻转6次,图形向右平移4．∵2019=336×6+3,∴点B 3向右平移1344（即336×4）到点B 2019．∵B 3的坐标为（2,0）,∴B 2019的坐标为（1346,0）,故答案为：D ．6.如图,在直角坐标系中,已知点A （﹣3,0）,B （0,4）,对△OAB 连续作旋转变换,依次得到△1,△2,△3,△4,…,则△2019的直角顶点的坐标为（）A．（8076,0）B．（8064,0）C．（8076,125）D．（8064,125）【答案】A．【解析】解：∵点A（﹣3,0）、B（0,4）,由勾股定理得：AB＝5,由图可知,三个三角形为一个循环,经历一次循环前进的水平距离为：12,2019÷3＝673,直角顶点在x轴上,673×12＝8076,∴△2019的直角顶点的坐标为（8076,0）．故答案为：A．7.如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点（1,0）作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为．【答案】（21008,21009）．【解析】解：由图可知：A1（1,2）,A2（﹣2,2）,A3（﹣2,﹣4）,A4（4,﹣4）,A5（4,8）,…,∵2017=504×4+1,∴点A2017在第一象限,∵2017=1008×2+1,∴A2n+1（（﹣2）n,2（﹣2）n）（n为自然数）．∴A2017的坐标为（（﹣2）1008,2（﹣2）1008）=（21008,21009）．故答案为：（21008,21009）．8.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为（1,0）,那么点B2018的坐标为（）A．（1,1）B．（）C．（）D．（﹣1,1）【答案】D．【解析】解：∵四边形OABC是正方形,OA＝1,∴B（1,1）,连接OB,在Rt△OAB中,由勾股定理得：OB,由旋转性质得：OB＝OB1＝OB2＝OB3,∴B1（,B2（﹣1,1）,B3,0）,…,360÷45=8,每8次一循环,2018÷8＝252……2,∴点B2018的坐标为（﹣1,1）.故答案为：D．9.将直角三角形纸板OAB按如图所示方式放置在平面直角坐标系中,OB在x轴上,OB＝4,OA＝．将三角形纸板绕原点O逆时针旋转,每秒旋转60°,则第2019秒时,点A的对应点A′的坐标为（）A．（﹣3,﹣3）B．（3,﹣3）C．（﹣3,3）D．（0,2 3）【答案】A．【解析】解：360÷60=6,即每6秒一循环,2019÷6=336……3,即2019秒时, 点A与其对应点A′关于原点O对称,∵OA＝4,∠AOB＝30°,可得：A(3, 3),∴第2019秒时,点A的对应点A′的坐标为(－3, －3),故答案为：A.10.正方形ABCD的位置在坐标中如图所示,点A、D的坐标反别为（1,0）、（0,2）,延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为【答案】4032352⎛⎫⎪⎝⎭．【解析】解：∵四边形ABCD是正方形,∴AD=AB,∠DAB=∠ABC=∠ABA1=90°=∠DOA, ∴∠ADO+∠DAO=90°,∠DAO+∠BAA1=90°, ∴∠ADO=∠BAA1,∵∠DOA=∠ABA1,∴△DOA∽△ABA1,∴11 2OA BAOD AB==,由勾股定理得：AB=AD=5,∴BA1,∴第2个正方形A1B1C1C的边长A1C=A1B+BC,面积=2⎝⎭,同理,第3个正方形的面积为：232⎛⎝⎭,第4个正方形的面积为：23322⎛⨯⎝⎭,……∴第2017个正方形的面积为：4032352⎛⎫⎪⎝⎭.即答案为：4032352⎛⎫⎪⎝⎭.11.如图所示,一动点从半径为 2 的⊙O 上的A0 点出发,沿着射线A0O 方向运动到⊙O 上的点A1 处,再向左沿着与射线A1O 夹角为60°的方向运动到⊙O 上的点A2 处；接着又从A2 点出发,沿着射线A2O 方向运动到⊙O 上的点A3 处,再向左沿着与射线A3O 夹角为60°的方向运动到⊙O 上的点A4 处；……按此规律运动到点A2 017 处,则点A2 017 与点A0 间的距离是【答案】4.【解析】解：由图分析可知,A6点与A0点重合,2017÷6=336……1,即点A2 017 与A1重合,∵⊙O的半径为 2 ,∴点A2 017 与点A0 间的距离是4.12.如图,由一些点组成形如正多边形的图案,按照这样的规律摆下去,则第n（n＞0）个图案需要点的个数是．【答案】n 2+2n .【解析】解：由图知,第1个图形点数为3+0×3,第2个图形点数为4+1×4；第3个图形点数为5+2×5；第4个图形点数为6+3×6……第n 个图形点数为：（n +2）+（n －1）（n +2）=n 2+2n ,即答案为：n 2+2n .13..如图所示的坐标系中放置一菱形OABC ,已知∠ABC =60°,点B 在y 轴上,OA =1,先将菱形OABC 沿x 轴的正方形无滑动翻转,每次翻转60°,连续翻转2017次,点B 的落点分别是B 1,B 2,B 3,……,则B 2017的坐标为【答案】（.【解析】解：由题意知：OB 即B∴B 1,=32,即B 1(32),由图可知,每翻折6次,图形向右平移4个单位,2017=336×6+1,求得：B 2017（336×4+ 32,即B 2017（）,故答案为：（.14.如图,在平面直角坐标系中,点A 1,A 2,A 3,……和点B 1,B 2,B 3,……分别在直线15y x b =+和x 轴上,△OA 1B 1,△B 1A 2B 2,△B 2A 3B 3……都是等腰直角三角形,若点A 1(1,1),则点A 2019的纵坐标是【答案】201832⎛⎫ ⎪⎝⎭.【解析】解：如图,分别过A 1,A 2,A 3作x 轴的垂线,∵点A (1,1)在直线15y x b =+上, ∴b =45, 由△OA 1B 1是等腰直角三角形,得：OB 1=2,设A 2(x ,y ),则B 1C 2=x －2,y = x －2,∴x －2=1455x +,解得：x =72,y =32,即A 2的纵坐标为：32；同理可得：A 3的纵坐标为：29342⎛⎫= ⎪⎝⎭, 即A n 的纵坐标是A n －1纵坐标的32倍, 即A 2019的纵坐标为：201832⎛⎫ ⎪⎝⎭.15.在平面直角坐标系中,正方形 ABCD 的位置如图所示,点 A 的坐标为(1,0),点 D 的坐标为(0,2),延长CB 交x 轴于点A 1,作正方形 A 1CC 1B 1；延长 C 1B 1 交 x 轴于点 A 2,作正方形 A 2C 1C 2B 2；…,按照这样的规律作正方形,则点B2 019的纵坐标为．【答案】201932⎛⎫⎪⎝⎭.【解析】解：过B作BH⊥x轴于H,由一线三直角模型,可知△ADO≌△BAH,即BH=OA=1,即B点纵坐标为1,同理得：B1点纵坐标为32,B2点纵坐标为232⎛⎫⎪⎝⎭,B3点纵坐标为332⎛⎫⎪⎝⎭,……B2019点纵坐标为201932⎛⎫⎪⎝⎭,即答案为：2019 32⎛⎫⎪⎝⎭.。

2021年中考数学压轴题提升训练正确分析函数图象含解析

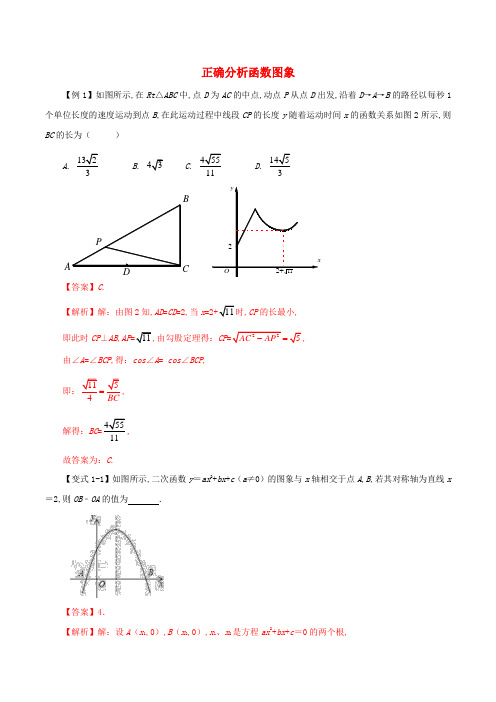
正确分析函数图象【例1】如图所示,在Rt △ABC 中,点D 为AC 的中点,动点P 从点D 出发,沿着D →A →B 的路径以每秒1个单位长度的速度运动到点B ,在此运动过程中线段CP 的长度y 随着运动时间x 的函数关系如图2所示,则BC 的长为（） AB. CD【答案】C .【解析】解：由图2知,AD =CD =2,当x,CP 的长最小, 即此时CP ⊥AB ,AP由勾股定理得：CP=由∠A =∠BCP ,得：cos ∠A = cos ∠BCP ,即：4BC=, 解得：BC故答案为：C .【变式1-1】如图所示,二次函数y ＝ax 2+bx +c （a ≠0）的图象与x 轴相交于点A ,B ,若其对称轴为直线x ＝2,则OB ﹣OA 的值为．【答案】4．【解析】解：设A （x 1,0）,B （x 2,0）,x 1、x 2是方程ax 2+bx +c ＝0的两个根,BC∵抛物线的对称轴是：x ＝2, ∴﹣2ba＝2, ∴ba＝﹣4, 由图可知：x 1＜0,x 2＞0, ∴OB ﹣OA ＝x 2﹣（﹣x 1）＝x 2+x 1 ＝﹣ba＝4, 故答案为：4．【变式1-2】如图1,正方形ABCD 在直角坐标系中,其中AB 边在y 轴上,其余各边均与坐标轴平行,直线l ：y ＝x ﹣5沿y 轴的正方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD 的边所截得的线段长为m ,平移的时间为t （秒）,m 与t 的函数图象如图2所示,则图2中b 的值为（）图1 图2A ．B ．C ．D ．【答案】C .【解析】解：在y ＝x ﹣5中,当y ＝0时, x ＝5；当x ＝0,y ＝﹣5, ∴直线y ＝x ﹣5与坐标轴围成的三角形为等腰直角三角形, ∴直线l 与直线BD 平行,由图2可得,t ＝3时,直线l 经过点A , ∴AO ＝5﹣3×1＝2,即A （﹣2,0）,t ＝15时,直线l 经过点C ,∴当t ＝9时,直线l 经过B ,D 两点, ∴AD ＝6,∴BD ＝,即b ＝,故答案为：C．【例2】如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),下列结论：①b2＞4ac；②ax2+bx+c≥-6；③若点(-2,m),(-5,n)在抛物线上,则m＞n；④关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1,其中正确的是__________．【解析】解：由图象知,抛物线与x轴有2个公共点,∴b2－4ac＞0,即①正确；抛物线有最低点,当x=－3时,y有最小值－6,即ax2+bx+c≥-6,故②正确；抛物线的对称轴为x=－3,点(-2,m),(-5,n)在抛物线上,∴m<n,故③错误；由图象知,当x=－1时,y=－4,由对称性可知,当x=－5时,y=－4,故④正确；综上,答案为：①②④.【变式2-1】如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是（）A．乙前4秒行驶的路程为48米B．在0到8秒内甲的速度每秒增加4米/秒C．两车到第3秒时行驶的路程相同D．在4到8秒内甲的速度都大于乙的速度【答案】C.【解析】解：根据图象可得：乙前4秒匀速运动,速度为12米/秒,行驶的路程为12×4=48米,故A正确；0~8秒内甲的速度是一条过原点的直线,甲的速度每秒增加4米/秒,故B正确；甲的速度与时间的关系为：v=4t,t=3时,v=12,即在t=3时,甲乙速度相等,在0~3秒时甲的速度小于乙的速度,故两车行驶路程不相等,故C错误；在4至8秒内甲的速度图象一直在乙的上方,所以甲的速度都大于乙的速度,故D正确；故答案为：C．【变式2-2】如图,若二次函数y＝ax2+bx+c（a≠0）图象的对称轴为x＝1,与y轴交于点C,与x轴交于点A、点B（﹣1,0）,则①二次函数的最大值为a+b+c；②a﹣b+c＜0；③b2﹣4ac＜0；④当y＞0时,﹣1＜x ＜3．其中正确的个数是（）A．1 B．2 C．3 D．4【答案】B．【解析】解：①∵二次函数y＝ax2+bx+c图象的对称轴为x＝1,且开口向下,∴当x＝1时,y＝a+b+c,y取最大值,即二次函数的最大值为a+b+c,所以①正确；②当x＝﹣1时,a﹣b+c＝0,所以②错误；③图象与x轴有2个交点, b2﹣4ac＞0,所以③错误；④∵图象的对称轴为x＝1,与x轴交于点A、点B（﹣1,0）,∴A（3,0）,当y＞0时,﹣1＜x＜3,所以④正确．所以答案为：B．【例3】如图1,在矩形ABCD中,动点E从A出发,沿AB→BC方向运动,当点E到达点C时停止运动,过点E作FE⊥AE,交CD于F点,设点E运动路程为x,FC＝y,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是25,则矩形ABCD的面积是（）A ．235B ．5C ．6D ．254【答案】B .【解析】解：若点E 在BC 上时,如图∵∠EFC +∠AEB ＝90°,∠FEC +∠EFC ＝90°, ∴∠CFE ＝∠AEB , ∴△CFE ∽△BEA , ∴CF CEBE AB=, 当E 在BC 中点时,CF 有最大值,BE ＝CE ＝x ﹣52, 即2552CEBE=,∴BE ＝CE ＝1, ∴BC ＝2,AB ＝52, ∴矩形ABCD 的面积为2×52＝5；故答案为：B ．【变式3-1】如图1,则等边三角形ABC 中,点P 为BC 边上的任意一点,且∠APD ＝60°,PD 交AC 于点D ,设线段PB 的长度为x ,CD 的长度为y ,若y 与x 的函数关系的大致图象如图2,则等边三角形ABC 的面积为．【答案】．【解析】解：由题可得,∠APD＝60°,∠ABC＝∠C＝60°, ∴∠BAP＝∠CPD,∴△ABP∽△PCD,∴AB CP BP CD=,设AB＝a,则a a xx y-=,∴y＝2x axa-+=21124ax aa⎛⎫--+⎪⎝⎭,当x＝12a时,y取得最大值2,可得：a=8,即等边三角形的边长为8,∴S×82＝故答案为：．【变式3-2】如图1,四边形ABCD中,AB∥CD,∠ADC＝90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图2所示,当P运动到BC中点时,△APD的面积为（）图1 图2A．4 B．5 C．6 D．7【答案】B．【解析】解：根据题意得：四边形ABCD是梯形,AB+BC＝6,CD＝4,12AD×CD＝8,得：AD＝4,∵12AD×AB＝2,∴AB＝1,当P运动到BC中点时,△APD的高为12（AB+CD）＝52,∴△PAD的面积＝12×52×4＝5；所以答案为：B．1.一个寻宝游戏的寻宝通道如图1所示,通道由在同一平面内的AB,BC,CA,OA,OB,OC组成．为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器．设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为（）图1 图2A．A→O→B B．B→A→C C．B→O→C D．C→B→O【答案】C.【解析】解：A、从A点到O点y随x的增大而减小,从O到B是先减小后增发,观察图2,A不符合题意；B、从B到A点y随x的增大先减小再增大,在A点达到最大值,从A到C点y随x的增大先减小再增大,观察图2,B不符合题意；C、从B到O点y随x的增大先减小再增大,从O到C点y随x的增大先减小再增大,在B、C点距离最大,观察图2,C符合题意；D、从C到B点y随x的增大先减小后增大,在到达M点时y=0,与图象不符,D不符合题意；所以答案为：C．2.小明家、食堂,图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家,如图反映了这个过程中,小明离家的距离y（km）与时间x（min）之间的对应关系,根据图象,下列说法正确的是（）A．小明吃早餐用了25minB．食堂到图书馆的距离为0.6kmC．小明读报用了30minD．小明从图书馆回家的速度为0.8km/min【答案】C．【解析】解：由图象可得,小明吃早餐用25﹣8＝17min,故选项A错误；食堂到图书馆的距离为：0.8﹣0.6＝0.2km,故选项B错误；小明读报用了58﹣28＝30min,故选项C正确；小明从图书馆回家的速度为：0.8÷（68﹣58）＝0.08km/min,故选项D错误；所以答案为：C．3.已知二次函数y＝ax2+bx+c中,函数y与自变量x的部分对应值如表所示：x…﹣5 ﹣4 ﹣3 ﹣2 ﹣1 …y…﹣8 ﹣3 0 1 0 …当y＜﹣3时,x的取值范围是．【答案】x ＜﹣4或x ＞0．【解析】解：由表可知,二次函数的对称轴为直线x ＝﹣2,抛物线的开口向下, 由x =﹣4时,y =-3得：x ＝0时,y ＝﹣3, ∴y ＜﹣3时,x 的取值范围为x ＜﹣4或x ＞0．故答案为：x ＜﹣4或x ＞0．4.如图,抛物线y ＝ax 2+bx +c （a ≠0）与x 轴交于点A （1,0）,对称轴为直线x ＝﹣1,当y ＞0时,x 的取值范围是（）A ．﹣1＜x ＜1B ．﹣3＜x ＜﹣1C ．x ＜1D ．﹣3＜x ＜1【答案】D ．【解析】解：∵抛物线y ＝ax 2+bx +c 与x 轴交于点A （1,0）,对称轴为直线x ＝﹣1, ∴抛物线与x 轴的另一交点坐标是（﹣3,0）, ∴当y ＞0时,x 的取值范围是﹣3＜x ＜1．所以答案为：D ．5.在矩形ABCD 中,AD =2AB =4,E 是AD 的中点,一块足够大的三角板的直角顶点与点E 重合,将三角板绕点E 旋转,三角板的两直角边分别交AB ,BC （或它们的延长线）于点M ,N ,设∠AEM =α（0°＜α＜90°）,给出下列四个结论：①AM =CN ； ②∠AME =∠BNE ； ③BN ﹣AM =2； ④S △EMN =22cos．上述结论中正确的个数是（）A．1 B．2 C．3 D．4【答案】C．【解析】解：①过E作EF⊥BC于点F,∵矩形ABCD,AD=2AB,E是AD的中点,∴AB=AE=EF=FC,∠MAE=∠NFE=90°,∵∠AEM+∠DEN=90°,∠FEN+∠DEN=90°, ∴∠AEM=∠FEN,∴△AME≌△FNE,∴AM=FN,∴MB=CN．∵M不一定是AB的中点,∴AM不一定等于CN,故①错误,②由Rt△AME≌Rt△FNE,得∠AME=∠BNE, 故②正确,③由①知,AM=NF,∵AD=2AB=4,∴BC=4,AB=2∴BN﹣AM=BN﹣NF =BF=AE=2,故③正确,④由①知,△AME≌△FNE,∴EM=EN,可得△EMN 为等腰直角三角形,在Rt △AEM 中,EM = cos AE α, ∴S △EMN = 212cos AE α⎛⎫ ⎪⎝⎭=22cos α, 故④正确．故答案为：C ．6.已知二次函数y =ax 2+bx +c （a ≠0）的图象如图所示,并且关于x 的一元二次方程ax 2+bx +c ﹣m =0有两个不相等的实数根,下列结论：①b 2﹣4ac ＜0；②abc ＞0；③a ﹣b +c ＜0；④m ＞﹣2,其中,正确的个数有（）A ．1B ．2C ．3D ．4【答案】B ．【解析】解：如图所示：图象与x 轴有两个交点,则b 2﹣4ac ＞0,故①错误；∵图象开口向上,∴a ＞0,∵对称轴在y 轴右侧,∴a ,b 异号,b ＜0,∵图象与y 轴交于x 轴下方,∴c ＜0,∴abc ＞0,故②正确；当x =﹣1时,a ﹣b +c ＞0,故③错误；∵由图象知,y ≥﹣2,∴关于x 的一元二次方程ax 2+bx +c ﹣m =0有两个不相等的实数根,则m ＞﹣2,故④正确．故答案为：B ．7.阅读对话,解答问题：（1）分别用a、b表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用树状图法或列表法写出（a,b）的所有取值；（2）求在（a,b）中使关于x的一元二次方程x2﹣ax+2b=0有实数根的概率．【答案】见解析．【解析】解：（1）（a,b）对应的表格为：1 2 31 （1,1）（1,2）（1,3）2 （2,1）（2,2）（2,3）3 （3,1）（3,2）（3,3）4 （4,1）（4,2）（4,3）（2）由方程x2﹣ax+2b=0有实数根,得：△=a2﹣8b≥0．由（1）中表格知：使a2﹣8b≥0的（a,b）有：（3,1）,（4,1）,（4,2）三组,∴p（△≥0）=14．8.如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动（点D与点B、C不重合）,作BE⊥AD 于E,CF⊥AD于F,则BE+CF的值（）A．不变B．增大C．减小D．先变大再变小【答案】C．【解析】解：S△ABC=S△ABD+S△ACD=12×AD×BE+12×AD×CF=12×AD×(BE+ CF),∵S△ABC是定值,∴BE+ CF=2ABCSAD,由图知,AD的长逐渐变大,则BE+ CF的值逐渐减小,故答案为：C.9.如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论：①ED⊥BC；②∠A=∠EBA；③EB平分∠AED；④ED=12AB中,一定正确的是（）A．①②③B．①②④C．①③④D．②③④【答案】B.【解析】解：由作图知,P在线段BC的垂直平分线上,而D是BC中点, ∴PD是线段BC的垂直平分线,即①正确；∴EB=CE=AE,即E是AC的中点,即∠A=∠EBA,②正确；由上可知,DE是△ABC的中位线,∴ED=12AB,④正确；只有当∠A=60°时,∠BED=∠AEB=60°,∴③错误；综上所述,答案为：B.10.一般情况下,中学生完成数学家庭作业时,注意力指数随时间x（分钟）的变化规律如图所示（其中AB、BC为线段,CD为双曲线的一部分）．（1）分别求出线段AB和双曲线CD的函数关系式；（2）若学生的注意力指数不低于40为高效时间,根据图中信息,求出一般情况下,完成一份数学家庭作业的高效时间是多少分钟？【答案】见解析.【解析】解：（1）设直线AB的解析式为：y=kx+b,将（0,30）,（10,50）代入得：b=30,10k+b=50,解得：k=2,b=30,即直线AB的解析式为：y=2x+30（0≤x≤10）；设双曲线CD的解析式为：myx =,将点C(44,50)代入得：m=2200,即双曲线CD的解析式为：2200yx=（x≥44）；（2）在y=2x+30中,当y=40时,x=5,在2200yx=中,当y=40时,x=55,55－5=50,即一般情况下,完成一份数学家庭作业的高效时间是50分钟.11.如图,正方形ABCD的边长为a,点E在边AB上运动（不与点A,B重合）,∠DAM＝45°,点F在射线AM上,且AF BE,CF与AD相交于点G,连接EC,EF,EG,则下列结论：①∠ECF＝45°；②△AEG的周长为（）a；③BE2+DG2＝EG2；④△EAF的面积的最大值18a2．其中正确的结论是．（填写所有正确结论的序号）【答案】①④.【解析】解：在BC上截取BH＝BE,连接EH,∵BE＝BH,∠EBH＝90°,∴EH BE,∵AF BE,∴AF＝EH,∵∠DAM＝∠EHB＝45°,∠BAD＝90°,∴∠FAE＝∠EHC＝135°,∵BA＝BC,BE＝BH,∴AE＝HC,∴△FAE≌△EHC,∴EF＝EC,∠AEF＝∠ECH,∵∠ECH+∠CEB＝90°,∴∠AEF+∠CEB＝90°,∴∠FEC＝90°,∴∠ECF＝∠EFC＝45°,故①正确,延长AD到H,使得DH＝BE,则△CBE≌△CDH,∴∠ECB＝∠DCH,∴∠ECH＝∠BCD＝90°,∴∠ECG＝∠GCH＝45°,∵CG＝CG,CE＝CH,∴△GCE≌△GCH,∴EG＝GH,∵GH＝DG+DH,DH＝BE,∴EG＝BE+DG,故③错误,△AEG的周长＝AE+EG+AG＝AE+AH＝AD+DH+AE＝AE+EB+AD＝AB+AD＝2a,故②错误,设BE＝x,则AE＝a﹣x,AF,∴S△AEF＝12•（a﹣x）x＝﹣12（x﹣12a）2+18a2,∴x＝12a时,△AEF的面积的最大值为18a2．故④正确,即答案为：①④．12.如图1,E为矩形ABCD边AD上的一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B 沿BC运动到点C时停止,它们运动的速度都是2 cm/s．若P,Q同时开始运动,设运动时间为t（s）,△BPQ的面积为y（cm2）,已知y与t的函数关系图象如图2,则CDBE的值为（）A3B C D图1 图2 【答案】D .【解析】解：由图2知,8≤t ≤10时,△BPQ 的面积不变,则P 在线段DE 上运动,∴BE =8×2=16cm ,DE =2×2=4cm ,t =8时,BQ =16,此时y,∴=12×BQ ×CD ,即：=12×16×CD , 解得：CD, ∴CD BE=164 即答案为：D .13.在矩形ABCD 中,AB >CD ,对角线AC ,BD 相交于点O ,动点P 由点A 出发,沿AB →BC →CD 向点D 运动．设点P 的运动路程为x ,△AOP 的面积为y ,y 与x 的函数关系图象如图②所示,则AD 边的长为（）A . 3B . 4C . 5D .6【答案】B .【解析】解：当P 点在AB 上运动时,y 逐渐增大,当P 点到达B 点时,y 最大为3． ∴12AB •12＝3,即AB •BC ＝12．当P 点在BC 上运动时,y 逐渐减小,当P 点到达C 点时,y 为0,此时结合图象可知P 点运动路径长为7, ∴AB +BC ＝7．图1图2则BC＝7﹣AB,代入AB•BC＝12,得：AB2﹣7AB+12＝0,解得：AB＝4或3,∵AB＜AD,∴AB＝3,BC＝4．即AD=BC=4,故答案为：B.14.在正方形ABCD中,点P从点D出发,沿着D→A方向匀速运动,到达点A后停止运动,点Q从点D出发,沿着D—C—B—A的方向匀速运动,到达点A后停止运动. 已知点P的运动速度为4,图②表示P、Q两点同时出发x秒后,△APQ的面积为y与x的函数关系,则点Q的运动速度可能是（）A. 2B. 3C. 8D. 12图①图②【答案】12.【解析】解：由图②知函数图象有三段,设正方形的边长为1,则点Q在线段AB上时,点P仍在运动,设点Q的速度为v,∴2134v v ≤<,∴8<v≤12,故答案为：12.15.如图,在矩形ABCD中,动点P从点B出发,沿B-C-D-A方向运动到点A停止,运动速度为1单位每秒. 设点P的运动路程为x,△ABP的面积为y,若y与x的函数关系式如图2所示,则△ABC的面积为【答案】10.【解析】解：由题意知,AB=4×1=4,BC=(9-4)×1=5,∴S△ABC=12×4×5=10,即答案为：10.16.如图,在矩形ABCD中,动点P从点A出发,沿A→B→C运动,设PA=x点D到直线PA的距离为y且y 关于x的函数图象如图所示,则当△PCD和△PAB的面积相等时,y的值为____.【答案】125.【解析】解：由题意知,AB=3,AD=4, 当x=5时,△PCD和△PAB的面积相等,此时△APD的面积为：12×3×4=6,即12xy=6,得：y=125,故答案为：125.17.如图 1,四边形ABCD 中,AB∥CD,∠B=90°,AC=AD．动点P 从点B 出发,沿折线B-A-D-C 方向以1 单位/秒的速度匀速运动,在整个运动过程中,△BCP 的面积S 与运动时间t（秒）的函数图象如图 2 所示,则AD 等于图1 图2【解析】解：过A作AE⊥CD于E,则四边形ABCE 是矩形,E 是CD 中点,由题意知,AB =3,∴CD =6,由图2知,S 最大值为15, 即12·BC ·CD =15, ∴BC =5,由勾股定理得：AC 即AD18.二次函数y =ax 2+bx +c 的大致图象如图所示,顶点坐标为（-2,-9a ）,下列结论：①4a +2b +c >0；②5a -b +c =0；③若方程a (x +5)(x -1)=-1有两个根x 1,x 2,且x 1<x 2,则-5< x 1< x 2<1；④若方程|ax 2+bx +c |=1有四个根,则这四个根的和为-4,其中正确的结论有（） A . 1个 B .2个 C . 3个 D .4个【答案】B .【解析】解：由图象知,a >0,∵顶点坐标为（-2,-9a ）,∴22b a-=-,2494ac b a a -=-, ∴b =-4a ,c =-5a ,抛物线的解析式为：y =ax 2+4ax -5a ,∴4a +2b +c =7a >0,故①正确；5a -b +c =-4a <0,故②错误；0=ax 2+4ax -5a ,解得：x =1或x =-5,即抛物线与x 轴交于点（1,0）,（-5,0）,∵方程a (x +5)(x -1)=-1有两个根x 1,x 2,且x 1<x 2,∴-5< x 1< x 2<1,故③正确；∵方程|ax 2+bx +c |=1有四个根,∴这四个根的和为：2×（b a -）=-8,故④错误；即答案为：B.19.如图1,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设点P的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图2所示,当P运动到BC中点时,△PAD的面积为（）A．4 B．8 C．6 D．5图1 图2【答案】D.【解析】解：由图象知,AB+BC=6,AB+BC+CD=10,∴CD=4,当点P运动到点C时S最大,最大值为8,即12AD·CD=8,∴AD=4,当点P运动到B点时,S=2,即12AB·AD=2,∴AB=1,当P运动到BC中点时,S=12×12（AB+CD）×AD=5,故答案为：D.。

2021年中考数学重难点专项突破—分析判断函数图象试题课件(24张PPT)

(2020·遵义)新龟兔赛跑的故事：龟兔从同一地点同时出发后，兔子很快把乌龟远远甩在后头．骄傲自满的兔子觉得自己遥遥领先，就躺在路边呼呼大睡起来．当它一觉醒来，发现乌龟已经超过它，于是奋力直追，最后同时到达终点．用S1，S2分别表示乌龟和兔子赛跑的路程，t为赛跑时间，则下列图象中与故事情节相吻合的是 ( C )
(2020·淮南二模)如图，两个全等的等腰直角三角板(斜边长为2)如图放置，其中一块三角板45°角的顶点与另一块三角板ABC的直角顶点A重合．若三角板ABC固定，当另一个三角板绕点A旋转时，它的直角边和斜边所在的直线分别与边BC交于点E，F. 设BF＝x，CE＝y，则y关于x的函数图象大致是 ( )
一段笔直的公路AC长20千米，途中有一处休息点B，AB长15千米．甲、乙两名长跑爱好者同时从点A出发，甲以15千米/时的速度匀速跑至点B，原地休息半小时后，再以10千米/时的速度匀速跑至终点C；乙以12千米/时的速度匀速跑至终点C. 下列选项，能正确反映甲、乙两人出发后2小时内运动路程y(千米)与时间x(时)函数关系的图象是（ A ）
符合题意的只有A选项
解题技巧： ①找起点：结合题干中所给自变量及因变量的取值范围，在图象中找出相对应的点； ②找特殊点(交点或转折点)：说明图象在此点处将发生变化； ③判断图象趋势：判断出函数的增减性； ④看是否与坐标轴相交．
甲、乙两位同学同时从400 m环形跑道上的同一起跑线出发，同向而行，甲的速度为6 m/s，乙的速度为4 m/s，设经过x s后，跑道上两人的距离(较短部分)为y(单位：m)，则y与x(0≤x≤300)之间的函数关系的图象是( C )
已知函数y＝－(x－m)(x－n)(其中m＜n)的图象如图所示，则一次函数y＝mx＋n与反比例函数y＝的图象可能是（ B ）

热点专题8 二次函数压轴题(原卷版) 2021年中考数学冲刺

热点专题8 二次函数压轴题二次函数与几何图形相结合的综合性问题，是近年来全国各地中考的热点题型，也是大部分地区全卷的压轴题。

近6年一直作为河南中考数学压轴题第23题呈现，其题型、题序及分值都比较稳定，题目综合性强，难度大，占11分。

二次函数压轴题，常考查函数解析式、交点坐标、图形面积或周长、存在性问题、图形的平移、对称、旋转等，是数与形的相互结合，相互渗透。

河南省中考考试说明要求掌握数形结合，分类讨论等数学思想方法。

具有阅读理解能力、收集处理信息的能力和运用数学知识对问题的探究能力等。

考向1与线段长、角度有关的二次函数问题1.（河南省新乡市长垣市2020届九年级上学期期末调研测试数学试题）如图，直线y ＝﹣x+5与x轴交于点B，与y轴交于点D，抛物线y＝﹣x2+bx+c与直线y＝﹣x+5交于B，D两点，点C是抛物线的顶点．（1）求抛物线的解析式；（2）点M是直线BD上方抛物线上的一个动点，其横坐标为m，过点M作x轴的垂线，交直线BD于点P，当线段PM的长度最大时，求m的值及PM的最大值．（3）在抛物线上是否存在异于B、D的点Q，使△BDQ中BD边上的高为23，若存在求出点Q的坐标；若不存在请说明理由．2.（2019年河南省许昌市中考数学二模试卷）如图，抛物线y1＝ax2+bx+与x轴交于点A （﹣3，0），点B，点D是抛物线y1的顶点，过点D作x轴的垂线，垂足为点C（﹣1，0）．（1）求抛物线y1所对应的函数解析式；（2）如图1，点M在抛物线y1上，横坐标为m，连接MC，若∠MCB＝∠DAC，求m 的值；（3）如图2，将抛物线y1平移后得到顶点为B的抛物线y2．点P为抛物线y1上的一个动点，过点P作y轴的平行线，交抛物线y2于点Q，过点Q作x轴的平行线，交抛物线y2于点R．当以点P，Q，R为顶点的三角形与△ACD全等时，请直接写出点P的坐标．考向2 与周长、面积有关的二次函数问题1.（2019年河南省中原名校中考第三次大联考数学试卷）如图，直线y＝﹣x+5与x轴交于点B，与y轴交于点C，抛物线y＝﹣x2+bx+c与直线y＝﹣x+5交于B，C两点，已知点D 的坐标为（0，3）（1）求抛物线的解析式；（2）点M，N分别是直线BC和x轴上的动点，则当△DMN的周长最小时，求点M，N的坐标，并写出△DMN周长的最小值；（3）点P是抛物线上一动点，在（2）的条件下，是否存在这样的点P，使∠PBA＝∠ODN？若存在，请直接写出点P的坐标；若不存在，请说明理由．2.(2019年河南省实验外国语学校中考数学模拟试卷)如图，直线y＝-12x-3与x轴，y轴分别交于点A，C，经过点A，C的抛物线y＝ax2+bx﹣3与x轴的另一个交点为点B(2，0)，点D 是抛物线上一点，过点D作DE⊥x轴于点E，连接AD，D C．设点D的横坐标为m．(1)求抛物线的解析式；(2)当点D在第三象限，设△DAC的面积为S，求S与m的函数关系式，并求出S的最大值及此时点D的坐标；(3)连接BC，若∠EAD＝∠OBC，请直接写出此时点D的坐标．考向3 与特殊三角形有关的二次函数问题1.（2019年河南省实验中学中考三模数学试卷）.如图，矩形OABC 中，点O 为原点，点A 的坐标为（0，8），点C 的坐标为（6，0）．抛物线249y x bx c =-++经过A 、C 两点，与AB 边交于点D ．（1）求抛物线的函数表达式；（2）点P 为线段BC 上一个动点（不与点C 重合），点Q 为线段AC 上一个动点，AQ =CP ，连接PQ ，设CP =m ，△CPQ 的面积为S ．①求S 关于m 的函数表达式，并求出m 为何值时，S 取得最大值；②当S 最大时，在抛物线249y x bx c =-++的对称轴l 上若存在点F ，使△FDQ 为直角三角形，请直接写出所有符合条件的F 的坐标；若不存在，请说明理由．2.（新乡市名校联考2019-2020学年九年级上学期期末数学试题）如图，抛物线2y 2ax x c =++经过(1,0)A -，B 两点，且与y 轴交于点(0,3)C ，抛物线与直线1y x =--交于A，E两点．（1）求抛物线的解析式；∆是以AE为底边的等腰三角形？若存在，请直（2）坐标轴上是否存在一点Q，使得AQE接写出点Q的坐标；若不存在，说明理由．∆相似，（3）P点在x轴上且位于点B的左侧，若以P，B，C为顶点的三角形与ABE求点P的坐标．考向4 与特殊四边形有关的二次函数问题1.（河南省外国语中学2019届九年级中招适应性测试卷数学试题）如图，在平面直角坐标系xOy中，已知抛物线y=ax2-2x+c与直线y=kx+b都经过A（0，-3）、B（3，0）两点，该抛物线的顶点为C．（1）求此抛物线和直线AB 的解析式；（2）设直线AB 与该抛物线的对称轴交于点E ，在射线EB 上是否存在一点M ，过M 作x 轴的垂线交抛物线于点N ，使点M 、N 、C 、E 是平行四边形的四个顶点？若存在，求点M 的坐标；若不存在，请说明理由；（3）设点P 是直线AB 下方抛物线上的一动点，当△P AB 面积最大时，求点P 的坐标，并求△P AB 面积的最大值．2.（河南省洛阳市2019-2020学年九年级上学期期中数学试题）如图，抛物线2y x bx c=-++交x 轴于A ，B 两点，交y 轴于点C .直线122y x =-+经过点B ，C .（1）求抛物线的解析式；（2）点P 是直线BC 上方抛物线上一动点，设点P 的横坐标为m .①求PBC ∆面积最大值和此时m 的值；②Q 是直线BC 上一动点，是否存在点P ，使以A 、B 、P 、Q 为顶点的四边形是平行四边形，若存在，直接写出点P 的坐标.3.（河南省濮阳市县区2019-2020学年九年级上学期期末数学试题）如图，已知抛物线23)0(y a bx a =++≠经过点1,0A 和点()3,0B ，与y 轴交于点C .（1）求此抛物线的解析式；（2）若点P 是直线BC 下方的抛物线上一动点（不点B ，C 重合），过点P 作y 轴的平行线交直线BC 于点D ，设点P 的横坐标为m .①用含m 的代数式表示线段PD 的长；②连接PB ，PC ，求PBC ∆的面积最大时点P 的坐标；（3）设抛物线的对称轴与BC 交于点E ，点M 是抛物线的对称轴上一点，N 为y 轴上一点，是否存在这样的点M 和点N ，使得以点C 、E 、M 、N 为顶点的四边形是菱形？如果存在，请直接写出点M 的坐标；如果不存在，请说明理由.考向5 与三角形相似有关的二次函数问题1.（河南省新乡市辉县市2019-2020学年九年级上学期期末数学试题）已知抛物线23y ax bx =++与x 轴分别交于(3,0)A -，(1,0)B 两点，与y 轴交于点C ．（1）求抛物线的表达式及顶点D 的坐标；（2）点F 是线段AD 上一个动点．①如图1，设AF k AD =，当k 何值时，2CF AD =1. ②如图2，以A ，F ，O 为顶点的三角形是否与ABC ∆相似？若相似，求出点F 的坐标；若不相似，请说明理由．2.（2020年河南省中考数学一模试题）如图，抛物线2y ax bx c =++与x 轴交于点(1,0)A -，点(3,0)B ，与y 轴交于点C ，且过点(2,3)D -．点P 、Q 是抛物线2y ax bx c =++上的动点．(1)求抛物线的解析式；(2)当点P 在直线OD 下方时，求POD ∆面积的最大值．(3)直线OQ 与线段BC 相交于点E ，当OBE ∆与ABC ∆相似时，求点Q 的坐标．。

2021年九年级数学中考一轮复习专项突破训练：二次函数图象分析(附答案)

2021年九年级数学中考一轮复习专项突破训练：二次函数图象分析（附答案）1．如图为二次函数y＝ax2+bx+c（a≠0）的图象，则下列说法：①a＞0 ②2a+b＝0③a+b+c＞0 ④当﹣1＜x＜3时，y＞0其中正确的个数为（）A．1B．2C．3D．42．如图，二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），对称轴为直线x ＝1，与y轴的交点B在（0，2）和（0，3）之间（包括这两点），下列结论：①当x＞3时，y＜0；②3a+b＜0；③﹣1≤a≤﹣；④4ac﹣b2＞8a；其中正确的结论是（）A．①③④B．①②③C．①②④D．①②③④3．如图，二次函数y＝ax2+bx+c（a≠0）的图象经过点（1，2）且与x轴交点的横坐标分别为x1，x2，其中﹣1＜x1＜0，1＜x2＜2，下列结论：①4a+2b+c＜0，②2a+b＜0，③b2+8a ＞4ac，④a＜﹣1，其中结论正确的有（）A．1个B．2个C．3个D．4个4．如图，已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＞0；②b﹣a＞c；③4a+2b+c＞0；④3a＞﹣c；⑤a+b＞m（am+b）（m≠1的实数）．其中正确结论的有（）A．①②③B．②③⑤C．②③④D．③④⑤5．如图，抛物线y＝ax2+bx+c（a≠0）过点（﹣1，0）和点（0，﹣3），且顶点在第四象限，设P＝a+b+c，则P的取值范围是（）A．﹣3＜P＜﹣1B．﹣6＜P＜0C．﹣3＜P＜0D．﹣6＜P＜﹣3 6．如图是抛物线y＝ax2+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间．则下列结论：①a﹣b+c＞0；②3a+b＝0；③b2＝4a（c﹣n）；④一元二次方程ax2+bx+c＝n﹣1有两个不相等的实数根．其中正确结论的个数是（）A．1个B．2个C．3个D．4个7．如图是抛物线y1＝ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标A（1，3），与x 轴的一个交点B（4，0），直线y2＝mx+n（m≠0）与抛物线交于A，B两点，下列结论：①2a+b＝0；②abc＞0；③方程ax2+bx+c＝3有两个相等的实数根；④抛物线与x轴的另一个交点是（﹣1，0）；⑤当1＜x＜4时，有y2＜y1，其中正确的是（）A．①②③B．①③④C．①③⑤D．②④⑤8．如图，是二次函数y＝ax2+bx+c（a≠0）的图象的一部分，给出下列命题：①a+b+c＝0；②b＞2a；③ax2+bx+c＝0的两根分别为﹣3和1；④a﹣2b+c＞0．其中正确的命题是（）A．①②B．②③C．①③D．①②③④9．二次函数y＝ax2+bx+c的图象如图所示，对称轴是直线x＝1．下列结论：①abc＜0；②3a+c ＞0；③（a+c）2﹣b2＜0；④a+b≤m（am+b）（m为实数）．其中结论正确的个数为（）A．1个B．2个C．3个D．4个10．已知二次函数y＝ax2+bx+c（a≠0）的图象如图，则下列结论中正确的是（）A．abc＞0B．b2﹣4ac＜0C．9a+3b+c＞0D．c+8a＜011．已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，现给出下列结论：①abc＞0；②9a+3b+c＝0；③b2﹣4ac＜8a；④5a+b+c＞0．其中正确结论的个数是（）A．1B．2C．3D．412．二次函数y＝ax2+bx+c的图象如图所示，对称轴是直线x＝﹣1，有以下结论：①abc＞0；②4ac＜b2；③2a+b＝0；④a﹣b+c＞2．其中正确的结论的个数是（）A．1B．2C．3D．413．如图，抛物线y＝ax2+bx+c的对称轴是x＝﹣1．且过点（，0），有下列结论：①abc ＞0；②a﹣2b+4c＝0；③25a﹣10b+4c＝0；④3b+2c＞0；⑤a﹣b≥m（am﹣b）；其中所有正确的结论是．（填写正确结论的序号）14．如图，二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于A，B两点，与y轴交于点C，且OA＝OC，则下列结论：①abc＜0；②；③ac﹣b+1＝0；④OA•OB＝﹣．其中正确结论的序号是．15．已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列4个结论：①abc＞0；②b ＜a+c；③4a+2b+c＞0；④b2﹣4ac＞0；其中正确的结论有．（填序号）16．如图，已知二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和（0，﹣1）之间（不包括这两点），对称轴为直线x＝1．下列结论：①abc＞0；②4a+2b+c＞0；③4ac﹣b2＜﹣4a；④＜a＜；⑤b＞c．其中正确结论有（填写所有正确结论的序号）．17．已知二次函数y＝x2﹣4x+k的图象的顶点在x轴下方，则实数k的取值范围是．18．抛物线y＝ax2+bx+c（a，b，c为常数）的顶点为P，且抛物线经过点A（﹣1，0），B （m，0），C（﹣2，n）（1＜m＜3，n＜0），下列结论：①abc＞0，②3a+c＜0，③a（m﹣1）+2b＞0，④a＝﹣1时，存在点P使△P AB为直角三角形．其中正确结论的序号为．19．二次函数y＝x2﹣2mx+1，在x≤1时y随x增大而减小，则m的取值范围是．20．如图，抛物线y＝ax2+c的顶点为B，A、C两点在该抛物线上，O为坐标原点，四边形ABCO为正方形，则ac＝．21．二次函数y＝ax2+bx+c（a≠0）图象如图，下列结论：①abc＞0；②2a+b＝0；③当m ≠1时，a+b＞am2+bm；④a﹣b+c＞0；⑤若ax12+bx1＝ax22+bx2，且x1≠x2，x1+x2＝2．其中正确的有．22．如图是二次函数y＝ax2+bx+c图象的一部分，其对称轴为x＝﹣1，且过点（﹣3，0）．下列说法：①abc＜0；②2a﹣b＝0；③4a+2b+c＜0；④若（﹣5，y1），（，y2）是抛物线上两点，则y1＞y2．其中说法正确的是．23．已知二次函数y＝ax2+bx+c的图象如图，其对称轴x＝﹣1，给出下列结果：①b2＞4ac；②abc＞0；③2a+b＝0；④a﹣b+c＜0；⑤3a+c＞0．其中正确结论的序号是．24．已知二次函数y＝ax2+bx+c的图象如图所示，则下列四个代数式：①ac；②a+b+c；③2a+b；④b2﹣4ac中；其值大于0的为．25．已知二次函数y＝ax2+bx+c的图象如图所示，顶点为（﹣1，0），有下列结论：①abc ＜0；②b2﹣4ac＝0；③a＞2；④4a﹣2b+c＞0．其中，正确结论有．26．二次函数y＝ax2+bx+c的图象过点（3，1），（6，﹣5），若当3＜x＜6时，y随着x的增大而减小，则实数a的取值范围是．27．已知当﹣1＜x＜0时，二次函数y＝x2﹣3mx+2的值恒大于1，则m的取值范围为．28．若函数y＝x2﹣2x+b的图象与坐标轴有三个交点，则b的取值范围是．29．如图，已知二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于点A（﹣1，0），与y轴的交点B在（0，﹣2）和C（0，﹣1）之间（不包括这两点），对称轴为直线x＝1，下列结论：①abc＞0；②4a+2b+c＞0；③4ac﹣b2＜8a；④；⑤b＜c．其中含所有正确结论的选项是．30．已知二次函数y＝（x﹣2a）2+（a﹣1）（a为常数），当a取不同的值时，其图象构成一个“抛物线系”，如图分别是当a＝﹣1，a＝0，a＝l，a＝2时二次函数的图象．它们的顶点在一条直线上，这条直线的解析式是．31．二次函数y＝ax2+bx+c的图象如图所示，对称轴为x＝1，给出下列结论：①abc＜0；②b2＞4ac；③4a+2b+c＜0；④2a+b＝0．其中正确的结论有．32．在平面直角坐标系xOy中，已知抛物线y＝x2﹣2（k﹣1）x+k2﹣k（k为常数）．（1）若抛物线经过点（1，k2），求k的值；（2）若抛物线经过点（2k，y1）和点（2，y2），且y1＞y2，求k的取值范围；（3）若将抛物线向右平移1个单位长度得到新抛物线，当1≤x≤2时，新抛物线对应的函数有最小值﹣，求k的值．33．在平面直角坐标系xOy中，直线y＝4x+4与x轴，y轴分别交于点A，B，抛物线y＝ax2+bx ﹣3a经过点A，将点B向右平移5个单位长度，得到点C．（1）求点C的坐标；（2）求抛物线的对称轴；（3）若抛物线与线段BC恰有一个公共点，结合函数图象，求a的取值范围．34．在平面直角坐标系xOy中，抛物线y＝ax2+bx﹣与y轴交于点A，将点A向右平移2个单位长度，得到点B，点B在抛物线上．（1）求点B的坐标（用含a的式子表示）；（2）求抛物线的对称轴；（3）已知点P（，﹣），Q（2，2）．若抛物线与线段PQ恰有一个公共点，结合函数图象，求a的取值范围．35．在平面直角坐标系中，已知抛物线C：y＝ax2+2x﹣1（a≠0）和直线l：y＝kx+b，点A （﹣3，﹣3），B（1，﹣1）均在直线l上．（1）若抛物线C与直线l有交点，求a的取值范围；（2）当a＝﹣1，二次函数y＝ax2+2x﹣1的自变量x满足m≤x≤m+2时，函数y的最大值为﹣4，求m的值；（3）若抛物线C与线段AB有两个不同的交点，请直接写出a的取值范围．36．在平面直角坐标系xOy中，抛物线y＝mx2﹣6mx+9m+1（m≠0）．（1）求抛物线的顶点坐标；（2）若抛物线与x轴的两个交点分别为A和B点（点A在点B的左侧），且AB＝4，求m的值．（3）已知四个点C（2，2）、D（2，0）、E（5，﹣2）、F（5，6），若抛物线与线段CD 和线段EF都没有公共点，请直接写出m的取值范围．37．如图，抛物线y＝ax2+bx﹣1（a≠0）经过A（﹣1，0），B（2，0）两点，与y轴交于点C．（1）求抛物线的解析式及顶点D的坐标；（2）点P在抛物线的对称轴上，当△ACP的周长最小时，求出点P的坐标；（3）若点M为抛物线第四象限内一点，连接BC、CM、BM，求当△BCM的面积最大时点M的坐标．38．如图，平面直角坐标系中，抛物线y＝﹣x2+4x+m﹣4（m为常数）与y轴的交点为C，M（3，0）与N（0，﹣2）分别是x轴、y轴上的点（1）当m＝1时，求抛物线顶点坐标．（2）若3≤x≤3+m时，函数y＝﹣x2+4x+m﹣4有最小值﹣7，求m的值．（3）若抛物线与线段MN有公共点，直接写出m的取值范围是．参考答案1．解：①图象开口向下，能得到a＜0；②对称轴在y轴右侧，x＝＝1，则有﹣＝1，即2a+b＝0；③当x＝1时，y＞0，则a+b+c＞0；④由图可知，当﹣1＜x＜3时，y＞0．故选：C．2．解：①由抛物线的对称性可求得抛物线与x轴令一个交点的坐标为（3，0），当x＞3时，y＜0，故①正确；②抛物线开口向下，故a＜0，∵x＝﹣＝1，∴2a+b＝0．∴3a+b＝0+a＝a＜0，故②正确；③设抛物线的解析式为y＝a（x+1）（x﹣3），则y＝ax2﹣2ax﹣3a，令x＝0得：y＝﹣3a．∵抛物线与y轴的交点B在（0，2）和（0，3）之间，∴2≤﹣3a≤3．解得：﹣1≤a≤﹣，故③正确；④．∵抛物线y轴的交点B在（0，2）和（0，3）之间，∴2≤c≤3，由4ac﹣b2＞8a得：4ac﹣8a＞b2，∵a＜0，∴c﹣2＜∴c﹣2＜0∴c＜2，与2≤c≤3矛盾，故④错误．故选：B．3．解：由抛物线的开口向下知a＜0，与y轴的交点为在y轴的正半轴上，得c＞0，对称轴为x＝＜1，∵a＜0，∴2a+b＜0，而抛物线与x轴有两个交点，∴b2﹣4ac＞0，当x＝2时，y＝4a+2b+c＜0，当x＝1时，a+b+c＝2．∵＞2，∴4ac﹣b2＜8a，∴b2+8a＞4ac，∵①a+b+c＝2，则2a+2b+2c＝4，②4a+2b+c＜0，③a﹣b+c＜0．由①，③得到2a+2c＜2，由①，②得到2a﹣c＜﹣4，4a﹣2c＜﹣8，上面两个相加得到6a＜﹣6，∴a＜﹣1．故选：D．4．解：①∵对称轴在y轴的右侧，∴ab＜0，由图象可知：c＞0，∴abc＜0，故①不正确；②当x＝﹣1时，y＝a﹣b+c＜0，∴b﹣a＞c，故②正确；③由对称知，当x＝2时，函数值大于0，即y＝4a+2b+c＞0，故③正确；④∵x＝﹣＝1，∴b＝﹣2a，∵a﹣b+c＜0，∴a+2a+c＜0，3a＜﹣c，故④不正确；⑤当x＝1时，y的值最大．此时，y＝a+b+c，而当x＝m时，y＝am2+bm+c，所以a+b+c＞am2+bm+c（m≠1），故a+b＞am2+bm，即a+b＞m（am+b），故⑤正确．故②③⑤正确．故选：B．5．解：∵抛物线y＝ax2+bx+c（c≠0）过点（﹣1，0）和点（0，﹣3），∴0＝a﹣b+c，﹣3＝c，∴b＝a﹣3，∵当x＝1时，y＝ax2+bx+c＝a+b+c，∴P＝a+b+c＝a+a﹣3﹣3＝2a﹣6，∵顶点在第四象限，a＞0，∴b＝a﹣3＜0，∴a＜3，∴0＜a＜3，∴﹣6＜2a﹣6＜0，即﹣6＜P＜0．故选：B．6．解：∵抛物线与x轴的一个交点在点（3，0）和（4，0）之间，而抛物线的对称轴为直线x＝1，∴抛物线与x轴的另一个交点在点（﹣2，0）和（﹣1，0）之间．∴当x＝﹣1时，y＞0，即a﹣b+c＞0，所以①正确；∵抛物线的对称轴为直线x＝﹣＝1，即b＝﹣2a，∴3a+b＝3a﹣2a＝a，所以②错误；∵抛物线的顶点坐标为（1，n），∴＝n，∴b2＝4ac﹣4an＝4a（c﹣n），所以③正确；∵抛物线与直线y＝n有一个公共点，∴抛物线与直线y＝n﹣1有2个公共点，∴一元二次方程ax2+bx+c＝n﹣1有两个不相等的实数根，所以④正确．故选：C．7．解：∵抛物线的顶点坐标A（1，3），∴抛物线的对称轴为直线x＝﹣＝1，∴2a+b＝0，所以①正确；∵抛物线开口向下，∴a＜0，∴b＝﹣2a＞0，∵抛物线与y轴的交点在x轴上方，∴c＞0，∴abc＜0，所以②错误；∵抛物线的顶点坐标A（1，3），∴x＝1时，二次函数有最大值，∴方程ax2+bx+c＝3有两个相等的实数根，所以③正确；∵抛物线与x轴的一个交点为（4，0）而抛物线的对称轴为直线x＝1，∴抛物线与x轴的另一个交点为（﹣2，0），所以④错误；∵抛物线y1＝ax2+bx+c与直线y2＝mx+n（m≠0）交于A（1，3），B点（4，0）∴当1＜x＜4时，y2＜y1，所以⑤正确．故选：C．8．解：∵x＝1时，y＝0，∴a+b+c＝0，所以①正确；∵x＝﹣＝﹣1，∴b＝2a，所以②错误；∵点（1，0）关于直线x＝﹣1对称的点的坐标为（﹣3，0），∴抛物线与x轴的交点坐标为（﹣3，0）和（1，0），∴ax2+bx+c＝0的两根分别为﹣3和1，所以③正确；∵抛物线与y轴的交点在x轴下方，∴c＜0，而a+b+c＝0，b＝2a，∴c＝﹣3a，∴a﹣2b+c＝﹣3b，∴﹣3b＜0，所以④错误．故选：C．9．解：①∵抛物线开口向上，∴a＞0，∵抛物线的对称轴在y轴右侧，∴b＜0∵抛物线与y轴交于负半轴，∴c＜0，∴abc＞0，①错误；②当x＝﹣1时，y＞0，∴a﹣b+c＞0，∵，∴b＝﹣2a，把b＝﹣2a代入a﹣b+c＞0中得3a+c＞0，所以②正确；③当x＝1时，y＜0，∴a+b+c＜0，∴a+c＜﹣b，当x＝﹣1时，y＞0，∴a﹣b+c＞0，∴a+c＞b，∴|a+c|＜|b|∴（a+c）2＜b2，即（a+c）2﹣b2＜0，所以③正确；④∵抛物线的对称轴为直线x＝1，∴x＝1时，函数的最小值为a+b+c，∴a+b+c≤am2+mb+c，即a+b≤m（am+b），所以④正确．10．解：A．∵二次函数的图象开口向下，图象与y轴交于y轴的正半轴上，∴a＜0，c＞0，∵抛物线的对称轴是直线x＝1，∴﹣＝1，∴b＝﹣2a＞0，∴abc＜0，故本选项错误；B．∵图象与x轴有两个交点，∴b2﹣4ac＞0，故本选项错误；C．∵对称轴是直线x＝1，与x轴一个交点是（﹣1，0），∴与x轴另一个交点的坐标是（3，0），把x＝3代入二次函数y＝ax2+bx+c（a≠0）得：y＝9a+3b+c＝0，故本选项错误；D．∵当x＝3时，y＝0，∵b＝﹣2a，∴y＝ax2﹣2ax+c，把x＝4代入得：y＝16a﹣8a+c＝8a+c＜0，故选：D．11．解：①由图象可知：a＞0，c＜0，∴由于对称轴＞0，∴b＜0，∴abc＞0，故①正确；②抛物线过（3，0），∴x＝3，y＝9a+3b+c＝0，故②正确；③顶点坐标为：（，）由图象可知：＜﹣2，∵a＞0，∴4ac﹣b2＜﹣8a，即b2﹣4ac＞8a，故③错误；④由图象可知：＞1，a＞0，∴2a+b＜0，∵9a+3b+c＝0，∴c＝﹣9a﹣3b，∴5a+b+c＝5a+b﹣9a﹣3b＝﹣4a﹣2b＝﹣2（2a+b）＞0，故④正确；故选：C．12．解：∵抛物线开口向下，∴a＜0，∵抛物线的对称轴为直线x＝﹣＝﹣1，∴b＝2a＜0，∵抛物线与y轴的交点在x轴上方，∴c＞0，∴abc＞0，所以①正确；∵抛物线与x轴有2个交点，∴△＝b2﹣4ac＞0，所以②正确；∵b＝2a，∴2a﹣b＝0，所以③错误；∵抛物线开口向下，x＝﹣1是对称轴，所以x＝﹣1对应的y值是最大值，∴a﹣b+c＞2，所以④正确．故选：C．13．解：由抛物线的开口向下可得：a＜0，根据抛物线的对称轴在y轴左边可得：a，b同号，所以b＜0，根据抛物线与y轴的交点在正半轴可得：c＞0，∴abc＞0，故①正确；直线x＝﹣1是抛物线y＝ax2+bx+c（a≠0）的对称轴，所以﹣＝﹣1，可得b＝2a，a﹣2b+4c＝a﹣4a+4c＝﹣3a+4c，∵a＜0，∴﹣3a＞0，∴﹣3a+4c＞0，即a﹣2b+4c＞0，故②错误；∵抛物线y＝ax2+bx+c的对称轴是x＝﹣1．且过点（，0），∴抛物线与x轴的另一个交点坐标为（，0），当x＝﹣时，y＝0，即，整理得：25a﹣10b+4c＝0，故③正确；∵b＝2a，a+b+c＜0，∴，即3b+2c＜0，故④错误；假设结论正确可得：a﹣b+c≥m2a﹣mb+c∴am2﹣mb+b﹣a≤0，∵△＝（b）2﹣4ab；b＝2a∴△＝4a2﹣4a（b﹣a）＝0，∴关于y＝am2﹣mb+b的图象与x轴有一个交点，又∵a＜0，∴y＝am2﹣mb+b﹣a有最大值ymax＝0，所以⑤正确；故答案为：①③⑤．14．解：观察函数图象，发现：开口向下⇒a＜0；与y轴交点在y轴正半轴⇒c＞0；对称轴在y轴右侧⇒﹣＞0；顶点在x轴上方⇒＞0．①∵a＜0，c＞0，﹣＞0，∴b＞0，∴abc＜0，①成立；②∵＞0，∴＜0，②不成立；③∵OA＝OC，∴x A＝﹣c，将点A（﹣c，0）代入y＝ax2+bx+c中，得：ac2﹣bc+c＝0，即ac﹣b+1＝0，③成立；④∵OA＝﹣x A，OB＝x B，x A•x B＝，∴OA•OB＝﹣，④成立．综上可知：①③④成立．故答案为：①③④．15．解：∵抛物线开口朝下，∴a＜0，∵对称轴x＝1＝﹣，∴b＞0，∵抛物线与y轴的交点在x轴的上方，∴c＞0，∴abc＜0，故①错误；根据图象知道当x＝﹣1时，y＝a﹣b+c＜0，∴a+c＜b，故②错误；根据图象知道当x＝2时，y＝4a+2b+c＞0，故③正确；根据图象知道抛物线与x轴有两个交点，∴b2﹣4ac＞0，故④正确．故答案为：③④．16．解：①∵函数开口方向向上，∴a＞0；∵对称轴在y轴右侧∴ab异号，∵抛物线与y轴交点在y轴负半轴，∴c＜0，∴abc＞0，故①正确；②∵图象与x轴交于点A（﹣1，0），对称轴为直线x＝1，∴图象与x轴的另一个交点为（3，0），∴当x＝2时，y＜0，∴4a+2b+c＜0，故②错误；③∵二次函数y＝ax2+bx+c的图象与y轴的交点在（0，﹣1）的下方，对称轴在y轴右侧，a＞0，∴最小值：＜﹣1，∵a＞0，∴4ac﹣b2＜﹣4a；∴③正确；④∵图象与y轴的交点B在（0，﹣2）和（0，﹣1）之间，∴﹣2＜c＜﹣1∴﹣2＜﹣3a＜﹣1，∴＞a＞；故④正确⑤∵a＞0，∴b﹣c＞0，即b＞c；故⑤正确．综上所述，正确的有①③④⑤，故答案为：①③④⑤．17．解：∵二次函数y＝x2﹣4x+k中a＝1＞0，图象的开口向上，又∵二次函数y＝x2﹣4x+k的图象的顶点在x轴下方，∴△＝（﹣4）2﹣4×1×k＞0，解得：k＜4，故答案为：k＜4．18．解：将A（﹣1，0），B（m，0），C（﹣2，n）代入解析式y＝ax2+bx+c，∴对称轴x＝，∴﹣＝m﹣1，∵1＜m＜3，∴ab＜0，∵n＜0，∴a＜0，∴b＞0，∵a﹣b+c＝0，∴c＝b﹣a＞0①abc＜0；错误；②当x＝3时，y＜0，∴9a+3b+c＝9a+3（a+c）+c＝12a+4c＝4（3a+c）＜0，②正确；③a（m﹣1）+2b＝﹣b+2b＝b＞0，③正确；④a＝﹣1时，y＝﹣x2+bx+c，∴P（，b+1+），若△P AB为直角三角形，则△P AB为等腰直角三角形，∴AP的直线解析式是y＝x+1，∴b+1+＝+1，∴b＝﹣2或0，∵b＞0，∴不存在点P使△P AB为直角三角形．④错误；故答案为②③．19．解：二次函数y＝x2﹣2mx+1的对称轴为x＝m，∵a＝1＞0，∴在对称轴的左侧（即当x≤m），y随x的增大而减小，又∵在x≤1时y随x增大而减小，∴m的取值范围为m≥1．故答案为：m≥1．20．解：∵抛物线y＝ax2+c的顶点B点坐标为（0，c），四边形ABCO是正方形，∴∠COB＝45°，CO＝BC，∴△COB是等腰直角三角形，∴C点横纵坐标绝对值相等，且等于BO长度一半，∴C点坐标为（﹣，），将点C代入抛物线方程中得ac＝﹣2．故答案为：﹣2．21．解：∵抛物线开口向下，∴a＜0，∵抛物线对称轴为x＝﹣＝1，即b＝﹣2a，∴b＞0，∵抛物线与y轴的交点在x轴上方，∴c＞0，∴abc＜0，所以①错误；∴2a+b＝0，所以②正确；∵x＝1时，函数值最大，∴a+b+c＞am2+bm+c，即a+b＞am2+bm（m≠1），所以③正确；∵抛物线与x轴的交点到对称轴x＝1的距离大于1，∴抛物线与x轴的一个交点在点（2，0）与（3，0）之间，∴抛物线与x轴的另一个交点在点（0，0）与（﹣1，0）之间，∴x＝﹣1时，y＜0，∴a﹣b+c＜0，所以④错误；当ax12+bx1＝ax22+bx2，则ax12+bx1+c＝ax22+bx2+c，∴x＝x1和x＝x2所对应的函数值相等，∴x2﹣1＝1﹣x1，∴x1+x2＝2，所以⑤正确；故答案为②③⑤．22．解：①∵二次函数的图象开口向上，∴a＞0，∵二次函数的图象交y轴的负半轴于一点，∴c＜0，∵对称轴是直线x＝﹣1，∴﹣＝﹣1，∴b＝2a＞0，故①正确；②∵b＝2a，∴2a﹣b＝0，故②正确；③∵抛物线的对称轴为x＝﹣1，且过点（﹣3，0），∴抛物线与x轴另一交点为（1，0）．∵当x＞﹣1时，y随x的增大而增大，∴当x＝2时y＞0，即4a+2b+c＞0，故③错误；④∵（﹣5，y1）关于直线x＝﹣1的对称点的坐标是（3，y1），又∵当x＞﹣1时，y随x的增大而增大，3＞，∴y1＞y2，故④正确；故答案为：①②④．23．解：∵图象和x轴有两个交点，∴b2﹣4ac＞0，∴b2＞4ac，∴①正确；∵从图象可知：a＞0，c＜0，﹣＝﹣1，b＝2a＞0，∴abc＜0，∴②错误；∵b＝2a＞0∴2a+b＝4a＞0，∴③错误；∵x＝﹣1时，y＜0，∴a﹣b+c＜0，∴④正确；∵x＝1时，y＞0，∴a+b+c＞0，把b＝2a代入得：3a+c＞0，选项⑤正确；故答案为①④⑤．24．解：①由二次函数的图象可知，该函数图象开口向下，则a＜0；该函数图象与y轴交于负半轴，则c＜0，∴ac＞0；②由图象可知，当x＝1时，y＞0，即y＝a+b+c＞0∴a+b+c＞0；③由图象可知，对称轴为0＜﹣＜1∵a＜0∴2a+b＜0④由图象可知，抛物线与x轴有两个交点，则b2﹣4ac＞0综上，其值大于0的有①②④．故答案为：①②④．25．解：∵抛物线开口向上，∴a＞0，∵对称轴为直线x＝﹣＝﹣1，∴b＝2a＞0，∵抛物线与y轴的交点在x轴上方，∴c＞0，∴abc＞0，所以①错误；∵抛物线的顶点在x轴上，∴△＝b2﹣4ac＝0，所以②正确；∵x＝﹣1时，y＝0，∴a﹣b+c＝0，即a﹣2a+c＝0，∴c＝a，而c＞2，∴a＞2，所以③正确；∵x＝﹣2时，y＞0，∴4a﹣2b+c＞0，所以④正确．故答案为②③④．26．解：将点（3，1），（6，﹣5），代入二次函数表达式得：，解得：，当a＞0时，则函数对称轴在x＝6的右侧，即x＝﹣≥6，即≥6，解得：a≤，同理当a＜0时，则函数对称轴在x＝3的左侧，即x＝﹣≤3，即≤3，解得：a ≥﹣，故答案为：﹣≤a≤且a≠0．27．解：二次函数y＝x2﹣3mx+2的图象是一条开口向上的抛物线，（1）当抛物线的对称轴x＝m≤﹣1时，即m≤﹣，要使二次函数解析式的值﹣1＜x＜0时恒大于1，只要x＝﹣1，y＝1+3m+2＝3m+3＞1，解得：m＞﹣，∴m无解；（2）当抛物线的对称轴x＝m≥0时，即m≥0时，要使二次函数解析式的值﹣1＜x＜0时恒大于1，只要m≥0即可；（3）当抛物线的对称轴x＝m在区间﹣1＜x＜0时，即﹣＜m＜0，要使二次函数解析式的值﹣1＜x＜0时恒大于1，只要x＝m时，y＞1即可；即y＝x2﹣3mx+2＝（m）2﹣3m×m+2＞1且﹣＜m＜0，解得：﹣＜m＜0；综上所述：m的取值范围是：m＞﹣．28．解：∵函数y＝x2﹣2x+b的图象与坐标轴有三个交点，∴，解得b＜1且b≠0．故答案为b＜1且b≠0．29．解：①由抛物线开口向上，则a＞0，对称轴为x＝1，因此b＜0，且2a+b＝0，﹣2＜c ＜﹣1，因此abc＞0，①是正确的；②当x＝2时，y＝4a+2b+c＜0，因此②不正确，③由b2﹣4ac＞0，推出4ac﹣b2＜0，∵8a＞0，4ac﹣b2＜8a，因此③正确；④∵图象与x轴交于点A（﹣1，0）和（3，0），∴ax2+bx+c＝0的两根为﹣1和3，∴a﹣b+c＝0，又2a+b＝0，∴3a+c＝0∴﹣3＝，∴c＝﹣3a，∴﹣2＜﹣3a＜﹣1，∴＜a＜；故④正确；⑤抛物线过（﹣1，0），a﹣b+c＝0，即，b＝a+c，因为a＞0，所以b＞c，因此⑤不正确；故答案为：①③④30．解：由已知得抛物线顶点坐标为（2a，a﹣1），设x＝2a①，y＝a﹣1②，①﹣②×2，消去a得，x﹣2y＝2，即．故答案为：．31．解：∵抛物线开口向下，∴a＜0，∵﹣＝1，∴b＞0，2a+b＝0，故④正确，∵抛物线交y轴于正半轴，∴c＞0，∴abc＜0，故①正确，∵抛物线与x轴有交点，∴b2﹣4ac＞0，即b2＞4ac，故②正确，∵x＝2时，y＞0，∴4a+2b+c＞0，故③错误，故正确的结论是①②④．32．解：（1）把点（1，k2）代入抛物线y＝x2﹣2（k﹣1）x+k2﹣k，得k2＝12﹣2（k﹣1）+k2﹣k解得k＝（2）把点（2k，y1）代入抛物线y＝x2﹣2（k﹣1）x+k2﹣k，得y1＝（2k）2﹣2（k﹣1）•2k+k2﹣k＝k2+k把点（2，y2）代入抛物线y＝x2﹣2（k﹣1）x+k2﹣k，得y2＝22﹣2（k﹣1）×2+k2﹣k＝k2﹣k+8∵y1＞y2∴k2+k＞k2﹣k+8解得k＞1（3）抛物线y＝x2﹣2（k﹣1）x+k2﹣k解析式配方得y＝（x﹣k+1）2+（﹣）将抛物线向右平移1个单位长度得到新解析式为y＝（x﹣k）2+（﹣）当k＜1时，1≤x≤2对应的抛物线部分位于对称轴右侧，y随x的增大而增大，∴x＝1时，y最小＝（1﹣k）2﹣k﹣1＝k2﹣k，∴k2﹣k＝﹣，解得k1＝1，k2＝都不合题意，舍去；当1≤k≤2时，y最小＝﹣k﹣1，∴﹣k﹣1＝﹣解得k＝1；当k＞2时，1≤x≤2对应的抛物线部分位于对称轴左侧，y随x的增大而减小，∴x＝2时，y最小＝（2﹣k）2﹣k﹣1＝k2﹣k+3，∴k2﹣k+3＝﹣解得k1＝3，k2＝（舍去）综上，k＝1或3．33．解：（1）与y轴交点：令x＝0代入直线y＝4x+4得y＝4，∴B（0，4），∵点B向右平移5个单位长度，得到点C，∴C（5，4）；（2）与x轴交点：令y＝0代入直线y＝4x+4得x＝﹣1，∴A（﹣1，0），将点A（﹣1，0）代入抛物线y＝ax2+bx﹣3a中得0＝a﹣b﹣3a，即b＝﹣2a，∴抛物线的对称轴x＝﹣＝﹣＝1；（3）∵抛物线y＝ax2+bx﹣3a经过点A（﹣1，0）且对称轴x＝1，由抛物线的对称性可知抛物线也一定过A的对称点（3，0），①a＞0时，如图1，将x＝0代入抛物线得y＝﹣3a，∵抛物线与线段BC恰有一个公共点，∴﹣3a＜4，a＞﹣，将x＝5代入抛物线得y＝12a，∴12a≥4，a≥，∴a≥；②a＜0时，如图2，将x＝0代入抛物线得y＝﹣3a，∵抛物线与线段BC恰有一个公共点，∴﹣3a＞4，a＜﹣；③当抛物线的顶点在线段BC上时，则顶点为（1，4），如图3，将点（1，4）代入抛物线得4＝a﹣2a﹣3a，解得a＝﹣1．综上所述，a≥或a＜﹣或a＝﹣1．34．解：（1）A（0，﹣）点A向右平移2个单位长度，得到点B（2，﹣）；（2）A与B关于对称轴x＝1对称，∴抛物线对称轴x＝1；（3）∵对称轴x＝1，∴b＝﹣2a，∴y＝ax2﹣2ax﹣，①a＞0时，当x＝2时，y＝﹣＜2，当y＝﹣时，x＝0或x＝2，∴函数与PQ无交点；②a＜0时，当y＝2时，ax2﹣2ax﹣＝2，x＝或x＝当≤2时，a≤﹣；∴当a≤﹣时，抛物线与线段PQ恰有一个公共点；35．解：（1）点A（﹣3，﹣3），B（1，﹣1）代入y＝kx+b，∴，∴，∴y＝x﹣；联立y＝ax2+2x﹣1与y＝x﹣，则有2ax2+3x+1＝0，∵抛物线C与直线l有交点，∴△＝9﹣8a≥0，∴a≤且a≠0；（2）根据题意可得，y＝﹣x2+2x﹣1，∵a＜0，∴抛物线开口向下，对称轴为直线x＝1，∵m≤x≤m+2时，y有最大值﹣4，∴当y＝﹣4时，有﹣x2+2x﹣1＝﹣4，∴x＝﹣1或x＝3，①在对称轴直线x＝1左侧，y随x的增大而增大，∴x＝m+2＝﹣1时，y有最大值﹣4，∴m＝﹣3；②在对称轴直线x＝1右侧，y随x增大而减小，∴x＝m＝3时，y有最大值﹣4；综上所述：m＝﹣3或m＝3；（3）①a＜0时，x＝1时，y≤﹣1，即a≤﹣2；②a＞0时，x＝﹣3时，y≥﹣3，即a≥，直线AB的解析式为y＝x﹣，抛物线与直线联立：ax2+2x﹣1＝x﹣，∴ax2+x+＝0，△＝﹣2a＞0，∴a＜，∴a的取值范围为≤a＜或a≤﹣2；36．解：（1）∵y＝mx2﹣6mx+9m+1＝m（x﹣3）2+1，∴抛物线的顶点坐标为（3，1）；（2）∵对称轴为直线x＝3，且AB＝4，∴A（1，0），B（5，0），将点A的坐标代入抛物线，可得：m＝﹣；（3）如图：①当m＞0时满足，解得：m＞；②当m＜0时满足，解得：m＜﹣1；综上，m＜﹣1或m＞．37．解：（1）∵抛物线y＝ax2+bx﹣1（a≠0）经过A（﹣1，0），B（2，0）两点，∴，∴，∴抛物线解析式为y＝x2﹣x﹣1＝（x﹣）2﹣，∴抛物线的顶点坐标为（，﹣）；（2）如图1，连接BC与抛物线对称轴的交点就是点P，连接AC，AP，∵点A，B关于抛物线对称轴对称，∴P A＝PB，∵B（2，0），C（0，﹣1），∴直线BC解析式为y＝x﹣1，∵点P在抛物线对称轴上，∴点P的横坐标为，∴点P的纵坐标为﹣，∴P（，﹣）；（3）设M（x，），过点M作x轴的垂线交BC于点N，则点N（x，）∴＝＝﹣x2+x＝﹣（x﹣1）2+，故当x＝1时，S△BMC最大，此时，所以当△BCM的面积最大时点M的坐标为（1，﹣1）．38．解：（1）当m＝1时，y＝﹣x2+4x﹣3＝﹣（x﹣2）2+1，∴顶点坐标为（2，1）；（2）由抛物线y＝﹣x2+4x+m﹣4（m为常数）可知：开口向上，函数的对称轴为直线x ＝2，∴当3≤x≤3+m时，y随x的增大而减小，∴当x＝m+3时，y有最小值﹣7，∴﹣（m+3）2+4（m+3）+m﹣4＝﹣7，解得m1＝2，m2＝﹣3（舍去），∴m＝2；（3）∵M（3，0），N（0，﹣2），∴直线MN的解析式为y＝x﹣2，∵抛物线与线段MN有公共点，则方程﹣x2+4x+m﹣4＝x﹣2，即x2﹣x﹣m+2＝0中△≥0，且m﹣4≤﹣2，∴（﹣）2﹣4（﹣m+2）≥0，解得﹣≤m≤2，故答案为﹣≤m≤2。

2021年中考数学压轴题冲刺提升专题动点与函数图象(原卷版)

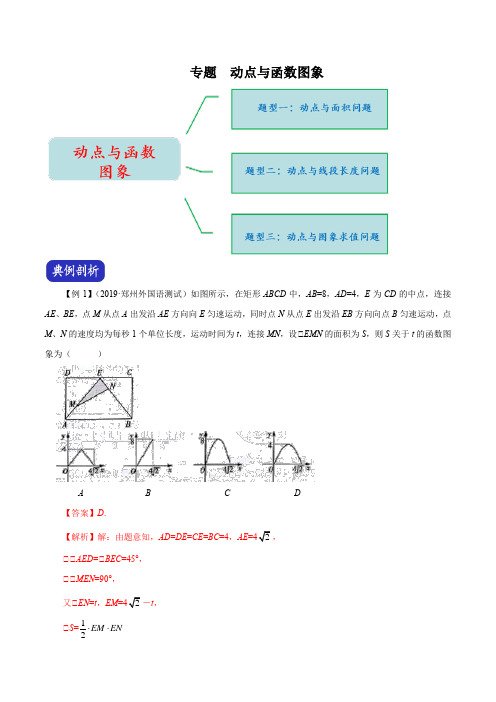
专题动点与函数图象【例1】（2019·郑州外国语测试）如图所示，在矩形ABCD中，AB=8，AD=4，E为CD的中点，连接AE、BE，点M从点A出发沿AE方向向E匀速运动，同时点N从点E出发沿EB方向向点B匀速运动，点M、N的速度均为每秒1个单位长度，运动时间为t，连接MN，设△EMN的面积为S，则S关于t的函数图象为（）A B C D【答案】D.【解析】解：由题意知，AD=DE=CE=BC=4，AE，△△AED=△BEC=45°，△△MEN=90°，又△EN=t，EM－t，△S=12EM EN ⋅⋅=()12t t ⋅⋅=(2142t -⋅-+，（0≤t ）图象为抛物线，开口朝下，当x 时，S 取最大值，故答案为D .【变式1-1】（2019·洛阳二模）如图，点 P 是边长为 2 cm 的正方形 ABCD 的边上一动点，O 是对角线的交点，当点 P 由 A →D →C 运动时，设 DP =x cm ，则△POD 的面积 y （cm 2）随 x （cm ）变化的关系图象为（）A BC D【变式1-2】（2019·叶县一模）如图，在△ABC 中，△ABC ＝60°，△C ＝45°，点D ，E 分别为边AB ，AC上的点，且DE △BC ，BD ＝DE ＝2，CE ＝52，BC ＝245．动点P 从点B 出发，以每秒1个单位长度的速度沿B →D →E →C 匀速运动，运动到点C 时停止．过点P 作PQ △BC 于点Q ，设△BPQ 的面积为S ，点P 的运动时间为t ，则S 关于t 的函数图象大致为（）A．B．C．D．【例2】（2019·省实验一模）如图，正方形ABCD，对角线AC和BD交于点E，点F是BC边上一动点（不与点B，C重合），过点E作EF的垂线交CD于点G，连接FG交EC于点H．设BF＝x，CH＝y，则y与x的函数关系的图象大致是（）A．B．C．D．【答案】A.【解析】解：△四边形ABCD是正方形，△△EBF＝△ECG＝45°，AC△BD，EB＝EC，△EF △EG ，△△BEC ＝△FEG ＝90°， △△BEF ＝△CEG ， △△BEF △△CEG ， △EF ＝EG ， △△EFG ＝45°， △△CFH ＝△BEF ， △△BEF △△CFH ，△BE BECH CF =， △x y =，△y ＝﹣x 2x （0＜x ），图象为一段开口朝下的抛物线，即答案为：A ．【变式2-1】（2019·名校模考）如图1，在矩形ABCD 中，AB ＜BC ，点E 为对角线AC 上的一个动点，连接BE ，DE ，过E 作EF △BC 于F ．设AE ＝x ，图1中某条线段的长为y ，若表示y 与x 的函数关系的图象大致如图2所示，则这条线段可能是图1中的（）A ．线段BEB ．线段EFC ．线段CED ．线段DE【变式2-2】（2018·洛宁县模拟）如图1，正△ABC 的边长为4，点P 为BC 边上的任意一点，且△APD =60°，PD 交AC 于点D ，设线段PB 的长度为x ，图1中某线段的长度为y ，y 与x 的函数关系的大致图象如图2，则这条线段可能是图1中的（）图1 图2 A ．线段AD B ．线段APC ．线段PDD ．线段CD【例3】（2019·周口二模）如图1，E 为矩形ABCD 边AD 上的一点，点P 从点B 沿折线BE -ED -DC 运动到点C 时停止，点Q 从点B 沿BC 运动到点C 时停止，它们运动的速度都是2 cm /s ．若P ，Q 同时开始运动，设运动时间为t （s ），△BPQ 的面积为y （cm 2），已知y 与t 的函数关系图象如图2，则CDBE的值为（） ABCD图1 图2【答案】D .【解析】解：由图象可知，t =8时，P 点与E 点重合；t =10时，P 与D 点重合， △P 点的运动速度为2cm /s ，△DE =4，BE =16， S △BCE =12·BC ·CD =8 CD ，即8 CD，即CD， △CD BE, 故答案为：D .【变式3-1】（2019·枫杨外国语三模）如图 1，动点 K 从△ABC 的顶点 A 出发，沿 AB ﹣BC 匀速运动到点 C 停止．在动点 K 运动过程中，线段 AK 的长度 y 与运动时间 x 的函数关系如图 2所示，其图1图2中点Q为曲线部分的最低点，若△ABC的面积是，则a的值为图1 图2【变式3-2】（2019·中原名校大联考）如图1，在矩形ABCD中，动点M从点A出发，沿A→B→C方向运动，当点M到达点C时停止运动，过点M作MN△AM交CD于点N，设点M的运动路程为x，CN＝y，图2表示的是y与x的函数关系的大致图象，则矩形ABCD的面积是（）A．20B．18C．10D．91. （2019·濮阳二模）如图，点A在x轴上，点B，C在反比例函数y＝kx（k＞0，x＞0）的图象上．有一个动点P从点A出发，沿A→B→C→O的路线（图中“→”所示路线）匀速运动，过点P作PM△x轴，垂足为M，设△POM的面积为S，点P的运动时间为t，则S关于t的函数图象大致为（）A．B．C．D．2.（2019·南阳模拟）如图，已知△ABC为等边三角形，AB＝2，点D为边AB上一点，过点D作DE△AC，交BC于E点；过E点作EF△DE，交AB的延长线于F点．设AD＝x，△DEF的面积为y，则能大致反映y 与x函数关系的图象是（）A．B．C．D．3.（2019·平顶山三模）如图，正方形ABCD的边长为4，点P、Q分别是CD、AD的中点，动点E从点A向点B运动，到点B时停止运动；同时，动点F从点P出发，沿P→D→Q运动，点E、F的运动速度相同．设点E的运动路程为x，△AEF的面积为y，能大致刻画y与x的函数关系的图象是（）A．B．C．D．4.如图甲，点E为矩形ABCD边AD上一点，点P，Q同时从B点出发，点P沿BE→ED→DC运动到点C停止，点Q沿BC运动到点C停止，它们的运动速度都是1cm/s，设P、Q出发t秒时，△BPQ的面积为y（cm2），已知y与t的函数关系的图象如图乙（曲线OM为抛物线的一部分），则下列结论：△当0＜t≤5时，y=25t2 △tan△ABE=34△点H的坐标为（11，0）△△ABE与△QBP不可能相似．其中正确的是（把你认为正确结论的序号都填上）5.（2019·焦作二模）如图1，在等边△ABC中，点D是BC边的中点，点P为AB边上的一个动点，设xAP ，图1中线段DP的长为y，若表示y与x的函数关系的图象如图2所示，则等边△ABC的面积为.6.（2019·三门峡一模）如图，边长分别为1和2的两个等边三角形，开始它们在左边重合，大三角形固定不动，然后把小三角形自左向右平移直至移出大三角形外停止．设小三角形移动的距离为x，两个三角形重叠面积为y，则y关于x的函数图象是（）ABCD．7.（2019·许昌月考）如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG，动点P 从点A出发，沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止（不含点A和点B），则△ABP 的面积S随着时间t变化的函数图象大致是（）A．B．C．D．8.（2019·信阳模拟）如图1，在△ABC中，△C=90°，动点P从点C出发，以1cm/s的速度沿折线CA→AB 匀速运动，到达点B时停止运动，点P出发一段时间后动点Q从点B出发，以相同的速度沿BC匀速运动，当点P到达点B时，点Q恰好到达点C，并停止运动，设点P的运动时间为t s，△PQC的面积为S cm2，S 关于t的函数图象如图2所示（其中0＜t≤3，3≤t≤4时，函数图象均为线段（不含点O），4＜t＜8时，函数图象为抛物线的一部分）给出下列结论：△AC =3cm ；△当S =65时，t =35或6．下列结论正确的是（）A ．△△都对B ．△△都错C ．△对△错D ．△错△对9.（2018·新乡一模）如图，平行四边形ABCD 中，ABcm ，BC =2cm ，△ABC =45°，点P 从点B 出发，以1cm /s 的速度沿折线BC →CD →DA 运动，到达点A 为止，设运动时间为t (s )，△ABP 的面积为S (cm 2)，则S 与t 的函数表达式为.10.（2019·郑州外国语模拟）如图，在等腰△ABC 中，AB =AC =4cm ，△B =30°，点P 从点Bcm /s 的速度沿BC 方向运动到点C 停止，同时点Q 从点B 出发以2cm /s 的速度沿B →A →C 运动到点C 停止，若△BPQ 的面积为y ，运动时间为t （s ），则y 与t 的函数关系式为：.11.（2019·安阳一模）如图，在四边形ABCD 中，AD △BC ，DC △BC ，DC =4 cm ，BC =6 cm ，AD =3 cm ，动点P ，Q 同时从点B 出发，点P 以2 cm /s 的速度沿折线BA -AD -DC 运动到点C ，点Q 以1 cm /s 的速度沿BC 运动到点C ，设P ，Q 同时出发t s 时，△BPQ 的面积为y cm 2，则y 与t 的函数图象大致是（）BBA B CD12.（2019·开封模拟）如图，菱形ABCD的边长是4 cm，△B=60°，动点P以1 cm/s的速度从点A出发沿AB方向运动至点B停止，动点Q以2cm/s的速度从点B出发沿折线BCD运动至点D停止．若点P，Q 同时出发，运动了t s，记△BPQ的面积为S cm2，则下面图象中能表示S与t之间的函数关系的是（）A．B．C．D．13. 如图，矩形ABCD中，AB＝2AD＝4cm，动点P从点A出发，以lcm/s的速度沿线段AB向点B运CD动，动点Q同时从点A出发，以2cm／s的速度沿折线AD→DC→CB向点B运动，当一个点停止时另一个点也随之停止．设点P的运动时间是x（s）时，△APQ的面积是y（cm2），则能够反映y与x之间函数关系的图象大致是（）14.（2019·信阳一模）如图,锐角三角形ABC中,BC=6,BC边上的高为4,直线MN交边AB于点M,交AC 于点N,且MN△BC,以MN为边作正方形MNPQ,设其边长为x(x>0),正方形MNPQ与△ABC公共部分的面积为y,则y与x的函数图象大致是()A B C D15.（2018·开封二模）如图，在平面直角坐标系中，已知A(0,1),B0)，以线段AB为边向上作菱形ABCD，且点D在y轴上. 若菱形ABCD以每秒2个单位长度的速度沿射线AB滑行，直至顶点D落在x轴上时停止．设菱形落在x轴下方部分的面积为S，则表示S与滑行时间t的函数关系的图象为（）图1 图2A B C D。

2021年中考数学压轴题专项训练一次函数含解析

2021年中考数学压轴题专项训练《一次函数》1．甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中.甲、乙两车离开A城的距离y（千米）与行驶时间x（小时）之间的函数关系如图所示.已知甲对应的函数关系式为y ＝60x.根据图象提供的信息.解决下列问题：（1）求乙离开A城的距离y与x的关系式；（2）求乙出发后几小时追上甲车？解：（1）设乙对应的函数关系式为y＝kx+b将点（4.300）.（1.0）代入y＝kx+b得：解得：.∴乙对应的函数关系式y＝100x﹣100；（2）易得甲车对应的函数解析式为y＝60x.联立.解得：.2.5﹣1＝1.5（小时）.∴乙车出发后1.5小时追上甲车．2．如图①所示.甲、乙两车从A地出发.沿相同路线前往同一目的地.途中经过B地．甲车先出发.当甲车到达B地时.乙车开始出发．当乙车到达B地时.甲车与B地相距km设甲、乙两车与B地之间的距离为.y1（km）.y2（km）.乙车行驶的时间为x（h）.y1.y2与x的函数关系如图②所示．（1）A.B两地之间的距离为20 km；（2）当x为何值时.甲、乙两车相距5km？解：（1）A.B两地之间的距离为20km．故答案为：20；（2）乙车的速度为：20÷＝120（km/h）.甲车的速度为：＝100（km/h）.甲比乙早出发的时间为：20÷100＝0.2（h）.相遇前：（20+100x）﹣120x＝5.解得x＝0.75；相遇后：120x﹣（20+100x）＝5.解得x＝1.25；答：当x为0.75或1.25时.甲、乙两车相距5km．3．在平面直角坐标系中.直线y＝x+2与x轴.y轴分别交于点A.B.点D的坐标为（0.3）.点E是线段AB上的一点.以DE为腰在第二象限内作等腰直角△DEF.∠EDF＝90°．（1）请直接写出点A.B的坐标：A（﹣2 . 0 ）.B（0 . 2 ）；（2）设点F的坐标为（a.b）.连接FB并延长交x轴于点G.求点G的坐标．解：（1）∵直线y＝x+2与x轴.y轴分别交于点A.B.∴点A（﹣2.0）.点B（0.2）故答案为：（﹣2.0）.（0.2）（2）如图.过点F作FM⊥y轴.过点E作EN⊥y轴.∴∠FMD＝∠EDF＝90°∴∠FDM+∠DFM＝90°.∠FDM+∠EDN＝90°.∴∠DFM＝∠EDN.且FD＝DE.∠FMD＝∠END＝90°.∴△DFM≌△EDN（AAS）∴EN＝DM.FM＝BN.∵点F的坐标为（a.b）.∴FM＝DN＝﹣a.DM＝b﹣3.∴点E坐标（﹣b+3.3+a）.∵点E是线段AB上的一点.∴3+a＝﹣b+3+2∴a+b＝2.∴点F（a.2﹣a）设直线BF的解析式为y＝kx+2.∴2﹣a＝ka+2∴k＝﹣1.∴直线BF的解析式为y＝﹣x+2.∴点G（2.0）4．某学校甲、乙两名同学去爱国主义教育基地参观.该基地与学校相距2400米．甲从学校步行去基地.出发5分钟后乙再出发.乙从学校骑自行车到基地．乙骑行到一半时.发现有东西忘带.立即返回.拿好东西之后再从学校出发．在骑行过程中.乙的速度保持不变.最后甲、乙两人同时到达基地．已知.乙骑行的总时间是甲步行时间的．设甲步行的时间为x（分）.图中线段OA表示甲离开学校的路程y（米）与x（分）的函数关系的图象．图中折线B﹣C﹣D和线段EA表示乙离开学校的路程y（米）与x（分）的函数关系的图象．根据图中所给的信息.解答下列问题：（1）甲步行的速度和乙骑行的速度；（2）甲出发多少时间后.甲、乙两人第二次相遇？（3）若s（米）表示甲、乙两人之间的距离.当15≤x≤30时.求s（米）关于x（分）的函数关系式．解：（1）由题意得：（米/分）.＝240（米/分）；（2）由题意可得：C（10.1200）.D（15.0）.A（30.2400）.设线段CD的解析式为：y＝kx+b.则.解得∴线段CD的解析式为：y＝﹣240x+3600.易知线段OA的解析式为：y＝80x.根据题意得240x+3600＝80x.解得：x＝.∴甲出发分后.甲、乙两人第二次相遇；（3）∵E（20.0）.A（30.2400）.设线段EA的解析式为：y＝mx+n..解得.∴线段EA的解析式为：y＝240x﹣4800.∴当15≤x≤20时.s＝y OA﹣0＝80x.当20＜x≤30时.s＝y OA﹣y EA＝80x﹣（240x﹣4800）＝﹣160x+4800.∴．5．对于给定的△ABC.我们给出如下定义：若点M是边BC上的一个定点.且以M为圆心的半圆上的所有点都在△ABC的内部或边上.则称这样的半圆为BC边上的点M关于△ABC的内半圆.并将半径最大的内半圆称为点M 关于△ABC的最大内半圆．若点M是边BC上的一个动点（M不与B.C重合）.则在所有的点M关于△ABC的最大内半圆中.将半径最大的内半圆称为BC关于△ABC的内半圆．（1）在Rt△ABC中.∠BAC＝90°.AB＝AC＝2.①如图1.点D在边BC上.且CD＝1.直接写出点D关于△ABC的最大内半圆的半径长；②如图2.画出BC关于△ABC的内半圆.并直接写出它的半径长；（2）在平面直角坐标系xOy中.点E的坐标为（3.0）.点P在直线y＝x上运动（P 不与O重合）.将OE关于△OEP的内半圆半径记为R.当≤R≤1时.求点P的横坐标t 的取值范围．解：（1）①如图1.过D作DE⊥AC于E.∵Rt△ABC中.∠BAC＝90°.AB＝AC＝2.∴∠C＝∠B＝45°.∵CD＝1.∴BD＝2﹣1＞CD.∴D到AC的距离小于到AB的距离.∵△DEC是等腰直角三角形.∴DE＝.即点D关于△ABC的最大内半圆的半径长是；②当D为BC的中点时.BC关于△ABC的内半圆为⊙D.如图2.∴BD＝BC＝.同理可得：BC关于△ABC的内半圆半径DE＝1．（2）过点E作EF⊥OE.与直线y＝x交于点F.设点M是OE上的动点.i）当点P在线段OF上运动时（P不与O重合）.OE关于△OEP的内半圆是以M为圆心.分别与OP.PE相切的半圆.如图3.连接PM.∵直线OF：y＝x∴∠FOE＝30°由（1）可知：当M为线段中点时.存在OE关于△OEP的内半圆.∴当R＝时.如图3.DM＝.此时PM⊥x轴.P的横坐标t＝OM＝；如图4.当P与F重合时.M在∠EFO的角平分线上.⊙M分别与OF.FE相切.此时R＝1.P的横坐标t＝OE＝3；∴当≤R≤1时.t的取值范围是≤t≤3．ii）当点P在OF的延长线上运动时.OE关于△OEP的内半圆是以M为圆心.经过点E且与OP相切的半圆.如图5．∴当R＝1 时.t的取值范围是t≥3．iii）当点P在OF的反向延长上运动时（P不与O重合）.OE关于△OEP的内半圆是以M 为圆心.经过点O且与EP相切的半圆.如图6．∵∠FOE＝∠OPE+∠OEP＝30°.∴∠OEP＜30°.∴OM＜1.当R＝时.如图6.过P作PA⊥x轴于A.N是切点.连接MN.MN⊥PE.此时OM＝MN＝.ME ＝3﹣＝.∴EN＝＝＝.Rt△OPA中.∠POA＝30°.OA＝﹣t.∴PA＝﹣t.∵∠ENM＝∠EAP＝90°.∠MEN＝∠AEP.∴△EMN∽△EPA.∴.即＝解得：t＝﹣.∴当≤R＜1时.t的取值范围是t≤﹣．综上.点P在直线y＝x上运动时（P不与O重合）.当≤R≤1时.t的取值范围是t ≤﹣或t≥．6．已知.一次函数y＝﹣x+6的图象与x轴、y轴分别交于点A、点B.与直线y＝x相交于点C．过点B作x轴的平行线l．点P是直线l上的一个动点．（1）求点A.点B的坐标．（2）若S△AOC＝S△BCP.求点P的坐标．（3）若点E是直线y＝x上的一个动点.当△APE是以AP为直角边的等腰直角三角形时.求点E的坐标．解：（1）一次函数y＝﹣x+6的图象与x轴、y轴分别交于点A、点B.则点A、B的坐标分别为：（8.0）、（0.6）；（2）联立y＝﹣x+6、y＝x并解得：x＝3.故点C（3.）.S△AOC＝8×＝15＝S△BCP＝BP×（yP﹣yC）＝BP×（6﹣）.解得：BP＝.故点P（.6）或（﹣.6）（3）设点E（m. m）、点P（n.6）；①当∠EPA＝90°时.如左图.∵∠MEP+∠MPE＝90°.∠MPE+∠NPA＝90°.∴∠MEP＝∠NPA.AP＝PE.∵△EMP≌△PNA（AAS）.则ME＝PN＝6.MP＝AN.即|m﹣n|＝6. m﹣6＝8﹣n.解得：m＝或16.故点E（.）或（14.）；②当∠EAP＝90°时.如右图.同理可得：△AMP≌△ANE（AAS）.故MP＝EN.AM＝AN＝6.即m＝n﹣8.|8﹣m|＝6.解得：m＝2或14.故点E（2.）或（16.20）；上.E（.）或（14.）或；（2.）或（16.20）．7．如图.A.B是直线y＝x+4与坐标轴的交点.直线y＝﹣2x+b过点B.与x轴交于点C．（1）求A.B.C三点的坐标；（2）当点D是AB的中点时.在x轴上找一点E.使ED+EB的和最小.画出点E的位置.并求E点的坐标．（3）若点D是折线A﹣B﹣C上一动点.是否存在点D.使AACD为直角三角形.若存在.直接写出D点的坐标；若不存在.请说明理由．解：（1）在y＝x+4中.令x＝0.得y＝4.令y＝0.得x＝﹣4.∴A（﹣4.0）.B（0.4）．把B（0.4）代入.y＝﹣2x+b.得b＝4∴直线BC为：y＝﹣2x+4．在y＝﹣2x+4中.令y＝0.得x＝2.∴C点的坐标为（2.0）；（2）如图点E为所求点D是AB的中点.A（﹣4.0）.B（0.4）．∴D（﹣2.2）．点B关于x轴的对称点B1的坐标为（0.﹣4）．设直线DB1的解析式为y＝kx+b．把D（﹣2.2）.B1（0.﹣4）代入一次函数表达式并解得：故该直线方程为：y＝﹣3x﹣4．令y＝0.得E点的坐标为．（3）存在.D点的坐标为（﹣1.3）或．①当点D在AB上时.由OA＝OB＝4得到：∠BAC＝45°.由等腰直角三角形求得D点的坐标为（﹣1.3）；②当点D在BC上时.如图.设AD交y轴于点F．在△AOF与△BOC中.∠FAO＝∠CBO.∠AOF＝∠BOD.AO＝BO.∴△AOF≌△BOC（ASA）．∴OF＝OC＝2.∴点F的坐标为（0.2）.易得直线AD的解析式为.与y＝﹣2x+4组成方程组并解得：x＝.∴交点D的坐标为．8．（1）模型建立：如图1.等腰直角三角形ABC中.∠ACB＝90°.CB＝CA.直线ED经过点C.过A作AD⊥ED于D.过B作BE⊥ED于E．求证：△BEC≌△CDA；（2）模型应用：①如图2.一次函数y＝﹣2x+4的图象分别与x轴、y轴交于点A、B.以线段AB为腰在第一象限内作等腰直角三角形ABC.则C点的坐标为C（4.6）或C（6.2）（直接写出结果）②如图3.在△ABC和△DCE中.CA＝CB.CD＝CE.∠CAB＝∠CED＝45°.连接BD、AE.作CM ⊥AE于M点.延长MC与BD交于点N.求证：N是BD的中点．解：（1）∵AD⊥ED.BE⊥ED.∴∠D＝∠E＝90°.∠ACD＝∠CAD＝90°.∵∠ACB＝90°.∴∠ACD＝∠BCE＝90°.∴∠BCE＝∠CAD.在△BEC和△CDA中.∴△BEC≌△CDA（AAS）；（2）①根据题意可得点C的坐标为C（4.6）或C（6.2）；故答案为： C（4.6）或C（6.2）；②如图.作BP⊥MN交MN的延长线于P.作DQ⊥MN于Q∵∠BCP+∠BCA＝∠CAM+∠AMC.∵∠BCA＝∠AMC.∴∠BCP＝∠CAM.在△CBP与△ACM中..∴△CBP≌△ACM（AAS）.∴MC＝BP.同理.CM＝DQ.∴DQ＝BP在△BPN与△DQN中..∵△BPN≌△DQN（AAS）.∴BN＝ND.∴N是BD的中点．9．如图.在平面直角坐标系xOy中.直线l：y＝﹣x+4与x轴、y轴分别相交于B、A两点.点C是AB的中点.点E、F分别为线段AB、OB上的动点.将△BEF沿EF折叠.使点B的对称点D恰好落在线段OA上（不与端点重合）．连接OC分别交DE、DF于点M、N.连接FM．（1）求tan∠ABO的值；（2）试判断DE与FM的位置关系.并加以证明；（3）若MD＝MN.求点D的坐标．解：（1）直线l：y＝﹣x+4与x轴、y轴分别相交于B、A两点. 则点A、B的坐标分别为：（0.4）、（3.0）；tan∠ABO＝＝＝tanα；（2）DE与FM的位置关系为相互垂直.理由：点C是AB的中点.则∠COB＝∠CBO＝∠EDF＝α.∠ONF＝∠DNM.∴∠DMN＝∠DFO.∴O、F、M、D四点共圆.∴∠DMF+∠DOF＝180°.∴∠DOF＝90°.即：DE⊥FM；（3）MD＝MN.∴∠MDN＝∠MND＝α.而∠COB＝α.∠DNM＝∠ONF＝α.即△OCF为以ON为底.底角为α的等腰三角形.则tan∠NFO＝＝＝tanβ.则cosβ＝（证明见备注）；设OF＝m.则DF＝FB＝3﹣m.cos∠DFO＝cosβ＝.解得：m＝.OD2＝DF2﹣OF2＝（3﹣m）2﹣m2＝；则OD＝.故点D（0.）．备注：如下图.过点N作HN⊥OF于点H.tanα＝.则sinα＝.作FM⊥ON于点M.设FN＝OF＝5a.则FN＝4a.则ON＝6a.同理可得：NH＝.tan∠NFO＝＝＝tanβ.则cosβ＝．10．如图.直线l1：y＝x+与y轴的交点为A.直线l1与直线l2：y＝kx的交点M的坐标为M（3.a）．（1）求a和k的值；（2）直接写出关于x的不等式x+＜kx的解集；（3）若点B在x轴上.MB＝MA.直接写出点B的坐标．解：（1）∵直线l1与直线l2的交点为M（3.a）.∴M（3.a）在直线y＝x+上.也在直线y＝kx上.∴a＝×3+＝3.∴M（3.3）.∴3＝3k.解得k＝1；（2）不等式x+＜kx的解集为x＞3；（3）作MN⊥x轴于N.∵直线l1：y＝x+与y轴的交点为A.∴A（0.）.∵M（3.3）.∴AM2＝（3﹣0）2+（3﹣）2＝.∵MN＝3.MB＝MA.∴BN＝＝.∴B（.0）或B（.0）．11．如图.长方形OBCD的OB边在x轴上.OD在y轴上.把OBC沿OC折叠得到OCE.OE与CD 交于点F．（1）求证：OF＝CF；（2）若OD＝4.OB＝8.写出OE所在直线的解析式．解：（1）∵四边形OBCD为矩形.∴DO＝BC.∠OBC＝∠ODC．由翻折的性质可知∠E＝∠OBC.CE＝BC.∴OD＝CE.∠E＝∠ODC．在△ODF和△CEF中.∴△ODF≌△CEF（AAS）.∴OF＝CF．（2）∵OF＝CF．设DF＝x.则OF＝CF＝8﹣x．在Rt△ODF中.OD＝4.根据勾股定理得.OD2+DF2＝OF2.∴42+x2＝（8﹣x）2.解得x＝3.∴F（3.4）.设直线OE的解析式为y＝kx.把F（3.4）代入得4＝3k.解得k＝.∴OE所在直线的解析式y＝x．12．如图.在平面直角坐标系中.直线y＝﹣x+m过点A（5.﹣2）且分别与x轴、y轴交于点B、C.过点A画AD∥x轴.交y轴于点D．（1）求点B、C的坐标；（2）在线段AD上存在点P.使BP+CP最小.求点P的坐标．解：（1）∵y＝﹣x+m过点A（5.﹣2）.∴﹣2＝﹣5+m.∴m＝3.∴y＝﹣x+3.令y＝0.∴x＝3.∴B（3.0）.令x＝0.∴y＝3.∴C（0.3）；（2）过C作直线AD对称点Q.可得Q（0.﹣7）.连结BQ.交AD与点P可得直线BQ：.令y′＝﹣2.∴.∴．13．如图.直线l1的函数表达式为y＝3x﹣2.且直线l1与x轴交于点D．直线l2与x轴交于点A.且经过点B（4.1）.直线l1与l2交于点C（m.3）．（1）求点D和点C的坐标；（2）求直线l2的函数表达式；（3）利用函数图象写出关于x.y的二元一次方程组的解．解：（1）在y＝3x﹣2中令y＝0.即3x﹣2＝0 解得x＝.∴D（.0）.∵点C（m.3）在直线y＝3x﹣2上.∴3m﹣2＝3.∴m＝.∴C（.3）；（2）设直线l2的函数表达式为Y＝KX+B（K≠0）.由题意得：.解得：.∴y＝﹣x+；（3）由图可知.二元一次方程组的解为．14．如图.在平面直角坐标系中.一次函数y＝kx+b的图象与x轴交于点A（﹣3.0）.与y轴交于点B.且与正比例函数y＝x的图象交点为C（m.4）．（1）求一次函数y＝kx+b的解析式；（2）求△BOC的面积；（3）若点D在第二象限.△DAB为等腰直角三角形.则点D的坐标为（﹣2.5）或（﹣5.3）或（.）．解：（1）∵点C在正比例函数图象上.∴m＝4.解得：m＝3.∵点C（3.4）、A（﹣3.0）在一次函数图象上.∴代入一次函数解析式可得.解这个方程组得. ∴一次函数的解析式为y＝x+2；（2）在中.令x＝0.解得y＝2.∴B（0.2）∴S△BOC＝×2×3＝3；（3）过点D1作D1E⊥y轴于点E.过点D2作D2F⊥x轴于点F.如图. ∵点D在第二象限.△DAB是以AB为直角边的等腰直角三角形. ∴AB＝BD2.∵∠D1BE+∠ABO＝90°.∠ABO+∠BAO＝90°.∴∠BAO＝∠EBD1.∵在△BED1和△AOB中.∴△BED1≌△AOB（AAS）.∴BE＝AO＝3.D1E＝BO＝2.即可得出点D的坐标为（﹣2.5）；同理可得出：△AFD2≌△AOB.∴FA＝BO＝2.D2F＝AO＝3.∴点D的坐标为（﹣5.3）.∵∠D1AB＝∠D2BA＝45°.∴∠AD3B＝90°.∴D3（.）.综上可知点D的坐标为（﹣2.5）或（﹣5.3）或（.）．故答案为：（﹣2.5）或（﹣5.3）或（.）．15．如图1中的三种情况所示.对于平面内的点M.点N.点P.如果将线段PM绕点P顺时针旋转90°能得到线段PN.就称点N是点M关于点P的“正矩点”．（1）在如图2所示的平面直角坐标系xOy中.已知S（﹣3.1）.P（1.3）.Q（﹣1.﹣3）.M （﹣2.4）．①在点P.点Q中. 点P是点S关于原点O的“正矩点”；②在S.P.Q.M这四点中选择合适的三点.使得这三点满足：点S是点P关于点M的“正矩点”.写出一种情况即可；（2）在平面直角坐标系xOy中.直线y＝kx+3（k＜0）与x轴交于点A.与y轴交于点B.点A关于点B的“正矩点”记为点C.坐标为C（x c.y c）．①当点A在x轴的正半轴上且OA小于3时.求点C的横坐标x c的值；②若点C的纵坐标y c满足﹣1＜y c≤2.直接写出相应的k的取值范围．解：（1）①在点P.点Q中.点S绕点O顺时针旋转90°能得到线段OP.故S关于点O的“正矩点”为点P.故答案为点P；②点S是点P关于点M的“正矩点”（答案不唯一）；故答案为：S.P.M；（2）①如图1.作CE⊥x轴于点E.作CF⊥y轴于点F.∠BFC＝∠AOB＝90°.点B（0.3）.点A（﹣.0）.∵∠ABO+∠CBO＝90°.∠CBO+∠BCF＝90°.∴∠BCF＝∠ABO.BC＝BA.∴△BCF≌△AOB（AAS）.∴FC＝OB＝3.故点C的坐标为：（﹣3.3+）.即点C的横坐标x c的值为﹣3；②点C（﹣3.3+）.如图2.﹣1＜y c≤2.即：﹣1＜3+≤2.则﹣3≤k．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

专题正确分析函数图象【例1】（2019·郑州一中模拟）如图所示，在Rt △ABC 中，点D 为AC 的中点，动点P 从点D 出发，沿着D →A →B 的路径以每秒1个单位长度的速度运动到点B ，在此运动过程中线段CP 的长度y 随着运动时间x 的函数关系如图2所示，则BC 的长为（） A.B. C.D.【答案】C .【解析】解：由图2知，AD =CD =2，当xCP 的长最小，即此时CP ⊥AB ，APCP= 由∠A =∠BCP ，得：cos ∠A = cos ∠BCP ，即：4BC=, 解得：BC,故答案为：C .BC【变式1-1】（2019·郑州联考）如图所示，二次函数y ＝ax 2+bx +c （a ≠0）的图象与x 轴相交于点A ，B ，若其对称轴为直线x ＝2，则OB ﹣OA 的值为．【变式1-2】（2019·郑州实验中学模拟）如图1，正方形ABCD 在直角坐标系中，其中AB 边在y 轴上，其余各边均与坐标轴平行，直线l ：y ＝x ﹣5沿y 轴的正方向以每秒1个单位的速度平移，在平移的过程中，该直线被正方形ABCD 的边所截得的线段长为m ，平移的时间为t （秒），m 与t 的函数图象如图2所示，则图2中b 的值为（）图1 图2A ．B ．C ．D ．【例2】（2019·开封模拟）如图，已知顶点为(-3，-6)的抛物线y =ax 2+bx +c 经过点(-1，-4)，下列结论：①b 2＞4ac ；②ax 2+bx +c ≥-6；③若点(-2，m )，(-5，n )在抛物线上，则m ＞n ；④关于x 的一元二次方程ax 2+bx +c =-4的两根为-5和-1，其中正确的是__________．【解析】解：由图象知，抛物线与x 轴有2个公共点，∴b 2－4ac ＞0，即①正确；抛物线有最低点，当x=－3时，y有最小值－6，即ax2+bx+c≥-6，故②正确；抛物线的对称轴为x=－3，点(-2，m)，(-5，n)在抛物线上，∴m<n，故③错误；由图象知，当x=－1时，y=－4，由对称性可知，当x=－5时，y=－4，故④正确；综上，答案为：①②④.【变式2-1】（2018·信阳一模）如图是甲、乙两车在某时段速度随时间变化的图象，下列结论错误的是（）A．乙前4秒行驶的路程为48米B．在0到8秒内甲的速度每秒增加4米/秒C．两车到第3秒时行驶的路程相同D．在4到8秒内甲的速度都大于乙的速度【变式2-2】（2019·南阳模拟）如图，若二次函数y＝ax2+bx+c（a≠0）图象的对称轴为x＝1，与y轴交于点C，与x轴交于点A、点B（﹣1，0），则①二次函数的最大值为a+b+c；②a﹣b+c＜0；③b2﹣4ac ＜0；④当y＞0时，﹣1＜x＜3．其中正确的个数是（）A．1 B．2 C．3 D．4【例3】（2019·河南中考仿真卷）如图1，在矩形ABCD中，动点E从A出发，沿AB→BC方向运动，当点E到达点C时停止运动，过点E作FE⊥AE，交CD于F点，设点E运动路程为x，FC＝y，如图2所表示的是y与x的函数关系的大致图象，当点E在BC上运动时，FC的最大长度是25，则矩形ABCD的面积是（）A ．235B ．5C ．6D ．254【答案】B .【解析】解：若点E 在BC 上时，如图∵∠EFC +∠AEB ＝90°，∠FEC +∠EFC ＝90°， ∴∠CFE ＝∠AEB ， ∴△CFE ∽△BEA ， ∴CF CEBE AB=，当E 在BC 中点时，CF 有最大值，BE ＝CE ＝x ﹣52，即2552CEBE=，∴BE ＝CE ＝1，∴BC ＝2，AB ＝52，∴矩形ABCD 的面积为2×52＝5；故答案为：B ．【变式3-1】（2019·三门峡二模）如图1，则等边三角形ABC 中，点P 为BC 边上的任意一点，且∠APD ＝60°，PD 交AC 于点D ，设线段PB 的长度为x ，CD 的长度为y ，若y 与x 的函数关系的大致图象如图2，则等边三角形ABC 的面积为．【变式3-2】（2019·商丘二模）如图1，四边形ABCD中，AB∥CD，∠ADC＝90°，P从A点出发，以每秒1个单位长度的速度，按A→B→C→D的顺序在边上匀速运动，设P点的运动时间为t秒，△P AD的面积为S，S关于t的函数图象如图2所示，当P运动到BC中点时，△APD的面积为（）图1 图2A．4B．5C．6D．71.（2018·焦作一模）一个寻宝游戏的寻宝通道如图1所示，通道由在同一平面内的AB，BC，CA，OA，OB，OC组成．为记录寻宝者的行进路线，在BC的中点M处放置了一台定位仪器．设寻宝者行进的时间为x，寻宝者与定位仪器之间的距离为y，若寻宝者匀速行进，且表示y与x的函数关系的图象大致如图2所示，则寻宝者的行进路线可能为（）图1 图2A．A→O→B B．B→A→C C．B→O→C D．C→B→O2.（2019·开封二模）小明家、食堂，图书馆在同一条直线上，小明从家去食堂吃早餐，接着去图书馆读报，然后回家，如图反映了这个过程中，小明离家的距离y（km）与时间x（min）之间的对应关系，根据图象，下列说法正确的是（）A．小明吃早餐用了25minB．食堂到图书馆的距离为0.6kmC．小明读报用了30minD．小明从图书馆回家的速度为0.8km/min3.（2019·商丘二模）已知二次函数y＝ax2+bx+c中，函数y与自变量x的部分对应值如表所示：x…﹣5﹣4﹣3﹣2﹣1…y…﹣8﹣3010…当y＜﹣3时，x的取值范围是．4.（2019·开封模拟）如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点A（1，0），对称轴为直线x＝﹣1，当y＞0时，x的取值范围是（）A．﹣1＜x＜1B．﹣3＜x＜﹣1C．x＜1D．﹣3＜x＜15.在矩形ABCD中，AD=2AB=4，E是AD的中点，一块足够大的三角板的直角顶点与点E重合，将三角板绕点E旋转，三角板的两直角边分别交AB，BC（或它们的延长线）于点M，N，设∠AEM=α（0°＜α＜90°），给出下列四个结论：①AM=CN；②∠AME=∠BNE；③BN﹣AM=2；④S △EMN =22cos．上述结论中正确的个数是（）A ．1B ．2C ．3D ．46.已知二次函数y =ax 2+bx +c （a ≠0）的图象如图所示，并且关于x 的一元二次方程ax 2+bx +c ﹣m =0有两个不相等的实数根，下列结论：①b 2﹣4ac ＜0；②abc ＞0；③a ﹣b +c ＜0；④m ＞﹣2，其中，正确的个数有（）A ．1B ．2C ．3D ．47.阅读对话，解答问题：（1）分别用a 、b 表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字，请用树状图法或列表法写出（a ，b ）的所有取值；（2）求在（a ，b ）中使关于x 的一元二次方程x 2﹣ax +2b =0有实数根的概率．8.（2019·许昌月考）如图，已知在Rt△ABC中，∠ABC=90°，点D沿BC自B向C运动（点D与点B、C不重合），作BE⊥AD于E，CF⊥AD于F，则BE+CF的值（）A．不变B．增大C．减小D．先变大再变小9.（2018·洛宁县模拟）如图，已知在Rt△ABC中，∠ABC=90°，点D是BC边的中点，分别以B、C 为圆心，大于线段BC长度一半的长为半径画弧，两弧在直线BC上方的交点为P，直线PD交AC于点E，连接BE，则下列结论：①ED⊥BC；②∠A=∠EBA；③EB平分∠AED；④ED=12AB中，一定正确的是（）A．①②③B．①②④C．①③④D．②③④10.（2018·洛宁县模拟）一般情况下，中学生完成数学家庭作业时，注意力指数随时间x（分钟）的变化规律如图所示（其中AB、BC为线段，CD为双曲线的一部分）．（1）分别求出线段AB和双曲线CD的函数关系式；（2）若学生的注意力指数不低于40为高效时间，根据图中信息，求出一般情况下，完成一份数学家庭作业的高效时间是多少分钟？11.（2019·实验中学三模）如图，正方形ABCD的边长为a，点E在边AB上运动（不与点A，B重合），∠DAM＝45°，点F在射线AM上，且AF BE，CF与AD相交于点G，连接EC，EF，EG，则下列结论：①∠ECF ＝45°；②△AEG 的周长为（）a ；③BE 2+DG 2＝EG 2；④△EAF 的面积的最大值18a 2．其中正确的结论是．（填写所有正确结论的序号）12.（2019·周口二模）如图1，E 为矩形ABCD 边AD 上的一点，点P 从点B 沿折线BE -ED -DC 运动到点C 时停止，点Q 从点B 沿BC 运动到点C 时停止，它们运动的速度都是2 cm /s ．若P ，Q 同时开始运动，设运动时间为t （s ），△BPQ 的面积为y （cm 2），已知y 与t 的函数关系图象如图2，则CDBE的值为（） A．3BCD图1 图213.(2019·洛阳联考)在矩形ABCD 中，AB >CD ，对角线AC ，BD 相交于点O ，动点P 由点A 出发，沿AB →BC →CD 向点D 运动．设点P 的运动路程为x ，△AOP 的面积为y ，y 与x 的函数关系图象如图②所示，则AD 边的长为（）A . 3B . 4C . 5D .614.（2019·大联考）在正方形ABCD 中，点P 从点D 出发，沿着D →A 方向匀速运动，到达点A 后停止运动，点Q 从点D 出发，沿着D —C —B —A 的方向匀速运动，到达点A 后停止运动. 已知点P的运动速图1图2度为4，图②表示P、Q两点同时出发x秒后，△APQ的面积为y与x的函数关系，则点Q的运动速度可能是（）A. 2B. 3C. 8D. 12图①图②15.如图，在矩形ABCD中，动点P从点B出发，沿B-C-D-A方向运动到点A停止，运动速度为1单位每秒. 设点P的运动路程为x，△ABP的面积为y，若y与x的函数关系式如图2所示，则△ABC的面积为16.（2019·洛阳模拟）如图,在矩形ABCD中,动点P从点A出发,沿A→B→C运动,设P A=x点D到直线P A的距离为y且y关于x的函数图象如图所示,则当△PCD和△P AB的面积相等时,y的值为____.17.（2019·郑州二模）如图1，四边形ABCD 中，AB∥CD，∠B=90°，AC=AD．动点P 从点B 出发，沿折线B-A-D-C 方向以 1 单位/秒的速度匀速运动，在整个运动过程中，△BCP 的面积S 与运动时间t（秒）的函数图象如图2 所示，则AD 等于图1 图218.（2019·河南模拟）二次函数y=ax2+bx+c的大致图象如图所示，顶点坐标为（-2，-9a），下列结论：①4a+2b+c>0；②5a-b+c=0；③若方程a(x+5)(x-1)=-1有两个根x1，x2，且x1<x2，则-5< x1< x2<1；④若方程|ax2+bx+c|=1有四个根，则这四个根的和为-4，其中正确的结论有（）A. 1个B.2个C. 3个D.4个19.（2019·商丘二模）如图1，四边形ABCD中，AB∥CD，∠ADC=90°，P从A点出发，以每秒1个单位长度的速度，按A→B→C→D的顺序在边上匀速运动，设点P的运动时间为t秒，△P AD的面积为S，S关于t的函数图象如图2所示，当P运动到BC中点时，△P AD的面积为（）A．4B．8C．6D．5图1 图2。