[医学]人工神经网络建模matlab.ppt
合集下载
人工神经网络建模(Artificial Neuron Nets)
人工神经网络建模(Artificial Neuron Nets)
• 一、引例
• 1981年生物学家格若根(W. Grogan)和维什(W.Wirth)发现了两 类蚊子(或飞蠓midges).他们测量了这两类蚊子每个个体的翼长和触角 长,数据如下: • • • • • • • • • 翼长 1.78 1.96 1.86 1.72 2.00 2.00 1.96 1.74 触角长 类别 1.14 Apf 1.18 Apf 1.20 Apf 1.24 Af 1.26 Apf 1.28 Apf 1.30 Apf 1.36 Af
m
例如,若记
z wi xi
i 1
m
ቤተ መጻሕፍቲ ባይዱ
• 取激发函数为符号函数
1, x 0, sgn( x) 0, x 0.
则
1, y f ( z) 0,
• S型激发函数:
w x w x
i 1 i i 1 m i
m
i
, ,
i
1 f ( x) , x 1 e
• 规 定 目 标 为 : 当 t(1)=0.9 时 表 示 属 于 Apf 类 , t(2)=0.1表示属于Af类。 • 设两个权重系数矩阵为:
w1 (1,1) w1 (1,2) w1 (1,3) W1 w1 (2,1) w1 (2,2) w1 (2,3)
( p) l
( p1) l
(i, j) a ( j),
( p) ( p) l l 1
l 1,...,L,
(10)
w (i, j )
表示第-1层第个元对第层第个元输入 的第次迭代时的权重
( p) l
其中
( p) L
• 一、引例
• 1981年生物学家格若根(W. Grogan)和维什(W.Wirth)发现了两 类蚊子(或飞蠓midges).他们测量了这两类蚊子每个个体的翼长和触角 长,数据如下: • • • • • • • • • 翼长 1.78 1.96 1.86 1.72 2.00 2.00 1.96 1.74 触角长 类别 1.14 Apf 1.18 Apf 1.20 Apf 1.24 Af 1.26 Apf 1.28 Apf 1.30 Apf 1.36 Af
m
例如,若记
z wi xi
i 1
m
ቤተ መጻሕፍቲ ባይዱ
• 取激发函数为符号函数
1, x 0, sgn( x) 0, x 0.
则
1, y f ( z) 0,
• S型激发函数:
w x w x
i 1 i i 1 m i
m
i
, ,
i
1 f ( x) , x 1 e
• 规 定 目 标 为 : 当 t(1)=0.9 时 表 示 属 于 Apf 类 , t(2)=0.1表示属于Af类。 • 设两个权重系数矩阵为:
w1 (1,1) w1 (1,2) w1 (1,3) W1 w1 (2,1) w1 (2,2) w1 (2,3)
( p) l
( p1) l
(i, j) a ( j),
( p) ( p) l l 1
l 1,...,L,
(10)
w (i, j )
表示第-1层第个元对第层第个元输入 的第次迭代时的权重
( p) l
其中
( p) L
人工神经网络-95页PPT文档资料

MATLAB名字由MATrix和 LABoratory 两词的前三个字 母组合而成。20世纪七十年代后期,时任美国新墨西 哥大学计算机科学系主任的Cleve Moler教授出于减轻 学生编程负担的动机,为学生设计了一组调用LINPACK 和EISPACK库程序的“通俗易用”的接口,此即用 FORTRAN编写的萌芽状态的MATLAB。
《医学信息分析与决策》课程组
10
一、神经网络简介
神经网络的基本功能
传统分类能力
ANN 分类能力
分类与识别功能
2019/11/29
• ①“初值:步长:终值” 产生一个行向量(行矩 阵)。当步长为1时可以省略。如:1:5;1:2:6
• ②特殊命令:linspace(x,x2,n): ones(n)
(3)用input指令输入单个参数 (4)用小型矩阵或用数据文件输入
2019/11/29
《医学信息分析与决策》课程组
28
二、MATLAB简介
25
二、MATLAB简介
数值与变量
①数值
②变量:
• 变量名、函数名是对大小写很敏感的,两个字符串 表示的变量,字母都相同,大小写不同,也视为不 同的变量;
• 第一个字母必须是英文字母; • 字符间不可留空格; • 最多只能有31个字符(只能用英文字母、数字和下
连字符) • 一行中“%”后的内容仅作注释用,对MATLAB的计
《医学信息分析与决策》课程组
11
一、神经网络简介
《医学信息分析与决策》课程组
10
一、神经网络简介
神经网络的基本功能
传统分类能力
ANN 分类能力
分类与识别功能
2019/11/29
• ①“初值:步长:终值” 产生一个行向量(行矩 阵)。当步长为1时可以省略。如:1:5;1:2:6
• ②特殊命令:linspace(x,x2,n): ones(n)
(3)用input指令输入单个参数 (4)用小型矩阵或用数据文件输入
2019/11/29
《医学信息分析与决策》课程组
28
二、MATLAB简介
25
二、MATLAB简介
数值与变量
①数值
②变量:
• 变量名、函数名是对大小写很敏感的,两个字符串 表示的变量,字母都相同,大小写不同,也视为不 同的变量;
• 第一个字母必须是英文字母; • 字符间不可留空格; • 最多只能有31个字符(只能用英文字母、数字和下
连字符) • 一行中“%”后的内容仅作注释用,对MATLAB的计
《医学信息分析与决策》课程组
11
一、神经网络简介
matlab_人工神经网络 ppt课件

matlab_人工神经网络
• (4)通信。自适应均衡、回波抵消、路由选 择和ATM网络中的呼叫接纳识别和控制。
• (5)空间科学。空间交汇对接控制、导航信 息智能管理、飞行器制导和飞行程序优化管理 等。
matlab_人工神经网络
• 大脑可视作为1000多亿神经元组成的神经网络
• 图1 神经元的解剖图
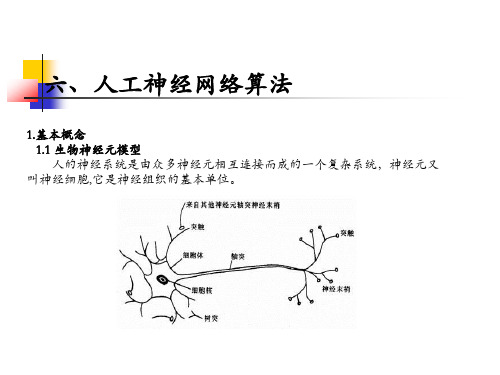
• 神经元的信息传递和处理是一种电化学活动。树 突由于电化学作用接受外界的刺激;通过胞体内 的活动体现为轴突电位,当轴突电位达到一定的 值则形成神经脉冲或动作电位;再通过轴突末梢 传递给其它的神经元.从控制论的观点来看;这 一过程可以看作一个多输入单输出非线性系统的 动态过程
matlab_人工神经网络
电脉冲
输 入
树 突
细胞体 形成 轴突
突
输
触
Байду номын сангаас
出
信息处理
传输
图12.2 生物神经元功能模型
• 归纳一下生物神经元传递信息的过程:生物神经 元是一个多输入、单输出单元。常用的人工神经 元模型可用图2模拟。
图2 人工神经元(感知器)示意图
x • 当神经元j有多个输入 i (i=1,2,…,m)和单个输出
yj 时,输入和输出的关系可表示为:
s
j
m
wij xi
i 1
j
y j f (s j )
• 其中 j 为阈值,w ij 为从神经元i到神经元j的
连接权重因子,f( )为传递函数,或称激励函 数。
matlab_人工神经 网络
m
z wixi i1
• 取激发函数为符号函数
sgnx()10,,
matlab_人工神经网络
第6章人工神经网络算法ppt课件
1.基本概念 1.3 主要的神经网络模型 目前使用的比较典型的一些神经网络模型主要有以下几类:
4.随机型神经网络 随机型神经网络其基本思想是:不但让网络的误差和能量函数向减小的方
向变化,而且还可按某种方式向增大的方向变化,目的是使网络有可能跳出局部 极小值而向全局最小点收敛。随机型神经网络的典型算法是模拟退火算法。
曲线越陡。
六、人工神经网络算法
1.基本概念 1.2 人工神经元模型 神经元采用了不同的激活函数,使得神经元具有不同的信息处理特性,并且
神经元的信息处理特性是决定神经网络整体性能的主要因素之一。 下面介绍四种常用的激活函数形式:
(4)高斯函数。高斯函数(也称钟型函数)也是极为重要的一类激活函数,常用 于径向基神经网络(RBF网络),其表达式为:
通过调整权值和阈值,使得误差能量达到最小时,网络趋于稳定状态,学习
结束。
(1)输出层与隐含层之间的权值调整。对每一个 wjk 的修正值为:
w jk
E
w jk
E
netk
netk w jk
J
式中: 为学习步长,取值介于(0,1),对式 netk wjkOj 求偏导得:
j0
netk wjk
Oj
x1
w1i
x2
w2ifΒιβλιοθήκη yixnwni
x0 1
六、人工神经网络算法
1.基本概念 1.2 人工神经元模型 在神经元中,对信号进行处理采用的是数学函数,通常称为激活函数、激励
函数或挤压函数,其输入、输出关系可描述为
u j
f
n
wij xi
j
i1
y f uj
式中xi i 1,2,,n是从其它神经元传来的输入信号; j 是该神经元的阈值;
4.随机型神经网络 随机型神经网络其基本思想是:不但让网络的误差和能量函数向减小的方
向变化,而且还可按某种方式向增大的方向变化,目的是使网络有可能跳出局部 极小值而向全局最小点收敛。随机型神经网络的典型算法是模拟退火算法。
曲线越陡。
六、人工神经网络算法
1.基本概念 1.2 人工神经元模型 神经元采用了不同的激活函数,使得神经元具有不同的信息处理特性,并且
神经元的信息处理特性是决定神经网络整体性能的主要因素之一。 下面介绍四种常用的激活函数形式:
(4)高斯函数。高斯函数(也称钟型函数)也是极为重要的一类激活函数,常用 于径向基神经网络(RBF网络),其表达式为:
通过调整权值和阈值,使得误差能量达到最小时,网络趋于稳定状态,学习
结束。
(1)输出层与隐含层之间的权值调整。对每一个 wjk 的修正值为:
w jk
E
w jk
E
netk
netk w jk
J
式中: 为学习步长,取值介于(0,1),对式 netk wjkOj 求偏导得:
j0
netk wjk
Oj
x1
w1i
x2
w2ifΒιβλιοθήκη yixnwni
x0 1
六、人工神经网络算法
1.基本概念 1.2 人工神经元模型 在神经元中,对信号进行处理采用的是数学函数,通常称为激活函数、激励
函数或挤压函数,其输入、输出关系可描述为
u j
f
n
wij xi
j
i1
y f uj
式中xi i 1,2,,n是从其它神经元传来的输入信号; j 是该神经元的阈值;
人工神经网络算法基础精讲ppt课件

30
2.3学习规则
学习规则
在神经网络的学习中,各神经元的连接权值需按一定的规则
调整,这种权值调整规则称为学习规则。下面介绍几种常见的学习
规则。
1.Hebb学习规则
2.Delta(δ)学习规则
3.LMS学习规则
4.胜者为王学习规则
5.Kohonen学习规则
6.概率式学习规则
2.3学习规则
1.Hebb学习规则
突触结构示意图
1.3生物神经元的信息处理机理
电脉冲
输 入
树 突
细胞体 形成 轴突
突
输
触
出
信息处理
传输
图 12.2 生物神经元功能模型
神经元的兴奋与抑制
当传入神经元冲动,经整和使细胞膜电位升高,超过动作电位 的阈值时,为兴奋状态,产生神经冲动,由轴突经神经末稍传出。 当传入神经元的冲动,经整和,使细胞膜电位降低,低于阈值时, 为抑制状态,不产生神经冲动。
④神经元的输出和响应是个输入值的综合作用的结果。
⑤兴奋和抑制状态,当细胞膜电位升高超过阈值时,细胞进入兴奋 状态,产生神经冲动;当膜电位低于阈值时,细胞进入抑制状态。
13
1.6激活函数
神经元的描述有多种,其区别在于采用了不同的激活函数,不 同的激活函数决定神经元的不同输出特性,常用的激活函数有如下 几种类型:
1957年,F.Rosenblatt提出“感知器”(Perceptron)模型,第一 次把神经网络的研究从纯理论的探讨付诸工程实践,掀起了人工神 经网络研究的第一次高潮。
4
1.1人工神经网络发展简史
20世纪60年代以后,数字计算机的发展达到全盛时期,人们误以 为数字计算机可以解决人工智能、专家系统、模式识别问题,而放 松了对“感知器”的研究。于是,从20世纪60年代末期起,人工神 经网络的研究进入了低潮。
2.3学习规则
学习规则
在神经网络的学习中,各神经元的连接权值需按一定的规则
调整,这种权值调整规则称为学习规则。下面介绍几种常见的学习
规则。
1.Hebb学习规则
2.Delta(δ)学习规则
3.LMS学习规则
4.胜者为王学习规则
5.Kohonen学习规则
6.概率式学习规则
2.3学习规则
1.Hebb学习规则
突触结构示意图
1.3生物神经元的信息处理机理
电脉冲
输 入
树 突
细胞体 形成 轴突
突
输
触
出
信息处理
传输
图 12.2 生物神经元功能模型
神经元的兴奋与抑制
当传入神经元冲动,经整和使细胞膜电位升高,超过动作电位 的阈值时,为兴奋状态,产生神经冲动,由轴突经神经末稍传出。 当传入神经元的冲动,经整和,使细胞膜电位降低,低于阈值时, 为抑制状态,不产生神经冲动。
④神经元的输出和响应是个输入值的综合作用的结果。
⑤兴奋和抑制状态,当细胞膜电位升高超过阈值时,细胞进入兴奋 状态,产生神经冲动;当膜电位低于阈值时,细胞进入抑制状态。
13
1.6激活函数
神经元的描述有多种,其区别在于采用了不同的激活函数,不 同的激活函数决定神经元的不同输出特性,常用的激活函数有如下 几种类型:
1957年,F.Rosenblatt提出“感知器”(Perceptron)模型,第一 次把神经网络的研究从纯理论的探讨付诸工程实践,掀起了人工神 经网络研究的第一次高潮。
4
1.1人工神经网络发展简史
20世纪60年代以后,数字计算机的发展达到全盛时期,人们误以 为数字计算机可以解决人工智能、专家系统、模式识别问题,而放 松了对“感知器”的研究。于是,从20世纪60年代末期起,人工神 经网络的研究进入了低潮。
MATLAB教学课件.ppt

直接输入法:将矩阵的元素用方括号括起来,按矩阵行的顺 序输入各元素,同一行的各元素之间用空格或逗号分隔,不同 行的元素之间用分号分隔。(也可以用回车键代替分号)
例如,键入命令: A=[1 2 3;4 5 6;7 8 9] 输出结果是: A = 1 2 3
456
789
四. 矩阵运算
1.建立矩阵
3.图形功能
MATLAB提供了两个层次的图形命令:一种是对图形句柄进 行的低级图形命令,另一种是建立在低级图形命令之上的高 级图形命令。利用MATLAB的高级图形命令可以轻而易举地 绘制二维、三维乃至四维图形,并可进行图形和坐标的标识、 视角和光照设计、色彩精细控制等等。
4.应用工具箱
基本部分和各种可选的工MATLAB最基本的数据对象,MATLAB的大部分运算 或命令都是在矩阵运算的意义下执行的。在MATLAB中,不需 对矩阵的维数和类型进行说明,MATLAB会根据用户所输入的 内容自动进行配置。
1.建立矩阵
建立矩阵可以用:直接输入法、利用函数建立矩阵和利 用M文件建立矩阵。
一. MATLAB特点:
一. MATLAB特点:
1. 数值计算和符号计算功能
MATLAB的数值计算功能包括:矩阵运算、多项式和有 理分式运算、数据统计分析、数值积分、优化处理等。符 号计算将得到问题的解析解。
2.MATLAB语言
MATLAB除了命令行的交互式操作以外,还可以程序方式 工作。使用MATLAB可以很容易地实现C或FORTRAN语言的 几乎全部功能,包括Windows图形用户界面的设计。
基本部分中有数百个内部函数。
其工具箱分为两大类:功能性工具箱和学科性工具箱。 功能性工具箱主要用来扩充其符号计算功能、可视建模仿真 功能及文字处理功能等。学科性工具箱专业性比较强,如控 制系统工具箱、信号处理工具箱、神经网络工具箱、最优化 工具箱、金融工具箱等,用户可以直接利用这些工具箱进行 相关领域的科学研究。
例如,键入命令: A=[1 2 3;4 5 6;7 8 9] 输出结果是: A = 1 2 3
456
789
四. 矩阵运算
1.建立矩阵
3.图形功能
MATLAB提供了两个层次的图形命令:一种是对图形句柄进 行的低级图形命令,另一种是建立在低级图形命令之上的高 级图形命令。利用MATLAB的高级图形命令可以轻而易举地 绘制二维、三维乃至四维图形,并可进行图形和坐标的标识、 视角和光照设计、色彩精细控制等等。
4.应用工具箱
基本部分和各种可选的工MATLAB最基本的数据对象,MATLAB的大部分运算 或命令都是在矩阵运算的意义下执行的。在MATLAB中,不需 对矩阵的维数和类型进行说明,MATLAB会根据用户所输入的 内容自动进行配置。
1.建立矩阵
建立矩阵可以用:直接输入法、利用函数建立矩阵和利 用M文件建立矩阵。
一. MATLAB特点:
一. MATLAB特点:
1. 数值计算和符号计算功能
MATLAB的数值计算功能包括:矩阵运算、多项式和有 理分式运算、数据统计分析、数值积分、优化处理等。符 号计算将得到问题的解析解。
2.MATLAB语言
MATLAB除了命令行的交互式操作以外,还可以程序方式 工作。使用MATLAB可以很容易地实现C或FORTRAN语言的 几乎全部功能,包括Windows图形用户界面的设计。
基本部分中有数百个内部函数。
其工具箱分为两大类:功能性工具箱和学科性工具箱。 功能性工具箱主要用来扩充其符号计算功能、可视建模仿真 功能及文字处理功能等。学科性工具箱专业性比较强,如控 制系统工具箱、信号处理工具箱、神经网络工具箱、最优化 工具箱、金融工具箱等,用户可以直接利用这些工具箱进行 相关领域的科学研究。
第四课 MATLAB NN工具箱 人工神经网络理论及应用 教学课件

第九页,共24页。
Net对象属性(shǔxìng):函数属性 (shǔxìng)
定义了在权值调整,初始化,性能计算或训 练时采用的算法
adaptFcn:权值/阈值(yùzhí)调整 initFcn:初始化权值/阈值(yùzhí) performFcn:性能指标函数 trainFcn:训练函数信号处理
w (k 1 ) w (k ) Δ (k w 1 )
训练函数(hánshù):traingdm 演示 :nnd12mo
第十七页,共24页。
MATLAB BP算法: 学习(xuéxí)速率 可变BP
(k1) k kd ine c c((k k))
J(k1)J(k) J(k1)J(k)
训练(xùnliàn)函数:traingdx 演示 :nnd12vl
25 训练周期
net.trainParam.time inf 最多训练时间
不同训练函数对应参数可能不同
第十二页,共24页。
Net对象(duìxiàng)属性:权值/阈 值
基于权值和阈值属性的访问方式(fāngshì): IW 输入权值; LW 网络层权值; b 阈值(输入层+网络层)
演示
第十三页,共24页。
支持以下 (yǐxià)NN模型:
感知器 BP网络 RBFN网络 竞争型网络 自组织网络 反响网络
时延网络(wǎngluò)
NARX网络 (wǎngluò)
自定义网络 (wǎngluò)
第三页,共24页。
MATLAB NN工具箱功能 (gōngnéng)
NNET 5.0含近200个工具箱函数,包括 (bāokuò):
பைடு நூலகம்Δ(k w ) g (k) 0
训练(xùnliàn)函数:trainrp
Net对象属性(shǔxìng):函数属性 (shǔxìng)
定义了在权值调整,初始化,性能计算或训 练时采用的算法
adaptFcn:权值/阈值(yùzhí)调整 initFcn:初始化权值/阈值(yùzhí) performFcn:性能指标函数 trainFcn:训练函数信号处理
w (k 1 ) w (k ) Δ (k w 1 )
训练函数(hánshù):traingdm 演示 :nnd12mo
第十七页,共24页。
MATLAB BP算法: 学习(xuéxí)速率 可变BP
(k1) k kd ine c c((k k))
J(k1)J(k) J(k1)J(k)
训练(xùnliàn)函数:traingdx 演示 :nnd12vl
25 训练周期
net.trainParam.time inf 最多训练时间
不同训练函数对应参数可能不同
第十二页,共24页。
Net对象(duìxiàng)属性:权值/阈 值
基于权值和阈值属性的访问方式(fāngshì): IW 输入权值; LW 网络层权值; b 阈值(输入层+网络层)
演示
第十三页,共24页。
支持以下 (yǐxià)NN模型:
感知器 BP网络 RBFN网络 竞争型网络 自组织网络 反响网络
时延网络(wǎngluò)
NARX网络 (wǎngluò)
自定义网络 (wǎngluò)
第三页,共24页。
MATLAB NN工具箱功能 (gōngnéng)
NNET 5.0含近200个工具箱函数,包括 (bāokuò):
பைடு நூலகம்Δ(k w ) g (k) 0
训练(xùnliàn)函数:trainrp
神经网络控制系统教程PPT(MATLAB基于Simulink的三种典型神经网络控制系统学习资料)

22
1. 基于传统控制理论的神经控制将神经网络作为传统控制系统中的一个或几个部分,用以充当辨识器,或对象模型,或控制器,或估计器,或优化计算等。这种方式很多,常见的一些方式归纳如下:
22
(a)
(b)
图3-3 神经直接逆动态控制系统
1).神经直接逆动态控制神经直接逆动态控制采用受控对象的一个逆模型,它与受控对象串联,以便使系统在期望响应(网络输入
22
(2)神经间接自校正控制间接自校正控制一般称为自校正控制。自校正控制是一种利用辨识器将对象参数进行在线估计,用控制器实现参数的自动整定相结合的自适应控制技术,它可用于结构已知而参数未知但恒定的随机系统,也可用于结构已知而参数缓慢变化的随机系统。
图3-4 神经自校正控制系统
22
神经自校正控制结构如图3-4所示,它由一个自校正控制器和一个能够在线辨识的神经网络辨识器组成。自校正控制器与被控对象构成反馈回路,根据神经网 络辨识器和控制器设计规则,以得到控制器的参数。 可见,辨识器和自校正控制器的在线设计是自校正控 制实现的关键。
22
上述两种分类并无本质差别,只是后者划分更细一些,几乎涉及到传统控制、系统辨识。滤波和预报等所有方面,这也间接地反映了随着神经网络理论和应用研究的深入,将向控制领域、信息领域等进一步透。为了更能从本质上认识神经网络在实现智能控制中的作用和地位。1998年李士勇将神经网络控制从它与传统控制和智能控制两大门类的结合上考虑分为两大类:即基于传统控制理论的神经控制和基于神经网络的智能控制两大类。
神经网络控制系统
1
神经网络控制理论基于Simulink的三种典型神经网络控制系统
神经网络发展至今已有半个多世纪的历史,概括起来经历了三个阶段:20世纪40 60年代的发展初期; 70年代的研究低潮期;80年代,神经网络的理论研究取得了突破性进展。神经网络控制是将神经网络在相应的控制系统结构中当做控制器或辨识器。神经网络控制的发展,虽仅有十余年的历史,但已有了多种控制结构。
1. 基于传统控制理论的神经控制将神经网络作为传统控制系统中的一个或几个部分,用以充当辨识器,或对象模型,或控制器,或估计器,或优化计算等。这种方式很多,常见的一些方式归纳如下:
22
(a)
(b)
图3-3 神经直接逆动态控制系统
1).神经直接逆动态控制神经直接逆动态控制采用受控对象的一个逆模型,它与受控对象串联,以便使系统在期望响应(网络输入
22
(2)神经间接自校正控制间接自校正控制一般称为自校正控制。自校正控制是一种利用辨识器将对象参数进行在线估计,用控制器实现参数的自动整定相结合的自适应控制技术,它可用于结构已知而参数未知但恒定的随机系统,也可用于结构已知而参数缓慢变化的随机系统。
图3-4 神经自校正控制系统
22
神经自校正控制结构如图3-4所示,它由一个自校正控制器和一个能够在线辨识的神经网络辨识器组成。自校正控制器与被控对象构成反馈回路,根据神经网 络辨识器和控制器设计规则,以得到控制器的参数。 可见,辨识器和自校正控制器的在线设计是自校正控 制实现的关键。
22
上述两种分类并无本质差别,只是后者划分更细一些,几乎涉及到传统控制、系统辨识。滤波和预报等所有方面,这也间接地反映了随着神经网络理论和应用研究的深入,将向控制领域、信息领域等进一步透。为了更能从本质上认识神经网络在实现智能控制中的作用和地位。1998年李士勇将神经网络控制从它与传统控制和智能控制两大门类的结合上考虑分为两大类:即基于传统控制理论的神经控制和基于神经网络的智能控制两大类。
神经网络控制系统
1
神经网络控制理论基于Simulink的三种典型神经网络控制系统
神经网络发展至今已有半个多世纪的历史,概括起来经历了三个阶段:20世纪40 60年代的发展初期; 70年代的研究低潮期;80年代,神经网络的理论研究取得了突破性进展。神经网络控制是将神经网络在相应的控制系统结构中当做控制器或辨识器。神经网络控制的发展,虽仅有十余年的历史,但已有了多种控制结构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 哪一分类直线才是正确的呢?
• 因此如何来确定这个判别直线是一个值得研究的 问题.一般地讲,应该充分利用已知的数据信息 来确定判别直线.
• 再如,如下的情形已经不能用分类直线的办法:
• 新思路:将问题看作一个系统,飞蠓的数据作为输 入,飞蠓的类型作为输出,研究输入与输出的关系。
二、神经元与神经网络
• 分类结果:(1.24,1.80),(1.28,1.84)属 于Af类;(1.40,2.04)属于 Apf类.
图2 分类直线图
• •缺陷:根据什么原则确定分类直线?
• 若取A=(1.46,2.10), B=(1.1,1.6)不变,则分类直线 变为 y=1.39x+0.071
分类结果变为: (1.24,1.80), (1.40,2.04) 属于Apf类; (1.28,1.84)属于Af类
• 记 wij 表示递推一次的修改量,则有
wijwijwij (3)
y f( wixi ) i1
• θ 为阈值,f(X)是激发函数;它可以是线性
函数,也可以是非线性函数.
例如,若记
m
z wixi i1
• 取激发函数为符号函数
sgnx)(10,,
x0,
(z)
1,
0,
m
wi xi ,
i1 m
• 记wij为从输入向量的第j (j=1,…,m) 个分量到输出向量的第i (i=1,…,n)个分量的权重。通常理论值与实际值有一误差, 网络学习则是指不断地把与比较,并根据极小原则修改参 数wij,使误差平方和达最小:
n
min (tpiopi)2 • (p=1,…,P) • (2) i1
• Delta学习规则:
人工神经网络建模 matlab.ppt
• 问:如果抓到三只新的蚊子,它们的触角长和翼长 分别为(l.24,1.80); (l.28,1.84);(1.40,2.04).问 它们应分别属于哪一个种类?
• 解法一:
• 把翼长作纵坐标,触角长作横坐标;那么 每个蚊子的翼长和触角决定了坐标平面的一个 点.其中 6个蚊子属于 APf类;用黑点“·”表 示;9个蚊子属 Af类;用小圆圈“。”表示.
(2)网络说话
• 人们把一本教科书用网络把它读出来(当然需 要通过光电,电声的信号转换);开始网络说 的话像婴儿学语那样发出“巴、巴、巴”的声 响;但经过B-P算法长时间的训练竟能正确读 出英语课本中 90%的词汇.
• 从此用神经网络来识别语言和图象形成一个新 的热潮.
4、人工神经网络的基本特点
• (1)可处理非线性
• (2)并行结构.对神经网络中的每一个神经元来 说;其运算都是同样的.这样的结构最便于计算 机并行处理.
• (3)具有学习和记忆能力.一个神经网络 可以通过训练学习判别事物;学习某一种规 律或规则.神经网络可以用于联想记忆.
• (4)对数据的可容性大.在神经网络中 可以同时使用量化数据和质量数据(如 好、中、差、及格、不及格等).
wi xi ,
i1
• S型激发函数:
1
f (x)
,
1ex
0f(x)1;
或
f
(x)
ex ex
ex ex
,
1f(x)1.
• 注:若将阈值看作是一个权系数,-1是一个固定的 输入,另有m-1个正常的输入,则(1)式也可表 示为: (1)‘
m
y f ( wixi) i1
• (5)神经网络可以用大规模集成 电路来实现.如美国用 256个神经 元组成的神经网络组成硬件用于识 别手写体的邮政编码.
四、反向传播算法(B-P算法)
• Back propagation algorithm
• 算法的目的:根据实际的输入与输出数据, 计算模型的参数(权系数)
• 1.简单网络的B-P算法
• 大脑可视作为1000多亿神经元组成的神经网络 • 神经元的解剖图
• 图3 神经元的解剖图
• 神经元的信息传递和处理是一种电化学活 动.树突由于电化学作用接受外界的刺激;通 过胞体内的活动体现为轴突电位,当轴突电位 达到一定的值则形成神经脉冲或动作电位;再 通过轴突末梢传递给其它的神经元.从控制论 的观点来看;这一过程可以看作一个多输入单 输出非线性系统的动态过程
• 图6 简单网络
• 假设有P个训练样本,即有P个输入输出对 • (Ip, Tp),p=1,…,P, • 其中
• 输入向量为 , Ip (ip1,..i.p,m )T
• 目标输出向量为(实际上的)
Tp (tp1,..t.p,n)T
O(o,..o.,)T
• 网络输出向量为 (理论上的)
p p1 pn
• 神经网络研究的两个方面 • 从生理上、解剖学上进行研究 • 从工程技术上、算法上进行研究
三、人工神经网络(Artificial Neuron Nets, 简称 ANN)
• 神经元的数学模型
• 图4神经元的数学模型
• 其中x=(x1,…xm)T 输入向量,y为输出,
wi是权系数;输入与输出具有如下关系: m
• 得到的结果见图1
• 图1 飞蠓的触角长和翼长
• 思路:作一直线将两类飞蠓分开
• 例如;取A=(1.44,2.10)和 B=(1.10,1.16), 过A B两点作一条直线:
•
y= 1.47x - 0.017,
• 其中X表示触角长;y表示翼长.
• 分类规则:设一个蚊子的数据为(x, y), • 如果y≥1.47x - 0.017,则判断蚊子属Apf类; • 如果y<1.47x - 0.017;则判断蚊子属Af类.
• (1)‘
• 参数识别:假设函数形式已知,则可以从已有的 输入输出数据确定出权系数及阈值。
2、神经网络的数学模型
• 众多神经元之间组合形成神经网络,例如下图 的含有中间层(隐层)的B-P网络
• 图5 带中间层的B-P网络
3、量变引起质变------神经网络的作用
• (1)蚂蚁群
• 一个蚂蚁有50个神经元,单独的一个蚂蚁不能做 太多的事;甚至于不能很好活下去.但是一窝蚂蚁; 设有 10万个体,那么这个群体相当于500万个神经元 (当然不是简单相加,这里只为说明方便而言);那 么它们可以觅食、搬家、围攻敌人等等.
• 因此如何来确定这个判别直线是一个值得研究的 问题.一般地讲,应该充分利用已知的数据信息 来确定判别直线.
• 再如,如下的情形已经不能用分类直线的办法:
• 新思路:将问题看作一个系统,飞蠓的数据作为输 入,飞蠓的类型作为输出,研究输入与输出的关系。
二、神经元与神经网络
• 分类结果:(1.24,1.80),(1.28,1.84)属 于Af类;(1.40,2.04)属于 Apf类.
图2 分类直线图
• •缺陷:根据什么原则确定分类直线?
• 若取A=(1.46,2.10), B=(1.1,1.6)不变,则分类直线 变为 y=1.39x+0.071
分类结果变为: (1.24,1.80), (1.40,2.04) 属于Apf类; (1.28,1.84)属于Af类
• 记 wij 表示递推一次的修改量,则有
wijwijwij (3)
y f( wixi ) i1
• θ 为阈值,f(X)是激发函数;它可以是线性
函数,也可以是非线性函数.
例如,若记
m
z wixi i1
• 取激发函数为符号函数
sgnx)(10,,
x0,
(z)
1,
0,
m
wi xi ,
i1 m
• 记wij为从输入向量的第j (j=1,…,m) 个分量到输出向量的第i (i=1,…,n)个分量的权重。通常理论值与实际值有一误差, 网络学习则是指不断地把与比较,并根据极小原则修改参 数wij,使误差平方和达最小:
n
min (tpiopi)2 • (p=1,…,P) • (2) i1
• Delta学习规则:
人工神经网络建模 matlab.ppt
• 问:如果抓到三只新的蚊子,它们的触角长和翼长 分别为(l.24,1.80); (l.28,1.84);(1.40,2.04).问 它们应分别属于哪一个种类?
• 解法一:
• 把翼长作纵坐标,触角长作横坐标;那么 每个蚊子的翼长和触角决定了坐标平面的一个 点.其中 6个蚊子属于 APf类;用黑点“·”表 示;9个蚊子属 Af类;用小圆圈“。”表示.
(2)网络说话
• 人们把一本教科书用网络把它读出来(当然需 要通过光电,电声的信号转换);开始网络说 的话像婴儿学语那样发出“巴、巴、巴”的声 响;但经过B-P算法长时间的训练竟能正确读 出英语课本中 90%的词汇.
• 从此用神经网络来识别语言和图象形成一个新 的热潮.
4、人工神经网络的基本特点
• (1)可处理非线性
• (2)并行结构.对神经网络中的每一个神经元来 说;其运算都是同样的.这样的结构最便于计算 机并行处理.
• (3)具有学习和记忆能力.一个神经网络 可以通过训练学习判别事物;学习某一种规 律或规则.神经网络可以用于联想记忆.
• (4)对数据的可容性大.在神经网络中 可以同时使用量化数据和质量数据(如 好、中、差、及格、不及格等).
wi xi ,
i1
• S型激发函数:
1
f (x)
,
1ex
0f(x)1;
或
f
(x)
ex ex
ex ex
,
1f(x)1.
• 注:若将阈值看作是一个权系数,-1是一个固定的 输入,另有m-1个正常的输入,则(1)式也可表 示为: (1)‘
m
y f ( wixi) i1
• (5)神经网络可以用大规模集成 电路来实现.如美国用 256个神经 元组成的神经网络组成硬件用于识 别手写体的邮政编码.
四、反向传播算法(B-P算法)
• Back propagation algorithm
• 算法的目的:根据实际的输入与输出数据, 计算模型的参数(权系数)
• 1.简单网络的B-P算法
• 大脑可视作为1000多亿神经元组成的神经网络 • 神经元的解剖图
• 图3 神经元的解剖图
• 神经元的信息传递和处理是一种电化学活 动.树突由于电化学作用接受外界的刺激;通 过胞体内的活动体现为轴突电位,当轴突电位 达到一定的值则形成神经脉冲或动作电位;再 通过轴突末梢传递给其它的神经元.从控制论 的观点来看;这一过程可以看作一个多输入单 输出非线性系统的动态过程
• 图6 简单网络
• 假设有P个训练样本,即有P个输入输出对 • (Ip, Tp),p=1,…,P, • 其中
• 输入向量为 , Ip (ip1,..i.p,m )T
• 目标输出向量为(实际上的)
Tp (tp1,..t.p,n)T
O(o,..o.,)T
• 网络输出向量为 (理论上的)
p p1 pn
• 神经网络研究的两个方面 • 从生理上、解剖学上进行研究 • 从工程技术上、算法上进行研究
三、人工神经网络(Artificial Neuron Nets, 简称 ANN)
• 神经元的数学模型
• 图4神经元的数学模型
• 其中x=(x1,…xm)T 输入向量,y为输出,
wi是权系数;输入与输出具有如下关系: m
• 得到的结果见图1
• 图1 飞蠓的触角长和翼长
• 思路:作一直线将两类飞蠓分开
• 例如;取A=(1.44,2.10)和 B=(1.10,1.16), 过A B两点作一条直线:
•
y= 1.47x - 0.017,
• 其中X表示触角长;y表示翼长.
• 分类规则:设一个蚊子的数据为(x, y), • 如果y≥1.47x - 0.017,则判断蚊子属Apf类; • 如果y<1.47x - 0.017;则判断蚊子属Af类.
• (1)‘
• 参数识别:假设函数形式已知,则可以从已有的 输入输出数据确定出权系数及阈值。
2、神经网络的数学模型
• 众多神经元之间组合形成神经网络,例如下图 的含有中间层(隐层)的B-P网络
• 图5 带中间层的B-P网络
3、量变引起质变------神经网络的作用
• (1)蚂蚁群
• 一个蚂蚁有50个神经元,单独的一个蚂蚁不能做 太多的事;甚至于不能很好活下去.但是一窝蚂蚁; 设有 10万个体,那么这个群体相当于500万个神经元 (当然不是简单相加,这里只为说明方便而言);那 么它们可以觅食、搬家、围攻敌人等等.
