U来公益贵州金星小学三年级数学思维训练
小学数学三年级思维训练练习题及答案

小学数学三年级思维训练练习题及答案题目:小学数学三年级思维训练练习题及答案说明:下面是小学三年级数学课堂上的一些思维训练练习题,希望同学们通过解题,培养自己的逻辑思维能力和数学运算能力。
每道题都附有答案,同学们可以对比自己的答案,并及时纠正。
祝同学们取得好成绩!一、填空题1. 以下哪一个数是奇数?A. 6B. 9C. 14答案:B2. 在下列数中,哪一个是最大的?A. 503B. 550C. 487答案:B3. 一共有8个小朋友,他们每人吃了3块糖果,那么一共吃了多少块糖果?A. 21B. 24C. 32答案:B二、选择题1. 下列哪一个数是一个偶数?A. 13B. 36C. 41答案:B2. 计算:35 - 17 = ?A. 18B. 22C. 26答案:A3. 小华家有36个苹果,小明家有27个苹果,那么两家一共有多少个苹果?A. 53B. 63C. 73答案:C三、解答题1. 用算式表示下列问题:小明和小红一共有15个饼干,小明比小红多5个饼干。
请用字母表示小红所拥有的饼干的数量,并写出算式。
答案:设小红拥有的饼干的数量为X,算式为:X + (X + 5) = 152. 请列出所有4的倍数,并将它们的倍数填写在下面的方框中:答案:4, 8, 12, 16, 20, ...四、应用题1. 一根铁丝长60厘米,小明需要将铁丝剪成相等的两段,每段铁丝长度是多少厘米?答案:将60厘米分成相等的两段,每段铁丝长度为60除以2,得到30厘米。
2. 一年级有30个学生,三年级有40个学生,五年级有35个学生。
请问一共有多少个学生?答案:一共有30 + 40 + 35 = 105个学生。
答案:一、填空题1. B2. B3. B二、选择题1. B2. A3. C三、解答题1. X + (X + 5) = 152X + 5 = 152X = 10X = 52. 4, 8, 12, 16, 20, ...四、应用题1. 30厘米2. 105个学生以上是小学数学三年级思维训练练习题及答案,希望同学们能认真思考并解答出正确答案。
三年级(下册)数学思维训练习题附答案

三年级(下册)数学思维训练习题单元目录第一单元除数是一位数的除法第二单元除数是一位数除法的应用题第三单元年、月、日第四单元年、月、日的应用题第五单元平移和旋转第六单元两位数乘两位数的乘法第七单元两位数乘两位数的乘法应用题第八单元认识千米第九单元认识吨第十单元轴对称图形第十一单元认识分数(一)第十二单元认识分数(二)第十三单元长方形和正方形面积(一)第十四单元长方形和正方形面积(二)第十五单元统计与平均数第十六单元认识小数(一)第十七单元认识小数(二)第十八单元观察物体第一单元除数是一位数的除法1、要使□36÷4的商是三位数,□里最小填()。
要使□36÷4的商是两位数,□里最大填()。
要使2□8÷8的商是三十多,□里可能填()。
2、一个三位数除以7商是75,有余数,余数最大是(),这时被除数是()。
3、在□里填上什么数,商中间有0?6)6□24、在□÷7=9……□中,被除数可能有几个?其中最大是几?最小是几?5、 3 □□)3 □□□□□□□ 386、7 □5)□□□□ 5□□4 57、□□□)□□□5 62 □2 8第二单元除数是一位数除法的应用题8、养殖场有300只鸡,鸡的只数是兔的3倍,把兔放在4个笼子里,平均每个笼子里有多少只兔?9、两个水桶共盛水60千克,如果第一桶水倒出4千克则两个桶中的水同样多,求第一桶里原来盛水多少千克?10、小明与小华共有图书160本,已知小明图书的本数是小华的3倍,求小明、小华各有图书多少本?11、王庄有小麦、水稻田共180亩,小麦的亩数是水稻的2倍。
王庄有小麦、水稻各多少亩?12、学校图书馆有科技书和文艺书共2400本,文艺书的本数是科技书的4倍。
两种书各有多少本?13、爸爸与儿子的年龄和是45岁,又知爸爸的年龄是儿子的4倍,爸爸与儿子今年各多少岁?第三单元年、月、日14、从上午8时到下午5时经过()。
A、9小时B、8小时C、10小时15、从6月8日到6月15日经过()。
三年级学生的数学思维训练方法

三年级学生的数学思维训练方法数学思维对学生的综合能力培养至关重要,特别是在他们的学习早期。
因此,为了帮助三年级学生提升数学思维能力,我们可以采用一些有效的训练方法。
本文将介绍一些适用于三年级学生的数学思维训练方法,以帮助他们在数学学习中取得更好的成绩。
一、启发学生的创造力思维数学不仅仅是记忆和应用公式,更是一门需要发挥创造力的学科。
为了培养学生的创造力思维,我们可以采用以下方法:1. 提供有趣的数学问题:给学生们一些有趣且有挑战性的数学问题,激发他们思考并寻找解决问题的方法。
例如:“如何用八块砖头搭建一个三层高的塔?”这样的问题能够让学生动脑筋,并培养他们的创造性思维。
2. 鼓励自由探索:在数学课堂上,给学生提供一些自由探索的机会,让他们自己去发现问题的规律和解决方法。
例如,让学生通过观察一些数列的规律来找出其中的规律,并写出下一个数。
二、培养学生的逻辑思维能力逻辑思维是数学学习中必不可少的能力,它能帮助学生分析问题、推理和验证结论。
以下是一些培养学生逻辑思维能力的方法:1. 进行逻辑谜题:数学谜题是培养学生逻辑思维的好方法。
在课堂上,教师可以出一些逻辑谜题,要求学生根据题目中的条件进行推理和判断。
这样的练习不仅能培养学生的逻辑思维,还能锻炼他们的解决问题的能力。
2. 引导学生进行证明:在教学中,鼓励学生自己去进行证明。
例如,可以给学生一个几何定理,要求他们自己推导出证明过程。
这样可以锻炼学生的逻辑思维,并提高他们的数学理解能力。
三、注重问题解决能力训练问题解决能力是数学思维的核心,它帮助学生应对现实生活中的实际问题,并找到最佳解决方案。
以下是一些训练学生问题解决能力的方法:1. 引导学生提出问题:在数学课堂上,教师可以引导学生提出与学习内容相关的问题,并协助他们找到解决问题的路径。
这样能够激发学生的主动学习和问题解决能力。
2. 创设数学情境:通过创设一些数学情境,让学生在实际应用中掌握数学知识,提高他们的问题解决能力。
小学三年级校本教材系列《数学思维训练》31页word

校本教材系列-----数学思维训练(三年级)第1讲等差数列1、下面是按规律排列的一串数,问其中的第1995项是多少?解答:2、5、8、11、14、……。
从规律看出:这是一个等差数列,且首项是2,公差是3,这样第1995项=2+3×(1995-1)=59842、在从1开始的自然数中,第100个不能被3除尽的数是多少?解答:我们发现:1、2、3、4、5、6、7、……中,从1开始每三个数一组,每组前2个不能被3除尽,2个一组,100个就有100÷2=50组,每组3个数,共有50×3=150,那么第100个不能被3除尽的数就是150-1=149.3、把1988表示成28个连续偶数的和,那么其中最大的那个偶数是多少?解答:28个偶数成14组,对称的2个数是一组,即最小数和最大数是一组,每组和为:1988÷14=142,最小数与最大数相差28-1=27个公差,即相差2×27=54,这样转化为和差问题,最大数为(142+54)÷2=98。
4、在大于1000的整数中,找出所有被34除后商与余数相等的数,那么这些数的和是多少?解答:因为34×28+28=35×28=980<1000,所以只有以下几个数:34×29+29=35×2934×30+30=35×3034×31+31=35×3134×32+32=35×3234×33+33=35×33以上数的和为35×(29+30+31+32+33)=54255、盒子里装着分别写有1、2、3、……134、135的红色卡片各一张,从盒中任意摸出若干张卡片,并算出这若干张卡片上各数的和除以17的余数,再把这个余数写在另一张黄色的卡片上放回盒内,经过若干次这样的操作后,盒内还剩下两张红色卡片和一张黄色卡片,已知这两张红色的卡片上写的数分别是19和97,求那张黄色卡片上所写的数。
三数思维训练(数阵图)
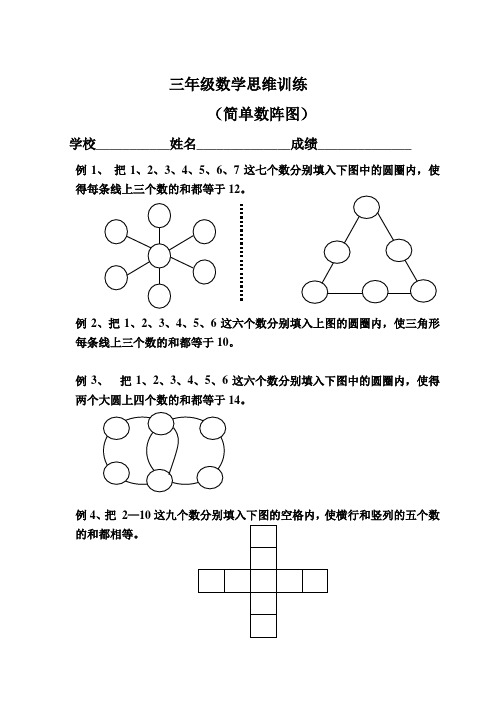
三年级数学思维训练
(简单数阵图)
学校___________姓名______________成绩______________
例1、把1、2、3、4、5、6、7这七个数分别填入下图中的圆圈内,使得每条线上三个数的和都等于12。
例2、把1、2、3、4、5、6这六个数分别填入上图的圆圈内,使三角形每条线上三个数的和都等于10。
例3、把1、2、3、4、5、6这六个数分别填入下图中的圆圈内,使得两个大圆上四个数的和都等于14。
例4、把2—10这九个数分别填入下图的空格内,使横行和竖列的五个数
的和都相等。
练习:1、把1、2、3、4、5、6、7这七个数分别填入下图中的圆圈内,使得每条线上三个数的和都等于10。
2、把1、2、
3、
4、
5、6这六个数分别填入上图的圆圈内,使三角形每条线上三个数的和都等于11。
3、把1~5
4、把5~9这五个数填入图中的○里(已
填入5)
思考:把1、2、3、4、5、6、7、8这八个数分别填入下图中的圆圈内,使得两个大圆上五个数的和都等于21。
小学三年级数学思维训练(速算与巧算一)(2021年整理)

小学三年级数学思维训练(速算与巧算一)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(小学三年级数学思维训练(速算与巧算一)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为小学三年级数学思维训练(速算与巧算一)(word版可编辑修改)的全部内容。
小学三年级数学思维训练(上册) 第一讲速算与巧算(一)一、加法中的巧算1.什么叫“补数”?两个数相加,若能恰好凑成整十、整百、整千、整万…,就把其中的一个数叫做另一个数的“补数"。
如:1+9=10,3+7=10,2+8=10,4+6=10,5+5=10.又如:11+89=100,33+67=100,22+78=100,44+56=100,55+45=100,在上面算式中,1叫9的“补数”;89叫11的“补数",11也叫89的“补数”。
也就是说两个数互为“补数"。
对于一个较大的数,如何能很快地算出它的“补数”来呢?一般来说,可以这样“凑”数:从最高位凑起,使各位数字相加得9,到最后个位数字相加得10。
如:87655→12345, 46802→53198,87362→12638,…下面讲利用“补数"巧算加法,通常称为“凑整法”。
2.互补数先加。
例1 巧算下面各题:①36+87+64②99+136+101③ 1361+972+639+28解:①式=(36+64)+87=100+87=187②式=(99+101)+136=200+136=336③式=(1361+639)+(972+28)=2000+1000=30003.拆出补数来先加。
小学三年级数学思维训练速算与巧算二

小学三年级数学思维训练速算与巧算二Document number【SA80SAB-SAA9SYT-SAATC-SA6UT-SA18】小学三年级数学思维训练(上册)第二讲速算与巧算(二)一、乘法中的巧算1.两数的乘积是整十、整百、整千的,要先乘.为此,要牢记下面这三个特殊的等式:5×2=1025×4=100125×8=1000例1 计算①123×4×25②125×2×8×25×5×4解:①式=123×(4×25)=123×100=12300②式=(125×8)×(25×4)×(5×2)=1000×100×10=10000002.分解因数,凑整先乘。
例 2计算①24×25②56×125③125×5×32×5解:①式=6×(4×25)=6×100=600②式=7×8×125=7×(8×125)=7×1000=7000③式=125×5×4×8×5=(125×8)×(5×5×4)=1000×100=1000003.应用乘法分配律。
例3 计算①175×34+175×66②67×12+67×35+67×52+6解:①式=175×(34+66)=175×100=17500②式=67×(12+35+52+1)=67×100=6700(原式中最后一项67可看成67×1)例4 计算①123×101 ②123×99解:①式=123×(100+1)=123×100+123=12300+123=12423②式=123×(100-1)=12300-123=121774.几种特殊因数的巧算。
与时俱进的数学思维三年级数学下册综合数学思维训练题

与时俱进的数学思维三年级数学下册综合数学思维训练题与时俱进的数学思维——三年级数学下册综合数学思维训练题数学在我们的日常生活中扮演着重要的角色,它帮助我们解决问题、培养逻辑思维能力,并带来乐趣。
作为三年级学生,我们需要通过综合数学思维训练题来提高数学素养和解决问题的能力。
本文将为大家介绍一些与时俱进的数学思维练习题。
一、快乐计算1. 将所给数字按照从小到大的顺序排列:64,27,42,89,53。
2. 在下图中填入适当的数字,使每个相邻两个数字之和都等于8。
(图略)3. 一个正整数,它加上15等于37,这个正整数是多少?4. 用合适的算式计算下面的题目:(a) 96 ÷ 6(b) 57 + 24(c) 85 - 18(d) 39 × 55. 使用每个数字只能使用一次,填入适当的数字,使得等式成立:_ ÷ _ = 4。
二、巧妙运算1. 找出下列数中的偶数:29,18,41,36,57。
2. 一个数的两倍再加上6等于20,这个数是多少?3. 小明有10元钱,他想买2元一杯的红茶,请问他最多能买几杯红茶,还剩多少钱?4. 用合适的运算符号填空,使等式成立:(a) 16 _ 4 _ 2 = 26(b) 15 _ 9 _ 3 = 99(c) 18 _ 6 _ 3 = 65. 一个数加上天数,等于31,这个数是多少?三、数学推理1. 找出下列数中的质数:20,37,44,53,66。
2. 口袋里有苹果、香蕉和橘子,共有8个水果,其中苹果的数量是香蕉和橘子的数量之和,香蕉的数量是4个,那么口袋里有几个苹果和几个橘子?3. 1小时有60分钟,蓝色的小球比红色的小球多两倍,现在蓝色的小球个数是红色的小球个数的两倍减去3,那么蓝色的小球有几个,红色的小球有几个?4. 用合适的算式计算下面的题目:(a) 21 + 18 - 9(b) 56 ÷ (8 - 2)(c) 36 × (5 - 2)(d) 63 - 48 ÷ 65. 请找出一组数字,使得123加上这组数字等于222。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江西省南昌市2015-2016学年度第一学期期末试卷(江西师大附中使用)高三理科数学分析一、整体解读试卷紧扣教材和考试说明,从考生熟悉的基础知识入手,多角度、多层次地考查了学生的数学理性思维能力及对数学本质的理解能力,立足基础,先易后难,难易适中,强调应用,不偏不怪,达到了“考基础、考能力、考素质”的目标。
试卷所涉及的知识内容都在考试大纲的范围内,几乎覆盖了高中所学知识的全部重要内容,体现了“重点知识重点考查”的原则。
1.回归教材,注重基础试卷遵循了考查基础知识为主体的原则,尤其是考试说明中的大部分知识点均有涉及,其中应用题与抗战胜利70周年为背景,把爱国主义教育渗透到试题当中,使学生感受到了数学的育才价值,所有这些题目的设计都回归教材和中学教学实际,操作性强。
2.适当设置题目难度与区分度选择题第12题和填空题第16题以及解答题的第21题,都是综合性问题,难度较大,学生不仅要有较强的分析问题和解决问题的能力,以及扎实深厚的数学基本功,而且还要掌握必须的数学思想与方法,否则在有限的时间内,很难完成。
3.布局合理,考查全面,着重数学方法和数学思想的考察在选择题,填空题,解答题和三选一问题中,试卷均对高中数学中的重点内容进行了反复考查。
包括函数,三角函数,数列、立体几何、概率统计、解析几何、导数等几大版块问题。
这些问题都是以知识为载体,立意于能力,让数学思想方法和数学思维方式贯穿于整个试题的解答过程之中。
二、亮点试题分析1.【试卷原题】11.已知,,A B C 是单位圆上互不相同的三点,且满足AB AC →→=,则AB AC →→⋅的最小值为( )A .14-B .12-C .34-D .1-【考查方向】本题主要考查了平面向量的线性运算及向量的数量积等知识,是向量与三角的典型综合题。
解法较多,属于较难题,得分率较低。
【易错点】1.不能正确用OA ,OB ,OC 表示其它向量。
2.找不出OB 与OA 的夹角和OB 与OC 的夹角的倍数关系。
【解题思路】1.把向量用OA ,OB ,OC 表示出来。
2.把求最值问题转化为三角函数的最值求解。
【解析】设单位圆的圆心为O ,由AB AC →→=得,22()()OB OA OC OA -=-,因为1OA OB OC ===,所以有,OB OA OC OA ⋅=⋅则()()AB AC OB OA OC OA ⋅=-⋅-2OB OC OB OA OA OC OA =⋅-⋅-⋅+ 21OB OC OB OA =⋅-⋅+设OB 与OA 的夹角为α,则OB 与OC 的夹角为2α所以,cos 22cos 1AB AC αα⋅=-+2112(cos )22α=--即,AB AC ⋅的最小值为12-,故选B 。
【举一反三】【相似较难试题】【2015高考天津,理14】在等腰梯形ABCD 中,已知//,2,1,60AB DC AB BC ABC ==∠= ,动点E 和F 分别在线段BC 和DC 上,且,1,,9BE BC DF DC λλ==则AE AF ⋅的最小值为 .【试题分析】本题主要考查向量的几何运算、向量的数量积与基本不等式.运用向量的几何运算求,AE AF ,体现了数形结合的基本思想,再运用向量数量积的定义计算AE AF ⋅,体现了数学定义的运用,再利用基本不等式求最小值,体现了数学知识的综合应用能力.是思维能力与计算能力的综合体现. 【答案】2918【解析】因为1,9DF DC λ=12DC AB =,119199918CF DF DC DC DC DC AB λλλλλ--=-=-==, AE AB BE AB BC λ=+=+,19191818AF AB BC CF AB BC AB AB BC λλλλ-+=++=++=+,()221919191181818AE AF AB BC AB BC AB BC AB BCλλλλλλλλλ+++⎛⎫⎛⎫⋅=+⋅+=+++⋅⋅ ⎪ ⎪⎝⎭⎝⎭19199421cos1201818λλλλ++=⨯++⨯⨯⨯︒2117172992181818λλ=++≥+= 当且仅当2192λλ=即23λ=时AE AF ⋅的最小值为2918. 2.【试卷原题】20. (本小题满分12分)已知抛物线C 的焦点()1,0F ,其准线与x 轴的交点为K ,过点K 的直线l 与C 交于,A B 两点,点A 关于x 轴的对称点为D . (Ⅰ)证明:点F 在直线BD 上; (Ⅱ)设89FA FB →→⋅=,求BDK ∆内切圆M 的方程. 【考查方向】本题主要考查抛物线的标准方程和性质,直线与抛物线的位置关系,圆的标准方程,韦达定理,点到直线距离公式等知识,考查了解析几何设而不求和化归与转化的数学思想方法,是直线与圆锥曲线的综合问题,属于较难题。
【易错点】1.设直线l 的方程为(1)y m x =+,致使解法不严密。
2.不能正确运用韦达定理,设而不求,使得运算繁琐,最后得不到正确答案。
【解题思路】1.设出点的坐标,列出方程。
2.利用韦达定理,设而不求,简化运算过程。
3.根据圆的性质,巧用点到直线的距离公式求解。
【解析】(Ⅰ)由题可知()1,0K -,抛物线的方程为24y x =则可设直线l 的方程为1x my =-,()()()112211,,,,,A x y B x y D x y -,故214x my y x =-⎧⎨=⎩整理得2440y my -+=,故121244y y m y y +=⎧⎨=⎩则直线BD 的方程为()212221y y y y x x x x +-=--即2222144y y y x y y ⎛⎫-=- ⎪-⎝⎭令0y =,得1214y yx ==,所以()1,0F 在直线BD 上.(Ⅱ)由(Ⅰ)可知121244y y m y y +=⎧⎨=⎩,所以()()212121142x x my my m +=-+-=-,()()1211111x x my my =--= 又()111,FA x y →=-,()221,FB x y →=-故()()()21212121211584FA FB x x y y x x x x m →→⋅=--+=-++=-,则28484,93m m -=∴=±,故直线l 的方程为3430x y ++=或3430x y -+=213y y -===±,故直线BD 的方程330x -=或330x -=,又KF 为BKD ∠的平分线,故可设圆心()(),011M t t -<<,(),0M t 到直线l 及BD 的距离分别为3131,54t t +--------------10分 由313154t t +-=得19t =或9t =(舍去).故圆M 的半径为31253t r +== 所以圆M 的方程为221499x y ⎛⎫-+= ⎪⎝⎭【举一反三】【相似较难试题】【2014高考全国,22】 已知抛物线C :y 2=2px(p>0)的焦点为F ,直线y =4与y 轴的交点为P ,与C 的交点为Q ,且|QF|=54|PQ|.(1)求C 的方程;(2)过F 的直线l 与C 相交于A ,B 两点,若AB 的垂直平分线l′与C 相交于M ,N 两点,且A ,M ,B ,N 四点在同一圆上,求l 的方程.【试题分析】本题主要考查求抛物线的标准方程,直线和圆锥曲线的位置关系的应用,韦达定理,弦长公式的应用,解法及所涉及的知识和上题基本相同. 【答案】(1)y 2=4x. (2)x -y -1=0或x +y -1=0. 【解析】(1)设Q(x 0,4),代入y 2=2px ,得x 0=8p,所以|PQ|=8p ,|QF|=p 2+x 0=p 2+8p.由题设得p 2+8p =54×8p ,解得p =-2(舍去)或p =2,所以C 的方程为y 2=4x.(2)依题意知l 与坐标轴不垂直,故可设l 的方程为x =my +1(m≠0). 代入y 2=4x ,得y 2-4my -4=0. 设A(x 1,y 1),B(x 2,y 2), 则y 1+y 2=4m ,y 1y 2=-4.故线段的AB 的中点为D(2m 2+1,2m), |AB|=m 2+1|y 1-y 2|=4(m 2+1).又直线l ′的斜率为-m ,所以l ′的方程为x =-1m y +2m 2+3.将上式代入y 2=4x ,并整理得y 2+4m y -4(2m 2+3)=0.设M(x 3,y 3),N(x 4,y 4),则y 3+y 4=-4m,y 3y 4=-4(2m 2+3).故线段MN 的中点为E ⎝ ⎛⎭⎪⎫2m2+2m 2+3,-2m ,|MN|=1+1m 2|y 3-y 4|=4(m 2+1)2m 2+1m 2.由于线段MN 垂直平分线段AB ,故A ,M ,B ,N 四点在同一圆上等价于|AE|=|BE|=12|MN|,从而14|AB|2+|DE|2=14|MN|2,即 4(m 2+1)2+⎝ ⎛⎭⎪⎫2m +2m 2+⎝ ⎛⎭⎪⎫2m 2+22=4(m 2+1)2(2m 2+1)m 4,化简得m 2-1=0,解得m =1或m =-1, 故所求直线l 的方程为x -y -1=0或x +y -1=0.三、考卷比较本试卷新课标全国卷Ⅰ相比较,基本相似,具体表现在以下方面: 1. 对学生的考查要求上完全一致。
即在考查基础知识的同时,注重考查能力的原则,确立以能力立意命题的指导思想,将知识、能力和素质融为一体,全面检测考生的数学素养,既考查了考生对中学数学的基础知识、基本技能的掌握程度,又考查了对数学思想方法和数学本质的理解水平,符合考试大纲所提倡的“高考应有较高的信度、效度、必要的区分度和适当的难度”的原则. 2. 试题结构形式大体相同,即选择题12个,每题5分,填空题4 个,每题5分,解答题8个(必做题5个),其中第22,23,24题是三选一题。
题型分值完全一样。
选择题、填空题考查了复数、三角函数、简易逻辑、概率、解析几何、向量、框图、二项式定理、线性规划等知识点,大部分属于常规题型,是学生在平时训练中常见的类型.解答题中仍涵盖了数列,三角函数,立体何,解析几何,导数等重点内容。
3. 在考查范围上略有不同,如本试卷第3题,是一个积分题,尽管简单,但全国卷已经不考查了。
四、本考试卷考点分析表(考点/知识点,难易程度、分值、解题方式、易错点、是否区分度题)。
