第1章 质点运动学与牛顿定律(1)
大学物理(西南交大)作业参考答案1

NO.1 质点运动学和牛顿定律班级 姓名 学号 成绩一、选择1. 对于沿曲线运动的物体,以下几种说法中哪种是正确的: [ B ] (A) 切向加速度必不为零. (B) 法向加速度必不为零(拐点处除外). (C) 由于速度沿切线方向,法向分速度必为零,因此法向加速度必为零. (D) 若物体作匀速率运动,其总加速度必为零.(E) 若物体的加速度a为恒矢量,它一定作匀变速率运动.2.一质点作一般曲线运动,其瞬时速度为V ,瞬时速率为V ,某一段时间内的平均速度为V,平均速率为V ,它门之间的关系为:[ D ](A )∣V ∣=V ,∣V ∣=V ; (B )∣V ∣≠V ,∣V∣=V ; (C )∣V ∣≠V ,∣V ∣≠V ; (D )∣V ∣=V ,∣V∣≠V .3.质点作曲线运动,r 表示位置矢量,v 表示速度,a表示加速度,S 表示路程,a τ表示切向加速度,下列表达式中, [ D ](1) d /d t a τ=v , (2) v =t r d /d , (3) v =t S d /d , (4) d /d t a τ=v .(A) 只有(1)、(4)是对的. (B) 只有(2)、(4)是对的.(C) 只有(2)是对的. (D) 只有(1)、(3)是对的.(备注:经过讨论认为(1)是对的)4.某物体的运动规律为t k t 2d /d v v -=,式中的k 为大于零的常量.当0=t 时,初速为0v ,则速度v 与时间t 的函数关系是 [ C ](A) 0221v v +=kt , (B) 0221v v +-=kt , (C) 02121v v +=kt , (D) 02121v v +-=kt 5.质点作半径为R 的变速圆周运动时的加速度大小为(v 表示任一时刻质点的速率) [ D ](A) t d d v .(B) 2v R . (C) R t 2d d vv +.(D) 2/1242d d ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛R t v v .6.质点沿x 方向运动,其加速度随位置的变化关系为:a=31+3x 2. 如在x=0处,速度v 0=5m.s -1,则在x=3m处的速度为:[ A ](A )9 m.s -1; (B )8 m.s -1; (C )7.8 m.s -1; (D )7.2 m.s -1 .7.如图所示,假设物体沿着竖直面上圆弧形轨道下滑,轨道是光滑的,在从A 至C 的下滑过程中,下面哪个说法是正确的?[ E ](A) 它的加速度大小不变,方向永远指向圆心. (B) 它的速率均匀增加.(C) 它的合外力大小变化,方向永远指向圆心. (D) 它的合外力大小不变.(E) 轨道支持力的大小不断增加.8.物体作圆周运动时,正确的说法是:[ C ] (A )加速度的方向一定指向圆心;(B )匀速率圆周运动的速度和加速度都恒定不变; (C )必定有加速度,且法向分量一定不为零;(D )速度方向一定在轨道的切线方向,法向分速度为零,所以法向加速度一定为零;9.以下五种运动形式,a保持不变的运动是 [ E ]A(A )单摆的运动;(B )匀速圆周运动;(C )圆锥摆运动;(D )行星的椭圆轨道运动;(E )抛体运动; 二、填空1.已知一质点在Oxy 平面内运动,其运动学方程为22(192)r ti t j =++;r的单位为m ,t 的单位为s ,则位矢的大小rv = 24i t j + ,加速度a =4(/)j m s 。
第1章-质点运动学
z A.
(t )
.B
的变化情况,定义:质点
的平均加速度为
(t t )
O
a t
y
24
x
质点的(瞬时)加速度定义为:
d d r a lim 2 t 0 t dt dt
2
即:质点在某时刻或某位置的(瞬时)加速度等于
速度矢量 对时间的一阶导数,或等于矢径 r 对时
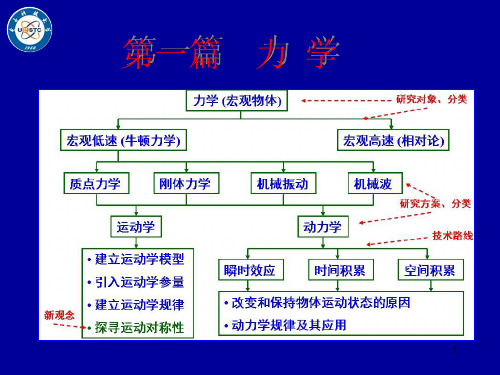
第一篇 力 学
1
内容提要
第一章 运动学 第二章 质点动力学(牛顿运动定律) 第三章 刚体力学
第四章 振动学基础
第五章 第六章 波动学基础
狭义相对论
2
第1章 质点运动学
§1-1 参考系、坐标系和理想模型
运动的可认知性——绝对运动与相对静止的辩证统一
案例讨论:关于物质运动属性的两种哲学论断 赫拉克利特:“人不能两次踏进同一条河流”
y
y
位置矢量 r 的大小(即质点P到原点o的距离)为
2 2 2 r r x y z
方向余弦: cos=x/r, cos=y/r, cos=z/r 式中 , , 取小于180°的值。
z
r
P(x,y,z)
z
C
cos2 + cos2 + cos2 =1
x
A
运动方程
—— 轨道方程。
11
消去时间t得:x2+y2=62
§1-3 位移 速 度
一.位移和路程
如图所示,质点沿曲线C运动。时刻t在A点,时 刻t+t在B点。 从起点A到终点B的有向线 段AB=r,称为质点在时间t内 的位移。 而A到B的路径长度S为 路程。
大学物理C复习提纲

第一章 质点运动学 第二章牛顿定律1、掌握质点运动学第二类问题的计算。
2、掌握牛顿定律的应用举例。
练习:1、已知一质量为m 的质点在x 轴上运动,质点只受到指向原点的引力作用,引力大小与质点离原点的距离x 的平方成反比,即2/x k f −=,k 是比例常数.设质点在A x =时的速度为零,求质点在4/A x =处的速度的大小。
2、质量为m 的子弹以速度0v 水平射入沙土中,设子弹所受阻力与速度成正比,比例系数为k ,忽略子弹的重力,求(1)子弹射入沙土后,,速度随时间变化的函数关系式;(2) 子弹射入沙土的最大深度。
第三章 动量守恒定律和能量守恒定律1、掌握冲量的概念。
2、掌握动量守恒定律。
3、掌握保守力的概念及保守力作功的特点:保守力做功只与始末位置有关,而与路径无关。
练习:1、在一定时间间隔内质点系的动量守恒,则在该时间间隔内,质点系所受A 、外力矩始终为零B 、外力做功始终为零C 、外力矢量和始终为零D 、内力矢量和不为零2、以下说法正确的是A 、大力的冲量一定比小力的冲量大B 、小力的冲量有可能比大力的冲量大C 、速度大的物体动量一定大D 、质量大的物体动量一定大第四章 刚体的转动1、掌握力矩的定义。
2、理解合外力矩与合外力的关系。
3、掌握决定刚体转动惯量大小的因素。
4、掌握转动定律。
5、刚体定轴转动的角动量:JW L =及角动量守恒定律。
练习:1、一质量为m 的质点作半径为r 的匀速圆周运动,则作用于质点的合力F 相对于圆心的力矩M= 。
2、刚体定轴转动惯量的大小由刚体的质量、质量分布和转轴位置决定。
3、以下说法正确的是A 、合外力为零,合外力矩一定为零B 、合外力为零,合外力矩一定不为零C 、合外力为零,合外力矩可以不为零D 、合外力不为零,合外力矩一定不为零4、在定轴转动中,如果合外力矩的方向与角速度方向一致,则以下说法正确的是A 、合力矩增大时,物体角速度一定增大B 、合力矩减小时,物体角速度一定减小C 、合力矩减小时,物体角加速度不一定变小D 、合力矩增大时,物体角加速度不一定增大5、芭蕾舞演员可绕过脚尖的铅直轴旋转,当她伸长两手时的转动惯量为J 0,角速度为ω0,当她突然收臂使转动惯量减小为J 0/2时,其角速度应为A 、ω0/4B 、4ω0C 、ω0/2D 、2ω0第五章 静电场 第六章 静电场中的导体与电介质1、 掌握静止电荷在其周围空间中只产生电场,而运动电荷在其周围空间既产生电场,又产生磁场。
第1章_质点运动学

17
1-2 质点运动的描述
r
m
求:(1)物体在圆周上运动的距离与时间的关系; (2)要维持物体这样的运动,绳子的拉力应为多少。
21
1-2 质点运动的描述
解:(1)物体在圆周上运动距离为物体经过的圆弧的长度
t
由
dv at dt
得
v v0
cdt v
0
0
ct
ds 由 v dt
1 2 得 s s 0 v0 t ct 2
1-1 物理基准 1-2 质点运动的描述 1-3 相对运动 1-4 牛顿运动定律 1-5 动量 1-6 能量
6
1-1 物理基准
一、长度、时间和质量标准 物体运动相关的单位有三个——长度、时间和质量。 1、长度的国际单位是米(m):一米等于光在真空 中传播1/299,792,458秒所走的距离。 2、时间的国际单位是秒(s):一秒是从铯原子中放射 出9,192,631,770次光振动所需要的时间。
质点是研究真实物体运动的一个理想模型,物体在其 大小和形状可以被忽略的情况下,可以视为一个质点。
4
引言
地球绕太阳公转时地球可视一个质点。 一切平动的物体,都可以视为一个质点。
如果物体的大小与形状不能忽略,则把物体上 每一小部分视为一个质点,把整个物体视为有许多 质点所组成的系统,称为质点系。
5
目录
第1章--质点运动学与牛顿定律

习题1 选择题1.1一质点在平面上运动,已知质点位置矢量的表达式为 r = a t 2 i + b t 2 j (其中a 、b 为常量), 则该质点作( ) (A) 匀速直线运动 (B) 变速直线运动 (C) 抛物线运动 (D) 一般曲线运动解 首先要判断的是质点的轨迹,由质点的位置矢量表达式 r = a t 2 i + b t 2 j 知2x at =,2y bt =。
消去t 可得质点的轨迹方程为by x a=,由此可知质点的轨迹为直线。
其次要判断的是状态的变化,也就是考察速度和加速度,22d at bt dt==+rυi j ,22a b =+a i j 。
由此可知质点作变速直线运动,故选B 。
1.2 如图所示,用水平力F 把木块压在竖直的墙面上并保持静止。
当F 逐渐增大时,木块所受的摩擦力( )(A )不为零, 但保持不变(B )随F 成正比地增大(C )开始随F 增大, 达到某一最大值后, 就保持不变 (D )无法确定解 由题意可知物体的状态是静止,根据牛顿第二定律物体所受的合外力为零。
在竖直方向上物体受重力和摩擦力两个力的作用,两个力大小相等 、方向相反。
故选A 。
1.3一质点沿x 轴运动,其速度与时间的关系为:24m/s t =+v ,当3s t =时,质点位于9m x =处,则质点的运动方程为( )(A)214123x t t =+- (B)2142x t t =+(C)23x t =+ (D)314123x t t =++解 因为质点沿x 轴运动,由dx dtυ=有dx dt υ=,通过积分2(4)dx dt t dt υ==+⎰⎰⎰得到2143x t t C =++。
当3s t =时,质点位于9m x =处,可求得12C =-。
故选A 。
1.4 质点作曲线运动,其瞬时速度为υ,瞬时速率为υ,平均速度为υ,平均速率为υ,则它们之间的下列四种关系中哪一种是正确的? ( ) (A ),υυ==υυ (B ),υυ≠=υυ习题1.2图(C ),υυ=≠υυ (D ),υυ≠≠υυ 解 ,,,d d s sd t d t t tυυ∆∆====∆∆r r υυ;d d s =r s ∆≠∆r 。
大学物理学复习资料

大学物理学复习资料第一章 质点运动学 主要公式:1.笛卡尔直角坐标系位失r=x i +y j +z k,质点运动方程(位矢方程):k t z j t y i t x t r)()()()(++=参数方程:。
t t z z t y y t x x 得轨迹方程消去→⎪⎩⎪⎨⎧===)()()(2.速度:dt r d v =3.加速度:dt vd a =4.平均速度:trv ∆∆=5.平均加速度:t va ∆∆=6.角速度:dt d θω=7.角加速度:dtd ωα=8.线速度与角速度关系:ωR v = 9.切向加速度:ατR dtdva ==10.法向加速度:Rv R a n 22==ω11.总加速度:22n a a a +=τ第二章 牛顿定律 主要公式:1.牛顿第一定律:当0=合外F时,恒矢量=v。
2.牛顿第二定律:dtP d dt v d m a m F=== 3.牛顿第三定律(作用力与反作用力定律):F F '-=第三章 动量与能量守恒定律 主要公式:1.动量定理:P v v m v m dt F I t t∆=-=∆=⋅=⎰)(12212.动量守恒定律:0,0=∆=P F合外力当合外力3、 动能定理:)(21212221v v m E dx F W x x k -=∆=⋅=⎰合 4.机械能守恒定律:当只有保守内力做功时,0=∆E 第五章 机械振动 主要公式:1.)cos(ϕω+=t A x Tπω2= 弹簧振子:mk=ω,k m T π2=单摆:lg =ω,g lT π2=2.能量守恒:动能:221mv E k =势能:221kx E p =机械能:221kA E E E Pk =+= 3.两个同方向、同频率简谐振动得合成:仍为简谐振动:)cos(ϕω+=t A x 其中:⎪⎩⎪⎨⎧++=∆++=22112211212221cos cos sin sin cos 2ϕϕϕϕϕϕA A A A arctg A A A A Aa. 同相,当相位差满足:πϕk 2±=∆时,振动加强,21A A A MAX +=;b. 反相,当相位差满足:πϕ)12(+±=∆k 时,振动减弱,21A A A MIN -=。
质心运动课件

一.质心动能定理 (科尼希定理)
一个质点组的质心在C,如图.
z S
ric C
mi
rc
对某参照系S, 定义:
O
ri
EC
1 2
MvC2
——质心动能
x
y
是否相等?
Ek
i
1 2
mi
vi2——质点组总动能
可以证明:
对 质某点参组照 总系 动, 能:Ek EC ErC
——质心动能定理 (科尼希定理)
质点组总动能 = 质心动能 + 质点组相对质心的动能
ErC
vrriiCC
i
1 2
mi
vi2C
是质点组相对质心的总动能
是第i个质点相对于质心C的位 速率矢
18
科尼希定理: Ek EC ErC 证明如下: z
r riC
是第i
个质点相对于质心C的位矢
如图:对某参照系S,
ri
v
2 i
rC
i
1 2
mi vi2C
i
1 2
mi
2vC
viC
19
Ek
i
1 2
mi vC2
i
1 2
mi vi2C
i
rr mivC viC
r r r mivC viC vC
r mi viC
vC
0
0
i
i
质心系中质点组总动量
=质心系中的质心动量
Ek
i
1 2
dLrC dt
M rC
质点组对质心的 角动量变化定理
质点组的角动
质点组相对于质心的角动量的时间 量变化定理在
变化率 = 各外力对质心的总力矩
第1章 质点运动学共48页文档

(2) 位矢法 以O点为参考点
r
x(
t
)i
y(
t
)j
R
cos
t
i
R
sin
t
j
(3) 自然法
以O’点为参考点,逆时为正。
S R t
第一章 质点运动学
7
§1-2 质点的位移、速度和加速度
一、位移 描述质点位置变化的物理量
S
几何描述: 数学描述:
PrQ
r(
t
t
)
r(
t
)
r( t ) r( t t )
2、联系 从数学上看是微分与积分的关系
微分法 r a 积分法
微分法
积分法
ar ra
第一类问题(微分法) 第二类问题(积分法)
第一章 质点运动学
14
例:直杆AB两端可以分别在两固定而 相互垂直的直线导槽上滑动,已知杆 的倾角按φ=ωt 随时间变化,试求杆 上M点的运动规律。(运动方程、轨 迹、速度、加速度)
直角坐标系
j
i
k
i jk
分别是x、y、z方 向的单位矢量
在直角坐标系中可写成:
r xi yj zk
a
x i y axi ay
j
z
k
j azk
(A)
大小
2 x
2 y
2 z
a
ax2
a
2 y
az2
第一章 质点运动学
12
由基本关系式
有:
dx
i
dy
j
dz
k
dt dt dt
a
dx
b
2
sin
t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
质点p 在一直线上运动,其坐标x 与时间t 有如下关系:x =-A sin ω t (SI) (A 为常数) 任意时刻t,质点的加速度a =___ ____。
t A ωωsin 2-(没有负号)质点p 在一直线上运动,其坐标x 与时间t 有如下关系:x =-A sin ω t (SI) (A 为常数) 任意时刻t,质点速度为零的时刻t =____ _ ()ωπ+1221n (n = 0,1,… )一质点作半径为 0.1 m 的圆周运动,其角位置的运动学方程为: 2214πt +=θ (SI)则其切向加速度为t a =________0.1m/s 2a t =dv/dt=Rd ω/dt=R α/dt=0.1质点沿半径为R 的圆周运动,运动学方程为 223t +=θ (SI) ,则t时刻质点的法向加速度大小为a n = ① . 16 R t 2a n =v 2/R=R ω2=R(d θ/dt)2一物体质量M =2 kg ,在合外力i t F)23(+= (SI )的作用下,从静止开始运动,式中i 为方向一定的单位矢量, 则当t=1 s 时物体的速度1v=__ _②_____1 m/sa=F/m, v=∫adt假设作用在一质量为10 kg 的物体上的力,在4秒内均匀地从零增加到50 N ,使物体沿力的方向由静止开始作直线运动.则物体最后的速率v =_______________.10 m · s -1a= 12.5t, v=∫adt一质点沿直线运动,其运动学方程为x = 6 t -t 2 (SI),则在t 由0至4s 的时间间隔内,质点的位移大小为 ___________,在t 由0到4s 的时间间隔内质点走过的路程为_________________.8m 10mv =dx/dt=6-2t,当t=3时,质点停止运动,3s-4s 质点反向加速一质点在力F = 5m (5 - 2t ) (SI)的作用下,t =0时从静止开始作直线运动,式中m为质点的质量,t 为时间,则当t = 5 s 时,质点的速率为 [ ] (A) 50 m ·s -1. . (B) 25 m ·s -1. (C) 0. (D) -50 m ·s -1.Ca=F/m, v=∫adt几个不同倾角的光滑斜面,有共同的底边,顶点也在同一竖直面上.若使一物体(视为质点)从斜面上端由静止滑到下端的时间最短,则斜面的倾角应选 (A) 60°. (B) 45°. (C) 30°. (D) 15°. B设底边为x,加速度a=gsin θ,下落时间t=(4x/gsin2θ)½质量为m 的物体自空中落下,它除受重力外,还受到一个与速度平方成正比的阻力的作用,比例系数为k ,k 为正值常量.该下落物体的收尾速度(即最后物体作匀速运动时的速度)将是 (A) kmg. (B) k g 2 . (C) gk . (D)gk .A物体做匀速直线运动满足mg=kv 2质点沿半径为R 的圆周作匀速率运动,每T 秒转一圈.在2T 时间间隔中,其平均速度大小与平均速率大小分别为(A) 2πR /T , 2πR/T . (B) 0 , 2πR /T (C) 0 , 0. (D) 2πR /T , 0.B升降机内地板上放有物体A ,其上再放另一物体B ,二者的质量分别为M A 、M B .当升降机以加速度a 向下加速运动时(a <g ),物体A 对升降机地板的压力在数值上等于(A) M A g. (B) (M A +M B )g. (C) (M A +M B )(g +a ). (D) (M A +M B )(g -a ). D一运动质点在某瞬时位于矢径()y x r ,的端点处, 其速度大小为(A) t r d d (B) t rd d (C) tr d d (D)22d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛t y t x D一段路面水平的公路,转弯处轨道半径为R ,汽车轮胎与路面间的摩擦系数为μ,要使汽车不致于发生侧向打滑,汽车在该处的行驶速率 (A) 不得小于gR μ. (B) 不得大于gR μ. (C) 必须等于gR 2. (D) 还应由汽车的质量M 决定. B摩擦力最多提供μmg 的向心力质点作曲线运动,r表示位置矢量,v 表示速度,a 表示加速度,S 表示路程,ta 表示切向加速度,下列表达式中,(1) a t = d /d v , (2) v =t r d /d , (3) v =t S d /d , (4) t a t =d /d v.(A) 只有(1)、(4)是对的. (B) 只有(2)、(4)是对的.(C) 只有(2)是对的. (D) 只有(3)是对的.D在作匀速转动的水平转台上,与转轴相距R 处有一体积很小的工件A ,如图所示.设工件与转台间静摩擦系数为μs ,若使工件在转台上无滑动,则转台的角速度ω应满足(A) Rgs μω≤. (B) R g s 23μω≤. (C) R gs μω3≤. (D) Rg s μω2≤. A对于沿曲线运动的物体,切向加速度必不为零.×匀速率圆周运动的切向加速度为零对于沿曲线运动的物体,若物体作匀速率运动,其总加速度必为零.×匀速率圆周运动的总加速度不为零加速度恒定不变时,物体运动方向也不变.×先减速后反向加速对于沿曲线运动的物体,法向加速度必不为零(拐点处除外).√在直线运动中,质点的加速度和速度的方向相同。
×减速的条件下不一样一质点沿x 轴运动,其加速度为a = 4t (SI),已知t = 0时,质点位于x 0=10 m 处,初速度v 0 = 0.试求其位置和时间的关系式.解: =a d v /d t 4=t , d v 4=t d t ⎰⎰=vv 0d 4d tt t v 2=t 2 4分v d =x /d t 2=t 2 t t x txx d 2d 020⎰⎰= x 2= t 3 /3+x 0 (SI) 4分有一质点沿x 轴作直线运动,t 时刻的坐标为x = 4.5 t 2 – 2 t 3 (SI) .试求: (1) 第2秒末的瞬时速度; (2) 第2秒内的路程.解:(1) v = d x /d t = 9t - 6t 2 v (2) =-6 m/s 4分 (2) S = |x (1.5)-x (1)| + |x (2)-x (1.5)| = 2.25 m 4分当t=1.5s 时,质点速度为零,后反向加速一质点沿x 轴运动,其加速度a 与位置坐标x 的关系为a =2+6 x 2 (SI)如果质点在原点处的速度为零,试求其在任意位置处的速度.解:设质点在x 处的速度为v ,62d d d d d d 2x txx t a +=⋅==v v 3分 ()x x xd 62d 02⎰⎰+=v v v3分()1322 x x=+v 2分(可以判断质点速度总是大于零的,故上述v 只保留一个根) dx/dt= v,然后分离变量,解一个微分方程一质点从静止开始作直线运动,开始时加速度为a 0,此后加速度随时间均匀增加,经过时间τ后,加速度为2a 0,经过时间2τ后,加速度为3 a 0 ,…求经过时间n τ后,该质点的速度和走过的距离.解:设质点的加速度为 a = a 0+α t ∵ t = τ 时, a =2 a 0 ∴ α = a 0 /τ 即 a = a 0+ a 0 t /τ , 2分由 a = d v /d t , 得 d v = a d tt t a atd )/(d 000τ⎰⎰+=vv∴ 2002t a t a τ+=v 2分 由 v = d s /d t , d s = v d tt t a t a t s ttsd )2(d d 2000τ+==⎰⎰⎰v 302062t a t a s τ+=2分t = n τ 时,质点的速度 ττ0)2(21a n n n +=v 1分 质点走过的距离 202)3(61ττa n n s n += 1分一质点沿x 轴运动,其加速度为a =6 t 2(SI),已知t = 0时,质点位于x 0=10 m 处,初速度v 0 = 0.试求其位置和时间的关系式.解: =a d v /d t 6=t 2 , d v 6=t 2 d t20d 6d tt t =⎰⎰vvv 2=t 34分v d =x /d t 2=t 330d 2d xtx x t t =⎰⎰x =t 4 /2 + x 0 =t 4 /2 + 10 (SI) 4分质点的运动方程为)(2015;301022SI t t y t t x -=+-=试求: (1)初速度的大小; (2)加速度的大小。
. 解:(1) v x =-10+60t ,v y =15-40t ; 2分v 0=()()221510-+=18ms -1 2分 (2) a x =60,a y =-40; 2分 a=()()224060-+=72.1ms -2 2分。
