中考试题相似三角形有关的综合问题2课后练习一及详解.docx
(完整word版)九年级数学相似三角形综合练习题及答案

九年级数学相似三角形综合练习题及答案1填空(本题14 分)(1 )若a=8cm , b=6cm , c=4cm ,贝U a 、b 、c 的第四比例项 d= ; a 、c 的比例中项 x=_。
(2) (2 x):x x:(1 x)。
贝U x= _______________ 。
(3) _______________________________________________________________ 在比例尺为1: 10000的地图上,距离为 3cm 的两地实际距离为 _________________________________ 公里。
(4) _______________________________ 圆的周长与其直径的比为 。
a 5 a b(5 )右,贝V= 。
b 3 b(6) 若 a :b : c=1 : 2: 3, 且 a bc 6,贝U a= ________ , b= ______ , c= _______ 。
ABACBC3CE(7) 如图 1, -- —— --- -,则(1)——(2)若 BD=10cm ,则 AD= cm 。
ADAE DE 2BC ,AB16cm ,则△ ABC 的周长为 (8)若点AEABc是线段AB的黄金分割点,且AC CB ,竺AC2•选择题 (1) 根据 A . 0 B .(2) 若线段bA.- d d C.—c(本题 9分)ab=cd ,共可写出以a 为第四比例项的比例式的个数是(1 C .2 D . 3a 、b 、c 、d 成比例,则下列各式中一定能成立的是(d b bC . DB AB ADEC AC AEBC DB ECECAB ACa3•已知:即3。
求(1)严3;;(2)愛。
(本题10分)4.若x: y:z=2: 7:5, x 2y 3z 6,求的值。
(本题6 分)za c e 25.已知:& d f 3,且2b d 5f 18。
(完整word)相似三角形综合题锦(含答案),推荐文档

一、相似三角形中的动点问题1.如图,在RtA ABC 中,/ ACB=90°, AC=3, BC=4,过点B作射线BB1// AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC 方向以每秒3个单位的速度运动.过点D作DH丄AB于H, 过点E作EF丄AC交射线BB1于F, G是EF中点,连接DG设点D运动的时间为t秒.(1)当t为何值时,AD=AB,并求出此时DE的长度;(2)当△ DEG与^ ACB相似时,求t的值. 4.如图所示,在^ ABC 中,BA= BC= 20cm , AC= 30cm, 点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,当P点到达B点时,Q点随之停止运动•设运动的时间为x.(1)当x为何值时,PQ// BC?(2)△ APQ与△ CQB能否相似?若能,求出AP的长;若不能说明理由.2.如图,在△ ABC中,^ ABC= 90° AB=6m, BC=8m,动点P 以2m/s的速度从A点出发,沿AC向点C移动•同时,动点Q以1m/s的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.(1)① 当t=2.5s时,求△CPQ的面积;②求△CPQ的面积S (平方米)关于时间t (秒)的函数解析式;(2)在P, Q移动的过程中,当△ CPQ为等腰三角形时,求出t的值. 5.如图,在矩形ABCD 中,AB=12cm, BC=6cm,点沿AB边从A开始向点B以2cm/s的速度移动;点沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t (S)表示移动的时间(0v t < 6)。
(1)当t为何值时,△ QAP为等腰直角三角形?(2)当t为何值时,以点Q、A、P为顶点的三角形与^ ABC相似?在RtAABC 中,/ ACB= 90° AC= 6, BC= 8, 3.如图1 ,点D在边AB上运动,DE平分三CDB交边BC于点E,EM丄BD,(1)当AD= CD 时,求证:DE/ AC;垂足为M, EN丄CD,垂足为N.(2)探究:AD为何值时,△ BME与^ CNE相似?C/V /V z二、构造相似辅助线一一双垂直模型6.在平面直角坐标系xOy中,点正比例函数y=kx的图象与线段OA的夹角是45。
中考相似三角形经典练习题(附答案)

中考相似三角形经典练习题(附答案)一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.2.如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.(1)求证:△CDF∽△BGF;(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.3.如图,点D,E在BC上,且FD∥AB,FE∥AC.求证:△ABC∽△FDE.4.如图,已知E是矩形ABCD的边CD上一点,BF⊥AE于F,试说明:△ABF∽△EAD.5.已知:如图①所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.(1)求证:①BE=CD;②△AMN是等腰三角形;(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证:△PBD∽△AMN.6.如图,E是▱ABCD的边BA延长线上一点,连接EC,交AD于点F.在不添加辅助线的情况下,请你写出图中所有的相似三角形,并任选一对相似三角形给予证明.7.如图,在4×3的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC=_________ °,BC= _________ ;(2)判断△ABC与△DEC是否相似,并证明你的结论.8.如图,已知矩形ABCD的边长AB=3cm,BC=6cm.某一时刻,动点M从A点出发沿AB方向以1cm/s 的速度向B点匀速运动;同时,动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动,问:(1)经过多少时间,△AMN的面积等于矩形ABCD面积的?(2)是否存在时刻t,使以A,M,N为顶点的三角形与△ACD相似?若存在,求t的值;若不存在,请说明理由.9.如图,在梯形ABCD中,若AB∥DC,AD=BC,对角线BD、AC把梯形分成了四个小三角形.(1)列出从这四个小三角形中任选两个三角形的所有可能情况,并求出选取到的两个三角形是相似三角形的概率是多少;(注意:全等看成相似的特例)(2)请你任选一组相似三角形,并给出证明.10.如图△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连接AE.(1)写出图中所有相等的线段,并加以证明;(2)图中有无相似三角形?若有,请写出一对;若没有,请说明理由;(3)求△BEC与△BEA的面积之比.11.如图,在△ABC中,AB=AC=a,M为底边BC上的任意一点,过点M分别作AB、AC的平行线交AC于P,交AB于Q.(1)求四边形AQMP的周长;(2)写出图中的两对相似三角形(不需证明);(3)M位于BC的什么位置时,四边形AQMP为菱形并证明你的结论.12.已知:P是正方形ABCD的边BC上的点,且BP=3PC,M是CD的中点,试说明:△ADM∽△MCP.13.如图,已知梯形ABCD中,AD∥BC,AD=2,AB=BC=8,CD=10.(1)求梯形ABCD的面积S;(2)动点P从点B出发,以1cm/s的速度,沿B⇒A⇒D⇒C方向,向点C运动;动点Q从点C出发,以1cm/s的速度,沿C⇒D⇒A方向,向点A运动,过点Q作QE⊥BC于点E.若P、Q两点同时出发,当其中一点到达目的地时整个运动随之结束,设运动时间为t秒.问:①当点P在B⇒A上运动时,是否存在这样的t,使得直线PQ将梯形ABCD的周长平分?若存在,请求出t的值;若不存在,请说明理由;②在运动过程中,是否存在这样的t,使得以P、A、D为顶点的三角形与△CQE相似?若存在,请求出所有符合条件的t的值;若不存在,请说明理由;③在运动过程中,是否存在这样的t,使得以P、D、Q为顶点的三角形恰好是以DQ为一腰的等腰三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.14.已知矩形ABCD,长BC=12cm,宽AB=8cm,P、Q分别是AB、BC上运动的两点.若P自点A出发,以1cm/s的速度沿AB方向运动,同时,Q自点B出发以2cm/s的速度沿BC方向运动,问经过几秒,以P、B、Q为顶点的三角形与△BDC相似?15.如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿BC边向点C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似.16.如图,∠ACB=∠ADC=90°,AC=,AD=2.问当AB的长为多少时,这两个直角三角形相似.17.已知,如图,在边长为a的正方形ABCD中,M是AD的中点,能否在边AB上找一点N(不含A、B),使得△CDM与△MAN相似?若能,请给出证明,若不能,请说明理由.18.如图在△ABC中,∠C=90°,BC=8cm,AC=6cm,点Q从B出发,沿BC方向以2cm/s的速度移动,点P从C出发,沿CA方向以1cm/s的速度移动.若Q、P分别同时从B、C出发,试探究经过多少秒后,以点C、P、Q为顶点的三角形与△CBA相似?19.如图所示,梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3,试在腰AB上确定点P的位置,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似.20.△ABC和△DEF是两个等腰直角三角形,∠A=∠D=90°,△DEF的顶点E位于边BC的中点上.(1)如图1,设DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,于是,除(1)中的一对相似三角形外,能否再找出一对相似三角形并证明你的结论.21.如图,在矩形ABCD中,AB=15cm,BC=10cm,点P沿AB边从点A开始向B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似.22.如图,路灯(P点)距地面8米,身高1.6米的小明从距路灯的底部(O点)20米的A点,沿OA 所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?23.阳光明媚的一天,数学兴趣小组的同学们去测量一棵树的高度(这棵树底部可以到达,顶部不易到达),他们带了以下测量工具:皮尺,标杆,一副三角尺,小平面镜.请你在他们提供的测量工具中选出所需工具,设计一种测量方案.(1)所需的测量工具是:_________ ;(2)请在下图中画出测量示意图;(3)设树高AB的长度为x,请用所测数据(用小写字母表示)求出x.24.问题背景在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:甲组:如图1,测得一根直立于平地,长为80cm的竹竿的影长为60cm.乙组:如图2,测得学校旗杆的影长为900cm.丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm.任务要求:(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;(2)如图3,设太阳光线NH与⊙O相切于点M.请根据甲、丙两组得到的信息,求景灯灯罩的半径.(友情提示:如图3,景灯的影长等于线段NG的影长;需要时可采用等式1562+2082=2602)25.阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC=8.7m,窗口高AB=1.8m,求窗口底边离地面的高BC.26.如图,李华晚上在路灯下散步.已知李华的身高AB=h,灯柱的高OP=O′P′=l,两灯柱之间的距离OO′=m.(1)若李华距灯柱OP的水平距离OA=a,求他影子AC的长;(2)若李华在两路灯之间行走,则他前后的两个影子的长度之和(DA+AC)是否是定值请说明理由;(3)若李华在点A朝着影子(如图箭头)的方向以v1匀速行走,试求他影子的顶端在地面上移动的速度v2.27.如图①,分别以直角三角形ABC三边为直径向外作三个半圆,其面积分别用S1,S2,S3表示,则不难证明S1=S2+S3.(1)如图②,分别以直角三角形ABC三边为边向外作三个正方形,其面积分别用S1,S2,S3表示,那么S1,S2,S3之间有什么关系;(不必证明)(2)如图③,分别以直角三角形ABC三边为边向外作三个正三角形,其面积分别用S1、S2、S3表示,请你确定S1,S2,S3之间的关系并加以证明;(3)若分别以直角三角形ABC三边为边向外作三个一般三角形,其面积分别用S1,S2,S3表示,为使S1,S2,S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件证明你的结论;(4)类比(1),(2),(3)的结论,请你总结出一个更具一般意义的结论.28.已知:如图,△ABC∽△ADE,AB=15,AC=9,BD=5.求AE.29.已知:如图Rt△ABC∽Rt△BDC,若AB=3,AC=4.(1)求BD、CD的长;(2)过B作BE⊥DC于E,求BE的长.30.(1)已知,且3x+4z﹣2y=40,求x,y,z的值;(2)已知:两相似三角形对应高的比为3:10,且这两个三角形的周长差为560cm,求它们的周长.参考答案与试题解析一.解答题(共30小题)1.如图,在△ABC中,DE∥BC,EF∥AB,求证:△ADE∽△EFC.考点:相似三角形的判定;平行线的性质。
相似三角形(包含答案和解析)

相似三角形综合检测题一、选择题(共18小题)1.(2011•深圳)如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为()A.:l B.:l C.5:3 D.不确定2.(2012•鄂州)在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为()A.B.C.D.3.(2012•攀枝花)如图,△ABC≌△ADE且∠ABC=∠ADE,∠ACB=∠AED,BC、DE交于点O.则下列四个结论中,①∠1=∠2;②BC=DE;③△ABD∽△ACE;④A、O、C、E四点在同一个圆上,一定成立的有()A.1个B.2个C.3个D.4个4.(2010•威海)在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x 轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第2010个正方形的面积为()A.B.C.D.5.(2000•天津)以下有四个结论:①顺次连接对角线相等的四边形各边中点,所得的四边形是菱形;②等边三角形是轴对称图形,但不是中心对称图形;③顶点在圆上的角叫做圆周角;④边数相同的正多边形都是相似形.其中正确的有()A.1个B.2个C.3个D.4个6.(1999•哈尔滨)如图,在△ABC中,AD是高,△ABC的外接圆直径AE交BC边于点G,有下列四个结论:①AD2=BD•CD;②BE2=EG•AE;③AE•AD=AB•AC;④AG•EG=BG•CG.其中正确结论的个数是()A.1个B.2个C.3个D.4个7.(2010•江汉区)如图,半圆O的直径AB=7,两弦AC、BD相交于点E,弦CD=,且BD=5,则DE等于()A.B.C.D.8.(2007•天门)如图所示,O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连接DF交BE的延长线于点H,连接OH交DC于点G,连接HC.则下列结论:①OH∥BF;②∠CHF=45°;③GH=BC;④FH2=HE•HB,正确的是()A.①②③B.②③④C.①②④D.①③④9.(2002•十堰)如图,若DC∥FE∥AB,则有()A.B.C.D.10.(2005•太原)如图,在正方形ABCD中,点E、F分别在边BC,CD上,如果AE=4,EF=3,AF=5,那么正方形ABCD的面积等于()A.B.C.D.11.(2002•烟台)如图,△ABC中,已知MN∥BC,DN∥MC.小红同学由此得出了以下四个结论:(1);(2);(3);(4).其中正确结论的个数为()A.1B.2C.3D.412.(2000•绍兴)如图,梯形ABCD中,AD∥BC,∠ABC=Rt∠,对角线AC⊥BD于P点.已知AD:BC=3:4,则BD:AC的值是()A.B.C.D.13.(2004•杭州)如图,在Rt△ABC中,AF是斜边上的高线,且BD=DC=FC=1,则AC的长为()A.B.C.D.14.(2010•鄂州)如图,已知AB是⊙O的直径,C是⊙O上的一点,连接AC,过点C作直线CD⊥AB交AB于点D.E是OB上的一点,直线CE与⊙O交于点F,连接AF交直线CD于点G,AC=2,则AG•AF是()A.10 B.12 C.8D.1615.(2010•聊城)如图,点P是矩形ABCD的边AD上的一个动点,矩形的两条边AB、BC 的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是()A.B.C.D.不确定16.(2010•鸡西)在锐角△ABC中,∠BAC=60°,BD、CE为高,F是BC的中点,连接DE、EF、FD.则以下结论中一定正确的个数有()①EF=FD;②AD:AB=AE:AC;③△DEF是等边三角形;④BE+CD=BC;⑤当∠ABC=45°时,BE=DE.A.2个B.3个C.4个D.5个17.(2002•杭州)1米长的标杆直立在水平的地面上,它在阳光下的影长为0.8米,此时,若某电视塔的影长为100米,则此电视塔的高度应是()A.80米B.85米C.120米D.125米18.(2000•重庆)如图,在△ABC中,∠BAC=90°,D是BC中点,AE⊥AD交CB的延长线于E,则下列结论正确的是()A.△AED∽△ACB B.△AEB∽△ACD C.△BAE∽△ACE D.△AEC∽△DAC二、填空题(共10小题)(除非特别说明,请填准确值)19.(2004•海淀区)如图所示,在圆O中,弧AB=弧AC=弧CD,AB=3,AE•ED=5,则EC 的长为_________.20.(2003•上海)在△ABC中,点D、E分别在边AB、AC上,CD平分∠ACB,DE∥BC.如果AC=10,AE=4,那么BC=_________.21.(2010•江津区)已知:在面积为7的梯形ABCD中,AD∥BC,AD=3,BC=4,P为边AD上不与A、D重合的一动点,Q是边BC上的任意一点,连接AQ、DQ,过P作PE∥DQ 交AQ于E,作PF∥AQ交DQ于F,则△PEF面积最大值是_________.22.(2004•襄阳)如图,梯形ABCD中,AD∥BC,AC、BD相交于点O,且AD=1,BC=3,则S△AOD:S△AOB=_________.23.(2005•重庆)如图,四边形ABCD是⊙O的内接正方形,P是弧AB的中点,PD与AB交于E点,则=_________.24.(2001•江西)如图,在△ABC中,AB>AC,过AC上一点D作直线DE,交AB于E,使△ADE和△ABC相似,这样的直线可作_________条.25.(2000•河南)如图,在△ABC中,点D在线段BC上,∠BAC=∠ADC,AC=8,BC=16,那么CD=_________.26.(2002•济南)在Rt△ABC中,∠A=90°,AB=3cm,AC=4cm,以斜边BC上距离B点3cm的点P为中心,把这个三角形按逆时针方向旋转90°到Rt△DEF,则旋转前后两个直角三角形重叠部分的面积为_________cm2.27.(2006•绵阳)如图,在△ABC中,D为AC边上的中点,AE∥BC,ED交AB于G,交BC延长线于F.若BG:GA=3:1,BC=10,则AE的长为_________.28.(2006•河南)如图,要拼出和图中的菱形相似的较长对角线为88cm的大菱形(如图)需要图1中的菱形的个数为_________.相似三角形综合检测题参考答案与试题解析一、选择题(共20小题)1.(2011•深圳)如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为()A.:l B.:l C.5:3 D.不确定考点:相似三角形的判定与性质;等边三角形的性质。
完整版)九年级数学相似三角形综合练习题及答案

完整版)九年级数学相似三角形综合练习题及答案1.填空题:1) 若$a=8$cm,$b=6$cm,$c=4$cm,则$a$、$b$、$c$的第四比例项$d=\underline{12}$;$a$、$c$的比例中项$x=\underline{5}$。
2) $(2-x):x=x:(1-x)$。
则$x=\underline{1}$。
3) 在比例尺为1:的地图上,距离为3cm的两地实际距离为\underline{30}公里。
4) 圆的周长与其直径的比为\underline{$\pi$}。
5) $\frac{a^5-ab}{b^3}=\frac{a^4}{b^2}$,则$\frac{a}{b}=\underline{a^2}$。
6) 若$a:b:c=1:2:3$,且$a-b+c=6$,则$a=\underline{2}$,$b=\underline{1}$,$c=\underline{3}$。
7) 如图1,则$\frac{AB}{AC}=\frac{BC}{CE}=\underline{\frac{3}{2}}$;若$BD=10$cm,则$AD=\underline{6}$cm;若$\triangle ADE$的周长为16cm,则$\triangle ABC$的周长为\underline{24}cm。
8) 若点$c$是线段$AB$的黄金分割点,且$AC>CB$,则$\frac{AC}{AB}=\underline{\frac{1+\sqrt{5}}{2}}$,$\frac{CB}{AB}=\underline{\frac{\sqrt{5}-1}{2}}$。
2.选择题:1) 根据$ab=cd$,共可写出以$a$为第四比例项的比例式的个数是()A.$1$,B.$2$,C.$3$,D.$4$。
答案:B。
2) 若线段$a$、$b$、$c$、$d$成比例,则下列各式中一定能成立的是()A.$abcd=1$,B.$a+b=c+d$,C.$\frac{a}{b}=\frac{c}{d}$,D.$a^2+b^2=c^2+d^2$。
2020年中考数学专题 相似三角形综合练习(含答案)

2020年中考数学专题 相似三角形综合(含答案)一、单选题(共有10道小题)1.如图,在△ABC 中,∠ACB= 90,CD ⊥AB ,垂足为D ,点E 是AB 的中点,CD=DE=a ,则AB 的长为( )A .2aB .a 22C .3aD . 2.根据下列条件,△ABC 和△111C B A 不相似的是()A.∠A=68°,∠B=40°,∠A 1=68°,∠B 1=72°B.∠B=∠B 1,BC=2,BC:A 1 B 1= A B: B 1C 1C.AB=1,BC=2, CA=1.5,A 1 B 1=4, B 1 C 1 =8,D.AB=12,BC=15,CA=24,A 1 B 1=24,A 1 B 1=20,B 1 C 1 =25,A 1 C 1=32 3.用作位似图形的方法,可以将一个图形放大或缩小,位似中心( ) A.只能选在原图形的外部B.只能选在原图形的内部C.只能选在原形的边上D.可以选择任意位置4.如图,AB ,CD 都是BD 的垂线,AB=4,CD=6,BD=14。
P 是BD 上一点,连接AP ,CP ,所得两个三角形相似,则BP 的长是( )A.2B.5.6C.12D.上述都有可能5.如图,是一束平行的光线从教室窗户射入教室的示意图,测得光线与地面所成的角∠AMC=30°,窗户的高在教室地面上的影长MN=32m ,窗户的下沿到教室地面的距离BC=1m (点M ,N ,CC 在同一直线上),则窗户的高CAA B CD a 3346.如图,在□ABCD 中,EF ∥AB 交AD 于点E ,交BD 于点F ,DE:EA=3:4,EF=3,则CD 的长为( )A.4B.7C.3D.127.如图1,已知在△ABC 中,点D 、E 、F 分别是边AB 、AC 、BC 上的点,DE ∥BC ,EF ∥AB ,且AD:DB = 3:5,那么CF ∶CB 等于( ) A. 5:8 B. 3:8 C. 3:5 D.8.如图,如果点C 是线段AB 的黄金分割点(AC>BC ),则下列比例式正确的是( )A.AB ACAC BC= B.AB BC BC AC = C. AC BC BC AB = D. AC ABAB BC=9.如图,P 为平行四边形ABCD 的边AD 上的一点,E 、F 分别为PB ,PC 的中点,△PEF ,△PDC ,△PAB 的面积分别为12,,S S S ,若3S =,则12S S +的值为()A.24B.12C.6D.3 10.如图,在□ABCD 中,点E 是边AD 的中点,EC 交对角线BD 于点F ,则EF:FC 等于( ) A.3:2 B.3:1 C.1:1 D.1:2 二、填空题(共有8道小题)11.如图,梯形ABCD 的对角线相交于O ,G 是BD 的中点.若AD = 3,BC = 9,则GOBG=A B C DE F A B C P A BCDE F E F A B CD12.如图,平行四边形中,是边上的点,交于点,如果, 那么 .13.如图,正五边形ABCDE 与五边形A ’B ’C ’D ’E ’是位似图形,且相似比为21。
初三最详细相似三角形解答题以及答案

一.解答题(共7小题)1.(2003•常德)如图1,D是△ABC的BC边上的中点,过点D的一条直线交AC于F,交BA的延长线于E,AG∥BC 交EF于G,我们可以证明EG•DC=ED•AG成立(不要求考生证明).(1)如图2,若将图1中的过点D的一条直线交AC于F,改为交CA的延长线于F,交BA的延长线于E,改为交BA于E,其它条件不变,则EG•DC=ED•AG还成立吗?如果成立,请给出证明;如果不成立,请说出理由;(2)根据图2,请你找出EG、FD、ED、FG四条线段之间的关系,并给出证明;(3)如图3,若将图1中的过点D的一条直线交AC于F,改为交CA的反向延长线于F,交BA的延长线于E,改为交BA于E,其它条件不变,则(2)得到的结论是否成立?2.(2003•厦门)如图,BD、BE分别是∠ABC与它的邻补角∠ABP的平分线,AE⊥BE,AD⊥BD,E、D为垂足.(1)求证:四边形AEBD是矩形;(2)若=3,F、G分别为AE、AD上的点,FG交AB于点H,且=3,求证:△AHG是等腰三角形.3.(2003•金华)如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.(1)当x为何值时,PQ∥BC;(2)当,求的值;(3)△APQ能否与△CQB相似?若能,求出AP的长;若不能,请说明理由.4.(2003•绍兴)已知∠AOB=90°,OM是∠AOB的平分线,按以下要求解答问题:(1)将三角板的直角顶点P在射线OM上移动,两直角边分别与边OA,OB交于点C,D.①在图甲中,证明:PC=PD;②在图乙中,点G是CD与OP的交点,且PG=PD,求△POD与△PDG的面积之比;(2)将三角板的直角顶点P在射线OM上移动,一直角边与边OB交于点D,OD=1,另一直角边与直线OA,直线OB分别交于点C,E,使以P,D,E为顶点的三角形与△OCD相似,在图丙中作出图形,试求OP的长.5.(2002•盐城)已知:如图,在直角三角形ABC中,∠BAC=90°,AB=AC,D为BC的中点,E为AC上一点,点G在BE上,连接DG并延长交AE于F,若∠FGE=45°.(1)求证:BD•BC=BG•BE;(2)求证:AG⊥BE;(3)若E为AC的中点,求EF:FD的值.6.(2002•黄冈)已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明成立(不要求考生证明).若将图中的垂线改为斜交,如图,AB∥CD,AD,BC相交于点E,过点E作EF∥AB交BD于点F,则:(1)还成立吗?如果成立,请给出证明;如果不成立,请说明理由;(2)请找出S△ABD,S△BED和S△BDC间的关系式,并给出证明.7.如图,已知直角梯形ABCD中,AB∥CD,∠D=90°,AB=AC,AE⊥AC且AE=AD,连BE交AC于F.(1)如图1,若CD=AD,试猜想BF与EF的数量关系;(2)如图2,若CD≠AD,问题(1)BF与EF的数量关系是否仍然成立?若成立,请证明.若不成立,请说明理由;(3)如图2,在第(2)问的条件下,取BC中点M,问线段MF与线段BD之间是否存在某种确定的数量关系?若存在,证明你的结论,若不存在,说明理由.答案与评分标准一.解答题(共7小题)1.(2003•常德)如图1,D是△ABC的BC边上的中点,过点D的一条直线交AC于F,交BA的延长线于E,AG∥BC 交EF于G,我们可以证明EG•DC=ED•AG成立(不要求考生证明).(1)如图2,若将图1中的过点D的一条直线交AC于F,改为交CA的延长线于F,交BA的延长线于E,改为交BA于E,其它条件不变,则EG•DC=ED•AG还成立吗?如果成立,请给出证明;如果不成立,请说出理由;(2)根据图2,请你找出EG、FD、ED、FG四条线段之间的关系,并给出证明;(3)如图3,若将图1中的过点D的一条直线交AC于F,改为交CA的反向延长线于F,交BA的延长线于E,改为交BA于E,其它条件不变,则(2)得到的结论是否成立?考点:相似三角形的判定与性质。
相似三角形综合题锦(含标准答案)
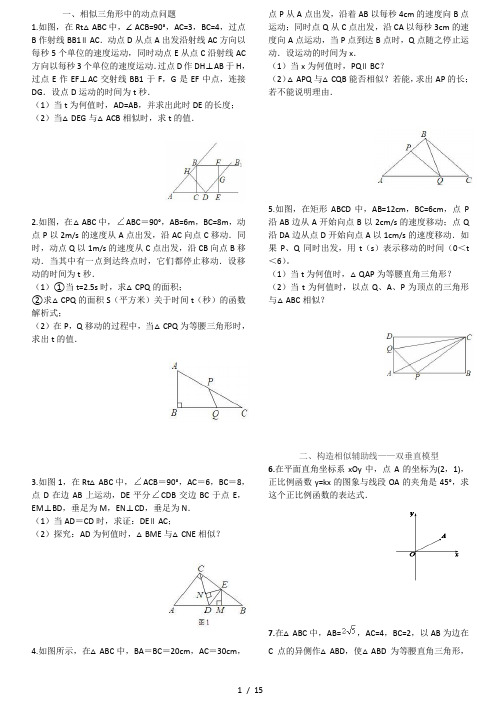
一、相似三角形中的动点问题1.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC 方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.(1)当t为何值时,AD=AB,并求出此时DE的长度;(2)当△DEG与△ACB相似时,求t的值.2.如图,在△ABC 中,ABC=90°,AB=6m,BC=8m,动点P以2m/s的速度从A点出发,沿AC向点C移动.同时,动点Q以1m/s的速度从C点出发,沿CB向点B移动.当其中有一点到达终点时,它们都停止移动.设移动的时间为t秒.(1)①当t=2.5s时,求△CPQ的面积;②求△CPQ的面积S(平方米)关于时间t(秒)的函数解析式;(2)在P,Q移动的过程中,当△CPQ为等腰三角形时,求出t的值.3.如图1,在Rt△ABC 中,ACB=90°,AC=6,BC=8,点D在边AB上运动,DE 平分CDB交边BC于点E,EM⊥BD,垂足为M,EN⊥CD,垂足为N.(1)当AD=CD时,求证:DE∥AC;(2)探究:AD为何值时,△BME与△CNE相似?4.如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,当P点到达B点时,Q点随之停止运动.设运动的时间为x.(1)当x为何值时,PQ∥BC?(2)△APQ与△CQB能否相似?若能,求出AP的长;若不能说明理由.5.如图,在矩形ABCD中,AB=12cm,BC=6cm,点P 沿AB边从A开始向点B以2cm/s的速度移动;点Q 沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(s)表示移动的时间(0<t <6)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学科:数学
专题:相似三角形有关的综合问题2
主讲教师:黄炜北京四中数学教师
金题精讲
题一:
题面:在平面直角坐标系xOy中,已知抛物线y=ax2+bx-2经过(2,1)和(6,-5)两点.
(1)求此抛物线的解析式;
(2)设此抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于C点,点P是在直线x=4右侧的抛物线上一点,过点P作PM⊥x轴,垂足为M,若以A、P、M为顶点的三角形与△OCB相似,求点P 的坐标.
满分冲刺
题一:
题面:如图,在平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,E为BC边上的一个动点(不与B、C重合).过E作直线AB的垂线,垂足为F.FE与DC的延长线相交于点G,连结DE,DF.(1)求证:△BEF∽△CEG;
(2)当点E在线段BC上运动时,△BEF和△CEG的周长之间有什么关系?并说明你的理由.
题二:
题面:如图,已知抛物线y=1
4
x2﹣
1
4
(b+1)x+
4
b
(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位
于点B的左侧),与y轴的正半轴交于点C.
(1)求点B的坐标,点C的坐标(用含b的代数式表示);
(2)请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说明理由;
(3)请你进一步探索在第一象限内是否存在点Q,使得△QCO,△QOA和△QAB中的任意两个三角形均相似(全等可作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
课后练习详解
金题精讲
题一:
答案:(1)抛物线的解析式为y =12-x 2+52x -2;(2)点P 的坐标为(8,-14)或(5,-2). 详解:(1)把(2,1)和(6,-5)两点坐标代入得4a +2b −2=1,36a +6b −2=−5, 解这个方程组,得 a =12-,b =52,
故抛物线的解析式为y =12-x 2+52x -2;
(2)令y =0,得12-x 2+52x -2=0,
解这个方程,得x 1=1,x 2=4.
∴A (1,0),B (4,0).
令x =0,得y = -2.
∴C (0,-2).
设P (m ,215222m m -+-),
∵∠COB =∠AMP =90°, ①当
OC OB MA MP =时,△OCB ∽△MAP . ∴224151222
m m m =--+, 解这个方程,得m 1=8,m 2=1(舍).
∴点P 的坐标为(8,-14), ②当
OC OB MP MA =时,△OCB ∽△MP A , ∴242151222
m m m =--+, 解这个方程,得m 1=5,m 2=1(舍).
∴点P 的坐标为(5,-2).
∴综上,点P 的坐标为(8,-14)或(5,-2).
满分冲刺
题一:
答案:(1)△BEF ∽△CEG ;(2)24. 详解:(1)因为四边形ABCD 是平行四边形,所以AB ∥D G ,
所以∠B =∠GCE ,∠G =∠BFE ,
所以△BEF ∽△CEG .
(2)△BEF 与△CEG 的周长之和为定值.过点C 作FG 的平行线交直线AB 于H , 因为GF ⊥AB ,所以四边形FHCG 为矩形.
所以FH =CG ,FG =CH ,
因此,△BEF 与△CEG 的周长之和等于BC +CH +BH ,
∵∠B =∠B ,∠AMB =∠BHC =90°
∴△ABM ∽△CBH ,
∴AB AM BC CH
. 由BC =10,AB =5,AM =4,
可得CH =8,
∴BH =6,
所以BC +CH +BH =24.
题二:
答案:(1)(b ,0),(0,4b );(2)P 的坐标为(
,);(3)存在点Q (1,2+)或Q (1,4),使
得△QCO ,△QOA 和△QAB 中的任意两个三角形均相似.
详解:(1)令y =0,即y =14x 2﹣14(b +1)x +4
b =0, 解得:x =1或b ,
∵b 是实数且b >2,点A 位于点B 的左侧,
∴点B 的坐标为(b ,0),
令x =0,
解得:y =4
b ,
∴点C 的坐标为(0,4b ),
故答案为:(b ,0),(0,4b );
(2)存在,
假设存在这样的点P ,使得四边形PCOB 的面积等于2b ,且△PBC 是以点P 为直角顶点的等腰直角三角形.
设点P 的坐标为(x ,y ),连接OP .
则S 四边形POCB =S △PCO +S △POB =12•4b •x +12•b •y =2b ,
∴x +4y =16.
过P 作PD ⊥x 轴,PE ⊥y 轴,垂足分别为D 、E ,
∴∠PEO =∠EOD =∠ODP =90°.
∴四边形PEOD 是矩形.
∴∠EPO =90°.
∴∠EPC =∠DPB .
∴△PEC ≌△PDB ,∴PE =PD ,即x =y .
由416x y x y =⎧⎨+=⎩解得165165x y ⎧=⎪⎪⎨⎪=⎪⎩ 由△PEC ≌△PDB 得EC =DB ,即
﹣4b =b ﹣, 解得b =>2符合题意.
∴P 的坐标为(
,); (3)假设存在这样的点Q ,使得△QCO ,△QOA 和△QAB 中的任意两个三角形均相似.
∵∠QAB =∠AOQ +∠AQO ,
∴∠QAB >∠AOQ ,∠QAB >∠AQO .
∴要使△QOA 与△QAB 相似,只能∠QAO =∠BAQ =90°,即QA ⊥x 轴.
∵b >2,
∴AB >OA ,
∴∠QOA >∠ABQ .
∴只能∠AOQ =∠AQB .此时∠OQB =90°,
由QA ⊥x 轴知QA ∥y 轴.
∴∠COQ =∠OQA .
∴要使△QOA 与△OQC 相似,只能∠QCO =90°或∠OQC =90°.
(I )当∠OCQ =90°时,△CQO ≌△QOA .
∴AQ =CO =4b .
由AQ 2=OA •AB 得:(4
b
)2=b ﹣1. 解得:b =8±
4. ∵b >2,
∴b =8+4.
∴点Q 的坐标是(1,2+).
(II )当∠OQC =90°时,△QCO ∽△QOA ,
∴CO OQ =QO
AQ ,即OQ 2=OC •AQ . 又OQ 2=OA •OB ,
∴OC •AQ =OA •OB .即4
b •AQ =1×
b . 解得:AQ =4,此时b =17>2符合题意,
∴点Q 的坐标是(1,4).
∴综上可知,存在点Q (1,2+)或Q (1,4),使得△QCO ,△QOA 和△QAB 中的任意两个三角形均相似.
初中数学试卷
鼎尚图文**整理制作。
