全等三角形之手拉手模型倍长中线截长补短法
浙教版八年级数学上册 全等三角形之手拉手模型、倍长中线-截长补短法
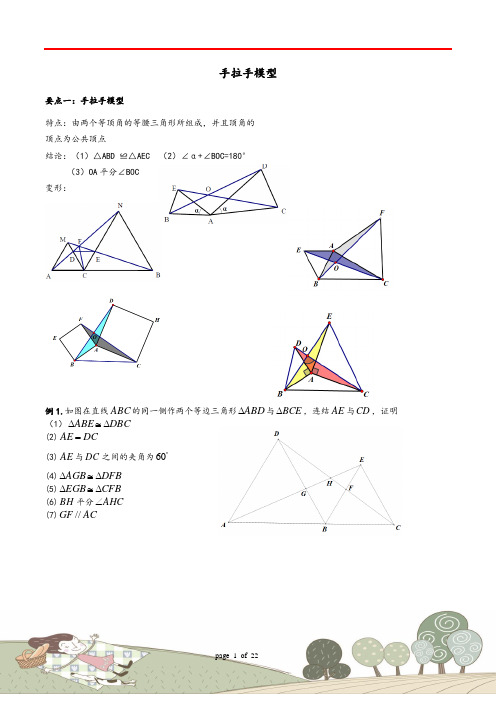
手拉手模型要点一:手拉手模型特点:由两个等顶角的等腰三角形所组成,并且顶角的 顶点为公共顶点结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180° (3)OA 平分∠BOC 变形:例1.如图在直线ABC 的同一侧作两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明 (1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60 (4)DFB AGB ∆≅∆ (5)CFB EGB ∆≅∆ (6)BH 平分AHC ∠ (7)AC GF //变式精练1:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD , 证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD , 证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,BH 平分AHC ∠例2:如图,两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H 问:(1)CDE ADG ∆≅∆是否成立? (2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度? (4)HD 是否平分AHE ∠?例3:如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H 问:(1)CDE ADG ∆≅∆是否成立? (2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度? (4)HD 是否平分AHE ∠?例4:两个等腰三角形ABD ∆与BCE ∆,其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD , 问:(1)DBC ABE ∆≅∆是否成立? (2)AE 是否与CD 相等?(3)AE 与CD 之间的夹角为多少度? (4)HB 是否平分AHC ∠?例5:如图,点A. B. C 在同一条直线上,分别以AB 、BC 为边在直线AC 的同侧作等边三角形△ABD 、△BCE.连接AE 、DC ,AE 与DC 所在直线相交于F ,连接FB.判断线段FB 、FE 与FC 之间的数量关系,并证明你的结论。
全等三角形重要题型(手拉手模型、截长补短、中线倍长)

全等三角形重要题型(手拉手模型、截长
补短、中线倍长)
全等三角形是高中数学中的重要题型之一。
其中,手拉手模型是一种常用的构造方法。
这种模型由两个等腰三角形或正方形组成,且顶角的顶点为公共顶点。
例如,在直线ABC的
同侧作两个等边三角形ΔABD和ΔBCE,连结AE和CD,可
以证明ΔABE≅ΔDBC,AE=DC,且AE与DC之间的夹角为
60度。
此外,还可以得到ΔAGB≅ΔDFB和ΔEGB≅ΔCFB,
BH平分∠AHC,XXX等结论。
除此之外,截长补短法也是证明线段和差倍分关系时常用的方法。
具体来说,截长法是在较长线段中截取一段等于另外两条线段中的一条,然后证明剩下部分等于另一条;而补短法则是将一条较短线段延长,延长部分等于另一条较短线段,然后证明新线段等于较长线段或延长一条较短线段等于较长线段,然后证明延长部分等于另一条较短线段。
举个例子,如果有两个正方形ABCD和DEFG,连结AG
和CE,二者相交于点H,我们可以通过全等三角形来证明
ΔADG≅ΔCDE,AG=CE,以及AG与CE之间的夹角为多少度。
另外,也可以考虑是否有HD平分∠AHE。
在另一个例子中,如果有两个等腰直角三角形ADC和XXX,连结AG和CE,二者相交于点H,同样可以采用全等三角形的方法来证明ΔADG≅ΔCDE,AG=CE,以及AG与CE之间的夹角为多少度,同时还可以考虑是否有HD平分∠AHE。
全等三角形重要题型(手拉手模型、截长补短、中线倍长)
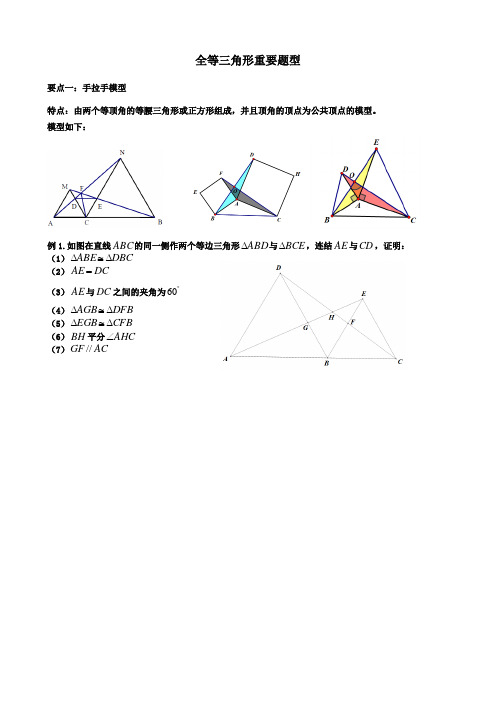
全等三角形重要题型要点一:手拉手模型特点:由两个等顶角的等腰三角形或正方形组成,并且顶角的顶点为公共顶点的模型。
模型如下:例1.如图在直线ABC 的同一侧作两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明: (1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60 (4)DFB AGB ∆≅∆ (5)CFB EGB ∆≅∆ (6)BH 平分AHC ∠ (7)AC GF //变式精练1:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD , 证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,BH 平分AHC ∠例2:如图,两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H问:(1)CDE ADG ∆≅∆是否成立? (2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度? (4)HD 是否平分AHE ∠?例3:如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H 问:(1)CDE ADG ∆≅∆是否成立? (2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度? (4)HD 是否平分AHE ∠?例4:两个等腰三角形ABD ∆与BCE ∆,其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ,问:(1)DBC ABE ∆≅∆是否成立? (2)AE 是否与CD 相等?(3)AE 与CD 之间的夹角为多少度? (4)HB 是否平分AHC ∠?要点二:截长补短法若遇到证明线段的和差倍分关系时,通常考虑截长补短法,构造全等三角形。
全等三角形之手拉手模型、倍长中线-截长补短法(西城专用)
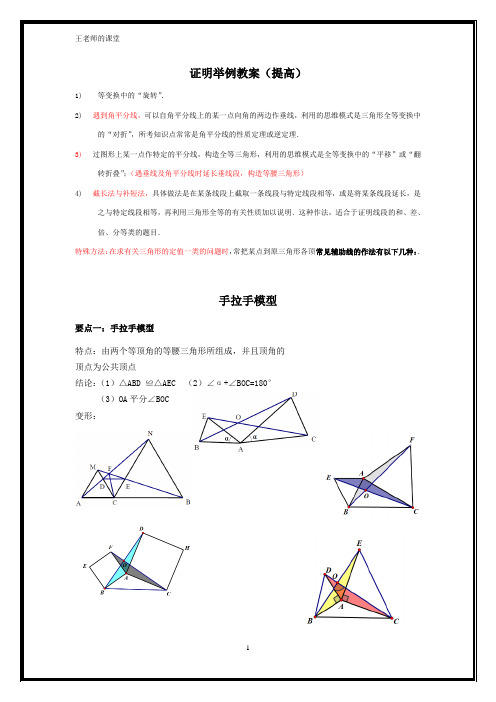
证明举例教案(提高)1)等变换中的“旋转”.2)遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.3)过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折叠”;(遇垂线及角平分线时延长垂线段,构造等腰三角形)4)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶常见辅助线的作法有以下几种:.手拉手模型要点一:手拉手模型特点:由两个等顶角的等腰三角形所组成,并且顶角的顶点为公共顶点结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180°(3)OA平分∠BOC变形:例 1.如图在直线ABC 的同一侧作两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)DFB AGB ∆≅∆ (5)CFB EGB ∆≅∆ (6)BH 平分AHC ∠ (7)AC GF //变式精练1:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,BH 平分AHC ∠例2:如图,两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H问:(1)CDE ADG ∆≅∆是否成立? (2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度? (4)HD 是否平分AHE ∠?例3:如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H问:(1)CDE ADG ∆≅∆是否成立? (2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度? (4)HD 是否平分AHE ∠?例4:两个等腰三角形ABD ∆与BCE ∆,其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD , 问:(1)DBC ABE ∆≅∆是否成立? (2)AE 是否与CD 相等?(3)AE 与CD 之间的夹角为多少度? (4)HB 是否平分AHC ∠?倍长与中点有关的线段倍长中线类☞考点说明:凡是出现中线或类似中线的线段,都可以考虑倍长中线,倍长中线的目的是可以旋转等长度的线段,从而达到将条件进行转化的目的。
三角形全等之手拉手模型、倍长中线、截长补短法、旋转、寻找三角形全等方法归纳总结49762
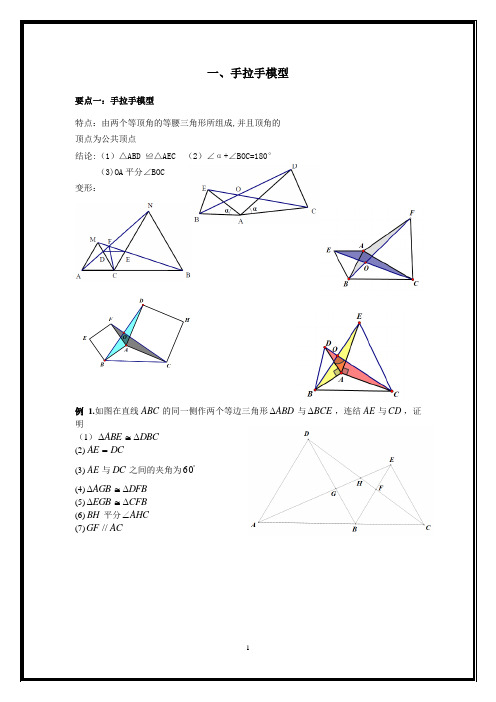
一、手拉手模型要点一:手拉手模型特点:由两个等顶角的等腰三角形所组成,并且顶角的 顶点为公共顶点结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180° (3)OA 平分∠BOC 变形:例 1.如图在直线ABC 的同一侧作两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60 (4)DFB AGB ∆≅∆ (5)CFB EGB ∆≅∆ (6)BH 平分AHC ∠ (7)AC GF //变式精练1:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD , 证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,BH 平分AHC ∠例2:如图,两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H问:(1)CDE ADG ∆≅∆是否成立? (2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度? (4)HD 是否平分AHE ∠?例3:如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H问:(1)CDE ADG ∆≅∆是否成立? (2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度? (4)HD 是否平分AHE ∠?例4:两个等腰三角形ABD ∆与BCE ∆,其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD , 问:(1)DBC ABE ∆≅∆是否成立? (2)AE 是否与CD 相等?(3)AE 与CD 之间的夹角为多少度? (4)HB 是否平分AHC ∠?二、倍长与中点有关的线段倍长中线类☞考点说明:凡是出现中线或类似中线的线段,都可以考虑倍长中线,倍长中线的目的是可以旋转等长度的线段,从而达到将条件进行转化的目的。
三角形全等之手拉手模型、倍长中线、截长补短法、旋转、寻找三角形全等方法归纳总结49762
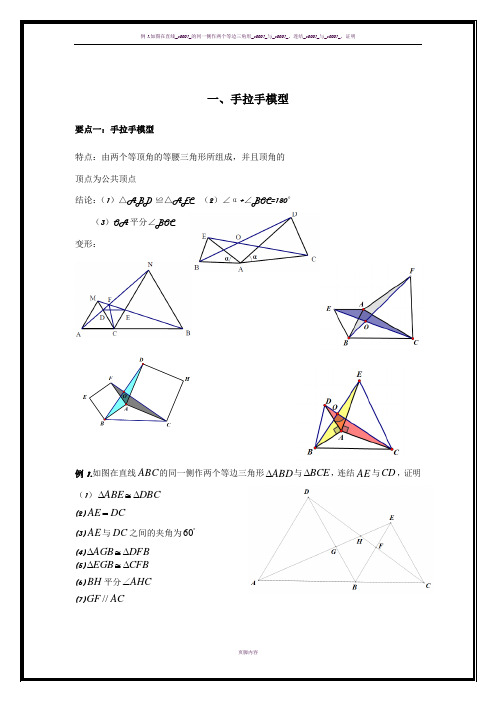
一、手拉手模型要点一:手拉手模型特点:由两个等顶角的等腰三角形所组成,并且顶角的 顶点为公共顶点结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180° (3)OA 平分∠BOC 变形:例1.如图在直线ABC 的同一侧作两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明 (1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60 (4)DFB AGB ∆≅∆ (5)CFB EGB ∆≅∆ (6)BH 平分AHC ∠ (7)AC GF //变式精练1:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,BH 平分AHC ∠例2:如图,两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H问:(1)CDE ADG ∆≅∆是否成立? (2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度?(4)HD 是否平分AHE ∠?例3:如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H问:(1)CDE ADG ∆≅∆是否成立? (2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度? (4)HD 是否平分AHE ∠?例4:两个等腰三角形ABD ∆与BCE ∆,其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ,问:(1)DBC ABE ∆≅∆是否成立? (2)AE 是否与CD 相等?(3)AE 与CD 之间的夹角为多少度? (4)HB 是否平分AHC ∠?二、倍长与中点有关的线段倍长中线类☞考点说明:凡是出现中线或类似中线的线段,都可以考虑倍长中线,倍长中线的目的是可以旋转等长度的线段,从而达到将条件进行转化的目的。
三角形全等之手拉手模型、倍长中线、截长补短法、旋转、寻找三角形全等方法归纳总结

i n ga re与,连结与,证BCE ∆AE CDosrofdoogeragnii rb ei n ga re go od fo r二、倍长与中点有关的线段考点说明:凡是出现中线或类似中线的线段,都可以考虑倍长中线,倍长中线的目的是可以旋转等长度的线段,从而达到将条件进行转化的目的。
.1()2AB AC <+Aean dAl l t h i ng si nt he i rb ei n ga re go 三、截长补短问题1:垂直平分线(性质)定理是_______________________________________________________问题2:角平分线(性质)定理是__________________________________________________________问题3:等腰三角形的两个底角________,简称______________;如果一个三角形有两个角相等,那么它们所对的边也______,简称____________.问题4:当见到线段的______________考虑截长补短,构造全等或等腰转移____、转移____,然后和_________重新组合解决问题.三角形全等之截长补短(一)一、单选题(共4道,每道25分)1.已知,如图,BM 平分∠ABC,P 为BM 上一点,PD⊥BC 于点D ,BD=AB+CD .求证:∠BAP+∠BCP=180°.请你仔细观察下列序号所代表的内容:①;②∵∠1=∠2;③∠A=∠BEP;④AP=PE;⑤;⑥;⑦;⑧.以上空缺处依次所填最恰当的是( )A.①③⑥⑦B.①③⑤⑧C.②③⑥⑦D.②④⑤⑧2.已知,如图,BM 平分∠ABC,点P 为BM 上一点,PD⊥BC 于点D ,BD=AB+DC .求证:∠BAP+∠BCP=180°.e an dAl l t h i ng si nt he i rb ei n ga re go od fo rs o 请你仔细观察下列序号所代表的内容:①延长BA ,过点P 作PE⊥BA 于点E ;②延长BA 到E ,使AE=DC ,连接PE ;③延长BA 到E ,使DC=AE ;④;⑤;⑥;⑦.以上空缺处依次所填最恰当的是( )A.②④⑦B.①⑤⑥C.③④⑥D.①⑤⑦3.已知,如图,在五边形ABCDE 中,AB=AE ,AD 平分∠CDE,∠BAE=2∠CAD,求证:BC+DE=CD .e an dAl l t h i ng si nt he i rb ei n ga re go od fo rs o 请你仔细观察下列序号所代表的内容:①在CD 上截取CF=CB ,连接AF ;②在DC 上截取DF=DE ,连接AF ;③在DC 上截取DF=DE ;④AE=AF;⑤AF=AE,∠4=∠3;⑥∠4=∠3;⑦;⑧;⑨.以上空缺处依次所填最恰当的是( )A.①④⑨ B.③⑤⑧ C.①⑥⑦ D.②⑤⑨4.已知,如图,在五边形ABCDE 中,AB=AE ,∠BAE=2∠CAD,∠ABC+∠AED=180°,求证:BC+DE=CD .请你仔细观察下列序号所代表的内容:①延长DE 到F ,使EF=BC ,连接AF ;②延长DE 到F ,使BC=EF ;e an dAl l t h i ng si nt he i rb ei n ga re go od fo rs o ③延长DE 到F ,连接AF ;④;⑤;⑥;⑦;⑧;⑨.以上空缺处依次所填最恰当的是( )A.③⑤⑥⑧B.①④⑥⑨C.①⑤⑥⑨D.②④⑦⑧r四、三角形全等旋转与截长补短专题问题一:题中出现什么的时候,我们应该想到旋转?(构造旋转的条件)问题二:旋转都有哪些模型?【例1】如图,P 是正△ABC 内的一点,若将△PBC 绕点B 旋转到△P 'BA ,则∠PBP '的度数是( ) A .45°B .60° C .90° D .120°【例2】如图,正方形BAFE 与正方形ACGD 共点于A ,连接BD 、CF ,求证:BD =CF 并求出∠DOH 的度数。
全等三角形之手拉手模型、倍长中线-截长补短法(西城专用)

全等三角形之手拉手模型、倍长中线-截长补短法(西城专用)手拉手模型是由两个等腰三角形组成的,它们共享一个顶点,并且顶角是等于的。
根据这个模型,可以得出结论:(1)△ABD≌△AEC,(2) ∠α+∠BOC=180°,(3) OA平分∠BOC。
举例来说,对于图中的直线ABC的同一侧,作两个等边三角形△ABD与△BCE,并连接AE与CD,可以证明(1)△ABE≅△DBC,(2) AE=DC,(3) AE与DC之间的夹角为60度,(4) △AGB≅△DFB,(5) △EGB≅△CFB,(6) BH平分∠AHC,(7) XXX。
除了手拉手模型,倍长中线也是一个常见的几何模型,它可以用来旋转等长度的线段,从而转化条件。
例如,在△ABC中,如果已知AM是中线,可以证明AMXXX。
例2】如图所示,已知在三角形ABC中,AD是BC边上的中线,E是AD上一点,延长BE交AC于F,且AF=EF,证明AC=BE。
已知AD是BC边上的中线,所以AD=DC。
又因为AE=ED,所以AD=DC=CE。
又因为BE=AC,所以XXX。
而因为AF=EF,所以AE=EF,所以CE=CF。
因此,AC+CD=CE+BE=2CE=2AC,所以AC=BE,证毕。
练2】如图所示,在三角形ABC中,AD交BC于点D,点E是BC中点,EF∥AD交CA的延长线于点F,交AB于点G,若BG=CF,证明AD为三角形ABC的角平分线。
因为E是BC的中点,所以AD是BC边上的中线,所以AD=DC。
又因为EF∥AD,所以AF=FD。
因为BG=CF,所以AG=AB-BG=AB-CF=AF。
所以AG=AF,所以AD是角A 的平分线,证毕。
练3】如图所示,已知三角形ABC中,AD平分∠BAC,E、F分别在BD、AD上,DE=CD,EF=AC,证明EF∥AB。
因为AD平分∠BAC,所以∠EAD=∠FAD,所以∠XXX∠XXX。
因为DE=CD,所以∠XXX∠XXX,所以∠AED=∠XXX。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
手拉手模型要点一:手拉手模型特点:由两个等顶角的等腰三角形所组成,并且顶角的 顶点为公共顶点结论:(1)△ABD ≌△AEC (2)∠α+∠BOC=180° (3)OA 平分∠BOC 变形:例1.如图在直线ABC 的同一侧作两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明 (1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60 (4)DFB AGB ∆≅∆ (5)CFB EGB ∆≅∆ (6)HB 平分AHC ∠ (7)AC GF //变式精练1:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD ,证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,BH 平分AHC ∠变式精练2:如图两个等边三角形ABD ∆与BCE ∆,连结AE 与CD , 证明(1)DBC ABE ∆≅∆ (2)DC AE =(3)AE 与DC 之间的夹角为︒60(4)AE 与DC 的交点设为H ,HB 平分AHC ∠例2:如图,两个正方形ABCD 与DEFG ,连结CE AG ,,二者相交于点H(2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度? (4)HD 是否平分AHE ∠?例3:如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H 问:(1)CDE ADG ∆≅∆是否成立? (2)AG 是否与CE 相等?(3)AG 与CE 之间的夹角为多少度? (4)HD 是否平分AHE ∠?例4:两个等腰三角形ABD ∆与BCE ∆,其中BD AB =,,EB CB =α=∠=∠CBE ABD ,连结AE 与CD ,(2)AE是否与CD相等?(3)AE与CD之间的夹角为多少度?∠?(4)HB是否平分AHC例5:如图,点A. B. C在同一条直线上,分别以AB、BC为边在直线AC的同侧作等边三角形△ABD、△BCE.连接AE、DC,AE与DC所在直线相交于F,连接FB.判断线段FB、FE与FC之间的数量关系,并证明你的结论。
【练1】如图,三角形ABC和三角形CDE都是等边三角形,点A,E,D,同在一条直线上,且角EBD=62°,求角AEB的度数倍长与中点有关的线段倍长中线类☞考点说明:凡是出现中线或类似中线的线段,都可以考虑倍长中线,倍长中线的目的是可以旋转等长度的线段,从而达到将条件进行转化的目的:将题中已知和未知条件集中在一对三角形中、构造全等三角形、平移线段。
【方法精讲】常用辅助线添加方法——倍长中线△ABC 中方式1: 延长AD到E , AD 是BC 边中线使DE=AD ,连接BE方式2:间接倍长作CF ⊥AD 于F ,延长MD 到N , 作BE ⊥AD 的延长线于使DN=MD , 连接BE 连接CD【例1】 已知:ABC ∆中,AM 是中线.求证:1()2AM AB AC <+.MCBA【练1】在△ABC 中,59AB AC ==,,则BC 边上的中线AD 的长的取值范围是什么?【练2】如图所示,在ABC ∆的AB 边上取两点E 、F ,使AE BF =,连接CE 、CF ,求证:AC BC +>EC FC +.F E CBA【练3】如图,在等腰三角形ABC 中,AB=AC ,D 是AB 上一点,F 是AC 延长线上的一点,且BD=CF ,连结DF 交BC 于E .求证:DE=EF(倍长中线、截长补短)【例2】 如图,已知在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,延长BE 交AC 于F ,AF EF =,求证:AC BE =.FEDC BA【练1】如图,已知在ABC ∆中,AD 是BC 边上的中线,E 是AD 上一点,且BE AC =,延长BE 交AC 于F ,求证:AF EF =FEDCBA【练2】如图,在△ABC 中,AB>AC ,E 为BC 边的中点,AD 为∠BAC 的平分线,过E 作AD 的平行线,交AB 于F ,交CA 的延长线于G .求证:BF=CG .【练3】如图,在ABC ∆中,AD 交BC 于点D ,点E 是BC 中点,EF AD ∥交CA 的延长线于点F ,交AB 于点G ,若BG CF =,求证:AD 为ABC ∆的角平分线.GFEDCBA【练4】如图所示,已知ABC ∆中,AD 平分BAC ∠,E 、F 分别在BD 、AD 上.DE CD =,EF AC =.求证:EF ∥ABFA CD E B【例3】已知AM 为ABC ∆的中线,AMB ∠,AMC ∠的平分线分别交AB 于E 、交AC 于F .求证:BE CF EF +>.FEMCBA【练1】在Rt ABC ∆中,F 是斜边AB 的中点,D 、E 分别在边CA 、CB 上,满足90DFE ∠=︒.若3AD =,4BE =,则线段DE 的长度为_________.FEDC BA【练2】如图,△ABC中,AB=2AC,AD平分BC且AD⊥AC,则∠BAC=______.【练3】在ABC∆中,点D为BC的中点,点M、N分别为AB、AC上的点,且MD ND⊥.(1)若90A∠=︒,以线段BM、MN、CN为边能否构成一个三角形?若能,该三角形是锐角三角形、直角三角形或钝角三角形?(2)如果2222BM CN DM DN+=+,求证()22214AD AB AC=+.M NDAB【例4】如图,等腰直角ABC∆与等腰直角BDE∆,P为CE中点,连接PA、PD.探究PA、PD的关系.(证角相等方法)【练1】如图,两个正方形ABDE和ACGF,点P为BC的中点,连接PA交EF于点Q.探究AP与EF的数量关系和位置关系.(证角相等方法)【练2】如图,在ABC∆中,ABCD=,BDABAD∠=∠,AE是BD边的中线.求证:AEAC2=【例5】如图所示,在ABC∆中,AB AC=,延长AB到D,使BD AB=,E为AB的中点,连接CE、CD,求证2CD EC=.ECBA【练1】已知ABC∆中,AB AC=,BD为AB的延长线,且BD AB=,CE为ABC∆的AB边上的中线.求证:2CD CE=E DCBA【练2】如图,CB、CD分别是钝角△AEC和锐角△ABC中线,且AC=AB,∠ACB=∠ABC.求证CE=2CD.【例16】如图,两个正方形ABDE 和ACGF ,点P 为BC 的中点,连接PA 交EF 于点Q . 探究AP 与EF 的数量关系和位置关系.(倍长中线与手拉手模型综合应用)【练1】已知:如图,正方形ABCD 和正方形EBGF ,点M 是线段DF 的中点. ⑴试说明线段ME 与MC 数量关系和关系.⑵如图,若将上题中正方形EBGF 绕点B 顺时针旋转α度数(︒<90α),其他条件不变,上述结论还正确吗?若正确,请你证明;若不正确,请说明理由.★全等之截长补短:人教八年级上册课本中,在全等三角形部分介绍了角的平分线的性质,这一性质在许多问题里都有着广泛的应用.而“截长补短法”又是解决这一类问题的一种特殊方法(把长边截成两个短边或把两个短边放到一起;出现角平分线进行翻折;有具体角的度数说明要求角的度数,进而得到角相等,D O ECB A全等)【例10】 如图所示,ABC ∆中,0045,90=∠=∠B C ,AD 平分BAC ∠交BC 于D 。
求证:AB=AC+CD 。
【练1】如图所示,在ABC ∆中,060=∠B ,ABC ∆的角平分线AD 、CE 相交于点O 。
求证:AE+CD=AC 。
【练2】已知ABC ∆中,ο60=∠A ,BD 、CE 分别平分ABC ∠和ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.【练2】如图,在四边形ABCD 中,AD ∥BC ,AE 平分∠BAD 交DC 于点E ,连接BE ,且AE ⊥BE ,求证:AB=AD+BC.【练3】已知:如图,在△ABC 中,∠A=90∘,AB=AC ,BD 是∠ABC 的平分线。
求证:BC=AB+AD.DCOEDBNMDCBA【练4】点M,N在等边三角形ABC的AB边上运动,BD=DC,∠BDC=120°,∠MDN=60°,求证MN=MB+NC.【例11】已知如图所示,在△ABC中,AD是角平分线,且AC=AB+BD,试说明∠B=2∠C(不只是边,倍角也适用)【练1】如图,在△ABC中,AB=AC,BD⊥AC交AC于点D.求证:∠DBC=21∠BAC.【例12】如图所示,已知21∠=∠,P为BN上一点,且BCPD⊥于D,AB+BC=2BD,求证:180=∠+∠BCPBAP。
21DMCPNACEDBCADCBA【练1】如图,在四边形ABCD 中,BC >BA,AD =CD ,BD 平分ABC ∠, 求证: 0180=∠+∠C A【例13】如图所示,在ABC Rt ∆中,AB=AC ,090=∠BAC ,CBD ABD ∠=∠,CE 垂直于BD 的延长线于E 。
求证:BD=2CE 。
【练1】已知:如图示,在Rt △ABC 中,∠A=90°,∠ABC=2∠C ,BD 是∠ABC 的平分线.求证:CD=2AD .【练2】如图所示,在ABC ∆中,090=∠ABC ,AD 为BAC ∠的平分线,C ∠=300,AD BE ⊥于E 点,求证:AC-AB=2BE 。
DCE【练3】正方形ABCD,E 是BC 上一点,AE ⊥EF,交∠DCH 的平分线于点F ,求证AE=EF【练4】已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE【例14】如图所示,已知AB //CD ,BCD ABC ∠∠,的平分线恰好交于AD 上一点E ,求证:BC=AB+CD 。
EBAFCAD【练1】如图,已知AD∥BC,∠PAB的平分线与∠CBA的平分线相交于E,CE的连线交AP于D.求证:AD+BC=AB.【练2】如图,在正方形ABCD中,F是CD的中点,E是BC边上的一点,且AF平分∠DAE,求证:AE=EC+CD.【练3】在△ABC中,AD是BC边上的高,∠B=2∠C.求证:CD=AB+BD.【练4】如图所示,在三角形ABC中,∠ACB=90°,AC=BC,D为三角形ABC外一点,且AD=BD,DE⊥AC交AC的延长线于点E.试探求ED、AE和BC之间有何数量关系【练5】在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F。
试探究线段AB与AF、CF之间的数量关系,并证明你的结论EAB CPEDCBA【例15】如图在△ABC 中,AB >AC ,∠1=∠2,P 为AD 上任意一点,求证:AB-AC >PB-PC A【练1】已知AM 为ABC ∆的中线,AMB ∠,AMC ∠的平分线分别交AB 于E 、交AC 于F .求证:BE CF EF +>.MFECBA如图,E 是AOB ∠的平分线上一点,OA EC ⊥,OB ED ⊥,垂足为C 、D 。
