2015-2016年新北师版九年级数学中考数学 实数计算题
初三数学一轮复习1.1实数部分2015,2016真题

(2015济南)﹣6的绝对值是( )
A.6B.﹣6C.±6D.0
(2015•济南)计算: +(﹣3)0=
(2015绍兴)计算 的结果是
A. -3 B.-2 C. 2 D. 3
(2015绍兴)据中国电子商务研究中心监测数据显示,2015年第一季度中国轻纺城市场群的商品成交额达27 800 000 000元,将27 800000 000用科学计数法表示为
(2015广东)在0,2,(-3)0,-5这四个数中,最大的数是
A.0B.2C.(-3)0D.-5
(2015六盘山)下列说法正确的是( )
A.-2的绝对值是-2B.0的倒数是0
C.4的平方根是2D.-3的相反数是3
(2015六盘山)如图3, 表示的点在数轴上表示时,所在哪两个字母之间( )
A.C与D B.A与B C.A与C D.B与C
A. 2.78×1010B. 2.78×1011C. 27.8×1010D. 0.278×1011
(2015绍兴)计算:
(2016南平)﹣3的倒数是( )
A.3B.﹣3C. D.
(2016南平)计算:( )2=______.
(2016•南平)计算:(2π)0+|﹣6|﹣ .
(2016河南)- 的相反数是( )
第一节实数
(2015北京)截止到2015年6月1日,北京市已建成34个地下调蓄设施,蓄水能力达到1 40 000立方平米。将140 000用科学记数法表示应为
A.14×104B.1.4×105C.1.4×106D.0.14×106
(2015北京)实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最大的是
(2016深圳)计算:
2015-2016新北师大版数学九年级上期末试卷2

1.已知1=x 是方程022=++ax x 的一个根,则方程的另一个根为( )A .2B .2-C .3-D .32.在下列函数中,当x <0时,y 随x 增大而增大的是( ) A 、x y 31-= B 、3y x=- C 、y=-x -3 D 、32+=x y 3.若函数xk y 1-=(k ≠1)在每一象限内,y 随x 的增大而减小,则k 的取值范围是( ) A 、k >1 B 、k <1 C 、k >0 D 、k <04.如右图,DE 是ΔABC 的中位线,则ΔADE 与ΔABC 的面积之比是( )A .1:1B .1:2C .1:3D .1:45.函数y=kx (k ≠0)和x k y =(k ≠0)在同一坐标系中的图象是( )6. 已知反比例函数xy 1=,下列结论中不正确的是( ) A.图象经过点(-1,-1) B.图象在第一、三象限 C.当1>x 时,10<<y D.当0<x 时,y 随着x 的增大而增大8.如图,ABCD 是正方形,E 是CD 的中点,P 是BC 边上的一点,下列条件中,不能推出△ABP 与△ECP 相似的是( )A. P 是BC 的中点B. ∠APE =90°C. ∠APB =∠EPCD. BP ︰BC =2︰39、如图,P (x ,y )是反比例函数xy 3=的图象在第一象限分支上的一个动点,PA ⊥x 轴于点A ,PB ⊥y 轴于点B ,随着自变量x 的增大,矩形OAPB 的面积( )A.增大B.减小C.不变D.无法确定10.若n (n ≠0)是关于x 的方程220x mx n ++=的根,则m+n 的值为( )A 、2 B、-2 C 、 0 D 、 1二、填空题:(18分)11.方程022=-x 的根是12.已知函数xk y =的图象如图所示,函数解析式为 13、13、为了估计不透明的袋子里装有多少白球,先从袋中摸出10个球都做上标记, 然后放回袋中去,充分摇匀后再摸出10个球,发现其中有一个球有标记,那么你估计袋中大约有 个白球.14.如左下图在Rt △ABC 中, ∠ACB =90°,CD ⊥AB 于D ,若AD =1,BD =4,则CD = .15.△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是16.(2013•三明)如图,已知一次函数y=kx+b的图象经过点P(3,2),与反比例函数y=(x>0)的图象交于点Q (m,n).当一次函数y的值随x值的增大而增大时,m的取值范围是.三、解答题:(52分)17.(6分)如左下图,△ABC为等边三角形,双向延长BC到D、E,使得∠DAE=120°,求证:BC2=BD CE.18.(6分)已知关于x的一元二次方程x2+3x+1-m=0(1)方程有两个不相等的实数根,求m的取值范围;(2)设x1、x2为方程的两个根,且m为最大的负整数,求x1x2+x1+x2的值.19.(6分)如右图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端在CB、CD上滑动,当CM多少时,ΔAED与N,M,C为顶点的三角形相似.20.(6分)(2013•曲靖)在一个暗箱中装有红、黄、白三种颜色的乒乓球(除颜色外其余均相同).其中白球、黄球各1个,若从中任意摸出一个球是白球的概率是.(1)求暗箱中红球的个数.(2)先从暗箱中任意摸出一个球记下颜色后放回,再从暗箱中任意摸出一个球,求两次摸到的球颜色不同的概率(用树形图或列表法求解).21.(6分)如图,在一正方形ABCD 中,E 为对角线AC 上一点,连接EB 、ED ,(1)求证:△BEC≌△DEC:(2)延长BE 交AD 于点F ,若∠DEB=140°.求∠AFE 的度数.解:22.(8分)如图,已知直线AB 与x 轴交于点C ,与双曲线x k y交于A (3,320)、B (-5,a )两点.AD ⊥x 轴于点D ,BE ∥x 轴且与y 轴交于点E .(1)求点B 的坐标及直线AB 的解析式;(2)判断四边形CBED 的形状,并说明理由.解:23.(2014•扬州14分)已知矩形ABCD 的一条边AD =8,将矩形ABCD 折叠,使得顶点B 落在CD 边上的P 点处.(1)如图1,已知折痕与边BC 交于点O ,连结AP 、OP 、O A .①求证:△OCP ∽△PDA ;②若△OCP 与△PDA 的面积比为1:4,求边AB 的长;(2)若图1中的点P 恰好是CD 边的中点,求∠OAB 的度数;(3)如图2,,擦去折痕AO 、线段OP ,连结BP .动点M 在线段AP 上(点M 与点P 、A 不重合),动点N 在线段AB 的延长线上,且BN =PM ,连结MN 交PB 于点F ,作ME ⊥BP 于点E .试问当点M 、N 在移动过程中,线段EF 的长度是否发生变化?若变化,说明理由;若不变,求出线段EF 的长度.。
2015-2016学年第一学期九年级数学北师大期中试题
8. 某中学准备建一个面积为 375 m2 的长方形游泳池,且游泳池的宽比长短 10 m。设游泳 题号 答案 1 2 3 4 5 6 7 8 9 10 池的长为 x m, 则可列方程为 ( A. x (x - 10)= 375 C. 2x (2x - 10)= 375 1. 关于 x 的方程 (m + 1) x2 + 2mx - 3 = 0 是一元二次方程, 则 m 的取值范围是 ( A. 任意实数 B. m ≠ 1 )
所以这个箱子底部长为 5 米, 宽为 3 米。 由长方体展开图可知, 所购买矩形铁皮面积为 (5 + 2) × (3 + 2)= 35 平方米 所以张大叔购买这张铁皮共花了 35×20 = 700 (元) 。 22、 (1)证明: 由折叠可知, CD = ED, ∠E = ∠C。 在矩形 ABCD 中, AB = CD, ∠A = ∠C, ∴ AB = ED, ∠A = ∠E ∵∠AFB=∠EFD, (2)四边形 BMDF 是菱形。 理由: 由折叠可知: BF=BM, DF=DM。 由 (1) 知△ABF ≌ △EDF, ∴BF=DF 23、 (1)解: FG⊥DE。理由如下: ∵△ABC 绕点 B 顺时针旋转 90毅至△DBE, ∴∠DEB = ∠ACB,
D
2 C. (x - 1 ) = 5 2 4
2 D. (x - 1 ) =1 2
A. 2 姨 3 B. 4 姨 3 C. 8 姨 2
B
A
E
3. 在平面直角坐标系中, 已知点 A (0, 2) , B (- 2 姨 3 , 0) , C (0, - 2) , D (2 姨 3 , 0) , 则以这 四个点为顶点的四边形 ABCD 是 ( A. 矩形 B. 菱形 九数 (北师大) (一) ) C. 正方形 第 1 页(共 8 页) D. 梯形
北师版2015-2016学年度上学期九年级数学期末考综合练习(附详细解答)
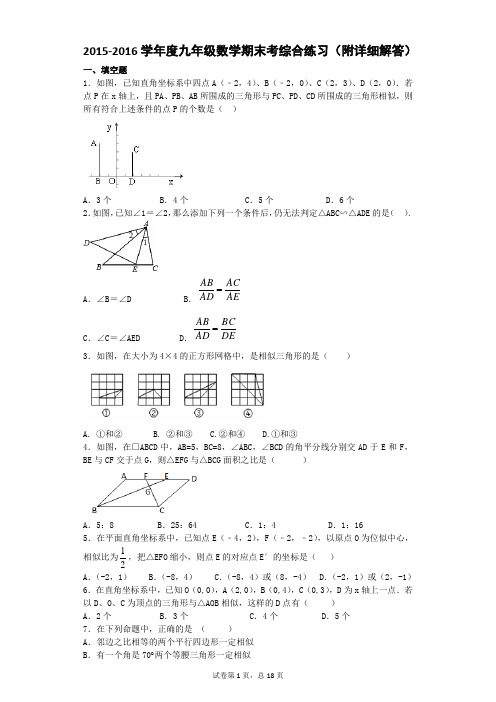
2015-2016学年度九年级数学期末考综合练习(附详细解答)一、填空题1.如图,已知直角坐标系中四点A (﹣2,4)、B (﹣2,0)、C (2,3)、D (2,0).若点P 在x 轴上,且PA 、PB 、AB 所围成的三角形与PC 、PD 、CD 所围成的三角形相似,则所有符合上述条件的点P 的个数是( )A .3个B .4个C .5个D .6个 2.如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC ∽△ADE 的是( ).A .∠B =∠D B .AE ACAD AB =C .∠C =∠AED D .DE BC AD AB = 3.如图,在大小为4×4的正方形网格中,是相似三角形的是( )A. ①和②B. ②和③C.②和④D.①和③4.如图,在□ABCD 中,AB=5,BC=8,∠ABC ,∠BCD 的角平分线分别交AD 于E 和F ,BE 与CF 交于点G ,则△EFG 与△BCG 面积之比是( )A .5:8B .25:64C .1:4D .1:16 5.在平面直角坐标系中,已知点E (﹣4,2),F (﹣2,﹣2),以原点O 为位似中心,相似比为21,把△EFO 缩小,则点E 的对应点E′的坐标是( ) A .(-2,1) B .(-8,4) C .(-8,4)或(8,-4) D .(-2,1)或(2,-1) 6.在直角坐标系中,已知O (0,0),A (2,0),B (0,4),C (0,3),D 为x 轴上一点.若以D 、O 、C 为顶点的三角形与△AOB 相似,这样的D 点有( ) A .2个 B .3个 C .4个 D .5个 7.在下列命题中,正确的是 ( )A .邻边之比相等的两个平行四边形一定相似B .有一个角是70︒两个等腰三角形一定相似C .两个直角三角形一定相似D .有一个角是60︒的两个菱形一定相似8.如图,Rt △ABC 中,AC ⊥BC ,AD 平分∠BAC 交BC 于点D ,DE ⊥AD 交AB 于点E ,M 为AE 的中点,BF ⊥BC 交CM 的延长线于点F ,BD =4,CD =3.下列结论:①∠AED =∠ADC ;②DE 1DA 2= ;③AC ·BE =12;④3BF =4AC .其中正确结论的个数有( )A .1个B .2个C .3个D .4个9.如图,在△ABC 中,DE 与BC 不平行,那么下列条件中,不能判断△ADE ∽△ACB 的是( )A .∠ADE=∠CB .∠AED=∠BC .BCDE AB AD = D .AB AEAC AD =10.如图,在平面直角坐标系中,点C 的坐标为(0,4),动点A 以每秒1个单位长的速度,从点O 出发沿x 轴的正方向运动,M 是线段AC 的中点.将线段AM 以点A 为中心,沿顺时针方向旋转90°,得到线段AB .过点B 作x 轴的垂线,垂足为E ,过点C 作y轴的垂线,交直线BE 于点D ,运动时间为t 秒.当S △BCD =254 时,t 的值为 ( )A .2或2+.2或2+.3或3+.3或3+11.如图,在△ABC 中,点D 是AC 上一点,添加下列哪个条件不能得到△CBD ∽△CAB 的是( )A .∠CDB=∠CBAB .∠CBD=∠AAC .BC ·AB =BD ·ACD .BC 2=CD ·AC12.如图,P 为线段AB 的黄金分割点,且AP> BP ,则下列结论成立的个数是( )⑴AB APAP BP = ⑵AB :AP=AP :PB ⑶BP 2=AP ·AB⑷AB AP≈0.618A .1个B .2个C .3个D . 4个 13.下列说法正确的是( ) A .所有的等边三角形都相似 B .所有的菱形都相似C .所有的等腰三角形都相似D .所有的矩形都相似14.如图,在△ABC 中,EF ∥BC ,AE 1EB 2=,8=BEFC S 四边形,则=∆ABC S ( )A .9B .10C .12D .1315.如图,△ABC 中,∠B=90°,AB=5,BC=12,将△ABC 沿DE 折叠,使点C 落在AB 边上的C '处,并且D C '∥BC ,则CD 的长是( )A .25156 B .6 C .96601 D .21316.下列各组中的四条线段是成比例线段的是( )A .a=6,b=4,c=10,d=5B .a=3,b=7,c=2,d= 9C .a=2,b=4,c=3,d=6D .a=4,b=11,c=3,d=217.如图,在□ABCD 中,点E 为AD 的中点,连接BE 交AC 于点F ,则AF ∶CF= ( )A .1∶2B .1∶3C .2∶3D .2∶518.已知点C 是线段AB 的黄金分割点,且AC >BC ,则下列等式成立的是( )A .AC 2=BC·AB B.AC 2=2BC·ABC .AB 2=AC·BC D.BC 2=AB·AC二、填空题19.点C 是线段AB 的黄金分割点,已知AB=4,则AC= .20.如图,测量小玻璃管口径的量具ABC ,AB 的长为10cm ,AC 被分为60等份.如果小玻璃管口DE 正好对着量具上20等份处(DE ∥AB ),那么小玻璃管口径DE 是 cm .21.已知53=+yx x ,则yx = .22.如图,△ABC 中,AE 交BC 于点D ,∠C =∠E ,AD :DE =3:5,AE =8,BD =4,则DC 的长等于 .23.如图,线段AB =1,点P 1是线段AB 的黄金分割点(AP 1<BP 1),点P 2是线段AP 1的黄金分割点(AP 2<P 1P 2),点P 3是线段AP 2的黄金分割点(AP 3<P 2P 3),…,依次类推,则AP n 的长度是_________。
2015-2016学年北师大附中初三上学期数学期中试卷

2015年北京师范大学附属实验中学初三上学期数学期中试卷一、选择题(本大题共10小题,每小题只有唯一正确答案.每小题3分,共30分) #1.抛物线2(2)3y x =+-的顶点坐标是( ). A .(2,3)- B .(2,3)-- C .(2,3)- D .(2,3)【答案】B【解析】抛物线的顶点为(2,3)--,故答案为B .#2.在Rt ABC △中,90C ∠=︒,若5AB =,2BC =,则sin B 的值为( ). A .5B .25C .12D .2【答案】A【解析】在Rt ABC △中,22541AC AB BC =-=-=,则5sin 5B ==.故选A .#3.如图,在ABC △中,点D 、E 分别在AB 、AC 边上,DE BC ∥,若6AD =,2BD =,9AE =,则EC 的长是( ). A .8 B .6C .4D .3 【答案】D【解析】∵DE BC ∥,∴ABC ADE ∽△△. ∴AD AE AB AC =, ∴632AD AE BD EC ===, ∴3EC =.#4.如图,点A 、B 、C 均在⊙O 上,35ACB ∠=︒,则AOB ∠的度数为( ). A .20︒ B .40︒ C .60︒ D .70︒【答案】D【解析】圆心角是其所对圆弧圆周角的2倍,即270AOB ACB ∠=∠=︒.故答案为D .#5.端午节吃粽子是中华民族的传统习俗,妈妈买了2个红豆粽、3个碱水粽、5个咸肉粽,粽子除内部馅料不同外其它均相同.小颖任意吃一个,吃到红豆粽的概率是( ).A .110B .15C .13D .12【答案】B 【解析】粽子的总数为23510++=,其中红豆综有2个,所以任意吃一个吃到红豆综的概率是21105=.故答案为B .#6.将抛物线23y x =向右平移2个单位,再向上平移3个单位,得到的抛物线的解析式是( ). A .23(2)3y x =++B .23(2)3y x =+-C .23(2)3y x =-+D .23(2)3y x =--OCBA【答案】C【解析】将抛物线23y x =向右平移2个单位得到23(2)y x =-,再向上平移3个单位得到23(2)3y x =-+.故答案为C .#7.如图,⊙O 的直径CD 垂直弦AB 于点E ,且2CE =,8DE =,则AB 的长为( ). A .2 B .4C .6D .8【答案】D【解析】根据圆的性质可知,圆的半径11()(28)522r CE DE =+=+=,在Rt BOE △中,2222AB BE OB OE ==-,其中523OE OC CE =-=-=,所以222538AB =-=.故答案为D .#8.二次函数2y ax bx c +=+(0a ≠)的图象如图所示,则下列关系式不正确...的是( ). A .0abc < B .0a b c ++< C .20a b -> D .40a b c -+<【答案】C【解析】由图象可知,该二次函数开口向下,所以0a <;对称轴为1x =-,即12ba-=-,即20b a =<;顶点为(1,)a b c --+在x 轴上半部分,所以0a b c -+>;与y 轴的交点在y 轴负半轴上,所以0c <.所以0abc <;1x =时,0y <,即0a b c ++<;20a b -=,故C 错误.#9.将矩形纸片ABCD 按如图所示的方式折叠,AE 、EF 为折痕,30BAE ∠=︒,3AB =,折叠后,点C 落在AD 边上的1C 处,并且点B 落在1EC 边上的1B 处.则BC 的长为( ). A .3 B .2C .3D .23【答案】C【解析】根据折叠的性质可知,130BAE C AB ∠=∠=︒,在Rt ABE △中,30BAE ∠=︒,3AB =,则tan301BE AB =⋅︒=, 在1Rt ABC △中,1tan301BC AB =⋅︒=,所以12EC =,又11=(1802)302FEC AEB ∠︒-∠=︒,在1Rt C EF △中,143cos303C E EF ==︒, 在Rt ECF △中,cos302CE EF =⋅︒=, 所以3BC BE CE =+=.故答案为C .#10.如图,正方形ABCD 中,8 cm AB =,对角线AC 、BD 相交于点O ,点E ,F分别从B 、C 两点同时出发,以1 cm /s 的速度沿BC 、CD 运动,到点C 、D 时停止运动,设运动时间为t (s ),OEF △的面积S (2cm ),则S (2cm )与t (s )的函数关系可用图象表示为( ).A .B .C .D .【答案】B【解析】根据题意BE CF t ==,8CE t =-, ∵四边形ABCD 为正方形,∴OB OC =,45OBC OCD ∠=∠=︒, ∵在OBE △中和OCF △中, OB OC OBE OCF BE CF =⎧⎪∠=∠⎨⎪=⎩, ∴OBE △≌OCF △(SAS ), ∴OBE OCF S S =△△,∴218164OBC OECF S S ==⨯=四边形△,∴2211116(8)416(4)8222CEF OECF S S S t t t t t =-=--⋅=-+=-+四边形△(08t ≤≤),∴S (2cm )与t (s )的函数图象为抛物线一部分,顶点为(4,8),自变量为08t ≤≤. 故答案为B .二、填空题(本大题共6小题,每小题3分,共18分)#11.请写出一个开口向下,且经过点(0,1)-的二次函数解析式:__________. 【答案】21y x =--【解析】开口向下,所以0a <,此时只需满足21y ax =-,即可符合条件.#12.如图,已知AB 是ABC △外接圆的直径,35A ∠=︒,则B ∠的度数是__________. 【答案】55︒【解析】∵AB 是ABC △外接圆的直径, ∴90ACB ∠=︒,又35A ∠=︒,此时55B ∠=︒. 故答案为55︒.#13.在阳光下,身高1.7m 的小强在地面上的影长为2m ,在同一时刻,测得学校的旗杆在地面上的影长为18m .则旗杆的高度为__________m . 【答案】15.3【解析】由于太阳光可近似看作平行线, 所以可根据相似定理可得,旗杆高度为21815.31.m 7h =⋅=. 故答案为15.3.#14.在一个不透明的口袋中装有4张相同的纸牌,它们分别标有数字1、2、3、4.随机地摸一张纸牌然后放回,再随机摸取出一张纸牌,则两次摸取纸牌上数字之和为5的概率是__________. 【答案】14【解析】摸两张牌所得结果有(1,1)、(1,2)、(1,3)、(1,4)、(2,1)、(2,2)、(2,3)、(2,4)、(3,1)、(3,2)、(3,3)、(3,4)、(4,1)、(4,2)、(4,3)、(4,4),则两次摸取纸牌上数字之和为5的样本情况为(1,4)、(2,3)、(3,2)、(4,1),其概率为41164=.故答案为14.#15.已知二次函数228y x x m =++,自变量123x =-+对应的函数值为1y ,自变量24x =-对应的函数值为2y ,则1y __________2y (填“>”、“<”或“=”). 【答案】<【解析】212(23)8(23)2y m m =-++-++=-,222(4)8(4)y m m =⋅-+⋅-+=,此时12y y <.故答案为<.#16.边长为1的正方形111OA B C 的顶点1A 在x 轴的正半轴上,如图将正方形111OA B C 绕顶点O 顺时针旋转75︒得正方形OABC ,使点B 恰好落在函数2y ax =(0a <)的图象上,则a 的值为__________. 【答案】23-【解析】将正方形111OA B C 绕顶点O 顺时针旋转75︒得正方形OABC ,即75xOA ∠=︒,又45AOB ∠=︒,所以30xOB ∠=︒,所以点B 的坐标为62(,)-, 而点B 的坐标为2(,)x ax , 解得:6x =,2a =-. 故答案为2-.三、解答题(本大题共30分,每小题5分) #17.计算:2sin453tan302tan60cos30︒+︒-︒⋅︒.【答案】2.【解析】2sin453tan302tan60cos30︒+︒-︒⋅︒2332323233=⨯+⨯-⨯=+-.#18.如图所示,图中的小方格都是边长为1的正方形,ABC △与A B C '''△是以点O 为位似中心的位似图形,它们的顶点都在小正方形的顶点上. @(1)画出位似中心O .【答案】【解析】画出位似中心O ,见答案.@(2)ABC △与A B C '''△的位似比为__________,面积比为__________.【答案】2:1,4:1【解析】根据图中ABC △与A B C '''△的边长可知21AC A C='',即位似比为2:1; 三角形面积比是边长比的平方,即为4:1.#19.已知:如图,在菱形ABCD 中,E 为BC 边上一点,AED B ∠=∠.@(1)求证:ABE DEA ∽△△. 【答案】ABE DEA ∽△△【解析】证明:∵四边形ABCD 是菱形, ∴AD BC ∥. 又∵B AED ∠=∠, ∴ABE DEA ∽△△@(2)若4AB =,求AE DE ⋅的值. 【答案】16【解析】∵ABE DEA ∽△△, ∴AE ABDA DE=. ∴AE DE AB DA ⋅=⋅.∵四边形ABCD 是菱形,4AB =, ∴4AB DA ==. ∴216AE DE AB ⋅==.#20.若二次函数2y ax bx c=++的x与y的部分对应值如下表:x4-3-2-1-0 y5-0343【答案】223y x x-=-+【解析】由表知,抛物线的顶点坐标为(1,4)-,∴设()214y a x=++,∵抛物线过(0,3),∴()20143a++=,∴1a=-,∴抛物线的解析式为()214y x=-++,即223y x x-=-+.@(2)画出此函数图象(不用列表).xyO【答案】【解析】如图.@(3)结合函数图象,当41x-<≤时,写出y的取值范围.【答案】y的取值范围是54y-<≤.【解析】当41x-<<-时,y单调递增,4x=-时,5y=-;1x=-时,max4y=;11x-<<时,y单调递减,1x =时,0y =.所以y 的取值范围是54y -<≤.#21.已知:如图,在ABC △中,30A ∠=︒,3tan 4B =,18AC =,求BC 、AB 的长. 【答案】15BC =,9312AB =+. 【解析】过D 点作CD AB ⊥于D , ∴90ADC BDC ∠=∠=︒, 在Rt ACD △中, ∵30A ∠=︒,∴1118922CD AC ==⨯=,3cos 1893AD AC A =⋅=⨯=, 在Rt BCD △中, ∵tan CDB BD =, ∴9123tan 4CD BD B ===, ∴2215BC BD CD =+=, ∴9312AB AD BD =+=+.#22.如图,某学校新建了一座吴玉章雕塑,小林站在距离雕塑2.7米的A 处自B 点看雕塑头顶D 的仰角为45︒,看雕塑底部C 的仰角为30︒,求塑像CD 的高度.(最后结果精确到0.1米,参考数据:3 1.7≈)【答案】1.2【解析】根据题意,得45DBE ∠=︒,30CBE ∠=︒, 2.7BE =, 在Rt DEB △中,45DBE ∠=︒, ∴tan45 2.7DE BE =⋅︒=米, ∴tan300.93CE BE =⋅︒=米, ∴ 2.70.93 1.2CD DE CE =-=-≈米. 故塑像CD 的高度大约为1.2米.四、解答题(本题共20分,每小题5分)#23.已知:如图,面积为22cm 的四边形ABCD 内接于⊙O ,对角线AC 经过圆心,45BAD ∠=︒,2cm CD =,求AB 的长.【答案】6【解析】延长BC 、AD 交于点E . ∵直径AC ,∴90ADC B ∠=∠=︒, ∵45BAD ∠=︒, ∴904545E ∠=︒-︒=︒, ∴2DE CD ==,∴3ABE S =△,∴132AB BE ⋅=, ∵45BAD E ∠=∠=︒, ∴AB BE =, ∴6AB =.#24.某文具店销售一种进价为每本10元的笔记本,为获得高利润,以不低于进价进行销售,结果发现,每月销售量y 与销售单价x 之间的关系可以近似地看作一次函数:50150y x =-+,物价部门规定这种笔记本每本的销售单价不得高于18元.@(1)当每月销售量为70本时,获得的利润为多少元? 【答案】420【解析】当70y =时,515070x -+=,解得16x =, ∴(1610)70420-⨯=元.@(2)该文具店这种笔记本每月获得利润为w 元,求每月获得的利润w 元与销售单价x 之间的函数关系式,并写出自变量的取值范围. 【答案】1018x ≤≤【解析】2(10)(5150)52001500w x x x x =--+=-+-, ∵1005150018x x x -≥⎧⎪-+≥⎨⎪≤⎩, ∴自变量的取值范围是1018x ≤≤.@(3)当销售单价定为多少元时,每月可获得最大利润,最大利润为多少元? 【答案】当销售单价定为18元时,每月可获得最大利润,最大利润为480元. 【解析】22520015005(20)500w x x x =-+-=--+, ∵50a =-<,∴当1018x ≤≤时,w 随x 的增大而增大. ∴当18x =时,w 有最大值为480元.答:当销售单价定为18元时,每月可获得最大利润,最大利润为480元.#25.如图,AB 是⊙O 的直径,弦CD AB ⊥与点E ,点P 在⊙O 上,1C ∠=∠.@(1)求证:CB PD ∥. 【答案】证明见解析.【解析】∵C P ∠=∠,又∵1C ∠=∠, ∴1P ∠=∠,∴CB PD ∥. @(2)若3BC =,3sin 5P ∠=,求⊙O 的直径. 【答案】5 【解析】连接AC , ∵AB 是⊙O 的直径, ∴90ACB ∠=︒,又∵CD AB⊥,∴BC BD=,∴P CAB∠=∠,∴3 sin5CAB∠=,即35 BCAB=,又知,3BC=,∴5AB=,∴直径为5.#26.阅读下列材料:小华遇到这样一个问题:已知:如图1,在ABC△中,三边的长分别为AB=,AC=2BC=,求A∠的正切值.小华是这样解决问题的:如图2所示,先在一个正方形网格(每个小正方形的边长均为1)中画出格点ABC△(ABC△三个顶点都在小正方形的顶点处),然后在这个正方形网格中再画一个和ABC△相似的格点DEF△,从而使问题得解.CBA图2D EFBA图1@(1)图2中与A∠相等的角为__________,A∠的正切值为__________.【答案】D∠,12.【解析】2BC=,AC=AB所以cos A==,从而1tan2A=,在DEF△中,1tan2D=,故D A∠=∠.@(2)参考小华解决问题的方法,利用图4中的正方形网格(每个小正方形的边长均为1)解决问题:如图3,在GHK△中,2HK=,HG=KG=,延长HK,请写出求αβ∠+∠度数的解题思路(需写出计算结果).【答案】45αβ∠+∠=︒.【解析】根据已知,把GHK △放到正方形网格中,连结GM , ∵可得2KM =,22MG =,∴4HM =,210HG =22MG =,25KG =2KM =,∴MKG MGH ∽△△, ∴1α∠=∠,∴45αβ∠+∠=︒.αβG KHM11M HGβα1MHβα五、解答题(本题共22分,第27题7分,第28题7分,第29题8分) #27.已知抛物线2154(3)22m y x m x -=--+. @(1)求证:无论m 为任何实数,抛物线与x 轴总有两个交点. 【答案】证明见解析.【解析】证明:令0y =,则2154(3)022mx m x ---+=. ∴[]222154(3)424(1)322m m m m m -∆=---⨯⨯=-+=-+. ∵不论m 为任何实数,都有2(13)0m -+>,即0∆>, ∴无论m 为任何实数,抛物线与x 轴总有两个交点.@(2)若抛物线对称轴1x =-,且反比例函数(0,0)ky k x x =>>的图象与抛物线在第一象限内的交点的横坐标为0x ,且满足023x <<,求k 的取值范围. 【答案】518k <<.【解析】∵抛物线2154(3)22m y x m x -=--+的对称轴为(3)3122m x m --=-=-⨯. 又∵抛物线对称轴1x =-, ∴31m -=-,即2m =, ∴抛物线的解析式为21322y x x =+-. 当23x <<时,αβG KHM1对于21322y x x =+-,y 随着x 的增大而增大, 对于(0,0)k y k x x =>>,y 随着x 的增大而减小. 所以当02x =时,由反比例函数图象在二次函数图象上方,得21333223k ⨯+->,解得18k <. 所以k 的取值范围为518k <<.#28.如图,点O 为矩形ABCD 的对称中心,10cm AB =,12cm BC =,点E 、F 、G 分别从A 、B 、C 三点同时出发,沿矩形的边按逆时针方向匀速运动,点E 的运动速度为1cm /s ,点F 的运动速度为3cm /s ,点G 的运动速度为1.5cm /s ,当点F 到达点C (即点F 与点C 重合)时,三个点随之停止运动.在运动过程中,EBF △关于直线EF 的对称图形是EB F '△.设点E 、F 、G 运动的时间为t (单位:s ).@(1)当t =__________s 时,四边形EBFB '为正方形.【答案】2.5.【解析】当四边形EBFB '为正方形时,45B EF BEF '∠=∠=︒,BEF △为等腰直角三角形. 此时10EB t =-,3BF t =,即103t t -=,解得 2.5t =.@(2)若以点E 、B 、F 为顶点的三角形与以点F ,C ,G 为顶点的三角形相似,求t 的值.【答案】2.8或14269-+.【解析】分两种情况,讨论如下:①若EBF FCG ∽△△,则有EB BF FC CG =,即103123 1.5t t t t-=-, 解得: 2.8t =; ②若EBF GCF ∽△△,则有EB BF CG FC =,即1031.5123t t t t-=-,解得:14269t =--(不合题意,舍去)或14269t =-+. ∴当 2.8t s =或(14269)t s =-+时,以点E 、B 、F 为顶点的三角形与以点F ,C ,G 为顶点的三角形相似.@(3)是否存在实数t ,使得点B '与点O 重合?若存在,求出t 的值;若不存在,请说明理由.【答案】不存在,理由见解析.【解析】假设存在实数t ,使得点B '与点O 重合.如图,过点O 作OM BC ⊥于点M ,则在Rt OFM △中,3OF BF t ==,1632FM BC BF t =-=-,5OM =, 由勾股定理得:222OM FM OF +=,即:2225(63)(3)t t +-=,解得:6136t =; 过点O 作ON AB ⊥于点N ,则在Rt OEN △中,10OE BE t ==-,1055EN BE BN t t =-=--=-,6ON =, 由勾股定理得:222ON EN OE +=,即:2226(5)(10)t t +-=-,解得: 3.9t =.∵61 3.936≠,∴不存在实数t ,使得点B '与点O 重合.#29.如图,在平面直角坐标系中,抛物线()20y ax bx a =+>与双曲线k y x=有交点A 、B ,已知点()2,2B --,tan 4AOX ∠=.@(1)求k 的值以及抛物线的解析式.【答案】4k =,23y x x =+.【解析】∵()2,2B --在双曲线上,∴()()224k=-⨯-=.∵tan 4AOx ∠=,∴可设(),4A m m ,∵A 在双曲线上,∴44m m ⋅=,∴1m =(1m =-舍去),∴()1,4A ,∵抛物线过点A 、B ,∴()()22222114a b a b ⎧-+-=-⎪⎨⋅+⋅=⎪⎩, 解得()(),1,3a b =,∴4k =,23y x x =+.@(2)过抛物线上点A 作直线AC x ∥轴,交抛物线于另一点C ,求所有满足EOC AOB ∽△△的点E 的坐标(注:这里E 、O 、C 与A 、O 、B 分别为对应点).【答案】G 点能落在⊙O 上,此时2x =.【解析】如图,设抛物线与x 轴负半轴的交点为D .由(1)知,抛物线的解析式是23y x x =+, ∵AC x ∥轴,∴()4,4C -,42OC =.又OB = ∴2OC OB=. ∵45COD BOD ∠=∠=︒,∴90COB ∠=︒,要BOA COE ∽△△,必须BOA COE ∠=∠,则点E 在直线CO 的两旁. ①将BOA △绕点O 顺时针转90︒,得到B OA ''△. 此时,点()2,2B '-是OC 的中点,点()14,1A -.延长'OA 至点1E ,使得112OE OA =,连接1CE ,此时()18,2E -. ②取点1E 关于直线OC 的对称点()22,8E -.@(3)点P 为抛物线上一动点,从O 点出发(含O 点)沿着抛物线向左运动,已知在此过程中,ABP △的面积ABP S △恰好有两次取到值m ,请直接写出m 的取值范围__________(P 与B 重合时规定0ABP S =△).【答案】03m <<或278m =. 【解析】见答案.。
2015-2016学年第一学期九年级数学北师大期中试题

(2)猜想与证明: 连接 FC, 判断 ABCF 是什么四边形, 并证明。
3
21. (本题 8 分) 已知: 如图, 平行四边形 ABCD 中, 点 O 是 CD 的中点, 连接 AO 并延长, 交 BC 的延长线于点 E。 (1)求证: △AOD ≌ △EOC;
A. m>- 1
8. 连接四边形 ABCD 各边中点得到的四边形是菱形,则四边形 ABCD 是 ( A. 矩形 C. 对角线相等的四边形 B. 菱形 D. 平行四边形 )
3. 某县为发展教育事业, 加强对教育经费的投入, 2013 年投入 4000 万元, 2015 年投入 7000 万元, 设教育经费的年平均增长率为 x, 根据题意, 下面所列方程正确的是 (
2 A. 4000 (1 + x) = 7000
)
9. 若 n (n≠0) 是关于 x 的方程 x2 + mx + 2n = 0 的根, 则 m + n 的值为 ( A. 1 B. 2 九数 (北师大) (A) C. - 1 第 2 页(共 8 页)
D. - 2
九数 (北师大) (A)
第 1 页(共 8 页)
B E C
17. 解方程。 (8 分) (1)解方程 2x2 - 5x - 3 = 0。 (配方法)
)
A
D F
得分
ቤተ መጻሕፍቲ ባይዱ评卷人
二、 填空题(每小题 3 分, 共 18 分)
(2)当 x 为何值时, x2 - x 的值与 3x2 - 5x + 2 的值相等?
11. 在平行四边形 ABCD 中, 添加一个条件 _______________ (写出一个即可) , 使平行四 边形 ABCD 是菱形。 12. 若关于 x 的方程 2x2 - 3x + c = 0 的一个根是 1, 则另一个根是 __________。 13. 经过某十字路口的汽车, 它可以继续前行, 也可以向左转或向右转, 如果这三种可能 性大小相同, 则两辆汽车经过这个十字路口全部继续右行的概率是 _________。 14. 三角形两边分别为 2 和 6, 第三边是方程 x2 - 10x + 21 = 0 的解, 则三角形的周长为 __________。 15. 如图, 点 E 是正方形 ABCD 内的一点, 连接 AE、 BE、 CE, 将△ABE 绕点 B 顺时针旋转 90毅到△CBE忆的位置。若 AE = 1, BE = 2, CE = 3, 则∠BE忆C = ________。
2015-2016学年北师大 数学上 九年级 期中测试试卷
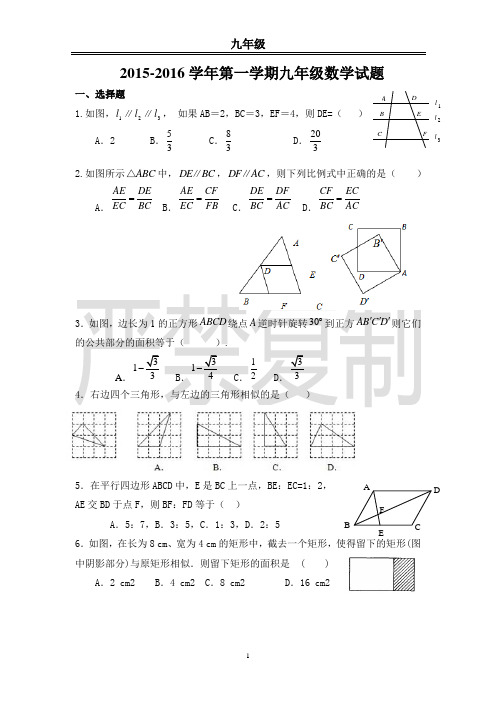
2015-2016学年第一学期九年级数学试题一、选择题1.如图,321l l l ∥∥, 如果AB =2,BC =3,EF =4,则DE=( )A .2B .53C .83D .2032.如图所示ABC △中,DE BC ∥,DF AC ∥,则下列比例式中正确的是( )A .AE DE EC BC =B .AE CF EC FB = C .DE DF BC AC =D .CF ECBC AC =3.如图,边长为1的正方形ABCD 绕点A 逆时针旋转30︒到正方AB C D '''则它们的公共部分的面积等于( ).A .313-B .314-C .12D .334.右边四个三角形,与左边的三角形相似的是( )5.在平行四边形ABCD 中,E 是BC 上一点,BE :EC=1:2, AE 交BD 于点F ,则BF :FD 等于( ) A .5:7,B .3:5,C .1:3,D .2:56.如图,在长为8 cm 、宽为4 cm 的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似.则留下矩形的面积是 ( ) A .2 cm2 B .4 cm2 C .8 cm2 D .16 cm2l 3l 2l 1F ED C BA F EDCBA7.如图,正方形ABCD 的对角线AC 、BD 相较于点O ,E 是BC 的中点,DE 交AC 于F ,若12DE ,则EF 等于( )A .8B .6C .4 D.38.如图所示,已知△ABC 中,AB=AC ,∠BAC=90°,直角∠EPF 的顶点P 是BC 中点,两边PE 、PF 分别交AB 、AC 于点E 、F ,给出以下四个结论:①AE=CF ;②△EPF 是等腰直角三角形;③S 四边形AEPF=21S △ABC ;④EF=AP .当∠EPF 在△ABC 内绕顶点P 旋转时(点E•不与A 、B 重合),上述结论中始终正确的有( ) A 、①④ B 、①② C 、①②③ D 、①②③④二、填空题9.若2===fed c b a ,且4=++f d b ,则=++e c a ______.10.如图,BD 和EC 相交于点A ,ED ∥BC ,BD =12,AD =4,EC =9, AC =______.11.如图,在同一时刻,小明测得他的影长为1米, 距他不远处的一棵槟榔树的影长为5米,已知小明的身 高为1.5米,则这棵槟榔树的高是__________米.12.有一个正十二面体,12个面上分别写有1~12这12个整数,投掷这个正十二面体一次,向上一面的数字是3的倍数或4的倍数的概率是 .13.如图,在四边形ABCD 中,AD ∥BC ,DE ⊥BC ,垂足为点E ,连接AC 交DE 于点F ,点G 为AF 的中点,∠ACD=2∠ACB .若DG=3,EC=1,则DE 的长为________.ABC D E FO14、如图,正方形ABCD 的面积为16,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线BD 上有一点P ,使PC+PE 的和最小,则这个最小值为15.如图所示,在正方形ABCD 的对角线BD 上取一点E ,使得∠BAE =15°,连接AE ,CE ,延长CE 到F ,连接BF ,使得BC =BF .若AB =1,有下列结论:①AE =CE ;②F 到BC 的距离为22;③BE EC EF +=;④S △AED=1248+;⑤S △EBF 312=.其中正确结论的序号是____________.三、解答题16.如左下图,BCAEAB DE AC AD ==. 求证:AE AB =17.如图,在△ABC 中,BC>AC , 点D 在BC 上,且DC =AC,∠ACB 的平分线CF 交AD 于F ,点E 是AB 的中点,连结EF. (1)求证:EF ∥BC.(2)若四边形BDFE 的面积为6,求△ABD 的面积.18.已知:如图,在ABC △中,AB AC =,点D 在BC 上,且DE AC ∥交AB 于E ,点F 在AC 上,且DF DC =。
2015年数学中考精选:北师大九年级上册(含答案)

2015年数学中考精选:北师大九年级上册一、选择题1.分式211x x -+的值为0,则x 的值为( ) A .1 B .-1 C .0 D .1±【答案】A2.某超市一月份的营业额为200万元,已知第一季度的总营业额共1000万元, 如果平均每月增长率为x,则由题意列方程应为( )A 、200(1+x )2=1000B 、200+200×2x=1000C 、200+200×3x=1000D 、200[1+(1+x )+(1+x )2]=1000【答案】D .3.同一时刻,小明在阳光下的影长为2米,与他邻近的旗杆的影长为6米,小明的身高为1.6米,则旗杆的高为( )A .3.2米B .4.8米C .5.2米D .5.6米【答案】B4.如图,已知在梯形ABCD 中,AD ∥BC ,2BC AD =,如果对角线AC 与BD 相交于点O ,△AOB 、△BOC 、△COD 、△DOA 的面积分别记作1S 、2S 、3S 、4S ,那么下列结论中,不正确的是( )A. 13S S =;B. 242S S =;C. 212S S =;D. 1324S S S S ⋅=⋅;【答案】B5.如图,过点C (1,2)分别作x 轴、y 轴的平行线,交直线y =-x +6于A 、B 两点,若反比例函数y =k x(x >0)的图像与△ABC 有公共点,则k 的取值范围是( )A .2≤k≤9B .2≤k≤8C .2≤k≤5D .5≤k≤8【答案】A .二、计算题6.(本题共4道小题,每小题5分,满分20分)(1)解方程:212270x x -+=(2)分解因式:2327x -(3)计算:101()2)4sin 4583--+- (4)先化简,再求值:22112111x x x x x x x --÷-++++,其中1x =. 【答案】(1)13x =,29x =;(2)3(3)(3)x x +-;(3)2;(4)11+x ,2.三、解答题7.试说明关于x 的方程012)208(22=+++-ax x a a 无论a 取何值,该方程都是一元二次方程。
