数理方程30题

合集下载

数理方程习题答案

数理方程习题答案数理方程习题答案数理方程是数学中一门重要的学科，它研究的是各种各样的方程。

在学习数理方程的过程中，习题是不可或缺的一部分。

通过解习题，我们可以加深对数理方程的理解，掌握解题的方法和技巧。

在这篇文章中，我将为大家提供一些数理方程习题的答案，希望能对大家的学习有所帮助。

1. 求解方程：2x + 5 = 17。

解：将方程化简，得到2x = 17 - 5，即2x = 12。

再将等式两边同时除以2，得到x = 6。

所以方程的解为x = 6。

2. 求解方程组：2x + y = 73x - 2y = 4解：可以使用消元法来求解这个方程组。

首先，将第一个方程乘以2，得到4x + 2y = 14。

然后将第二个方程与这个结果相加，得到7x = 18。

再将等式两边同时除以7，得到x = 18/7。

将x的值代入第一个方程，可以求得y的值为y = 7 - 2x = 7 - 2(18/7) = 7 - 36/7 = 7/7 - 36/7 = -29/7。

所以方程组的解为x = 18/7，y = -29/7。

3. 求解二次方程：x^2 - 5x + 6 = 0。

解：可以使用因式分解法来求解这个二次方程。

首先，将方程化简，得到(x - 2)(x - 3) = 0。

根据乘积为零的性质，可以得到x - 2 = 0或者x - 3 = 0。

解这两个方程，可以得到x = 2或者x = 3。

所以方程的解为x = 2或者x = 3。

4. 求解三次方程：x^3 - 3x^2 + 2x - 4 = 0。

解：可以使用综合除法来求解这个三次方程。

首先，将方程按照降幂排列，得到x^3 - 3x^2 + 2x - 4 = 0。

然后，尝试将方程的第一项x^3除以x的最高次数x^3，得到商为1。

将这个商乘以方程的所有项，得到x^3 - 3x^2 + 2x - 4 - (x^3 - 3x^2 + 2x - 4) = 0。

化简这个等式，可以得到0 = 0。

数理方程习题全解

（2） z 4 4 0 ；解 z 4 4 2 4 1 2 4 cos j sin
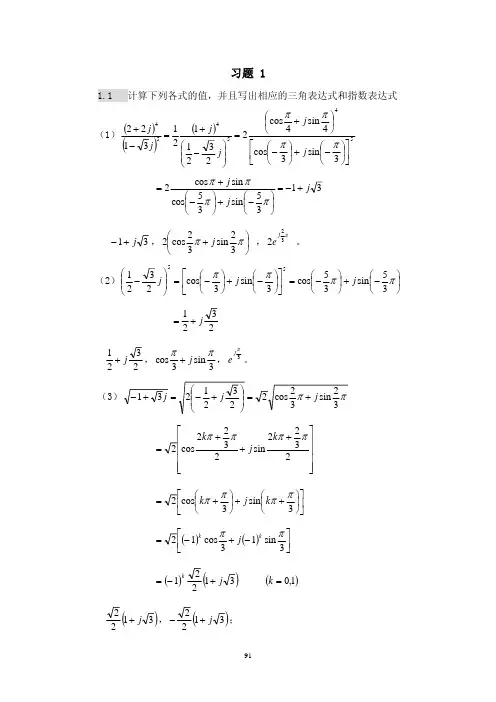
93

2k 1 j sin 2k 1 = 2 cos 4 4
k 0,1,2,3
1 1 k 0 ： z1 2 cos j sin 2 j 1 j 4 4 2 2 3 3 1 1 k 1 ： z2 2 cos j sin 2 j 1 j 4 4 2 2 5 5 1 1 k 2 ： z3 2 cos j sin 2 j 1 j 4 4 2 2 7 7 1 1 k 3 ： z4 2 cos j sin 2 j 1 j 4 4 2 2
3 8
k k 2 8 cos j sin 2 16 2 16
3 3 8 3
k 0,1,2,3
7 7 2 cos j sin ， 2 8 cos j sin ， 16 16 16 16 9 15 15 9 2 cos j sin ， 2 8 cos j sin ； 16 16 16 16
1 3 5 5 （2） j sin cos j sin 2 2 j cos 3 3 3 3 1 3 j 2 2
4
cos j sin 4 4
4
2
cos j sin 1 j 3 5 5 cos j sin 3 3

方程题100道带答案

方程题100道带答案1. 2x + 3 = 7，答案：x = 22. 5x 8 = 12，答案：x = 43. 3x + 4 = 19，答案：x = 54. 7x 15 = 14，答案：x =5.29（约等于5.3）5. 9x + 11 = 32，答案：x = 1.89（约等于1.9）6. 4x 6 = 18，答案：x = 6.57. 8x + 5 = 37，答案：x = 3.758. 6x 9 = 21，答案：x = 5.59. 10x + 13 = 53，答案：x = 410. 3x + 7 = 16，答案：x = 311. 2x 5 = 9，答案：x = 712. 4x + 8 = 24，答案：x = 413. 5x 3 = 22，答案：x = 514. 7x + 6 = 51，答案：x = 5.（约等于5.9）15. 9x 4 = 35，答案：x = 4.11（约等于4.1）16. 6x + 5 = 47，答案：x = 617. 8x 7 = 29，答案：x = 5.2518. 10x + 2 = 42，答案：x = 419. 3x 8 = 7，答案：x = 520. 5x + 9 = 44，答案：x = 5.2继续完善方程题100道带答案文档：21. 若4x 2 = 14，求x的值。

答案：x = 422. 解方程6x + 3 = 39，得x等于多少？答案：x = 623. 当7x 5 = 46时，x的值为多少？答案：x = 7.29（约等于7.3）24. 8x + 4 = 36，求x的值。

答案：x = 3.525. 如果9x 6 = 30，那么x等于多少？答案：x = 4.22（约等于4.2）26. 解方程3x + 5 = 14，得x的值。

答案：x = 327. 当5x 2 = 23时，求x的值。

答案：x = 528. 7x + 8 = 57，求x的值。

答案：x = 5.29（约等于5.3）29. 9x 3 = 42，求x的值。

数理方程练习题

数理方程练习题第二章定解问题与偏微分方程理论习题2.11. 密度为ρ均匀柔软的细弦线x =0端固定，垂直悬挂，在重力作用下，于横向拉它一下，使之作微小的横振动。

试导出振动方程。

2. 长为L ，均匀细杆，x = 0端固定，另一端沿杆的轴线方向被拉长b 静止后（在弹性限度内）突然放手，细杆作自由振动。

试写出振动方程的定解条件。

3. 长为L 、密度为ρ的底半径为R 的均匀圆锥杆（轴线水平）作纵振动，锥的顶点固定在x =0处。

导出此杆的振动方程。

4. 一根长为L 、截面面积为1的均匀细杆，其x =0端固定，以槌水平击其x =L 端，使之获得冲量I 。

试写出定解问题。

习题2.21. 一半径为r ，密度为ρ，比热为c ，热传导系数为k 的匀质圆杆，如同截面上的温度相同，其侧面与温度为u 1的介质发生热交换，且热交换的系数为k 1。

试导出杆上温度u 满足的方程。

4. 设有一根具有绝热的侧表面的均匀细杆，它的初始温度为)(x ?，两端满足下列边界条件之一：（1）一端（x =0）绝热，另一端（x = L ）保持常温u 0；（2）两端分别有热流密度q 1和q 2进入；（3）一端（x =0）温度为u 1(t )，另一端（x = L ）与温度为)(t θ的介质有热交换。

试分别写出上述三种热传导过程的定解问题。

习题2.41. 判断下列方程的类型：（1）04=+++++u cu bu au au au y x yy xy xx ；（2）02=+++++u cu bu au au au y x yy xy xx ；（3）02222=+++++u au bu au au au y x yy xy xx ；（4）0=+yy xx xu u 。

2. 求下列方程的通解（1）0910=++yy xy xx u u u ；（3）0384=++yy xy xx u u u 。

第三章分离变量法习题3.12. 求解下列定解问题（1）-====><<=====)(,00)0,0(,0002x L x u u u u t L x u a u t t t L x x xx tt3. 求下列边值问题的固有值和固有函数：（1）===+''==0,000L x x X X X X λ （3）0,0012===+'+''==e x x y y y y x y x λ 习题3.21.求定解问题：-===><<====)(0,0)0,0(,002x L x u u u t L x u a u t L x x xx t 习题3.52. 求解定解问题：===><<=+-===-00020,0)0,0(,0T u u u t L x Ae u a u t L x x x t xx α 0T 是常数。

方程题100道带答案大全

方程题100道带答案大全一、一元一次方程1. 3x 7 = 11答案：x = 62. 5 2x = 1答案：x = 23. 4x + 8 = 24答案：x = 44. 9 3x = 0答案：x = 35. 7x 14 = 0答案：x = 2二、一元二次方程6. x^2 5x + 6 = 07. x^2 + 3x 4 = 08. 2x^2 4x 6 = 09. 3x^2 + 12x + 9 = 010. x^2 8x + 16 = 0三、二元一次方程组11.x + y = 5x y = 312.2x + 3y = 83x 2y = 713.4x + y = 92x 3y = 514.3x 2y = 105x + y = 1615.2x + 5y = 12x 3y = 4四、不等式16. 3x 7 > 217. 2x + 5 < 1518. 4x 9 ≥ 119. 5x + 6 ≤ 2420. 7 3x > 2x + 1（文档第一部分完成，后续题目及答案将依次列出）五、分式方程21. 1/x + 2/(x+1) = 3答案：x = 1 或 x = 322. (2x+1)/(x2) = 3答案：x = 7/223. (3x2)/(x+3) + 4/(x1) = 024. (x+4)/(x3) (x2)/(x+2) = 2答案：x = 11/325. (2x+3)/(3x1) = (x+2)/(x1)答案：x = 1 或 x = 5/3六、绝对值方程26. |2x 5| = 3答案：x = 4 或 x = 127. |3x + 2| 4 = 7答案：x = 3 或 x = 5/328. |x 2| + |x + 3| = 8答案：x = 5 或 x = 129. |2x + 1| = |3x 4|答案：x = 1 或 x = 11/5 30. |x 4| |x + 1| = 3答案：x = 5 或 x = 1/2七、根式方程31. √(x 1) = 2答案：x = 532. √(3x + 4) + √(2x 1) = 5答案：x = 433. √(x + 2) √(x 3) = 1答案：x = 434. √(2x 5) = √(3x + 2) 135. √(4 x) + √(x + 3) = 5答案：x = 4八、指数方程36. 2^x = 16答案：x = 437. 3^(2x) = 9答案：x = 138. 4^(x1) = 1/2答案：x = 1/239. 5^(x+2) = 25答案：x = 140. (1/2)^x = 8答案：x = 3（文档内容持续更新，敬请期待剩余题目及答案）九、对数方程41. log₂(x 1) = 3答案：x = 942. log₃(2x + 3) = 2答案：x = 343. log₅(x) log₅(x + 2) = 1答案：x = 544. log₁₀(3x 1) + log₁₀(x + 4) = 1答案：x ≈ 0.645. log(x 2) log(x + 1) = log₂3答案：x ≈ 5.4十、三角方程46. sin(x) = 1/2, 0 ≤ x ≤ 2π答案：x = π/6 或5π/647. cos(x) = 0, 0 ≤ x ≤ 2π答案：x = π/2 或3π/248. tan(2x) = 1, 0 ≤ x ≤ π答案：x = π/8 或5π/849. 2sin²(x) sin(x) 1 = 0答案：x = π/6, 5π/6 或7π/6, 11π/650. cos²(x) + cos(x) 2 = 0答案：x = 2π/3, 4π/3十一、综合应用题51. 一辆汽车以60km/h的速度行驶，另一辆汽车以80km/h的速度行驶，两车相距100km，多久后两车相遇？答案：1小时后两车相遇。

数理方程练习题(作业)

数理方程练习题一（2009研）1. 设(,)u u x y =，求二阶线性方程20ux y∂=∂∂ 的一般解。

2. 设u f = 满足Laplace 方程22220u u x y ∂∂∂∂+=求函数u.3. 求Cauchy 问题22000(,)(0,)cos tt xx t t t u a u x t u x u x x ==⎧-=∈⨯∞⎪⎨==∈⎪⎩的解．4. 求解Cauchy 问题200cos (,)(0,)cos 010tt xx t t t u a u t x x t x x u x u x ==⎧-=∈⨯∞⎪≥⎧⎨==⎨⎪<⎩⎩5. 解在半无界问题20000(,)(0,)sin (0)0(0)tt xx t t t x u a u x t u x u x x u t +===⎧+=∈⨯∞⎪⎪==≤≤∞⎨⎪=≥⎪⎩6. 求解二维Cauchy 问题222200(,,)(0,)0()(,)tt t t t u a u x y t u u x x y x y ==⎧-∆=∈⨯∞⎪⎨==+∈⎪⎩求下列函数的Fourier 变换1 0()00axe xf x a x -⎧≥=>⎨<⎩2 1||()0||a x a x x a≤⎧∏=⎨>⎩3 2()x f x e -=7. 磁致伸缩换能器、鱼群探测换能器等器件的核心是两端自由的均匀杆，它作纵振动．研究两端自由棒的自由纵振动，即定解问题。

200,0(,0)(),(,0)()0(0,)(,)00tt xx t xx u a u x l t u x x u x x x l u t u l t t ϕψ⎧-=<<>⎪==≤≤⎨⎪==≥⎩8. 散热片的横截面为矩形。

它的一边y=b 处于较高温度V ，其他三边b=0，x=0，x=a 则处于冷却介质中因而保持较低的温度v 求解这横截面上的稳定温度分布Ux,y)即定解问题0;0(0,),(,)0(,0),(,)()0xx yy u u x a y b u y v u a y vy b u x v u x b V x x a +=<<<<⎧⎪==<<⎨⎪==<<⎩9. 求解定解问题2000cos sin 0,00,0ttxx x x x x l t t t x u a u A t lu u u u πω====⎧-=⎪⎪⎪==⎨⎪'==⎪⎪⎩10. 求解定解问题200sin 0,00t xx x x x l t u a u A tu u u ω===⎧-=⎪⎪==⎨⎪=⎪⎩ 11. 弦的x=0端固定而x=l 端受迫作谐振动sin A t ω，则弦的初始位移和初始速度都是零，求弦的振动。

数理方程试题

数理方程试题一．判断题（每题2分）.1. 2u u x y x y x+=是非线性偏微分方程.( )2. 绝对可积函数一定可做Fourier 积分变化.( )3. ()(1) 1.n n F x n Legendre F =是次正交多项式，则 ( )4. (,)0xy f x y =的解是调和函数.( )5. **12u u 已知,是线性偏微分方程(,)xx yy u u f x y +=的解，则**12u u -是0u ?= 的解.( )二．填空题（每题2分）.1. ()sin t xx yy u u u xt -+= 是____________型偏微分方程.2. 内部无热源的半径为R 的圆形薄板,内部稳态温度分布，当边界上温度为()t φ时，试建立方程的定解问题________________________.3. 2x 的Legendre 正交多项式的分解形式为__________________.4.某无界弦做自由振动,此弦的初始位移为()x φ,初始速度为()a x φ-,则弦振动规律为______________________________.5. []()____________.at m L e t s = 三．求解定解问题（12分）20sin ;0,0;0.t xx xx xx lt u a u A t u u u ω===-====四．用积分变换方法求解以下微分方程（每题12分，共24分）（1）1,0,0;1,1.xy x y u x y uy u===>>=+=（2） 00230, 1.tt t y y y e y y =='''+-='==五．某半无界弦的端点是自由的，初始位移为零，初始速度为cos x ，求弦的自由振动规律。

（12分）六．设有长为a ，宽为b 的矩形薄板，两侧面绝热，有三边的温度为零，另一边的温度分布为x ，内部没有热源，求稳定状态时板内的温度分布。

数理方程习题综合

例 1、1、1 设v=v(线x,y),二阶性偏微分方程v xy =xy 的通解。

解原方程可以写成 ð／ðx(ðv／ðy) =xy 两边对x 积分,得 v y =¢(y)+1/2 x 2Y ,其中¢(y)就是任意一阶可微函数。

进一步地,两边对y 积分,得方程得通解为v (x,y)=∫v y dy+f(x)=∫¢(y)dy+f(x)+1/4 x 2y 2=f(x)+g(y)+1/4 x 2y 2其中f(x),g(y)就是任意两个二阶可微函数。

例1、1、2即 u(ξ,η) = F(ξ) + G(η),其中F(ξ),G(η)就是任意两个可微函数。

例1、2、1设有一根长为L 的均匀柔软富有弹性的细弦,平衡时沿直线拉紧,在受到初始小扰动下,作微小横振动。

试确定该弦的运动方程。

取定弦的运动平面坐标系就是O XU ,弦的平衡位置为x 轴,弦的长度为L,两端固定在O,L 两点。

用u(x,t)表示弦上横坐标为x 点在时刻t 的位移。

由于弦做微小横振动,故u x ≈0、因此α≈0,cos α≈1,sin α≈tan α=u x ≈0,其中α表示在x 处切线方向同x 轴的夹角。

下面用微元法建立u 所满足的偏微分方程。

在弦上任取一段弧'MM ,考虑作用在这段弧上的力。

作用在这段弧上的力有张力与外力。

可以证明,张力T 就是一个常数,即T 与位置x 与时间t 的变化无关。

事实上,因为弧振动微小,则弧段'MM 的弧长dx u xx xx ⎰∆++=∆21s ≈x ∆。

这说明该段弧在整个振动过程中始终未发生伸长变化。

于就是由Hooke 定律,张力T 与时间t 无关。

因为弦只作横振动,在x 轴方向没有位移,故合力在x 方向上的分量为零,即T(x+x ∆)cos α’-T(x)cos α=0、由于co's α’≈1,cos α≈1,所以T(X+∆x)=T(x),故张力T 与x 无关。

数理方程习题

uyy + uzz = 0的解; (3) un (r, θ) = rn cos(nθ)), rn sin(nθ)) (n = 0, 1, 2, · · · )是拉普拉斯方程urr +
1 r ur 1 u r2 θθ
+
= 0的解. ut = −uxx , u(x, 0) = 1,
10. 说明定解问题
− auxx = 0的解.
((x, y ) ̸= (0, 0)), eax cos(ay ), eax sin(ay )均是二维 ((x, y, z ) ̸= (0, 0, 0))是三维拉普拉斯方程uxx +
拉普拉斯方程uxx + uyy = 0的解; (2) u(x, y, z ) = √
1 x2 + y 2 + z 2
证. (方法一) 极坐标系与直角坐标系之间的变换关系为 x = r cos θ, 或者为 r = (x2 + y 2 ) 2 , 于是 ∂r x = = cos θ, ∂x r ∂θ y sin θ =− 2 =− , 2 ∂x x +y r 从而 ∂u ∂r ∂u ∂θ ∂u ∂u sin θ ∂u = + = cos θ − , ∂x ∂r ∂x ∂θ ∂x ∂r ∂θ r ∂u ∂u ∂r ∂u ∂θ ∂u ∂u cos θ = + = sin θ + , ∂y ∂r ∂y ∂θ ∂y ∂r ∂θ r ∂r y = = sin θ, ∂y r ∂θ x cos θ = 2 = . 2 ∂y x +y r
习题1
1. 对下列偏微分方程, 指出它的阶, 并指出它是线性的、拟线性的还是非线性的. 若是线性的, 再指出它是齐次的还是非齐次的. (1) u3 x + 2uuy = xy ; (2) uuy − 6xyux = 0; (3) uxx − x2 uy = sin x;

数学解方程100道练习题

数学解方程100道练习题解题方法一：平方差公式法1. 解方程：x² - 9 = 02. 解方程：4x² - 16 = 03. 解方程：9x² - 4 = 04. 解方程：25x² - 49 = 05. 解方程：16x² + 9 = 06. 解方程：36x² + 25 = 07. 解方程：9x² - 16 = 08. 解方程：4x² - 25 = 09. 解方程：64x² - 16 = 010. 解方程：49x² - 4 = 0解题方法二：配方法11. 解方程：x² - 7x + 12 = 012. 解方程：x² + 5x + 6 = 013. 解方程：x² - 6x + 5 = 014. 解方程：x² + 6x + 9 = 015. 解方程：x² + 4x + 3 = 016. 解方程：x² - 4x + 4 = 017. 解方程：x² + 2x - 3 = 018. 解方程：x² - 9x + 14 = 019. 解方程：x² - 8x + 15 = 020. 解方程：x² + 3x - 10 = 0解题方法三：因式分解法21. 解方程：(x + 3)(x - 4) = 022. 解方程：(x - 2)(x + 7) = 023. 解方程：(x - 5)(x + 5) = 024. 解方程：(x + 1)(x + 4) = 025. 解方程：(x - 3)(x + 3) = 026. 解方程：(x + 2)(x - 2) = 027. 解方程：(x + 6)(x - 6) = 028. 解方程：(x - 9)(x + 9) = 029. 解方程：(x + 8)(x - 8) = 030. 解方程：(x - 7)(x + 7) = 0解题方法四：二次方程求根公式法31. 解方程：x² + 6x + 5 = 032. 解方程：x² - 4x + 4 = 033. 解方程：x² + 2x - 8 = 034. 解方程：x² + 5x + 6 = 035. 解方程：x² + 3x - 18 = 036. 解方程：x² + x - 12 = 037. 解方程：x² - 6x + 9 = 038. 解方程：x² - 9x + 20 = 039. 解方程：x² - 7x + 12 = 040. 解方程：x² - 8x + 15 = 0解题方法五：恒等变形法41. 解方程：3(x - 2) = 2x + 142. 解方程：2(x + 3) = 3x + 443. 解方程：(x - 4)² = 1644. 解方程：2(x + 5) - 3(x - 1) = 445. 解方程：5(x + 1) - (2x - 3) = 446. 解方程：4(2x - 3) - 3(4x + 5) = 847. 解方程：(2x - 1)³ = 12548. 解方程：(3x - 2)² = 4949. 解方程：√(x + 2) = 450. 解方程：2√(2x - 1) - 3 = 7解题方法六：代入法51. 解方程：2x + 3 = 752. 解方程：3x - 5 = 1653. 解方程：4x² + 3x = 754. 解方程：2x² - 5x + 3 = 055. 解方程：5x² + 2x = 356. 解方程：3x² - 4x + 1 = 057. 解方程：16x² + 8x - 1 = 058. 解方程：9x² - 12x + 4 = 059. 解方程：25x² - 14x - 3 = 060. 解方程：36x² + 30x - 5 = 0解题方法七：对数法61. 解方程：log₂(x + 3) = 262. 解方程：log₄(x - 2) = 363. 解方程：ln(x + 1) = 464. 解方程：log₇(x + 2) = 165. 解方程：log₅(x - 1) = 266. 解方程：log₃(x + 1) + log₃(x - 1) = 267. 解方程：log₆(2x - 1) + log₆(3x + 1) = 268. 解方程：log₈(x - 4) = 369. 解方程：log₂(x + 1) - log₂(x - 1) = 170. 解方程：log₉(2x - 1) - log₉(x - 1) = 1解题方法八：绝对值法71. 解方程：|x + 3| = 572. 解方程：|x - 4| = 373. 解方程：|x + 2| + |x - 2| = 674. 解方程：|x - 5| + |x + 5| = 1075. 解方程：2|x - 3| = 876. 解方程：3|x + 4| = 977. 解方程：|x - 9| = 778. 解方程：4|x + 8| = 3279. 解方程：|x - 7| - |x + 7| = 080. 解方程：|x + 6| - |x - 6| = 0解题方法九：分式方程法81. 解方程：(x + 2)/(3x - 1) = 4/382. 解方程：(2x - 1)/(x + 3) = 5/283. 解方程：(5x - 2)/(x - 4) = 3/284. 解方程：(3x + 1)/(2x - 3) = 7/585. 解方程：(x + 1)/(4x + 3) = 2/586. 解方程：(2x - 3)/(x + 2) - 3/(2x + 3) = 187. 解方程：(3x + 1)/(4x - 5) + 2/(3x - 1) = 17/1288. 解方程：2/(x + 3) + 3/(2x - 1) = 5/289. 解方程：(x - 2)/(4x + 5) - (2x - 3)/(5x + 2) = 1/390. 解方程：(2x + 1)/(x - 2) + (3x - 2)/(x + 3) = 5解题方法十：根号方程法91. 解方程：√(4x + 5) = 392. 解方程：√(x + 2) - 2 = 193. 解方程：√(x - 3) + 2 = 594. 解方程：√(x + 4) - √(x - 1) = 295. 解方程：√(2x + 3) = 496. 解方程：√(3x - 2) - √(2x + 1) = 297. 解方程：√(x - 1) - √(x + 2) = 198. 解方程：√(x - 4) + √(x + 3) = 699. 解方程：√(x + 1) + √(x - 1) = 4100. 解方程：√(2x + 1) + √(x - 2) = 5这些题目涵盖了数学解方程的常见方法和类型，希望通过这些练习题的练习，你能够熟练掌握解方程的技巧和方法。

数理方程课后习题答案

数理方程课后习题答案数理方程课后习题答案数理方程是数学中的一个重要分支，它研究的是各种数学模型中的方程。

在学习数理方程的过程中，课后习题是巩固知识、提高能力的重要途径之一。

本文将为大家提供一些数理方程课后习题的答案，希望能对大家的学习有所帮助。

1. 解方程：2x + 5 = 13解答：将方程中的常数项5移到等号右边，得到2x = 13 - 5，即2x = 8。

然后将2移到等号右边，得到x = 8/2，即x = 4。

所以方程的解为x = 4。

2. 解方程组：{2x + y = 7，x - y = 1}解答：可以使用消元法来解决这个方程组。

首先将第二个方程的系数取负，得到{-x + y = -1}。

然后将第二个方程乘以2，得到{-2x + 2y = -2}。

将这两个方程相加，得到{0x + 3y = -3}，即3y = -3。

解得y = -1。

将y的值代入第一个方程，得到2x - 1 = 7，即2x = 8。

解得x = 4。

所以方程组的解为x = 4，y = -1。

3. 解二次方程：x^2 - 5x + 6 = 0解答：可以使用因式分解法来解决这个二次方程。

将方程因式分解为(x - 2)(x - 3) = 0。

根据乘积为零的性质，得到x - 2 = 0或x - 3 = 0。

解得x = 2或x = 3。

所以方程的解为x = 2或x = 3。

4. 解三次方程：x^3 - 6x^2 + 11x - 6 = 0解答：可以使用因式分解法来解决这个三次方程。

观察方程，可以发现x = 1是一个解。

通过除以x - 1，得到(x - 1)(x^2 - 5x + 6) = 0。

将x^2 - 5x + 6进行因式分解，得到(x - 1)(x - 2)(x - 3) = 0。

根据乘积为零的性质，得到x - 1 = 0或x - 2 = 0或x - 3 = 0。

解得x = 1或x = 2或x = 3。

所以方程的解为x = 1或x = 2或x = 3。

数理方程复习试卷2014

一、（15分）用达朗贝尔公式求解定解问题：�ðð2uu ððtt 2=16ðð2uu ððxx 2，−∞<xx <+∞，tt >0uu |tt=0=3xx 2，ððuu ððtt |tt=0=9xx 解：∵uu (xx ,tt )=12[φφ(xx +aatt )+φφ(xx −aatt )]+12aa ∫ψψ(ξξ)ddξξxx+aatt xx−aatt∴φφ(xx )=3xx 2，ψψ(xx )=9xx , aa =4 ∴uu (xx ,tt )=12[3(xx +4tt )2+3(xx −4tt )2]+18∫9ξξddξξxx+4tt xx−4tt =3xx 2+9xxtt +48tt 2二、（15分）用分离变量法求解定解问题：⎩⎪⎨⎪⎧ðð2uu ððtt 2=aa 2ðð2uu ððxx 2，0<xx <ll ，tt >0uu |xx=0=0，uu xx |xx=ll =0uu |tt=0=5，uu tt |tt=0=3ssss ss 3ππxx 2ll 解：∵令uu (xx ,tt )=XX (xx )TT (tt )∴TT ,,(tt )aa 2TT (tt )=XX ,,(xx )XX (xx )=−λλ ∴�TT ,,(tt )+λλaa 2TT (tt )=0…①XX ,,(xx )+λλXX (xx )=0…②∵uu |xx=0=0，uu xx |xx=ll =0 ∴XX (0)=XX ,(ll )=0 （1）当λλ<0时，XX (xx )=AAee √−λλxx +BBee −√−λλxx ∵XX (0)=XX ,(ll )=0，则AA =BB =0 ∴λλ不能小于零。

数理方程题库

精品文档第一部分分离变量法一、 (1)求解特征值问题(2)验证函数系关于内积正交，并求范数二、用分离变量法求解定解问题的解的表达式，写出具体的分离变量过程. 进一步，当时，求和时的值 .三、（方程非齐次的情形）求定解问题四、（边界非齐次的情形）求定解问题五、（ Possion方程）求定解问题六、求定解问题：注意：1、考试只考四种边界条件，即还有以下三种：2)3)4)2、以上均为抛物型方程，还可以考双曲型方程（相应的初值条件变为两个）和椭圆型方程（无初值条件）；3、考试中除特别要求（如以上的第二题）外，不要求必须用分离变量法、特征函数法等方法求解，你可以自己选择方法（如上面的第三题）可以用Laplace 变换求解。

第二部分积分变换法一、请用下面三种方法求解无穷限波动问题2 u a22u,x, t 0t2x2u t0x,xux,xt t0(1)用积分变换法推导达朗贝尔公式(2)用特征线法推导达朗贝尔公式(3)用降维法推导达朗贝尔公式二、用积分变换法求解定解问题2u x2 y,x1, y 0x yx3 ,x1uy0u x1cos y,y0注意：只考应用 Fourier 变换和 Laplace变换求解方程的问题第三部分特征线问题一、判断方程的类型 .二、从达朗贝尔公式出发，证明在无界弦问题中(1)若初始位移x 和初始速度x 为奇函数，则u t,00(2)若初始位移x 和初始速度x 为偶函数，则u x t,00三、请用下列方法求解定解问题(1) 用特征线法求解(2) 用积分变换法求解第四部分Legendre 多项式一、将 fxx 2 在区间 1,1 内展成勒让德多项式的级数二、在半径为 1的球内求调和函数，使u r 1 3cos 21（提示：边界条件仅与有关，解也同样）第五部分 Green 函数20、证明：x limx （弱），其中1, xx20,x21、证明： limsin Nxx （弱）NNx22、证明：当时，弱收敛于23、求 x在 0, 上的余弦级数，并证明该级数若收敛于 x24、求x 0 在 0,上的正弦级数，并证明该级数若收敛于x。

50道数学方程挑战(打印版)

50道数学方程挑战(打印版) 50道数学方程挑战（打印版）1. 解一元一次方程题目：解方程：`3x - 7 = 2x + 5`答案：x = 122. 解一元一次方程题目：解方程：`5x + 8 = 3x - 8`答案：x = -163. 解一元一次方程题目：解方程：`2(x - 3) = 4x + 1` 答案：x = -14. 解一元一次方程题目：解方程：`7(x + 2) = 5x - 3` 答案：x = -135. 解一元一次方程题目：解方程：`4x - 9 = 3x + 12` 答案：x = 216. 解一元一次方程题目：解方程：`6x + 7 = 2(3x - 5)` 答案：x = 177. 解一元一次方程题目：解方程：`5(x - 2) = 3x + 7` 答案：x = 118. 解一元一次方程题目：解方程：`4x + 6 = 3(2x + 4)` 答案：x = 69. 解一元一次方程题目：解方程：`2(x + 3) = 5x - 1`答案：x = 710. 解一元一次方程题目：解方程：`3x - 8 = 4(x - 3)` 答案：x = 411. 解一元一次方程题目：解方程：`7x + 2 = 3(2x + 5)` 答案：x = 712. 解一元一次方程题目：解方程：`5(x - 1) = 2(3x + 4)` 答案：x = 313. 解一元一次方程题目：解方程：`4x - 3 = 2(2x + 1)` 答案：x = 114. 解一元一次方程题目：解方程：`6x + 5 = 3(x + 10)` 答案：x = 1515. 解一元一次方程题目：解方程：`2(x - 5) = 4x + 1` 答案：x = -1116. 解一元一次方程题目：解方程：`3x - 2 = 4(x - 3)` 答案：x = 217. 解一元一次方程题目：解方程：`5x + 8 = 2(3x - 1)` 答案：x = 418. 解一元一次方程题目：解方程：`6x - 1 = 3(2x + 5)` 答案：x = 719. 解一元一次方程题目：解方程：`4x + 3 = 2(x + 6)` 答案：x = 320. 解一元一次方程题目：解方程：`2(x - 4) = 5x + 1`答案：x = -921. 解一元一次方程题目：解方程：`3x + 4 = 2(2x - 1)` 答案：x = 222. 解一元一次方程题目：解方程：`5x - 9 = 3(x + 3)` 答案：x = 623. 解一元一次方程题目：解方程：`2x + 5 = 3(x - 2)` 答案：x = 1124. 解一元一次方程题目：解方程：`4x + 1 = 2(3x + 5)` 答案：x = 325. 解一元一次方程题目：解方程：`6x - 7 = 3(2x + 1)` 答案：x = 326. 解一元一次方程题目：解方程：`2(x - 3) = 4x + 6` 答案：x = -527. 解一元一次方程题目：解方程：`3x + 6 = 2(2x - 1)` 答案：x = 028. 解一元一次方程题目：解方程：`5x - 8 = 3(x + 4)` 答案：x = 829. 解一元一次方程题目：解方程：`2x + 3 = 2(x + 6)`答案：x = 930. 解一元一次方程题目：解方程：`4x - 5 = 3(x + 1)` 答案：x = 231. 解一元一次方程题目：解方程：`6x + 1 = 2(3x - 4)` 答案：x = 132. 解一元一次方程题目：解方程：`2(x - 2) = 4x + 1` 答案：x = -533. 解一元一次方程题目：解方程：`3x - 6 = 2(2x + 1)` 答案：x = 434. 解一元一次方程题目：解方程：`5x + 2 = 3(x + 10)` 答案：x = 2235. 解一元一次方程题目：解方程：`4x - 3 = 2(x + 6)` 答案：x = 936. 解一元一次方程题目：解方程：`2(x - 5) = 5x + 1` 答案：x = -1137. 解一元一次方程题目：解方程：`3x + 4 = 2(2x - 1)` 答案：x = 238. 解一元一次方程题目：解方程：`5x - 9 = 3(x + 3)` 答案：x = 639. 解一元一次方程题目：解方程：`2x + 5 = 3(x - 2)` 答案：x = 1140. 解一元一次方程题目：解方程：`4x + 1 = 2(3x + 5)`答案：x = 341. 解一元一次方程题目：解方程：`6x - 7 = 3(2x + 1)` 答案：x = 342. 解一元一次方程题目：解方程：`2(x - 3) = 4x + 6` 答案：x = -543. 解一元一次方程题目：解方程：`3x + 6 = 2(2x - 1)` 答案：x = 044. 解一元一次方程题目：解方程：`5x - 8 = 3(x + 4)` 答案：x = 845. 解一元一次方程题目：解方程：`2x + 3 = 2(x + 6)` 答案：x = 946. 解一元一次方程题目：解方程：`4x - 5 = 3(x + 1)` 答案：x = 247. 解一元一次方程题目：解方程：`6x + 1 = 2(3x - 4)` 答案：x = 148. 解一元一次方程题目：解方程：`2(x - 2) = 4x + 1` 答案：x = -549. 解一元一次方程题目：解方程：`3x - 6 = 2(2x + 1)`答案：x = 450. 解一元一次方程题目：解方程：`5x + 2 = 3(x + 10)` 答案：x = 22。

高考数学真题汇编 4：方程理试题

高考数学真题汇编 4：方程理试题
本文档将为您提供一些高考数学方程理论部分的真题试题。

以
下是一些典型的高考数学方程试题，供您参考和练。

第一部分：一元一次方程
1. 已知方程 $3x - 7 = 2x + 1$，求解此一元一次方程并给出结果。

2. 某商品的原价为$x$元，现在打七折出售，售价为630元，
求$x$的值。

3. 解方程 $\frac{x}{2} + \frac{x}{3} = x - 5$，给出$x$的解。

第二部分：一元二次方程
1. 求解方程 $x^2 - 5x + 6 = 0$，给出所有解。

2. 若方程 $2x^2 + kx + 8 = 0$ 的解为$x = 3$ 和$x =
\frac{2}{3}$，求$k$的值。

3. 解方程 $4x^2 + 8x + 3 = 0$，给出所有解。

第三部分：其他方程
1. 解方程 $\sqrt{x} + \sqrt[3]{x} = 5$，求出所有$x$的解。

2. 若方程 $2^x + 2^{-x} = 2$ 的解为$x = 1$ 和$x = -1$，求另一组解。

3. 解方程 $2^x + 3 \cdot 2^{-x} = 3$，给出$x$的解。

以上是一些高考数学方程的典型试题。

希望这些题目对您的练和准备有所帮助。

如果需要更多相关的试题或者有其他问题，请随时告诉我。

祝您学业有成，考试顺利！。

数学方程解题实例：50题(打印版)

数学方程解题实例：50题(打印版)数学方程解题实例：50题（打印版）目录1. 2x - 3y = 72. 5x + 4y = 233. 3x^2 - 5x + 2 = 04. 2x^2 + 7x - 11 = 05. 4x^3 - 6x^2 + 3x - 1 = 06. 5x^2 - 12x + 9 = 07. 2(x - 3)^2 = 138. (x - 1)(x + 4) = 09. 3x^2 + 14x - 21 = 010. 2x^3 - 5x^2 + 7x - 3 = 011. 4x^2 - 12x + 9 = 012. x^3 - 6x^2 + 9x - 1 = 013. 3(x - 2)^3 = 1914. x^2 - 5x + 6 = 015. 2x^3 + 7x^2 - 11x - 6 = 016. 5x^2 - 21x + 18 = 017. x^3 - 3x^2 + 5x - 2 = 018. 6(x - 1)^2 = 1119. x^2 - 4x + 4 = 020. 3x^3 - 8x^2 + 11x - 5 = 021. 4x^2 - 9x + 2 = 022. x^3 - 6x^2 + 11x - 4 = 023. 2(x - 3)^3 = 524. x^2 - 5x - 6 = 025. 2x^3 + 3x^2 - 7x - 4 = 026. 5x^2 - 10x + 2 = 027. x^3 - 2x^2 + 4x - 1 = 028. 6(x - 2)^2 = 729. x^2 - 3x + 2 = 030. 3x^3 - 5x^2 + 7x - 2 = 031. 4x^2 - 6x + 1 = 032. x^3 - 3x^2 + 6x - 2 = 033. 2(x - 1)^3 = 134. x^2 - 4x - 5 = 035. 2x^3 - 3x^2 + 5x - 1 = 036. 5x^2 - 12x - 3 = 037. x^3 - 6x - 7 = 038. 6(x - 3)^2 = 1339. x^2 - 2x + 1 = 040. 3x^3 - 8x^2 + 4x - 1 = 041. 4x^2 - 9x - 2 = 042. x^3 - 5x^2 + 10x - 3 = 043. 2(x - 2)^3 = 344. x^2 - 5x - 6 = 045. 2x^3 + x^2 - 3x - 2 = 046. 5x^2 - 10x - 2 = 047. x^3 - 2x^2 + 3x - 1 = 048. 6(x - 1)^2 = 849. x^2 - 3x + 2 = 050. 3x^3 - 5x^2 + 7x - 2 = 0 解题步骤1. 2x - 3y = 7解：将方程两边同时乘以3，得：6x - 9y = 21将方程两边同时乘以2，得：4x - 6y = 14将两个方程相减，得：2x + 3y = 7将上式两边同时乘以3，得：6x + 9y = 21将原方程与上式相加，得：12x = 28解得 x = 28 / 12 = 7 / 3将 x 代入原方程，得：2 * (7 / 3) - 3y = 7解得 y = 1 / 3所以，方程的解为 x = 7 / 3，y = 1 / 3。

初中三年级课外练习题数学题代数方程求解题20题及答案

初中三年级课外练习题数学题代数方程求解题20题及答案初中三年级课外练习题：数学题代数方程求解题1. 问题描述解下列各方程，并将解用集合表示：a) 2x + 3 = 7b) 5(x + 2) = 25c) 4x - 2(x + 3) = 3(2x - 5)2. 方程求解a) 2x + 3 = 7首先，我们将常数项移至等式右侧：2x = 7 - 32x = 4然后，将方程两边都除以2：x = 4 ÷ 2x = 2b) 5(x + 2) = 25首先，将括号内的表达式展开： 5x + 10 = 25然后，将常数项移至等式右侧： 5x = 25 - 105x = 15最后，将方程两边都除以5：x = 15 ÷ 5x = 3c) 4x - 2(x + 3) = 3(2x - 5)首先，将括号内的表达式展开： 4x - 2x - 6 = 6x - 15然后，将相似项合并得到：2x - 6 = 6x - 15接着，将常数项移至等式右侧：2x - 6 - 6x = -15-4x - 6 = -15将方程两边都加上6：-4x - 6 + 6 = -15 + 6-4x = -9最后，将方程两边都除以-4（注意符号的改变）： x = -9 ÷ -4x = 9/43. 解集表示a) 方程2x + 3 = 7的解为集合{x}，其中x = 2。

b) 方程5(x + 2) = 25的解为集合{x}，其中x = 3。

c) 方程4x - 2(x + 3) = 3(2x - 5)的解为集合{x}，其中x = 9/4。

注意：以上解集表示方式是用集合的形式表示方程的解。

这种表示方式可以简洁地表达多个解的情况。

4. 答案总结a) 方程2x + 3 = 7的解为x = 2。

b) 方程5(x + 2) = 25的解为x = 3。

c) 方程4x - 2(x + 3) = 3(2x - 5)的解为x = 9/4。

以上是解答给定的20道初中三年级数学代数方程求解题的过程及答案。