学而思五年级春季下学期超长123班讲义学案试题(8-13讲)
学而思2011年暑假超常123班难题汇总

学而思2011年暑假超常123班难题汇总第一讲 四边形中的基本图形1、【例8】长方形ABCD 中被嵌入了6个相同的正方形,已知AB =22厘米,BC =20厘米,那么每一个正方形的面积是多少平方厘米?【难度级别】★★★★★【解题思路】使用“弦图”求解。
什么叫“弦图”,解释一下。
一个斜着放的正方形,左右2个顶点做水平线,上下2个顶点做竖直线,可以将正方形分割成4个直角三角形和一个小正方形,如图。
这4个直角三角形是完全相同的。
假设直角三角形的长直角边长度为b ,短直角边长度为a ,斜边长度为c ,则a 平方+b 平方=c 平方。
对题目图中的6个小正方形都做出弦图来,做完弦图后,仔细数一数,发现:上下的长度由(3a+2b)构成,左右的长度由(3a+b)构成,所以:3a+2b =22,3a+b =20。
求得:a =6,b =2。
【答案】6×6+2×2=40。
课堂上,有一位同学,不会做但是懵对了,很神奇呀!DC2、【学案2】在四边形ABCD 中,线段BC 长为6厘米,∠ABC =90°,∠BCD =135°,且点A 到边CD的垂线段AE =12厘米,线段ED =5,求四边形ABCD的面积。
【难度级别】★★★★☆【解题思路】延长DC 和AB 相交于P ,三角形APD 的面积-三角形BPC 的面积,就是要求的四边形ABCD 的面积。
三角形BPC 是等腰直角三角形且BC 已知,面积可求。
三角形APD 的高AE 已知,求出底PD 即可,ED 已知,求PE ,三角形PEA 是等腰直角的,PE =AE 。
问题解决。
【答案】(12+5)×12÷2-6×6÷2=843、【学案3】等腰梯形ABCD 中,交于O 点的两条对角线互相垂直,三角形ECB 是直角三角形,OC 比AO 长20厘米。
已知三角形ADE 的面积是250平方厘米,则梯形ABCD 的面积是多少平方厘米?【难度级别】★★★★☆【解题思路】三角形BOC 、AOD 、EOC 均是等腰直角三角形,OE =OD+DE =OC ,OD =AO ,得到DE =20,由ADE 面积250,得到AO =25,所以OC =45,AC =25+45=70,BD =70。
学而思小学奥数个精彩讲座总汇全

第1讲计算综合(一)繁分数的运算,涉及分数与小数的定义新运算问题,综合性较强的计算问题.1.繁分数的运算必须注意多级分数的处理,如下所示:甚至可以简单地说:“先算短分数线的,后算长分数线的”.找到最长的分数线,将其上视为分子,其下视为分母.2.一般情况下进行分数的乘、除运算使用真分数或假分数,而不使用带分数.所以需将带分数化为假分数.3.某些时候将分数线视为除号,可使繁分数的运算更加直观.4.对于定义新运算,我们只需按题中的定义进行运算即可.5.本讲要求大家对分数运算有很好的掌握,可参阅《思维导引详解》五年级[第1讲循环小数与分数].1.计算:71147 18262 13581333416⨯+⨯-÷【分析与解】原式=7123723174612241488128131233+⨯=⨯=-2.计算:【分析与解】注意,作为被除数的这个繁分数的分子、分母均含有5199.于是,我们想到改变运算顺序,如果分子与分母在5199后的两个数字的运算结果一致,那么作为被除数的这个繁分数的值为1;如果不一致,也不会增加我们的计算量.所以我们决定改变作为被除数的繁分数的运算顺序.而作为除数的繁分数,我们注意两个加数的分母相似,于是统一通分为1995×.具体过程如下:原式=5919(3 5.22)19930.41.6910()52719950.5199519(6 5.22)950+-⨯÷+⨯-+=5191.3219930.440.40.59()519950.419950.5191.329-⨯⨯⨯÷+⨯⨯-=199320.41()19950.5+÷⨯=0.410.5÷=1143.计算:1111111987-+-【分析与解】原式=11198711986-+=198613973-=198739734.计算:已知=181111+12+1x+4=,则x等于多少【分析与解】方法一:1118x68114x112x7111+11148x62+214x1x+4+====+++++++交叉相乘有88x+66=96x+56,x=1.25.方法二:有11131118821x4+==+++,所以18222133x4+==++;所以13x42+=,那么x=.5.求944,43,443,...,44 (43)个这10个数的和.【分析与解】方法一:944+43+443...44 (43)++个=1044(441)(4441)...(44...41)+-+-++-个=104444444...44 (49)++++-个=1094(999999...999...9)99⨯++++-个=1004[(101)(1001)(10001)...(1000...01)]99⨯-+-+-++--个=914111.1009=49382715919⨯-个.方法二:先计算这10个数的个位数字和为39+4=31⨯;再计算这10个数的十位数字和为4×9=36,加上个位的进位的3,为36339+=;再计算这10个数的百位数字和为4×8=32,加上十位的进位的3,为32335+=;再计算这10个数的千位数字和为4×7=28,加上百位的进位的3,为28331+=;再计算这10个数的万位数字和为4×6=24,加上千位的进位的3,为24327+=;再计算这10个数的十万位数字和为4×5=20,加上万位的进位的2,为20222+=;再计算这10个数的百万位数字和为4×4=16,加上十万位的进位的2,为16218+=;再计算这10个数的千万位数字和为4×3=12,加上百万位的进位的1,为12113+=;再计算这10个数的亿位数字和为4×2=8,加上千万位的进位的1,为819+=;最后计算这10个数的十亿位数字和为4×1=4,加上亿位上没有进位,即为4.所以,这10个数的和为91.6.如图1-1,每一线段的端点上两数之和算作线段的长度,那么图中6条线段的长度之和是多少【分析与解】因为每个端点均有三条线段通过,所以这6条线段的长度之和为:1173(0.60.875)1+0.75+1.8+2.625=6.175=63440⨯+++=7.我们规定,符号“○”表示选择两数中较大数的运算,例如:3.5○=○=.符号“△”表示选择两数中较小数的运算,例如:△=△=.请计算:23155 (0.625)(0.4)33384 1235(0.3)( 2.25) 3104⨯+【分析与解】原式1550.6255155725384218384122562.253⨯=⨯÷=+8.规定(3)=2×3×4,(4)=3×4×5,(5)=4×5×6,(10)=9×10×11,….如果111(16)(17)(17)-=⨯,那么方框内应填的数是多少【分析与解】111(17)()1(16)(17)(17)(16)=-÷=-=161718111516175⨯⨯-=⨯⨯.9.从和式11111124681012+++++中必须去掉哪两个分数,才能使得余下的分数之和等于1【分析与解】因为1116124+=,所以12,14,16,112的和为l,因此应去掉18与110.10.如图1-2排列在一个圆圈上10个数按顺时针次序可以组成许多个整数部分是一位的循环小数,例如.那么在所有这种数中。
学而思五年级年度质量测评试卷及答案

2015年东学堂语文五年级年测试卷答案及解析第一部分基础知识一、B(4分)解析:本题考查的知识点是字音的正确性,只有B组字音完全正确,其余三组不正确的字音改正如下: A抖擞(sǒu) C 绫罗绸缎(líng) D旋风(xuàn)二、B(4分)解析:本题考查的知识点是字形的正确性,只有B组字形完全正确,其余三组不正确的字形改正如下: A迫不及待 C崇山峻岭 D、九霄云外三、D(4分)解析:本题考查的知识点是字义的准确性,A、B、C三组字义全部正确,D组不正确的字义改正如下:回顾.(顾:回头、张望)莫名.其妙(名:说出、讲出)四、C(4分)解析:本题考查的知识点是成语的使用,C句成语使用得当,其余三组成语使用不当原因如下:A巧夺天工用来形容人工建筑巧妙绝伦,不可修饰自然景观。
B凤毛麟角用来比喻好的东西十分稀有,不可用来形容“不自觉者”。
D死得其所用来形容好人死的很有价值,不可用来形容贪污罪犯。
五、A(4分)解析:本题考查的知识点是语句的准确性,A句没有语病,其余三组语病及其改正方法如下:B用词不当——将“庄严”改为“严肃”C语义矛盾——将“一定”或者“大概”去掉一个D搭配不当——将“一个班级”去掉第二部分文学常识六、文学常识(每空3分,共30分)1.枕中记南柯太守传2.东晋/晋干宝志怪3.于谦要留清白在人间4.无限山河泪/无限河山泪惯看秋月春风临江仙(注:第2小题第一空答“晋”也可得分;第4小题第一空答“无限河山泪”也可得分)解析:本题考查的知识点是文学常识的巧妙运用,只要学生平时注重文学常识的积累,此题难度不大。
题目的分值是每空3分,全部以汉字填写的形式出现,需要注意的是:出现错别字的空不得分。
七、四大名著(每空1分,共8分)解析:本题考查的知识点是我国“四大名著”的相关知识点,需要学生掌握的是“四大名著”的作者、 书中人物形象以及其所做之事。
八、作家作品(每组对应2分,共10分)席慕蓉——歌中有我父亲的草原母亲的河 余光中——而现在,乡愁是一湾浅浅的海峡海 子——我只愿面朝大海,春暖花开 徐志摩——在康河的柔波里,我甘心做一条水草 艾 青——因为我对这土地爱得深沉解析:本题考查的知识点是作家作品的对应,题中出现的作品名句均来自该作家名篇,要求学生重点掌握。
2013学而思五年级春季下学期超长123班讲义学案试题813讲
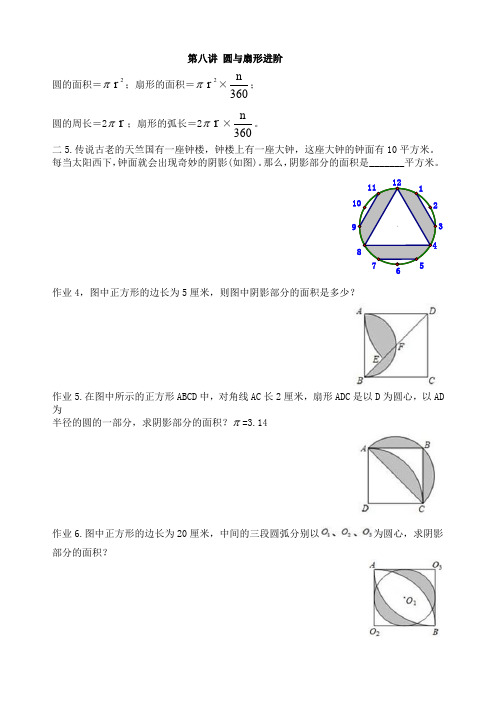
第八讲 圆与扇形进阶圆的面积=π2r ;扇形的面积=π2r ×360n ;圆的周长=2πr ;扇形的弧长=2πr ×360n。
二5.传说古老的天竺国有一座钟楼,钟楼上有一座大钟,这座大钟的钟面有10平方米。
每当太阳西下,钟面就会出现奇妙的阴影(如图)。
那么,阴影部分的面积是_______平方米。
作业4,图中正方形的边长为5厘米,则图中阴影部分的面积是多少?作业5.在图中所示的正方形ABCD 中,对角线AC 长2厘米,扇形ADC 是以D 为圆心,以AD 为半径的圆的一部分,求阴影部分的面积?π=3.14作业6.图中正方形的边长为20厘米,中间的三段圆弧分别以为圆心,求阴影部分的面积?第九讲 比较与估算 一.大小比较1.通分2.化成小数3.倒数法4.参考值法5.交叉相乘 6、糖水原理 1.ab <c a db ++<cd 7.糖水原理 2.a b<m a m b ++二.估算1、整体放缩2、部分放缩3、中项放缩4、分组放缩 一1.把32、53、75、1915按照从小到大的顺序排列。
一2.将250131、4021、0.5、0.52、0.5 从小到大排列,第三个数是_______。
一3.比较大小:2713和5728;1111111和111111111。
交叉相乘若ab >cd (a 、b 、c 、d 为正整数),则bc >ad 。
一5.下式中五个分数都是最简真分数,要使不等式成立,这些分母的和最小是多少? (__)1>(__)2>(__)3>(__)4>(__)5一.7设321311301++=a ,521511501491481++++=b ,则在a 与b 中,较大的数是______。
参考值法 二6.将178、2413、3518、5931按从小到大的顺序排列。
糖水原理-结论1 若0<ab <cd <1,则ab <ca db ++<cd导问4.如果一个班的女生人数占全班人数的31和83之间,这个班至少有多少人?补充.54<?25<65糖水原理-结论2 若0<ab <1,m >0,则ab <ma mb ++原理解读:(1)横向看:分子分母同时“+”一个常数,分数值变大;(2)纵向看:每个分数的“分母-分子”差是相同的,也就是说这个糖水原理的应用条件是:如果“分母-分子”差不同,可以通过扩倍变成差相同,之后就可以应用糖水原理 二2(2).比较75、2320、3329、161149的大小。
2013学而思五年级春季下学期超长123班讲义学案试题(1—7讲)
补充1,2013年华杯赛决赛最后一题第14题.不为零的自然数n既是2010个数字和相同的自然数之和,也是2012个数字和相同的自然数之和,还是2013个数字和相同的自然数之和,那么n最小是多少?
一4.(1)求(5412×852)÷9的余数。
(2)求 ÷9的余数;
(3)有一只猴子摘了一大堆香蕉,他把香蕉平分成3小堆,不多不少。又把其中一小堆再平分成5份,发现多了一根。如果他一开始就把香蕉平分成5堆,会多出几根?
(4)有一只猴子摘了一大堆香蕉,他把香蕉平分成6小堆,多了2根。又把其中一小堆再平分成5份,发现多了4根。如果他一开始就把香蕉平分成5堆,会多出几根?
7.一个半径为1厘米的圆,沿边长为10厘米的正六边形外围滚动一圈,求圆扫过的面积是多少?沿边长为10厘米的正八边形外围滚动一圈,求圆扫过的面积?
8.一个半径为1厘米的圆,沿半径为5厘米的圆外围滚动一圈,求小圆扫过的面积是多少?这次我们继续使用之前几问得到的方法来计算,结果是否仍然正确?
9.一个半径为r的圆,沿着周长为L的任意凸图形外围滚动一周,求圆扫过的面积?
(2)形如1444…4(n>1,n个4)的完全平方数有______个;
三5. + +1(m、n为自然数)能否为平方数?
学案1.称能表示成1+2+3+…+k的形式的自然数为三角数。有一个四位数N,它既是三角数,又是完全平方数,则N=______。
学而思五年级春季第八讲 同余

第八讲同余寒假班我们已经学习了余数问题,那一讲我们掌握了一些有关余数的基本性质,并解决了一些简单余数问题,本讲则是在此基础之上的进一步拓展与提高,因此本讲首先是基本性质应用的复习(例1、3、5),其次将是解决一些较复杂的综合余数问题(例2、4、6)。
一、基本性质的复习1、带余数除法算式:a÷b=q……r(a、b、q、r均为整数)从中我们应该得到:(1)b>r 除数大于余数(2)a-r=b×q 被除数减去余数则会出现整除关系,则带余数问题就可以转化为整数问题。
2、余数的性质:(1)可加性:和的余数等于余数的和。
即:两数和除以m的余数等于这两个数分别除以m的余数和。
例:7÷3=2……1 5÷3=1……2,则(7+5)÷3的余数就等于(1+2)÷3的余数0。
(2)可减性:差的余数等于余数的差。
即:两数差除以m的余数等于这两个数分别除以m的余数差。
例:17÷3=5……2 5÷3=1……2,则(17-5)÷3的余数就等于(2-2)÷3的余数0。
(3)可乘性:积的余数等于余数的积。
即:两数积除以m的余数等于这两个数分别除以m的余数积。
例:64÷7=9……1 45÷7=6……3,则(64×45)÷3的余数就等于(1×3)÷7的余数3。
二、同余式在生活中,若两个自然数a和b都除以同一个除数m时,余数相同该如何表示呢?在代数中我们称之为同余。
即:a与b同余于模m。
意思就是自然数a和b关于m来说是余数相同的。
用同余式表达为:a≡b(modm).注:若a与b同余于模m,则a与b的差一定被m整除。
(余数的可减性)三、例题讲解例1、分析:此题实际上是带余数除法算式的一个应用。
“1013除以一个两位数余数为12”,说明1013减去12以后就会被这个两位数整除,则这个两位数应该是1013-12=1001的因数,且是大于12的两位因数。
【教材同步】春季学期五年级奥数教程下册【讲义】

春季学期北师大版数学五年级奥数讲义2020年3月制目录第一讲多边形的面积1.1面积计算1.2等积变形1.3列方程求面积第二讲二元一次方程组第三讲牛吃草问题第四讲分数的简算(加减法)第五讲分数的简算(乘法)第六讲分数除法应用题第七讲较复杂分数应用题第八讲浓度问题(百分数)第九讲长方体和正方体的表面积第十讲长方体和正方体的体积第十一讲应用题综合练习(一)第十二讲应用题综合练习(二)第一讲多边形的面积面积的计算[同步巩固演练]1、求下图中每个小图形的阴影部分的面积(单位:厘米)[能力拓展平台]1、已知三角形ABC的周长是20厘米,三角形内一点到三角形三条边的距离都是3厘米,求三角形的面积。
第1题2、如图,ABCG是4×7的长方形,DEFG是2×10的长方形,那么三角形BCM的面积与三角形DEM的面积之差是多少?(单位:厘米)第2题3、求阴影部分的面积(单位:厘米)4、长方形ABCD 的边上有二点E 、F 、AF 、BE 、BE 把长方形分成若干块,其中三个小块的面积标注在图上,求阴影部分面积。
第4题5、(第五届华杯赛试题)涂阴影部分的小正六角星形面积是16平方厘米,问大正六角星的面积是多少平方厘米第5题等积变形[同步巩固演练]1、如图所示,已知矩形ABCD 中,BE=21EC ,则△ABE 和△ABC 的面积之比是多少?第1题2、如图所示,梯形ABCD 中共有8个三角形,其中,面积相等的三角形有多少对?第2题3、如图,三角形ABC 的面积是18平方厘米,BD=2DC ,AE=EC ,则三角形BDE 的面积是多少平方厘米?第3题4、如图已知BC=6BD ,AB=5BE ,三角形BDE 的面积是1,则三角形ABC 的面积是多少?第4题5、如图ABCD 是平行四边形,AE=32AB ,则梯形EBCD 的面积是三角形AED 的面积是多少倍?6、如图所示,三角形ABC 中,BD=DC ,ED=2AE ,BF=FD ,三角形ABC 的面积是1,三角形DFE 的面积是多少?第6题[能力拓展平台]1、如图E 、F 分别为平行四边形ABCD 两条邻边的中点,若平行四边行的面积是1,则图中面积为41的三角形有多少个。
学而思五年级春季下学期超长123班讲义学案试题(1—7讲)

1. 在如下图的圆中,正方形ABCD勺边长为8,圆心0到AB的距离为5,求正方形EFGH勺面积。
2. 如图,直角三角形ABC中,两直角边分别为7, 24,三角形内有一点P到各边的距离相等,这这个距离为多少3. 如图,对角线BD将矩形ABCD分割为两个三角形,AE和CF分别是两个三角形上的高,长度都等于6cm EF的长度为5 cm,求矩形ABCD勺面积2已知长方形长为8,宽为4,将长方形沿一条对角线折起压平,如图,求重叠部分△FBD的面积3. 如图:矩形ABCD AB=3cm,AD=9cn折叠矩形,使B点与D点重合,折痕为EF,则三角形BEF的面积是多少E三.2.在一个直径为一丈的圆形池中有一芦苇,高出水面1尺,风吹过,芦苇高刚好倒下碰到水面,芦苇到了岸边,那么水面的深度和芦苇的高度是多少学案1.如图所示,直角三角形PQR勺直角边为5厘米和9厘米,问图中3个正方形面积之和比4个三角形面积之和大多少学案3.下图是一个长为16,宽为10的长方形,沿着图中虚线的位置将这个长方形折叠成一个等腰梯形,则这个梯形的面积是_________ o补充1.将B点折到AD边上的E点,E是五等分点,AE= 1,求三角形BCF的面积。
BA F BD C补充2. 一根绳子在一个圆柱上从一端到另一端均匀的绕了4圈,圆柱的底面积周长为4米, 长12米,求绳子的长度第二讲完全平方数一 4.求一个最小的自然数,它乘以2后是完全平方数,乘以3后是完全立方数,乘以5后是五次方数。
一 5.从乘法算式1 X 2X 3X-X 15中至少要删除多少个数,才能使剩下的数的乘积为完全平方数一 6.从1!、2!、3!、…、100!这100个数中去掉一个数,使得剩下各数的乘积是一个完全平方数,请问:被去掉的那个数是什么二名同学,编号为1〜100,面向南站成一排,第1次全体同学向后转;第2次编号为2的倍数的同学向后转;第3次编号为3的倍数的同学向后转;……;第100次编号为100的倍数的同学向后转;这时,面向南的同学有_______ 名二名同学,编号为1〜100,面向南站成一排,第1次全体同学向右转;第2次编号为2的倍数的同学向右转;第3次编号为3的倍数的同学向右转;……;第100次编号为100的倍数的同学向右转;这时,面向东的同学有____________________ 名3. (1)形如11…1(n > 1, n个1)的完全平方数有________ 个;(2)形如1444…4(n > 1, n个4)的完全平方数有_______ 个;5. 3m+3n+1 (m n为自然数)能否为平方数学案1.称能表示成1+2+3+…+k的形式的自然数为三角数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第八讲 圆与扇形进阶圆的面积=π2r ;扇形的面积=π2r ×360n ;圆的周长=2πr ;扇形的弧长=2πr ×360n 。
二5.传说古老的天竺国有一座钟楼,钟楼上有一座大钟,这座大钟的钟面有10平方米。
每当太阳西下,钟面就会出现奇妙的阴影(如图)。
那么,阴影部分的面积是_______平方米。
作业4,图中正方形的边长为5厘米,则图中阴影部分的面积是多少?作业5.在图中所示的正方形ABCD 中,对角线AC 长2厘米,扇形A DC 是以D 为圆心,以A D为半径的圆的一部分,求阴影部分的面积?π=3.14作业6.图中正方形的边长为20厘米,中间的三段圆弧分别以为圆心,求阴影部分的面积?第九讲 比较与估算 一.大小比较 1.通分 2.化成小数 3.倒数法 4.参考值法 5.交叉相乘 6、糖水原理 1.a b <c a d b ++<c d 7.糖水原理 2.a b <ma mb ++ 二.估算1、整体放缩 2、部分放缩 3、中项放缩 4、分组放缩一1.把32、53、75、1915按照从小到大的顺序排列。
一2.将250131、4021、0.52o3o、0.523o、0.52o从小到大排列,第三个数是_______。
一3.比较大小:2713和5728;1111111和111111111。
交叉相乘若ab >cd (a 、b、c 、d 为正整数),则bc>ad 。
一5.下式中五个分数都是最简真分数,要使不等式成立,这些分母的和最小是多少? ﻩ(__)1>(__)2>(__)3>(__)4>(__)5一.7设321311301++=a ,521511501491481++++=b ,则在a 与b中,较大的数是______。
参考值法 二6.将178、2413、3518、5931按从小到大的顺序排列。
糖水原理-结论1 若0<ab <cd <1,则a b <c a d b ++<cd导问4.如果一个班的女生人数占全班人数的31和83之间,这个班至少有多少人?补充.54<?25<65糖水原理-结论2 若0<ab <1,m>0,则ab <ma mb ++原理解读:(1)横向看:分子分母同时“+”一个常数,分数值变大;(2)纵向看:每个分数的“分母-分子”差是相同的,也就是说这个糖水原理的应用条件是:如果“分母-分子”差不同,可以通过扩倍变成差相同,之后就可以应用糖水原理 二2(2).比较75、2320、3329、161149的大小。
二4(1).比较大小:9753⨯⨯,17151311⨯⨯,25232119⨯⨯。
二、估算本讲估算用到4种方法:整体放缩、部分放缩、中项放缩、分组放缩。
1、整体放缩指的是所有项都参与放缩,每一项都按照最大项、最小项估算得到最大值和最小值,得到算式估算的范围。
题目一般是求:整数部分。
2、部分放缩指的是:不是所有项都参与放缩,留一部分差别比较大的项参与计算,其它项再进行放缩,放缩也是找最大值和最小值。
题目一般也是求:整数部分。
3、中项放缩算式中的两项,找两项的中间数来表示,这种放缩方法叫作中项放缩。
三.3 (1)491 (32131)13011+++的整数部分是_______。
(2)281 (12)11111011+++的整数部分是_______。
三4. 1+21+31+41+51+61+71+81+91+101+111+121+131+141+151的整数部分是多少?4、分组放缩指的是,算式中+、-交错,对算式进行(+、-)分组和(-、+)分组,舍弃后面一些值较小的分组,可以得到算式的最大值和最小值。
三.5 514131211-+-++…+1001991981+-的整数部分是______。
补充1.(6141211-+-+…+1001981961+-)×10的整数部分是______。
补充2871651431211⨯-⨯+⨯-⨯+ (201020091)⨯+化成小数,小数点后第1位是_______。
作业4.个数字是多少?作业6.学案1. 选出若干个数使它们的和大于3,最少要选多少个数? 学案2.第十讲比例法解行程一7.从甲地到乙地,若速度提高0,2倍,则时间少用1小时,则原计划用多少小时?一3.甲乙二人分别从A、B两地同时出发,相向而行,甲乙的速度之比是4:3,二人相遇后继续前进,甲到达B地和乙到达A地后都立即返回,已知二人第二次相遇的地点距离第一次相遇的地点30千米,则A、B两地相距多少千米?二2. A、B两地相距600米,甲、乙分别从A、B两地同时出发,结果在距B地200米处相遇,如果乙的速度提高到原来的3倍,那么两人可提前2分钟到达,则甲的速度是每分钟多少米?二3.甲、乙两车分别从A、B两地同时出发,相向而行。
出发时,甲、乙的速度比是5:4,相遇后甲的速度减少20%,乙的速度增加20%。
这样当甲到达B地时,乙离A地还有10千米,那么A、B两地相距多少千米?二4.如图,C 、D为AB 的三等分点;8点整时甲从A 出发匀速向B行走,8点12分乙从B 出发匀速向A行走,再过几分钟后丙也从B 出发匀速向A 行走;甲、乙在C 点相遇时丙恰好走到D 点,甲、丙8:30相遇时乙恰好到A 。
那么,丙出发时是8点_____分。
三1.甲乙两车由A 地开往B 地,甲车速度是每小时80千米,乙车速度是70千米/时,甲车比乙车提前15分钟到达B 地,那么AB 两地的距离是多少?三2.乐乐从家到学校平时需要45分钟,今天乐乐起晚了,她需要用1.5倍的速度赶去学校,才刚好不会迟到,那么现在距离上课还有多少分钟?三3. 一辆汽车从甲地开往乙地,每分钟行750米,预计20分钟到达,但出发时被耽误了5分钟,如果仍需在预定的时间内到达,汽车每分钟必须比原来快多少米?三4.王叔叔开车从北京到上海,从开始出发,车速即比原计划的速度提高了91,结果提前一个半小时到达;返回时,按原计划的速度行驶280千米后,将车速提高61,于是提前1小时40分到达北京。
北京、上海的路程是多少千米?三5.上午8点整,甲从A地出发匀速去B地,20分钟后,甲与从B地出发匀速去A地的乙相遇;相遇后甲将速度提高到原来的3倍,乙速不变;8点30分,甲乙两人同时到达各自目的地,那么,乙从B地出发是8点______分?学案1.运动会上,康子和阿雪正在为10000米跑的冠军做最后冲刺,康子暂时领先阿雪10米,阿雪奋力追赶。
已知:阿雪跑5步的距离,康子只需跑4步;但阿雪跑9步的时间,康子只能跑7步。
现在阿雪离终点还有400米,如果两人都保持这个速度到终点,谁得冠军?学案2.甲、乙两人从相距490米的A、B两地同时步行出发,相向而行,丙与甲同时从A 出发,在甲、乙二人之间来回跑步(遇到乙立即返回,遇到甲也立即返回)。
已知丙每分钟跑240米,甲每分钟走40米,当丙第一次折返回来并与甲相遇时,甲、乙二人相距210米,那么乙每分钟走_____米;甲下一次遇到丙时,甲、乙相距_____米。
学案3.一列火车出发1小时后因故停车0.5小时,然后以原速的3/4前进,最终到达目的地晚1.5小时;若出发1小时后又前进90公里再因故停车0.5小时,然后同样以原速的3/4前进,则到达目的地仅晚1小时,那么整个路程为多少公里?作业3.李经理的司机每天早上7:30分到达李经理家接他去公司。
有一天李经理7点从家里出发去公司,路上遇到从公司按时来接他的车,再乘车去公司,结果比平时早到5分钟。
则李经理乘车的速度是步行速度的_______倍?作业5.如图:甲乙分别从A、C两地同时出发,匀速相向而行,他们的速度之比为5:4,相遇于B地后,甲继续以原来的速度向C地前进,而乙则立即调头返回,并且乙的速度比相遇前降低,这样当乙回到C地时,甲恰好到达离C地18千米的D处,那么A、C两地之间的距离是多少?A BC D作业6.一辆大货车与一辆小轿车同时从甲地开往乙地,小轿车到达乙地后立即返回,返回时速度提高50%。
出发2小时后,小轿车与大货车第一次相遇,当大货车到达乙地时,小轿车刚好走到甲乙两地的中点。
小轿车在甲乙两地往返一次(返回时提速)需要多长时间?补充1.甲乙两人从A、B两地同时出发,相向而行,在图C点处相遇;当甲乙相遇时,丙从B地出发,在图D点和甲相遇;相遇后甲立即掉头,并以原来速度的80﹪向A行走,最后和丙同时到达A地,而此时,乙离A地还有720米,已知CD=900米,求全程?A C D B十一.位值原理1、位值原理:错误!未定义书签。
=a×10000+b ×1000+c ×100+d ×10+e =错误!未定义书签。
×100+错误!2、m为原序数与其反序数的差一定是⎩⎨⎧为偶数的倍数,为奇数的倍数,m 9m 99。
3、三个互不相同的非零数字,组成的所有三位数之和一定是222的倍数。
位值原理题目,常用的解题方法有:提取公因数、不定方程等。
一6.一个六位数错误!未定义书签。
,如果满足4×错误!未定义书签。
=错误!,则称错误!未定义书签。
为“迎春数”(如4×102564=410256,则102564就是“迎春数”)。
请你求出所有“迎春数”的总和。
二3.一个四位数的反序数比它本身大8802,求这个四位数。
二5.已知一个五位回文数等于45与一个四位回文数的乘积(即错误!=45×错误!),那么这个五位回文数最大的可能是______。
三3.一个四位的完全平方数,它的前两位数字相同,后两位数字也相同,请找出所有符合条件的四位数。
三4.两个不同的数字组成的两个两位数的平方差,仍然是一个平方数,即=x方,求AB?三5.如果一个五位数,它的各位数字乘积恰好是它的各位数字和的25倍。
那么,这个五位数的最大值是_____,前两位的最大值是____。
学案1.设六位数错误!满足错误!未定义书签。
=f×错误!未定义书签。
,请写出这样的六位数。
学案2.错误!是一个七位回文数,其中相同的字母代表相同的数字,不同的字母代表不同的数字,已知这个七位数第一位能被2整除,前2位组成的两位数能被3整除,前3位组成的三位数能被4整除,……,前7位组成的七位数能被8整除,那么错误!=_______。
学案3.将4个不同的数字排在一起,可以组成24个不同的四位数。
将这24个四位数按从小到大的顺序排列的话,第二个是5的倍数;按从大到小的顺序排列的话,第二个是不能被4整除的偶数;按从小到大排列的第五个与第二十个的差在3000~4000之间。
求这24个四位数中最大的那个。
作业4.观察如图所示的减法算式,得数175和被减数571的数字顺序相反。
