Failure reasoning in multiple-strategy proof planning
高中英语阅读理解解题技巧ppt课件

Main idea extraction method
Finding topic sentences
Common misconceptions and coping strategies
Misconception 1
Translate word by word and sentence by sentence
Response strategy
Pay attention to the connections between paragraphs, understand the overall structure and logical relationship of the article.
CATALOGUE
目 录
• Vocabulary and Phrase Accumulation and Application
• Improving Reading Speed and Standardizing Answering Questions
• Simulated test exercise and explanation
Response strategy
Learn to read meaning groups, understand the relationship between the main body and modifying elements of sentences, and grasp the central idea of the article.
新视野大学英语第三版读写教程第四册Unit 1-Life and Logic教案

新视野大学英语读写教程第四册教案B4U1Unit 1Life and Logic*Teaching Objectives:Students will learn to use English to1.To practice the skimming and scanning reading skills2.To apply the phrases and patterns3.To master the writing pattern of a narrative essay4.To write an essay creatively based on the understanding of the text*Time Allotment: each unit 8 classes1st---2nd classes: Part I Warming up1.Lead-in : Background introduction and theme-2.Understanding of the text: Detailed understanding focusincluding Topic Sentence, Key Words, Logic Words, Reading Clues etc. in order to help students have a better understanding about the passage by asking some questions about it.3rd--4th classes:Part II Text Study3.Reading in Depth: Structure Analysis, Summary, Difficult sentences analysisnguage Focus: More practice in Language Points (language points explanation,Sentence Patterns, Useful Expressions)5th—6th classes:Part III Reflection5.Critical thinking: More speaking practice in discussion related to love and logic6.Writing Practice: Text writing• My first meeting with my roommate• My most embarrassing experience• A time I felt most proud of myself7th—8th classes: Part IV Assignment7. Post-reading activities: review words and expressions, role-play, exercises, etc8. Section B: Focus on fast reading and Practice in reading skillUNIT 1Section A Love and Logic: The Story of a FallacyPart I Warming up1. Lead-in:1) What do you know about logic?Tips:·It is the use and study of valid reasoning;·Most prominent in the subjects of philosophy, mathematics, and computerscience;·Established as a formal discipline by Aristotle;·One of the classical trivium (三学科), the other two being grammar and rhetoric (修辞);·Divided into three parts: inductive reasoning(归纳推理), abductive reasoning (反绎推理), and deductive reasoning(演绎推理).2) Do you think it is possible to deal with life in a completely rational and logical way?Tips:·When it comes to making a choice, many people tend to use rational and logical reasoning;·Rational world is not necessarily a wonderful one;·Rational individuals can make choices that are bad news for others;·It is ridiculous to deal with love in a logical way.3) The following are some statements to test your reasoning ability. Tell whetherthe conclusions after the word “Therefore”are true (T), false (F), or uncertain (U). Write your answer on the line before each statement.1. All odd numbers are integers (整数). All even numbers are integers. Therefore, all odd numbers are even numbers.2. There are no dancers that aren’t slim and no singers that aren’t dancers. Therefore, all singers are slim.3. A toothpick (牙签) is useful. Useful things are valuable. Therefore, a toothpick is valuable.4. Three pencils cost the same as two erasers. Four erasers cost the same as one ruler. Therefore, pencils are more expensive than rulers.5. Class A has a higher enrollment than Class B. Class C has a lower enrollment than Class B. Therefore, Class A has a lower enrollment than Class C.2. Cultural Background:1) What is a fallacy? And how is it used?Tips:·An error in reasoning that renders an argument logically invalid;·By accident or design, logical fallacies are often used in debate or propaganda;·To mislead people;·To distract people from the real issue for the purpose of winning an argument.2) How many types of fallacy do you know?Tips:Part II Text Study1. Global Reading:Tips for Reading: A Good Reader should1) Try to become an active reader.2) Learn to ask more questions. ( what, why, how)3) Do the efficient reading. (key points, topic sentence, key words, locatingwords, necessary and sufficient )4) Develop a habit of marking during reading.1.1 Answer Questions1) Why does the narrator want to have a beautiful and well-spoken girlfriend?Tips: He thinks a beautiful and well-spoken girlfriend will assist him to land a job and achieve success in an elite law company.2) Why does the narrator decide to teach Polly logic?Tips: Because he believes logic is essential to critical thinking. By teaching Polly logic, he can make her intelligent and well-spoken.3) Is the narrator successful in teaching Polly logic? How do you know?Tips: Yes. He is only too successful in teaching her because in the end when he asks Polly to be his girlfriend, Polly refuses his request by applying all the logical fallacies he has taught her.1.2 Structure Analysis:The text tells a humorous but ironic story. The narrator, a smart and promisingyoung student in a law school who seems to be able to attract beautiful girls easily, ends up in failure in his efforts to win a girl.Text A is a narrative, the focus of which is the plot. The structure of a narrative essay usually follows the Introduction –Body –Conclusion format.1.3 SummaryMy roommate Rob made a pact with me that he’d give me his girlfriend Polly in exchange for my jacket. And I agreed.Polly had the right background to be the girlfriend of a dogged, brilliant lawyer like myself. She was pretty, well-off, and radiant. Still, I want to dispense her enough pearls of wisdom to make her “well-spoken”.So I tried my best to teach her such logical fallacies as Dicto Simpliciter, Hasty Generalization, Ad Misericordiam, and False Analogy. After five nights of diligent work, I actually made a logician out of Polly. She was an analytical thinker at last. When I asked her to develop our relationship into a romantic one, however, she refuted my arguments as those logical fallacies I had taught her! And she refused my proposition by making full proposition: She liked Rob in leather, therefore, she had told him to make the pact with me so that Rob could have my jacket.为了给后代换来一个和平的环境,我们的革命先烈们抛头颅、洒热血。
财务报表分析与证券估值英文课件 (3)

The Big Picture for This Chapter
Understand the Difference Between:
ü Simple Valuation Schemes ü Stock Screening, and ü Fully Fledged Fundamental Analysis
CHAPTER THREE
McGraw-Hill/Irwin
Copyright © 2013 by The McGraw-Hill Companies, Inc. All rights reserved.
Prepared by: Stephen H. Penman – Columbia University
Unlevered (or Enterprise) Multiples (that are Unaffected by the Financing of Operations)
Unlevered Price/Sales Ratio Market Value of Equity Net Debt Sales
Understand how the financial statements are used in each of these types of analysis Understand how formal fundamental analysis is done Understand what generates value in a business:
Unlevered Price/ebit
Market Value of Equity Net Debt ebit Market Value of Equity Net Debt ebitda
理智与情感-英文

要点三
Increased selfawareness
Rational thinking fans selfawareness by encoding individuals to reflect on their emotional experiences and identify patterns in their emotional responses
The Regulation of Reason on Emotional Expression
Emotional suppression
Reason can regulate emotional expression by suppressing inappropriate or excessive displays of emotion, such as controlling factual expressions or vocal tones
The relationship between reason and emotion
• Interaction: Reason and emotion are not mutually exclusive; They interact and influence each other For example, emotions can provide valuable information that helps us make quick decisions, while reason can help us evaluate and justify those decisions
• Integration: In many cases, the best decisions are made by integrating both reason and emotion This allows us to take advantage of the strengths of both cultures while minimizing their weaknesses For example, we might use reason to objectively analyze a problem while also considering our emotional response to potential solutions
操作系统名词解释整理

==================================名词解释======================================Operating system: operating system is a program that manages the computer hardware. The operating system is the one program running at all times on the computer (usually called the kernel), with all else being systems programs and application programs.操作系统:操作系统一个管理计算机硬件的程序,他一直运行着,管理着各种系统资源Multiprogramming: Multiprogramming is one of the most important aspects of operating systems. Multiprogramming increases CPU utilization by organizing jobs (code and data) so that the CPU always has one to execute.多程序设计:是操作系统中最重要的部分之一,通过组织工作提高CPU利用率,保证了CPU始终在运行中。
batch system: A batch system is one in which jobs are bundled together with the instructions necessary to allow them to be processed without intervention.批处理系统:将许多工作和指令捆绑在一起运行,使得它们不必等待插入,以此提高系统效率。
SP706T_datasheet
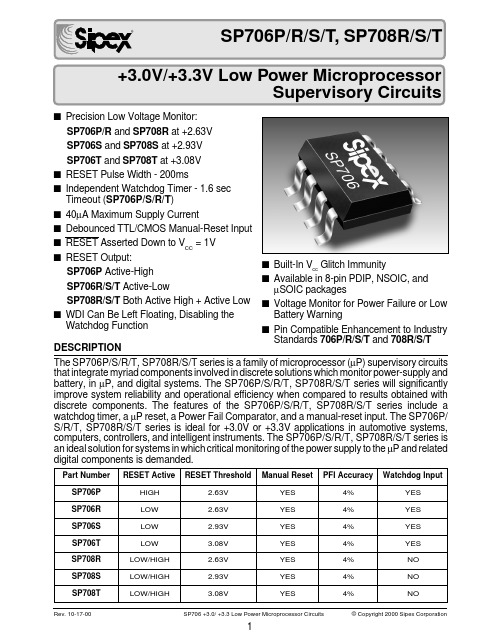
V
VRST(MAX)<VCC<3.6V
PARAMETER
MIN. TYP. MAX. UNITS CONDITIONS
WDO Output Voltage VOH VOL V
OH
VOL MR Pull-Up Current
MR Pulse Width, tMR
MR Input Threshold VIL VIH V
IL
VIH MR to Reset Out Delay, tMD
4.5V<V <5.5V, CC
I
SOURCE
=
800µA
4.5V<VCC<5.5V, ISINK = 3.2mA
µA MR = 0V,VRST(MAX)<VCC<3.6V MR = 0V,4.5V<VCC<5.5V
ns
VRST(MAX)<VCC<3.6V 4.5V<VCC<5.5V
VRST(MAX)<VCC<3.6V
DESCRIPTION
s Built-In Vcc Glitch Immunity s Available in 8-pin PDIP, NSOIC, and
基于平行多种群与冗余基因策略的置信规则库优化方法
基于平行多种群与冗余基因策略的置信规则库优化方法徐晓滨 1朱 伟 1徐晓健 1侯平智 1, 2常雷雷1摘 要 置信规则库(Belief rule base, BRB)的参数学习和结构学习共同影响着置信规则库的建模精度和复杂度. 为了提高BRB 结构学习和参数学习的优化效率, 本文提出了一种基于平行多种群(Parallel multi-population)策略和冗余基因(Redundant genes)策略的置信规则库优化方法. 该方法采用平行多种群策略以实现对具有不同数量规则BRB 同时进行优化的目的, 采用冗余基因策略以确保具有不同数量规则的BRB 能够顺利进行(交叉, 变异等)相关优化操作. 最终自动生成具有不同数量规则BRB 的最优解, 并得出帕累托前沿(Pareto frontier), 决策者可以根据自身偏好和实际问题需求, 综合权衡并在帕累托前沿中筛选最优解. 最后以某输油管道泄漏检测问题作为示例验证本文提出方法的有效性, 示例分析结果表明本文提出的方法可以一次生成具有多条规则BRB 的最优解, 并且可以准确绘制出帕累托前沿, 为综合决策提供较强的决策支持.关键词 平行多种群, 冗余基因, 置信规则库, 帕累托前沿引用格式 徐晓滨, 朱伟, 徐晓健, 侯平智, 常雷雷. 基于平行多种群与冗余基因策略的置信规则库优化方法. 自动化学报,2022, 48(8): 2007−2017DOI 10.16383/j.aas.c190580Belief Rule Base Optimization Method Based on ParallelMulti-population and Redundant Genes StrategyXU Xiao-Bin 1 ZHU Wei 1 XU Xiao-Jian 1 HOU Ping-Zhi 1, 2 CHANG Lei-Lei 1Abstract The parameter learning and structure learning of the belief rule base (BRB) affect accuracy and com-plexity of modeling. In order to improve the optimization efficiency of BRB structure learning and parameter learn-ing, this paper proposes a belief rule base optimization method based on parallel multi-population and redundant genes strategy. This method adopts parallel multi-population strategy to optimize simultaneously BRB with differ-ent quantity rules. Redundant genetic strategy is adopted to ensure that BRB with different number of rules can smoothly perform (crossover, mutation, etc.) optimization operations. Then, an optimal solution of BRB with differ-ent number of rules is automatically generated, and derived Pareto frontier. Decision maker can comprehensively se-lect the optimal solution based on their own mind and actual problem needs. Finally, this paper presents an ex-ample of pipeline leak detection to verity the method proposed. The experimental result shows that the proposed method can generate the optimal solution of BRB with multiple rules at one time and can accurately plot the Pareto frontier which provides strong decision support for decision maker.Key words Parallel population, redundant genes, belief rule base (BRB), Pareto frontierCitation Xu Xiao-Bin, Zhu Wei, Xu Xiao-Jian, Hou Ping-Zhi, Chang Lei-Lei. Belief rule base optimization method based on parallel multi-population and redundant genes strategy. Acta Automatica Sinica , 2022, 48(8): 2007−2017置信规则库(Belief rule base, BRB)是一种基于D-S (Dempster-Shafer)证据理论的复杂系统建模、分析与评价的专家系统方法. 该方法以置信规则(Belief rule)为基础, 能够较好地表示、建模和集成不确定条件下的多种类型信息[1−2]. 同时, 作为一种 “白箱(White box)”方法, BRB 还具有较强的可解释性, 专家可以更好地参与BRB 的建模、训练以及学习过程. 自提出以来, BRB 已成功应用于各个领域, 如智慧医疗[3]、多属性决策分析[4]以及军事能力评估[5]等.然而, BRB 的规模不宜过大, 否则将会给建模造成巨大的困难. 同时, 由于人的认知不完备或者数据缺失, 专家给定的初始化BRB 可能面临所筛选关键指标及其取值不准确的情况, 因此采用初始收稿日期 2019-08-20 录用日期 2020-02-07Manuscript received August 20, 2019; accepted February 7,2020浙江省杰出青年基金 (LR21F030001), 浙江省重点研发计划基金(2021C03015, 2018C01031), 国家自然科学基金 (61903108,U1709215), 浙江省自然科学基金(LY21F030011)资助Supported by Zhejiang Outstanding Youth Fund (LR21F 030001), Zhejiang Province Key Research and Development Projects (2021C03015, 2018C01031), National Natural Science Foundation of China (61903108, U1709215), and Natural Science Foundation of Zhejiang Province (LY21F030011)本文责任编委 莫红Recommended by Associate Editor MO Hong1. 杭州电子科技大学自动化学院 杭州 3100182. 杭州言实科技有限公司 杭州 3100181. Department of Automation, Hangzhou Dianzi University,Hangzhou 3100182. Hangzhou Yanshi S&T Co., Ltd., Hang-zhou 310018第 48 卷 第 8 期自 动 化 学 报Vol. 48, No. 82022 年 8 月ACTA AUTOMATICA SINICAAugust, 2022BRB进行建模、评估和预测时, 其结果精度可能不高. 为了解决这些问题, 需要对初始BRB进行学习优化以明确其规模和提高建模精度. 众多研究者在多个领域开展了相关研究, 主要可以分为3类: BRB 结构学习、BRB参数学习以及BRB结构与参数联合优化.BRB结构学习的目的是识别与筛选关键前提属性及其参考值. Chang等[5]首先提出了基于主成分分析等维度约减技术的BRB结构学习方法, 对装备体系综合能力评估问题开展了相关研究; Wang 等[6]提出动态调整BRB规则的结构学习方法; Li 等[7]提出了基于极小方差的前提属性参考值确定方法, 并基于此提出了安全性评估方法.BRB参数学习的目的是通过优化BRB相关参数的取值以提高建模精度. Yang等[8]提出BRB 优化模型优化BRB的参数. Zhou等[9]基于期望极大估计算法提出了在线参数学习方法, 对于时效性有较高要求的复杂决策问题提供了在线建模方法. Chen等[10]对前提属性参考值存在的约束进行分析,改进了BRB系统的优化模型, 将前提属性参考值作为被训练的参数进行参数学习, 并将原优化模型称为局部训练模型, 改进后的优化模型称为全局训练模型. Savan等[11]、Chang等[12]和马炫等[13]提出了基于演化算法(Evolutionary algorithms, EA)的BRB参数学习方法. Chang等[12]对比了多种演化算法的求解效率, 包括遗传算法(Genetic algorithm, GA)、差分进化(Differential evolutionary, DE)算法以及粒子群(Particle swarm optimization, PSO)算法等. 这些优化算法在解决解空间较大的理论与实践问题方面具有较强的优势.在结构学习和参数学习的基础上, Chang等[14−16]进一步提出了对BRB参数和结构进行优化的BRB 联合优化方法, 通过构建双层优化模型, 在外层模型中优化BRB结构, 在内层模型中优化BRB参数,实现对BRB参数与结构的联合优化. Yang等[16]提出BRB结构和参数的联合优化方法, 采用启发式策略(Heuristic strategy)优化BRB结构, 采用差分进化算法优化BRB参数.以上有关BRB结构学习、参数学习的相关工作仅关注单一层面, 而文献[14−16]虽然实现了对BRB 结构与参数的优化, 但是其对BRB结构和参数的优化仍然是分别开展, 更具体而言, 在外层模型中仅优化BRB结构, 在内层模型中仅优化BRB参数. 在本质上仍然属于迭代(Iterative)的过程, 并未实现对BRB结构与参数的同时优化.基于此, 本文提出一种基于平行多种群策略和冗余基因策略的BRB优化方法. 该方法中, 采用具有不同基因数量的多个种群来编码具有不同数量规则的BRB, 多个不同种群共同参与优化过程来实现对BRB结构与参数进行优化的目的; 在优化过程中, 为具有较少基因的个体(具有较少规则的BRB)补充部分冗余基因, 以确保不同长度个体能够同时参与优化过程. 采用该方法, 可以一次产生具有不同数量规则BRB的最优解, 并自动生成帕累托前沿, 决策者可以根据自身偏好或实际问题需求在帕累托前沿上筛选最优解. 最终以某输油管道泄漏检测问题为例对本文提出的方法进行验证.1 BRB理论基础及推理过程1.1 BRB基础k 在传统D-S证据理论的基础上, Yang等[8]进一步提出采用具有置信结构的IF-THEN规则来表达、建模与推理不确定条件下的多种类型信息, 包括定性定量信息、语义数值信息、完备与不完备信息等. 由具有同一置信结构的IF-THEN规则组合而成的规则库即称为置信规则库(BRB), 其中第条规则如式(1)所示:x m(m=1,···,M)mA k m(m=1,···,M;k=1,···,K)kmβn,k(n=1,···,N)k n D n∧θkδm km其中, 表示第个前提属性,表示第条规则中第个前提属性的参考值;表示第条规则中第个评估结果的置信度; “”表示规则满足交集假设; 和分别表示第条规则和第个前提属性的权重.相应的, 当置信规则建立在并集假设下时, 其表述形式如式(2)所示:∨其中, “”代表规则满足并集假设.作为一种具有白箱特征的专家系统方法, BRB 已经广泛应用于解决多复杂系统问题[17−18].1.2 BRB的推理BRB系统的规则推理过程主要有4个步骤.步骤 1. 计算前提属性与参考值之间的匹配度.x m x∗m jm对于给定前提属性的值为, 第条规则中第个属性的匹配度如式(3)所示:2008自 动 化 学 报48 卷x ∗m m A k +1m A kmm j 其中, 代表第 个属性的输入值, 和 表示相邻激活规则中的第 个属性的值. 第 条规则中的第 个属性的综合匹配度如式(4)所示:c m m m 其中, 表示第 个属性的置信度. 如果没有不完整的信息并且第 个属性的置信度为1, 则式(4)可以简化为式(5):步骤 2. 计算激活规则权重.θk k αkm k m x m w k >0k k 其中,表示第 条规则的相对权重; 表示第 条规则中第 个前提属性与参考值集合 之间的匹配度. 如果 , 表示第 条规则被激活, 否则第 条规则未被激活.βn n 步骤 3. 通过证据推理(Evidential reasoning,ER)算法融合被激活的规则, 如式(7) (见本页下方)和式(8) (见下页上方)所示. 式(7)和式(8)中,表示第 个评估结果的置信度.步骤 4. 输出结果.融合相应的规则后得到评估结果的置信分布形式, 如式(9)所示:D n U (D n )U 当评估结果输出为单一值时, 需要对步骤3中的结果进行集成. 假设评估等级 对应的效用值为, 则评估结果的综合效用 可根据式(10)进行计算.1.3 BRB 学习以及面临的问题当前BRB 的学习方法可大致分为3类:1) BRB 结构学习BRB 结构学习主要思想是缩减BRB 规模或者是确定BRB 的最佳结构. BRB 规模与前提属性的个数以及前提属性的参考值有关[5−7]. 因此, BRB 结构学习主要从这两方面考虑. BRB 结构学习所解决的是由前提属性的个数或者前提属性的参考值个数过多而导致的组合爆炸的问题.2) BRB 参数学习BRB 参数学习主要思想是优化BRB 的参数提高建模精度[8−10]. 由于人的认知不完备或者数据缺失, 专家给定的初始化BRB 可能面临所筛选关键指标及其取值不准确的情况, 因此采用初始BRB 进行建模、评估和预测时, 其结果精度可能不高. 因此提出BRB 参数学习以提高对复杂非线性系统的建模能力. BRB 的参数优化模型取均方误差或者绝对误差作为优化目标函数, 前提属性的参考值, 规则权重以及评估结果的置信度作为决策变量. 目前BRB 的优化方法主要有主成分分析法(Principal component analysis, PCA)、牛顿法以及演化算法(Evolutionary algorithm, EA).3) BRB 联合优化BRB 联合优化的主要思想是对BRB 结构和参数同时优化以减小建模复杂度和提高建模精度[14−16].当前针对BRB 参数和结构优化的BRB 联合优化方法[14−15]中, 首先推导出集成模型精度(由均方差表示)与复杂度(与规则数量相关)的综合优化目标, 然后构建双层优化模型, 并提出基于演化算法的优化模型求解算法, 最终实现对BRB 结构与参数的联合优化. 但是该方法对BRB 结构与参数的联合优化是迭代进行, 并未实现对BRB 结构与参数的同时优化.8 期徐晓滨等: 基于平行多种群与冗余基因策略的置信规则库优化方法2009[]综上所述, 当前BRB 学习相关研究中一般仅局限于结构学习或参数学习, 而开展的BRB 结构与参数联合优化的过程本质上也是迭代和分别进行, 并未实现对BRB 结构与参数同时进行优化的目的. 基于此, 本文提出采用平行多种群策略和冗余基因策略的BRB 优化方法, 实现对BRB 结构与参数进行同时优化的目的.2 基于平行多种群策略的BRB 优化模型2.1 平行多种群策略当前, 一般采用多种群策略来集成不同算子的优势以解决大规模优化问题[19−22]. 具体而言, 在不同种群中分别采用不同算子进行优化, 在优化过程中进行对比并将其作为下一代分配优化资源的依据,综合集成多种不同算子的共同优势. 这是由于传统优化问题中并不涉及结构优化. 因此, 在将多种群策略应用于优化算法时, 不同种群中的优化算子不同, 但个体长度(编码格式)仍是相同的. 但这与本文要解决的核心问题有本质区别: 本文研究的出发点是实现对BRB 结构和参数的同时优化, 因此在本文采用的多种群策略中, 不同种群中的个体长度(编码格式)不同.但是, 同时优化BRB 结构与参数所面临的最大挑战在于, 具有不同数量规则的BRB 规模不同,而采用演化算法进行求解时, 要求种群中所有个体K 的长度相同. 本文提出采用平行多种群策略解决这一问题. 将具有不同数量规则的BRB 按照其规则数量划分为多个种群, 在单一种群中BRB 具有相同数量规则(个体长度相同), 不同种群之间BRB 规则数量不同(个体长度不同). 换言之, 将BRB 中规则数量 , 也作为待优化参数之一引入第2.2节中的优化模型中, 以实现对BRB 结构与参数同时优化的目的.图1表示平行多种群策略将初始种群划分为具有不同规则数量的种群(种群规则数量相同), 但仍不能用于交叉变异, 需要添加冗余基因至所有个体长度相等(见第3节).2.2 BRB优化模型基于第2.1节提出的平行多种群策略, 建立同时包含BRB结构与参数的优化模型为初始种群初始种群中的个体初始种群中的个体对应的BRB图 1 平行多种群策略Fig. 1 Parallel multiple population strategy2010自 动 化 学 报48 卷k=1,···,K;n=1,···,N;m=1,···,M;p= q∈[1,···,M].K min K maxm lb m ub mm(0,1][0,1]∑Nn=1βn,k<1其中,式(11b)表示规则数量在预定的最小规则数和最大规则数之间. 式(11c)表示第个前件属性的参考值在下界和上界之间. 式(11d)和式(11e)表示第个前件属性的参考值的上下界必须包含在规则中. 式(11f)表示初始规则权重应该在内. 式(11g)表示评估结果的置信度应该在内. 式(11h)表示评估结果的置信度之和小于或者等于1 (当信息不完整时).3 基于冗余基因策略的BRB优化算法为了求解第2.2节中建立的优化模型, 本节提出基于冗余基因策略的BRB优化算法. 基于冗余基因策略, 对基因数量较少的个体(规则数量较少的BRB)补全部分冗余基因, 至所有个体的长度相等. 这样所有个体的长度即一致, 也就可以参与优化操作, 而并不参与适应度计算.基于冗余基因策略的BRB优化求解算法共包括6个步骤, 如图2所示.步骤 1. 参数识别参数识别主要包括演化算法的参数设值和BRB的参数设值. 演化算法的参数包括种群个数、迭代次数等. BRB的参数包括BRB的规则个数、前提属性(参考值)的个数、评估结果的置信度个数.步骤 2. 初始化(编码)K KK min K max每一个个体代表一个具体的BRB. 个体基因由BRB的参数组成. BRB的参数包括前提属性的参考值、规则权重、评估结果的置信度以及表示BRB中规则数量. 的取值为离散整数, 介于最小规则数和最大规则数之间.不同的BRB具有不同的规则数量, 不同个体之间的基因个数也不相等, 这就导致不同种群中的个体长度不同, 因此不能进入下一步的交叉变异操作.步骤 3. 交叉变异(补全冗余基因)在进行交叉变异操作之前, 首先需要对不同种群中的所有个体补全冗余基因, 以确保所有个体的长度相同(所有个体包含基因数量相同), 如图3所示.向各个个体中补全基因的操作步骤如下: 首先图 2 优化算法的6个步骤Fig. 2 Optimization algorithm with six steps8 期徐晓滨等: 基于平行多种群与冗余基因策略的置信规则库优化方法2011K 识别具有最多基因数量的个体(即具有最多规则数量的BRB), 以该个体的长度为标准长度; 然后依次对每个个体补全冗余基因, 需要注意补全基因应当满足所在位置的上下限要求, 且最后一位标志初始规则数量的基因 位置和取值不变.补全基因后, 所有个体长度将会相等, 均为初始具有最多基因数量个体的长度. 补全基因后个体将进入优化操作. 本文采用的是差分进化[19−21]算法作为优化引擎, 其优化操作包括交叉和变异.v ′i,j j CR z ′i,j 1−CR v ′i,j z ′i,j 交叉策略指出引入交叉算子可以增强种群的多样性. 为第 个基因的临时个体即交叉后的个体, 其交叉算子为 , 是当前个体, 其交叉算子为 . 每一个个体按照一定的概率选择交叉个体 , 否则生成原来的个体 .CR =0.9sn ∈[1,2,···,n ]其中, 交叉算子 , 是由每一个个体产生的随机整数.变异操作指出随机选取种群中两个不同个体,iv ′将其与待变异的个体进行合成, 得到新的个体. 第 个新个体 可以由式(13)得到z r 1z r 2z r 3r 1=r 2=r 3F =0.5其中, , 和 是3个随机产生的个体, 并且, 变异算子 .步骤 4. 适应度计算(删除冗余基因、解码)K 经过交叉, 变异操作后的个体中的基因已经得到优化, 在进行适应度计算之前需要首先根据每个个体最后一位标志初始长度的基因 删除在步骤3中添加的冗余基因, 换言之, 只有与初始BRB 相关的基因才会进入适应度计算当中, 步骤3中添加的冗余基因不参与适应度计算, 如图4所示.删除冗余基因之后, 根据基因编码方案对剩余个体的基因进行解码操作, 然后进入适应度计算,包括输入信息与前提属性的匹配度计算, 规则激活权重计算以及激活规则集成(见第1.2节).步骤 5. 选择通过比较个体的适应度值, 选择适应度值最小的个体作为最优个体作. 在选择适应度值的过程中,图 3 添加冗余基因Fig. 3 Add redundant genes不参与适应度计算图 4 删除冗余基因Fig. 4 Remove redundant genes2012自 动 化 学 报48 卷个体适应度值的比较仅局限于具有相同长度的个体或者具有相同规则数量的BRB. 最终的最优个体是由不同规则数量的BRB 组成, 而不是由特定数量规则的BRB 组成.i u t i 对于第 个个体 , 选择个体的适应度函数获得更低的额定值作为下一代.f (·)其中, 是适应度函数, 本文中是指均方差(Meansquare error, MSE).步骤 6. 权衡分析在选择最优的个体之后, 利用具有不同规则数量的最优BRB 导出帕累托前沿, 通过考虑决策者的偏好和具体要求, 进行权衡分析以产生最优解.(x 1,x 2)(x 1,x 2)x 2x 1图5说明了具有两个属性 问题的权衡分析概念[23]. 图5表示包含两个属性 的帕累托前沿; Ⅰ点表示偏好 的情况下决策者选择的解决方案; Ⅱ点表示偏好 的情况下决策者选择的解决方案.图 5 权衡分析Fig. 5 Tradeoff analysis4 案例分析本节以输油管道泄漏检测为例, 验证本文中所提出方法的有效性. 已知可以根据输油管道进出口的流量差(FlowDiff )和压力差(PressureDiff )推断出输油管道的泄漏尺寸值(Leaksize ). 流量差和压力差是检测管道中是否存在泄露并且与泄漏尺寸相关的两个重要属性. 因此选择流量差和压力差作为BRB 的前提属性, 泄露尺寸作为输出结果. 为了便于对比分析, 本文采用现有BRB 相关文献中多次使用的实验数据[9−10, 24], 该数据共包括从英国北部某地采集得到的2008组输油管道泄露数据.为了与当前方法的进行公平比较, BRB 的参数设置与当前方法保持一致. 首先构建BRB 的模型,BRB 采用5个评估等级评估管道泄漏情况, 其效用值分别为F lowDiff ∈[−10,2]P ressureDiff ∈[−0.02,0.04]前提属性流量差 , 压力差.本文研究的主要目的是实现BRB 结构和参数的同时优化, 平行多种群与冗余基因策略适用于演化算法, 如差分进化算法(DE), 遗传算法(GA), 粒子群算法(PSO)等. 在众多优化算法中, DE 算法取得了较好的优势, 即其具有优化效率高, 求解速度快且不易陷入局部最优解等优点. 因此本文采用DE 作为BRB 结构与参数优化模型的求解算法, 为了与当前方法进行比较, DE 优化算法的参数值和当前方法使用的参数值一致, 其设置如下:1) BRB 中规则数量取值范围为3 ~ 8条;2) 优化算法中个体数量设定为100; 迭代次数为1 000代;3) 交叉率和突变率设值为0.8和0.8;4) 算法共运行30次以验证平行多种群与冗余基因策略方法的稳定性.表1给出了算法运行30次之后具有不同数量规则的BRB 统计结果. 通过表1可以发现, 当规则数量为3 ~ 8条时, 不同BRB 的最小值/平均值都远小于其方差(小一个数量级), 这说明本文提出的方法具有较好的稳定性.图6进一步给出了本文提出方法在1 000代优化过程中帕累托前沿的优化过程.通过表1以及图6, 可以得出以下结论:1) 在1 000代的优化过程中, 帕累托前沿不断表 1 运行30次的数据结果Table 1 Statistics of 30 runs第 3 条第 4 条第 5 条第 6 条第 7 条第 8 条min 4.0389×101 3.2065×101 2.9210×101 2.9208×101 2.9200×101 2.9189×101 avg 5.3796×101 3.9717×101 3.7355×101 3.7332×101 3.6770×101 4.4892×101 vara9.5350×1025.2327×1023.4741×1023.2595×1024.3643×1022.4779×1028 期徐晓滨等: 基于平行多种群与冗余基因策略的置信规则库优化方法2013向前推进;2) 当优化至100代时(见图6(b)), 具有不同数量规则的BRB 实际上已经达到了比较稳定的可行解;3) 规则数量(即参数数量)对优化结果具有一定影响. 当优化到100代时, 由于规则数量较多的BRB 的参数数量较多, 此时具有6/7/8条规则的BRB 并未取得较优解, 也未在帕累托前沿上;4) 决策者可以根据自身偏好在帕累托前沿上选择最优BRB. 当不考虑偏好时, 具有5条规则BRB 具有明显优势, 其MSE 明显小于前者, 而后续随着规则数量增加, MSE 也并未明显大幅下降, 即具有5条规则的BRB 处于拐点(Elbow point)[25].表2给出了具有5条规则的BRB, 图7给出了模型预测结果与真实值之间的对比以及误差.表3进一步对比了本文所得结果与已有文献中针对该示例的计算结果. 通过对比, 可以发现:1) 与已有仅开展参数学习的研究[9−10, 24]相比,根据不同的优化模型, BRB 参数学习的优化参数数量为336 ~ 349. 其模型误差MSE 均处于较高水平.文献[6]提出动态优化方法, 该方法涉及到的优化参数个数从349降到39. 其在降低建模复杂度方面与上述3种方法相比取得了较好的结果. 而本文采用的并行多种群与冗余基因策略的方法取得的模型误差MSE 更小, 即本文提出方法相对参数学习具有优势.2) 本文所得结果稍劣于BRB 联合优化方法[14]所得到的结果. 原因在于: BRB 联合优化方法属于迭代方法, 即在对BRB 参数进行优化时, 并不优化其结构, 而本文提出的方法在一次优化过程中同时实现对BRB 结构和参数的优化. 换言之, 在给定资源条件下, BRB 联合优化仍然仅优化其参数(这是由其迭代优化的本质决定的), 而本文所提出方法可以同时实现对BRB 结构与参数. 在这种情况下, 本文提出方法仍能取得与当前最优解(0.267 9)十分接BRB 规则数量1010M S E (i n l o g )(a) 不同规模 BRB 的 MSE (第 1~1 000 轮迭代)(a) MSEs for different BRBs (Rounds 1~1 000)M S E (i n l o g )(b) 不同规模 BRB 的 MSE (第 100~1 000 轮迭代)(b) MSEs for different BRBs (Rounds 100~1 000)BRB 规则数量图 6 帕累托前沿的优化过程Fig. 6 Optimal process of the Pareto frontier2014自 动 化 学 报48 卷07:00:007:15:007:30:007:45:008:00:008:15:008:30:008:45:109:00:009:15:009:30:009:45:010:00:010:15:110:30:010:45:011:00:011:15:111:30:011:45:012:00:012:15:012:30:0输出(a) 具有 5 条规则的新 BRB 的输出(a) Output by new BRB with five rules时刻时刻07:00:007:15:007:30:007:45:008:00:008:15:008:30:008:45:109:00:009:15:009:30:009:45:010:00:010:15:110:30:010:45:011:00:011:15:111:30:011:45:012:00:012:15:012:30:0−−误差(b) 具有 5 条规则的新 BRB 的误差(b) Error by new BRB with five rules图 7 输油管道泄漏检测结果与误差对比Fig. 7 Pipeline leak detection test results and error comparison表 2 具有5条规则的最优BRB 参数Table 2 Optimal BRB parameters with five rules序号权重前提属性泄露大小流量差压力差0246810.8642−10.0000 −0.002 0.39500.06920.01940.01220.50422 1.0000−7.5000 −0.0176 0.78780.21090.00010.00000.001230.0911−1.7830 0.00650.01010.12450.05250.57940.233540.28380.384 50.00730.20130.20720.15130.21640.223850.24992.000 00.04000.65880.04980.09290.02430.1742表 3 基于不同BRB 优化方法的实验结果对比分析Table 3 Comparative analysis of experimental results based on different BRB optimization methods序号方法描述MSE (MAE)尺寸(训练/测试)NOR NOP 1其他方法ANFS 0.50739/2SVM 0.4219δ2=1C = 10, 3以前 BRB 学习方法局部训练[24]0.4049500/200 8563364在线更新[9]0.7880800/200 8563365适应性学习[10]0.3990500/200 8563496动态规则调整[6]0.5040900/200 8141080.44506397双层优化[15]0.2917500/200 85368一般并集 BRB 优化[26]0.3741500/200 83200.28485360.267912929本文方法平行多种群与冗余基因0.4038500/200 832400.29215注: “NOR”表示规则数量 (Number of rules), “NOP”表示参数数量 (Number of parameters)8 期徐晓滨等: 基于平行多种群与冗余基因策略的置信规则库优化方法2015近的结果(0.292 1)验证了本文提出方法的有效性.3) 相比BRB 联合优化方法, 本文的另一优势在于最终产生的结果以帕累托前沿的形式表示出来, 决策者既可以根据自身需求或问题特点在帕累托前沿上选择恰当的最优解, 又可以在不考虑偏好的情况下, 根据拐点原则通过权衡分析选择无偏最优解.5 结束语为了实现对置信规则库结构和参数同时优化的目的, 本文提出一种基于并行多种群与冗余基因策略的置信规则库优化方法. 通过输油管道泄漏检测的例子验证本文所提出方法的有效性. 主要结论如下:首先, 通过并行多种群策略, 具有不同规则数量的BRB 可以同时进入优化操作, 因此可以同时优化BRB 的结构和参数. 然后, 通过提出冗余基因策略, 具有不同长度的个体(BRB 具有不同的规则数量)可以进行交叉变异操作. 只有与初始BRB 相关的基因才会进入适应度计算当中. 最后, 输油管道泄漏检测的例子结果表明, 基于并行多种群与冗余基因策略的置信规则库优化方法可以同时优化具有不同规则数量的多个BRB, 随着BRB 的优化,帕累托前沿不断向前推进. 最后可以通过拐点原则识别最佳BRB, 也可以根据决策者的偏好来决定最佳BRB. 下一步工作, 需要对优化算法引擎展开进一步的研究. 优化算法引擎需要大量的参数, 这将导致优化效率下降. 所以迫切需要找到更好的优化技术去解决这些问题. 此外, 还应当在更多理论和实际问题中对本文提出方法进行验证.ReferencesYang J B, Singh M G. An evidential reasoning approach for multiple-attribute decision making with uncertainty. IEEE Transactions on Systems, Man, and Cybernetics , 1994, 24(1):1−181Yang J B, Liu J, Wang J, Sii H S, Wang H W. Belief rule-base inference methodology using the evidential reasoning approach-RIMER. IEEE Transactions on Systems, Man, and Cyberneti -cs — Part A: Systems and Humans , 2006, 36(2): 266−2852Hossain M S, Rahaman S, Kor A L, Andersson K, Pattinson C.A belief rule based expert system for datacenter PUE prediction under uncertainty. IEEE Transactions on Sustainable Comput-ing , 2017, 2(2): 140−1533Yang J B, Xu D L. Nonlinear information aggregation via evid-ential reasoning in multiattribute decision analysis under uncer-tainty. IEEE Transactions on Systems, Man, and Cybernetics —Part A: Systems and Humans , 2002, 32(3): 376−3934Chang L L, Zhou Y, Jiang J, Li M J, Zhang X H. Structure learning for belief rule base expert system: A comparative study.Knowledge-Based Systems , 2013, 39: 159−1725Wang Y M, Yang L H, Fu Y G, Chang L L, Chin K S. Dynam-ic rule adjustment approach for optimizing belief rule-base ex-6pert system. Knowledge-Based Systems , 2016, 96: 40−60Li G L, Zhou Z J, Hu C H, Chang L L, Zhou Z G, Zhao F J. A new safety assessment model for complex system based on the conditional generalized minimum variance and the belief rule base. Safety Science , 2017, 93: 108−1207Yang J B, Liu J, Xu D L, Wang J, Wang H W. Optimization models for training belief-rule-based systems. IEEE Transac-tions on Systems, Man, and Cybernetics — Part A: Systems and Humans , 2007, 37(4): 569−5858Zhou Z J, Hu C H, Xu D L, Yang J B, Zhou D H. Bayesian reasoning approach based recursive algorithm for online updat-ing belief rule based expert system of pipeline leak detection.Expert Systems with Applications , 2011, 38(4): 3937−39439Chen Y W, Yang J B, Xu D L, Zhou Z J, Tang D W. Inference analysis and adaptive training for belief rule based systems. Ex-pert Systems with Applications , 2011, 38(10): 12845−1286010Savan E E, Yang J B, Xu D L, Chen Y W. A genetic algorithm search heuristic for belief rule-based model-structure validation.In: Proceedings of the 2013 IEEE International Conference on Systems, Man, and Cybernetics. Manchester, UK: IEEE, 2013.1373−137811Chang L L, Zhou Z J, You Y, Yang L H, Zhou Z G. Belief rule based expert system for classification problems with new rule ac-tivation and weight calculation procedures. Information Sci-ences , 2016, 336: 75−9112Ma Xuan, Li Xing, Tang Rong-Jun, Liu Qing. A particle swarm optimization approach for symbolic regression. Acta Automat-ica Sinica , 2020, 46(8): 1714−1726(马炫, 李星, 唐荣俊, 刘庆. 一种求解符号回归问题的粒子群优化算法. 自动化学报, 2020, 46(8): 1714−1726)13Chang L L, Zhou Z J, Chen Y W, Xu X B, Sun J B, Liao T J,et al. Akaike information criterion-based conjunctive belief rule base learning for complex system modeling. Knowledge-Based Systems , 2018, 161: 47−6414Chang L L, Zhou Z J, Chen Y W, Liao T J, H u, Y, et al. Be-lief Rule Base Structure and parameter joint optimization un-der disjunctive assumption for nonlinear complex system model-ing. IEEE Transactions on Systems, Man, and Cybernetics: Sys-tems , 2018, 48(9): 1542−155415Yang L H, Wang Y M, Liu J, Martínez L. A joint optimization method on parameter and structure for belief-rule-based sys-tems. Knowledge-Based Systems , 2018, 142: 220−24016Chen Y, Chen Y W, Xu X B, Pan C C, Yang J B, Yang G K. A data-driven approximate causal inference model using the evid-ential reasoning rule. Knowledge-Based Systems , 2015, 88: 264−27217Zhou Z J, Hu C H, Xu D L, Yang J B, Zhou D H. New model for system behavior prediction based on belief rule systems. In-formation Sciences , 2010, 180(24): 4834−486418Wu G H, Mallipeddi R, Suganthan P N, Wang R, Chen H K.Differential evolution with multi-population based ensemble of mutation strategies. Information Sciences , 2016, 329: 329−34519Qu B Y, Suganthan P N, Liang J J. Differential evolution with neighborhood mutation for multimodal optimization. IEEE Transactions on Evolutionary Computation , 2012, 16(5): 601−61420Elsayed S, Sarker R, Coello C C. Enhanced multi-operator dif-ferential evolution for constrained optimization. In: Proceedings of the 2016 IEEE Congress on Evolutionary Computation (CEC). Vancouver, Canada: IEEE, 2016. 4191−4198212016自 动 化 学 报48 卷。
UJA1069TW24资料
• • • •
Advanced low-power concept Safe and controlled system start-up behavior Advanced fail-safe system behavior that prevents any conceivable deadlock Detailed status reporting on system and sub-system levels
• • • • • •
LIN transceiver compliant with LIN 2.0 and SAE J2602, and compatible with LIN 1.3 Advanced independant watchdog Dedicated voltage regulator for microcontroller Serial peripheral interface (full duplex) Local wake-up input port Inhibit/limp-home output port
The UJA1069 is designed to be used in combination with a microcontroller and a LIN controller. The fail-safe SBC ensures that the microcontroller is always started up in a defined manner. In failure situations the fail-safe SBC will maintain the microcontroller function for as long as possible, to provide full monitoring and software driven fall-back operation. The UJA1069 is designed for 14 V single power supply architectures and for 14 V and 42 V dual power supply architectures.
英语 博弈论术语
Sequential-move game:
即动态博弈
下棋、打牌……
斗地主!
Each player should figure out how the other players willrespondto his currentmove,how he will respond in turn.The player anticipates where his initial decisions will ultimatelylead,and uses thisinformationto calculate his current best choice.When thinking about how others willrespond,one must put oneself in theirshoes and think as they wound.
As we have known,confess in ThePrisoners’Dilemmafor each prisoner is theDominant strategy.
囚徒困境中,A与B,“坦白”均是占优。
从a角度而言,……
Dominated trategy
被占优策略
We can get to know it by comparing it toDominant strategy.
Prisoner’s dilemma
囚徒困境
智猪博弈:
可能存在多个纳什均衡的例子:
性别博弈:
斗鸡博弈:
Theyact at the same time ,
Linear chain of reasoning
直线推理
In my opinion, it’s base on the passing of time, this meansthatplayers who take part in this game make decision depend on others’behavior.In china, we may call it“螳螂捕蝉,黄雀在后”,so it like aline, andwe name it uponthis. Infact, you can better understand it when you think about play chess.
中英互译
Unit11.使用因特网access to the internet2.在因特网上运营的企业business run on the internet3.企业的内部运营internal functioning of the enterprise 4.提高生产力to improve the productivity5.到达一个更广泛的消费群体to reach a much wider consumer base 6.采购批发销售的产品to acquire wholesale products7.大幅削减成本to cut costs dramatically8.更好地跟踪和管理to better track and manageUnit21.实体店和网店之间的整合integration between the physical store and the online store2.展示其所做的市场分析demonstrate its market analysis3.写一份执行摘要write an executive summary4.在因特网上畅销sell well over the internet5.聚焦于缝隙市场focus on a niche market6.瞄准特定市场target a very specific market7.留下空白leave gaps8.有更大的机会获得成功have a better chance of successUnit31.确定的结果an assured outcome2.因特网公司的失败率the failure rate for online companies 3.以类似的方式开始to begin in a similar manner4.发现市场上存在的消费需求to identify a consumer need in the marketplace 5.启动资本start-up capital6.耗时和烦人的任务a time-consuming and tiresome task7.错误估计物流困难to misjudge the logistical problems 8.缺乏足够的商务技能to lack sufficient business skills Unit41.失去信誉lose credibility2.独特的客户体验unique customer experience3.从电子商务网站中获利profit from an e-commerce website4.简短详细的规格说明short and detailed specifications5.各种支付方式all kinds of payment options6.在最前面列出运费to list shipping costs upfront7.纸质支票和电子支票paper and electronic cheques8.客户支持customer support9.货币转换器a currency converter10.隐私政策 privacy policyUnit51.计算机代码computer code2.巨大成功a roaring success3.在线支付服务online payment services4.激光指示器a laser pointer5.起越来越大的作用play a growing role6.访问量最大的网站the most visited site7.企业对企业平台B2B(business-to-business)platform8.显示力量或权力flex the musclesTEXTB1.实际存在的,实体的brick and mortar2.品牌服装designer clothes3.家喻户晓的人或名字household name4.客户群customer base5.婴儿潮时期出生的人baby boomers6.卖场和网上bricks and clicks7.预期收益 expected revenue8.市场份额market shareUnit61.问题的一个重要解决途径one key answer to the problem2.一个组织内部的活动activities within an organization3.客户关系管理customer relationship management4.复写纸形式carbon-paper forms5.在一个理想的系统中in an ideal system6.获得并留住顾客obtain and retain customer7.局域网local network8.顾客的购买偏好customers’ buying preference 9.计算机辅助管理computer-facilitated management 10.更昂贵的综合性软件组合套装more expensive and integrated software suites Unit71.支付网关payment gateway2.服务条款terms of service3.安全证书security certificate4.结账流程checkout process5.定制页面设计customize page design6.新创公司start-up companies7.购物车shopping cart8.欺诈识别技术fraud detection technologyUnit81.另一方面on the other hand2.占据,占有take up3.专门从事specialize in4.应付,处理cope/deal with5.音/视频剪辑audio/video clips6.限于be restricted to7.集中concentrate upon8.依靠,取决于depend onText B1.search engine搜索引擎2.enter a query输入查询的问题3.provision, access and retrieval of documents文件的提供、存取和检索4.web page 网页5.case-based reasoning基于案例的推理6.NLP自然语言处理器puting power计算能力8.filename文件名Unit91.电子商务营销策略e-business marketing strategy 2.绩效营销performance marketing3.战略合作伙伴strategic partner4.社会关系网络social networking5.电子邮件营销email marketing6.分销联盟计划affiliate networking(program)7.提升销量和流量boost sales and traffic8.成倍增加在线收入exponentially grow your online revenue Unit101.解决争端resolve disputes2.资产保护protection of assets3.经商conduct business4.无数变量numerous variables5.监管机构supervisory/regulatory authority6.人力资源human resources7.关键因素key factors8.电子签名electronic signature9.商品活动business activity10.商业价值commercial value11.确保可执行性ensure enforceability12.信息产品information productsUnit111.建立安全措施institute security measures2.平息不安quell the uneasiness3.网络入侵者online intruders4.(像虫子一样)钻进worm one’s way into5.关闭电脑shut down the computer6.未授权访问unauthorized access7.备份协议a backup protocol8.令人瞩目的网站high-profile sites Text B风险意识risk consciousness风险评估risk assessment传输机制transport mechanism政策实施与执行policy implementation and enforcement安全策略security strategy系统效能system effectivenessunit121.当今的趋势the current trends2.地理区域geographic zones3.智能手机smart phones4.移动商务mobile commerce /business(m-commerce/business5.潜在客户potential customers6.网络账户online accounts7.搜索引擎优化服务SEO service8.零售业retail industry1.customer relationship management客户关系管理2.enterprise resource planning企业资源计划3. a comprehensive eCRM system综合电子客户关系管理系统4.department of customer service客户服务部门5.web technology 网络技术6.customized software按客户要求开发的软件,定制软件7.exchange customer information交换客户信息8.vertical market 纵向市场9.feedback from the customer客户的反馈10.business practices 商务运作,商务活动11.obtain and retain customers赢得和留住客户12.sales-force automation 销售队伍自动化13.customize these packages定制这些软件包14.browser-equipped phones and laptops配有浏览器的电话和手提电脑15.traditional contact management传统的客户接触管理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Failure Reasoning in Multiple-Strategy Proof PlanningAndreas Meier Erica MelisGerman Research Center for Artificial Intelligence(DFKI)Saarbr¨u cken,Germanyameier,melis@dfki.de,http://www.ags.uni-sb.de/{~ameier|~melis}AbstractThe control in multi-strategy proof planning goes beyond the control in other automated theorem proving approaches:not only the selection of the inference andthe facts for the next step can be guided by domain-specific heuristics but also thecombination of proof plan refinements such as step introduction,backtracking,andvariable instantiation.This enables a dynamic traversal of the search space and a dynamic construc-tion of the proof plan guided by mathematically motivated heuristics.This paperdiscusses how proof planning with multiple strategies exploits failures to guide thesubsequent proof plan manipulations and refinements.1IntroductionEach automated theorem prover comprises some heuristics that select the next refine-ment step of the proof construction.Typically,e.g.,in provers based on the resolution principle,the control is based on“local”general-purpose heuristics that reason on the current proof facts and the possible inferences.As result,the control decisions are re-stricted to the selection of the inference rule and the premises for the next step in the proof derivation.Other decisions are often hard-coded into the system and not subject to reasoning about control.In particular,in search procedures involving backtrack-ing(e.g.,Artificial Intelligence planning)the combination of the different refinements step introduction and backtracking is typically hard-coded in some form,for instance, backtrack if and only if no step can be applied.Proof planning is an approach to mathematical theorem proving in which the proof of a theorem is planned at the abstract level of so-called methods.The knowledge-based proof planning developed in theΩmega group employs declarative meta-reasoning to guide the search[13].Mathematically motivated heuristics cannot only reason about the current goals and assumptions but also about the proof planning history and the planning context.Moreover,inΩmega’s automated multiple-strategy proof planner Multi the choice points that are subject to heuristic guidance are not restricted to the next goal and the next method.Rather,also the decisions on which strategy to choose can be guided,where strategies are independent proof plan operations,and different strategies can realize,for instance,different kinds of backtracking and different kinds of variable instantiation.1In certain situations,a step does not result in the expected progress or a refinement does not apply as it usually would.If a pattern of such failures and how to overcome and exploit them can be discovered,then the occurrence of the failure may hold the key to discover a solution proof plan for the problem at hand.In this paper,we shall describe two meta-reasoning patterns that productively use failures toflexibly guide subsequent proof plan manipulations and refinements.We explain how the meta-reasoning patterns are realized in Multi and how they are applied to proof plan -δ-problems.The paper is structured as follows.First,we introduce the basics of proof planning with multiple strategies in section2.Afterwards,we explain the application of Multi to tackle -δ-problems.Section4investigates the failure reasoning patterns and their application for -δ-problems.We conclude with the discussion of results and related work in section5.2Proof Planning with Multiple StrategiesProof planning was originally conceived as an extension of tactical theorem proving to implement automated theorem proving at the abstract level of tactics.Bundy’s key idea in[3]is to augment individual tactics with pre-and postconditions.This results in planning operators,so-called methods.In theΩmega[6]system proof planning is enriched by incorporating knowledge into the planning process[13]and the introduction of the additional hierarchical level of strategies[12].Domain-specific knowledge can be encoded in methods and control rules.Methods can encode not only general proving steps but also steps particular to a mathematical domain.Heuristics guiding the search can be encoded in control rules.The control rules are evaluated at choice points in the planning process and can express meta-level reasoning about the current proof planning state as well as about the entire history of the proof planning process and the proof context.Further domain-specific knowledge can be contained in external systems that are incorporated into the proof planning process. For proof planning -δ-problems,which we shall discuss,in particular,the constraint solver C o SIE for equations and inequalities over the reals is important.Proof construction may require construction of mathematical objects,i.e.,instan-tiation of existentially quantified variables by witness terms.In proof planning,meta-variables are used as place holders for witness terms.When proof planning -δ-problems, equations and inequalities with meta-variables are passed to C o SIE,which checks the (in)consistency of the constraints and collects consistent constraints in a constraint store. Later,it tries to compute instantiations for the meta-variables that satisfy the collected constraints[15].The simplest version of proof planning searches at the level of methods,i.e.,it searches for applicable methods and applies the instantiated methods,which are called actions,until all goals are closed.Thefinal sequence of actions forms a solution plan. InΩmega’s previous simple proof planner further plan refinement and modification operations such as backtracking and meta-variable instantiation were hard-coded with the introduction of actions:backtrack one action in the plan if and only if no method is applicable and instantiate meta-variables only at the end if all goals are closed.Case-studies revealed that the somewhat inflexible proof planning fails on problems2for which moreflexibility is needed[12].1This motivated the development of proof planning with multiple strategies,which decomposes the previously monolithic proof planning process and replaces it by separated strategies,which are instances of param-eterized algorithms for different proof plan refinements and modifications.We implemented proof planning with multiple strategies in the automated proof planner Multi.Among others,Multi employs algorithms for action introduction, meta-variable instantiation,and backtracking.The algorithm for action introduction has parameters for a set of methods and a set of control rules.When Multi executes a strategy of this algorithm,the algorithm introduces only actions that use the methods specified in the strategy.The choices during the action computation and selection are guided by the control rules specified by the strategy.The algorithms for meta-variable instantiation and backtracking have one parameter,respectively.The parameter of the instantiation algorithm is a function that determines how the instantiation for a meta-variable is computed.If Multi applies an instantiation strategy with respect to a meta-variable mv,and if the computation function of the strategy yields a term t for mv, then the instantiation algorithm substitutes mv by t in the proof plan.The parameter of the backtrack algorithm is a function that computes a set of refinement steps of other algorithms that have to be deleted.When Multi applies a backtrack strategy,then the algorithm removes all refinement steps that are computed by the function parameter of the strategy as well as all steps that depend from these steps.Sample strategies of all three algorithms are discussed in the subsequent sections.In Multi no combination of strategies is pre-defined or hard-coded in a control cycle. Rather,Multi’s blackboard architecture enables theflexible cooperation of independent strategies guided by meta-reasoning in strategic control rules.In a nutshell,Multi operates according to the following cycle:Job Offers Strategies whose condition is true wrt.the current proof plan post their applicability in form of so-called job offers onto the blackboard.Guidance The strategic control rules are evaluated to order the job offers. Invocation The strategy who posed the highest ranked job offer is invoked. Execution The algorithm of the invoked strategy is executed with respect to the pa-rameter instantiation specified by the strategy.Note that the execution of an action introduction strategy can be interrupted(i.e., interruption is a choice point in the action introduction algorithm).In this case,Multi canfirst apply some other strategies and then re-invoke the interrupted strategy execu-tion.Failures in the action introduction algorithm,i.e.,a goal for which no method is applicable,are also interrupts.A detailed,technical description of the Multi system can be found in[9].3Proof Planning -δ-problems-δ-problems make statements about the limit,the continuity,and the derivative of a function f at a point a.The standard definitions of limit,continuity,and derivative comprise so-called –δcriterions.For instance,the definitions of limit and continuity are:f=l≡∀ (0<δ∧∀xlimx→a(0< ⇒∃δ(|x−a|<δ⇒|f(x)−f(a)|< )))An example theorem is the Cont-If-Deriv problem that states that,if a function f has a derivative f at point a2,then f is continuous at a.When the definitions of limit and continuity are expanded,then the problem’s assumption is∀ 1(0<δ1∧∀x1x1−a−f |< 1))) and the problem’s theorem is∀ (0<δ∧∀xf(x1)−f(a)2That is,if limx1→aStrategy:SolveInequalityinequality-goalAlgorithmMethodsAskCS ,Solve*-B ,F actorialEstimate ...prove-inequality ,...Table 1:The SolveInequality strategy.Inequality and reduce a goal with formula |b |<e to simpler inequalities in case there is an assumption |a |<e and b =k ∗a +l holds for suitable terms k and l .The resulting simpler goals are |l |<e 2∗mv ,|k |≤mv ,and 0<mv ,where mv is a new meta-variable.As concrete application of ComplexEstimate consider the following situation during the proof planning process for the Cont-If-Deriv problem (see section 4.1).Thereis the goal |f (c x )−f (a )|<c and the assumption |f (mv x 1)−f (a )c x −a−f )+(f ∗c x −f ∗a )(i.e.,k =c x −a and l =f ∗c x −f ∗a in this linear combination of f (c x )−f (a )wrt.f (mv x 1)−f (a )2,mv 1<ct |<t to the three subgoals 0<mv F ,mv F <|t |,and |t |<t ∗mv F ,where mv F is a new meta-variable.A concrete application of F actorialEstimate is discussed in section 4.2.So,SolveInequality successively produces simpler inequalities until it reaches inequal-ities that are accepted by C o SIE .This approach –handle with C o SIE or simplify –is guided by the control rule prove-inequality .This rule first checks whether the current goal is an inequality.If this is the case,it prefers the methods of SolveInequal-ity in the desired order:TellCS ,AskCS ,Simplify ,Solve*-B ,ComplexEstimate ,F actorialEstimate ...To derive -δ-proofs Multi employs also the domain-independent action introduc-tion strategies NormalizeGoal and UnwrapAss .Both strategies contain general methods for the decomposition of logic connectives and quantifiers.Whereas applications of Nor-malizeGoal decompose goals to derive new goals,applications of UnwrapAss derive new assumptions by the decomposition of given assumptions.In order to instantiate meta-variables that occur in constraints collected by C o SIE ,Multi employs two instantiation strategies,InstIfDetermined and ComputeInstFromCS .The first is applicable only if C o SIE states that a meta-variable is already determined by the constraints collected so far.Then,the computation function connects to C o SIE and receives this instantiation for the puteInstFromCS is applicable to allmeta-variables for which constraints are stored in C o SIE.The computation function of this strategy requests from C o SIE to compute an instantiation for a meta-variable that is consistent with all constraints collected so far.Application and Cooperation of the StrategiesWhen proof planning an -δ-problem Multi typically proceeds as follows:First, it applies NormalizeGoal to decompose the initial goal.Afterwards,it applies Solve-Inequality to the resulting inequality goals.Some methods of SolveInequality can only be applied when suitable assumptions are available(e.g.,ComplexEstimate).In case SolveInequality detects promising subformulas of given assumptions,it interrupts(guided by one of its control rules)such that Multi can apply UnwrapAss to derive the promising subformula.Afterwards,SolveInequality can proceed and use the new assumption.The invocation of ComputeInstFromCS is delayed by a strategic control rule until all goals are closed.This delay of the computation of instantiations for meta-variables is sensible since the instantiations should not be computed before all constraints are collected,i.e.,only after all goals are closed.However,if the current constraints already determine a meta-variable,then a further delay of the corresponding instantiation is not necessary.Rather,immediate instantiations of determined meta-variables can simplify a problem[12].To allow for theflexible instantiation of determined meta-variables SolveInequality can interrupt and cooperate with the strategy InstIfDetermined.When SolveInequality runs into a deadend,i.e.,itfinds a goal to which no method is applicable,then Multi employs the backtrack strategy BackTrackActionToGoal,which removes the action that introduced the goal.4Failure Reasoning for -δ-problems and BeyondThe typical application and cooperation of strategies to accomplish -δ-proofs described at the end of the previous section is Multi’s“default”behavior.However,since Multi does not pre-define an order or combination of strategies,strategic control rules can be added which override the default behavior.One of the applications of control rules is failure reasoning:Control rules can analyze occurring failures and draw consequences for particular proof plan refinements and modifications.4.1Guiding the Introduction of Case-SplitsA well-known technique from mathematics to deal with complex problems is to split the problem into cases and to solve the cases separately.But how should the Eureka step case-split be controlled?That is,when should a case-split be introduced and which cases should be considered?We found a pattern that describes the need for a case-split,which can be spotted by failure reasoning.The failure and its solution exhibit the following general pattern:There is a main goal,which can be solved introducing some side goals,which we also call conditions.Afterwards,one of the conditions cannot be solved.In this situation,the partial success,i.e.,the solution of the main goal,gives rise to consider patching the proof attempt by introducing a case-split on the failing condition.Then,the main goal has to be proved several times under different case-split6hypotheses.As example for a -δ-problem that needs such meta-reasoning consider the Cont-If-Deriv problem introduced in section 3.When tackling this problem Multi starts as it is usual for -δ-proofs.It decomposes the theorem with the strategy NormalizeGoal and derives the inequality goals0<mv δand |f (c x )−f (a )|<c(where mv δis a new meta-variable and c x and c are new constants)to which it applies SolveInequality .SolveInequality passes the first goal with an application of the method TellCS as constraint to C o SIE but fails to reduce the second goal.Since in the initial assumption it detects |f (x 1)−f (a )mv x 1−a −f |<mv 1and the three new goals 0<mv 1,|mv x 1−a |<c δ1,and |mv x 1−a |>0(where mv x 1and mv 1are new meta-variables and c δ1is a new constant).With the new assumption SolveInequality closes the main goal |f (c x )−f (a )|<c in several steps (among these steps is the application of ComplexEstimate discussed in section 3as well as applications of TellCS to pass resulting simple inequality con-straints to C o SIE ).In between,SolveInequality interrupts once and switches to InstIfDe-termined ,which introduces the binding mv x 1→c x .Then,it tackles the new goals from the application of UnwrapAss .It succeeds in solving 0<mv 1and |mv x 1−a |<c δ1but fails to solve |mv x 1−a |>0,which meanwhile became |c x −a |>0wrt.the introduced binding mv x 1→c x .In this situation,Multi can solve the main goal with an assumption that has some conditions.When Multi uses the assumption,then it introduces the conditions as new ter,it fails to prove one of these side goals.The meta-reasoning patternIFfailing condition while main goal is solved THEN introduce case-split on failing conditionanalyzes the failure and suggests its “repair”.Technically,the “repair”is realized in Multi by two control rules,one strategic control rule and one method-level control rule in the strategy SolveInequality ,which guide suitable backtracking and the introduction of the case-split.This works as follows:if SolveInequality fails to prove a condition of an assumption that was used to prove the main goal,then the strategic control rule triggers the application of a backtrack strategy that backtracks all actions following the introduction of the failing condition.In our example,this strategy backtracks the application of UnwrapAss and all actions that depend on it such that |f (c x )−f (a )|<c becomes again a goal.When Multi re-invokes SolveInequality after the application of this backtrack strategy,then the con-trol rule in SolveInequality fires and suggests the application of the method CaseSplit for the failing condition and its negation.Afterwards,SolveInequality has to prove |f (c x )−f (a )|<c twice:once under hypothesis |c x −a |>0and once under hypothesis7¬(|c x−a|>0).For thefirst case it proceeds as already described above.The failing condition|c x−a|>0now follows from the hypothesis of the case.The second case is solved differently by SolveInequality.First,it simplifies the hypothesis¬(|c x−a|>0) to c x=a.Afterwards,it uses this equation to simplify the goal|f(c x)−f(a)|<c to 0<c ,which follows from an introduced hypothesis.Cont-If-Lim=f and Lim-If-Both-Sides-Lim are two other well-known problems from the limit domain that require this kind of failure reasoning.Cont-If-Lim=f states that a function f is continuous at point a if the limit at point a is f(a).The Lim-If-Both-Sides-Lim problem states that a function f has a limit l at point a,if both the right-hand and the left-hand limit of f at a are l.More such problems can be constructed.In other mathematical domains the same pattern occurs and can lead to a case-split introduction(see discussion of related work in section5).Whereas the failure reasoning pattern is domain independent,the actual case-split may depend on the mathematical domain.So far,we employ a general case-split into the cases cond and¬cond.Examples for possible domain dependent case-splits are:a>0,a<0,a=0n=1,n>1x∈S,x∈S4.2Meta-Reasoning for Repair of Constraint HandlingMulti provides the freedom to backtrack any actions in the proof plan under construc-tion.This allows for backtracking that targets the application of certain desirable steps rather than the traversal of the search space.In the following,we discuss a pattern in which such a backtracking is suggested by meta-reasoning on a highly desirable but blocked strategy.As example problem consider the problem LIM-DIV,which states that the limit of:the function1c∀ (0<δ∧∀x x−1c x−1c x∗c|<c .An application of F actorialEstimate to this goal results in the three goals0<mv f,|c x∗c|>mv f,and|c−c x|<mv f∗c (with the new meta-variable mv f).SolveInequality closes these three goals with TellCS.This results in the proof plan tree for|1c|<c infigure1,where[|c x−c|<mvδ]is an assumption that is created during the application of NormalizeGoal but is not used so far.Now all goals are closed and in the default behavior C o SIE is supposed to provide instantiations for the meta-variables mvδand mv f.That is,the strategy ComputeInst-FromCS,which asks C o SIE to compute the instantiations,becomes a highly desirable strategy.However,C o SIE fails to compute instantiations in this situation and Com-puteInstFromCS does not succeed.What is the problem?So far,C o SIE collected the constraints8[|c x−c|<mvδ]|c x∗c|>mv f TellCS|c−c x|1c|<c SimplifyFigure1:Initial proof plan tree for|1c|<c |c x−c|c has to be smallerthan mv f,which has to be smaller than|c x∗c|.These constraints are consistent,but a solution for mv f exists only,if|c x−c|2,mvδ≤c ∗mv f|0|<c ∗mv f mvδ≤c ∗mv f|−1|≤mv TellCS|c−c x|<mv f∗c ComplexEstimate Figure2:Refined proof plan tree for|c−c x|<mv f∗c Since C o SIE also fails on this extended constraint set the strategic control rule backtrack-to-unblock-cosie guides the backtracking of the application of TellCS that closes|c x∗c|>mv f(seefigure1).Again,SolveInequality reduces the re-opened goal with ComplexEstimate.This action makes again use of the assumption|c x−c|<mvδand reduces|c x∗c|>mv f to the new goals|c∗c|≥mv f∗2,mvδ≤mv f|c∗c|≥mv f∗2TellCS mv TellCS0<mvTellCS 2>0mvδ>0mvδ≤c ∗mv f2,and mvδ→min(c ∗c22∗(c+1)).Thefinal proof plan tree for|1c|<c results from replacing|c x∗c|>mv f and |c−c x|<mv f∗c in the tree infigure1by the proof plan trees infigure2andfigure3, respectively.All -δ-problems in which subgoals with fractions occur need to repair the constraint reasoning,for instance,lim x→21x+1=1|x|=0,limx→1x2−x+12,deriv(f,a)=f ⇒deriv(α∗f,a)=α∗f ,deriv(f,a)=f ∧deriv(g,a)=g ⇒deriv(f+g,a)=f +g .In other domains the same meta-reasoning to overcome blocked instantiations of constraint solvers is applicable.105Conclusion and Related WorkWe described two situations in which the multiple-strategy proof planner Multi pro-ductively exploits failures to guide particular,mathematically motivated modifications. The described failure reasoning and the repair modifications are possible since Multi does not enforce a pre-defined systematic backtracking(e.g.,backtrack always the last step).Rather,when a failure occurs,then strategic control rules can analyze the failure and can dynamically guide promising refinements and modifications.Further meta-reasoning patterns in Multi are discussed in[10]and[8].All the patterns are generally applicable rather than over-specific.Related WorkFailure reasoning in the proof planner CL a M is closely related to the introduction of case-splits in Multi.In[7],Bundy and Ireland describe critics as a means to patch failed proof attempts in CL a M by exploiting information on failures.The motivation for the introduction of critics is similar to our motivation for failure reasoning:failures in the proof planning process often hold the key to discover a solution proof plan.Critics in CL a M extend the hierarchy of inference rules,tactics,and methods.A critic is associated with one method–mostly with the wave method–and captures patchable exceptions to the application of this method.Critics are expressed in terms of preconditions and patches.The preconditions analyze the reasons why the method has failed to apply.The patch suggests a change to the proof plan.The situations that trigger case-splits in CL a M and Multi are very similar:unprov-able premises of conditional facts from the context.However,the critics mechanism in CL a M and failure reasoning in Multi considerably differ not only in minor technical is-sues but also in their conceptual design.Critics are a method-like entity directly bound to failing preconditions of a particular method.Moreover,part of a critic is a patch of the failure,which is a special procedure that changes the proof plan.In contrast, failure reasoning in Multi is conducted by declarative and separate control rules.These control rules are not associated with a particular method but rather test for particular situations that can occur during the proof planning process(independent of the strategy or method that caused the situation).The control rules can reason about the current proof plan and about other information such as the history.The patch of a failure is not implemented into special procedures but is carried out by methods and strategies whose application is suggested by the control rules.It is a common criticism of proof planning that it relies on over-specific knowledge (e.g.,see[4]).The introduction of case-splits in CL a M and Multi is based on the same meta-reasoning pattern(although technically realized quite differently),which is applied to different domains(problems provable by induction vs.limit problems).This observation is encouraging that this meta-reasoning pattern is general and promising also for other domains.So far,we applied the meta-reasoning pattern to -δ-problems only.Other problem classes tackled withΩmega’s proof planning(e.g.,see[11])did not require such failure reasoning.However,if necessary,the control rules implementing the meta-reasoning pattern could be easily extended to guide case-splits for problems from other domains as well.Typically,backtracking methods return to prior points in the spanned search tree and11thereby often erase meaningful progress towards a solution.As opposed thereto,Multi enables the goal-directed backtracking of selected steps(and all steps that explicitly depend on them).This can result in a new proof plan not in the search tree traversed so far.In[5]Ginsberg describes a backtracking approach for the solution of constraint satisfaction problems that is similar to Multi’s.His approach also enables the deletion of selected steps without removing all steps introduced after these steps(provided that these other steps do not explicitly depend on the steps selected for deletion).He uses the term“dynamic”backtracking because of the dynamic way in which the search is structured.References[1]R.G.Bartle and D.R.Sherbert.Introduction to Real Analysis.John Wiley&Sons,New York,1982.[2]W.W.Bledsoe.Challenge Problems in Elementary Analysis.Journal of AutomatedReasoning,6:341–359,1990.[3]A.Bundy.The Use of Explicit Plans to Guide Inductive Proofs.In Proceedings ofCADE–9,volume310of LNCS,pages111–120.Springer,1988.[4]A.Bundy.A Critique of Proof Planning.In Festschrift in Honour of RobortKowalski.2002.[5]M.L.Ginsberg.Dynamic Backtracking.Journal of Artificial Intelligence Research,1:25—46,1993.[6]TheΩmega Group.Proof Development with OMEGA.In Proceedings of CADE–18,number2392in LNAI,pages144–149.Springer,2002.[7]A.Ireland and A.Bundy.Productive Use of Failure in Inductive Proof.Journal ofAutomated Reasoning,16(1-2):79–111,1996.[8]A.Meier.Multi–Proof Planning with Multiple Strategies.PhD thesis,FachbereichInformatik,Universit¨a t des Saarlandes,Saarbr¨u cken,2004.[9]A.Meier.The Proof Planners ofΩmega:A Technical Description.Seki ReportSR-04-XY,FR Informatik,Saarland University,Saarbr¨u cken,Germany,2004. [10]A.Meier and E.Melis.Proof Planning Limit Problems with Multiple Strategies.Seki Report SR-04-YX,FR Informatik,Saarland University,Saarbr¨u cken,Ger-many,2004.[11]A.Meier,M.Pollet,and paring approaches to the exploration of thedomain of residue classes.Journal of Symbolic Computation,Special Issue on the Integration of Automated Reasoning and Computer Algebra Systems,34(4):287–306, 2002.[12]E.Melis and A.Meier.Proof Planning with Multiple Strategies.In CL-2000,volume1861of LNAI,pages644–659.Springer,2000.12。
