疲劳曲线计算
03_疲劳强度计算

m
1 N0
n
m i
n
i
i 1
Sca
1 e
S
2. 当量循环次数Ne计算法:
取不稳定循环诸变应力中数值最大的应力或循环次
数最多的应力(对疲劳损伤影响最大的那个应力),
作为计算基准应力,而将诸变应力i所对应的循环次
数ni转化为当量循环次数Ne,使得应力循环Ne次后,
对材料所造成的损伤与诸应力i各自循环ni次对材料所
lim m ax ae m e s
按静应力计算:
M m e, ae M m, a
Sca
lim
m ax max
s m a
S
N
N
H
工作应力分布在: OAGH :疲劳强度计算 HGC :静强度计算
3.变应力的最小应力保持不变,即 min C(如受轴向变载荷的紧螺栓)
4)计算安全系数:Sca
lim
m ax max
S
零件的极限应力
lim m ax m e ae
零件的极限应力点的确定:
按零件的载荷变化规律不同分:
• 变应力的应力比保持不变,即:r = C • 变应力的平均应力保持不变,即:m = C • 变应力的最小应力保持不变,即:min = C
M m e, ae M m, a
1)如果此线与AG线交于M( me ,ae ),则有:
m e m
,
ae
1
m
K
lim m ax ae m e 1
K
K
m
Sca
lim
m ax max
1
K
K m m a
S
2)如果此线与GC线交于N( me ,ae ),则有:
钢筋混凝土梁的疲劳性能计算方法

钢筋混凝土梁的疲劳性能计算方法一、引言钢筋混凝土结构是目前世界上最为广泛应用的一种结构形式,其优点主要体现在具有较高的强度和刚度、耐久性好、施工方便、经济实用等方面。
然而,在长期使用过程中,由于受到外界环境的影响和内部因素的作用,结构构件会出现疲劳现象,从而降低其使用寿命和安全性能。
因此,研究钢筋混凝土结构的疲劳性能,对于保证结构的安全性和经济性具有重要意义。
本文旨在介绍钢筋混凝土梁的疲劳性能计算方法,包括梁的疲劳破坏形式、影响因素、计算方法等内容。
二、梁的疲劳破坏形式梁的疲劳破坏形式主要有两种:裂纹扩展疲劳和弯曲疲劳。
1. 裂纹扩展疲劳在受到交变载荷作用下,钢筋混凝土梁中的裂纹会在应力循环作用下逐渐扩展,最终导致梁的破坏。
裂纹扩展疲劳是梁疲劳破坏的主要形式,其破坏机理是由于应力循环作用下,梁内部的裂纹逐渐扩展,最终导致梁的破坏。
2. 弯曲疲劳在受到交变载荷作用下,钢筋混凝土梁会发生弯曲变形,当弯曲应力超过梁的弯曲极限时,会导致梁的破坏。
弯曲疲劳是梁疲劳破坏的另一种形式,其破坏机理是由于交变载荷作用下,梁内部的应力逐渐增大,最终导致梁的破坏。
三、影响因素梁的疲劳性能受到多种因素的影响,主要包括以下几个方面:1. 周期数:梁的疲劳寿命与循环载荷的周期数有关,周期数越大,梁的疲劳寿命越长。
2. 应力幅值:梁的疲劳寿命与循环载荷的应力幅值有关,应力幅值越大,梁的疲劳寿命越短。
3. 载荷类型:不同类型的载荷对梁的疲劳寿命具有不同的影响,例如,交变载荷对梁的疲劳寿命的影响大于单向载荷。
4. 材料性质:材料的强度、韧性、断裂韧度等性质对梁的疲劳寿命具有重要影响。
5. 几何尺寸:梁的几何尺寸对疲劳寿命的影响主要体现在梁的截面尺寸和长度方面,截面尺寸越小、长度越长,梁的疲劳寿命越短。
四、计算方法梁的疲劳寿命计算方法主要有两种:应力范围法和循环应力法。
1. 应力范围法应力范围法是一种常用的疲劳寿命计算方法,其基本原理是根据材料的疲劳曲线,通过计算载荷的应力范围来确定梁的疲劳寿命。
§3-1 材料的疲劳特性.

通过对大量结构断裂事故分析表明,结构内部裂纹和缺陷的存在是 导致低应力断裂的内在原因。
对于高强度材料,一方面是它的强度高(即许用应力高),另一方 面则是它抵抗裂纹扩展的能力要随着强度的增高而下降。因此,用传统 的强度理论计算高强度材料结构的强度问题,就存在一定的危险性。 断裂力学——是研究带有裂纹或带有尖缺口的结构或构件的强度和 变形规律的学科。准确的说,上述裂纹是指宏观裂纹,即用肉眼或低倍 显微镜能看得见的裂纹。工程中常认为裂纹尺寸大于0.1mm,就称为宏 观裂纹。断裂力学建立了构件的裂纹尺寸、工作应力以及材料抵抗裂纹 扩展能力三者之间的定量关系。
z r s
m s rN N s rm N 0 C
s rN s r (N N D )
有限寿命区间内循环次数N与疲劳极限srN的关系为:
s rN s
m N0 r Nr
K Ns r
式中, sr、N0及m的值由材料试验确定。KN寿命系数.
三、等寿命疲劳曲线(极限应力线图)
材料的疲劳特性
不同应力比时材料的疲劳极限也不相同,可用极限应力线图表示。
第三章 机械零件的强度
§3-1 材料的疲劳特性
§3-2 机械零件的疲劳强度计算 §3-3 机械零件的抗断裂强度 §3-4 机械零件的接触强度
材料的疲劳特性
二、 s-N疲劳曲线 疲劳极限:应力循环特性r一定时,应力经 过N次循环而材料不发生疲劳破坏的最大应 力。 r一定时,极限应力与应力循环次数的关系 曲线称为疲劳曲线。
二、 材料的疲劳曲线
材料的疲劳特性
材料的疲劳特性
疲劳曲线
机械零件的疲劳大多发生在s-N曲线的 CD段,可用下式描述:
m s rN N C ( NC N ND ) D点以后的疲劳曲线呈一水平线,代表着 无限寿命区其方程为:
疲劳测试与疲劳曲线

疲劳测试与疲劳曲线导读:1860年,维勒(Wöh l e r)在解决火车轴断裂时,首先提出了疲劳曲线和疲劳极限的概念,所以后人也称该曲线为维勒曲线。
1954年1月10日,B O A C的一架“彗星”在意大利厄尔巴岛上空7800米处解体。
4月8日,B O A C的又一架“彗星”栽入意大利那不勒斯湾,机上21人罹难。
至此,“彗星”全部停飞。
“彗星”频繁陨落,震惊了世界。
当时,英国首相丘吉尔下令,要不惜一切代价搞清事故原因。
为此,英国海军出动舰队,将厄尔巴岛附近海域失事的飞机残骸从上百米深的海底打捞起来,送到英国皇家飞机研究院进行调查。
调查发现,空难死者的肺部有因气体膨胀而引起的裂痕,说明失事前机舱内气压突然减小,使肺内气体急剧膨胀而导致肺部破裂。
而对飞机残骸的研究表明,部分舷窗出现了裂痕,这一发现与尸检结论相吻合。
与此同时,德哈维兰公司对正在生产和已停飞的飞机进行严格检查,试验进行了9000多个小时,飞机蒙皮出现了裂痕,与失事飞机残骸上的裂痕一样。
经过技术人员研究分析,事故是由制造飞机机体结构的金属材料“疲劳”所致。
机械零件在交变压力作用下,经过一段时间后,在局部高应力区形成微小裂纹,再由微小裂纹逐渐扩展以致断裂。
疲劳破坏具有在时间上的突发性、位置上的局部性及对环境和缺陷的敏感性等特点,不易被及时发现。
“彗星”飞机方形舷窗处的蒙皮,在反复增压和减压的冲击下,产生变形、裂纹,最终导致金属疲劳断裂。
作为世界上第一种喷气式客机,“彗星”比其他客机都飞得快,承受的压力自然也大,更容易产生金属疲劳问题。
由此,通过对“彗星”事故的调查,诞生了一门新的学科---“疲劳力学”。
今天咱们就来熟悉和了解一下关于:疲劳曲线及基本疲劳力学性能。
01疲劳曲线和对称循环疲劳曲线(一)疲劳曲线和疲劳极限疲劳曲线:是疲劳应力与疲劳寿命的关系曲线,即S-N曲线,是确定疲劳极限、建立疲劳应力判据的基础。
对于一般具有应变时效的金属材料,如碳钢、球铁等,当循环应力水平降到某一临界值时,低应力段变为水平线段,表明试样可以经无限次应力循环也不发生疲劳断裂,故将对应的应力称为疲劳极限,记为σ-1(对称循环,r=-1)。
第三讲 P-S-N曲线,疲劳统计学
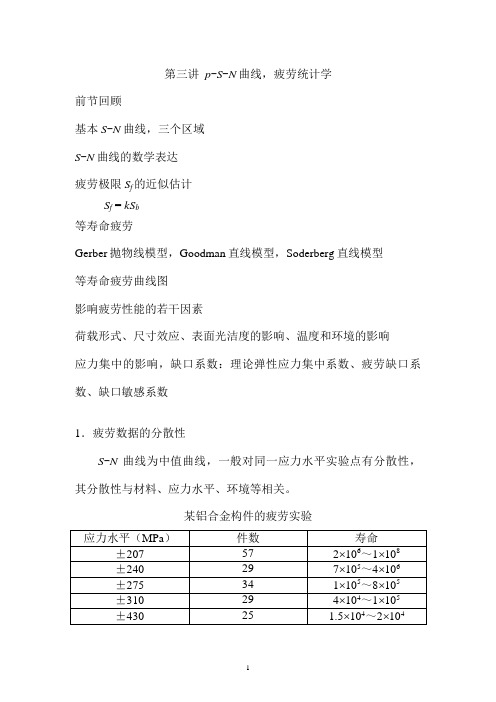
第三讲p-S-N曲线,疲劳统计学前节回顾基本S-N曲线,三个区域S-N曲线的数学表达疲劳极限S f的近似估计S f = kS b等寿命疲劳Gerber抛物线模型,Goodman直线模型,Soderberg直线模型等寿命疲劳曲线图影响疲劳性能的若干因素荷载形式、尺寸效应、表面光洁度的影响、温度和环境的影响应力集中的影响,缺口系数:理论弹性应力集中系数、疲劳缺口系数、缺口敏感系数1.疲劳数据的分散性S-N曲线为中值曲线,一般对同一应力水平实验点有分散性,其分散性与材料、应力水平、环境等相关。
某铝合金构件的疲劳实验应力水平低则寿命 长,分散性也大,在同 样应力水平下,疲劳寿 命可以相差几十到几百 倍。
2.p -S -N 曲线p -S -N 曲线是组成不同成活率p 下的S -N 曲线集,这一曲线集给出了:1)在给定应力水平下失效循环次数N 的分布数据;2)在给定的有限寿命下疲劳强度S 的分布数据;3)无限寿命或N > N L 的疲劳强度-疲劳极限的分布数据。
p -S -N 曲线由成组实验获得。
p -S -N 曲线在有限寿命段(103 < N <106)在双对数坐表系上近似为直线。
3.疲劳寿命与疲劳强度 概率分布之间的关系疲劳破坏是疲劳损伤 逐渐累积的结果,材料中 宏观或微观的不可逆变形 是疲劳损伤的主要形式。
lg NSlg NS疲劳寿命概率分布:在给定疲劳强度下构件的疲劳寿命概率分布形式。
一般可由疲劳实验获得。
疲劳强度概率分布:在给定疲劳寿命下构件的疲劳强度概率分布形式。
设在一疲劳荷载作用下,构件在给定疲劳强度S *下的疲劳寿命N 的概率分布密度为f (n |S *),而在给定疲劳寿命N *下的疲劳强度S 的概率分布密度为g (s |N *),则可以证明ds N s g dn S n f S N )()(***0*⎰⎰=即在给定的疲劳强度S *下 疲劳寿命N 小于或等于N *的 概率与在给定的疲劳寿命N * 下疲劳强度S 小于或等于S * 的概率相等。
材料的疲劳特

减载槽
济性后,采用具有高疲劳强度的材料,并配以适当的热处理和各种
表面强化处理。
适当提高零件的表面质量,特别是提高有应力集中部位的表面加工 质量,必要时表面作适当的防护处理。
尽可能地减少或消除零件表面可能发生的初始裂纹的尺寸,对于延 长零件的疲劳寿命有着比提高材料性能更为显著的作用。
机械零件的抗断裂强度
力点M或N。
相应的疲劳极限应力应是极限应力曲线
上的某一个点所代表的应力(s m ,s a ) 。
计算安全系数及疲劳强度条件为:
Sca
s m ax s max
s m s a sm sa
S
根据零件工作时所受的约束来确定应力可能发生的变化规律,从而决定
以哪一个点来表示极限应力。
机械零件可能发生的典型的应力变化规律有以下三种:
用A'G'C折线表示零件材料的极限应力线图是其中一种近似方法。
A'G'直线的方程为: s 1 s a ss m
CG'直线的方程为:
s a s m s s
σ为试件受循环弯曲应力时的材 料常数,其值由试验及下式决定:
s
2s 1 s 0 s0
对于碳钢,σ≈0.1~0.2,对于合金钢,σ≈0.2~0.3。
s
m rN
N
C ( N C
N
ND)
D点以后的疲劳曲线呈一水平线,代表着
无限寿命区其方程为:
s rN s r (N ND )
由于ND很大,所以在作疲劳试验时,常 规定一个循环次数N0(称为循环基数),用N0
s-N疲劳曲线
及其相对应的疲劳极限σr来近似代表ND和 σr∞,于是有:
s
m rN
N
疲劳强度计算

疲劳强度计算一、变应力作用下机械零件的失效特征1、失效形式:疲劳(破坏)(断裂)——机械零件的断裂事故中,有80%为疲劳断裂。
2、疲劳破坏特征:1)断裂过程:①产生初始裂反(应力较大处);②裂纹尖端在切应力作用下,反复扩展,直至产生疲劳裂纹。
2)断裂面:①光滑区(疲劳发展区);②粗糙区(脆性断裂区)(图2-5)3)无明显塑性变形的脆性突然断裂4)破坏时的应力(疲劳极限)远小于材料的屈服极限。
3、疲劳破坏的机理:是损伤的累笱4、影响因素:除与材料性能有关外,还与γ,应力循环次数N ,应力幅a σ主要影响 当平均应力m σ、γ一定时,a σ越小,N 越少,疲劳强度越高二、材料的疲劳曲线和极限应力图疲劳极限)(N N γλτσ—循环变应力下应力循环N 次后材料不发生疲劳破坏时的最大应力称为材料的疲劳极限疲劳寿命(N )——材料疲劳失效前所经历的应力循环次数N 称为疲劳寿命1、疲劳曲线(N γσ-N 曲线):γ一定时,材料的疲劳极限N γσ与应力循环次数N 之间关系的曲线0N —循环基数 γσ—持久极限1)有限寿命区当N <103(104)——低周循环疲劳——疲劳极限接近于屈服极限,可接静强度计算 )10(1043≥N ——高周循环疲劳,当043)10(10N N ≤≤时,N γσ随N ↑→N σσ↓2)无限寿命区,0N N ≥ γγσσ=N 不随N 增加而变化γσ——持久极限,对称循环为1-σ、1-τ,脉动循环时为0σ、0τ注意:有色金属和高强度合金钢无无限寿命区,如图所示。
3)疲劳曲线方程))10(10(043N N ≤≤C N N m m N =⋅=⋅0γγσσ——常数∴疲劳极限:γγγσσσ⋅==N m N K NN 0 (2-9) m N NN K 0=——寿命系数 几点说明:①0N 硬度≤350HBS 钢,7010=N ,当7010=>N N 时,取7010==N N ,1=N K≥350HBS 钢,70701025,10)25~10(⨯=>⨯=N N N 时,取701025⨯==N N ,1=N K有色金属,(无水平部分),规定当71025⨯>N 时,取701025⨯==N N②m —指数与应力与材料的种类有关。
压力容器疲劳02

4、日本超高压容器设计规则(HPIS-C-103-1989)中的疲劳曲线(1)理论基础Langer公式:1100ln 100a E S σψ-=+-试验:针对三个级别的材料,确定Langer 公式的材料常数,如下表。
适用范围:交变载荷100-1000MPa ; 壁温-50-350℃最佳疲劳曲线:40.540.540.54.52103144.58103993.9210481a f a f a fS N S NS N---=⨯⨯+=⨯⨯+=⨯⨯+设计疲劳曲线:在最佳疲劳曲线基础上考虑安全系数和E 350后求得。
原则上,寿命次数取安全系数15,对应力幅取安全系数1.6。
(2)圆筒的疲劳设计计算 对象:内压圆筒无侧向开孔 a 、交变应力幅按最大剪应力强度理论求得如下(不计自增强残余应力):21322211()()221()1a u e u e u e K S p p p p K Kp p K σσ⎡⎤-+==---+⎢⎥-⎣⎦=--p u ,p e ----上限压力与下限压力,MPa 。
b.内壁平均应力()221Rm u e K p p K θσσ=-+- 平均应力的真实值----实际疲劳寿命计算中所用的平均应力值为:////20,00a m sa sa m s m mm m s a a m s a s mm a s m ifandthenandσσσσσσσσσσσσσσσσσσσσσσσσ+≤≤+≤⇒=⎧>⇒=-⎪+><⇒⎨⎪<⇒=⎩=⇒=c.当量交变应力幅/1aeq m bσσσσ=-d.循环次数根据当量交变应力幅查S-N 曲线,可得设计(许用)循环次数。
注:自增强残余应力和热应力可组合到平均应力中去,但要考虑自增强残余应力在使用中的衰减。
5、影响低周疲劳的因素(1)疲劳曲线是基于标准试件得到的。
标准试样及试验:6-10mm 圆棒,表面磨光,无刻痕、凹槽,夹持端和试件标长段有足够大的圆角过渡;试验是在室温、无腐蚀、辐射等环境下,以及对称循环载荷下进行的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例题3.2 一杆件如图所示,受脉动循环拉力F=0N~3×105 N,r=常数,材料为 40Mn钢,调质处理,200HB~230HB,σB =735MPa, σS =471MPa,圆角精铣加工 (相当于精车),要求应力循环次数不低于5×105 ,求圆角处危险截面的安全 系数Sσ。
解: 2. 求σ-1 和σ0
3.求寿命系数KN
例题3.2 一杆件如图所示,受脉动循环拉力F=0N~3×105 N,r=常数,材料为 40Mn钢,调质处理,200HB~230HB,σB =735MPa, σS =471MPa,圆角精铣加工 (相当于精车),要求应力循环次数不低于5×105 ,求圆角处危险截面的安全 系数Sσ。
知识点:疲劳曲线
疲劳曲线:表示循环次数N与疲劳极限间的关系的曲线。
有限寿命区内:
循环次数N0、疲劳极限σr 则N次循环时疲劳极限 N
例题3.1
已知 45钢的σ-1 =300MPa,N0 =107 ,m=9,用对数坐标绘出该材料的疲劳 曲线图。
解: 在对数坐标上取一点B,其坐标为: lgN0 =lg107 lg σ-1 =lg300
解题思路:
由 r、σmin、σmax 可求σa、σm
通过许用疲劳应力图求解
例题3.2 一杆件如图所示,受脉动循环拉力F=0N~3×105 N,r=常数,材料为 40Mn钢,调质处理,200HB~230HB,σB =735MPa, σS =471MPa,圆角精铣加工 (相当于精车),要求应力循环次数不低于5×105 ,求圆角处危险截面的安全 系数Sσ。
过B做斜率等于-1/9的直线,即为所求
知识点:疲劳极限应力图
σa : 应力幅 σ-1:对称循环疲劳极限 σs: 屈服极限
σm: 平均应力 σ0: 脉动循环疲劳极限 σB:强度极限
许用疲劳极限应力图
KN :寿命系数
(Kσ)D : 综合影响系数 Kσ :应力集中系数 βσ:表面状态系数
试验证明:应力集中、零件尺 寸和表面状态都只对应力幅有 影响。
解: 1. 求σm 和σa
例题3.2 一杆件如图所示,受脉动循环拉力F=0N~3×105 N,r=常数,材料为 40Mn钢,调质处理,200HB~230HB,σB =735MPa, σS =471MPa,圆角精铣加工 (相当于精车),要求应力循环次数不低于5×105 ,求圆角处危险截面的安全 系数Sσ。
r=常数时的安全系数计算简图
例题3.2 一杆件如图所示,受脉动循环拉力F=0N~3×105 N,r=常数,材料为 40Mn钢,调质处理,200HB~230HB,σB =735MPa, σS =471MPa,圆角精铣加工 (相当于精车),要求应力循环次数不低于5×105 ,求圆角处危险截面的安全 系数Sσ。
6. 用图解法求安全系数 (r=常数) 1)计算疲劳强度安全系数:
2)计算屈服强度安全系数: Nhomakorabea解: 4. 求综合应力系数
Kσ :应力集中系数 βσ:表面状态系数
例题3.2 一杆件如图所示,受脉动循环拉力F=0N~3×105 N,r=常数,材料为 40Mn钢,调质处理,200HB~230HB,σB =735MPa, σS =471MPa,圆角精铣加工 (相当于精车),要求应力循环次数不低于5×105 ,求圆角处危险截面的安全 系数Sσ。
