八上第11讲 期中专题一 将军饮马类题型全覆盖
八年级将军饮马问题例题讲解

八年级将军饮马问题例题讲解哎呀,今天咱们聊聊八年级的将军饮马问题,听名字就觉得特别有意思,对吧?咱们先来个开门见山,将军带着他的军队,经过一条河,得给马喝水。
这问题看似简单,但其实里面藏着不少小玄机,真的是个大考验,脑袋瓜得动一动。
想象一下,这将军带着一帮士兵,行军走到河边,嗨,口渴得不行,马儿们更是想喝水。
可是,问题来了,河边的水不深,能让马儿们喝到,但不让它们掉进水里。
将军一边心急如焚,一边得想办法。
怎么让这些马儿在喝水的时候不掉进河里呢?这时候就得用到一些小技巧了。
咱们可以想象一下,马儿们得排队,得一个一个地喝水。
将军心里想着,得控制好马儿的喝水速度,别让它们都挤在一起,这样容易出事。
也许能用一些方法,比如说把马儿们牵得远一些,慢慢地让它们喝,像是在参加比赛一样,嘿嘿,真是有意思的场景。
想想马儿们排成一队,乖乖的,一个个慢慢走过来喝水,真是可爱。
这时候就得算一算了,马儿们得喝多少水,每匹马喝水的速度又有多快。
嘿,可能是三两口就满足了,也可能是急着想喝个痛快,一口气喝个干净。
将军得根据情况来调整策略,真是够麻烦的。
不过,思来想去,最好的办法还是得让马儿们分批来,排着队,井然有序。
然后,咱们再来想象一下,如果马儿们不听话,乱跑,那可就麻烦了。
想象一下将军那个急得直挠头的样子,心里想着:这马儿也太不听话了!要不就得用点小办法,比如说放一块香饽饽在河边,吸引它们过来,嘿嘿,果然,马儿们就乖乖走过来喝水了。
就像小朋友看到喜欢的玩具一样,立马就冲过去了,真是太可爱了。
接着咱们来讨论一下,假设这条河不宽,马儿们很快就能喝到水,那将军得加快速度,不能让马儿们等太久。
想想那画面,马儿们都急得不行,口水都快流下来了,哈哈,真是个搞笑的场景。
将军这时候就得使出浑身解数,调整路线,确保马儿们能尽快喝水。
但是,事情总是没那么简单。
马儿喝水喝得急,可能还会打架,踩到脚,这可就不好了。
所以,将军得一边指挥,一边安抚,真是一场心力交瘁的战斗。
初二数学将军饮马相关题目及解答

这是总纲:【序号一】文章引言- 对“初二数学将军饮马相关题目及解答”进行简单介绍和解释。
【序号二】初步理解将军饮马问题- 对问题进行初步描述,解释将军饮马问题的背景和相关概念。
- 分析将军饮马问题中的关键因素和要点,引导读者初步理解问题。
【序号三】盘点各类将军饮马问题- 总结各类将军饮马问题,包括常见的类型、变种及相关的难点。
- 分析各类问题的特点和难点,并介绍解题的一般思路和方法。
【序号四】深度解析具体的将军饮马问题- 选取一到两个典型的将军饮马问题进行详细分析,展示深度解题的过程和技巧。
- 重点突出解题思路和方法,引导读者掌握解决具体问题的技巧和策略。
【序号五】对将军饮马问题的个人理解和观点- 共享个人对将军饮马问题的理解和感悟,探讨解题过程中的心得和体会。
- 提出对将军饮马问题的个人见解和观点,展示对问题的深刻理解和思考。
【序号六】总结和回顾- 对全文进行总结和回顾,强调将军饮马问题的重要性和解题的技巧。
- 突出对变种问题的解题策略和技巧,鼓励读者深入探索相关问题,提升解题能力。
【序号七】结语- 对全文进行简短的结语,表达对将军饮马问题的重视和对读者的鼓励。
假设最终文章大致如下:序号一:文章引言在初二数学学习中,将军饮马问题一直是一个经典而又充满挑战的题目。
它不仅考验着学生的数学思维和逻辑能力,同时也对解题技巧和方法提出了很高的要求。
在接下来的文章中,我们将对将军饮马问题进行全面的探讨和分析,并共享解题的一般思路和方法。
序号二:初步理解将军饮马问题将军饮马问题是一个著名的逻辑问题,通常以丰富的形式出现在中学数学教科书中。
它涉及到将军与士兵、马与草地之间的复杂关系,要求学生通过数学方法解决实际问题,锻炼逻辑推理和数学建模的能力。
让我们来看一下一个常见的例子。
假设有一名将军带着三十个士兵和三十匹马要过草原。
草原上有三十个不同的点,它们是将军要经过的地方。
将军每次只能带十匹马经过,但他有几个条件:1. 每匹马每次必须有骑手骑着; 2. 每个地点只能经过一次; 3. 带着马过草地时必须带上骑手;问题是,如何保证士兵、马、将军都能安全地过草地?透过这个简单的例子,我们初步了解了将军饮马问题的背景和相关概念。
初二将军饮马练习题及答案

初二将军饮马练习题及答案题目一:将军饮马练习阅读下面的短文,然后根据短文内容回答问题。
春秋时期,楚国的将军薛将军因在战场上立下赫赫战功,受到国王的嘉奖,被封为将军。
薛将军深感自己取得的成就来之不易,为了更好地提升自己的军事才能,他经常利用业余时间练习骑射。
一天,他饮酒之后,心血来潮,决定骑马练习。
他醉醺醺地骑在马背上,手握弓箭,身姿挺拔。
突然,他抬头目视远方的鹰,大声喊道:“马儿,你好生奔放,将你的速度发挥到极致。
”马儿似乎听懂了薛将军的话,使出浑身解数奔驰起来。
薛将军稳稳地坐在马背上,准备放箭。
问题:1. 薛将军为什么经常练习骑射?2. 为什么薛将军喊马儿将速度发挥到极致?3. 薛将军的骑射练习中有哪些亮点?答案:1. 薛将军经常练习骑射是为了提升自己的军事才能。
2. 薛将军喊马儿将速度发挥到极致是为了更好地测试自己的骑射技巧。
3. 薛将军的骑射练习中的亮点包括:饮酒后决定进行练习,以更高难度的状态来挑战自己;喊马儿将速度发挥到极致,考验自己的射击准确性和反应能力。
题目二:将军饮马练习答案解析问题:1. 薛将军为什么经常练习骑射?答案解析:薛将军经常练习骑射是为了更好地提升自己的军事才能。
他深感自己在战场上立下的赫赫战功来之不易,因此希望通过练习骑射来增强自己的战斗力。
2. 为什么薛将军喊马儿将速度发挥到极致?答案解析:薛将军喊马儿将速度发挥到极致是为了更好地测试自己的骑射技巧。
他希望在马儿飞驰的情况下,能够准确地射箭,展现出自己的高超技艺。
3. 薛将军的骑射练习中有哪些亮点?答案解析:薛将军的骑射练习中的亮点包括:a) 饮酒后决定进行练习:饮酒之后,薛将军心血来潮,决定骑马练习。
这展现了他的勇气和自信,也体现了他对自己技艺的自豪感。
b) 喊马儿将速度发挥到极致:薛将军对马儿的速度要求极高,希望它能够发挥出最快的速度。
这要求他自己的反应能力和射击准确性都必须达到非常高的水平。
总结:薛将军通过练习骑射来提升自己的军事才能,展示了他在战场上立下的赫赫战功所带来的成就感。
将军饮马问题例题

将军饮马问题例题
例题:一个将军饮马,有三个酒坛,其中一个酒坛里装着毒酒,另外两个酒坛里装着普通的酒。
这三个酒坛外观相同,将军无法通过外观来判断哪个酒坛是有毒的。
在喝下一杯毒酒后,将军将会立即死亡。
现在将军有一匹马,这匹马可以闻出毒酒,如果马喝下一杯毒酒,它将会在30分钟后死亡。
将军只有30
分钟的时间来确定哪个酒坛里装着毒酒,并且不允许酒坛之间进行任何类型的测量。
解法:将军可以按照以下步骤确定毒酒所在的酒坛:
1. 为了节省时间,将将军的马分成三组,每组10匹马。
标记
这三组马为A、B、C。
2. 让A组的马尝试第一个酒坛,让B组尝试第二个酒坛,C
组尝试第三个酒坛。
3. 让所有的马者都喝下一杯酒。
4. 等待15分钟。
5. 如果A组的马中有马死亡,那么第一个酒坛是有毒的;如
果B组的马中有马死亡,那么第二个酒坛是有毒的;如果C
组的马中有马死亡,那么第三个酒坛是有毒的。
6. 如果在15分钟内没有任何马死亡,那么第一个酒坛是安全的,因此第二个酒坛是有毒的;如果A和B组的马都没有死
亡,那么第三个酒坛是有毒的。
这样,将军可以在30分钟内确定哪个酒坛里装着毒酒。
中考复习:“将军饮马”类题型大全

“将军饮马”类题型大全一.求线段和最值1(一)两定一动型例1:如图,AM⊥EF,BN⊥EF,垂足为M、N,MN=12m,AM=5m,BN=4m, P是EF 上任意一点,则PA+PB的最小值是______m.分析:这是最基本的将军饮马问题,A,B是定点,P是动点,属于两定一动将军饮马型,根据常见的“定点定线作对称”,可作点A关于EF的对称点A’,根据两点之间,线段最短,连接A’B,此时A’P+PB即为A’B,最短.而要求A’B,则需要构造直角三角形,利用勾股定理解决.解答:作点A关于EF的对称点A’,过点A’作A’C⊥BN的延长线于C.易知A’M=AM=NC=5m,BC=9m,A’C=MN=12m,在Rt△A’BC中,A’B=15m,即PA+PB的最小值是15m.变式:如图,在边长为2的正三角形ABC中,E,F,G为各边中点,P为线段EF上一动点,则△BPG周长的最小值为_________.分析:考虑到BG为定值是1,则△BPG的周长最小转化为求BP+PG的最小值,又是两定一动的将军饮马型,考虑作点G关于EF的对称点,这里有些同学可能看不出来到底是哪个点,我们不妨连接AG,则AG⊥BC,再连接EG,根据“直角三角形斜边中线等于斜边的一半”,可得AE=EG,则点A就是点G关于EF的对称点.最后计算周长时,别忘了加上BG的长度.解答:连接AG,易知PG=PA,BP+PG=BP+PA,当B,P,A三点共线时,BP+PG=BA,此时最短,BA=2,BG=1,即△BPG周长最短为3.2(二)一定两动型例2:如图,在△ABC中,AB=AC=5,D为BC中点,AD=5,P为AD上任意一点,E 为AC上任意一点,求PC+PE的最小值.分析:这里的点C是定点,P,E是动点,属于一定两动的将军饮马模型,由于△ABC 是等腰三角形,AD是BC中线,则AD垂直平分BC,点C关于AD的对称点是点B,PC+PE=PB+PE,显然当B,P,E三点共线时,BE更短.但此时还不是最短,根据“垂线段最短” 只有当BE⊥AC时,BE最短.求BE时,用面积法即可.解答:作BE⊥AC交于点E,交AD于点P,易知AD⊥BC,BD=3,BC=6,则AD·BC=BE·AC,4×6=BE·5,BE=4.8变式:如图,BD平分∠ABC,E,F分别为线段BC,BD上的动点,AB=8,△ABC的周长为20,求EF+CF的最小值________.分析:这里的点C是定点,F,E是动点,属于一定两动的将军饮马模型,我们习惯于“定点定线作对称”,但这题这样做,会出现问题.因为点C的对称点C’必然在AB上,但由于BC长度未知,BC’长度也未知,则C’相对的也是不确定点,因此我们这里可以尝试作动点E关于BD的对称点.解答:如图,作点E关于BD的对称点E’,连接E’F,则EF+CF=E’F+CF,当E’,F,C三点共线时,E’F+CF=E’C,此时较短.过点C作CE’’⊥AB于E’’,当点E’ 与点E’’重合时,E’’C最短,E’’C为AB边上的高,E’’C=5.(三)两定两动型例3:如图,∠AOB=30°,OC=5,OD=12,点E,F分别是射线OA,OB上的动点,求CF+EF+DE的最小值.分析:这里的点C,点D是定点,F,E是动点,属于两定两动的将军饮马模型,依旧可以用“定点定线作对称”来考虑.作点C关于OB的对称点,点D关于OA的对称点.解答:作点C关于OB的对称点C’,点D关于OA的对称点D’,连接C’D’. CF+EF+DE=C’F+ EF+D’E,当C’,F, E,D’四点共线时,CF+EF+DE=C’D’最短.易知∠D’OC’=90°,OD’=12,OC’=5,C’D’=13,CF+EF+DE最小值为13.变式:(原创题)如图,斯诺克比赛桌面AB宽1.78m,白球E距AD边0.22m,距CD 边1.4m,有一颗红球F紧贴BC边,且距离CD边0.1m,若要使白球E经过边AD,DC,两次反弹击中红球F,求白球E运动路线的总长度.分析:本题中,点E和点F是定点,两次反弹的点虽然未知,但我们可以根据前几题的经验作出,即分别作点E关于AD边的对称点E’,作点F关于CD边的对称点F’,即可画出白球E的运动路线,化归为两定两动将军饮马型.解答:作点E关于AD边的对称点E’,作点F关于CD边的对称点F’,连接E’F’,交AD于点G,交CD于点H,则运动路线长为EG+GH+HF长度之和,即E’F’长,延长E’E交BC于N,交AD于M,易知E’M=EM=0.22m,E’N=1.78+0.22=2m,NF’=NC+CF’=1.4+0.1=1.5m,则Rt△E’NF’中,E’F’=2.5m,即白球运动路线的总长度为2.5m.小结:以上求线段和最值问题,几乎都可以归结为“两定一动”“一定两动”“两定两动”类的将军饮马型问题,基本方法还是“定点定线作对称”,利用“两点之间线段最短”“垂线段最短”的2条重要性质,将线段和转化为直角三角形的斜边,或者一边上的高,借助勾股定理,或者面积法来求解.当然,有时候,我们也需学会灵活变通,定点对称行不通时,尝试作动点对称.(二)求角度例1:P为∠AOB内一定点,M,N分别为射线OA,OB上一点,当△PMN周长最小时,∠MPN=80°.(1)∠AOB=_____°(2)求证:OP平分∠MPN分析:这又是一定两动型将军饮马问题,我们应该先将M,N的位置找到,再来思考∠AOB 的度数,显然作点P关于OA的对称点P’,关于OB的对称点P’’,连接P’P’’,其与OA交点即为M,OB交点即为N,如下图,易知∠DPC与∠AOB互补,则求出∠DPC的度数即可.解答:(1)法1:如图,∠1+∠2=100°,∠1=∠P’+∠3=2∠3,∠2=∠P’’+∠4=2∠4,则∠3+∠4=50°,∠DPC=130°,∠AOB=50°.再分析:考虑到第二小问要证明OP平分∠MPN,我们就连接OP,则要证∠5=∠6,显然很困难,这时候,考虑到对称性,我们再连接OP’,OP’’,则∠5=∠7,∠6=∠8,问题迎刃而解.解答:(1)法2:易知OP’=OP’’,∠7+∠8=∠5+∠6=80°,∠P’OP’’=100°,由对称性知,∠9=∠11,∠10=∠12,∠AOB=∠9+∠10=50°(2)由OP’=OP’’,∠P’OP’’=100°知,∠7=∠8=40°,∠5=∠6=40°,OP平分∠MPN.变式:如图,在五边形ABCDE中,∠BAE=136°,∠B=∠E=90°,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为________.分析:这又是典型的一定两动型将军饮马问题,必然是作A点关于BC、DE的对称点A′、A″,连接A′A″,与BC、DE的交点即为△AMN周长最小时M、N的位置.解答:如图,∵∠BAE=136°,∴∠MA′A+∠NA″A=44°由对称性知,∠MAA′=∠MA′A,∠NAA″=∠NA″A,∠AMN+∠ANM=2∠MA′A+2∠NA″A=88°思考题:1.(2017·安顺)如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为_______.2.(2017·安徽改编)如图,在矩形ABCD中,AB=4,AD=3.P为矩形ABCD内一点,若矩形ABCD面积为△PAB面积的4倍,则点P到A,B两点距离之和PA+PB 的最小值为________.。
【中考数学】最全“将军饮马”类问题(类型大全+分类汇编)总复习
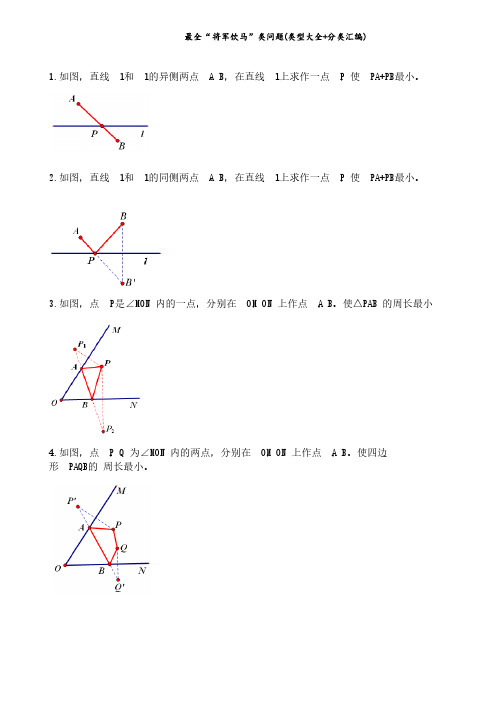
最全“将军饮马”类问题(类型大全+分类汇编)1.1.如图,直线如图,直线如图,直线 l l 和 l 的异侧两点的异侧两点的异侧两点 A A 、B ,在直线,在直线 l l 上求作一点上求作一点上求作一点 P P ,使,使,使 PA+PB PA+PB 最小。
最小。
最小。
2.2.如图,直线如图,直线如图,直线 l l 和 l 的同侧两点的同侧两点的同侧两点 A A 、B ,在直线,在直线 l l 上求作一点上求作一点上求作一点 P P ,使,使,使 PA+PB PA+PB 最小。
最小。
最小。
3.3.如图,点如图,点如图,点 P P 是∠是∠是∠MON MON 内的一点,分别在内的一点,分别在 OM OM ,ON 上作点上作点 A A ,B 。
使△。
使△PAB PAB 的周长最小的周长最小4.4.如图,点如图,点如图,点 P P ,Q 为∠为∠MON MON 内的两点,分别在内的两点,分别在 OM OM ,ON 上作点上作点 A A ,B 。
使四边形 PAQB 的 周长最小。
周长最小。
5.5.如图,点如图,点如图,点 A A 是∠是∠是∠MON MON 外的一点,在射线外的一点,在射线 OM OM 上作点上作点上作点 P P ,使,使,使 PA PA 与点与点与点 P P 到射线到射线到射线 ON ON 的距离的距离之和最小之和最小6. .如图,点如图,点如图,点 A A 是∠是∠是∠MON MON 内的一点,在射线内的一点,在射线 OM OM 上作点上作点上作点 P P ,使,使,使 PA PA 与点与点与点 P P 到射线到射线到射线 ON ON 的距的距离之和最小离之和最小EMME HM30°二、常见题型三角形问题1.如图,在等边△如图,在等边△ABC ABC ABC 中,中,中,AB = 6AB = 6AB = 6,,AD AD⊥⊥BC BC,,E E 是是 AC AC 上的一点,上的一点,上的一点,M M M 是是 AD AD 上的一点,若上的一点,若上的一点,若 AE = 2 AE = 2 AE = 2,求,求,求 EM+EC EM+EC EM+EC 的最小值的最小值 A解:∵点解:∵点 C C C 关于直线关于直线关于直线 AD AD AD 的对称点是点的对称点是点的对称点是点 B B B,,A∴连接∴连接 BE BE BE,交,交,交 AD AD AD 于点于点于点 M M M,则,则,则 ME+MD ME+MD 最小,过点过点 B B B 作作 BH BH⊥⊥AC AC 于点于点于点 H H H,, 则 EH = AH EH = AH –– AE = 3 AE = 3 –– 2 = 1,BH = BC2 - CH2 = 62 - 32 = 3 3在直角△在直角△BHE BHE BHE 中,中,中,BE = BE = BH2 + HE2B=(3 3)2 + 12 = 2 7DCBDC2.如图,在锐角△如图,在锐角△ABC ABC ABC 中,中,中,AB = 4 2AB = 4 2AB = 4 2,∠,∠,∠BAC BAC BAC=45°,∠=45°,∠=45°,∠BAC BAC BAC 的平分线交的平分线交的平分线交 BC BC BC 于点于点于点 D D D,,M 、N N 分别是分别是分别是 AD AD AD 和和 AB AB 上的动点,上的动点,则 BM+MN BM+MN 的最小值是的最小值是 .解:作点解:作点 B B B 关于关于关于 AD AD AD 的对称点的对称点 B'B',,过点过点 B' B' B'作作 B'E B'E⊥⊥AB AB 于点于点 E ,交,交 AD AD AD 于点于点于点 F F F,, 则线段则线段 B'E B'E B'E 的长就是的长就是的长就是 BM BM BM+MN的最小值+MN的最小值 在等腰等腰 Rt Rt Rt△△AEB'AEB'中,中, 根据勾股定理得到,根据勾股定理得到,B'E B'E = 4CB'M FDAN EB3.如图,△如图,△ABC ABC ABC 中,中,中,AB=2AB=2AB=2,∠BAC=30°,若在,∠BAC=30°,若在,∠BAC=30°,若在 AC AC AC、、AB AB 上各取一点上各取一点上各取一点 M M M、、N ,使,使 BM+MN BM+MN BM+MN 的值最小,则这个最小值的值最小,则这个最小值C解:作解:作 AB AB AB 关于关于关于 AC AC AC 的对称线段的对称线段 AB'AB',,过点过点 B' B' B'作作 B'N B'N⊥⊥AB AB,垂足为,垂足为,垂足为 N N N,交,交,交 AC AC AC 于点于点 M , 则 B'N = MB'+MN = MB+MN B'N B'N 的长就是的长就是的长就是 MB+MN MB+MN MB+MN 的最小值的最小值则∠则∠B'AN = 2B'AN = 2B'AN = 2∠∠BAC= 60BAC= 60°,°,°,AB' = AB = 2AB' = AB = 2AB' = AB = 2,, ∠ANB'= 90ANB'= 90°,∠°,∠°,∠B' = 30B' = 30B' = 30°。
将军饮马问题例题及应用
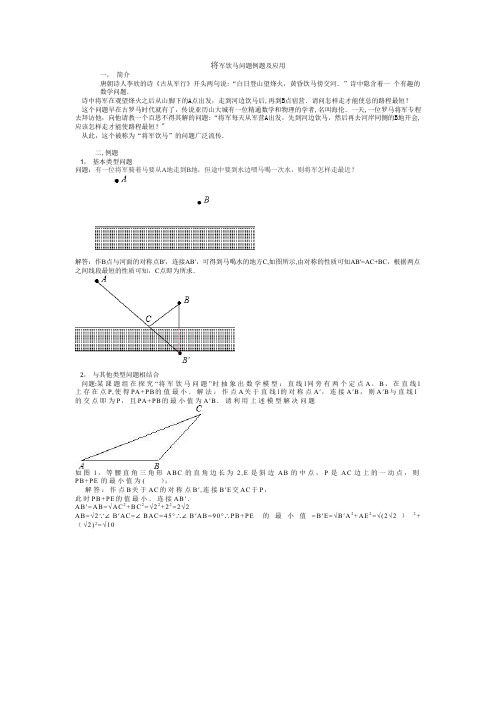
将军饮马问题例题及应用一,简介唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题.诗中将军在观望烽火之后从山脚下的A点出发,走到河边饮马后,再到B点宿营.请问怎样走才能使总的路程最短?这个问题早在古罗马时代就有了,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:“将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短?"从此,这个被称为“将军饮马”的问题广泛流传.二,例题1,基本类型问题问题:有一位将军骑着马要从A地走到B地,但途中要到水边喂马喝一次水,则将军怎样走最近?解答:作B点与河面的对称点B′,连接AB′,可得到马喝水的地方C,如图所示,由对称的性质可知AB′=AC+BC,根据两点之间线段最短的性质可知,C点即为所求.2,与其他类型问题相结合问题:某课题组在探究“将军饮马问题”时抽象出数学模型:直线l同旁有两个定点A、B,在直线l 上存在点P,使得PA+PB的值最小.解法:作点A关于直线l的对称点A′,连接A′B,则A′B与直线l 的交点即为P,且PA+PB的最小值为A′B.请利用上述模型解决问题如图1,等腰直角三角形A B C的直角边长为2,E是斜边AB的中点,P是AC边上的一动点,则PB+PE的最小值为( );解答:作点B关于AC的对称点B′,连接B′E交AC于P,此时PB+PE的值最小.连接AB′.AB′=AB=√AC2+B C2=√22+22=2√2AB=√2∵∠B′AC=∠B AC=45°∴∠B′AB=90°∴PB+PE的最小值=B′E=√B′A2+AE2=√(2√2)2+(√2)2=√10。
将军饮马问题例题及应用
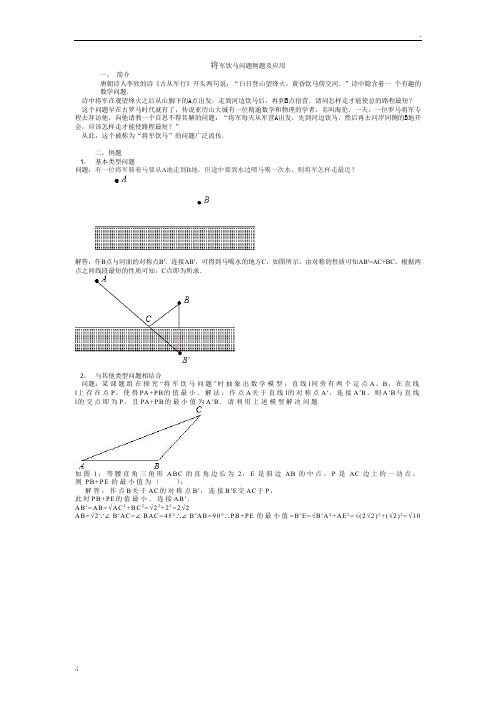
..; 将军饮马问题例题及应用一, 简介唐朝诗人李欣的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一 个有趣的数学问题.诗中将军在观望烽火之后从山脚下的A 点出发,走到河边饮马后,再到B 点宿营.请问怎样走才能使总的路程最短? 这个问题早在古罗马时代就有了,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:“将军每天从军营A 出发,先到河边饮马,然后再去河岸同侧的B 地开会,应该怎样走才能使路程最短?”从此,这个被称为“将军饮马”的问题广泛流传.二,例题1, 基本类型问题问题:有一位将军骑着马要从A 地走到B 地,但途中要到水边喂马喝一次水,则将军怎样走最近?解答:作B 点与河面的对称点B ′,连接AB ′,可得到马喝水的地方C ,如图所示,由对称的性质可知AB ′=AC+BC ,根据两点之间线段最短的性质可知,C 点即为所求.2, 与其他类型问题相结合问题:某课题组在探究“将军饮马问题”时抽象出数学模型:直线l 同旁有两个定点A 、B ,在直线l 上存在点P ,使得PA+PB 的值最小.解法:作点A 关于直线l 的对称点A ′,连接A ′B ,则A ′B 与直线l 的交点即为P ,且PA+PB 的最小值为A ′B .请利用上述模型解决问题如图1,等腰直角三角形A B C 的直角边长为2,E 是斜边AB 的中点,P 是AC 边上的一动点,则PB +PE 的最小值为( );解答:作点B 关于AC 的对称点B ′,连接B ′E 交AC 于P ,此时PB +PE 的值最小.连接AB ′.AB ′=AB =√AC 2+B C 2=√22+22=2√2AB =√2∵∠B ′AC =∠B AC =45°∴∠B ′AB =90°∴PB +PE 的最小值=B ′E=√B ′A 2+AE 2=√(2√2)2+(√2)2=√10。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
时间飞逝,下周将进入考试周,考前计划两讲内容,第一讲,主要是对初二阶段将军饮马专题再作一个归纳,第二讲,主要对常考易错知识点进一步辨析.
今天我们主要是对“将军饮马”专题中求线段和最值与求角度做整理.
一.求线段和最值
1
(一)两定一动型
例1:
如图,AM⊥EF,BN⊥EF,垂足为M、N,MN=12m,AM=5m,BN=4m,P是EF上任意一点,则PA+PB的最小值是______m.
分析:
这是最基本的将军饮马问题,A,B是定点,P是动点,属于两定一动将军饮马型,根据常见的“定点定线作对称”,可作点A关于EF的对称点A’,根据两点之间,线段最短,连接A’B,此时A’P+PB即为A’B,最短.而要求A’B,则需要构造直角三角形,利用勾股定理解决.
解答:
作点A关于EF的对称点A’,过点A’作A’C⊥BN的延长线于C.易知A’M =AM=NC=5m,BC=9m,A’C=MN=12m,在Rt△A’BC中,A’B=15m,即PA+PB的最小值是15m.
变式:
如图,在边长为2的正三角形ABC中,E,F,G为各边中点,P为线段EF上一动点,则△BPG周长的最小值为_________.
分析:
考虑到BG为定值是1,则△BPG的周长最小转化为求BP+PG的最小值,又是两定一动的将军饮马型,考虑作点G关于EF的对称点,这里有些同学可能看不出来到底是哪个点,我们不妨连接AG,则AG⊥BC,再连接EG,根据“直角三角形斜边中线等于斜边的一半”,可得AE=EG,则点A就是点G关于EF的对称点.最后计算周长时,别忘了加上BG的长度.
解答:
连接AG,易知PG=PA,BP+PG=BP+PA,当B,P,A三点共线时,BP+PG=BA,此时最短,BA=2,BG=1,即△BPG周长最短为3.
2
(二)一定两动型
例2:
如图,在△ABC中,AB=AC=5,D为BC中点,AD=5,P为AD上任意一点,E为AC上任意一点,求PC+PE的最小值.
这里的点C是定点,P,E是动点,属于一定两动的将军饮马模型,由于△ABC 是等腰三角形,AD是BC中线,则AD垂直平分BC,点C关于AD的对称点是点B,PC+PE=PB+PE,显然当B,P,E三点共线时,BE更短.但此时还不是最短,根据“垂线段最短” 只有当BE⊥AC时,BE最短.求BE时,用面积法即可.
解答:
作BE⊥AC交于点E,交AD于点P,易知AD⊥BC,BD=3,BC=6,
则AD·BC=BE·AC,
4×6=BE·5,BE=4.8
变式:
如图,BD平分∠ABC,E,F分别为线段BC,BD上的动点,AB=8,△ABC的周长为20,求EF+CF的最小值________.
这里的点C是定点,F,E是动点,属于一定两动的将军饮马模型,我们习惯于“定点定线作对称”,但这题这样做,会出现问题.因为点C的对称点C’必然在AB上,但由于BC长度未知,BC’长度也未知,则C’相对的也是不确定点,因此我们这里可以尝试作动点E关于BD的对称点.
解答:
如图,作点E关于BD的对称点E’,连接E’F,则EF+CF=E’F+CF,当E’,F,C三点共线时,E’F+CF=E’C,此时较短.过点C作CE’’⊥AB于E’’,当点E’ 与点E’’重合时,E’’C最短,E’’C为AB边上的高,E’’C =5.
3
(三)两定两动型
例3:
如图,∠AOB=30°,OC=5,OD=12,点E,F分别是射线OA,OB上的动点,求CF+EF+DE的最小值.
分析:
这里的点C,点D是定点,F,E是动点,属于两定两动的将军饮马模型,依旧可以用“定点定线作对称”来考虑.作点C关于OB的对称点,点D关于OA 的对称点.
解答:
作点C关于OB的对称点C’,点D关于OA的对称点D’,连接C’D’.CF +EF+DE=C’F+EF+D’E,当C’,F,E,D’四点共线时,CF+EF +DE=C’D’最短.易知∠D’OC’=90°,OD’=12,OC’=5,C’D’=13,CF+EF+DE最小值为13.
变式:
(原创题)如图,斯诺克比赛桌面AB宽1.78m,白球E距AD边0.22m,距CD边1.4m,有一颗红球F紧贴BC边,且距离CD边0.1m,若要使白球E经过边AD,DC,两次反弹击中红球F,求白球E运动路线的总长度.
分析:
本题中,点E和点F是定点,两次反弹的点虽然未知,但我们可以根据前几题的经验作出,即分别作点E关于AD边的对称点E’,作点F关于CD边的对称点F’,即可画出白球E的运动路线,化归为两定两动将军饮马型.
解答:
作点E关于AD边的对称点E’,作点F关于CD边的对称点F’,连接E’F’,交AD于点G,交CD于点H,则运动路线长为EG+GH+HF长度之和,即E’F’长,延长E’E交BC于N,交AD于M,易知E’M=EM=0.22m,E’N=1.78+0.22=2m,NF’=NC+CF’=1.4+0.1=1.5m,则Rt△E’NF’中,E’F’=2.5m,即白球运动路线的总长度为2.5m.
小结:
以上求线段和最值问题,几乎都可以归结为“两定一动”“一定两动”“两定两动”类的将军饮马型问题,基本方法还是“定点定线作对称”,利用“两点之间
线段最短”“垂线段最短”的2条重要性质,将线段和转化为直角三角形的斜边,或者一边上的高,借助勾股定理,或者面积法来求解.
当然,有时候,我们也需学会灵活变通,定点对称行不通时,尝试作动点对称.
(二)求角度
例1:
P为∠AOB内一定点,M,N分别为射线OA,OB上一点,当△PMN周长最小时,∠MPN=80°.
(1)∠AOB=_____°
(2)求证:OP平分∠MPN
分析:
这又是一定两动型将军饮马问题,我们应该先将M,N的位置找到,再来思考∠AOB的度数,显然作点P关于OA的对称点P’,关于OB的对称点P’’,连接P’P’’,其与OA交点即为M,OB交点即为N,如下图,易知∠DPC 与∠AOB互补,则求出∠DPC的度数即可.
解答:
(1)法1:
如图,∠1+∠2=100°,∠1=∠P’+∠3=2∠3,∠2=∠P’’+∠4=2∠4,则∠3+∠4=50°,∠DPC=130°,∠AOB=50°.
再分析:
考虑到第二小问要证明OP平分∠MPN,我们就连接OP,则要证∠5=∠6,显然很困难,这时候,考虑到对称性,我们再连接OP’,OP’’,则∠5=∠7,∠6=∠8,问题迎刃而解.
解答:
(1)法2:
易知OP’=OP’’,∠7+∠8=∠5+∠6=80°,∠P’OP’’=100°,由对称性知,∠9=∠11,∠10=∠12,∠AOB=∠9+∠10=50°
(2)
由OP’=OP’’,∠P’OP’’=100°知,∠7=∠8=40°,∠5=∠6=40°,OP平分∠MPN.
变式:
如图,在五边形ABCDE中,∠B AE=136°,∠B=∠E=90°,在BC、DE上分别找一点M、N,使得△AMN的周长最小时,则∠AMN+∠ANM的度数为________.
分析:
这又是典型的一定两动型将军饮马问题,必然是作A点关于BC、DE的对称点A′、A″,连接A′A″,与BC、DE的交点即为△AMN周长最小时M、N的位置.解答:
如图,
∵∠BAE=136°,
∴∠MA′A+∠NA″A=44°
由对称性知,
∠MAA′=∠MA′A,
∠NAA″=∠NA″A,
∠AMN+∠ANM
=2∠MA′A+2∠NA″A=88°
本讲思考题:
1.(2017·安顺)如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD PE的和最小,则这个最小值为_______.
本讲思考题:
2.(2017·安徽改编)如图,在矩形ABCD中,AB=4,AD=3.P为矩形ABCD 内一点,若矩形ABCD面积为△PAB面积的4倍,则点P到A,B两点距离之和PA PB的最小值为________.。
