海浪波长以及波浪力计算
波浪力计算公式

波浪力计算公式引言:在海洋工程中,波浪力是一个重要的参数,用于估计波浪对结构物的作用力。
波浪力的计算可以通过波浪力计算公式来实现。
本文将介绍波浪力计算公式的原理和应用,并探讨波浪力计算的相关问题。
一、波浪力计算公式的原理波浪力计算公式是根据波浪理论和结构动力学原理推导出来的。
其基本原理是根据波浪的特性和结构物的几何形状,通过计算波浪作用下的压力和力矩,进而得到波浪力的大小和方向。
二、常用的波浪力计算公式1. Morison公式:Morison公式是最常用的波浪力计算公式之一,适用于波浪作用下的柱状结构物。
该公式基于马克思-赫茨伯格(Morison)定律,考虑了波浪作用下的惯性力和阻力。
其表达式为:F = 0.5 * ρ * Cd * A * (dV/dt) + ρ * Cp * A * V * |V|其中,F为波浪力,ρ为水的密度,Cd和Cp分别为阻力系数和惯性系数,A为结构物的横截面积,V为波浪速度,dV/dt为波浪加速度。
2. Goda公式:Goda公式是一种改进的波浪力计算公式,适用于不规则波浪作用下的结构物。
该公式考虑了波浪的频率谱和结构物的响应特性,能更准确地估计波浪力。
其表达式为:F = ∫∫ (0.5 * ρ * Hs * g * S(f) * A * R(f)^2 * |H(f)|^2 * cos(θ))^0.5 df dθ其中,F为波浪力,ρ为水的密度,Hs为波浪高度,g为重力加速度,S(f)为波浪频率谱密度函数,A为结构物的横截面积,R(f)为结构物的响应函数,H(f)为波浪高度频谱密度函数,θ为波浪方向。
三、波浪力计算的应用波浪力计算公式广泛应用于海洋工程中的结构设计和安全评估。
通过计算波浪力,可以评估结构物的稳定性和安全性,为结构物的设计和施工提供依据。
例如,在海上风电场中,需要计算波浪力来评估风机基础的稳定性;在海岸工程中,需要计算波浪力来评估海堤的稳定性。
四、波浪力计算的相关问题1. 如何确定阻力系数和惯性系数?阻力系数和惯性系数是波浪力计算公式中的重要参数,可以通过试验或数值模拟来确定。
波浪理论的计算方法

波浪理论的计算方法波浪理论是用来描述海洋和湖泊中波浪的性质和行为的科学理论。
它是基于一系列基本方程和边界条件的数学模型,可以用来计算和预测波浪的高度、速度、周期等特性。
下面将介绍波浪理论的计算方法。
波浪的基本方程为水流动的欧拉方程和连续性方程,通过线性化和加入适当的边界条件,可以得到简化的一维波浪方程。
这个方程被称为波浪方程或爱舍尔-盖伊尔(Airy-Gay-Lussac)方程,是解决波浪传播和干涉问题最常用的工具。
波浪方程的一般形式如下:∂^2η/∂t^2=g∇^2η其中,∂^2η/∂t^2是波浪面随时间的加速度,g是重力加速度,∇^2是波浪面的拉普拉斯算子。
在一维情况下,波浪方程可以被进一步简化为:∂^2η/∂t^2=g∂^2η/∂x^2其中,x是水平方向的坐标。
求解这个波浪方程,可以得到波浪的解析表达式或数值解。
下面介绍几种常用的计算方法。
1. 艾尔金(Airy)线性理论:该方法假设波浪是以线性和无散动态传播的,适用于小振幅的波浪。
它利用波浪的线性性质,通过傅里叶级数展开和代数运算,可以得到波浪的频谱分布和波浪高度的概率分布。
2.快速海洋波浪传播(SWAN)模型:该模型是一种基于频谱方法的波浪模拟模型。
它将波浪场视作由多个波浪成分组成的矢量叠加,利用频谱分布和相干关系,通过解耦和复合波浪成分,可以计算出各个频段的波浪高度和方向。
3.深水波浪传播模型:该模型假设波浪在无限深水域传播,适用于大范围的波浪传播问题。
它利用波浪动能守恒和动量守恒原理,通过波浪的能量传递和波浪平衡状态的概念,可以计算出波浪随距离变化的特性。
4.海洋预报模型:该模型结合海洋动力学和波浪动力学,通过数值离散和积分方法求解波浪方程。
它将海洋和大气的相互作用考虑在内,可以计算出波浪与海流、风速等环境因素的相互作用,从而得到更准确的波浪预报结果。
这些方法都有各自的优缺点,选择适合的方法需要考虑波浪的性质、计算的精度要求和计算的效率等因素。
水中的波动现象和波浪力的计算分析

水中的波动现象和波浪力的计算分析在我们日常生活中,水是一个非常常见和重要的自然元素。
水对于地球上的生命形态和自然环境起着至关重要的作用。
而水中的波动现象和波浪力的计算分析是一个非常有趣和有挑战性的课题。
当我们观察到水面上产生的波浪时,我们往往会感到它们的美丽和神秘。
波浪是由外力在水中产生的扰动所引起的。
当这种扰动传播到水面上时,就会形成波浪。
波浪有许多不同的形态,它们可以是简单的正弦波,也可以是复杂的交错波。
在水中的波动中,存在着波长、波速和波浪力等重要的物理参数。
波长是指波浪连续的两个相邻的峰或谷之间的距离,用λ表示。
波速是指波浪传播的速度,用v表示。
波速与波长之间存在着直接的关系,即波速等于波长除以波周期。
而波周期是指波浪从一个峰到相邻的下一个峰所需的时间。
波浪力是指波浪对固体表面施加的力量。
在航海和海洋工程等领域,对波浪力进行准确的计算和分析非常重要。
波浪力的计算和分析可以通过海洋工程中的波浪观测和力学模型来实现。
波浪观测通常使用专门的仪器来测量波浪的高度、周期和速度等参数。
这些观测数据可以帮助我们对波浪力进行科学的计算和分析。
同时,在海洋工程中,研究人员还开发了一系列数学和计算模型来模拟和预测波浪力。
这些模型通常基于流体力学的原理,结合了波浪的物理特性和海洋环境的变化。
通过这些模型,研究人员可以更好地理解和预测波浪力的特性和作用。
对波浪力的计算和分析不仅可以帮助我们更好地理解水中的波动现象,还可以为海洋工程和船舶设计等领域提供重要的参考和指导。
在海洋工程中,波浪力是一个非常重要的参数,它可以影响结构物的稳定性和安全性。
因此,准确地计算和分析波浪力可以帮助我们设计更安全和可靠的海洋工程结构。
而在船舶设计中,波浪力也是一个重要的参考因素,它可以影响船体的稳定性和航行性能。
因此,对波浪力的计算和分析可以帮助我们设计更高效和舒适的船舶。
总之,水中的波动现象和波浪力的计算分析是一个非常有趣和有挑战性的课题。
第七章 波浪理论及其计算原理

第七章 波浪理论及其计算原理在自然界中;常可以观察到水面上各式各样的波动,这就是常讲的波浪运动,它造成海洋结构的疲劳破坏,也影响船的航行和停泊的安全。
波浪的动力作用也常引起近岸浅水地带的水底泥沙运动,致使岸滩崩塌,建筑物前水底发生淘刷,港口和航道发生淤积,水深减小,影响船舶的通航和停泊。
为了海洋结构物、驾驶船舶和船舶停靠码头的安全,必须对波浪理论有所了解。
一般讲,平衡水面因受外力干扰而变成不平衡状态,但表面张力、重力等作用力则使不平衡状态又趋于平衡,但由于惯性的作用。
这种平衡始终难以达到,于是,水体的自由表面出现周期性的有规律的起伏波动,而波动部位的水质点则作周期性的往复振荡运动。
这就是波浪现象的特性。
波浪可按所受外界的干扰不同进行分类。
由风力引起的波浪叫风成波。
由太阳、月亮以及其它天体引起的波浪叫潮汐波。
由水底地震引起的波浪叫地震水波由船舶航行引起的波浪叫船行波。
其中对海洋结构安全影响最大的是风成波。
风成波是在水表面上的波动,也称表面波。
风是产生波动的外界因素,而波动的内在因素是重力。
因此,从受力的来看;称为重力波。
视波浪的形式及运动的情况,波浪有各种类型。
它们可高可低,可长司短。
波可是静止的一一驻波(即两个同样波的相向运动所产生的波,也可以是移动的——推进波以一定的速度将波形不变地向一个方向传播的波),可以是单独的波,也可以是一个接一个的一系列波所组成的波群。
§7-1 液体波动理论一、流体力学基础1、速度场 描述海水质点的速度随空间位置和时间的变化规律的一个矢量。
),,,(t z y x V V =它的三个分量为:x 方向的量:),,,(t z y x u u =y 方向的量:),,,(t z y x v v =z 方向的量:),,,(t z y x w w =2、速度势 对于作无旋运动的液体,存在一个函数,它能反映出速度的变化,但仅仅是反映速度大小的变化,这个函数称为速度v的势函数,简称速度势: ),,,(t z y x φφ=3、速度与速度势的关系x u ∂∂=φ, y v ∂∂=φ, zw ∂∂=φ 二、海水运动的基本假设1、海水无粘性,只有重力是唯一的外力;2、液体自由液面上的压力为常数;3、液体波动振幅相对于波长为无限小;4、液体作无旋运动。
流体力学中的流体波长

流体力学中的流体波长流体力学是研究流体运动的学科,其中涉及到一系列的物理量和概念。
流体波长是流体力学中一个重要的概念之一,用于描述流体中波动的特性。
本文将介绍流体波长的定义、计算方法以及其在不同领域的应用。
一、流体波长的定义在流体力学中,流体波长是指一定时间内波浪所传播的距离。
它与波速和频率有关,可以用以下公式来表示:λ = v/f其中,λ表示流体波长,v表示波速,f表示频率。
这个公式告诉我们,流体波长与波速成正比,与频率成反比。
二、流体波长的计算方法在实际应用中,计算流体波长的方法根据具体情况有所不同。
下面以两种常见的情况为例进行介绍。
1. 静态流体的波长计算当流体处于静态状态时,即没有波浪或涡流的情况下,可以采用如下方法计算流体波长。
首先,我们需要确定波速v。
对于静态流体而言,波速为零,因此流体波长也为零。
这是因为在静态情况下,并不存在波动的传播。
2. 动态流体的波长计算当流体处于动态状态时,即存在波浪或涡流时,可以采用如下方法计算流体波长。
首先,我们需要确定频率f。
对于给定的波动现象,频率可以通过实验或理论分析得到。
然后,我们需要确定波速v。
波速的计算方法因具体情况而异。
在一维波动中,波速可以简单地通过公式v = λf 计算得到。
在复杂的三维流体波动中,波速的计算需要考虑更多的因素,如流体的密度、粘性等。
最后,我们可以利用公式λ = v/f 计算得到流体波长。
三、流体波长的应用流体波长在众多领域有着广泛的应用。
以下将介绍其中几个常见的应用场景。
1. 海洋学中的流体波长应用在海洋学研究中,流体波长是一个重要的参数,可以用来描述海浪的特性。
通过测量海浪的频率和波速,可以计算得到海浪的波长,并进一步分析海浪的形成机制、传播规律等。
2. 声波传播中的流体波长应用在声波传播研究中,流体波长被用来描述声波在流体中传播的距离。
通过测量声波的频率和波速,可以计算得到声波的波长,并用于声学系统的设计和优化。
船舶操纵运动波浪力计算

船舶操纵运动波浪力计算2.1 不规则波入射力计算模型依据概率统计理论,不规则波的波面可以看作是由一系列具有不同的频率、波数、波幅、传播方向以及随机分布初相位角的规则波叠加而成。
在实际应用中寻求海浪的统计特性,通常采用“波能谱”的概念来描述海浪。
海浪形成的过程是风把能量传递给水的过程。
这一过程大致可分为两个阶段,第一阶段为波浪生长阶段,当风最初作用于海面上时,海面开始出现较小的波,随着时间的增长,风不断地把能量传递给水,波浪越来越大,显然这一阶段海浪是比较复杂,其统计特性随时间不断变化,这一阶段的海浪描述描述相当复杂。
但是,当波浪渐趋稳定时,波的能量达到一定值,其统计特征基本上不随时间变化,为了这一阶段海浪的数学描述,应用波谱密度函数,从大量观察分析结果表明海浪以及船舶在波浪中的运动等均属于狭带谱的正态随机过程,因此基于以下假设:1.波浪为弱平稳的、各态历经的、均值为零的正态(高斯)随机过程。
2.波谱的密度函数为窄带。
3.波峰(最大值)为统计上独立的。
由波的方向性谱密度,不规则波的波面可用下列随机积分表示来描述:⎰⎰-∞+-+=220),(2)],()sin cos (cos[),,(ππςθωθωθωεωθηθξηξςd d S t k t (2-1)其中,),(θωςS 为波谱密度函数,表示了不规则波浪中各种频率波的能量在总能量中所占的份量。
仅考虑波沿主浪向运动的情况,并将式(2-1)转化为随船坐标系下表示为:⎰∞+--=0)(2)]()sin cos (cos[),,(ωωωεωμμςςd S t y x k t y x e (2-2)为了方便计算,将波能谱密度函数进行离散,用求和形式代替上式的积分如下:∑=+--∆=ni i ei i i t y x k S t y x 1])sin cos (cos[)(2),,(εωμμωωςς (2-3)其中,相位角i ε可视为均匀分布在(0,2π)区间内的随机变量。
海洋学第5章海浪
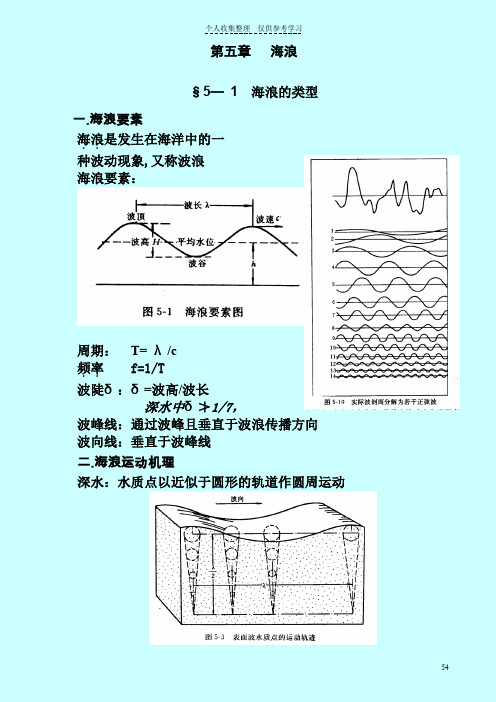
第五章海浪§5—1海浪的类型一.海浪要素海浪..是发生在海洋中的一种波动现象,又称波浪海浪要素:周期:T= λ/c频率.. f=1/T波陡δ:δ=波高/波长深水中δ≯1/7,波峰线:通过波峰且垂直于波浪传播方向波向线:垂直于波峰线二.海浪运动机理深水:水质点以近似于圆形的轨道作圆周运动运动半径:随着水深的增加而减小h=λ/2时;r↓→4% r0(r0=a)浅水:(h<λ/20)运动波及海底。
三.海浪的分类1.按海水深度分深度深: 表面波(深水波):h↑→r↓深度浅: 长波(浅水波h<λ/20)运动波及海底。
2.按周期分3.按生成原因分:.......风浪、潮波、海啸4.按受力情况分:自由波:涌浪受迫波:潮波5.按波形前进与否分:进行波;驻波。
6.按边界条件分①微小振幅波H/λ很小,H可忽略所有运动方程式都是线性的。
②有限振幅波:H不可忽略a.斯托克斯波有“质量运移”b.孤立波H/λ<1/10; 运动集中在波峰附近c.摆线波7.内波§5—2 海浪的形成一.海浪形成假说(1)形成毛细波(2)风以法向压力形式给波浪传递能量(3)空气小涡流加强了水质点的运动(4) 波长较短的波由风取得能量转给波长较长的波二、海浪的消衰1.分子粘滞性消耗的能量2.涡动消耗能量3.空气的阻力4.海底摩擦5.波浪破碎三.海浪的状态1.海浪三要素风速:大于0风时:状态相同的风作用的时间风区:状态相同的风作用的海区风大不一定浪大.......2.定常状态风区一定,海浪达最大;风区增加,海浪高度增加;风区是限制因素。
3.过渡状态风区一定,海浪未达最大;时间增加,海浪高度增加;风时是限制因素。
4.海浪的充分成长状态能量收支平衡;海浪达最大;风区、时间增加,海浪高度不增加。
5.判断海浪状态的标准a.最小风时成长至最大海浪所需的时间;未达最小风时:过渡状态b.最小风区成长至最大海浪所需的风区。
达最小风时,未达最小风区:定常状态最小风时、风区均满足:充分成长状态四. 涌浪离开风区的海浪称为涌浪1.涌浪的特点:(1)波长小的浪衰减快(2)传播中涌浪的周期和波长都在增加原因:选择消衰作用,使周期小的波消衰得快.(3)波长比波高大40~100倍;先头涌可达1000倍以上有时是台风来临的征兆(4)传播距离远:可达10000公里以上2. 涌浪传播速度:Cg =λπ23.涌浪波高消衰原因(1) 粘滞性消耗:空气的阻力和海水的涡动粘滞性消耗(2)离散:各个波的波速不同而引起;(3)角散:侧向散开五. 观测到的大洋中的最大海浪北太平洋:波高34m,周期14.8s,波速为28.3m/s印度洋:观测到24.9m的波高;及波长超过350m的风暴波大西洋:观测到波长824m,周期为23s的大浪,其波速达35.8m/s。
波浪理论及其计算原理

设:
忽略常数项,得四阶近似的波面方程为:
五阶近似。Skjelbreia和Hendrickson(1960)提出了Stokes波的五阶近似。为了便于工程上的计算应用,采用列表方式给出各系数。计算时只要查表,把系数代入简单的代数式即可获得波浪的各项特性参数。各计算公式如下:
(7-1)
式中: 、 、 为水质点速度在 、 、 三个坐标轴方向上的分量; 为海水的密度; 为流体所受的表面力; 为重力加速度。
用欧拉法描述流场时,可得到运动方程为:
(7-2)
二、连续方程
流体在运动时,必须遵循质量守恒定律,也就是必须满足连续方程。
今在流体内取一由闭曲面 所围成的固定几何空间,其体积为 。则在单位时间内所取空间内流体质量的增加量为:
三阶近似。取式(7-39)的前三项,得:
设:
代入上式,并除以 之后,得:
忽略方次在 以上的各项,并按 的方次排列,有:
由此可得:
代入 ,得到 的波形表达式:
为了简化上式,设:
用摄动法求解 ,令:
代入前式,得:
将上式展开,保留 的三次方以下各项,有:
于是得:
, ,
代回到 的表达式,得(到三次方)
再代回到上面的 表达式,有
(7-13)
(7-14)
不过,运动是无旋还是有旋的还不清楚,一般当作是有旋的,并引进流函数 ,则 , ,将这些代入式(7-13)和(7-14),消去 后,得:
(7-15)
令:
(7-16)
将式(7-16)代入式(7-15),得:
(7-17)
因为 ,所以 。相反,如把 代入这个关系式,得:
(7-18)
上式所表示的运动是无旋的。因此,开始时可以将速度势 引入,即 , ,得:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Option ExplicitDim L1 As Single, L2 As Single, t As Single, d!, k!, kd!, thkd!, H!, D1!Dim CD As Single, CM As Single, l As Single, Ko As SingleDim Fhdmax As Single, Fhlmax As Single, Mhdmax As Single, Mhlmax!, Fhmax!, Mhmax!Dim θ As Si ngleConst Pi = 3.141592653Const G = 9.8Const γ = 1025Private Sub Command1_Click()Dim r As IntegerDo While TrueL1 = Val(InputBox("请输入波长L1:", "求解设计波长:", "100"))t = Val(InputBox("请输入设计波周期T:", "请输入", "6"))d = Val(InputBox("请输入设计水深d:", "请输入", "20"))If L1 <= 0 Thenr = MsgBox("请输入一个正数!", 5, "输入错误")If r = 2 ThenEndEnd IfElseExit DoEnd IfLoopk = 2 * Pi / L1kd = k * dthkd = (Exp(kd) - Exp(-kd)) / (Exp(kd) + Exp(-kd))L2 = G * (t ^ 2) * thkd / (2 * Pi)Do Until Abs(L2 - L1) < 0.001L1 = L2k = 2 * Pi / L1kd = k * dthkd = (Exp(kd) - Exp(-kd)) / (Exp(kd) + Exp(-kd))L2 = G * (t ^ 2) * thkd / (2 * Pi)LoopPrint "设计波长是:"; L2Print "波数:"; Format$(k, "0.0000")End SubPrivate Sub Command2_Click()EndEnd SubPrivate Sub Command3_Click()H = Val(InputBox("请输入设计波高H:", "请输入", "3"))D1 = Val(InputBox("请输入桩柱直径D1:", "请输入", "2"))l = Val(InputBox("请输入桩柱间距l:", "请输入", "15"))If d / L2 < 0.5 ThenPrintPrint "相对水深d/L2:"; d / L2Print "采用线性波理论计算:"ElseMsgBox "重新选择计算理论"End IfPrint "波陡:"; H / L2Print "相对柱径:"; D1 / L2If D1 / L2 < 0.2 ThenPrint "属于小直径桩柱"ElsePrint "属于大直径桩柱"End IfCD = Val(InputBox("请输入拖曳力系数:", "请输入", "1.0"))CM = Val(InputBox("请输入质量系数:", "请输入", "2.0")) PrintPrint "选用拖曳力系数:"; CDPrint "选用质量系数:"; CMDim LD As SingleLD = l / D1Print "桩柱相对间距:"; LDPrint "群桩系数Ko:";If LD > 4 ThenKo = 1Print KoElseIf LD < 4 And LD > 3 ThenKo = 1.25Print KoElseIf LD < 2 ThenKo = 1.5Print KoEnd IfEnd SubPrivate Sub Command4_Click()Dim K1 As Single, K2 As Single, K3 As Single, K4 As SingleDim e As Single, θo As SingleK1 = (2 * k * (d + H / 2) + sh(2 * k * (d + H / 2))) / (8 * sh(2 * k * d)) Fhdmax = CD * γ * G * D1 * (H ^ 2) * K1 / 2PrintPrint "K1值:"; Format$(K1, "0.0000")Print "单桩柱最大水平拖曳力Fhdmax:"; FhdmaxK2 = th(k * d)Fhlmax = CM * γ * G * Pi * (D1 ^ 2) * H * K2 / 8PrintPrint "K2值:"; Format$(K2, "0.0000")Print "单桩柱最大水平惯性力Fhlmax:"; FhlmaxK3 = (2 * (k ^ 2) * (d + H / 2) ^ 2 + 2 * k * (d + H / 2) * sh(2 * k * (d + H / 2)) - ch(2 * k * (d + H / 2)) + 1) / (32 * sh(2 * k * d))Mhdmax = CD * γ * G * D1 * (H ^ 2) * L2 * K3 / (2 * Pi)PrintPrint "K3值:"; Format$(K3, "0.0000")Print "单桩柱最大水平拖曳力矩Mhdmax:"; MhdmaxK4 = (k * d * sh(k * d) - ch(k * d) + 1) / ch(k * d)Mhlmax = CM * γ * G * (D1 ^ 2) * H * L2 * K4 / 16PrintPrint "K4值:"; Format$(K4, "0.0000")Print "单桩柱最大水平惯性力矩Mhlmax:"; MhlmaxIf Fhlmax >= 2 * Fhdmax ThenFhmax = Fhlmaxθo = 90ElseIf Fhlmax < 2 * Fhdmax ThenFhmax = Fhdmax * ((1 + (Fhlmax / Fhdmax) ^ 2) / 4)θo = arcsin(Fhlmax / (2 * Fhdmax))End IfPrintPrint "单桩柱最大水平波力Fhmax:"; FhmaxIf Mhlmax >= 2 * Mhdmax ThenMhmax = MhlmaxElseIf Mhlmax < 2 * Mhdmax ThenMhmax = Mhdmax * ((1 + (Mhlmax / Mhdmax) ^ 2) / 4)End IfPrintPrint "单桩柱最大水平波力矩Mhmax:"; MhmaxPrint "最大水平波力和最大水平波力矩的相位θo:"; θoe = Mhmax / FhmaxPrintPrint "最大水平波力作用点离海底的距离e:"; eEnd SubPublic Function sh(n) As Singlesh = (Exp(n) - Exp(-n)) / 2End FunctionPublic Function ch(n) As Singlech = (Exp(n) + Exp(-n)) / 2End FunctionPublic Function th(n) As Singleth = (Exp(n) - Exp(-n)) / (Exp(n) + Exp(-n))End FunctionPublic Function arcsin(n) As Singlearcsin = Atn(n / Sqr(-n * n + 1))End FunctionPublic Function FH(θ) As SingleFH = Fhdmax * Cos(θ) * Abs(Cos(θ)) + Fhlmax * Sin(θ)End FunctionPublic Function MH(θ) As SingleMH = Mhdmax * Cos(θ) * Abs(Cos(θ)) + Mhlmax * Sin(θ)End FunctionPrivate Sub Command5_Click()Dim i As IntegerOpen "C:\Documents and Settings\All Users\桌面\不同相位水平波力.txt" For Output As #1 Print #1, Tab(8); "相位角θ"; Spc(3); "cosθ"; Spc(3); "cosθ|cosθ|"; Spc(3); "sinθ"; Spc(3); "Fhdmaxcosθ|cosθ|"; Spc(3); "Fhlmaxsinθ"; Spc(6); "FH"For i = 0 To 180 Step 15θ = i * Pi / 180Print #1, Tab(10); i; Tab(20); Format$(Cos(θ), "0.0000");Print #1, Tab(30); Format$(Cos(θ) * Abs(Cos(θ)), "0.0000");Print #1, Tab(40); Format$(Sin(θ), "0.0000");Print #1, Tab(55); Format(Fhdmax * Cos(θ) * Abs(Cos(θ)), "0.00");Print #1, Tab(70); Format(Fhlmax * Sin(θ), "0.00");Print #1, Tab(85); Format(FH(θ), "0.00")Next iClose #1End SubPrivate Sub Command6_Click()Dim i As IntegerOpen "C:\Documents and Settings\All Users\桌面\不同相位水平波力矩.txt" For Output As #2Print #2, Tab(8); "相位角θ"; Spc(3); "cosθ"; Spc(3); "cosθ|cosθ|"; Spc(3); "sinθ"; Spc(3); "Fhdmaxcosθ|cosθ|"; Spc(3); "Mhlmaxsinθ"; Spc(6); "MH"For i = 0 To 180 Step 15θ = i * Pi / 180Print #2, Tab(10); i; Tab(20); Format$(Cos(θ), "0.0000");Print #2, Tab(30); Format$(Cos(θ) * Abs(Cos(θ)), "0.0000");Print #2, Tab(40); Format$(Sin(θ), "0.0000");Print #2, Tab(55); Format(Mhdmax * Cos(θ) * Abs(Cos(θ)), "0.00");Print #2, Tab(70); Format(Mhlmax * Sin(θ), "0.00");Print #2, Tab(85); Format(MH(θ), "0.00")Next iClose #2End SubPrivate Sub Command7_Click()Dim ψ As SingleDim ∑H As SingleDim i As IntegerDim t As Single, m As Integerψ = l * 360 / L2PrintPrint "前后两桩柱的波浪位相差ψ:"; ψt = 0For i = 0 To 180 - ψ∑H = FH(i) + FH(i + ψ)If t < ∑H Thent = ∑Hm = iEnd IfNext iPrint "发生最大水平合波力的相位:"; m Print "前后两桩柱的最大水平合波力为:"; t End SubPrivate Sub Command8_Click()ClsEnd SubPrivate Sub Command9_Click()Dim ψ As SingleDim ∑M As SingleDim i As IntegerDim t As Single, m As Integerψ = l * 360 / L2t = 0For i = 0 To 180 - ψ∑M = MH(i) + MH(i + ψ)If t < ∑M Thent = ∑Mm = iEnd IfNext iPrintPrint "发生最大水平合波力矩的相位:"; m Print "前后两桩柱的最大水平合波力矩为:"; t End Sub海洋环境作业计算结果:。
