大学物理复习衍射1
合集下载
《大学物理》光的衍射(一)
放映结束 感谢各位的批评指导！
谢 谢！
让我们共同进步
③影响衍射图样的a和
由暗纹条件： asin k 若λ 一定时，
sin 1 ： 缝越窄，衍射越显著，但a不能小于（a小于时 也有衍射，a但此时半波带理论不成立）；缝越宽，衍射越不明显， 条纹向中心靠近，逐渐变成直线传播。
由暗纹条件： asin k 若a一定时， sin λ 越大，衍射越显著，
20 2sin0 2 / a 1.092102 rad
易得中央明条纹的线宽度为
x=2 f tan0 2 f sin0 5.46103 m
（2）浸入水中，折射率改变，设折射率为n,则波长改变为
=/n 2
an
n ， ，即中央明条纹的角宽度减小
大学物理 习题练习 光的衍射
光的衍射
• 什么是光的衍射？
波在传播中遇到障碍物，使波面受到限制时，能够绕过障碍物 继续前进的现象。
光通过宽缝时，是沿直线传播的，若将缝的宽度减小到约104m及更 小时，缝后几何阴影区的光屏上将出现衍射条纹。
菲涅耳衍射
衍射屏、光源和接收屏之间（或 二者之一）均为有限远
夫琅禾费衍射
衍射屏与光源和接收屏三者之间 均为无限远。
单缝夫琅禾费衍射
衍射屏 透镜L
透镜L
B
S
*
a
Aδ f
f
观察屏
·p
0
衍射角:
①衍射图样中明、暗纹公式：
亮纹条件： a sin (2k 1)
2
（近似值）
暗纹条件： a sin 2k k
2
②单缝衍射条纹特点—条纹宽度
对K级暗纹有
大学物理101光的衍射(1)
解 ：(1) x0
2 f
a
4.0m m
(2) 单缝衍射明纹的角位置由a
sin
（2k
1）
2
确定，得：sin 2
5 ，
2a
x2
f
tan 2
f
sin 2
5
2a
f
5.0mm
(3) 由ain （2k 1） 知: 相应于第二级、三级衍射明纹, k分别为2、3，
2
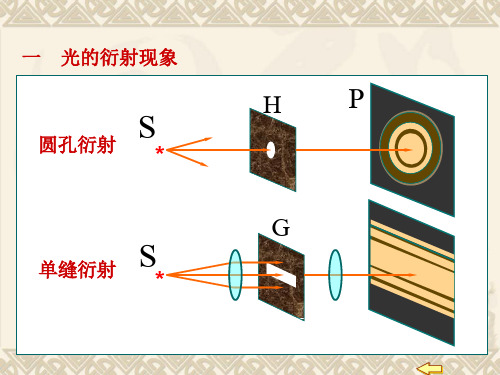
一 光的衍射现象
圆孔衍射
S
*
单缝衍射
S
*
HP
G
衍射 光在传播过程中绕过障碍物的边缘而偏离直线传 播的现象
说明
衍射现象是否明显取决于障碍物线度与波长的对 比，波长越大，障碍物越小，衍射越明显。
二 惠更斯 — 菲涅尔原理
n
S
rP *
S
t S ： 时刻波阵面
S ：波阵面上面元
(子波波源)
子波在 P点引起的振动振幅 s 并与 有关 .
当k=1时，λ=5000A0
当k=2时，λ=3000 A0
(3)中央明纹宽度为
x 2 f
a
5000 1010 2 1 0.5 103
在可见光范围内，入射光波长为λ=5000A0。 2 103 m
解：(1)对P点，由
(2)P点为第一级
tg x 1.5103 1.5103
f
1
明纹，k=1
sin 3 1.5103rad
2a
当θ很小， tgθ=sinθ=θ
半波带数为： 2k+1=3
由单缝衍射公式可知 2a sin 2atg 2k 1 2k
大学物理光的衍射
xk f
中央明纹线宽度：
x0
2
f
tg 0
2 f
a
其它(qítā)明纹线宽
a
度x： f k1 f k
f a 2021/12/19
1 2
x0
5 3
2a 2a
精品文档
B
I
0
f
a
3 5
2a 2a
·p
o
sin
中央(zhōngyāng)亮纹2角1宽度2：a 4、a, 相比拟时 ，条纹分散得开，衍
射现象明显；
2、中央(zhōngyāng)亮2纹1 角2宽a 度：
a
sin 1
a
中央两侧(liǎnɡ cè)第一暗纹之间。
I
a
5 3
2a
2a
0
精品文档
a
3
2a
5
2a
sin
3、中央(zhōngyāng)明
纹宽度为其它明纹宽
度的2倍：
A
k级暗纹： a sin k a
k xk
sin k
f k
tg k
光源—障碍物 —接收屏距离为
无限远。
平行光
点光源
菲涅耳衍射(yǎnshè)
夫朗和费衍射(yǎnshè)
点光源
实验室夫朗和 费衍射
精品文档
13—2 单缝夫琅和费衍射(yǎnshè)
一、单缝夫琅和费衍射(yǎnshè)
X
原理
S f1 L1
光 强
L2 f2
精品文档
二、菲涅耳半波带法 将衍射光束分成(fēn chénɡ)一组一组的平行光，每组平行光的衍射角 （与原入射方向的夹角）相同。
精品文档
浙江大学《大学物理》课件光的衍射1
这是具体的白光单缝夫琅禾费衍射
光的衍射
单缝夫琅禾费衍射图样特征的讨论： ③衍射效应还与缝宽 a、入射光的波长 密切相关。 只有 a~ 才有明显的衍射效应
分析书上P49页例17.1，注意各种物理量单位的统一
【例题】用单色平行光垂直照射到宽度为 a=0.5mm的单缝上， 在缝后放置一个焦距为 f=100cm的透镜，则在焦平面的屏幕 上形成衍射条纹，若在离屏上中央明纹中心距离为1.5mm处 的P点为一亮纹，试求： ①入射光的波长；②P点条纹的级数和该条纹对应的衍射角； ③狭缝处波面可分为几个半波带；④中央明纹的宽度。
②原中央明纹变为3 个小明纹，相当于 插入二条暗纹
光的衍射
2.振幅矢量叠加法：（只须了解其基本原理）
sinu u I A2 sin 2u 2 2 I 0 A0 u A A0
光的衍射
四、光栅衍射：
任何能周期性地分割波阵面的衍射屏------衍射光栅，相邻 两缝（或刻痕）中心间距称为光栅常数-----d
光的衍射
光栅衍射的整个过程是平行光先经各个单缝衍射后，再 进行多光束干涉！ 对光栅的每一条缝而言，单缝衍射的结论完全适用，故 光栅的衍射条纹应看作单缝衍射和多光束干涉的综合结果。
光的衍射
多缝衍射的明暗情况：
相邻的两个主 极大之间均有 N 1个极小 N 2个次极大
光的衍射
光的衍射
光栅衍射条纹的明暗条件为： dsin k k 0,1, 2,...主极大 k dsin k 1, 2,..., N 1, N 1,...极小 N
光的衍射
三、单缝夫琅禾费衍射：
原来垂直入射的平行光经过衍射能出射各种角度的平行光， 到达观察屏的光的强度是各个平行衍射光的相干叠加。
大学物理衍射1
2e + 0.5λ1= 0.5(2k +1)λ1,即2e = kλ1
改变波长后有： 改变波长后有：
k λ1 = k λ 2 − λ 2 , k = λ 2 /( λ 2 − λ1 ) 1 1 e = k λ1 = λ1λ 2 /( λ 2 − λ1 ) 2 2
第十一章 波动光学
第十一章 波动光学
1111-0 1111-1 1111-2 1111-3 教学基本要求 光的相干性 光程 分波面干涉 分振幅干涉
114-04 第四章教学基本要求 11光的衍射 114-05 第四章教学基本要求 11衍射光栅 114-06 第四章教学基本要求 11光的偏振
了解获得相干光的方法， 一 了解获得相干光的方法，理解光程的概念以及光程差与 相位差的关系，掌握光的干涉加强和减弱的条件. 相位差的关系，掌握光的干涉加强和减弱的条件 掌握杨氏双缝干涉和薄膜等厚干涉条纹的分布规律， 二 掌握杨氏双缝干涉和薄膜等厚干涉条纹的分布规律，了 解半波损失发生的条件，了解劈尖干涉的应用. 解半波损失发生的条件，了解劈尖干涉的应用 *三 了解迈克尔逊干涉仪的工作原理和迈克尔逊 莫雷实验 莫雷实验. 三 了解迈克尔逊干涉仪的工作原理和迈克尔逊—莫雷实验 了解惠更斯-菲涅尔原理 菲涅尔原理， 四 了解惠更斯 菲涅尔原理，能用菲涅尔半波带法分析单缝 夫琅禾费衍射条纹的分布规律， 夫琅禾费衍射条纹的分布规律，理解缝宽及波长对衍射条纹分布 的影响. 的影响 了解光栅衍射条纹的形成及特点， 五 了解光栅衍射条纹的形成及特点，理解并会应用光栅极 大方程，会分析光栅常数及波长对光栅衍射谱线分布的影响， 大方程，会分析光栅常数及波长对光栅衍射谱线分布的影响， 了解光栅衍射的应用. 了解光栅衍射的应用 *六 了解光栅方程的缺级现象，了解 射线的衍射及应用 射线的衍射及应用. 六 了解光栅方程的缺级现象，了解X射线的衍射及应用 理解自然光、线偏振光和部分偏振光的特征及检验方法， 七 理解自然光、线偏振光和部分偏振光的特征及检验方法， 理解马吕斯定律，理解布儒斯特定律， 理解马吕斯定律，理解布儒斯特定律，了解发射和折射时光的 偏振的应用. 偏振的应用
《大学物理》光的衍射(一)ppt课件
通过测量星光经过望远镜后的衍射斑大小，可以 推算出望远镜的分辨率，进而评估其观测能力。
2 3
显微镜的分辨率
利用光的衍射现象，显微镜能够分辨出非常微小 的物体或结构，其分辨率受到光源波长和物镜数 值孔径的限制。
摄影镜头的分辨率
摄影镜头通过控制光的衍射，可以在底片上形成 清晰的像，镜头的分辨率决定了照片的清晰度。
2024/1/24
激光全息技术在光学信息存储、三维显示和防伪等领域的应用
利用全息技术实现高密度光学信息存储、真彩色三维显示以及高级防伪措施等。
22
06
总结与展望
Chapter
2024/1/24
23
本节内容回顾与总结
光的衍射现象及其分类
介绍了光的衍射现象，包括菲涅尔衍射和夫 琅禾费衍射等，以及它们的特点和应用。
8
衍射图样分析
01
02
03
中央明纹
在屏幕中心形成的最亮区 域，宽度约为其他明纹的 两倍。
2024/1/24
明暗相间条纹
在中央明纹两侧形成一系 列明暗相间的条纹，离中 心越远，明纹亮度越低， 暗纹越暗。
条纹间距
相邻明纹或暗纹之间的距 离，与波长、缝宽和观察 距离有关。
9
缝宽对衍射图样的影响
缝宽增加
明暗条纹的间距减小，且离中央 明纹越远的明纹亮度越低。
2024/1/24
双缝间距减小
明暗条纹的间距增大，且离中央明 纹较远的明纹亮度也有所提高。
极限情况
当双缝间距趋近于零时，双缝衍射 图样趋近于单缝衍射图样。
14
04
光的衍射在生活中的应用
Chapter
2024//24
15
光学仪器的分辨率
2 3
显微镜的分辨率
利用光的衍射现象，显微镜能够分辨出非常微小 的物体或结构，其分辨率受到光源波长和物镜数 值孔径的限制。
摄影镜头的分辨率
摄影镜头通过控制光的衍射，可以在底片上形成 清晰的像，镜头的分辨率决定了照片的清晰度。
2024/1/24
激光全息技术在光学信息存储、三维显示和防伪等领域的应用
利用全息技术实现高密度光学信息存储、真彩色三维显示以及高级防伪措施等。
22
06
总结与展望
Chapter
2024/1/24
23
本节内容回顾与总结
光的衍射现象及其分类
介绍了光的衍射现象，包括菲涅尔衍射和夫 琅禾费衍射等，以及它们的特点和应用。
8
衍射图样分析
01
02
03
中央明纹
在屏幕中心形成的最亮区 域，宽度约为其他明纹的 两倍。
2024/1/24
明暗相间条纹
在中央明纹两侧形成一系 列明暗相间的条纹，离中 心越远，明纹亮度越低， 暗纹越暗。
条纹间距
相邻明纹或暗纹之间的距 离，与波长、缝宽和观察 距离有关。
9
缝宽对衍射图样的影响
缝宽增加
明暗条纹的间距减小，且离中央 明纹越远的明纹亮度越低。
2024/1/24
双缝间距减小
明暗条纹的间距增大，且离中央明 纹较远的明纹亮度也有所提高。
极限情况
当双缝间距趋近于零时，双缝衍射 图样趋近于单缝衍射图样。
14
04
光的衍射在生活中的应用
Chapter
2024//24
15
光学仪器的分辨率
大学物理光的衍射
XX,
汇报人：XX
01
02
03
04
05
06
光的衍射是指光在传播过程中遇到障碍物时，会绕过障碍物继续传播的现象。
光的衍射是光的波动性的表现，与光的干涉、反射等现象一起构成了光的传播规律。
光的衍射现象在光学、物理学、天文学等领域有着广泛的应用。 光的衍射现象的发现，为光的波动说提供了有力的证据，推动了光学的发展。
单缝衍射：光通过单缝时，形成明暗相间 的条纹
双缝干涉：光通过双缝时，形成明暗相间 的条纹
薄膜干涉：光通过薄膜时，形成彩色的条 纹
光栅衍射：光通过光栅时，形成彩色的条 纹
菲涅尔衍射：光通过菲涅尔透镜时，形成 彩色的条纹
光子衍射：光子通过狭缝时，形成明暗相 间的条纹
光的衍射：光在传 播过程中遇到障碍 物时，会发生衍射 现象
衍射图样：单缝衍 射图样是明暗相间 的条纹，条纹间距 与狭缝宽度有关
单缝衍射的条纹间距与狭缝 的宽度、光的波长和观察屏 的距离有关。
单缝衍射是光的衍射现象之 一，当光通过狭缝时，会在 其后形成明暗相间的条纹。
单缝衍射的条纹亮度与狭缝 的宽度和光的强度有关。
单缝衍射的条纹形状与狭缝 的形状有关，可以是直线、
光的波动性：光 波在传播过程中 具有周期性和振 幅变化的特点。
干涉现象：当两 束或多束相干光 波相遇时，它们 在空间某些区域 会相互加强或减 弱，形成明暗相 间的干涉条纹。
双缝干涉实验： 通过双缝干涉实 验可以观察到明 暗交替的干涉条 纹，证明了光波
的波动性。
干涉条件：只有 相干光波才能产 生干涉现象，而 相干光波需要满 足频率相同、振 动方向相同和相 位差恒定等条件。
曲线或折线等。
光学仪器制造：利用 单缝衍射现象制造各 种光学仪器，如望远 镜、显微镜等。
汇报人：XX
01
02
03
04
05
06
光的衍射是指光在传播过程中遇到障碍物时，会绕过障碍物继续传播的现象。
光的衍射是光的波动性的表现，与光的干涉、反射等现象一起构成了光的传播规律。
光的衍射现象在光学、物理学、天文学等领域有着广泛的应用。 光的衍射现象的发现，为光的波动说提供了有力的证据，推动了光学的发展。
单缝衍射：光通过单缝时，形成明暗相间 的条纹
双缝干涉：光通过双缝时，形成明暗相间 的条纹
薄膜干涉：光通过薄膜时，形成彩色的条 纹
光栅衍射：光通过光栅时，形成彩色的条 纹
菲涅尔衍射：光通过菲涅尔透镜时，形成 彩色的条纹
光子衍射：光子通过狭缝时，形成明暗相 间的条纹
光的衍射：光在传 播过程中遇到障碍 物时，会发生衍射 现象
衍射图样：单缝衍 射图样是明暗相间 的条纹，条纹间距 与狭缝宽度有关
单缝衍射的条纹间距与狭缝 的宽度、光的波长和观察屏 的距离有关。
单缝衍射是光的衍射现象之 一，当光通过狭缝时，会在 其后形成明暗相间的条纹。
单缝衍射的条纹亮度与狭缝 的宽度和光的强度有关。
单缝衍射的条纹形状与狭缝 的形状有关，可以是直线、
光的波动性：光 波在传播过程中 具有周期性和振 幅变化的特点。
干涉现象：当两 束或多束相干光 波相遇时，它们 在空间某些区域 会相互加强或减 弱，形成明暗相 间的干涉条纹。
双缝干涉实验： 通过双缝干涉实 验可以观察到明 暗交替的干涉条 纹，证明了光波
的波动性。
干涉条件：只有 相干光波才能产 生干涉现象，而 相干光波需要满 足频率相同、振 动方向相同和相 位差恒定等条件。
曲线或折线等。
光学仪器制造：利用 单缝衍射现象制造各 种光学仪器，如望远 镜、显微镜等。
(网工)《大学物理学》光的衍射练习题(解答) (1)
f
a
拓展题：在单缝衍射实验中，缝宽 a=0.2mm，透镜焦距 f=0.4m，入射光波长 =500nm，在距离中
央亮纹中心位置 2mm 处是亮纹还是暗纹？对应的波阵面分为几个半波带？
（D）
(A) 亮纹，3 个半波带； (B) 亮纹，4 个半波带；(C) 暗纹，3 个半波带； (D) 暗纹，4 个半波带。
(C) 不变；
(D) 改变无法确定。
【提示：衍射光栅公式变为 d sin a sin ' k ，最高级次 k 变大】
5．在光栅光谱中，假如所有偶数级次的主极大都恰好在单缝衍射的暗纹方向上，因而实际上不出
现，那么此光栅每个透光缝宽度 a 和相邻两缝间不透光部分宽度 b 的关系为
（B）
/2
/2
拓展题：在单缝夫琅和费衍射中，若单缝两边缘点 A、B 发出的单色平行光到空间某点 P 的光程差
为 1.5 ，则 A、B 间可分为 个半波带，P 点处为 （填明或暗）条纹。若光程差为 2 ，则
A、B 间可分为 个半波带，P 点处为 （填明或暗）条纹。
a sin
【提示：根据公式
n 判断， n 3 ，奇数半波带对应明 条纹，2 是 4 个 / 2 ，偶数半波带对应
相等，则光谱上呈现的全部级数为
（B）
(A) 0 、 1、 2 、 3 、 4 ； (B) 0 、 1、 3 ；(C) 1、 3 ； (D) 0 、 2 、 4 。
【 提 示 ： 根 据 衍 射 光 栅 公 式 d sin k ， 取 =900 k 4.16 ， 可 判 断 kmax 4 。 又 由 缺 级 公 式
ab
【提示：由缺级公式 k
k ' ，取 k 3k ' 】
大学物理光的衍射
k1bsin
2
b213000A &
对于 , k1是明纹
则 bsin（2k1）
2
b s in 3 0 0 3， 4 3 3 （ 0A & )是 紫 光
2
.
例1：如图，波长为
的单色平行光垂直照 A
射单缝，若由单缝边
缘发出的光波到达屏
上P、Q、R三点的光
o
程差分别为2、2.5
P
3.5 ，比较P、Q、 R B
.
离得远 可分辨
瑞利判据 刚能分辨
离得太近 不能分辨 小孔（直径D）对两个靠近的遥远的点光源的分辨
.
S1
D
*
0
*
I
S2
最小分辨角
分辨本领
1
1.22 D
R 1 D
1.22
.
D
R
望远镜： 不可选择，可D R
▲ 世界上最大的光学望远镜： D=8m
建在了夏威夷山顶。 ▲世界上最大的射电望远镜：
f
Q
三点的亮度。
R
解题思路：2＝22 第二级暗纹
2.5(221)
2
第二级明纹
2
3.5(231) 第三级明纹
2.
例：在单缝夫朗和费衍射实验中，屏上第3级暗纹 对应的单缝处波面可划分为——6 —个半波带？若 将缝宽缩小一半，原来第3级暗纹处将是明——纹。
例：波长为600nm的单色平行光，垂直入射 到缝宽为b=0.60mm的单缝上，缝后有一焦 距f=60cm的透镜。在透镜焦平面上观察衍射 图样. 则中央明纹宽度为—1— .2m—m。两个第3级暗纹之 间的距离为—3.6—m—m 。
sb
显 示
几何
大学物理第12章光的衍射
衍射规律
光通过狭缝后，会向四周扩散，形成 衍射现象。衍射图样的形状和大小与 狭缝的宽度和光波长有关。
多缝干涉与衍射的应用
光学仪器设计
干涉和衍射原理被广泛应用于光学仪器设计，如望远镜、显微镜 等，以提高成像质量和分辨率。
物理实验研究
多缝干涉和衍射实验是研究光波性质的重要手段，有助于深入理解 光的波动性和相干性。
光源
圆孔
选择单色光源，如激光， 以产生相干性好的光束。
制作一个具有特定直径 的圆孔，作为衍射的障
碍物。
屏幕
放置在圆孔后方，用于 接收衍射后的光束。
测量工具
测量衍射图案的直径、 形状和强度分布。
圆孔衍射的规律
中央亮斑
通过圆孔衍射形成的中央亮斑是各向同性的，其 直径与圆孔的直径成正比。
衍射角
衍射角与波长和圆孔直径有关，随着波长的增加， 衍射角减小。
该理论可以解释光的干涉、衍射和散射等现象，是光学领域的重要理论之一。
03 单缝衍射
单缝衍射实验装置
01
02
03
光源
使用单色光作为光源，如 激光，以保证光的相干性。
单缝
单缝的宽度决定了衍射的 程度，缝宽越窄，衍射现 象越明显。
屏幕
用于接收衍射光斑，记录 衍通过单缝后，会在屏幕中央形成最亮的光斑。
夜空中星星发出的光在穿过大气层时， 由于大气的密度和温度变化，使得星 光发生衍射，产生了闪烁现象。
02 光的衍射理论
惠更斯-菲涅尔原理
惠更斯-菲涅尔原理是光的衍射理论的基础，它指出波前上的 每一点都可以被视为新的波源，这些波源发出的波在空间中 相互叠加，形成衍射现象。
该原理可以解释光的直线传播、反射和折射等现象，是光学 领域的重要理论之一。
光通过狭缝后，会向四周扩散，形成 衍射现象。衍射图样的形状和大小与 狭缝的宽度和光波长有关。
多缝干涉与衍射的应用
光学仪器设计
干涉和衍射原理被广泛应用于光学仪器设计，如望远镜、显微镜 等，以提高成像质量和分辨率。
物理实验研究
多缝干涉和衍射实验是研究光波性质的重要手段，有助于深入理解 光的波动性和相干性。
光源
圆孔
选择单色光源，如激光， 以产生相干性好的光束。
制作一个具有特定直径 的圆孔，作为衍射的障
碍物。
屏幕
放置在圆孔后方，用于 接收衍射后的光束。
测量工具
测量衍射图案的直径、 形状和强度分布。
圆孔衍射的规律
中央亮斑
通过圆孔衍射形成的中央亮斑是各向同性的，其 直径与圆孔的直径成正比。
衍射角
衍射角与波长和圆孔直径有关，随着波长的增加， 衍射角减小。
该理论可以解释光的干涉、衍射和散射等现象，是光学领域的重要理论之一。
03 单缝衍射
单缝衍射实验装置
01
02
03
光源
使用单色光作为光源，如 激光，以保证光的相干性。
单缝
单缝的宽度决定了衍射的 程度，缝宽越窄，衍射现 象越明显。
屏幕
用于接收衍射光斑，记录 衍通过单缝后，会在屏幕中央形成最亮的光斑。
夜空中星星发出的光在穿过大气层时， 由于大气的密度和温度变化，使得星 光发生衍射，产生了闪烁现象。
02 光的衍射理论
惠更斯-菲涅尔原理
惠更斯-菲涅尔原理是光的衍射理论的基础，它指出波前上的 每一点都可以被视为新的波源，这些波源发出的波在空间中 相互叠加，形成衍射现象。
该原理可以解释光的直线传播、反射和折射等现象，是光学 领域的重要理论之一。
大学普通物理光的衍射
(11)
2πR rm 2πR r0 + m 2 ∆S m = ∫rm−1rdr = R + r0 ∫r0 + ( m −1) λ2 rdr R + r0 1 λ π Rλ [r0 + ( m − ) ] = R + r0 2 2 π Rλ ∆S m
R + r0 π Rλ ∴ Am ∝ K (θ ) R + r0 ∴ A1＞ A2＞ A3＞ L ＞ Am rm
其中k=2π/λ πλ 其中
AQ ( R ) K (θ ) r
cos(ω t − kr )dS
(7)
S面在 点的光振动 面在P点的光振动 面在 点的光振动:
E=∫ C
Sቤተ መጻሕፍቲ ባይዱ
A (R)K(θ ) Q
E 或 =∫ C
S
r A (R)K(θ ) Q
cos(ωt − kr) ⋅ dS
r
e-i (ωt −kr)dS 菲涅耳积分
如右上图: 第一个波带被分为N个细环带 各个细环带在P点的 个细环带,各个细环带在 如右上图 第一个波带被分为 个细环带 各个细环带在 点的 振幅矢量其大小逐个递减,其相位逐个相差 振幅矢量其大小逐个递减 其相位逐个相差 π / N
m=1 r 个波带在P点处的振幅矢量 个波带在 Am : 第m个波带在 点处的振幅矢量
(24)
二、半波带法定明暗纹条件 1.半波带法 半波带法(half-wave zone method): 半波带法 三个半波带
B
四个半波带
θ
C
θ
A
{
2.明暗纹条件 明暗纹条件: 明暗纹条件 λ a ⋅sinθ = 2k
AC = 3⋅ 2 λ
大学物理 衍射1(单缝)
−7
(不可见) 不可见) (不可见) 不可见) (可见) 可见) (可见) 可见) (不可见) 不可见)
17
k = 3, λ3 = 6.0 × 10 m = 600nm;
−7
k = 4, λ4 = 4.7 ×10 −7 m = 470nm; k = 5, λ5 = 3.8 × 10 −7 m = 380nm.
惠更斯 e dS
n
·
Q
θ
r
S
k(θ)dS 2πr Ep = ∫ dE( p) = ∫C cos(ωt − ) S S r λ
3
§23.2 单缝的夫琅禾费衍射
一. 单缝夫琅禾费衍射的光路图 将衍射光束分成一组一组的平行光，每组平行光 将衍射光束分成一组一组的平行光， 与原入射方向的夹角为衍射角θ. 观察屏 E屏幕
S
E A
障碍物
B
接收屏
E
A
距离均为无限远。 远场) 距离均为无限远。(远场)
光源
障碍物
B
接收屏
2
二、惠更斯-费涅耳原理 惠更斯波传到的任何一 点都是子波的波源， 衍射时波场中各点 的强度由各子波在 该点的相干叠加决 定. 菲涅耳 波的衍射就是波阵面上 dE(p) 连续） （连续）无穷多子波波源 · 发出的波的相干叠加。 发出的波的相干叠加。 p
其中
sin u 2 I = I0 ( ) u
1 I / I0
π a sin θ u = λ
相对光强曲线
0.017 0.047
0.047
0.017
-2(λ /a) -(λ /a) 0 λ /a 2(λ /a)
sinθ θ
角增加时， 当θ角增加时，半波带数增加(asinθ=kλ/2)，未 角增加时 半波带数增加( ) 被抵消的半波带面积减少，所以光强变小. 被抵消的半波带面积减少，所以光强变小.
(不可见) 不可见) (不可见) 不可见) (可见) 可见) (可见) 可见) (不可见) 不可见)
17
k = 3, λ3 = 6.0 × 10 m = 600nm;
−7
k = 4, λ4 = 4.7 ×10 −7 m = 470nm; k = 5, λ5 = 3.8 × 10 −7 m = 380nm.
惠更斯 e dS
n
·
Q
θ
r
S
k(θ)dS 2πr Ep = ∫ dE( p) = ∫C cos(ωt − ) S S r λ
3
§23.2 单缝的夫琅禾费衍射
一. 单缝夫琅禾费衍射的光路图 将衍射光束分成一组一组的平行光，每组平行光 将衍射光束分成一组一组的平行光， 与原入射方向的夹角为衍射角θ. 观察屏 E屏幕
S
E A
障碍物
B
接收屏
E
A
距离均为无限远。 远场) 距离均为无限远。(远场)
光源
障碍物
B
接收屏
2
二、惠更斯-费涅耳原理 惠更斯波传到的任何一 点都是子波的波源， 衍射时波场中各点 的强度由各子波在 该点的相干叠加决 定. 菲涅耳 波的衍射就是波阵面上 dE(p) 连续） （连续）无穷多子波波源 · 发出的波的相干叠加。 发出的波的相干叠加。 p
其中
sin u 2 I = I0 ( ) u
1 I / I0
π a sin θ u = λ
相对光强曲线
0.017 0.047
0.047
0.017
-2(λ /a) -(λ /a) 0 λ /a 2(λ /a)
sinθ θ
角增加时， 当θ角增加时，半波带数增加(asinθ=kλ/2)，未 角增加时 半波带数增加( ) 被抵消的半波带面积减少，所以光强变小. 被抵消的半波带面积减少，所以光强变小.
大学物理Ⅰ13.7单缝夫琅禾费衍射衍射
x
f
tan
f
sin
(2k
1)
f
2a
k 1, 2...
暗纹中心： x f tan f sin k f k 1,2...
a
3）其他明纹的线宽度：相邻暗纹中心间的距离
即中央明纹宽度为其他明纹宽度的两倍。
4）单缝衍射的光强分布
x
f
O
k级亮纹对应（2k+1）个半波带；k级暗纹对应2k 个半波带.k越大，AB上波阵面分成的波带数就越多， 所以，每个半波带的面积就越小，在P点引起的光强 就越弱。因此，各级明纹随着级次的增加而亮度减弱。
2
则，必定有一个“半波带”发的光过透镜后会聚在 P
点不能被抵消，形成明纹。
若 不满足明暗条纹条件，则AB 不能被分成整数
个半波带，则或多或少总有一部分的振动不能被抵消， 此时，会聚在屏上的亮度处于明暗纹之间。
综上所述，可得单缝衍射明、暗条纹条件
1）若 BC asin 2 将缝分为两个半波带
由波动光学 :一个点光源经过透镜后所成的像是 以爱里斑为中心的一组衍射条纹。
如果两个物点相距太近，它们的爱里斑重叠过多， 这两个物点的像就无法分辨。
两物点相距多远时恰好能分辨呢？
瑞利判据：对于两个光强相等的非相干物点，如 果其一个像斑的中心恰好落在另一像斑的第一暗 纹处，则此两物点被认为是刚好可以分辨。
不是整数， km取整数部分）
为整数，则取km-1）
观察：单缝宽度变化，中央明纹宽度如何变化？ a减小，1增大，衍射效应越明显.
4）在单缝衍射中，若使单缝和单缝后透镜分 别稍向上移，则衍射条纹将如何变化？
单缝上移衍射光束向上平移经透镜聚焦后， 位置不变条纹不变
大学物理光的衍射
波导型器件
利用光的衍射原理，在光纤通信中实现光信 号的传输、调制和检测等功能。
阵列波导光栅（AWG）
用于光纤通信网络中，实现多路光信号的复 用和解复用。
衍射光栅
用于波分复用（WDM）系统中，将不同波 长的光信号分离或合成。
应用领域
光纤通信、光网络、数据中心等。
微型显示技术中衍射元件
微型显示技术
利用衍射元件实现微型化、高清晰度 的显示技术，如头戴式显示器 （HMD）、智能手机等。
02
典型衍射实验及观察
单缝衍射实验
实验装置
包括单色光源、单缝、屏幕等部 分。
光源要求
需要使用单色光，因为不同波长 的光在衍射时产生的干涉图样不 同，单色光可保证实验结果的准 确性。
单缝要求
单缝宽度要远小于光的波长，这 样才能产生明显的衍射现象。
观察结果
在屏幕上可以观察到明暗相间的 衍射条纹，中央条纹最亮，两侧
波动理论与衍射
波动理论
光具有波动性质，可以看作是一种电磁波。光的衍射现象可以用波动理论来解释。
衍射的解释
当光波遇到障碍物或小孔时，障碍物或小孔的尺寸与光波的波长相当或更小时，光 波会发生明显的衍射现象。这是因为光波在障碍物或小孔的边缘处发生弯曲，使得 光波的传播方向发生改变。
惠更斯-菲涅尔原理
惠更斯-菲涅尔原理
衍射光学与计算光学的融合
随着计算机技术的不断发展，计算光学在衍射光学中的应用将越来越广 泛。未来，衍射光学与计算光学的融合将成为光学领域的重要发展趋势， 为光学设计和制造带来更多的可能性。
THANKS
感谢观看
条纹依次递减。
双缝干涉与衍射比较
实验装置
双缝干涉实验与衍射实验装置类似，只是在单缝处 改为双缝。
利用光的衍射原理，在光纤通信中实现光信 号的传输、调制和检测等功能。
阵列波导光栅（AWG）
用于光纤通信网络中，实现多路光信号的复 用和解复用。
衍射光栅
用于波分复用（WDM）系统中，将不同波 长的光信号分离或合成。
应用领域
光纤通信、光网络、数据中心等。
微型显示技术中衍射元件
微型显示技术
利用衍射元件实现微型化、高清晰度 的显示技术，如头戴式显示器 （HMD）、智能手机等。
02
典型衍射实验及观察
单缝衍射实验
实验装置
包括单色光源、单缝、屏幕等部 分。
光源要求
需要使用单色光，因为不同波长 的光在衍射时产生的干涉图样不 同，单色光可保证实验结果的准 确性。
单缝要求
单缝宽度要远小于光的波长，这 样才能产生明显的衍射现象。
观察结果
在屏幕上可以观察到明暗相间的 衍射条纹，中央条纹最亮，两侧
波动理论与衍射
波动理论
光具有波动性质，可以看作是一种电磁波。光的衍射现象可以用波动理论来解释。
衍射的解释
当光波遇到障碍物或小孔时，障碍物或小孔的尺寸与光波的波长相当或更小时，光 波会发生明显的衍射现象。这是因为光波在障碍物或小孔的边缘处发生弯曲，使得 光波的传播方向发生改变。
惠更斯-菲涅尔原理
惠更斯-菲涅尔原理
衍射光学与计算光学的融合
随着计算机技术的不断发展，计算光学在衍射光学中的应用将越来越广 泛。未来，衍射光学与计算光学的融合将成为光学领域的重要发展趋势， 为光学设计和制造带来更多的可能性。
THANKS
感谢观看
条纹依次递减。
双缝干涉与衍射比较
实验装置
双缝干涉实验与衍射实验装置类似，只是在单缝处 改为双缝。
大学物理--第二章--光的衍射---副本资料
-(/d)
0
/d
-(/4d) /4d
sin
2/d
多光束干涉的结果：在几乎黑暗的背景上出现了 一系列又细又亮的明条纹
2. 单缝衍射的影响 透镜
(1). 光强调制
光栅衍射条纹 λ 是多缝干涉被
θ
a
d
θ
θ
单缝衍射调制
后的结果
f
光强曲线
I
I0单 II0单
衍射光相干叠加
I
sin
-2-2(/d) --1(/d) I0单00I单
2. 光学仪器分辩本领 刚可分辨
S1
D
*
0
*
I
S2
不可分辨
重叠区中心光强是艾里斑中心 光强的80％，人眼恰能分辨。
最小分辨角
1
1.22
D
瑞利判据:对于两个等光强的非相干物点,如果其一个
象斑的中心恰好落在另一象斑的边缘(第一暗纹处),则
此两物点被认为是刚刚可以分辨。
分辨本领 R 1 D 1.22
/d1
2/d 2 sin ( /a)
-2
-1
0
1
2 sin ( /a)
(2). 缺级现象
干涉明纹位置： d sin k，k 0,1,2,
若该方向同时满足单缝衍射暗纹位置，则有：
a sin k ，k 1,2,3,
此时k 级主极大缺级
干涉明纹缺级级次： k d k a
k 1,2,3
K级光栅衍射主极大出现缺级现象
3 P点所在位置为第三级明条纹，
对应缝宽可分为2k+1=7个半波带
§3 光学仪器的分辨本领
1.圆孔的夫琅禾费衍射 相对光
强曲线
衍射屏 L
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
a
L2
f2
半波带个数
P
N
2a
sin
中央，O点
O 0 N 0
亮纹，零级亮纹
若
a sin
2
,
N 1?
明亮程度变差，但不是暗纹
当asin 时, N 2 第一次出现暗纹
当
a
sin
3
2
时,
N
3
再次出现亮纹
N 偶数 , N 奇数 ,
a sin a sin
2k (2k
2
, 1)
k
,
1,2,3 k 1,2,3
k=3，=6000Å
(2）由上问知k=3或k=4
k=4，=4670Å
(3)由菲涅耳半波带法可知，可以分成 2k+1个半波带。即可分为7 或9 个。
例：某一波长的光在同一个单缝衍射中的第3级明纹中心与波长
为600nm的光的第2级明纹中心重合。试求该光波的波长。
解:
a
sin
3
(2
3
1)
1
2
a
s in 2
N a sin
2
A N A sin
I
I0
sin2 2
o
A
A
5.结果的讨论
(1)光强度分布
I
(
)
I0
sin 2 2
π
a
sin
(2)主极大(中央明纹)
0
0
(3)极小(暗纹)
k , k 1, 2,
o
I
sin 0
I I0
sin 0
a sin k
sin
k
a
I 0
解： 由第二暗纹 k=2 得： a sin 2
且距中央亮纹中心的距离为
x ftg f sin
x
x 1 2.0 1.0mm
a
2
f x ax 25cm
sin 2
例 在宽度a=0.6mm的狭缝后d=40cm处有一与狭缝平行的屏，如图 所示。如以平行单色光自左面垂直照射狭缝，在屏上形成衍射条纹 ，若在离O点为x=1.4mm的P点，看到的是明纹。试求 ：
4I0 cos 2
d sin
I
杨氏双缝
?
偶数个半波带
(4)次极大 I 的极大值
d d
(
sin
2
2
)
0
I
(
)
I0
sin 2 2
π
a
sin
1 1.43 , 2 2.46 , 3 3.47 ,
I
k (k 12)
以 sin 为横轴，亮纹分布近似等间距
sin
I1 4.7% I0 , I2 1.7% I0 , I3 0.8% I0 ,
光栅衍射
P 缝宽：a 不透光间隔：b
d a b 光栅常数
b
O 光栅缝的总数 N
多光束干涉 d sin
a
光栅 透镜
d sin
f
A(
)
屏
A0
sin N , sin
2
I I0
A( ) A0
sin2 N sin2
sin
N 2
sin
2
考虑 N = 2 的情形
I
I0
sin2 2 sin2
(1)该入射光的波长；(2) P点的条纹级数；
(3)从P点来看，对该光波而言，狭缝的波振面可分半波带的数目。
解：(1)
P
x d x tg sin
d
x
由单缝衍射加强条件得： a
O
a sin 2k 1 / 2
d
k 1，2， 3
0.6 0.0014 / 0.4 2k 1 / 2
可间光范围内，k=3.4
o
A
这是多个同方向、同频率，同振幅、初 相依次差一个恒量的简谐振动的合成。
A
A
A
sin N
sin /
/ 2
2
A
sin
N
/ 2
/
2
AN
sin N /
N / 2
2
A A sin N / 2 A sin N / 2 AN sin N / 2
sin / 2
/ 2
N / 2
2 a sin N
(2
2
1)
600 2
2 3
7 1 5 600 1 429 nm
例：单缝衍射实验,=605.8nm的光垂直入射，缝宽a = 0.3mm，
透镜焦距 f=1m。求：(1)中央明纹的宽度；(2)第二级明纹
中心至中央明纹中心的距离；(3)相应于第二级和第三级明
纹，单缝可分出多少个半波带，每个半波带的宽度是多少？
解:
(1) x0
2 f
a
4.0mm
(2) asin(2k Nhomakorabea1)
2
x2
f
tan 2
5
2a
f
sin 2
5.0mm
5
2a
(3) a sin
(2k
1)
2
可分出5个和7个半波带
半波带宽度分别为
0.3 5
mm
和
0.3 7
mm
三、光栅衍射
衍射光栅分类： 透射光栅 反射光栅
光栅的衍射条纹：
单缝衍射 和 多缝干涉 的总效果
- 3 a
-
2 a
-
a
O
a
(5)条纹宽度
k 1
零级亮纹
a sin
k 0
2
a
x 2 f
a
其它亮纹
k 1
a
x f
a
2 3 aa
单缝宽度变化，中央明纹宽度如何变化？
a
x f
a
入射波长变化，衍射效应如何变化 ?
越大，
越大，衍射效应越明显.
1
例： 波长为 6000 埃的单色光垂直照射宽 a=0.30 mm 的单缝，在 缝后透镜的焦平面处的屏幕上，中央明纹上下两侧第二条暗纹之 间相距 2.0 mm ,求透镜焦距。
暗纹 亮纹
2
2
R
A
L
A1
C
B /2
R
A
L
A1
A2 C
B
/2
P
o
菲涅耳波带
a sin
2k
2
(2k 1)
暗纹 明纹
2
中央明纹的角宽度
P
a sin
o
2
a
x 2 f
a
单缝衍射的动态变化
R
fo
根据透镜成像原理衍射图不变 .
入射光非垂直入射时光 程差的计算
Δ DB BC
b(sin sin)
（中央明纹向下移动）
Δ BC DA
b(sin sin)
（中央明纹向上移动）
a
A
D
B
C
D A
b
C
B
3. 振幅矢量法
将缝分N个等宽的细窄条--子光源
每个子光源引起的光振幅相等,
a
相邻子光源的光程差 a sin
N
相位差 2 a sin N
Q点的合振幅A：就是各子光源的振幅 矢量和的模。
二、单缝的夫琅和费衍射
1.实验装置
L1
S
a
f1
L2
f2
a：缝宽
P
S：单色线光源 L1：凸透镜 O L2：凸透镜
：衍射角
2.菲涅耳半波带法
a
光程差均是 /2
半波带
半波带个数
B
N
2a
sin
若 asin , N 2
a
半波带 半波带
θ
1 2
1 2
相消 相消
A
λ
2 干涉相消形成暗纹
2
L1 S
a
f1