通过函数绘制一阶二阶传递函数伯德图
绘制伯德图
幅频和相频特性为:
A( ) (1 T 2 2 )2 (2 T )2, ( ) tg 1
1 T 1 ,o ,称为转折频率或交换频率。 T
Monday, March 09, 2015
可以用这两段渐近线近似的表示惯性环节的对数幅频特性。
3
惯性环节的Bode图
10 渐近线 0 -10 -20 0° -45° -90° 1 20T
20dB / Dec
图中,红、绿线分别是低频、高频渐近线,蓝线是实际曲线。
T
( )
2.0
-63.4
3.0
-71.5
4.0
-76
5.0
-78.7
7.0
-81.9
10
-84.3
20
-87.1
50
-88.9
100
-89.4
1 1 当 0时, (0) 0;当 时, ( ) ;当 时, () 。 T T 4 2 由图不难看出相频特性曲线在半对数坐标系中对于(0, -45°) 点是斜对称的,这是对数相频特性的一个特点。
当时间常数T 变化时,对数幅频特性和对数相频特性的形状 都不变,仅仅是根据转折频率1/T 的大小整条曲线向左或向 右平移即可。而当增益改变时,相频特性不变,幅频特性上 下平移。
Monday, March 09, 2015 6
振荡环节的频率特性
K Kn 2 ⒋ 振荡环节的频率特性: G( s) 2 2 T s 2Ts 1 s 2 n s n 2
0 L( ) 20 lg K 0 0
K 1 K 1 0 K 1
( )
180
K 0
log
如何绘制伯德图PPT课件

G( j ) 00
(5-63) (5-64)
100 00
900 1800
10 100 1000
图5-11 放大环节的Bode图
如图5-11所示,它是一条与角频率ω无关且与ω轴重合的直线。
5
(二)积分环节 积分环节的频率特性是
G( j) 1 j 1 1 e j90 j
7
当有n个积分环节串联时,即
dB L()
G(
j
)
(
1
j
)n
其对数幅频特性为
20 lg
G(
j )
20 lg
1
பைடு நூலகம்n
40
( 5-70 )
0
(5-71)
0.01 0.1
40 dB / dec
1
10
n 20 lg
G( j ) n 900
(5-72) 度 ()
6
设 ' 10 ,则有
20lg ' 20lg 10 20 20lg
dB L()
可见,其对数幅频特性是一条在
60
(5-68)
ω =1(弧度/秒)处穿过零分贝线 (ω 轴),且以每增加十倍频降 低20分贝的速度(-20dB/dec ) 变化的直线。
40
20dB / dec
1
L() dB
根据bode图求传递函数

ห้องสมุดไป่ตู้
s(s 1)(s
20)
s(s
1)(0.05s
1)
例4:根据对数幅频特性,求系统的传递函数。
L()
40
40
60
20 0
40
0.1 1 2.5
G(s) 100 (0.4s 1) s2 (10s 1)
放映结束 感谢各位批评指导!
谢 谢!
让我们共同进步
20lgk (3) 在交接频率处,曲线的斜率发生改变,改变多少取决于典型环
节种类。例如,在惯性环节后,斜率减少20dB/dec;在一阶微 分环节后斜率增加20dB/dec 。
绘制近似对数幅频曲线的步骤:
① 在半对数坐标上标出所有的转折频率(1/T);
② 确定低频段的斜率和位置;
③ 由低频段开始向高频段延伸,每经过一个转折频率,
由低频段开始向高频段延伸每经过一个转折频率由低频段开始向高频段延伸每经过一个转折频率曲线的斜率发生相应的变化
一般的近似对数幅频曲线特点: (1) 最左端直线的斜率为20NdB/dec,N是积分环节个数; (2) 低频段曲线表达式为20lgk-20vlgw
在 =1时,最左端直线(低频段曲线)或其延长线的分贝值等于
曲线的斜率发生相应的变化。
1
例1:已知最小相位系统的近似对数幅频特性曲线 如图所示。求系统的传递函数。
L()
-20
20
0 -20 20
0.1 1
(rad/s)
-40
解:系统低频段斜率为-20dB/dec,v=1,I型系统。
-20lgw+20lgK
k =1。
在ω1= 0.1处,渐近线变为水平线,故ω1对应的应是一 阶微分环节的转折频率。 对应的传递函数为:s 1
开环伯德图的绘制

( ) 90 arctan
2
arctan arctan
10
arctan
20
L() 0 A(c ) 1
c ?
?
g ?
h?
G( j )
1
2
10
100
1 1 G( j ) 100 (0.5 j 1) j ( j 1)
一个比例环节、积分环节、一阶惯性环节 和一阶微分环节构成
转角频率分别为 1
1 2 2 T2
1 1 T1
3
开环伯德图的绘制
L( ) 20dB / dec
40 20 40dB / dec 20dB / dec
G( s)
50( s 2) s( s 1)
50( j 2) G( j ) j ( j 1)
( ) ( j 2) j ( j 1) arctg 90 arctg
2
1
2 2
10 10
100 100
0.1
Байду номын сангаас1 2
( )
-90
10
100
1
( )
-92.8 -108.4 -108.4 -95.6 -90.5
4
-120
开环伯德图(习题一)
系统对数幅频特性如图所示,确定传递函数
L( ) 20dB / dec
0
20 20dB / dec
1. 确定每一个环节的转角频率30 2. 找到对应的典型环节 3. 确定变量的值
自动控制理论 5-2 频域:伯德图

Lω 20lg1 =0 dB
——低频渐近线为一条0dB的水平直线。
15
Lω 20lg 1 Tn ω
2
2 2
2ζ T ω
n
2
高频段,即ωTn>>1时
L() 20lg( Tn ) 40lg(Tn )
2 2
当ω增加10倍
ωTn 40 40lgωTn L() 40lg10
2
伯德图表示频率特性的优点: 把频率特性的乘除运算转变为加减运算; 在对系统作近似分析时,一般只需要画出 对数幅频特性曲线的渐近线,从而大大简 化了图形的绘制; 用实验方法,将测得系统频率响应的数据 画在半对数坐标纸上。根据所作出的曲线, 估计被测系统的传递函数。
3
二 典型因子的伯德图
5-2 对数坐标图
表示系统频率特性的图形有三种: 对数坐标图 极坐标图 对数幅相图
1
一、对数坐标图
1. 对数幅频特性图: 横坐标:用频率ω 的对数lgω 分度。 纵坐标:L(ω)= 20lg|G(jω)| (dB), 采用线性分 度;
2.相频特性图 横坐标:用频率ω 的对数lgω 分度。 纵坐标:频率特性的相角,以度为单位,采用线性 分度;
20lg 1 jω T 20lg 1 ω 2 T 2
ωT ω arct an
13
L ( )
dB
20
20 0
( )
90
1 10T
1 T
10 T
45 0
1 10T
1 T
10 T
一阶微分环节高频渐近线的斜率是+20dB/dec,其 相位变化范围由0°(ω=0)经+45°至90°(ω=∞)
如何绘制伯德图

。
6
设 ' 10 ,则有
20 lg 20 lg 10 20 20 lg
'
(5-68)
dB L( )
可见,其对数幅频特性是一条在 ω =1(弧度/秒)处穿过零分贝线 ( ω 轴),且以每增加十倍频降 低 20 分贝的速度( -20dB/dec ) 变化的直线。 积分环节的相频特性是
对数幅频特性为
20 lg G( j ) 20 lg K
(5-61)
当K>1时,20lgK>0,位于横轴上方;
当K=1时,20lgK=0,与横轴重合;
当K<1时,20lgK<0,位于横轴下方。
4
放大环节的对数幅频特性如图5-11所示,它是一条与角频 率ω 无关且平行于横轴的直线,其纵坐 标为20lgK。
0
100
1000
(5-63)
180
0
放大环节的相频特性是
G( j ) 0
0
图5-11 放大环节的Bode图
(5-64) 如图5-11所示,它是一条与角频率ω无关且与ω轴重合的直线。
5
(二)积分环节 积分环节的频率特性是
G ( j ) 1 j j 1
1
e
j 90
2 2 2
(5-85)
相频特性是
G ( j ) arctg 2 1
2 2
dB
40
(5-86)20
0
1 1 10
0
精确特性
40dB / dec
二阶微分环节与振荡节的Bode
1
图关于ω 轴对称,如图5-21 。
模拟电子课程波特图
w
(5)一阶微分环节
G 一阶微分环节的传递函数为: ( s) s 1
其频率特性表达式为:
G( jw) jw 1
幅频特性:
A( w) G( jw) 1 2 w2 20lg A( w) 20lg 1 2 w2
1、在低频段 w很小,即w 0
20lg A(w) 20lg 1 0(dB)
幅频特性:
A( w) G ( jw) w 20 lg A( w) 20 lg w
20lg A(w) 20lg w
w每增大 倍,放大倍数就上升 dB 10 20 而且,当w 1时, lg A( w) 0dB 20
20 lg A( w)
20
10
0
10
20
0.1 1 10 100
对数相频特性是 (w)和频率w的关系曲线
(w)
1
2
4
10
20
40
100
w
下面我们只研究对数幅频特性
四、典型环节的对数幅频特性 (1)比例环节
比例环节的传递函数为: G(s) K 常数
其频率特性表达式为: G( jw) K 常数
幅频特性:
A( w) G ( jw) K 20 lg A( w) 20 lg K
w每增大 10倍,放大倍数就下降 dB 20
20 lg A( w)
20
10
当w 1 / T时, lg A( w) 0dB, 20 和低频渐近线相交
0
10
20 0.1/ T
1/ T
10/T
w
3、误差 实际曲线和渐近线有误差,但不大。
当w 1 / T时,误差最大。 1 20 lg A(1 / T ) 20 lg 1 T 2 20 lg 2 3.01dB T 20 lg A( w)
MATLAB中bode图绘制技巧
Matlab中Bode图的绘制技巧2010-06-04 21:21:48 阅读54 评论0 字号:大中小订阅我们经常会遇到使用Matlab画伯德图的情况,可能我们我们都知道bode这个函数是用来画bode图的,这个函数是Matlab内部提供的一个函数,我们可以很方便的用它来画伯德图,但是对于初学者来说,可能用起来就没有那么方便了。
譬如我们要画出下面这个传递函数的伯德图:s^2H(s)=------------------------------------------------------------------------------------------s^4 + s^3 + s^2 + s +(这是一个用butter函数产生的2阶的,频率范围为[20 20K]HZ的带通滤波器。
) 我们可以用下面的语句:num=[ 0 0];den=[1 ];H=tf(num,den);bode(H)这样,我们就可以得到以下的伯德图:可能我们会对这个图很不满意,第一,它的横坐标是rad/s,而我们一般希望横坐标是HZ;第二,横坐标的范围让我们看起来很不爽;第三,网格没有打开(这点当然我们可以通过在后面加上grid on解决)。
下面,我们来看看如何定制我们自己的伯德图风格:在命令窗口中输入:bodeoptions我们可以看到以下内容:ans =Title: [1x1 struct]XLabel: [1x1 struct]YLabel: [1x1 struct]TickLabel: [1x1 struct]Grid: 'off'XLim: {[1 10]}XLimMode: {'auto'}YLim: {[1 10]}YLimMode: {'auto'}IOGrouping: 'none'InputLabels: [1x1 struct]OutputLabels: [1x1 struct]InputVisible: {'on'}OutputVisible: {'on'}FreqUnits: 'rad/sec'FreqScale: 'log'MagUnits: 'dB'MagScale: 'linear'MagVisible: 'on'MagLowerLimMode: 'auto'MagLowerLim: 0PhaseUnits: 'deg'PhaseVisible: 'on'PhaseWrapping: 'off'PhaseMatching: 'off'PhaseMatchingFreq: 0PhaseMatchingValue: 0我们可以通过修改上面的每一项修改伯德图的风格,比如我们使用下面的语句画我们的伯德图:P=bodeoptions;='on';={[10 40000]};={'manual'};='HZ';num=[ 0 0];den=[1 ];H=tf(num,den);bode(H,P)这时,我们将会看到以下的伯德图:上面这张图相对就比较好了,它的横坐标单位是HZ,范围是[10 40K]HZ,而且打开了网格,便于我们观察-3DB处的频率值。
如何绘制伯德图
低频高频渐近线的交点为:20log K 20log K 20logT ,得:
T 1,o
1 T
,称为转折频率或交换频率。
T可uesd以ay,用Mar这ch 3两1, 2段020渐近线近似的表示惯性环节的对数幅频特性。 4
惯性环节的Bode图
10 渐近线
0
-10
20dB / Dec
-20
0°
-45°
T T T 20T 10T 5T
112 2T T T
5 10 20 TTT
一阶微分环节的波德图
惯性环节的波德图
Tuesday, March 31, 2020
17
二阶微分环节的频率特性
③ 二阶微分环节: G(s) T 2s2 2Ts 1
幅频和相频特性为:
A()
(1
T
2
2
)2
(2T
)2,
(
)
tg 1
第三节 典型环节的频率特性 之一 波德图
Tuesday, March 31, 2020
1
比例环节的bode图
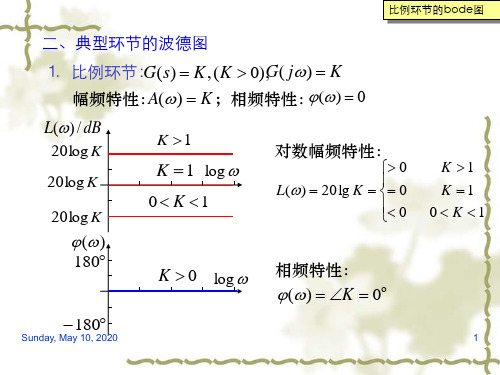
二、典型环节的波德图
⒈ 比例环节:G(s) K, (K 0),G( j) K 幅频特性:A() K;相频特性:() 0
L() / dB
20log K
20log K
20log K
()
频率特性分别为:
G( j) j G( j) 1 jT G( j) 1 T 2 2 j2T
Tuesday, March 31, 2020
14
纯微分环节的波德图
① 纯微分: A( )
L( )(dB)
20
L( ) 20 log A( ) 20 log
典型环节传递函数及伯德图
1 T
10 T
j
20
20dB / dec
0
0 0.01
0.1
1
10
( )()
0 0.01 -30 -60 -90
0.1
1
10
3. 理想微分环节
微分环节的特点:输出量与输入量的微分成正比例,即输出量与输入 量无关而与输入量的变化率正比例。 微分环节的微分方程:
微分环节的传递函数
3. 理想微分环节
而测厚信号
与厚差信号
之间关系为
6. 延迟环节
G( s) es
G( j) 1 L() 20lg G( j) 0dB
L( )(dB)
20
G( j) e j G( j) (rad) 57.3(度)
( ) 57.3(度)
j
0 0.1 1 0
( ) arctan
和惯性 比差一
dB
20
20 0
( )
90
1 10T
1 T
10 T
45 0
1 10T
1 T
10 T
6. 延迟环节
延迟环节的特点:输出量与输入量变化形式完全相同,但在时间上有一定的 滞后。 延迟环节的微分方程:
延迟环节的传递函数:
对于延迟时间很小的延迟环节,常常将它按泰勒 级数展开,并略去高次项,得如下简化的传递函数
1.比例环节(放大环节)
比例环节的特点:输出量与输入量之间的关系是一种固定 的比例关系,也就是输出量能无失真、无滞后地按一定比 例复现输入量。 比例环节的微分方程:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于一阶二阶传递函数的伯德图
一阶惯性系统的通式为:
将式子两边同时除以a0得
令0
0a K b =为系统静态灵敏度; 0
1a a =τ为系统时间常数; 则有
)()()1(
s KX s Y s =+τ
故有 )
1()()()(+==s K s X s Y s H τ 以液柱式温度计为例,传递函数为 )1(1)()()(+==s s X s Y s H τ
可得频率响应函数
)1j (1)(+=
τωs H )()()(001t x b t y a dt
t dy a =+)()()(0001t x a b t y dt t dy a a =+
可得传递函数的幅频与相频特性 2)1(1
)()(τωωω+==j H A
ωτωωϕarctan )()(-=∠=j H 在MATLAB 上输入程序(此时令1=τ)
num=[1];
den=[1,1];
figure
sys=tf(num,den);
bode(sys);grid on
可得bode 图
二阶惯性系统的通式为:
将式子两边同时除以a 0得
令0
0a K b =为系统静态灵敏度; 20
n a a =ω为系统无阻尼固有频率;
1
012a a a =ξ为系统阻尼器 传递函数为
12)
()()(22++==n n
s s K s X s Y s H ωξω
可得传递函数的幅频与相频特性 2222)(4)1(1
)()(2n n K j H A ωωξωωωω+-==
)()()()(001222t x b t y a dt
t dy a dt t y d a =++)()()()(00012202t x a b t y dt t dy a a dt t y d a a =++
2212arctan )()(n n j H ωωωωξωωϕ--=∠= 例如传递函数
12)()()(2++==s s s X s Y s H
在MATLAB 上输入程序 num=[2];
den=[1,1,1]; figure
sys=tf(num,den); bode(sys);grid on 可得bode 图。
