两类阶次分布参数系统的控制研究
自控原理 二阶系统

自控原理二阶系统自控原理是控制工程的基础知识之一,其中的二阶系统更是控制工程中的重要组成部分。
二阶系统通常由两个一阶系统级联或串联而成,具有比一阶系统更高的动态性能和控制精度。
在现实生活中,我们常常可以遇到二阶系统的例子。
比如,我们乘坐的汽车通常都是由发动机和传动系统来控制车辆的速度和行驶方向,这就是一个典型的二阶系统。
在这个系统中,发动机和传动系统分别起到加速和减速的作用,通过调节二者之间的协调关系来实现对汽车行驶状态的控制。
二阶系统的特点之一是具有振荡性。
在控制工程中,我们常常会遇到振荡现象,就好比一个摆动的钟摆。
这种振荡现象往往会对系统的稳定性产生负面影响,因此在设计二阶系统时需要注意对振荡进行控制。
控制二阶系统的一种常用方法是PID控制器,即比例-积分-微分控制器。
PID控制器通过对系统进行反馈调节,根据系统输出与期望输出之间的差异进行比例、积分和微分运算,从而实现对系统的精确调节和控制。
除了PID控制器,还有许多其他的控制方法可以应用于二阶系统。
例如,模糊控制和神经网络控制等,这些方法能够通过建立适当的数学模型来实现对二阶系统的控制。
在实际应用中,二阶系统广泛应用于各个领域,如航空航天、工业自动化、医疗仪器等等。
在飞行器中,二阶系统可以用来控制飞机的姿态和高度;在工业领域中,二阶系统可以用于控制机器人的运动和精确定位;在医疗仪器中,二阶系统可以用来控制心脏起搏器的工作频率和波形等。
总之,二阶系统作为自控原理中的重要组成部分,具备振荡性和动态性能较高的特点。
通过合理设计和选择控制方法,我们可以对二阶系统进行精确的调节和控制,从而实现对系统的稳定性和性能的优化。
在实际应用中,我们可以根据具体情况选择适当的控制方法,以满足系统的要求,提高生产效率和工作质量。
二阶系统分析

573.3 二阶系统的时间响应及动态性能3.3.1 二阶系统传递函数标准形式及分类常见二阶系统结构图如图3-6所示其中K ,T 为环节参数。
系统闭环传递函数为Ks s T Ks ++=Φ21)(化成标准形式2222)(nn ns s s ωξωω++=Φ (首1型) (3-5) 121)(22++=Φs T s T s ξ (尾1型) (3-6)式中,KT T 1=,11T K T n ==ω,1121KT =ξ。
ξ、n ω分别称为系统的阻尼比和无阻尼自然频率,是二阶系统重要的特征参数。
二阶系统的首1标准型传递函数常用于时域分析中,频域分析时则常用尾1标准型。
二阶系统闭环特征方程为02)(22=++=n n s s s D ωξω其特征特征根为122,1-±-=ξωξωλn n若系统阻尼比ξ取值范围不同,则特征根形式不同,响应特性也不同,由此可将二阶系统分类,见表3-3。
58数学上,线性微分方程的解由特解和齐次微分方程的通解组成。
通解由微分方程的特征根决定,代表自由响应运动。
如果微分方程的特征根是1λ,2λ,, n λ且无重根,则把函数te1λ,te 2λ,, tn eλ称为该微分方程所描述运动的模态,也叫振型。
如果特征根中有多重根λ,则模态是具有tte λ, ,2t e t λ形式的函数。
如果特征根中有共轭复根ωσλj ±=,则其共轭复模态t e )j (ωσ+与te )j (ωσ-可写成实函数模态t etωσsin 与t e t ωσcos 。
每一种模态可以看成是线性系统自由响应最基本的运动形态,线性系统自由响应则是其相应模态的线性组合。
3.3.2 过阻尼二阶系统动态性能指标计算设过阻尼二阶系统的极点为()n T ωξξλ11211---=-= ()n T ωξξλ11222-+-=-= )(21T T > 系统单位阶跃响应的拉氏变换sT s T s s R s s C n1)1)(1()()()(212++==ωΦ进行拉氏反变换,得出系统单位阶跃响应 111)(211221-+-+=--T T eT T e t h T t T t0≥t (3-7)59过阻尼二阶系统单位阶跃响应是无振荡的单调上升曲线。
二阶系统闭环参数ω和对时域响应ξ的影响

二阶系统闭环参数ω和对时域响应ξ的影响闭环系统的参数ω和ξ对系统的动态响应有着重要的影响。
ω是系统的自然频率,决定了系统的振荡速度;ξ是系统的阻尼比,决定了系统的振荡衰减速度。
本文将从时间域分析闭环系统对ω和ξ的影响,具体表现在系统的稳态误差、超调量、上升时间和振荡周期等方面。
首先,稳态误差是指系统在输入信号稳定后的偏差大小。
对于二阶系统,稳态误差与ω和ξ有关。
当ω较大时,系统的自然频率高,响应速度快,稳态误差较小。
相反,当ω较小时,系统的自然频率低,响应速度慢,稳态误差较大。
对于ξ来说,当ξ较大时,系统的阻尼比高,响应速度快,稳态误差较小。
当ξ较小时,系统的阻尼比低,响应速度慢,稳态误差较大。
其次,超调量是指系统响应的最大偏差值与系统稳定值之间的差别。
对于二阶系统,超调量也与ω和ξ有关。
当ω较大时,系统的自然频率高,响应速度快,超调量较小。
相反,当ω较小时,系统的自然频率低,响应速度慢,超调量较大。
对于ξ来说,当ξ较大时,系统的阻尼比高,响应速度快,超调量较小。
当ξ较小时,系统的阻尼比低,响应速度慢,超调量较大。
再次,上升时间是指系统从0%到100%响应稳定值所需的时间。
在二阶系统中,上升时间与ω和ξ有关。
当ω较大时,系统的自然频率高,响应速度快,上升时间较短。
相反,当ω较小时,系统的自然频率低,响应速度慢,上升时间较长。
对于ξ来说,当ξ较大时,系统的阻尼比高,响应速度快,上升时间较短。
当ξ较小时,系统的阻尼比低,响应速度慢,上升时间较长。
最后,振荡周期是指系统响应从一次峰值到下一次峰值所经历的时间。
对于二阶系统,振荡周期也与ω和ξ有关。
当ω较大时,系统的自然频率高,振荡周期较短。
相反,当ω较小时,系统的自然频率低,振荡周期较长。
对于ξ来说,当ξ较大时,系统的阻尼比高,振荡周期较短。
当ξ较小时,系统的阻尼比低,振荡周期较长。
综上所述,二阶系统的参数ω和ξ对系统的动态响应有着重要的影响。
其中,ω决定了系统的振荡速度,ξ决定了系统的振荡衰减速度。
二阶系统的控制方法

二阶系统的控制方法
有多种控制方法可用于二阶系统,以下是其中几种常见的控制方法:
1. 比例控制(P控制):在比例控制中,控制器的输出与误差
信号成正比。
该控制方法能够提供输出信号的调节,但无法解决系统的稳定性和超调问题。
2. 比例-积分控制(PI控制):在比例-积分控制中,控制器的
输出由误差信号的比例和积分组成。
积分项可以消除稳态误差,并提供更好的稳定性和抗干扰能力。
3. 比例-微分控制(PD控制):在比例-微分控制中,控制器
的输出由误差信号的比例和微分组成。
微分项可以提供更快的响应速度,并减小超调现象。
4. 比例-积分-微分控制(PID控制):PID控制是最常用的控
制方法之一,将比例、积分和微分三个项结合起来。
PID控制
器能够提供快速响应、稳态精度和抗干扰能力。
此外,还有一些高级控制方法适用于二阶系统,如模糊控制、自适应控制和最优控制等。
选择合适的控制方法需要考虑到系统的性能指标、控制要求和实际应用等因素。
二阶系统的频率响应与频率特性测量
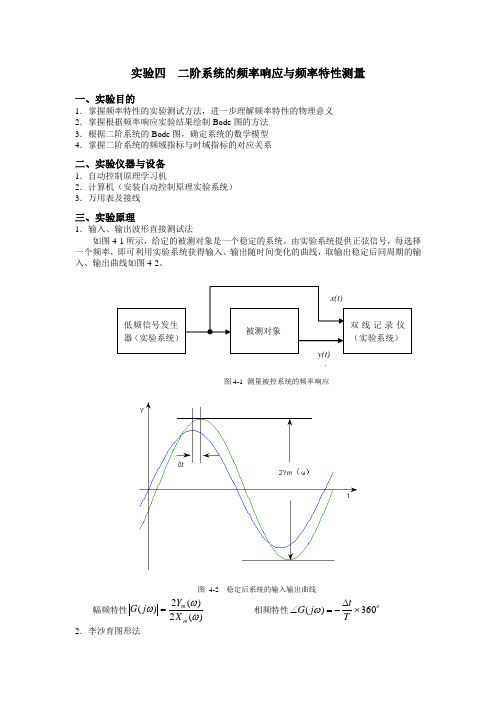
实验四二阶系统的频率响应与频率特性测量一、实验目的1.掌握频率特性的实验测试方法,进一步理解频率特性的物理意义2.掌握根据频率响应实验结果绘制Bode图的方法3.根据二阶系统的Bode图,确定系统的数学模型4.掌握二阶系统的频域指标与时域指标的对应关系二、实验仪器与设备1.自动控制原理学习机2.计算机(安装自动控制原理实验系统)3.万用表及接线三、实验原理1.输入、输出波形直接测试法如图4-1所示,给定的被测对象是一个稳定的系统。
由实验系统提供正弦信号,每选择一个频率,即可利用实验系统获得输入、输出随时间变化的曲线,取输出稳定后同周期的输入、输出曲线如图4-2。
图4-1 测量被控系统的频率响应图4-2 稳定后系统的输入输出曲线幅频特性)(2)(2)(ωωωmmXYjG=相频特性oTtjG360)(⨯∆-=∠ω2.李沙育图形法取被测对象某一选定频率下的输入信号x (t )和输出信号y (t )(去掉不稳定部分),利用实验系统做X-Y 图,得到一个椭圆图形,如图4-3所示。
图4-3 李沙育图形幅频特性:)(2)(2)(ωωωm m X Y j G =相频特性:如图4-3,椭圆长轴在第一、三象限,()()()ωωωφm 01-2Y 2Y sin=若椭圆长轴在第二、四象限,()()()ωωωφm 01-o 2Y 2Y sin-180=随着角频率的增加,大多数情况下椭圆逆时针运动,表明输出信号Y (t )滞后于输入信号X (t ),相位的计算结果要添加一个负号,如果椭圆顺时针运动,Y (t )超前于X (t ),计算结果为正。
幅值取两倍是为了便于测量。
3.测试频率的选取选取合适的实验测试频率范围是准确确定系统频率特性的关键。
控制系统多为低通滤波器,在频率很低时,系统的输出能够复现输入信号,通常,取被测对象转折频率的1/10作为起始测试频率,若对象模型未知,则先确定最大测试频率,方法是先测出输入信号频率为0时输出的幅值Y (0),逐渐增大输入信号频率,直至输出幅值Y m 为Y (0)/(50-100),此时频率便可确定为最大测试频率,测试频率可以在0与max ω之间选取若干点。
二阶系统的最优控制

二阶系统的最优控制Ξ肖 滨(海军潜艇学院 青岛 266071) 摘 要 应用最优控制理论验证了二阶系统最优控制为典型的Bang 2Bang 控制,通过理论推导得出了其相轨迹,并讨论了二阶系统最优控制的实现。
关键词 最优控制 二阶系统 Bang 2Bang 控制The Opti m al Con trol of Second -Order SystemX iao B in(N avy S ub m arine A cad e m y ,Q ing d ao ,266071) ABSTRACT T h is paper demo strated that the op ti m al contro l of second 2o rder system is the typ ical Bang 2Bang contro l by app lying the Op ti m al Contro l T heo ry .T he state track about th is contro l m ethod is obtained also by using theo ry inference ,and how to realize the op ti m al contro l of second 2o rder system is discussed deep ly at last .KEY WOR D S op ti m al contro l ,second 2o rder system ,Bang 2Bang contro l在雷达声纳等控制系统中,都涉及到目标自动搜索及跟踪问题,而其控制一般都采用闭环自动控制和调整实现,对于二阶系统而言,如何获得最优控制,使系统动态性能达到最快速的跟踪控制效果,一直是人们所关注的问题。
二阶系统的传递函数为 H (S )=k mS (S T m +1)(1)采用图1所示的闭环控制后,其传递函数为H (S )=K m T mS 2+S T m +K m T m (2)图2是二阶闭环系统阶跃响应曲线,可以看出:当系统阻尼太大时,系统响应时间长;而当系统阻尼太小时,输出超调量又太大。
典型二阶系统的z变换

典型二阶系统的z变换摘要:1.引言2.二阶系统的定义和特点3.Z 变换的定义和性质4.典型二阶系统的z 变换方法5.典型二阶系统的z 变换应用6.结论正文:1.引言在控制系统中,二阶系统是一种常见的系统类型,其动态性能和稳定性至关重要。
为了更好地分析这类系统,我们需要了解其数学模型以及相关的变换方法。
其中,Z 变换是一种常用的数学工具,可以有效地分析和设计二阶系统。
本文将介绍典型二阶系统的Z 变换方法及其应用。
2.二阶系统的定义和特点二阶系统是指其传递函数中包含两个存储器的系统,通常用一阶系统G(s) 和二阶系统H(s) 的串联或并联组合来描述。
二阶系统的特点是其阶跃响应存在超调量和稳态误差,且系统的稳定性取决于系统的阻尼比。
3.Z 变换的定义和性质Z 变换是一种在复平面上的积分变换,可以将系统的时域信号转换为频域信号。
其定义为:Z 变换Y(z) = ∫X(s)e^(-s/z)ds,其中X(s) 为输入信号,Y(z) 为输出信号,z 为复变量。
Z 变换具有以下性质:线性性、时域卷积定理、时域微分定理、初值定理等。
4.典型二阶系统的z 变换方法对于典型的二阶系统,我们可以通过求解微分方程或传递函数的方式得到其Z 变换。
具体方法如下:(1) 求解微分方程:首先将系统的微分方程转换为传递函数G(s),然后通过Z 变换求解得到输出信号的Z 域表示。
(2) 传递函数直接求解:对于已知的传递函数G(s),可以直接利用Z 变换的定义进行计算。
5.典型二阶系统的z 变换应用(1) 分析系统稳定性:通过求解系统的Z 变换,可以得到系统的频率响应,从而分析系统的稳定性和稳态误差。
(2) 设计系统控制器:根据系统的Z 变换,可以设计合适的控制器,以满足系统的性能要求。
(3) 系统仿真和实验:通过Z 变换,可以在频域上进行系统的仿真和实验,便于观察系统的动态性能。
6.结论典型二阶系统的Z 变换是一种重要的数学工具,可以有效地分析和设计控制系统。
二阶系统的模糊控制
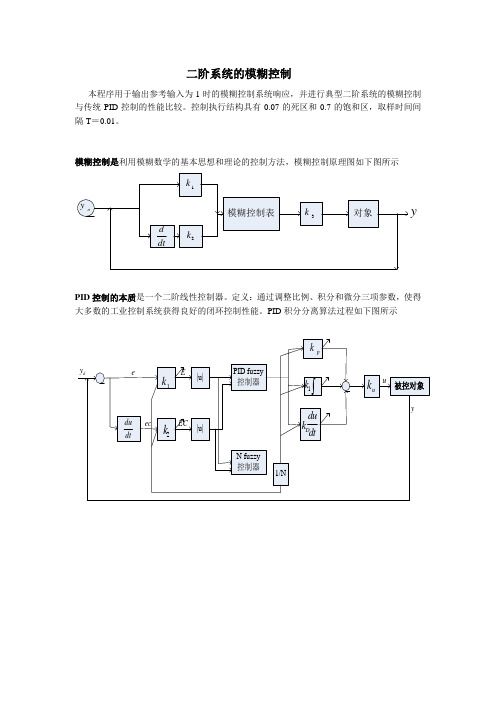
二阶系统的模糊控制本程序用于输出参考输入为1时的模糊控制系统响应,并进行典型二阶系统的模糊控制与传统PID控制的性能比较。
控制执行结构具有0.07的死区和0.7的饱和区,取样时间间隔T=0.01。
模糊控制是利用模糊数学的基本思想和理论的控制方法,模糊控制原理图如下图所示yPID控制的本质是一个二阶线性控制器。
定义:通过调整比例、积分和微分三项参数,使得大多数的工业控制系统获得良好的闭环控制性能。
PID积分分离算法过程如下图所示在本模糊系统中输入变量有两个,e和ec,e代表系统的误差,ec代表系统误差的微分,e 与ec的范围都是-6到+6:a=addvar(a,'input','e',[-6 6]);a=addvar(a,'input','ec',[-6 6]);输出变量有一个,u表示对系统的控制,范围是-3到+3:a=addvar(a,'output','u',[-3 3]);PID控制与模糊控制的阶跃响应如下图所示模糊控制器的输入输出曲面如下图所示程序如下clc;num=10;den=[2,8,1];[a1,b,c,d]=tf2ss(num,den);x=[0;0];T=0.01;h=T;umin=0.07;umax=0.7;td=0.02;Nd=td/T;N=500;R=1*ones(1,N);%传统PID控制e=0;ec=0;ie=0;kp=5;ki=0.1;kd=0.001;for k=1:Nuu1(1,k)=-(kp*e+ki*ec+kd*ie);%延迟环节u=uu1(1,k-Nd);%死区和饱和环节if abs(u)<=uminu=0;elseif abs(u)>umaxu=sign(u)*umax;end%利用龙格-库塔法进行系统仿真k0=a1*x+b*u;k1=a1*(x+h*k0/2)+b*u;k2=a1*(x+h*k1/2)+b*u;k3=a1*(x+h*k2)+b*u;x=x+(k0+2*k1+2*k2+k3)*h/6;y=c*x+d*u;%计算误差、微分和积分e1=e;e=y-R(1,k)ec=(e-e1)/T;ie=e*T+ie;yy1(1,k)=y;end%模糊控制a=newfis('simple');a=addvar(a,'input','e',[-6 6]);a=addmf(a,'input',1,'NB','trapmf',[-6 -6 -5 -3]); a=addmf(a,'input',1,'NS','trapmf',[-5 -3 -2 0]); a=addmf(a,'input',1,'ZR','trimf',[-2 0 2]);a=addmf(a,'input',1,'PS','trapmf',[0 2 3 5]);a=addmf(a,'input',1,'PB','trapmf',[3 5 6 6]);a=addvar(a,'input','ec',[-6 6]);a=addmf(a,'input',2,'NB','trapmf',[-6 -6 -5 -3]); a=addmf(a,'input',2,'NS','trapmf',[-5 -3 -2 0]); a=addmf(a,'input',2,'ZR','trimf',[-2 0 2]);a=addmf(a,'input',2,'PS','trapmf',[0 2 3 5]);a=addmf(a,'input',2,'PB','trapmf',[3 5 6 6]);a=addvar(a,'output','u',[-3 3]);a=addmf(a,'output',1,'NB','trapmf',[-3 -3 -3 -2]); a=addmf(a,'output',1,'NS','trimf',[-2 -1 0]);a=addmf(a,'output',1,'ZR','trimf',[-1 0 1]);a=addmf(a,'output',1,'PS','trimf',[0 1 2]);a=addmf(a,'output',1,'PB','trapmf',[2 3 3 3]);%模糊规则矩阵rr=[5 5 4 4 35 4 4 3 34 4 3 3 24 3 3 2 23 3 2 2 1];r1=zeros(prod(size(rr)),3);k=1;for i=1:size(rr,1)for j=1:size(rr,2)r1(k,:)=[i,j,rr(i,j)];k=k+1;endend[r,s]=size(r1);r2=ones(r,2);rulelist=[r1,r2];a=addrule(a,rulelist);%采用模糊控制器的二阶系统仿真e=0;ec=0;x=[0;0];ke=60;kec=2.5;ki=0.01;ku=0.8;for k=1:N %输入变量变换到论域e1=ke*e;ec1=kec*ec;if e1>=6e1=6;elseif e1<=-6e1=-6;endif ec1>=6ec1=6;elseif ec1<=-6ec1=-6;endin=[e1,ec1]uu(1,k)=ku*evalfis(in,a)-ki*ie;if k<=Ndu=0elseu=uu(1,k-Nd)endif abs(u)<=uminu=0;elseif abs(u)>umaxu=sign(u)*umax;endk0=a1*x+b*u;k1=a1*(x+h*k0/2)+b*u;k2=a1*(x+h*k1/2)+b*u;k3=a1*(x+h*k2)+b*u;x=x+(k0+2*k1+2*k2+k3)*h/6;y=c*x+d*u;%计算误差、微分和积分e1=e;e=y(1,1)-R(1,k)ec=(e-e1)/T;ie=e*T+ie;yy(1,k)=y;end%绘制结果曲线kk=[1:N]*T;figure(1);plot(kk,R,'k',kk,yy,'r',kk,yy1,'b'); xlabel('时间(0.01秒)');ylabel('输出');gtext('模糊控制');gtext('PID控制'); figure(2);gensurf(a);。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两类阶次分布参数系统的控制研究
一般而言,整数阶分布参数系统可以描述扩散过程,分数阶分布参数系统可以描述反常扩散过程和分数阶反应扩散过程。
这两类阶次系统广泛应用于工程、生态、社会、环境等领域,因而受到了人们的关注。
本文主要研究整数阶分布参数系统(通常简称为分布参数系统)和分数阶分布参数系统这两类阶次分布参数系统的控制问题,具体的研究工作如下:1.借助于静态传感器网络和PI控制器,研究了带有静态或移动污染源的扩散系统的控制问题。
通过构造优化执行器位置的目标函数和质心化的Voronoi剖分(centroidal Voronoi tessellations,CVTs)获得了执行器移动的路径。
基于Lyapunov稳定性理论证明了执行器位置的收敛性,也就是在带有PI控制器的控制输入的作用下执行器位置收敛到各自Voronoi单元的质心。
另外,再构造优化喷洒作用的目标函数来确立用于喷洒控制的PI控制器,使得喷洒量与污染物量的差异最小且避免喷洒过量造成二次污染。
最后建立了修正的整数阶仿真平台(Diff-MAS2D-PID仿真平台),并借此验
证了PI控制器对扩散过程的控制效果优于P控制器效果。
2.针对加权调和反常扩散系统的控制问题,将分数阶PI控制器引入系统的控制过程中用于移动执行器的运动控制和喷洒控制。
首次应用Lyapunov稳定性理论证明了移动执行器在带有分数阶PI控制器的控制输入作用下分别收敛到各自Voronoi区域的质心。
进一步而言,建立了一种基于分数阶PI控制器的新型CVT算法和一种修正的分数阶仿真平台(FO-Diff-MAS2D-FOPI仿真平台)。
最后,给出该反常扩散过程的数值仿真验证了所提分数阶PI控制器的有效性。
3.将反步法引入到具有混合或Robin边界条件的分数阶反应扩散系统,探讨了该系统的边界反馈控制问题。
这里系统的扩散率是不依赖于空间的,即扩散系数为常数。
基于反步法设计了Dirichlet,Neumann和Robin三种边界反馈控制器。
通过积分变换将在设计的控制器作用下的系统转化为Mittag-Leffler稳定的目标系统,控制问题转化为
求解积分变换的核函数问题。
应用分数阶Lyapunov方法证明了设计的边界反馈控制器可以使得闭环系统Mittag-Leffler稳定。
数值仿真表明了所提方法的有效性。
4.考虑了仅在边界
可测量具有混合边界条件的分数阶反应扩散系统的输出反馈控制问题。
在传感器和执行器同位和异位(即传感器和执行器在边界同一端和不同端)
两种情形下,分别设计了在Dirichlet执行力作用下的状态观测器,再结合前面
设计的基于反步法的边界反馈控制器得到了输出反馈控制器。
借助分数阶Lyapunov方法证明了该输出反馈控制器可以使得闭环系统Mittag-Leffler稳定。
数值仿真进一步验证了理论结果。
5.研究了含有空间依赖(非常数)扩散率的分数阶分布参数系统(原系统)的
边界镇定性问题。
该问题可以视为常数扩散率问题的推广,且更加符合实际情况。
通过变量变换将该系统转化为更具一般性的非常数扩散率的分数阶反应扩散系
统(新系统)。
利用反步法、积分变换设计新系统的边界反馈控制器,再根据给定的变量变换得到原系统的边界反馈控制器。
基于分数阶Lyapunov方法获得了在该边界反馈控制器作用下的原系统Mittag-Leffler稳定的充分条件。
数值仿真验证了该闭环系统的Mittag-Leffler稳定性。
