C语言实现FFT(快速傅里叶变换)
傅里叶变换c程序
傅里叶变换c程序傅里叶变换是一种用于分析和处理信号的重要数学工具，广泛应用于信号处理、图像处理、通信系统等领域。
在数学上，傅里叶变换可以将一个时域上的连续或离散信号转换为频域上的连续或离散信号，从而提供了一种将信号从时域转换为频域表示的方法。
在计算机科学中，傅里叶变换也有很大的应用。
通过使用傅里叶变换算法，可以对信号进行频谱分析，提取信号的频率成分，并在频域上进行滤波、去噪等处理。
傅里叶变换的计算可以使用多种方法，包括连续傅里叶变换（FFT）和离散傅里叶变换（DFT）。
为了实现傅里叶变换的计算，可以使用C语言编写相应的程序。
下面是一个简单的傅里叶变换C程序的示例：```c#include <stdio.h>#include <stdlib.h>#include <math.h>#define PI 3.14159265typedef struct {double real;double imag;} Complex;void fft(Complex* x, int N) {if (N <= 1) {}Complex* even = (Complex*) malloc(N/2 * sizeof(Complex)); Complex* odd = (Complex*) malloc(N/2 * sizeof(Complex)); for (int i = 0; i < N/2; i++) {even[i] = x[2*i];odd[i] = x[2*i + 1];}fft(even, N/2);fft(odd, N/2);for (int k = 0; k < N/2; k++) {Complex t;double angle = -2 * PI * k / N;t.real = cos(angle) * odd[k].real + sin(angle) * odd[k].imag; t.imag = cos(angle) * odd[k].imag - sin(angle) * odd[k].real; x[k].real = even[k].real + t.real;x[k].imag = even[k].imag + t.imag;x[k + N/2].real = even[k].real - t.real;x[k + N/2].imag = even[k].imag - t.imag;}free(even);}int main(void) {int N = 8;Complex* x = (Complex*) malloc(N * sizeof(Complex));// 初始化输入信号for (int i = 0; i < N; i++) {x[i].real = i;x[i].imag = 0;}fft(x, N);printf("傅里叶变换结果：\n");for (int i = 0; i < N; i++) {printf("X[%d] = %.2f + %.2fi\n", i, x[i].real, x[i].imag);}free(x);return 0;}```该程序演示了如何通过C代码实现傅里叶变换。
快速傅里叶变换fft的c程序代码实现
快速傅里叶变换fft的c程序代码实现标题：一种高效实现快速傅里叶变换(FFT)的C语言程序代码导言：快速傅里叶变换（Fast Fourier Transform，FFT）是一种在信号处理、图像处理、通信系统等领域广泛应用的重要算法。
它通过将输入信号从时域转换到频域，实现了对信号的频谱分析和频率成分提取。
在实际应用中，为了获得高效的FFT计算过程，我们需要使用合适的算法和优化技巧，并将其转化为高质量的C语言代码。
本文将介绍一种基于Cooley-Tukey算法的快速傅里叶变换的C语言程序代码实现。
我们将从原理开始详细讲解FFT算法，然后逐步引入代码实现的步骤，并进行相关优化。
我们将总结整个实现过程，并分享一些个人对FFT算法的理解和观点。
一、快速傅里叶变换（FFT）的原理（1）傅里叶级数与离散傅里叶变换傅里叶级数是将一个周期函数分解为一系列正弦和余弦函数的和的方法。
然而，实际数字信号往往是离散的。
我们需要离散傅里叶变换（Discrete Fourier Transform，DFT）来对离散信号进行频谱分析。
（2）DFT的定义及其计算复杂度离散傅里叶变换通过对离散信号的变换矩阵进行乘法运算，得到其频谱表示。
然而，直接使用定义式计算DFT的时间复杂度为O(N^2)，其中N为信号长度，这对于大规模信号计算是不可接受的。
（3）引入快速傅里叶变换 (FFT)Cooley-Tukey算法是一种最常用的FFT算法，通过将DFT分解为多个较小规模的DFT计算来降低计算复杂度。
FFT的时间复杂度为O(NlogN)，大大提高了计算效率。
二、快速傅里叶变换（FFT）的C语言实现（1）算法流程和数据结构设计以一维FFT为例，我们需要定义合适的数据结构来表示复数和存储输入输出信号，同时设计实现FFT的主要流程。
（2）递归实现方法递归实现是最直观的FFT实现方法，基于Cooley-Tukey算法的思想。
将输入信号分为偶数和奇数两部分，然后递归计算它们的FFT。
c语言傅里叶处理函数
c语言傅里叶处理函数C语言傅里叶处理函数傅里叶变换是一种重要的信号处理方法，广泛应用于图像处理、音频处理、通信等领域。
在C语言中，我们可以使用傅里叶处理函数来实现对信号的频域分析和频谱变换。
本文将介绍C语言中常用的傅里叶处理函数及其使用方法。
一、傅里叶变换简介傅里叶变换是一种将时域信号转换为频域信号的数学方法，可以将信号分解为一组不同频率的正弦和余弦函数的叠加。
傅里叶变换的基本原理是利用正弦和余弦函数的周期性特点，将信号分解为不同频率的谐波分量，从而得到信号的频谱信息。
二、C语言中的傅里叶处理函数在C语言中，我们可以使用多种库函数或自定义函数来实现傅里叶变换。
以下是常用的傅里叶处理函数及其功能介绍。
1. FFT（快速傅里叶变换）FFT是一种高效的傅里叶变换算法，能够快速计算离散信号的频域分析。
在C语言中，我们可以使用FFTW库或自己实现FFT算法来进行快速傅里叶变换。
2. DFT（离散傅里叶变换）DFT是一种将离散信号转换为离散频谱的变换方法。
在C语言中，我们可以使用库函数如fftw_plan_dft_1d()来计算离散傅里叶变换。
3. IFFT（逆傅里叶变换）IFFT是傅里叶变换的逆运算，可以将频域信号恢复为时域信号。
在C语言中，我们可以使用库函数如fftw_plan_dft_1d()和fftw_execute()来计算逆傅里叶变换。
三、傅里叶处理函数的使用方法使用傅里叶处理函数进行信号处理的一般步骤如下：1. 导入相关库函数或自定义函数。
2. 定义输入信号和输出信号的数组。
3. 对输入信号进行傅里叶变换或逆傅里叶变换。
4. 分析或处理得到的频谱数据。
5. 可选地进行逆傅里叶变换，将频域信号恢复为时域信号。
以下是一个简单的示例，展示了如何使用FFTW库函数进行傅里叶变换和逆傅里叶变换：```c#include <stdio.h>#include <fftw3.h>#define N 16int main() {double in[N], out[N];fftw_complex *out_complex;fftw_plan plan;// 初始化输入信号for (int i = 0; i < N; i++) {in[i] = i;}// 创建傅里叶变换的输入输出数组out_complex = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * (N/2+1));// 创建傅里叶变换的计划plan = fftw_plan_dft_r2c_1d(N, in, out_complex, FFTW_ESTIMATE);// 执行傅里叶变换fftw_execute(plan);// 输出频谱数据for (int i = 0; i < N/2+1; i++) {printf("频率%d: 幅度%f 相位%f\n", i, cabs(out_complex[i]), carg(out_complex[i]));}// 销毁计划和临时数组fftw_destroy_plan(plan);fftw_free(out_complex);return 0;}```四、总结本文介绍了C语言中常用的傅里叶处理函数及其使用方法。
c实现快速傅里叶变换输出频谱
标题：C语言实现快速傅里叶变换输出频谱一、简介在信号处理和频域分析中，快速傅里叶变换（FFT）是一种常用的算法，用于将时域的信号转换为频域的频谱。
在C语言中实现快速傅里叶变换可以帮助我们对信号进行高效的频域分析。
本文将从基础开始，介绍C语言实现快速傅里叶变换并输出频谱的方法。
二、快速傅里叶变换概述快速傅里叶变换是一种将离散信号转换为频域表示的算法，它将N个离散时间域采样点转换成N个频域采样点。
快速傅里叶变换算法的核心是分治法，通过递归地将信号分解为奇偶部分，然后合并计算，从而实现高效的频谱分析。
三、C语言实现快速傅里叶变换1. 我们需要定义一个复数结构体，用于表示实部和虚部。
在C语言中，可以使用结构体来表示复数，例如：```ctypedef struct {double real; // 实部double imag; // 虚部} Complex;```2. 接下来，我们可以编写一个函数来实现快速傅里叶变换。
在函数中，我们可以按照快速傅里叶变换的递归算法，将信号分解为奇偶部分，并进行合并计算，最终得到频域表示的频谱。
```cvoid FFT(Complex* x, int N, int inv) {// 实现快速傅里叶变换的代码// ...}```3. 在实现快速傅里叶变换的过程中，我们还需要编写一些辅助函数，例如计算旋转因子和进行信号分解合并等操作。
四、输出频谱在C语言中实现快速傅里叶变换后，我们可以将得到的频域表示的频谱输出到文件或者直接在终端进行可视化。
通过频谱分析，我们可以了解信号的频域特性，包括频率成分、频谱密度等信息。
五、个人观点和理解C语言实现快速傅里叶变换需要深入理解算法的原理，同时对C语言的数据结构和递归算法有一定的掌握。
在实际应用中，我们可以将快速傅里叶变换应用于音频处理、图像处理、通信系统等领域，对信号的特性进行频域分析。
六、总结通过本文的介绍，我们了解了C语言实现快速傅里叶变换并输出频谱的方法。
c语言快速傅里叶变
c语言快速傅里叶变快速傅里叶变换的实现可以使用递归或迭代两种方式：1. 递归实现递归版本的快速傅里叶变换（FFT）是一种标准实现方法，它的时间复杂度为O(n * log2(n))。
快速傅里叶变换的代码实现如下：```void fft(double complex* x, int n){if(n == 1)return;double complex odd[n/2], even[n/2];for(int i=0, j=0; i<n; i+=2, j++){even[j] = x[i];odd[j] = x[i+1];}fft(even, n/2);fft(odd, n/2);for(int i=0; i<n/2; i++){double complex t = cexp(-I * 2 * M_PI * i / n) * odd[i];x[i] = even[i] + t;x[i+n/2] = even[i] - t;}}```2. 迭代实现迭代实现 FFT 的主要思路是根据蝴蝶定理将一次变换的复杂度降为 O(n)，多次迭代后复杂度为 O(n*logn)。
代码实现如下：```void fft(double complex* x, int n){int k = log2(n);double complex w[n/2];for (int i=0; i<n/2; i++)w[i] = cexp(-I * 2 * M_PI * i / n);for (int i=0; i<k; i++)for (int j=0; j<n; j++)if (!(j & (1<<i))){int x1 = j, x2 = j | (1<<i);double complex t = x[x2] * w[x2 & ((1<<i)-1)];x[x2] = x[x1] - t;x[x1] += t;}}```以上两种方式都是可行的，但是迭代实现方式更加快速。
fft的C语言实现
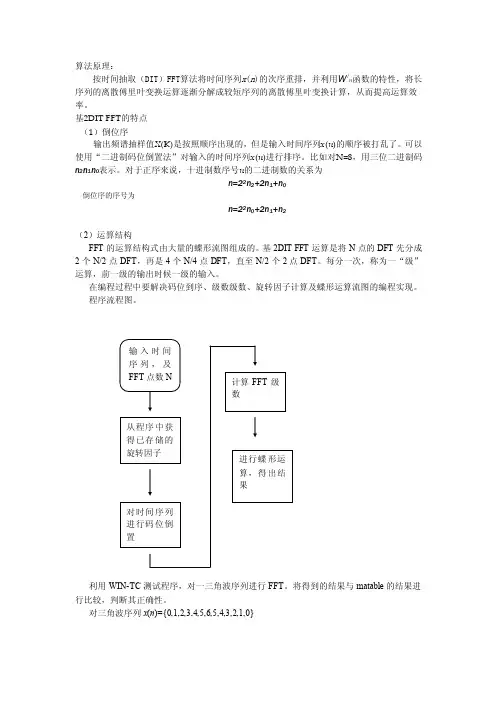
算法原理：按时间抽取（DIT）FFT算法将时间序列x(n)的次序重排，并利用W i n函数的特性，将长序列的离散傅里叶变换运算逐渐分解成较短序列的离散傅里叶变换计算，从而提高运算效率。
基2DIT FFT的特点（1）倒位序输出频谱抽样值X(K)是按照顺序出现的，但是输入时间序列x(n)的顺序被打乱了。
可以使用“二进制码位倒置法”对输入的时间序列x(n)进行排序。
比如对N=8，用三位二进制码n2n1n0表示。
对于正序来说，十进制数序号n的二进制数的关系为n=22n2+2n1+n0倒位序的序号为n=22n0+2n1+n2（2）运算结构FFT的运算结构式由大量的蝶形流图组成的。
基2DIT FFT运算是将N点的DFT先分成2个N/2点DFT，再是4个N/4点DFT，直至N/2个2点DFT。
每分一次，称为一“级”运算，前一级的输出时候一级的输入。
在编程过程中要解决码位到序、级数级数、旋转因子计算及蝶形运算流图的编程实现。
程序流程图。
利用WIN-TC测试程序，对一三角波序列进行FFT。
将得到的结果与matable的结果进行比较，判断其正确性。
对三角波序列x(n)={0,1,2,3,4,5,6,5,4,3,2,1,0}在WIN-TC进行128点FFT，得到前6个结果Matable仿真的前6个结果是XKN2 =Columns 1 through 636.0000 34.2084 -10.3770i 29.1007 -19.4445i 21.4292 -26.1115i 12.2946 -29.6817i 2.9501 -29.9525i前半段波形对比显示WIN-TC结果能保证小数点后2位的精度。
对方波序列x(n),长度为64，前32为1，幅值为1的序列在WIN-TC进行128点FFT，得到前6个结果Matable仿真的前6个结果是Columns 1 through 632.0000 20.8677 -19.8677i 1.0000 -20.3555i -6.2783 - 7.2783i 04.5539 - 3.5539i仿真波形对比显示WIN-TC结果能保证小数点后2位的精度。
[C++]频谱图中FFT快速傅里叶变换C++实现
![[C++]频谱图中FFT快速傅里叶变换C++实现](https://img.taocdn.com/s3/m/f1be4c19773231126edb6f1aff00bed5b9f373d0.png)
[C++]频谱图中FFT快速傅⾥叶变换C++实现在项⽬中，需要画波形频谱图，因此进⾏查找，不是很懂相关知识，下列代码主要是针对这篇⽂章。
//快速傅⾥叶变换/*⼊⼝参数：inv： =1,傅⾥叶变换; =-1,逆傅⾥叶变换N：输⼊的点数，为偶数，⼀般为2的幂次级，2,4,8,16...k: 满⾜N=2^k（k>0）,实质上k是N个采样数据可以分解为偶次幂和奇次幂的次数real[]: inv=1时，存放N个采样数据的实部，inv=-1时，存放傅⾥叶变换的N个实部imag[]: inv=1时，存放N个采样数据的虚部，inv=-1时，存放傅⾥叶变换的N个虚部出⼝参数：real[]: inv=1时，返回傅⾥叶变换的实部，inv=-1时，返回逆傅⾥叶变换的实部imag[]: inv=1时，返回傅⾥叶变换的虚部，inv=-1时，返回逆傅⾥叶变换的虚部*/void FFT::dealFFT(double real[], double imag[], double dSp[], int N, int k, int inv){int i, j, k1, k2, m, step, factor_step;double temp_real, temp_imag, factor_real, factor_imag;if (inv != 1 && inv != -1)return;//double *real = new double[N];//double *imag = new double[N];//倒序j = 0;for (i = 0; i < N; i++){if (j>i){temp_real = real[j];real[j] = real[i];real[i] = temp_real;temp_imag = imag[j];imag[j] = imag[i];imag[i] = temp_imag;}m = N / 2;while (j >= m&&m != 0){j -= m;m >>= 1;}j += m;}//蝶形运算for (i = 0; i < k; i++){step = 1 << (i + 1);factor_step = N >> (i + 1); //旋转因数变化速度//初始化旋转因⼦factor_real = 1.0;factor_imag = 0.0;for (j = 0; j < step / 2; j++){for (k1 = j; k1 < N; k1 += step){k2 = k1 + step / 2; //蝶形运算的两个输⼊/* temp_real = real[k1] + real[k2] * factor_real - imag[k2] * factor_imag;temp_imag = imag[k1] + real[k2] * factor_imag + imag[k2] * factor_real;real[k2] = real[k1] - (real[k2] * factor_real - imag[k2] * factor_imag);imag[k2] = imag[k1] - (real[k2] * factor_imag + imag[k2] * factor_real);real[k1] = temp_real;imag[k1] = temp_imag;*///上⾯⽅法虽然直⽩，但效率太低，稍微改变结构如下：temp_real = real[k2] * factor_real - imag[k2] * factor_imag;temp_imag = real[k2] * factor_imag + imag[k2] * factor_real;real[k2] = real[k1] - temp_real;imag[k2] = imag[k1] - temp_imag;real[k1] = real[k1] + temp_real;imag[k1] = imag[k1] + temp_imag;}factor_real = inv*cos(-2 * PI*(j + 1)*factor_step / N);factor_imag = inv*sin(-2 * PI*(j + 1)*factor_step / N);}}if (inv == -1){for (i = 0; i <= N - 1; i++){real[i] = real[i] / N;imag[i] = imag[i] / N;}}for (i = 0; i<N;i++){dSp[i] = sqrt(real[i] * real[i] + imag[i] * imag[i]);}}⼀般好像需要进⾏下转换，即后半部分和前半部分置换，即1234变成3412.void FFT::FFTShift(double dp[], int len){for (int i = 0; i < len / 2; i++){double tmp = dp[i];dp[i] = dp[i + len / 2];dp[i + len / 2] = tmp;}}此时得到的应该是实部和虚部解出来的频谱图的Y轴电压值，⼀般频谱图Y轴为dB，因此需要进⾏转换void FFT::getFFT(double dRe[], double dIm[], double dSp[], int len, int nBits, double dWorkingImpedance){dealFFT(dRe, dIm, dSp, len, nBits, 1);FFTShift(dSp,len); //此时得到的应该是实部和虚部解出来的频谱图的Y轴电压值，还需要转换////dBW = 10lg(电压^2/阻抗);dBm =dBW+30，注意电压单位是Vfor (int i = 0; i<len; i++){dSp[i] = 10 * log10(dSp[i] * dSp[i] / dWorkingImpedance)+30;}}getFFT()输出之后的dp才是要的频谱图Y轴值，频谱图X轴的坐标得到通过以下⽅式：//X轴精确度，采样频率/数据个数 = 步长m_DeltaX_S = m_dataPara.nSampleFrequency / nDataNumOfPage_S;data_SX[i / 2] = m_dataPara.nCenterFrequency + count*m_DeltaX_S - m_dataPara.nWorkingBandWidth/2;//中⼼频率+当前点*步长-带宽/2在项⽬中，实际代码如下：int count = 0;for (int i = 0; i < nDataNumOfPage_S * 2; i++){if (i % 2 == 0)data_SQ[i / 2] = data_S[i] * m_DeltaY_S;elsedata_SI[i / 2] = data_S[i] * m_DeltaY_S;if (i % 2 == 0){count++;data_SX[i / 2] = m_dataPara.nCenterFrequency + count*m_DeltaX_S - m_dataPara.nWorkingBandWidth/2;}}m_dataPara.nWorkingImpedance = 50;FFT fft;int nBits = log10(nDataNumOfPage_S) / log10(2);//因为参数需要是2的N次⽅fft.getFFT(data_SQ, data_SI, data_SS, nDataNumOfPage_S, nBits, m_dataPara.nWorkingImpedance); LoadData_S(data_SX, data_SS, nDataNumOfPage_S);。
fft算法c语言实现
fft算法c语言实现快速傅里叶变换（FFT）是一种高效的离散傅里叶变换算法，用于计算信号在频域的表示。
下面是一个简单的使用 C 语言实现的 FFT 算法示例，它可以用于对输入的时域信号进行离散傅里叶变换。
```c#include <stdio.h>#include <stdlib.h>#include <math.h>#define N 16// 复数结构体typedef struct {double real;double imag;} Complex;// 初始化复数void initComplex(Complex *c, double real, double imag) {c->real = real;c->imag = imag;}// FFT 算法void fft(Complex *c, int n) {int i, j, k;Complex w, u, v;// 层次遍历for (i = 1; i < n; i <<= 1) {// 旋转因子w.real = cos(2 * M_PI * i / n);w.imag = -sin(2 * M_PI * i / n);for (j = 0; j < n; j += i) {for (k = 0; k < i / 2; k++) {u.real = c[j + k].real;u.imag = c[j + k].imag;v.real = c[j + i / 2 + k].real;v.imag = c[j + i / 2 + k].imag;c[j + k].real = u.real + w.real * v.real - w.imag * v.imag; c[j + k].imag = u.imag + w.real * v.imag + w.imag * v.real; c[j + i / 2 + k].real = u.real - w.real * v.real + w.imag * v.imag; c[j + i / 2 + k].imag = u.imag - w.real * v.imag - w.imag * v.real; }}}}// 打印复数void printComplex(Complex c) {printf("%f + %fi\n", c.real, c.imag);}int main() {Complex c[N];// 输入的时域信号for (int i = 0; i < N; i++) {c[i].real = rand() / RAND_MAX;c[i].imag = rand() / RAND_MAX;}printf("输入的时域信号：\n");// 打印输入的时域信号for (int i = 0; i < N; i++) {printComplex(c[i]);}fft(c, N);printf("经过 FFT 变换后的频域信号：\n");// 打印经过 FFT 变换后的频域信号for (int i = 0; i < N; i++) {printComplex(c[i]);}return 0;}```上述代码是一个简单的 C 语言实现的 FFT 算法示例。