合肥工业大学材料力学习题册答案

合集下载

材料力学课后习题答案详细

Rr (R r) (3 104 ) (60 30) 0.009mm
变形厚的壁厚：
(R r) | (R r) | 30 0.009 29.991(mm)
[习题 2-11] 受轴向拉力 F 作用的箱形薄壁杆如图所示。已知该材料的弹性
常数为 E, ，试求 C 与 D 两点间的距离改
22

N 22 A

10 103 N 400mm 2
25MPa
33

N 33 A
10 103 N 400mm 2
25MPa
[习题 2-3] 试求图示阶梯状直杆横截面 1-1、2-2 和平 3-3 上的轴力，并作
轴力图。若横截面面积 A1 200mm2 ， A2 300mm2 ， A3 400mm2 ，并求各横截面上的应力。
A1 11.503cm2 1150.3mm2
AE

N EA A

366.86 103 N 2 1150.3mm2
159.5MPa
EG

N EG A

357.62 103 N 2 1150.3mm2
155.5MPa
[习题 2-5] 石砌桥墩的墩身高 l 10m ，其横截面面尺寸如图所示。荷载
22

N 22 A2

10 103 N 300mm 2
33.3MPa
3
33

N 33 A
10 103 N 400mm 2
25MPa
[习题 2-4] 图示一混合屋架结构的计算简图。屋架的上弦用钢筋混凝土制
成。下面的拉杆和中间竖向撑杆用角钢构成，其截面均
为两个 75mm 8mm 的等边角钢。已知屋面承受集度为

材料力学习题册参考答案

材料力学习题册参考答案材料力学习题册参考答案（无计算题）第1章：轴向拉伸与压缩一：1（ABE ）2（ABD ）3（DE ）4（AEB ）5（C ）6（ＣＥ）７（ABD ）8（C ）9（BD ）10（ADE ）11（ACE ）12（D ）13（CE ）14（D ）15（ＡＢ）１６（BE ）17（D ）二：1对2错3错4错5对6对7错8错9错10错11错12错13对14错15错三：1：钢铸铁 2：比例极限p σ 弹性极限e σ 屈服极限s σ 强度极限b σ3.横截面 45度斜截面4. εσE =， EAFl l =5.强度，刚度，稳定性；6.轴向拉伸（或压缩）；7. llb b ?μ?=8. 1MPa=106 N/m 2 =1012 N/mm 2 9. 抵抗伸缩弹性变形，加载方式 10. 正正、剪 11.极限应力 12. >5% <5% 13. 破坏s σ b σ 14.强度校核截面设计荷载设计15. 线弹性变形弹性变形 16.拉应力 45度 17.无明显屈服阶段的塑性材料力学性能参考答案：1. A 2. C 3. C 4. C 5. C 6. 5d ; 10d 7. 弹塑8. s2s 9. 0.1 10. 压缩11. b 0.4σ 12. <；< 剪切挤压答案：一：1.（C ），2.（B ），3.（A ），二：1. 2bh db 2. b(d+a) bc 3. 4a δ a 2 4. F第2章：扭转一：1.（B ） 2.（C D ） 3.（C D ） 4. （C ） 5. （A E ） 6. （A ）7. （D ）8. （B D ） 9.（C ） 10. （B ） 11.（D ） 12.（C ）13.（B ）14.（A ） 15.（A E ）二：1错 2对 3对 4错 5错 6 对三：1. 垂直 2. 扭矩剪应力 3.最外缘为零4. p ττ< 抗扭刚度材料抵抗扭转变形的能力5. 不变不变增大一倍6. 1.5879τ7.实心空心圆8. 3241)(α- 9. m ax m in αττ= 10. 长边的中点中心角点 11.形成回路（剪力流）第3章：平面图形的几何性质一：1.（C ），2.（A ），3.（C ），4.（C ），5.（A ），6.（C ），7.（C ），8.（A ），9.（D ）二：1）. 1；无穷多；2）4)4/5(a ； 3），84p R I π=p 4z y I 16R I I ===π4）12/312bh I I z z ==；5）)/(/H 6bh 6BH W 32z -= 6）12/)(2211h b bh I I I I z y z y +=+=+；7）各分部图形对同一轴静矩8）两轴交点的极惯性矩；9）距形心最近的；10）惯性主轴；11）图形对其惯性积为零三：1：64/πd 114； 2.（0 , 14.09cm ）(a 22，a 62)3： 4447.9cm 4， 4：0.00686d 4 ，5: 77500 mm 4 ;6: 64640039.110 23.410C C C C y y z z I I mm I I mm ==?==?第4章：弯曲内力一：1.（A B ）2.（D ）3.（B ）4.（A B E ）5.（A B D ）6.（ACE ） 7.（ABDE ） 8.（ABE ）9. （D ） 10. （D ） 11.（ACBE ） 12.（D ） 13.（ABCDE ）二：1错 2错 3错 4对 5错 6对 7对三：1. 以弯曲变形 2.集中力 3. KNm 2512M .max =4. m KN 2q = 向下 KN 9P = 向上5.中性轴6.荷载支撑力7. 小8. 悬臂简支外伸9. 零第5章：弯曲应力一：1（ＡＢＤ）２．（C ）3.（BE ）4.（A ）5.（C ）6.（C ）7.（B ）8.（C ）9.（BC ）二：1对 2错 3错 4 对 5 错 6错 7 对三：1.满足强度要求更经济、更省料2. 变成曲面，既不伸长也不缩短3.中性轴4.形心主轴5.最大正应力6.剪力方向7.相等8.平面弯曲发生在最大弯矩处9.平面弯曲第6章：弯曲变形一：1（B ），2（B ），3（A ），4（D ），5（C ），6（A ），7（C ），8（B ），9（A ）10（B ），11（A ）二：1对2错3错4错5错6对7错8错9错10对11错12对三：1.（转角小量:θθtan ≈）（未考虑高阶小量对曲率的影响）2. 挠曲线采用近似微分方程导致的。

合工大 05-06二学期材料力学(Ⅱ)试卷B答案(重修)(柳).doc

一、简答题（37分）1．若将圆形截面杆的直径增加一倍，试问杆的抗拉（压）刚度、抗扭刚度和抗弯刚度各增加多少倍？（6分）解：直径为d 的圆杆件：4 321d GI P π=，4 641d EI Z π=，2 41d EA π= 直径为2d 的圆杆件：()42 321d GI P π=，()42 641d EI Z π=，()22 41d EA π= 所以，抗拉压刚度增加3倍，抗扭刚度和抗弯刚度各增加15倍2. 试求图示平面图形的形心坐标。

设D b a << ,，挖去部分可看作矩形。

（5分）解：0=C xabD abab D ab y C 44422--=--=ππ3．试写出用积分法求图示梁弯曲变形时确定积分常数的边界条件和连续条件。

（4分）qa2/2光滑连续性条件是：右左右左＝，＝θθ ,y y a x =4．试画出图示1-1截面上a 、b 两点的单元体图。

（具体应力值不需计算）。

（6分）解： A 点B 点5. 试求图示矩形截面细长压杆的临界压力。

材料的弹性模量为E 。

（8分）解，压杆为细长杆件，所以临界压力可以使用欧拉公式计算。

即:()()962121 ,143min2min2d d d I u ul EI F cr =⎪⎭⎫⎝⎛===π∴ 24296lEd F cr π=6. 重量为P 的重物自高度h 处自由下落至抗弯刚度为EI 的悬臂梁中点C 处。

试求动荷系数d K 。

（8分）解：EIPa st 33=δ336113211211Pa hEIPa EI h hK std ++=∙++=++=δ二、计算题（63分）1. 图示为铰接的正方形结构，各杆的横截面面积均为A ，材料均为铸铁，其许用压应力与许用拉应力的比值为3]/[][t c =σσ解：AB ，BC ，CD ，AD ，CA 各杆件的受力是：F F AB 2-=F F BC =，F F CD =，F F CA 2-=，0=AD F由于各杆件的横截面积均为A压杆AB 杆危险：[][]t c AB c A F A F σσσ32=≤==，[][]A F t σ23=⇒拉杆BC 或者CD 杆危险：[]t BC t AFA F σσ≤==，[][]A F t σ=⇒(b )2/A B∴ 结构的许可载荷为[][][]3AA F c t σσ==2. 试作图示悬臂梁的剪力图和弯矩图，并给出max ||M 和max Q ||F 。

材料力学完整课后习题答案

习题2-2一打入基地内的木桩如图所示，杆轴单位长度的摩擦力fkx2，试做木桩的后力图。

解：由题意可得：l 1 0 fdx F 有kl 3 F k 3F / l 3 3 l FN x1 3Fx 2 / l 3dx F x1 / l 3 0习题2-3 石砌桥墩的墩身高l 10m ，其横截面面尺寸如图所示。

荷载 F 1000kN ，材料的密度2.35kg / m 3 ，试求墩身底部横截面上的压应力。

解：墩身底面的轴力为：N F G F Alg 2-3 图1000 3 2 3.14 12 10 2.35 9.8 3104.942kN 墩身底面积： A 3 2 3.14 12 9.14m 2 因为墩为轴向压缩构件，所以其底面上的正应力均匀分布。

N 3104.942kN 339.71kPa 0.34MPa A 9.14m 2习题2-7 图示圆锥形杆受轴向拉力作用，试求杆的伸长。

2-7 图解：取长度为dx 截离体（微元体）。

则微元体的伸长量为：Fdx l F F l dx d l ，l dx EA x 0 EA x E 0 A x r r1 x r r d d1 d ，r 2 1 x r1 2 x 1 ，r2 r1 l l 2l 2 d d1 d d1 d d1 2 d d A x 2 x 1 u2 ，d 2 x 1 du 2 dx 2l 2 2l 2 2l 2l 2l dx d d 2l du dx du ，2 2 1 du 2 d 2 d1 A x u d1 d 2 u l F F l dx 2 Fl l du 因此，l dx 0 u 2 0 EA x E 0 A x E d1 d 2 l 2 Fl 1 l 2 Fl 1 u E d d d d E d1 d 2 0 2 2 d 1 1 x 1 2l 2 0 2 Fl 1 1 E d1 d 2 d 2 d 1 dd1 l 1 2l 2 2 2 Fl 2 2 4 Fl E d1 d 2 d 2 d1 Ed 1 d 2习题2-10 受轴向拉力 F 作用的箱形薄壁杆如图所示。

合肥工业大学工程力学练习册答案5—12章-c10f1d744431b90d6c85c77e

五轴向拉伸与压缩
5– 1 试求图示各杆横截面 1-1、2-2、3-3上的轴力，并作轴
力图。
2-2上的正应力。
解： 1．轴力
由截面法可求得，杆各横截面上的轴力为
2．应力
Pa
MPa
Pa
MPa
5– 2 一根中部对称开槽的直杆如图所示。试求横截面 1-1和
5– 3 一桅杆起重机如图所示。起重杆 AB的横截面是外径为 20
剪应力。
8–8长度为 250mm，截面尺寸为
的薄钢尺，由于
两端外力偶的作用而弯成中心角为的圆弧。已知弹性模量。试求钢尺横截面上的最大正应力。
解：根据题意，
可以得到
故钢尺横截面上的最大正应力为
解： 1．求 1-1截面上的剪力和弯矩
：
，
∴ 1-1截面上的剪力和弯矩为：
，
2．求 1-1截面上 a、b两点的应力
3．当 P和共同作用时，
(b) 1．当 q单独作用时，查表得
由剪切强度条件
≤ ，可得
MPa
≥
m
mm
解：设每个螺栓承受的剪力为 Q，则由
可得
螺栓的剪应力
MPa ∴ 螺栓满足剪切强度条件。
Pa 11-7
6– 3矩形截面木拉杆的接头如图所示。已知轴向拉力
kN，截面
宽度
mm，木材的顺纹容许挤压应力
MPa，顺纹的容许
剪应力
MPa，求接头处所需的尺寸 L和 a。
6– 4螺栓接头如图所示。已知
每个螺栓承受的轴向为
由螺栓强度条件 ≤
可得螺栓的直径应为 ≥
11-4
5– 9一铰接结构由杆 AB和 AC组成如图所示。杆 AC的长度为杆 AB的两

(完整版)材料力学课后习题答案

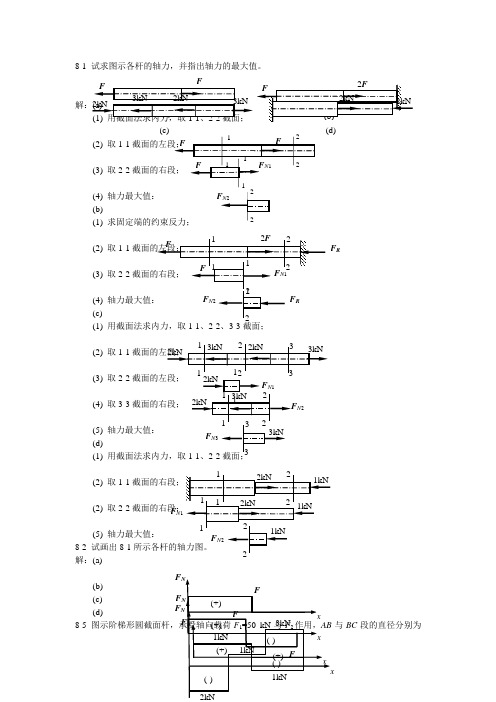
8-1 试求图示各杆的轴力，并指出轴力的最大值。

(2) 取1-1(3) 取2-2(4) 轴力最大值： (b)(1) 求固定端的约束反力； (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力，取1-1、2-2、3-3截面；(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段；(5) 轴力最大值： (d)(1) 用截面法求内力，取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值： 8-2 试画出8-1解：(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求载荷F 2之值。

解：(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ，如欲使AB 与BC 段横截面上的正应力相同，试求BC 段的直径。

解：(1)用截面法求出1-1、2-2截面的轴力；(2) 求1-1、2-2截面的正应力，利用正应力相同；8-7 图示木杆，承受轴向载荷F =10 kN 作用，杆的横截面面积A =1000 mm 2，粘接面的方位角θ= 450，试计算该截面上的正应力与切应力，并画出应力的方向。

解：(1) (2) 8-14 2=20 mm ，两杆F =80 kN 作用，试校核桁架的强度。

解：(1) 对节点A(2) 列平衡方程解得： (2) 8-15 图示桁架，杆1A 处承受铅直方向的载荷F 作用，F =50 kN ，钢的许用应力[σS ] =160 MPa ，木的许用应力[σW ] =10 MPa 。

解：(1) 对节点A (2) 84 mm 。

8-16 题8-14解：(1) 由8-14得到的关系；(2) 取[F ]=97.1 kN 。

8-18 图示阶梯形杆A 2=100 mm 2，E =200GPa ，试计算杆AC 的轴向变形解：(1) (2) AC 8-22 图示桁架，杆1与杆2的横截面面积与材料均相同，在节点A 处承受载荷F 作用。

材料力学课后习题答案详细

由对称性可知，受力CH图 0
N1 N 2 0.5F 0.5 20 10(kN )
10
（2）求 C 点的水平位移与铅垂位移。变形协调图
A
点的铅垂位移：l1

N1l EA1

10000N 1000mm 210000N / mm2 100mm2
0.476mm
B 点的铅垂位移： l2
材料可认为符合胡克定律，其弹性模量 E 10GPa 。如不计柱的自重，试求：
（1）作轴力图；
（2）各段柱横截面上的应力；
（3）各段柱的纵向线应变；
（4）柱的总变形。
解：（1）作轴力图
N AC 100kN NCB 100 160 260(kN )
轴力图如图所示。
（2）计算各段上的应力
第二章轴向拉(压)变形
[习题 2-1] 试求图示各杆 1-1 和 2-2 横截面上的轴力，并作轴力图。（a）解：（1）求指定截面上的轴力
N11 F N 22 2F F F
（2）作轴力图轴力图如图所示。
（b）解：（1）求指定截面上的轴力
N11 2F N 22 2F 2F 0
如以表示斜截面与横截面的夹角，试求当 0o ,30o ,45o ,60o ,90o 时各斜截面
上的正应力和切应力，并用图表示其方
向。
解：斜截面上的正应力与切应力的公式
为：
5
0 cos 2

0 2
sin 2
式中， 0

N A

10000 N 100mm 2
100MPa ，把
示。
由平平衡条件可得：
X 0
N EG N EA cos 0

材料力学全部习题解答

弹性模量
b
E 2 2 0 M P a 2 2 0 1 0 9P a 2 2 0 G P a 0 .1 0 0 0
s
屈服极限 s 240MPa
强度极限 b 445MPa
伸长率 ll010000m ax2800
由于 280;故0该50 材0料属于塑性材料;
13
解：1由图得
弹性模量 E0 3.550110063700GPa
A x l10.938m m
节点A铅直位移
A ytan 4 l150co sl4 2503.589m m
23
解：1 建立平衡方程由平衡方程
MB 0 FN1aFN22aF2a
FN 2 FN1
得： FN12F1N22F
l1
l2
2.建立补充方程
3 强度计算联立方程1和方
程（2）;得
从变形图中可以看出;变形几何关
l
l0
断面收缩率
AAA110000d22d22d2121000065.1900
由于 2故.4 属6 % 于塑5 性% 材料;
15
解：杆件上的正应力为
F A
4F D2 -d2
材料的许用应力为
要求
s
ns
由此得
D 4Fns d2 19.87mm
s
取杆的外径为
D19.87m m
16
FN1 FN 2
Iz= I（ za） I（ zR ） =1 a2 4
2R4 a4 R 4 =
64 12 4
27
Z
解 a沿截面顶端建立坐标轴z;，y轴不变; 图示截面对z，轴的形心及惯性矩为
0 .1
0 .5
y d A 0 .3 5 y d y2 0 .0 5 y d y

(完整版)材料力学习题集(有答案)汇总

11. 12. ；椭圆形13. 14.＞，=
一、是非题
2.1使杆件产生轴向拉压变形的外力必须是一对沿杆件轴线的集中力。（）
2.2轴力越大，杆件越容易被拉断，因此轴力的大小可以用来判断杆件的强度。（）
2.3内力是指物体受力后其内部产生的相互作用力。（）
2.4同一截面上， σ 必定大小相等，方向相同。（）
答：
扭转
1.一直径为的实心轴，另一内径为d,外径为D,内外径之比为的空心轴，若两轴横截面上的扭矩和最大切应力均分别相等，则两轴的横截面面积之比有四种答案：
(A) ；(B) ；(C) ；(D) 。
2.圆轴扭转时满足平衡条件，但切应力超过比例极限，有下述四种结论：
(A) (B) (C) (D)
切应力互等定理：成立不成立不成立成立
1.图示木接头，水平杆与斜杆成角，其挤压面积为为
（A）；（B）；
（C）；（D）。
答：C
2.图示铆钉连接，铆钉的挤压应力有如下四个答案
（A）；（B）；
（C）；（D）。
答：B
3.切应力互等定理是由单元体
（A）静力平衡关系导出的；（B）几何关系导出的；
（C）物理关系导出的；（D）强度条件导出的。
(A) ; (B) ; (C) ; (D) 。
2.对于没有明显屈服阶段的塑性材料，通常以表示屈服极限。其定义有以下四个结论，正确的是哪一个？
(A)产生2%的塑性应变所对应的应力值作为屈服极限；
(B)产生0.02%的塑性应变所对应的应力值作为屈服极限；
(C)产生0.2%的塑性应变所对应的应力值作为屈服极限；
(A)外径和壁厚都增大；(B)外径和壁厚都减小；
(C)外径减小，壁厚增大；(D)外径增大，壁厚减小。

材料力学习题大全及答案

习题2-1图习题2-2图习题2-3图习题2-4图习题2-5图习题2-6图材料力学习题大全及答案第1章引论1－1 图示矩形截面直杆，右端固定，左端在杆的对称平面内作用有集中力偶，数值为M 。

关于固定端处横截面A －A 上的内力分布，有四种答案，根据弹性体的特点，试分析哪一种答案比较合理。

正确答案是 C 。

1－2 图示带缺口的直杆在两端承受拉力F P 作用。

关于A －A 截面上的内力分布，有四种答案，根据弹性体的特点，试判断哪一种答案是合理的。

正确答案是 D 。

1－3 图示直杆ACB 在两端A 、B 处固定。

关于其两端的约束力有四种答案。

试分析哪一种答案最合理。

正确答案是 D 。

1－4 等截面直杆在两端承受沿杆轴线的拉力F P 。

关于杆中点处截面A －A 在杆变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试判断哪一种答案是正确的。

正确答案是 D 。

1－5 图示等截面直杆在两端作用有力偶，数值为M ，力偶作用面与杆的对称面一致。

关于杆中点处截面A －A 在杆变形后的位置（对于左端，由A A '→；对于右端，由A A ''→），有四种答案，试判断哪一种答案是正确的。

正确答案是 C 。

习题2-1图习题2-2图习题2-3图习题2-4图1－6 等截面直杆，其支承和受力如图所示。

关于其轴线在变形后的位置（图中虚线所示），有四种答案，根据弹性体的特点，试分析哪一种是合理的。

正确答案是 C 。

第2章杆件的内力分析2－1 平衡微分方程中的正负号由哪些因素所确定？简支梁受力及Ox 坐标取向如图所示。

试分析下列平衡微分方程中哪一个是正确的。

（A ）d d Q x F d M（B ）d d Q x F （C ）d d Q x F （D ）d d Q xF 2－2 对于图示承受均布载荷q 的简支梁，其弯矩图凸凹性与哪些因素相关？试判断下列四种答案中哪几种是正确的。

材料力学习题册答案-第3章扭转

第三章扭转之老阳三干创作一、是非判断题1.圆杆受扭时,杆内各点处于纯剪切状态. （×）2.杆件受扭时,横截面上的最年夜切应力发生在距截面形心最远处. （×）3.薄壁圆管和空心圆管的扭转切应力公式完全一样. （×）4.圆杆扭转变形实质上是剪切变形. （×）5.非圆截面杆不能应用圆截面杆扭转切应力公式,是因为非圆截面杆扭转时“平截面假设”不能成立. （√）6.资料相同的圆杆,他们的剪切强度条件和扭转强度条件中,许用应力的意义相同,数值相等. （×）7.切应力互等定理仅适用于纯剪切情况. （×）8.受扭杆件的扭矩,仅与杆件受到的转矩（外力偶矩）有关,而与杆件的资料及其横截面的年夜小、形状无关. （√）9.受扭圆轴在横截面上和包括轴的纵向截面上均无正应力.（√）10.受扭圆轴的最年夜切应力只呈现在横截面上. （×）11.受扭圆轴内最年夜拉应力的值和最年夜切应力的值相等.（√）12.因木材沿纤维方向的抗剪能力差,故若受扭木质圆杆的轴线与木材纤维方向平行,当扭距到达某一极限值时,圆杆将沿轴线方向呈现裂纹. （×）二、选择题1.内、外径之比为α的空心圆轴,扭转时轴内的最年夜切应力为τ,这时横截面上内边缘的切应力为（ B）A τ；B ατ；C 零； D（2.实心圆轴扭转时,不发生屈服的极限扭矩为T,若将其横截面面积增加一倍,则极限扭矩为（ C ）3.两根受扭圆轴的直径和长度均相同,但资料C分歧,在扭矩相同的情况下,它们的最年夜切应力τ、τ和扭转角ψ、ψ之间的关系为（ B ）τ2,φ1=φ2 τ2,φ 2 τ2,φ1=φ2 D2,φ24.阶梯圆轴的最年夜切应力发生在（ D ）A 扭矩最年夜的截面；B 直径最小的截面；C 单元长度扭转角最年夜的截面；D 不能确定.5.空心圆轴的外径为D,内径为d, α=d／D,其抗扭截面系数为（ D ）6.对受扭的圆轴,关于如下结论：①最年夜剪应力只呈现在横截面上；②在横截面上和包括杆件的纵向截面上均无正应力；③圆轴内最年夜拉应力的值和最年夜剪应力的值相等.现有四种谜底,正确的是（ A ）A ②③对B ①③对C ①②对D 全对D ）杆件.A 任意杆件；B 任意实心杆件；C 任意资料的圆截面；D 线弹性资料的圆截面.θ与（A ）无关.A 杆的长度；B 扭矩；C 资料性质；D 截面几何性质.9.若将受扭实心圆轴的直径增加一倍,则其刚度是原来的（ D ）A 2倍；B 4倍；C 8倍； D 16倍.三、计算题1.试用截面法求出图示圆轴各段内的扭矩T,并作扭矩图⑴试画出该轴的扭,扭矩图有何变动？,最年夜扭矩变小.3.如图所示的空心圆轴,外径D=100㎜,内径d=80㎜,l=500㎜,M=6kN/m,M=4kN/m. 请绘出轴的扭矩图,并求出最年夜剪应力解：扭矩图如上,则轴面极惯性矩I P则最年夜剪应力τmax4．图示圆形截面轴的抗扭刚度为每段长1m,试画出其扭矩图并计算出圆轴两真个相对扭转角.解：φAD=φAB+φBC+φCD φφ所以φ5.如图所示的阶梯形传动轴中,A轮输入的转矩M=800N•m,B﹑C和D••m.传动轴的许用切应力[τ]=400Mpa,许用扭转角[θ]=1°/m,资料的剪切弹性模量G=80Gpa.⑴试根据轴的强度条件和刚度条件,确定传动轴各段的直径.⑵若将传动轴改为等截面空心圆轴,并要求内外直径之比α=d/D=0.6,试确定轴的外径；并比力两种情况下轴的重量.解：（1τ］对AB 段同理得AC 段的d 段d 所以d 1应取值38.5mm,d 2应取值43.7mm,d 36.图示的传动轴长l=510㎜,直径D=50㎜.现将此轴的一段钻成内径d=25㎜的内腔,而余下一段钻成d=38㎜的内腔.若资料的许用切应力[τ]=70Mpa,试求：⑵若要求两段轴内的扭转角相等,则两段的长度应分别为几多？ρ即7.如图所示钢轴AD 的资料许用切应力[τ]=50Mpa,切变模量G=80Gpa,许用扭转角[θ°／m.作用在轴上的转矩M=800N •m,1200N •m,M=400N •m.试设计此轴的直径.解：由题意轴中最年夜扭矩为800N •Mg 根据轴的强度条件ττ］所以根据轴的刚度条件所以即轴的直径应取值43.4mm.8. 钻探机钻杆外经D=60㎜,内径d=㎜,功率P=7.355KW,轴的转速n=180r/min,杆钻入土层的深度l=40m,资料的切变模量G=80Gpa,许用切应力[τ]=40Mpa,假设土壤对钻杆的阻力沿长度均匀分布,试求：⑴土壤对钻杆单元长度的阻力矩m ； ⑵作钻杆的扭矩图,并进行强度校核；⑶计算A 、B 截面的相对扭转角.解：（1）由ML-T=0 则(2)扭矩图如图所示（3）两端截面的相对扭转角为Φ感谢土木0902班石李、臧明远同学！。

合肥工业大学工程力学练习册答案—章重点

五轴向拉伸与压缩试求图示各杆横截面1-1、2-2、3-3上的轴力，并作轴N 1= 10kNN 2= -15kN N 3= -18kN一根中部对称开槽的直杆如图所示。

试求横截面1-1和2-2解： 1．轴力由截面法可求得，杆各横截面上的轴力为 P N -= 2．应力 63111111104201014----⨯⨯⨯-=-==A P A N σPa 175-=MPa ()6322222210410201014----⨯⨯-⨯-=-==A P A N σPa 350-=MPa一桅杆起重机如图所示。

起重杆AB 的横截面是外径为18 mm 的圆环，钢丝绳CB 的横截面面积为10 mm 2。

试求起重杆和钢丝绳横截面上的应力。

解： 1．轴力取节点B 为研究对象，受力如图所示，0=∑X ： 045cos 30cos =++ P N N AB BC0=∑Y ： 030sin 45sin =--AB N P由此解得： 83.2-=AB N kN ， 04.1=BC N kN 2．应力起重杆横截面上的应力为 ()622310182041083.2-⨯-⨯⨯-==πσAN AB ABPa 4.47-=MPa 钢丝绳横截面上的应力为6310101004.1-⨯⨯==A N BC BC σPa 104=MPa 铜和钢的弹性模量分1001=GPa 和2102=E GPa 。

若杆的总伸长为126.0=l ∆ mm ，试求杆横截面上的应力和载荷P 。

解：1．横截面上的应力由题意有 ⎪⎪⎭⎫⎝⎛+=+=∆+∆=∆2211221121E l E l A E Pl A E Pl l l l σ 由此得到杆横截面上的应力为9922111021040010100600126.0⨯+⨯=+∆=E l E l l σPa 9.15=MPa2．载荷62610404109.15-⨯⨯⨯⨯==πσA P N 20=kN200=E GPa解：1．最大正应力在BC 段的任一横截面上，即127.3M P aPa 102041040623min max =⨯⨯⨯==-σA N 2．杆的总伸长mm 57.0m 1020108001040104001020010404 444623623932221222121=⎪⎪⎭⎫⎝⎛⨯⨯+⨯⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛+=+=+=+=----ππππ∆∆∆d l d l E P d EPl d EPl EA Pl EA Pll l l BC AB BC AB BCAB BC ABAB 和AC 组成如图所示。

材料力学习题册_参考答案(1-9章)

（图 1）
（图 2）
3．有 A、B、C 三种材料，其拉伸应力—应变实验曲线如图 3 所示，曲线( B )材料
的弹性模量 E 大，曲线( A )材料的强度高，曲线( C )材料的塑性好。
4．材料经过冷作硬化后，其( D )。
A．弹性模量提高，塑性降低
B．弹性模量降低，塑性提高
C．比例极限提AB 梁的中点
D 任意点
14. 轴向拉伸杆，正应力最大的截面和剪应力最大的截面 ( A )
A 分别是横截面、450 斜截面
B 都是横截面
C 分别是 450 斜截面、横截面
D 都是 450 斜截面
15. 设轴向拉伸杆横截面上的正应力为σ，则 450 斜截面上的正应力和剪应力( D )。
A σ＝Eε＝300MPa
B σ＞300MPa
C 200MPa＜σ＜300Mpa
D σ＜200MPa
21．图 9 分别为同一木榫接头从两个不同角度视图，则（ B ）。
A. 剪切面面积为 ab,挤压面面积为 ch； B. 剪切面面积为 bh,挤压面面积为 bc；
C. 剪切面面积为 ch,挤压面面积为 bc； D. 剪切面面积为 bh,挤压面面积为 ch。
F
p
.D
.
.
.
.
...
解：设每个螺栓受力为 F，由平衡方程得
根据强度条件，有［σ］≥
故螺栓的内径取为 24mm。 4．图示一个三角架，在节点 B 受铅垂荷载 F 作用，其中钢拉杆 AB 长 l1=2m，截面面
积 A1=600mm2，许用应力 [ ]1 160MPa ，木压杆 BC 的截面面积 A2=1000mm2，许用应力 [ ]2 7MPa 。试确定许用荷载[F]。

合肥工业大学工程力学习题册答案

YB
YC
XC
B
XB
P
B B FA D
FB
A
P
FF
FA F’C
B FB
理论力学习题册解答
1
二、平面汇交力系
2 – 1 五个力作用于一点，如图所示图中方格的边长
为 1cm，求力系的合力。 [解] 由解析法有 500N y 1000N
RX X 1000 cos 1 500 cos 2 450 750 cos 3 800 cos 4 549.3N
C
30
YB = 60 KN ;
∑X = 0: X ∑Y = 0 : Y
解得：
B
B
− N C cos 60° = 0
20KN/m
+ N C sin 60° − 20 × 6 = 0
X B = 34.64 KN ;
XB B YB C 60 NC
N C = 69.28 KN ;
再取 AB 为研究对象，AB 杆受力如图：
d= MO = 45.96cm R
3 – 3 求下列各图中平行分布力系的合力和对于 A 点之矩。
L A q (a) [解] A a L (b) (a) 对 A 点之矩为: (b) 对 A 点之矩为: q q1 B A L (c) (c) 对 A 点之矩为： B q2
1 M A = −qa × a 2 1 = − qa 2 2
m
i
0 : FA OA sin 30 m2 0
可解得：
m1 即
O1 B A m2 B NO NO1 A FA FB
FA 5N ;
FB 5N ;
FB FA O
② BO1 杆受力如图,

材料力学习题册答案-第3章扭转(完整资料).doc

此文档下载后即可编辑第三章扭转一、是非判断题1.圆杆受扭时，杆内各点处于纯剪切状态。

（×）2.杆件受扭时，横截面上的最大切应力发生在距截面形心最远处。

（×）3.薄壁圆管和空心圆管的扭转切应力公式完全一样。

（×）4.圆杆扭转变形实质上是剪切变形。

（×）5.非圆截面杆不能应用圆截面杆扭转切应力公式，是因为非圆截面杆扭转时“平截面假设”不能成立。

（√）6.材料相同的圆杆，他们的剪切强度条件和扭转强度条件中，许用应力的意义相同，数值相等。

（×）7.切应力互等定理仅适用于纯剪切情况。

（×）8.受扭杆件的扭矩，仅与杆件受到的转矩（外力偶矩）有关，而与杆件的材料及其横截面的大小、形状无关。

（√）9.受扭圆轴在横截面上和包含轴的纵向截面上均无正应力。

（√）10.受扭圆轴的最大切应力只出现在横截面上。

（×）11.受扭圆轴内最大拉应力的值和最大切应力的值相等。

（√ ）12.因木材沿纤维方向的抗剪能力差，故若受扭木质圆杆的轴线与木材纤维方向平行，当扭距达到某一极限值时，圆杆将沿轴线方向出现裂纹。

（ × ）二、选择题1.内、外径之比为α的空心圆轴，扭转时轴内的最大切应力为τ，这时横截面上内边缘的切应力为（ B ）A τ；B ατ；C 零；D （1- 4α）τ 2.实心圆轴扭转时，不发生屈服的极限扭矩为T ，若将其横截面面积增加一倍，则极限扭矩为（ C ）A0 B 20T 0 D 40T 3.两根受扭圆轴的直径和长度均相同，但材料C 不同，在扭矩相同的情况下，它们的最大切应力τ、τ和扭转角ψ、ψ之间的关系为（ B ）A 1τ=τ2, φ1=φ2B 1τ=τ2, φ1≠φ2C 1τ≠τ2, φ1=φ2D 1τ≠τ2, φ1≠φ2 4.阶梯圆轴的最大切应力发生在（ D ）A 扭矩最大的截面；B 直径最小的截面；C 单位长度扭转角最大的截面；D 不能确定。

(完整版)材料力学习题册答案..

练习1 绪论及基本概念1-1 是非题（1）材料力学是研究构件承载能力的一门学科。

（是）（2）可变形固体的变形必须满足几何相容条件，即变形后的固体既不可以引起“空隙”，也不产生“挤入”现象。

（是）（3）构件在载荷作用下发生的变形，包括构件尺寸的改变和形状的改变。

（是）（4）应力是内力分布集度。

（是）（5）材料力学主要研究构件弹性范围内的小变形问题。

（是）（6）若物体产生位移，则必定同时产生变形。

（非）（7）各向同性假设认为，材料沿各个方向具有相同的变形。

（F ）（8）均匀性假设认为，材料内部各点的力学性质是相同的。

（是）（9）根据连续性假设，杆件截面上的内力是连续分布的，分布内力系的合力必定是一个力。

（非）（10）因为构件是变形固体，在研究构件的平衡时，应按变形后的尺寸进行计算。

（非）1-2 填空题（1）根据材料的主要性质对材料作如下三个基本假设：连续性假设、均匀性假设、各向同性假设。

（2）工程中的强度，是指构件抵抗破坏的能力；刚度，是指构件抵抗变形的能力。

（3）保证构件正常或安全工作的基本要求包括强度，刚度，和稳定性三个方面。

（4）图示构件中，杆1发生拉伸变形，杆2发生压缩变形，杆3发生弯曲变形。

（5）认为固体在其整个几何空间内无间隙地充满了物质，这样的假设称为连续性假设。

根据这一假设构件的应力，应变和位移就可以用坐标的连续函数来表示。

（6）图示结构中，杆1发生弯曲变形，构件2发生剪切变形，杆件3发生弯曲与轴向压缩组合。

变形。

（7）解除外力后，能完全消失的变形称为弹性变形，不能消失而残余的的那部分变形称为塑性变形。

（8）根据小变形条件，可以认为构件的变形远小于其原始尺寸。

1-3 选择题（1）材料力学中对构件的受力和变形等问题可用连续函数来描述；通过试件所测得的材料的力学性能，可用于构件内部的任何部位。